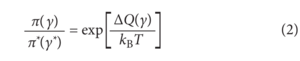“耗散适应理论”的版本间的差异
| 第7行: | 第7行: | ||
下面内容将从 热平衡、 Crooks relation进而引入耗散适应。 | 下面内容将从 热平衡、 Crooks relation进而引入耗散适应。 | ||
| − | |||
| − | |||
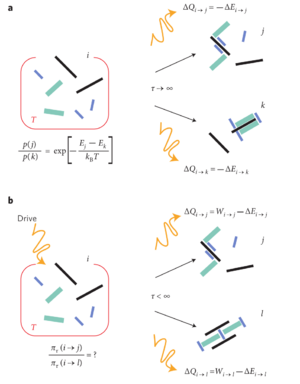
'''热平衡'''。当一个系统长时间与温度为T的热源接触而不受干扰时,我们说它达到了热平衡。在此条件下,一般假设微观排列j和k分别具有能量Ej和Ek,将以波尔兹曼分布给出的相对概率(p) : | '''热平衡'''。当一个系统长时间与温度为T的热源接触而不受干扰时,我们说它达到了热平衡。在此条件下,一般假设微观排列j和k分别具有能量Ej和Ek,将以波尔兹曼分布给出的相对概率(p) : | ||
| 第27行: | 第25行: | ||
公式2 | 公式2 | ||
| − | + | 结合图2,γ:正向微观状态演化轨迹 i->j->k,γ*:逆向微观状态演化轨迹 k->j->i,π(γ):γ轨迹的概率,π(γ*):γ*轨迹的概率。这个方程表明,微轨迹γ比它的时间反转更有可能是正热量的指数因子,当正路径被穿越时,释放到周围热储层的热量。这种关系即使在任意时变的外部场来驱动系统沿整个轨迹运行时也成立,只要时间变化是向后的(*),可以计算反向轨迹的概率。因此,热ΔQ(γ)通常由两部分贡献:系统从开始到结束的内能变化ΔE,以及外加场在整个过程中所做的功W。 | |
[[文件:Figure 2 Dynamical irreversibility and heat production.png|缩略图|图2 动态不可逆性和产热]] | [[文件:Figure 2 Dynamical irreversibility and heat production.png|缩略图|图2 动态不可逆性和产热]] | ||
2022年5月2日 (一) 10:09的最新版本
此词条由自生成结构读书会词条梳理志愿者(The)构建,未经专家审核,带来阅读不便,请见谅。
系统中任何既定的改变大多数都是随机的,但当系统恰巧可以更好地吸收和耗散能量时,这些结构上的变化就会出现最持久和最不可逆的变化。随着时间流逝,这些不可逆变化被优先积累了下来,于是在耗散发生时系统更倾向于形成类似的构型。回顾这一非平衡过程的可能形成历史,我们会发现这一结构已经自我组织成一种可以很好地适应环境条件的状态,这就是耗散适应(dissipative adaptation)现象。
下面内容将从 热平衡、 Crooks relation进而引入耗散适应。
热平衡。当一个系统长时间与温度为T的热源接触而不受干扰时,我们说它达到了热平衡。在此条件下,一般假设微观排列j和k分别具有能量Ej和Ek,将以波尔兹曼分布给出的相对概率(p) :
p(j) / p(k) = exp [ - (E_j - E_k) / k_B T] (公式1)
这里,k_B是波尔兹曼常数。
图1
如图1a所示,在经典的平衡统计力学情景中,系统与温度为T的热储层接触长时间τ,丢失了其初始状态i的所有记忆,因此,微观状态j和k的相对概率(p)是这些状态各自能量的简单指数函数。由于能量守恒,在从一种状态转变到另一种状态的过程中,释放到浴槽中的热量(ΔQ)与在这一过程中发生的内能(ΔE)的变化相等且相反。
然而,如图1b所示,当引入一个外部驱动,并且在有限的时间内观察系统,发现系统处于给定状态的概率通常取决于初始条件和系统是如何被驱动的。非平衡统计力学的挑战是试图用热力学量来表达这种概率分布,热力学量现在不仅包括最终态的内能,还包括在态间过渡期间驱动器所做的功。对于同一实验的单一实现,热(ΔQ)是一个波动的随机变量,它是由驱动过程中所做的功(W)和内能变化(ΔE)之间的差决定的。
Crooks relation。为了取得进一步的进展,有必要认识到,非平衡系统的统计行为不能用某一时刻个体微观状态的局部性质来理解,而必须通过动态轨迹之间的比较来表示。1999年,Gavin Crooks将时间反转对称性和能量守恒结合起来,推导出了一个热波动系统可能采取的不同动力学路径的相对可能性的精确表达式
公式2
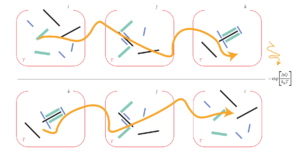
结合图2,γ:正向微观状态演化轨迹 i->j->k,γ*:逆向微观状态演化轨迹 k->j->i,π(γ):γ轨迹的概率,π(γ*):γ*轨迹的概率。这个方程表明,微轨迹γ比它的时间反转更有可能是正热量的指数因子,当正路径被穿越时,释放到周围热储层的热量。这种关系即使在任意时变的外部场来驱动系统沿整个轨迹运行时也成立,只要时间变化是向后的(*),可以计算反向轨迹的概率。因此,热ΔQ(γ)通常由两部分贡献:系统从开始到结束的内能变化ΔE,以及外加场在整个过程中所做的功W。
图2 动态不可逆性和产热
图2则展示了当系统与热储接触时,在时变场的特定模式(大箭头)驱动下,观察到特定配置序列的概率与在时间反转驱动下观察到事件的时间反转序列的概率有一个设定的比率。特别是,当系统按照对应于比率分子的模式驱动时,这两个概率的差异与释放到储层的热量的指数因子有关(ΔQ;(小箭头)。
耗散适应。为了解决利用热力学预测任意非平衡演化路径这一更重要的挑战,我们需要回到公式(2),并从不同的角度分析它。如果我们能重新排列这个方程,以比较某些过程的结果,这将有助于理解这个方程中最有趣的一些结果。在这些过程中,物质是由任意的强迫场驱动的,或在存在热波动的情况下由外部施加的电流驱动的。通过累加不同可能的微轨迹及其相关的概率,我们得到:
公式3
其中,角括号表示所有微轨迹的加权平均值,起始点(i)和结束点(j, k)是固定的。式中右侧主导因子$e^{\triangle E_{jk}/ (k_B T)}$的影响意义明显:如果没有外部驱动(W=0)并等待很长时间来平衡(π_{\infty}*(j* -> i*) /π_{\infty}*(k* -> i*) = 1)。系统会朝着从外部驱动中吸收更多功,向环境中放热更大的方向演化,耗散也越大。 j 比 k 的内能E越小,i -> j 的所有路径上做的平均功越大,演化到j的概率越高。
从驱动力中吸收的能量使系统结构能够穿越太高的激活障碍,而仅靠热波动无法快速跳跃,如果跳跃后能量被耗散,则无法帮助系统回到最初的方向(图3)。
图3
图3中左图:在这个简单的势垒跳跃模型中,一个经历热波动的粒子位于一个受驱动的能量景观中,因此右边的状态和过渡状态的能量以正弦的方式随着时间同步振荡(最大值和最小值显示为黄色)。中间:当驱动引起的势垒高度的振荡暂时降低了跃迁的活化能时,粒子最有可能跃迁。右:这个系统的驱动被设计成使向左跳跃的障碍高度随时间固定,这意味着驱动优先加速向右跳跃。这种统计不可逆性立即意味着,在典型的向右跳跃时刻,右侧状态的能量将低于左侧状态,因此正热量被散发到周围的热源中(ΔQ >0).因此,不可逆性和散热是齐头并进的。
如果外部驱动力使得系统能垒和右侧的能量周期性同时降低的话,那么小球更可能从左侧跃过能垒到右侧,吸收环境中的功并放热,但从右侧跃过所需要的能垒没有变化。当有外部驱动力时,系统中不同的演化轨迹会吸收不同的功,不同的轨迹会在驱动力中竞争可以吸收的功,使得那些可以吸收更多功的轨迹的概率更高,体现出耗散适应。
耗散适应:
从 Crooks relation 可以推出从外部驱动中吸收更多功的轨迹发生的概率会相对更高。
系统会演化到一些特殊的状态:从起始状态到该状态的所有路径从外部驱动中获取的平均功更大的状态,通过耗散来适应外部驱动力。
待建立参考文献: England, Jeremy L. (4 November 2015). "Dissipative adaptation in driven self-assembly". Nature Nanotechnology. 10 (11): 919–923.
“此词条暂由(The)构建、整理。”