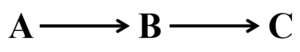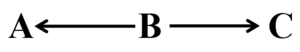“链接合,叉接合,对撞接合”的版本间的差异
(→链接合) |
(→编者推荐) |
||
| 第77行: | 第77行: | ||
[[文件:反叉式-对撞结构实例因果图.png|缩略图|对撞接合举例]] | [[文件:反叉式-对撞结构实例因果图.png|缩略图|对撞接合举例]] | ||
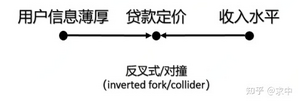
第二种叉接合在上节已经举过“鞋的尺码←孩子的年龄→阅读能力”,这里不再赘述,而第三种对撞结构,这里可以用确定用户贷款定价的方式作为例子,理论上来说一个用户的信息越薄,贷款定价越高;收入水平越高,贷款定价越低;而信息的薄厚与收入水平并没有明显的关系,但如果固定了贷款定价之后,可能收入水平越高,用户信息越薄;因为对两者的结果的筛选,导致了两者产生了一定联系。 | 第二种叉接合在上节已经举过“鞋的尺码←孩子的年龄→阅读能力”,这里不再赘述,而第三种对撞结构,这里可以用确定用户贷款定价的方式作为例子,理论上来说一个用户的信息越薄,贷款定价越高;收入水平越高,贷款定价越低;而信息的薄厚与收入水平并没有明显的关系,但如果固定了贷款定价之后,可能收入水平越高,用户信息越薄;因为对两者的结果的筛选,导致了两者产生了一定联系。 | ||
| + | |||
| + | == 相关文献推荐 == | ||
| + | |||
| + | # Pearl J.. Bayesian Networks A Model of Self-Activated Memory for Evidential Reasoning''. Conference of the Cognitive Science Society'', 1985 | ||
| + | # Verma, T., & Pearl, J. (1988). Influence diagrams and d-separation. UCLA, Computer Science Department. | ||
| + | # Thomas Verma, Judea Pearl. Equivalence and synthesis of causal models, 1991 | ||
| + | # Pearl, J.. Causal diagrams for empirical research''. Biometrika'', 1995, 82(4): 669-688 | ||
== 编者推荐 == | == 编者推荐 == | ||
2022年6月10日 (五) 00:03的版本
此词条由因果科学读书会词条梳理志愿者我是猫(74989)编撰,未经专家审核,带来阅读不便,请见谅。
参考链接
定义
接合(conjunction)是包含两个连接的三节点网络,是所有贝叶斯网络及因果网络的构建模块。接合有三种基本形式:链接合、叉接合、对撞接合
贝叶斯网络
贝叶斯网络的基本结构是一个有向无环图(Directed Acyclic Graph, DAG),由节点(nodes)和节点之间带有单向箭头的连线组成。贝叶斯网络的基础就是通过这三种基础结构形成的。
因果图
因果推断是一种通过事物的原因推导至某个肯定结果的逻辑方式。通过因果推断,人类可以很好的解决生活和科学中遇到的问题。而如果能够完全掌握这一方法,就能够在计算机上模拟因果推断,进而设计强大的自动化机器。机器最终可以帮助人类解决科学界悬而未决的问题,并最终从环境中不断的学习新的因果知识。
为了将语言中的因果关系使用数学形式表达,Pearl 提出了因果图。因果图是一种图形式的模拟,代表变量之间存在的因果关系。点代表变量,带有指向的边则表示了变量的因果关系影响。这种点-边的关系图被称为因果图。Pearl 认为因果图可以良好的展示因果关系。如果每个边带有一个权重,则可以表示不同因素对于这一结果的影响强度大小。
因果图基本三节点的路径结构主要包括三种:链式,叉式,反叉式/对撞式,这三种路径结构可以理解成由两个流向的信息流进行随机组合而成。
链接合
第一种结构为链式结构/链接合(也被称为head-to-tail),顾名思义,像一条链子一样,让信息从一端流到另一端。链结合是最简单的接合表现形式。在科学中,人们常常将B视为某种机制,或“中介物”,它将A的效应传递给C。链式结构中的链式与数学中常用的链式法则的链式有着接近相同的含义,指代着因果关系的层层递进,即A为B的因,B又为C的因,每一层的节点(或者说中介物)又屏蔽它的上层和下层;人类是很容易的依靠条件独立性,依靠与生俱来的筛选能力或者推断能力,确定相关信息和无关信息的界限,但是机器并没有这种能力,为机器配置这种因果图是推动机器学习更加鲁棒,更加智能不可或缺的必经之路。
规则1 (链结构中的条件独立性)
如果变量X和Y之间只有一条单向路径,Z是截断这条路径的任何一组变量,则在Z的条件下,X和Y是独立的。
例:“火灾→烟雾→警报”
在链结合中,中介物B“屏蔽”(screen off)了从A到C的信息或从C到A的信息。例如,一旦我们知道了烟雾的“值”,关于火的任何新信息便不会再以任何理由让我们增强或削弱对警报的信念。
换句话说,信息从A经过B流向C,因此A和C是相关的(即不是独立的)。考虑一个更复杂的链结构:A->C->D->E->B ,虽然变长了,但是信息还是能够从A流向B,因此A和B仍然是相关的。
叉接合
第二种结构为叉式结构/叉接合(也被称为tail-to-tail),旁边两个边类似一条路的分叉,信息从中间结点传输到两端。在叉接合中,B通常被视作A和C的共因(common cause)或混杂因子(confounder)。混杂因子会使A和C在统计学上发生关联,即使它们之间并没有直接的因果关系。
规则2 (分叉结构的条件独立性)
如果变量X是变量Y和Z的共同原因,并且Y和Z之间只有一条路径,则Y和Z在X的条件下独立。
直接观察图中的叉式结构的形状的话与叉子还有一定的差距,不过因果图中(或者说接合模块)在乎的是不同节点的拓扑关系,将中间节点向上或者向下移动之后就可以看出一个明显的叉子形状,这里中间节点B通常被视为A和C的共因(common cause)或混杂因子(confounder )。混杂因子会使A和C在统计学上发生关联,即使它们没有直接的关系,在pearl的the book of why 中举了一个非常经典例子:“鞋的尺码←孩子的年龄→阅读能力”,穿较大码的鞋的孩子年龄可能更大,所以往往有着更强的阅读能力,但当固定了年龄之后,A和C就条件独立了。换句话说,穿较大码的鞋的孩子往往阅读能力较强。但这种关系是非因果的——给孩子穿大一号的鞋不会让他有更强的阅读能力,相反,这两个变量的变化都可以通过第三个变量,即孩子的年龄来解释。越年长的孩子鞋码越大,他们的阅读能力也越强。
对于叉接合,信息从B流向A,也从B流向C,那么A和C就不是独立的。考虑一个更复杂的叉结构:A<-C<-D<-E->G->B ,信息从E流向A,也流向B,那么A和B就不是独立的。
对撞接合
最重要的是第三种,对撞式/反叉式结构,也叫对撞接合(也被称为head-to-head),像两个对撞的小行星一样,信息流入中间的节点。当以变量B为条件时,对撞接合与链接合或叉接合的运作方式正好相反。如果A和C原本是相互独立的,那么给定B将使它们彼此相关。进一步说,根据拓扑学中形式即内容的理念,当我们以中间变量B为条件时(即为某个变量遍历各个指定的值),这种对撞接合的运作方式与叉接合,链接合的运作方式又有所不同,给定B即固定了链接合和叉接合的某一节点的原因,导致A和C至少有一节点固定,从而阻断它们的相关性,而在对撞中给定B则为固定了它们的结果,导致对A和C采取了有偏选取,打乱了随机分布,从而因为两种分布的有偏呈现了一定程度的相关性。
规则3 (对撞结构中的条件独立性)
如果变量Z是变量X和Y之间的对撞节点,并且X和Y之间只有一条路径,那么X和Y就是无条件独立的,但是在Z和Z的任何子孙条件下是相互依赖的。
例:才华→名人←美貌
若只选著名演员的数据,那么我们就会看到才华与美貌之间出现了负相关,这种负相关可以解释为:发现某位名人并不美貌这一事实,会使我们更相信他富有才华。这种负相关有时被称为对撞偏倚或“辩解”效应(explain-away effect)
对于对撞接合,信息从A和C分别流向B,并且在B对撞。所以B也被称为对撞子(collider)。此时,A和C都影响B,但是信息没有从B流向A或者C,因此A和C是相互独立的。
更一般地,如果一条从A到B的路径中出现了对撞接合,那么A和B就不可能是相关的(至少针对这条路径而言,如果有别的路径那再另说)。所以,对于路径A->C<-D<-B ,信息分别从 A 和 B流入 ,并在此对撞。因此A和B仍然是不相关或者说相互独立的。
接合关系与信息流动
因果模型通过三种接合连接起来,构成了系统信息的传输,对于模型上信息的传输可以直观理解为:将连接看作一个管道,管道将信息从X点传递到Y点。其中信息的传递是双向的,既在因果方向传递,也在非因果方向传递,其中重要的是控制非因果路径,容易造成混杂,影响结论。
如何阻断信息在接合中的流动:
a. 链接合(A→B→C):控制B可防止有关A的信息流向C或C的信息流向A
b. 叉接合(A←B→C):控制B可以防止有关A的信息流向C或C的信息流向A
c. 对撞接合(A→B←C):控制B后由于辩解效应的存在,信息会在“管道”中流通
接合模式运作方式的现实例子
对撞结构和叉式、链式结构存在着完全不同的运作方式,而任何形式联系的运作均存在于事物状态的改变之中,在这里只考虑中间节点固定与否对其他的节点间的关系的影响,具体来说如下:
A. 对于叉式和链式结构,以中间变量B为条件,那么A和C的关系被阻断。
B. 对于对撞式结构,以中间变量B为条件,那么A和C产生了相关性。
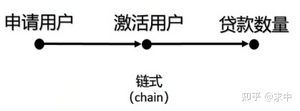
首先对于链接合来说,可以从银行信用卡贷款的例子来理解,申请信用卡的用户决定了最终激活确认的用户,最终激活确认的用户又直接影响了贷款数量,具体因果路径可用下图表示,此时可以说申请用户的情况和最终发生的贷款是相关的,但是如果我们以激活确认用户为条件时,我们便不能从更多的申请用户的信息确定贷款的状态。
第二种叉接合在上节已经举过“鞋的尺码←孩子的年龄→阅读能力”,这里不再赘述,而第三种对撞结构,这里可以用确定用户贷款定价的方式作为例子,理论上来说一个用户的信息越薄,贷款定价越高;收入水平越高,贷款定价越低;而信息的薄厚与收入水平并没有明显的关系,但如果固定了贷款定价之后,可能收入水平越高,用户信息越薄;因为对两者的结果的筛选,导致了两者产生了一定联系。
相关文献推荐
- Pearl J.. Bayesian Networks A Model of Self-Activated Memory for Evidential Reasoning. Conference of the Cognitive Science Society, 1985
- Verma, T., & Pearl, J. (1988). Influence diagrams and d-separation. UCLA, Computer Science Department.
- Thomas Verma, Judea Pearl. Equivalence and synthesis of causal models, 1991
- Pearl, J.. Causal diagrams for empirical research. Biometrika, 1995, 82(4): 669-688
编者推荐
集智学园课程
因果科学读书会第三季:因果+X
“因果”并不是一个新概念,而是一个已经在多个学科中使用了数十年的分析技术。通过前两季的分享,我们主要梳理了因果科学在计算机领域的前沿进展。如要融会贯通,我们需要回顾数十年来在社会学、经济学、医学、生物学等多个领域中,都是使用了什么样的因果模型、以什么样的范式、解决了什么样的问题。我们还要尝试进行对比和创新,看能否以现在的眼光,用其他的模型,为这些研究提供新的解决思路。
“因果+X”就是要让因果真正地应用于我们的科学研究中,不管你是来自计算机、数理统计领域,还是社会学、经济学、管理学领域,还是医学、生物学领域,我们希望共同探究出因果研究的范式,真正解决因果的多学科应用问题,乃至解决工业界的问题。