“干预”的版本间的差异
(→编者推荐) |
|||
| 第94行: | 第94行: | ||
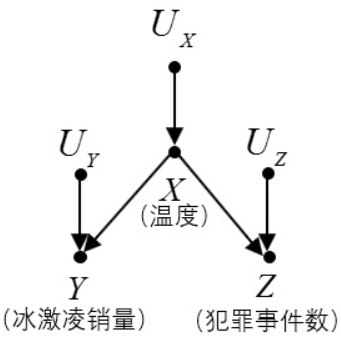
[[文件:因果模型.png|左|缩略图|342x342像素|图1 干预前]] | [[文件:因果模型.png|左|缩略图|342x342像素|图1 干预前]] | ||
[[文件:图1 干预模型.png|左|缩略图|344x344像素|图2 干预后]] | [[文件:图1 干预模型.png|左|缩略图|344x344像素|图2 干预后]] | ||
| + | |||
| + | |||
| + | |||
| + | |||
2022年6月10日 (五) 21:40的版本
此词条暂由因果科学读书会词条梳理志愿者我是猫(74989)翻译审校,未经专家审核,带来阅读不便,请见谅。
概念来源
干预是因果关系之梯的第二层级,在因果之梯第一层,即便是“以某个变量为条件(conditioning on)”的操作,也只是依据现有观测到的数据进行统计,并没有改变数据的分布。
干预(intervention)和以变量为条件(conditioning on)有着本质的区别。当我们在模型中对一个变量进行干预时,我们将固定这个变量的值。其他变量的值也随之改变。当我们以一个变量为条件时,我们什么也不会改变;我们只是将关注的范围缩小到样本的子集,选取其中我们感兴趣的变量的值。因此,以变量为条件改变的是我们看世界的角度,而干预则改变了世界本身。
当我们进行干预以确定一个变量的值时,我们就限制了该变量随其他自然变量而变化的自然趋势。在图模型中,干预的操作将删除所有指向该变量的边。
实际应用中,干预也非常重要。比如,当我们对一种新的抗癌药物进行研究时,我们试图确定当我们对病人进行药物干预时,病人的病情如何变化。当我们研究暴力电视节目和儿童的攻击行为之间的关系时,我们希望知道,干预减少儿童接触暴力电视节目是否会减少他们的攻击性行为。
在统计学中,我们为了研究这样的问题,一个变量是否引起另一个变量的变化。我们通常会进行一个随机对照试验,这也被成为统计学的黄金准则。在一个正确的随机对照试验中,除了输入变量,所有影响输出变量的因素要么不变,要么是随机变化的,因此输出变量的任何改变必然由这一输入变量引起。
不幸的是,很多问题不适合用随机对照试验来解决。比方说,研究暴力电视节目时,虽然可以随机选取参与者,但是很难有效的控制每个孩子看电视的行为,因此几乎不可能知道我们对孩子的控制是否有效,甚至在随机药物试验中,也会出现很多问题,参与者退出了,没有吃药,或者谎报吃药。在随机对照试验不可行的情况下,研究人员实施观察性研究,他们仅仅记录数据,而不是控制数据。这样方式很难将因果关系从相关关系中提取出来,因此产生干预模型,通过do演算将因果关系从相关关系中分离出来。
解决的问题
干预是一种解决问题的方式,对于查询到的基于特定模型提出的问题。人们通常进行实验(干预)来回答。干预措施的形式是固定一个模型中一个变量的值,并观察结果。
实验操作者指出实验明确地调整了牙膏的价格。从图形上看,这阻止了任何原本会影响该变量的因果因素。从图表上看,这清除了所有指向实验变量的因果箭头。
对于一个复杂的问题,可以进行更复杂的查询,其中将 do 运算符(值是固定的)应用于多个变量。
数学演算
do算子
我们在符号上区分变量X自然地取值x的情况和固定X取值x的情况,后者用do(X=x)来表示。因此,P(Y=y|X=x)表示X=x的条件下Y=y的概率;P(Y=y|X=x)表示通过干预使X=x时Y=y的概率。以分布的术语说,P(Y=y|X=x)反映了在X=x的值都是x的个体上Y的总体分布;另一方面,P(Y=y|do(X=x))反映了如果群体中的每个个体均将X的值固定为x时,Y的总体分布。类似的,用P(Y=y|do(X=x),Z=z)表示对于给定的Z=z,干预do(X=x)得到分布中Y=y的条件概率。
利用do-表达式和图模型,可以将因果关系从相关关系中分解出来。
do演算
do 演算是一组可用于将一个概率表达式转换为另一个概率表达式的操作,其总体目标是将包含 do 算子的表达式转换为不包含 do 算子的表达式。不包括do 算子的表达式可以单独从观察数据中估计出来,不需要实验进行干预。这就避免了某些实验中所需要的昂贵的,冗长的,甚至是不道德的实验要求。
do演算在进行转换时,利用一种规则集进行表示,这种规则集是完整的(可以用它来派生该系统中的每个真实表达式)。因此可以通过算法进一步确定,对于给定的模型,一个解是否在多项式时间内可计算。
do演算规则
Rules
这个表达式包含了三个涉及 do 运算符的条件概率表达式转换规则。
Rule 1
Rule 1 permits the addition or deletion of observations.:
in the case that the variable set Z blocks all paths from W to Y and all arrows leading into X have been deleted.
【终译】
规则1 允许对观察变量进行增加或者删除
在这个例子中,变量集合Z阻断了所有从W到Y的路径,并且所有指向X的箭头被删除
Rule 2
Rule 2 permits the replacement of an intervention with an observation or vice versa.:![]()
in the case that Z satisfies the back-door criterion.
【终译】
规则2允许用观察来替代干预,或者反之亦然
在这个例子中,变量集合Z满足后门标准
Rule 3
Rule 3 permits the deletion or addition of interventions.:
in the case where no causal paths connect X and Y.
【终译】
规则3允许对干预进行增加或者删除
在这个例子中,X和Y之间没有因果路径相连接
拓展
这些规则并不意味着可以删除任何查询的 do 运算符。在这些情况下,可以用一个受操纵的变量(例如饮食)来代替一个不受操纵的变量(例如血液胆固醇) ,然后这个变量可以被转化去除胆固醇。例子:
干预实例
以图1为例,如果我们要进行干预以降低冰激凌销量(比如,关闭所有冰激凌店),那么我们就去掉所有指向冰激凌销量 的边,并得到如图2所示的图模型。当我们在这个新的图模型中检验相关性时,我们发现犯罪率当然是与冰激凌销量完全独立的,因为冰激凌销量已经与天气温度无关了。换句话说,即使我们将 的值调整为另一个不变的值,这种变化也不会传递给可变的犯罪率 。我们看到,与以某个变量为条件不同,干预一个变量会导致一种完全不同的相关性关系,以某个变量为条件可以完全从数据中获得,但干预却会影响图模型结构的变化。
在符号的表达上,我们使用do算子来表达这种干预。比如,当我们固定Y的值为y时,我们用do(Y=y)来表示这种干预行为。所以P(Z=z|Y=y)表示当以Y=y为条件时Z=z的概率,而P(Z=z|do(Y=y))表示当我们干预Y的值使其为y时,Z=z的概率。从概率分布的角度来说, 表示的是在Y可取的所有值中, Y=y那部分样本对应的Z=z的概率,而P(Z=z|do(Y=y)) 表示的是将每一个样本的Y的值全部固定为y后Z=z的概率。这两者是完全不同的,干预改变了原始数据的分布,而以变量为条件不改变原始数据的分布。