“前门调整”的版本间的差异
(→编者推荐) |
(→编者推荐) |
||
| 第89行: | 第89行: | ||
“因果+X”就是要让因果真正地应用于我们的科学研究中,不管你是来自计算机、数理统计领域,还是社会学、经济学、管理学领域,还是医学、生物学领域,我们希望共同探究出因果研究的范式,真正解决因果的多学科应用问题,乃至解决工业界的问题。 | “因果+X”就是要让因果真正地应用于我们的科学研究中,不管你是来自计算机、数理统计领域,还是社会学、经济学、管理学领域,还是医学、生物学领域,我们希望共同探究出因果研究的范式,真正解决因果的多学科应用问题,乃至解决工业界的问题。 | ||
===文章总结=== | ===文章总结=== | ||
| + | [https://swarma.org/?p=24963 周日直播 | 从辛普森悖论谈起:因果效应中的混淆因子及可识别性 | 集智俱乐部 (swarma.org)] | ||
| + | |||
[https://swarma.org/?p=27916 因果推断:现代统计的思想飞跃 | 集智俱乐部 (swarma.org)] | [https://swarma.org/?p=27916 因果推断:现代统计的思想飞跃 | 集智俱乐部 (swarma.org)] | ||
2022年7月11日 (一) 16:32的版本
调整目的: 因果效应估计
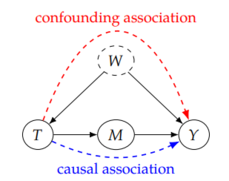
我们期望在给定如下因果图的情况下,判断治疗变量 T 对结果变量 Y 的因果效应 [math]\displaystyle{ P(y|do(t)) }[/math],其中 W 是一个未观测的混淆变量,M 是中介变量。(注意:我们现在观测不到W,无法进行后门调整.。)
主要步骤如下[1]:
- 估计T对M的因果效应[math]\displaystyle{ P(m|do(t)) }[/math] ,由于T-W-Y-M 这条路径被 阻断 (见 D-分离) [math]\displaystyle{ P(m|do(t))=P(m|t) }[/math].
- 估计M对Y的因果效应[math]\displaystyle{ P(y|do(m)) }[/math], 由于 T 阻断了后门路径 M<-T<-W ->Y, 根据后门调整 我们可以轻松得到[math]\displaystyle{ P(y|do(m))= \sum_t P(y|m,t) P(t) }[/math].
- 结合以上两种因果效应[math]\displaystyle{ P(y|do(t))= \sum_m P(y|do(m)) P(m| do(t)) }[/math].
前门准则[2]
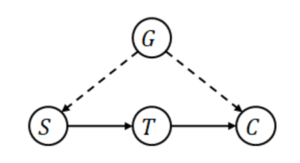
定义:我们说变量集 M 关于 T 和 Y 满足前门准则,若:
前门调整
若变量集M关于(T,Y)满足前门准则,并且我们有[math]\displaystyle{ P(t,m)\gt 0 }[/math], T对Y的因果效应是可识别的,
[math]\displaystyle{ P(y|do(t))= \sum_m P(m| t) \sum_{t'} P(y|m,t') P(t') }[/math].
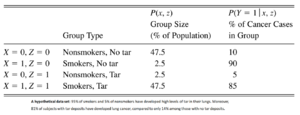
例子:吸烟与肺癌
| 组别 | P(x,z) (每个组别所占百分比) | P(Y=1|x,z) (每组内罹患癌症的百分比) | |
|---|---|---|---|
| X=0,Z=0 | 非吸烟者,肺内无焦油 | 47.5 | 10 |
| X=1,Z=0 | 吸烟者,肺内无焦油 | 2.5 | 90 |
| X=0,Z=1 | 非吸烟者,肺内有焦油 | 2.5 | 5 |
| X=1,Z=1 | 吸烟者,肺内有焦油 | 47.5 | 85 |
从数据中来看,似乎吸烟对肺癌有显著影响,但是烟草公司会从不同的角度争辩,从而给出不同的答案。若我们只看非吸烟者,体内有焦油可以的患癌率从10%降到了5%;若们只看吸烟者,体内有焦油可以的患癌率从90%降到了85%,可见焦油有防护作用。
数学上,前门调整可以被运用,
[math]\displaystyle{ P(Y=1|do(X=0))= 0.4975,P(Y=1|do(X=1))= 0.4525, }[/math]。
- ↑ https://www.bradyneal.com/Introduction_to_Causal_Inference-Dec17_2020-Neal.pdf
- ↑ Pearl, Judea. "Models, reasoning and inference." Cambridge, UK: CambridgeUniversityPress 19 (2000).
编者推荐
书籍推荐
这本书非常适合初学者入门因果科学,这里面涉及到对结构因果模型的详细定义和阐述,非常清晰易懂。
在本书中,人工智能领域的权威专家朱迪亚·珀尔及其同事领导的因果关系革命突破多年的迷雾,厘清了知识的本质,确立了因果关系研究在科学探索中的核心地位。
关于这本书集智俱乐部邀请白楚研究员用100分钟,为大家详细介绍了Judea Pearl绘制的因果科学蓝图,作为一个起点,去拥抱因果革命。可以查看对应的视频分享解读《为什么》:攀登因果之梯
课程推荐
这个视频邀请新加坡国立大学研究员冯福利老师介绍如何有效地将因果理论引入数据驱动的推荐模型,主要介绍通过引入后门调 整处理:1)流行度偏差;2)用户兴趣放大。
图灵奖得主朱迪亚·珀尔教授认为,当下正在进行一场改变数据科学的新革命 ”因果革命“。它以科学为中心,涉及从数据到政策、可解释性、机制的泛化,再到一些社会科学中的归因和公平性问题,甚至哲学中的创造性和自由意志 。本季读书会以Elements of Causal Inference一书为线索,主要展现因果科学在机器学习各个方向上的影响,包括强化学习、迁移学习、表示学习等等,并分享在工业界的部分应用成果。本季读书会梳理了因果科学的核心内容,理解它如何改变数据科学,助力 AI 系统超越曲线拟合和获得回答因果问题的能力。
因果推断与机器学习领域的结合已经吸引了越来越多来自学界业界的关注。第一季读书会主要关注了因果科学在机器学习方向上的前沿应用,为深入探讨、普及推广因果科学议题,第二季读书会着力于实操性、基础性,带领大家精读因果科学方向两本非常受广泛认可的入门教材:Causal inference in statistics: A primer和Elements of causal inference: foundations and learning algorithms。读书会以直播讨论为主,结合习题交流、夜谈、编程实践、前沿讲座等多类型内容,主要面向有机器学习背景、希望深入学习因果科学基础知识和重要模型方法、寻求解决相关研究问题的研究人员。
“因果”并不是一个新概念,而是一个已经在多个学科中使用了数十年的分析技术。通过前两季的分享,我们主要梳理了因果科学在计算机领域的前沿进展。如要融会贯通,我们需要回顾数十年来在社会学、经济学、医学、生物学等多个领域中,都是使用了什么样的因果模型、以什么样的范式、解决了什么样的问题。我们还要尝试进行对比和创新,看能否以现在的眼光,用其他的模型,为这些研究提供新的解决思路。
“因果+X”就是要让因果真正地应用于我们的科学研究中,不管你是来自计算机、数理统计领域,还是社会学、经济学、管理学领域,还是医学、生物学领域,我们希望共同探究出因果研究的范式,真正解决因果的多学科应用问题,乃至解决工业界的问题。
文章总结
周日直播 | 从辛普森悖论谈起:因果效应中的混淆因子及可识别性 | 集智俱乐部 (swarma.org)
因果推断:现代统计的思想飞跃 | 集智俱乐部 (swarma.org)
因果科学入门读什么书?Y. Bengio博士候选人的研读路径推荐
历时3个月,全球32位讲者,共同讲述因果科学与Causal AI的全景框架!
相关路径
- 因果科学与Casual AI读书会必读参考文献列表,这个是根据读书会中解读的论文,做的一个分类和筛选,方便大家梳理整个框架和内容。
- 因果推断方法概述,这个路径对因果在哲学方面的探讨,以及因果在机器学习方面应用的分析。
- 因果科学和 Causal AI入门路径,这条路径解释了因果科学是什么以及它的发展脉络。此路径将分为三个部分进行展开,第一部分是因果科学的基本定义及其哲学基础,第二部分是统计领域中的因果推断,第三个部分是机器学习中的因果(Causal AI)。
- 复杂网络动力学系统重构文献,这个路径是张江老师梳理了网络动力学重构问题,描述了动力学建模的常用方法和模型,并介绍了一些经典且重要的论文,这也是复杂系统自动建模读书会的主要论文来源,所以大部分都有解读视频。
- 因果纠缠集智年会——因果推荐系统分论坛关于因果推荐系统的参考文献和主要嘉宾介绍,来源是集智俱乐部的因果纠缠年会。