“动作电位”的版本间的差异
小 |
小 |
||
| 第85行: | 第85行: | ||
===起搏电位=== | ===起搏电位=== | ||
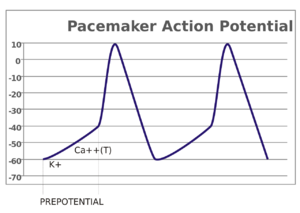
[[文件:Pacemaker potential.svg.png|替代=|缩略图|在起搏电位中,细胞自发地去极化(斜向上的直线),直到它发放动作电位。]] | [[文件:Pacemaker potential.svg.png|替代=|缩略图|在起搏电位中,细胞自发地去极化(斜向上的直线),直到它发放动作电位。]] | ||
| − | 感觉神经元中,动作电位是由外部刺激引起的。然而,一些兴奋性细胞不需要这样的刺激就可以发放动作电位:它们自发地使轴丘去极化,以特定的速率发放动作电位,像内部时钟一样。这种细胞的电位变化称为起搏电位(pacemaker potentials)。心脏窦房结( sinoatrial | + | 感觉神经元中,动作电位是由外部刺激引起的。然而,一些兴奋性细胞不需要这样的刺激就可以发放动作电位:它们自发地使轴丘去极化,以特定的速率发放动作电位,像内部时钟一样。这种细胞的电位变化称为起搏电位(pacemaker potentials)。心脏窦房结( sinoatrial node)的心肌起搏细胞(cardiac pacemaker cells)就是一个很好的例子。<ref name="noble_1960" group="lower-alpha">{{cite journal | vauthors = Noble D | title = Cardiac action and pacemaker potentials based on the Hodgkin-Huxley equations | journal = Nature | volume = 188 | issue = 4749 | pages = 495–7 | date = November 1960 | pmid = 13729365 | doi = 10.1038/188495b0 | bibcode = 1960Natur.188..495N | s2cid = 4147174 }}</ref> 虽然这种起搏电位有其自然节奏,但可以通过外部刺激进行调节;例如,药物以及交感神经和副交感神经发出的信号可以改变心率。外部刺激不是引起细胞动作电位的连续性发放,仅是改变其节奏。某些情况下,存在对发放频率更为复杂的调节,引起特定的动作电位模式,比如爆发(bursting)。 |
==动作电位的相位== | ==动作电位的相位== | ||
| 第116行: | 第116行: | ||
Once an action potential has occurred at a patch of membrane, the membrane patch needs time to recover before it can fire again. At the molecular level, this ''absolute refractory period'' corresponds to the time required for the voltage-activated sodium channels to recover from inactivation, i.e., to return to their closed state.{{sfn|Stevens|1966|pp=19–20}} There are many types of voltage-activated potassium channels in neurons. Some of them inactivate fast (A-type currents) and some of them inactivate slowly or not inactivate at all; this variability guarantees that there will be always an available source of current for repolarization, even if some of the potassium channels are inactivated because of preceding depolarization. On the other hand, all neuronal voltage-activated sodium channels inactivate within several milliseconds during strong depolarization, thus making following depolarization impossible until a substantial fraction of sodium channels have returned to their closed state. Although it limits the frequency of firing,{{sfn|Stevens|1966|pp=21–23}} the absolute refractory period ensures that the action potential moves in only one direction along an axon.{{sfn|Purves|Augustine|Fitzpatrick|Hall|2008|p=56}} The currents flowing in due to an action potential spread out in both directions along the axon.{{sfn|Bullock|Orkand|Grinnell|1977|pp=161–164}} However, only the unfired part of the axon can respond with an action potential; the part that has just fired is unresponsive until the action potential is safely out of range and cannot restimulate that part. In the usual [[orthodromic conduction]], the action potential propagates from the axon hillock towards the synaptic knobs(the axonal termini); propagation in the opposite direction—known as [[antidromic conduction]]—is very rare.{{sfn|Bullock|Orkand|Grinnell|1977|p=509}} However, if a laboratory axon is stimulated in its middle, both halves of the axon are "fresh", i.e., unfired; then two action potentials will be generated, one traveling towards the axon hillock and the other traveling towards the synaptic knobs. | Once an action potential has occurred at a patch of membrane, the membrane patch needs time to recover before it can fire again. At the molecular level, this ''absolute refractory period'' corresponds to the time required for the voltage-activated sodium channels to recover from inactivation, i.e., to return to their closed state.{{sfn|Stevens|1966|pp=19–20}} There are many types of voltage-activated potassium channels in neurons. Some of them inactivate fast (A-type currents) and some of them inactivate slowly or not inactivate at all; this variability guarantees that there will be always an available source of current for repolarization, even if some of the potassium channels are inactivated because of preceding depolarization. On the other hand, all neuronal voltage-activated sodium channels inactivate within several milliseconds during strong depolarization, thus making following depolarization impossible until a substantial fraction of sodium channels have returned to their closed state. Although it limits the frequency of firing,{{sfn|Stevens|1966|pp=21–23}} the absolute refractory period ensures that the action potential moves in only one direction along an axon.{{sfn|Purves|Augustine|Fitzpatrick|Hall|2008|p=56}} The currents flowing in due to an action potential spread out in both directions along the axon.{{sfn|Bullock|Orkand|Grinnell|1977|pp=161–164}} However, only the unfired part of the axon can respond with an action potential; the part that has just fired is unresponsive until the action potential is safely out of range and cannot restimulate that part. In the usual [[orthodromic conduction]], the action potential propagates from the axon hillock towards the synaptic knobs(the axonal termini); propagation in the opposite direction—known as [[antidromic conduction]]—is very rare.{{sfn|Bullock|Orkand|Grinnell|1977|p=509}} However, if a laboratory axon is stimulated in its middle, both halves of the axon are "fresh", i.e., unfired; then two action potentials will be generated, one traveling towards the axon hillock and the other traveling towards the synaptic knobs. | ||
| − | + | 细胞膜片上一旦发生动作电位,膜片需要时间恢复才能再次激活。在分子水平上,这个绝对不应期对应于电压激活的钠离子通道从失活状态恢复到关闭状态所需的时间。神经元中存在多种类型的电压激活钾通道。其中一些迅速失活(A 型电流),一些缓慢失活或从不失活;这种变异性保证了,即使一些钾离子通道因去极化而失活,总有电流来源使膜复极化。另一方面,去极化较强时,神经元所有的电压激活钠通道在几毫秒内失活,从而使去极化不可能发生,直到相当一部分的钠通道恢复到关闭状态。绝对不应期虽然限制了发放频率,但确保了动作电位沿轴突单向传播。动作电位产生的电流会沿轴突双向扩布。然而,只有未发放的轴突部位才能作出动作电位的反应;刚刚发放过的部位是没有反应的,直到动作电位移到安全范围,不能再刺激该部位。在通常的正向传导([[orthodromic conduction]])中,动作电位从轴丘向突触扣结(轴突末梢)传导,向相反方向传导的反向传导([[antidromic conduction]])现象非常罕见。不过,如果实验中从中间刺激轴突,两边的轴突都是“新鲜的”,即未被刺激,那么就会产生两个动作电位,一个传向轴丘,另一个传向突触扣结。 | |
===髓鞘和跳跃式传导=== | ===髓鞘和跳跃式传导=== | ||
| − | + | 为了在神经系统中快速高效地传递电信号,某些神经元的轴突上覆有髓鞘(myelin sheath)。髓鞘是多层膜,将轴突逐段包裹起来,段的间隔被称为郎飞结。它由专门的细胞产生:周围神经系统中是施万细胞([[Schwann cell]]s),中央神经系统中是少突胶质细胞([[oligodendrocyte]]s)。髓鞘减少了膜电容,并增加结间段的膜电阻,从而让动作电位在郎飞结之间快速、跳跃式的移动。<ref name="Zalc" group="lower-alpha">{{cite journal | vauthors = Zalc B | title = The acquisition of myelin: a success story | journal = Novartis Foundation Symposium | volume = 276 | pages = 15–21; discussion 21–5, 54–7, 275–81 | year = 2006 | pmid = 16805421 | doi = 10.1002/9780470032244.ch3 | isbn = 978-0-470-03224-4 | series = Novartis Foundation Symposia }}</ref><ref name="S. Poliak & E. Peles" group="lower-alpha">{{cite journal | vauthors = Poliak S, Peles E | title = The local differentiation of myelinated axons at nodes of Ranvier | journal = Nature Reviews. Neuroscience | volume = 4 | issue = 12 | pages = 968–80 | date = December 2003 | pmid = 14682359 | doi = 10.1038/nrn1253 | s2cid = 14720760 }}</ref><ref name=":2" group="lower-alpha">{{cite journal | vauthors = Simons M, Trotter J | title = Wrapping it up: the cell biology of myelination | journal = Current Opinion in Neurobiology | volume = 17 | issue = 5 | pages = 533–40 | date = October 2007 | pmid = 17923405 | doi = 10.1016/j.conb.2007.08.003 | s2cid = 45470194 }}</ref> 髓鞘形成(myelination)主要存在于脊椎动物,不过一些无脊椎动物也有类似的系统,比如某些种类的虾。<ref name=":3" group="lower-alpha">{{cite journal | vauthors = Xu K, Terakawa S | title = Fenestration nodes and the wide submyelinic space form the basis for the unusually fast impulse conduction of shrimp myelinated axons | journal = The Journal of Experimental Biology | volume = 202 | issue = Pt 15 | pages = 1979–89 | date = August 1999 | doi = 10.1242/jeb.202.15.1979 | pmid = 10395528 | url = http://jeb.biologists.org/cgi/pmidlookup?view=long&pmid=10395528 }}</ref> 脊椎动物中并不是所有的神经元都有髓鞘;例如,组成自主神经系统的神经元的轴突一般都没有髓鞘。髓鞘阻止了离子从髓鞘包裹的轴突部位出入。一般地,髓鞘增加了动作电位的传导速度,使其能效更高。不管是否跳跃,动作电位的平均传导速度范围从 1 米每秒(m/s)到 100 m/s 以上,一般而言,随轴突直径的增大而增大。<ref name="hursh_1939" group="lower-alpha">{{cite journal | vauthors = Hursh JB | year = 1939 | title = Conduction velocity and diameter of nerve fibers | journal = American Journal of Physiology | volume = 127 | pages = 131–39| doi = 10.1152/ajplegacy.1939.127.1.131 }}</ref> | |
| − | + | 动作电位不能在有髓鞘的轴突段的膜上传播。不过,电流经细胞质传输,足以使后面的一两个郎飞结去极化。就是说,一个郎飞结的动作电位产生的离子电流在下一个郎飞结引起另一个动作电位;动作电位的这种看似在郎飞结之间“跳跃”被称为跳跃式传导。跳跃式传导的机制在 1925 年就由 Ralph Lillie 提出,<ref name=":4" group="lower-alpha">{{cite journal | vauthors = Lillie RS | title = Factors Affecting Transmission and Recovery in the Passive Iron Nerve Model | journal = The Journal of General Physiology | volume = 7 | issue = 4 | pages = 473–507 | date = March 1925 | pmid = 19872151 | pmc = 2140733 | doi = 10.1085/jgp.7.4.473 }} See also {{harvnb|Keynes|Aidley|1991|p=78}}</ref> 但其首个实验证据来自 Ichiji Tasaki <ref name="tasaki_1939" group="lower-alpha">{{cite journal | vauthors = Tasaki I | year = 1939 | title = Electro-saltatory transmission of nerve impulse and effect of narcosis upon nerve fiber | journal = Am. J. Physiol. | volume = 127 | pages = 211–27| doi = 10.1152/ajplegacy.1939.127.2.211 }}</ref> 和 Taiji Takeuchi <ref name="tasaki_1941_1942_1959" group="lower-alpha">{{cite journal | vauthors = Tasaki I, Takeuchi T | year = 1941 | title = Der am Ranvierschen Knoten entstehende Aktionsstrom und seine Bedeutung für die Erregungsleitung | journal = Pflügers Archiv für die gesamte Physiologie | volume = 244 | pages = 696–711 | doi = 10.1007/BF01755414 | issue = 6 | s2cid = 8628858 }}<br />* {{cite journal | vauthors = Tasaki I, Takeuchi T | year = 1942 | title = Weitere Studien über den Aktionsstrom der markhaltigen Nervenfaser und über die elektrosaltatorische Übertragung des nervenimpulses | journal = Pflügers Archiv für die gesamte Physiologie | volume = 245 | pages = 764–82 | doi = 10.1007/BF01755237 | issue = 5 | s2cid = 44315437 }}</ref><ref name=":12">Tasaki, I in {{harvnb|Field|1959|pp=75–121}}</ref> 以及 Andrew Huxley 和 Robert Stämpflii。<ref name="huxley_staempfli_1949_1951" group="lower-alpha">{{cite journal | vauthors = Huxley AF, Stämpfli R | title = Evidence for saltatory conduction in peripheral myelinated nerve fibres | journal = The Journal of Physiology | volume = 108 | issue = 3 | pages = 315–39 | date = May 1949 | pmid = 16991863 | pmc = 1392492 | doi = 10.1113/jphysiol.1949.sp004335 | author-link1 = Andrew Huxley }}<br />* {{cite journal | vauthors = Huxley AF, Stampfli R | title = Direct determination of membrane resting potential and action potential in single myelinated nerve fibers | journal = The Journal of Physiology | volume = 112 | issue = 3–4 | pages = 476–95 | date = February 1951 | pmid = 14825228 | pmc = 1393015 | doi = 10.1113/jphysiol.1951.sp004545 | author-link1 = Andrew Huxley }}</ref> 而在无髓鞘的轴突,动作电位在紧邻的膜上引起另一个动作电位,并像波一样沿着轴突不断地移动。 | |
| − | + | [[Image:Conduction velocity and myelination.png|thumb|right|300px|猫的有髓鞘和无髓鞘轴突的传导速度的比较。有髓鞘神经元的传导速度 ''v'' 与轴突直径 ''d'' 大致呈线性变化(即 ''v'' ∝ ''d''),<ref name="hursh_1939" group="lower-alpha" /> 而无髓鞘神经元的速度大致与平方根呈线性变化(''v'' ∝√''d'')。<ref name="rushton_1951" group="lower-alpha">{{cite journal | vauthors = Rushton WA | title = A theory of the effects of fibre size in medullated nerve | journal = The Journal of Physiology | volume = 115 | issue = 1 | pages = 101–22 | date = September 1951 | pmid = 14889433 | pmc = 1392008 | doi = 10.1113/jphysiol.1951.sp004655 | author-link = W. A. H. Rushton }}</ref> 红色和蓝色曲线是实验数据的拟合,而虚线是其理论外推。|链接=Special:FilePath/Conduction_velocity_and_myelination.png]] | |
| − | + | 髓鞘具有两个重要的优势:传导速度快和能效高。粗于一个最小直径(大约 1 微米)的轴突,髓鞘通常能让动作电位的传导速度增加十倍。<ref name="hartline_2007" group="lower-alpha">{{cite journal | vauthors = Hartline DK, Colman DR | title = Rapid conduction and the evolution of giant axons and myelinated fibers | journal = Current Biology | volume = 17 | issue = 1 | pages = R29-35 | date = January 2007 | pmid = 17208176 | doi = 10.1016/j.cub.2006.11.042 | s2cid = 10033356 | doi-access = free }}</ref> 反之,相同的传导速度,有髓鞘的神经纤维比无髓的更细。例如,有髓鞘的蛙轴突和无髓鞘的乌贼巨轴突(squid giant axon)的动作电位传导速度大致相同(25 米/秒),但是青蛙的轴突直径要小 30 倍,横截面积要小 1000 倍。此外,因为离子电流被局限于郎飞结,离子的跨膜“泄漏”要少得多,节省了新陈代谢能量。考虑到人类神经系统消耗大约 20% 的身体代谢能量,这种节省有显著的选择优势([[natural selection|selective advantage]])。<ref name="hartline_2007" group="lower-alpha" /> | |
| − | + | 髓鞘包裹的轴突节段的长度对跳跃式传导的成功至关重要。它们应尽可能长,以最大限度地提高传导速度,但不能太长,以至于传过去的信号太弱,无法在下一个郎飞结触发动作电位。在自然界中,有髓鞘节段通常足够长,使信号被动传播至少两个结点而仍有足够的强度在第二、三结点触发动作电位。因此,跳跃式传导的安全系数很高,可以绕过损伤的郎飞结继续传播。然而,动作电位可能在安全系数较低的某些位置过早终止,即使在无髓神经元中也是如此;一个常见的例子是轴突分支成两个轴突的分支点。 | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | 有些疾病会降解髓鞘,破坏跳跃式传导,降低动作电位的传导速度。<ref name=":5" group="lower-alpha">{{cite journal | vauthors = Miller RH, Mi S | title = Dissecting demyelination | journal = Nature Neuroscience | volume = 10 | issue = 11 | pages = 1351–4 | date = November 2007 | pmid = 17965654 | doi = 10.1038/nn1995 | s2cid = 12441377 }}</ref> 其中最被人所知的是多发性硬化症(multiple sclerosis),髓鞘的降解削弱协调运动。<ref name=":13">Waxman, SG in {{harvnb|Waxman|2007|loc=''Multiple Sclerosis as a Neurodegenerative Disease'', pp. 333–346.}}</ref> | ||
===电缆学说=== | ===电缆学说=== | ||
| − | [[File:Cable theory Neuron RC circuit v3.svg|thumb|300x300px| | + | [[File:Cable theory Neuron RC circuit v3.svg|thumb|300x300px|电缆理论对神经元纤维的简化图。连接的 RC 电路对应于被动的神经突相邻的节段。(与胞内阻抗 ''r<sub>i</sub>'' 对应的)胞外阻抗 ''r<sub>e</sub>'' 未显示,因其通常小到可以忽略不计;细胞外液可以认为是处处电位相等。|链接=Special:FilePath/Cable_theory_Neuron_RC_circuit_v3.svg]] |
| − | |||
| − | |||
The flow of currents within an axon can be described quantitatively by [[cable theory]]<ref name="rall_1989">[[Wilfrid Rall|Rall, W]] in {{harvnb|Koch|Segev|1989|loc=''Cable Theory for Dendritic Neurons'', pp. 9–62.}}</ref> and its elaborations, such as the compartmental model.<ref name="segev_1989">{{cite book | vauthors = Segev I, Fleshman JW, Burke RE | chapter = Compartmental Models of Complex Neurons | title = Methods in Neuronal Modeling: From Synapses to Networks. | veditors = Koch C, Segev I | editor1-link = Christof Koch | date = 1989 | pages = 63–96 | publisher = The MIT Press | location = Cambridge, Massachusetts | isbn = 978-0-262-11133-1 | lccn = 88008279 | oclc = 18384545 }}</ref> Cable theory was developed in 1855 by [[William Thomson, 1st Baron Kelvin|Lord Kelvin]] to model the transatlantic telegraph cable<ref name="kelvin_1855" group=lower-alpha>{{cite journal | vauthors = Kelvin WT | year = 1855 | title = On the theory of the electric telegraph | journal = Proceedings of the Royal Society | volume = 7 | pages = 382–99 | doi = 10.1098/rspl.1854.0093| s2cid = 178547827 | author-link = William Thomson, 1st Baron Kelvin }}</ref> and was shown to be relevant to neurons by [[Alan Lloyd Hodgkin|Hodgkin]] and [[W. A. H. Rushton|Rushton]] in 1946.<ref name="hodgkin_1946" group=lower-alpha>{{cite journal | vauthors = Hodgkin AL, Rushton WA | title = The electrical constants of a crustacean nerve fibre | journal = Proceedings of the Royal Society of Medicine | volume = 134 | issue = 873 | pages = 444–79 | date = December 1946 | pmid = 20281590 | doi = 10.1098/rspb.1946.0024 | author-link1 = Alan Lloyd Hodgkin | bibcode = 1946RSPSB.133..444H | doi-access = free }}</ref> In simple cable theory, the neuron is treated as an electrically passive, perfectly cylindrical transmission cable, which can be described by a [[partial differential equation]]<ref name="rall_1989" /> | The flow of currents within an axon can be described quantitatively by [[cable theory]]<ref name="rall_1989">[[Wilfrid Rall|Rall, W]] in {{harvnb|Koch|Segev|1989|loc=''Cable Theory for Dendritic Neurons'', pp. 9–62.}}</ref> and its elaborations, such as the compartmental model.<ref name="segev_1989">{{cite book | vauthors = Segev I, Fleshman JW, Burke RE | chapter = Compartmental Models of Complex Neurons | title = Methods in Neuronal Modeling: From Synapses to Networks. | veditors = Koch C, Segev I | editor1-link = Christof Koch | date = 1989 | pages = 63–96 | publisher = The MIT Press | location = Cambridge, Massachusetts | isbn = 978-0-262-11133-1 | lccn = 88008279 | oclc = 18384545 }}</ref> Cable theory was developed in 1855 by [[William Thomson, 1st Baron Kelvin|Lord Kelvin]] to model the transatlantic telegraph cable<ref name="kelvin_1855" group=lower-alpha>{{cite journal | vauthors = Kelvin WT | year = 1855 | title = On the theory of the electric telegraph | journal = Proceedings of the Royal Society | volume = 7 | pages = 382–99 | doi = 10.1098/rspl.1854.0093| s2cid = 178547827 | author-link = William Thomson, 1st Baron Kelvin }}</ref> and was shown to be relevant to neurons by [[Alan Lloyd Hodgkin|Hodgkin]] and [[W. A. H. Rushton|Rushton]] in 1946.<ref name="hodgkin_1946" group=lower-alpha>{{cite journal | vauthors = Hodgkin AL, Rushton WA | title = The electrical constants of a crustacean nerve fibre | journal = Proceedings of the Royal Society of Medicine | volume = 134 | issue = 873 | pages = 444–79 | date = December 1946 | pmid = 20281590 | doi = 10.1098/rspb.1946.0024 | author-link1 = Alan Lloyd Hodgkin | bibcode = 1946RSPSB.133..444H | doi-access = free }}</ref> In simple cable theory, the neuron is treated as an electrically passive, perfectly cylindrical transmission cable, which can be described by a [[partial differential equation]]<ref name="rall_1989" /> | ||
| − | 轴突内电流的流动可以用电缆理论(cable theory)<ref name="rall_1989" /> | + | 轴突内电流的流动可以用电缆理论(cable theory)<ref name="rall_1989" /> 及其细化模型,如房室模型(compartmental model)来定量描述。<ref name="segev_1989" /> 电缆理论是 Lord Kelvin 在 1855 年提出的,用来对跨大西洋电报电缆进行建模 <ref name="kelvin_1855" group="lower-alpha" />,并于 1946 年被 Hodgkin 和 Rushton 证明描述神经元也很有用。<ref name="hodgkin_1946" group="lower-alpha" /> 简单的电缆理论中,神经元被看作是一个电被动的完美圆柱形的传输电缆,可用一个偏微分方程来描述<ref name="rall_1989" /> |
:<math> | :<math> | ||
\tau \frac{\partial V}{\partial t} = \lambda^2 \frac{\partial^2 V}{\partial x^2} - V | \tau \frac{\partial V}{\partial t} = \lambda^2 \frac{\partial^2 V}{\partial x^2} - V | ||
| 第157行: | 第140行: | ||
where ''V''(''x'', ''t'') is the voltage across the membrane at a time ''t'' and a position ''x'' along the length of the neuron, and where λ and τ are the characteristic length and time scales on which those voltages decay in response to a stimulus. Referring to the circuit diagram on the right, these scales can be determined from the resistances and capacitances per unit length.{{sfn|Purves|Augustine|Fitzpatrick|Hall|2008|pp=52–53}} | where ''V''(''x'', ''t'') is the voltage across the membrane at a time ''t'' and a position ''x'' along the length of the neuron, and where λ and τ are the characteristic length and time scales on which those voltages decay in response to a stimulus. Referring to the circuit diagram on the right, these scales can be determined from the resistances and capacitances per unit length.{{sfn|Purves|Augustine|Fitzpatrick|Hall|2008|pp=52–53}} | ||
| − | 其中 ''V(x'', ''t)'' 是时间 ''t'' 和沿神经元长度的位置 ''x'' | + | 其中 ''V(x'', ''t)'' 是时间 ''t'' 和沿神经元长度的位置 ''x'' 的跨膜电压,其中 λ 和 τ 是特征长度和时间尺度,对刺激的反应电位以这些尺度发生衰减。参考右边的电路图,这些尺度可以通过单位长度的电阻和电容来确定。 |
:<math> | :<math> | ||
| 第170行: | 第153行: | ||
These time and length-scales can be used to understand the dependence of the conduction velocity on the diameter of the neuron in unmyelinated fibers. For example, the time-scale τ increases with both the membrane resistance ''r<sub>m</sub>'' and capacitance ''c<sub>m</sub>''. As the capacitance increases, more charge must be transferred to produce a given transmembrane voltage (by [[capacitance|the equation ''Q'' = ''CV'']]); as the resistance increases, less charge is transferred per unit time, making the equilibration slower. In a similar manner, if the internal resistance per unit length ''r<sub>i</sub>'' is lower in one axon than in another (e.g., because the radius of the former is larger), the spatial decay length λ becomes longer and the [[conduction velocity]] of an action potential should increase. If the transmembrane resistance ''r<sub>m</sub>'' is increased, that lowers the average "leakage" current across the membrane, likewise causing ''λ'' to become longer, increasing the conduction velocity. | These time and length-scales can be used to understand the dependence of the conduction velocity on the diameter of the neuron in unmyelinated fibers. For example, the time-scale τ increases with both the membrane resistance ''r<sub>m</sub>'' and capacitance ''c<sub>m</sub>''. As the capacitance increases, more charge must be transferred to produce a given transmembrane voltage (by [[capacitance|the equation ''Q'' = ''CV'']]); as the resistance increases, less charge is transferred per unit time, making the equilibration slower. In a similar manner, if the internal resistance per unit length ''r<sub>i</sub>'' is lower in one axon than in another (e.g., because the radius of the former is larger), the spatial decay length λ becomes longer and the [[conduction velocity]] of an action potential should increase. If the transmembrane resistance ''r<sub>m</sub>'' is increased, that lowers the average "leakage" current across the membrane, likewise causing ''λ'' to become longer, increasing the conduction velocity. | ||
| − | + | 这些时间尺度和长度尺度可以用来理解无髓鞘纤维中传导速度依赖于神经元直径。比如,时间尺度 τ 随着膜电阻 ''r<sub>m</sub>'' 和膜电容 ''c<sub>m</sub>'' 的增大而增大。随着电容的增加,(根据公式 [[capacitance|''Q'' = ''CV'']])必须转移更多的电荷才能产生给定的跨膜电压;随着电阻的增加,每单位时间转移的电荷越少,越慢恢复平衡。同样,如果一个轴突的单位长度 ''r<sub>i</sub>'' 低于另一个轴突(比如,因为前者的半径较大),空间衰减长度 λ 变长,动作电位的传导速度应该增加。如果跨膜电阻 ''r<sub>m</sub>'' 增大,降低平均跨膜“泄漏”电流,同样导致 λ 变长,增加了传导速度。 | |
| − | == | + | ==动作电位的终止== |
===化学突触=== | ===化学突触=== | ||
| − | + | 一般而言,到达突触扣结(synaptic knobs)的动作电位会使神经递质释放到突触间隙。<ref name=":6" group="lower-alpha">{{cite book | vauthors = Süudhof TC | title = Pharmacology of Neurotransmitter Release | chapter = Neurotransmitter release | volume = 184 | issue = 184 | pages = 1–21 | year = 2008 | pmid = 18064409 | doi = 10.1007/978-3-540-74805-2_1 | isbn = 978-3-540-74804-5 | series = Handbook of Experimental Pharmacology }}</ref> 神经递质是可以打开突触后细胞离子通道的小分子;大多数轴突的所有末梢都有相同的神经递质。传来的动作电位打开了突触前膜上的电压敏感性钙通道,钙内流导致充满神经递质的突触囊泡(vesicle)迁移到细胞表面,并将其内容物释放到突触间隙(synaptic cleft)。<ref name=":7" group="lower-alpha">{{cite journal | vauthors = Rusakov DA | title = Ca2+-dependent mechanisms of presynaptic control at central synapses | journal = The Neuroscientist | volume = 12 | issue = 4 | pages = 317–26 | date = August 2006 | pmid = 16840708 | pmc = 2684670 | doi = 10.1177/1073858405284672 }}</ref> 引起破伤风([[tetanus]])的破伤风痉挛毒素(tetanospasmin)和引起肉毒中毒( [[botulism]])的肉毒杆菌毒素(botulinum toxin)等神经毒素会抑制这一复杂的过程。<ref name=":8" group="lower-alpha">{{cite journal | vauthors = Humeau Y, Doussau F, Grant NJ, Poulain B | title = How botulinum and tetanus neurotoxins block neurotransmitter release | journal = Biochimie | volume = 82 | issue = 5 | pages = 427–46 | date = May 2000 | pmid = 10865130 | doi = 10.1016/S0300-9084(00)00216-9 }}</ref> | |
| − | |||
| − | |||
[[Image:Gap cell junction-en.svg|thumb|right|兴奋性细胞之间的电突触让离子从一个细胞直接流到另一个细胞,比化学突触快得多。|链接=Special:FilePath/Gap_cell_junction-en.svg]] | [[Image:Gap cell junction-en.svg|thumb|right|兴奋性细胞之间的电突触让离子从一个细胞直接流到另一个细胞,比化学突触快得多。|链接=Special:FilePath/Gap_cell_junction-en.svg]] | ||
| 第184行: | 第165行: | ||
===神经肌肉接头=== | ===神经肌肉接头=== | ||
| − | + | 化学突触有个特例,就是运动神经元轴突末梢与肌纤维形成的神经肌肉接头(neuromuscular junction)。<ref name=":11" group="lower-alpha">{{cite journal | vauthors = Hirsch NP | title = Neuromuscular junction in health and disease | journal = British Journal of Anaesthesia | volume = 99 | issue = 1 | pages = 132–8 | date = July 2007 | pmid = 17573397 | doi = 10.1093/bja/aem144 | df = dmy-all | doi-access = free }}</ref> 运动神经元释放神经递质乙酰胆碱(acetylcholine),结合到肌膜(''[[sarcolemma]]'')上的内在膜蛋白乙酰胆碱受体(acetylcholine receptor)。<ref name=":12" group="lower-alpha">{{cite journal | vauthors = Hughes BW, Kusner LL, Kaminski HJ | title = Molecular architecture of the neuromuscular junction | journal = Muscle & Nerve | volume = 33 | issue = 4 | pages = 445–61 | date = April 2006 | pmid = 16228970 | doi = 10.1002/mus.20440 | s2cid = 1888352 }}</ref> 不过,乙酰胆碱结合后又很快解离并被位于突触中的乙酰胆碱酯酶([[acetylcholinesterase]])水解。这种酶能迅速减少对肌肉的刺激,从而使肌肉收缩的程度和时间受到精细的调控。一些毒药,例如神经毒剂沙林([[sarin]])和塔崩(tabun),<ref name="Newmark" group="lower-alpha">{{cite journal | vauthors = Newmark J | title = Nerve agents | journal = The Neurologist | volume = 13 | issue = 1 | pages = 20–32 | date = January 2007 | pmid = 17215724 | doi = 10.1097/01.nrl.0000252923.04894.53 | s2cid = 211234081 }}</ref> 以及杀虫剂二嗪农([[diazinon]])和马拉硫磷([[malathion]]),会使乙酰胆碱酯酶失活,从而阻断这种控制。<ref name=":13" group="lower-alpha">{{cite journal | vauthors = Costa LG | title = Current issues in organophosphate toxicology | journal = Clinica Chimica Acta; International Journal of Clinical Chemistry | volume = 366 | issue = 1–2 | pages = 1–13 | date = April 2006 | pmid = 16337171 | doi = 10.1016/j.cca.2005.10.008 }}</ref> | |
| − | |||
| − | |||
==其他细胞类型== | ==其他细胞类型== | ||
===心肌动作电位=== | ===心肌动作电位=== | ||
| − | [[Image:Ventricular myocyte action potential.svg|thumb|220px|[[文件:Ventricular myocyte action potential.svg.png|缩略图]] | + | [[Image:Ventricular myocyte action potential.svg|thumb|220px|[[文件:Ventricular myocyte action potential.svg.png|缩略图]]心肌动作电位的阶段。电压的急剧上升(“0”)对应于钠离子的内流,而两个下降(分别为“1”和“3”)对应于钠通道失活和复极化的钾离子外流。特征性平台(“2”)是由电压敏感性钙通道的打开产生的。|链接=Special:FilePath/Ventricular_myocyte_action_potential.svg.png]] |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | 心肌动作电位与神经元动作电位的不同之处在于,心肌动作电位有一个延长的平台期,即膜会保持几百毫秒高电位之后,才被钾电流复极化。<ref name="Kleber" group="lower-alpha">{{cite journal | vauthors = Kléber AG, Rudy Y | title = Basic mechanisms of cardiac impulse propagation and associated arrhythmias | journal = Physiological Reviews | volume = 84 | issue = 2 | pages = 431–88 | date = April 2004 | pmid = 15044680 | doi = 10.1152/physrev.00025.2003 | s2cid = 21823003 }}</ref> 这个平台是慢速钙通道打开的作用,使膜电位在钠通道失活之后,仍保持在其平衡电位附近。 | |
| − | === | + | 心肌动作电位在协调心脏收缩中起着重要作用。窦房结的心肌细胞提供了同步心脏的起搏电位。<ref name="Kleber" group="lower-alpha" /> 这些细胞的动作电位传导到并通过房室结(atrioventricular node)——心房和心室之间唯一的传导通路。房室结的动作电位通过希斯氏束(bundle of His)传递到浦肯野纤维(Purkinje fibers)。相对的,心肌动作电位的异常ーー无论是由于先天性基因突变还是损伤ーー都可能导致人类疾病,尤其是心律失常。<ref name="Kleber" group="lower-alpha" /> 几种抗心律失常药物作用于心肌动作电位,如奎尼丁([[quinidine]])、利多卡因([[lidocaine]])、 β 受体阻滞剂([[beta blocker]]s)和维拉帕米([[verapamil]])。<ref name=":14" group="lower-alpha">{{cite journal | vauthors = Tamargo J, Caballero R, Delpón E | title = Pharmacological approaches in the treatment of atrial fibrillation | journal = Current Medicinal Chemistry | volume = 11 | issue = 1 | pages = 13–28 | date = January 2004 | pmid = 14754423 | doi = 10.2174/0929867043456241 }}</ref> |
| − | |||
| − | + | ===肌肉动作电位=== | |
| + | 正常的骨骼肌细胞的动作电位与神经元的动作电位相似。动作电位是细胞膜(肌膜)去极化的结果,这种去极化开启了电压敏感的钠通道;这些电压敏感的钠通道失活,膜通过钾离子外向复极化。动作电位之前的静息电位通常是 -90mV,比典型的神经元稍微负。肌肉动作电位持续时间约为 2-4 ms,绝对不应期约为 1-3 ms,肌肉传导速率约为 5 m/s。动作电位释放钙离子,释放原肌球蛋白(tropomyosin),使肌肉收缩。肌肉动作电位是由突触前神经元动作电位传至神经肌肉接头引起的。神经肌肉接头是很多神经毒素的共同靶点。<ref name="Newmark" group="lower-alpha" /> | ||
===植物动作电位=== | ===植物动作电位=== | ||
| 第220行: | 第191行: | ||
However, the flytrap doesn't close after one trigger. Instead, it requires the activation of 2 or more hairs.<ref name=":1" /><ref name=":2" /> If only one hair is triggered, it throws the activation as a false positive. Further, the second hair must be activated within a certain time interval (0.75 s - 40 s) for it to register with the first activation.<ref name=":2" /> Thus, a buildup of calcium starts and slowly falls from the first trigger. When the second action potential is fired within the time interval, it reaches the Calcium threshold to depolarize the cell, closing the trap on the prey within a fraction of a second.<ref name=":2" /> | However, the flytrap doesn't close after one trigger. Instead, it requires the activation of 2 or more hairs.<ref name=":1" /><ref name=":2" /> If only one hair is triggered, it throws the activation as a false positive. Further, the second hair must be activated within a certain time interval (0.75 s - 40 s) for it to register with the first activation.<ref name=":2" /> Thus, a buildup of calcium starts and slowly falls from the first trigger. When the second action potential is fired within the time interval, it reaches the Calcium threshold to depolarize the cell, closing the trap on the prey within a fraction of a second.<ref name=":2" /> | ||
| − | + | 然而,捕蝇草不会在一次触发后闭合,而是需要激活 2 根或更多的毛。<ref name=":1" /><ref name=":2" /> 如果只有一根毛被触发,这个激活会被视为假阳性。而且第二根毛必须在一定的时间间隔(0.75 s - 40 s)内被激活,才能将其与第一次激活一起记录。<ref name=":2" /> 因此,钙的积累从第一次触发开始并且然后慢慢下降。当第二个动作电位在时间间隔内被激发时,它达到钙阈值使细胞去极化,在几分之一秒内关闭捕获物的陷阱。<ref name=":2" /> | |
Together with the subsequent release of positive potassium ions the action potential in plants involves an [[osmotic]] loss of salt (KCl). Whereas, the animal action potential is osmotically neutral because equal amounts of entering sodium and leaving potassium cancel each other osmotically. The interaction of electrical and osmotic relations in plant cells<ref name="Gradmann_1998" group="lower-alpha">{{cite journal | vauthors = Gradmann D, Hoffstadt J | title = Electrocoupling of ion transporters in plants: interaction with internal ion concentrations | journal = The Journal of Membrane Biology | volume = 166 | issue = 1 | pages = 51–9 | date = November 1998 | pmid = 9784585 | doi = 10.1007/s002329900446 | s2cid = 24190001 }}</ref> appears to have arisen from an osmotic function of electrical excitability in a common unicellular ancestors of plants and animals under changing salinity conditions. Further, the present function of rapid signal transmission is seen as a newer accomplishment of [[metazoan]] cells in a more stable osmotic environment.<ref name="Gradmann_1980"> | Together with the subsequent release of positive potassium ions the action potential in plants involves an [[osmotic]] loss of salt (KCl). Whereas, the animal action potential is osmotically neutral because equal amounts of entering sodium and leaving potassium cancel each other osmotically. The interaction of electrical and osmotic relations in plant cells<ref name="Gradmann_1998" group="lower-alpha">{{cite journal | vauthors = Gradmann D, Hoffstadt J | title = Electrocoupling of ion transporters in plants: interaction with internal ion concentrations | journal = The Journal of Membrane Biology | volume = 166 | issue = 1 | pages = 51–9 | date = November 1998 | pmid = 9784585 | doi = 10.1007/s002329900446 | s2cid = 24190001 }}</ref> appears to have arisen from an osmotic function of electrical excitability in a common unicellular ancestors of plants and animals under changing salinity conditions. Further, the present function of rapid signal transmission is seen as a newer accomplishment of [[metazoan]] cells in a more stable osmotic environment.<ref name="Gradmann_1980"> | ||
| 第274行: | 第245行: | ||
The study of action potentials has required the development of new experimental methods. The initial work, prior to 1955, was carried out primarily by [[Alan Lloyd Hodgkin]] and [[Andrew Fielding Huxley]], who were, along [[John Carew Eccles]], awarded the 1963 [[Nobel Prize in Physiology or Medicine]] for their contribution to the description of the ionic basis of nerve conduction. It focused on three goals: isolating signals from single neurons or axons, developing fast, sensitive electronics, and shrinking [[electrode]]s enough that the voltage inside a single cell could be recorded. | The study of action potentials has required the development of new experimental methods. The initial work, prior to 1955, was carried out primarily by [[Alan Lloyd Hodgkin]] and [[Andrew Fielding Huxley]], who were, along [[John Carew Eccles]], awarded the 1963 [[Nobel Prize in Physiology or Medicine]] for their contribution to the description of the ionic basis of nerve conduction. It focused on three goals: isolating signals from single neurons or axons, developing fast, sensitive electronics, and shrinking [[electrode]]s enough that the voltage inside a single cell could be recorded. | ||
| − | + | 动作电位的研究一直以来需要开发新的实验方法。在 1955 年之前最初的工作主要是由 [[Alan Lloyd Hodgkin]] 和 Andrew Fielding Huxley 完成的,他们因为在描述神经传导的离子基础方面做出的贡献,和 [[John Carew Eccles]] 一起被授予 1963 年诺贝尔生理学或医学奖。它聚焦于三个目标:从单个神经元或轴突中分离出信号,发展快速、灵敏的电子设备,以及缩小电极,使单个细胞内的电压能够被记录下来。 | |
The first problem was solved by studying the [[Squid giant axon|giant axons]] found in the neurons of the [[squid]] (''[[Loligo forbesii]]'' and ''[[Doryteuthis pealeii]]'', at the time classified as ''Loligo pealeii'').<ref name="keynes_1989" group="lower-alpha">{{cite journal | vauthors = Keynes RD | title = The role of giant axons in studies of the nerve impulse | journal = BioEssays | volume = 10 | issue = 2–3 | pages = 90–3 | year = 1989 | pmid = 2541698 | doi = 10.1002/bies.950100213 }}</ref> These axons are so large in diameter (roughly 1 mm, or 100-fold larger than a typical neuron) that they can be seen with the naked eye, making them easy to extract and manipulate.<ref name="hodgkin_1952" group="lower-alpha" /><ref name="Meunier" group="lower-alpha">{{cite journal | vauthors = Meunier C, Segev I | title = Playing the devil's advocate: is the Hodgkin-Huxley model useful? | journal = Trends in Neurosciences | volume = 25 | issue = 11 | pages = 558–63 | date = November 2002 | pmid = 12392930 | doi = 10.1016/S0166-2236(02)02278-6 | s2cid = 1355280 }}</ref> However, they are not representative of all excitable cells, and numerous other systems with action potentials have been studied. | The first problem was solved by studying the [[Squid giant axon|giant axons]] found in the neurons of the [[squid]] (''[[Loligo forbesii]]'' and ''[[Doryteuthis pealeii]]'', at the time classified as ''Loligo pealeii'').<ref name="keynes_1989" group="lower-alpha">{{cite journal | vauthors = Keynes RD | title = The role of giant axons in studies of the nerve impulse | journal = BioEssays | volume = 10 | issue = 2–3 | pages = 90–3 | year = 1989 | pmid = 2541698 | doi = 10.1002/bies.950100213 }}</ref> These axons are so large in diameter (roughly 1 mm, or 100-fold larger than a typical neuron) that they can be seen with the naked eye, making them easy to extract and manipulate.<ref name="hodgkin_1952" group="lower-alpha" /><ref name="Meunier" group="lower-alpha">{{cite journal | vauthors = Meunier C, Segev I | title = Playing the devil's advocate: is the Hodgkin-Huxley model useful? | journal = Trends in Neurosciences | volume = 25 | issue = 11 | pages = 558–63 | date = November 2002 | pmid = 12392930 | doi = 10.1016/S0166-2236(02)02278-6 | s2cid = 1355280 }}</ref> However, they are not representative of all excitable cells, and numerous other systems with action potentials have been studied. | ||
| 第335行: | 第306行: | ||
Mathematical and computational models are essential for understanding the action potential, and offer predictions that may be tested against experimental data, providing a stringent test of a theory. The most important and accurate of the early neural models is the [[Hodgkin–Huxley model]], which describes the action potential by a coupled set of four [[ordinary differential equation]]s (ODEs).<ref name="hodgkin_1952" group="lower-alpha" /> Although the Hodgkin–Huxley model may be a simplification with few limitations<ref name=":23">{{cite journal | vauthors = Baranauskas G, Martina M | title = Sodium currents activate without a Hodgkin-and-Huxley-type delay in central mammalian neurons | journal = The Journal of Neuroscience | volume = 26 | issue = 2 | pages = 671–84 | date = January 2006 | pmid = 16407565 | pmc = 6674426 | doi = 10.1523/jneurosci.2283-05.2006 }}</ref> compared to the realistic nervous membrane as it exists in nature, its complexity has inspired several even-more-simplified models,{{sfn|Hoppensteadt|1986}}<ref group="lower-alpha" name=":20">*{{cite journal | vauthors = Fitzhugh R | title = Thresholds and plateaus in the Hodgkin-Huxley nerve equations | journal = The Journal of General Physiology | volume = 43 | issue = 5 | pages = 867–96 | date = May 1960 | pmid = 13823315 | pmc = 2195039 | doi = 10.1085/jgp.43.5.867 }}<br />* {{cite journal | vauthors = Kepler TB, Abbott LF, Marder E | title = Reduction of conductance-based neuron models | journal = Biological Cybernetics | volume = 66 | issue = 5 | pages = 381–7 | year = 1992 | pmid = 1562643 | doi = 10.1007/BF00197717 | s2cid = 6789007 }}</ref> such as the [[Morris–Lecar model]]<ref name="morris_1981" group="lower-alpha">{{cite journal | vauthors = Morris C, Lecar H | title = Voltage oscillations in the barnacle giant muscle fiber | journal = Biophysical Journal | volume = 35 | issue = 1 | pages = 193–213 | date = July 1981 | pmid = 7260316 | pmc = 1327511 | doi = 10.1016/S0006-3495(81)84782-0 | bibcode = 1981BpJ....35..193M }}</ref> and the [[FitzHugh–Nagumo model]],<ref name="fitzhugh" group="lower-alpha">{{cite journal | vauthors = Fitzhugh R | title = Impulses and Physiological States in Theoretical Models of Nerve Membrane | journal = Biophysical Journal | volume = 1 | issue = 6 | pages = 445–66 | date = July 1961 | pmid = 19431309 | pmc = 1366333 | doi = 10.1016/S0006-3495(61)86902-6 | bibcode = 1961BpJ.....1..445F }}<br />* {{cite journal | vauthors = Nagumo J, Arimoto S, Yoshizawa S | year = 1962 | title = An active pulse transmission line simulating nerve axon | journal = Proceedings of the IRE | volume = 50 | pages = 2061–2070 | doi = 10.1109/JRPROC.1962.288235 | issue = 10 | s2cid = 51648050 }}</ref> both of which have only two coupled ODEs. The properties of the Hodgkin–Huxley and FitzHugh–Nagumo models and their relatives, such as the Bonhoeffer–Van der Pol model,<ref name="bonhoeffer_vanderPol" group="lower-alpha">{{cite journal | vauthors = Bonhoeffer KF | title = Activation of passive iron as a model for the excitation of nerve | journal = The Journal of General Physiology | volume = 32 | issue = 1 | pages = 69–91 | date = September 1948 | pmid = 18885679 | pmc = 2213747 | doi = 10.1085/jgp.32.1.69 }}<br />* {{cite journal | vauthors = Bonhoeffer KF | year = 1953 | title = Modelle der Nervenerregung | journal = Naturwissenschaften | volume = 40 | pages = 301–311 | doi = 10.1007/BF00632438|bibcode = 1953NW.....40..301B | issue = 11 | s2cid = 19149460 }}<br />* {{cite journal | vauthors = Van der Pol B | year = 1926 | title = On relaxation-oscillations | journal = Philosophical Magazine | volume = 2 | pages = 977–992| author-link = Balthasar van der Pol }}<br />* {{cite journal | year = 1928 | title = The heartbeat considered as a relaxation oscillation, and an electrical model of the heart | journal = Philosophical Magazine | volume = 6 | pages = 763–775| vauthors = Van der Pol B, Van der Mark J| author-link1 = Balthasar van der Pol | doi=10.1080/14786441108564652}}<br />* {{cite journal | year = 1929 | title = The heartbeat considered as a relaxation oscillation, and an electrical model of the heart | journal = Arch. Neerl. Physiol. | volume = 14 | pages = 418–443| vauthors = Van der Pol B, van der Mark J| author-link1 = Balthasar van der Pol }}</ref> have been well-studied within mathematics,<ref name="math_studies">Sato, S; Fukai, H; Nomura, T; Doi, S in {{harvnb|Reeke|Poznanski|Sporns|Rosenberg|2005|loc=''Bifurcation Analysis of the Hodgkin-Huxley Equations'', pp. 459–478.}}<br />* FitzHugh, R in {{harvnb|Schwann|1969|loc=''Mathematical models of axcitation and propagation in nerve'', pp. 12–16.}}<br />* {{harvnb|Guckenheimer|Holmes|1986|pp=12–16}}</ref><ref group="lower-alpha" name=":21">{{cite journal | vauthors = Evans JW | year = 1972 | title = Nerve axon equations. I. Linear approximations | journal = Indiana Univ. Math. J. | volume = 21 | pages = 877–885 | doi = 10.1512/iumj.1972.21.21071 | issue = 9| doi-access = free }}<br />* {{cite journal | vauthors = Evans JW, Feroe J | year = 1977 | title = Local stability theory of the nerve impulse | journal = Math. Biosci. | volume = 37 | pages = 23–50 | doi = 10.1016/0025-5564(77)90076-1 }}</ref> computation<ref name="computational_studies">Nelson, ME; Rinzel, J in {{harvnb|Bower|Beeman|1995|loc=''The Hodgkin-Huxley Model'', pp. 29–49.}}<br />* Rinzel, J & Ermentrout, GB; in {{harvnb|Koch|Segev|1989|loc=''Analysis of Neural Excitability and Oscillations'', pp. 135–169.}}</ref> and electronics.<ref name="keener_1983" group="lower-alpha">{{cite journal | vauthors = Keener JP | year = 1983 | title = Analogue circuitry for the Van der Pol and FitzHugh-Nagumo equations | journal = IEEE Transactions on Systems, Man and Cybernetics | volume = 13 | issue = 5 | pages = 1010–1014 | doi = 10.1109/TSMC.1983.6313098 | s2cid = 20077648 }}</ref> However the simple models of generator potential and action potential fail to accurately reproduce the near threshold neural spike rate and spike shape, specifically for the [[mechanoreceptors]] like the [[Pacinian corpuscle]].<ref name=":24">{{cite journal | vauthors = Biswas A, Manivannan M, Srinivasan MA | title = Vibrotactile sensitivity threshold: nonlinear stochastic mechanotransduction model of the Pacinian Corpuscle | journal = IEEE Transactions on Haptics | volume = 8 | issue = 1 | pages = 102–13 | year = 2015 | pmid = 25398183 | doi = 10.1109/TOH.2014.2369422 | s2cid = 15326972 | url = https://zenodo.org/record/894772 }}</ref> More modern research has focused on larger and more integrated systems; by joining action-potential models with models of other parts of the nervous system (such as dendrites and synapses), researchers can study [[neural computation]]{{sfnm|1a1=McCulloch|1y=1988|1pp=19–39, 46–66, 72–141|2a1=Anderson|2a2=Rosenfeld|2y=1988|2pp=15–41}} and simple [[reflex]]es, such as [[escape reflex]]es and others controlled by [[central pattern generator]]s.<ref name="cpg">Getting, PA in {{harvnb|Koch|Segev|1989|loc=''Reconstruction of Small Neural Networks'', pp. 171–194.}}</ref><ref name="pmid10713861" group="lower-alpha">{{cite journal | vauthors = Hooper SL | title = Central pattern generators | journal = Current Biology | volume = 10 | issue = 5 | pages = R176–R179 | date = March 2000 | pmid = 10713861 | doi = 10.1016/S0960-9822(00)00367-5 | citeseerx = 10.1.1.133.3378 | s2cid = 11388348 }}</ref> | Mathematical and computational models are essential for understanding the action potential, and offer predictions that may be tested against experimental data, providing a stringent test of a theory. The most important and accurate of the early neural models is the [[Hodgkin–Huxley model]], which describes the action potential by a coupled set of four [[ordinary differential equation]]s (ODEs).<ref name="hodgkin_1952" group="lower-alpha" /> Although the Hodgkin–Huxley model may be a simplification with few limitations<ref name=":23">{{cite journal | vauthors = Baranauskas G, Martina M | title = Sodium currents activate without a Hodgkin-and-Huxley-type delay in central mammalian neurons | journal = The Journal of Neuroscience | volume = 26 | issue = 2 | pages = 671–84 | date = January 2006 | pmid = 16407565 | pmc = 6674426 | doi = 10.1523/jneurosci.2283-05.2006 }}</ref> compared to the realistic nervous membrane as it exists in nature, its complexity has inspired several even-more-simplified models,{{sfn|Hoppensteadt|1986}}<ref group="lower-alpha" name=":20">*{{cite journal | vauthors = Fitzhugh R | title = Thresholds and plateaus in the Hodgkin-Huxley nerve equations | journal = The Journal of General Physiology | volume = 43 | issue = 5 | pages = 867–96 | date = May 1960 | pmid = 13823315 | pmc = 2195039 | doi = 10.1085/jgp.43.5.867 }}<br />* {{cite journal | vauthors = Kepler TB, Abbott LF, Marder E | title = Reduction of conductance-based neuron models | journal = Biological Cybernetics | volume = 66 | issue = 5 | pages = 381–7 | year = 1992 | pmid = 1562643 | doi = 10.1007/BF00197717 | s2cid = 6789007 }}</ref> such as the [[Morris–Lecar model]]<ref name="morris_1981" group="lower-alpha">{{cite journal | vauthors = Morris C, Lecar H | title = Voltage oscillations in the barnacle giant muscle fiber | journal = Biophysical Journal | volume = 35 | issue = 1 | pages = 193–213 | date = July 1981 | pmid = 7260316 | pmc = 1327511 | doi = 10.1016/S0006-3495(81)84782-0 | bibcode = 1981BpJ....35..193M }}</ref> and the [[FitzHugh–Nagumo model]],<ref name="fitzhugh" group="lower-alpha">{{cite journal | vauthors = Fitzhugh R | title = Impulses and Physiological States in Theoretical Models of Nerve Membrane | journal = Biophysical Journal | volume = 1 | issue = 6 | pages = 445–66 | date = July 1961 | pmid = 19431309 | pmc = 1366333 | doi = 10.1016/S0006-3495(61)86902-6 | bibcode = 1961BpJ.....1..445F }}<br />* {{cite journal | vauthors = Nagumo J, Arimoto S, Yoshizawa S | year = 1962 | title = An active pulse transmission line simulating nerve axon | journal = Proceedings of the IRE | volume = 50 | pages = 2061–2070 | doi = 10.1109/JRPROC.1962.288235 | issue = 10 | s2cid = 51648050 }}</ref> both of which have only two coupled ODEs. The properties of the Hodgkin–Huxley and FitzHugh–Nagumo models and their relatives, such as the Bonhoeffer–Van der Pol model,<ref name="bonhoeffer_vanderPol" group="lower-alpha">{{cite journal | vauthors = Bonhoeffer KF | title = Activation of passive iron as a model for the excitation of nerve | journal = The Journal of General Physiology | volume = 32 | issue = 1 | pages = 69–91 | date = September 1948 | pmid = 18885679 | pmc = 2213747 | doi = 10.1085/jgp.32.1.69 }}<br />* {{cite journal | vauthors = Bonhoeffer KF | year = 1953 | title = Modelle der Nervenerregung | journal = Naturwissenschaften | volume = 40 | pages = 301–311 | doi = 10.1007/BF00632438|bibcode = 1953NW.....40..301B | issue = 11 | s2cid = 19149460 }}<br />* {{cite journal | vauthors = Van der Pol B | year = 1926 | title = On relaxation-oscillations | journal = Philosophical Magazine | volume = 2 | pages = 977–992| author-link = Balthasar van der Pol }}<br />* {{cite journal | year = 1928 | title = The heartbeat considered as a relaxation oscillation, and an electrical model of the heart | journal = Philosophical Magazine | volume = 6 | pages = 763–775| vauthors = Van der Pol B, Van der Mark J| author-link1 = Balthasar van der Pol | doi=10.1080/14786441108564652}}<br />* {{cite journal | year = 1929 | title = The heartbeat considered as a relaxation oscillation, and an electrical model of the heart | journal = Arch. Neerl. Physiol. | volume = 14 | pages = 418–443| vauthors = Van der Pol B, van der Mark J| author-link1 = Balthasar van der Pol }}</ref> have been well-studied within mathematics,<ref name="math_studies">Sato, S; Fukai, H; Nomura, T; Doi, S in {{harvnb|Reeke|Poznanski|Sporns|Rosenberg|2005|loc=''Bifurcation Analysis of the Hodgkin-Huxley Equations'', pp. 459–478.}}<br />* FitzHugh, R in {{harvnb|Schwann|1969|loc=''Mathematical models of axcitation and propagation in nerve'', pp. 12–16.}}<br />* {{harvnb|Guckenheimer|Holmes|1986|pp=12–16}}</ref><ref group="lower-alpha" name=":21">{{cite journal | vauthors = Evans JW | year = 1972 | title = Nerve axon equations. I. Linear approximations | journal = Indiana Univ. Math. J. | volume = 21 | pages = 877–885 | doi = 10.1512/iumj.1972.21.21071 | issue = 9| doi-access = free }}<br />* {{cite journal | vauthors = Evans JW, Feroe J | year = 1977 | title = Local stability theory of the nerve impulse | journal = Math. Biosci. | volume = 37 | pages = 23–50 | doi = 10.1016/0025-5564(77)90076-1 }}</ref> computation<ref name="computational_studies">Nelson, ME; Rinzel, J in {{harvnb|Bower|Beeman|1995|loc=''The Hodgkin-Huxley Model'', pp. 29–49.}}<br />* Rinzel, J & Ermentrout, GB; in {{harvnb|Koch|Segev|1989|loc=''Analysis of Neural Excitability and Oscillations'', pp. 135–169.}}</ref> and electronics.<ref name="keener_1983" group="lower-alpha">{{cite journal | vauthors = Keener JP | year = 1983 | title = Analogue circuitry for the Van der Pol and FitzHugh-Nagumo equations | journal = IEEE Transactions on Systems, Man and Cybernetics | volume = 13 | issue = 5 | pages = 1010–1014 | doi = 10.1109/TSMC.1983.6313098 | s2cid = 20077648 }}</ref> However the simple models of generator potential and action potential fail to accurately reproduce the near threshold neural spike rate and spike shape, specifically for the [[mechanoreceptors]] like the [[Pacinian corpuscle]].<ref name=":24">{{cite journal | vauthors = Biswas A, Manivannan M, Srinivasan MA | title = Vibrotactile sensitivity threshold: nonlinear stochastic mechanotransduction model of the Pacinian Corpuscle | journal = IEEE Transactions on Haptics | volume = 8 | issue = 1 | pages = 102–13 | year = 2015 | pmid = 25398183 | doi = 10.1109/TOH.2014.2369422 | s2cid = 15326972 | url = https://zenodo.org/record/894772 }}</ref> More modern research has focused on larger and more integrated systems; by joining action-potential models with models of other parts of the nervous system (such as dendrites and synapses), researchers can study [[neural computation]]{{sfnm|1a1=McCulloch|1y=1988|1pp=19–39, 46–66, 72–141|2a1=Anderson|2a2=Rosenfeld|2y=1988|2pp=15–41}} and simple [[reflex]]es, such as [[escape reflex]]es and others controlled by [[central pattern generator]]s.<ref name="cpg">Getting, PA in {{harvnb|Koch|Segev|1989|loc=''Reconstruction of Small Neural Networks'', pp. 171–194.}}</ref><ref name="pmid10713861" group="lower-alpha">{{cite journal | vauthors = Hooper SL | title = Central pattern generators | journal = Current Biology | volume = 10 | issue = 5 | pages = R176–R179 | date = March 2000 | pmid = 10713861 | doi = 10.1016/S0960-9822(00)00367-5 | citeseerx = 10.1.1.133.3378 | s2cid = 11388348 }}</ref> | ||
| − | + | 数学和计算模型对于理解动作电位是必不可少的,通过将模型产生的预测与实验数据进行比对,为理论提供严格的检验。早期神经模型中最重要和最准确的是 Hodgkin-Huxley 模型,它通过一组四个常微分方程(ODEs)来描述动作电位。<ref name="hodgkin_1952" group="lower-alpha" /> 虽然 Hodgkin-Huxley 模型可能是一个带有限制的简化模型,<ref name=":20" group="lower-alpha" /> 但与实际存在的神经膜相比,它的局限性很小 <ref name=":23" />,其复杂性激发了几个更简化的模型,例如 Morris-Lecar 模型[[Morris–Lecar model|l]]<ref name="morris_1981" group="lower-alpha" /> a和 FitzHugh-Nagumo 模型,<ref name="fitzhugh" group="lower-alpha" /> 这两个模型都只有两个耦合的常微分方程。Hodgkin-Huxley 模型和 FitzHugh-Nagumo 模型以及它们的近亲,如 Bonhoeffer-Van der Pol 模型,<ref name="bonhoeffer_vanderPol" group="lower-alpha" /> 已经在数学中得到了很好的研究,<ref name="math_studies" /><ref name=":21" group="lower-alpha" /> 计算,<ref name="computational_studies" /> 和电子学。<ref name="keener_1983" group="lower-alpha" /> 然而,简单的生成电位和动作电位模型并不能准确地再现近阈值神经元刺激速率和刺激形态,特别是对于机械性受体如帕西尼氏小体(Pacinian corpuscle)<ref name=":24" /> 。更多的现代研究侧重于更大、更完整的系统;通过将动作电位模型与神经系统其他部分的模型(如树突和突触)结合起来,研究人员可以研究神经计算和简单反射,如逃逸反射和其他由中枢模式发生器控制的反射。<ref name="cpg" /><ref name="pmid10713861" group="lower-alpha" /> | |
| − | |||
| − | |||
| − | |||
| − | == References == | + | ==References== |
===Footnotes=== | ===Footnotes=== | ||
{{Reflist|32em}} | {{Reflist|32em}} | ||
2022年7月29日 (五) 21:53的版本
此词条由神经系统中的动力学模型读书会词条梳理志愿者 okxy 翻译审校,未经专家审核,带来阅读不便,请见谅。
生理学上,动作电位(action potential, AP)就是特定细胞位置的膜电位迅速上升又迅速下降的过程[1] :这种去极化(depolarization)会导致相邻位置同样地去极化。动作电位可在神经元、肌肉细胞、内分泌细胞等类型的称为兴奋性细胞(excitable cells)的动物细胞以及某些植物细胞中发生。
在神经元中,动作电位在细胞与细胞之间的通讯中起着中心作用,它可以以跳跃式传导(saltatory conduction )方式,协助神经信号沿着轴突向位于轴突末端的突触扣结(synaptic bouton 或 synaptic knob)传播(propagation);然后信号通过突触传递到其他神经元、运动细胞或腺体。在其他类型的细胞中,它们的主要功能是激活细胞内的反应过程。例如,在肌肉细胞中,动作电位是引起肌肉收缩的一系列事件的第一步。在胰腺的 β 细胞中,它们会刺激胰岛素的释放[lower-alpha 1]。神经元的动作电位也被称为“神经冲动(neural impulse)”或“脉冲(spike)”,神经元产生的动作电位的时间序列被称为“动作电位序列(spike train)”。神经元发出动作电位或神经冲动,也常说神经在“发放(fire)”。
动作电位是由细胞质膜内嵌的特殊类型的电压门控离子通道(voltage-gated ion channel)产生的[lower-alpha 2]。这些通道在膜电位处于细胞的静息电位(一个负数数值)附近时关闭,而在膜电位增加到精确定义的阈电位(threshold voltage)时迅速打开,从而使膜电位去极化[lower-alpha 2]。开放状态的通道让钠离子内流,改变电化学梯度,进而使膜电位趋升于零。这便导致更多的通道打开,产生更大的跨膜电流……这个过程爆发性地发生,直到所有可用的离子通道都打开,从而导致膜电位的大幅上升。钠离子的快速内流导致细胞质膜极性反转,随后离子通道迅速失活。随着钠离子通道的关闭,钠离子不再能进入神经元,然后以主动运输的方式被转运到质膜外。随后,钾离子通道被激活,产生一个外向的钾离子电流,使电化学梯度回到静息状态。动作电位发生后,会有短暂的负移,称为后超极化(afterhyperpolarization)。
动物细胞中存在两种基本类型的动作电位。一种是电压门控钠通道产生的,另一种是电压门控钙通道产生的。钠脉冲通常持续不到一毫秒,而钙脉冲可持续 100 毫秒甚至更长时间。在某些类型的神经元,持续稍久的钙脉冲为钠脉冲的长时间迸发提供驱动力。另一方面,在心肌细胞,初始的快速钠脉冲像“点火器”一样,迅速引发钙脉冲,从而产生肌肉收缩[2]。
概述
动物、植物和真菌的细胞膜几乎都在细胞外部和内部维持一个电压差,称为膜电位(membrane potential)。动物细胞的跨膜电压一般是 -70 mV。这意味着细胞内部相对于外部存在一个负电压。在大多数类型的细胞中,膜电位通常相当稳定。而某些类型的细胞具有电活性,即它们的电压随着时间而波动。在某些类型的有电活性的细胞,包括神经元和肌肉细胞中,电压波动的通常形式为迅速上升而后迅速下降。这些升降的循环即为动作电位。在某些类型的神经元中,整个升降循环在千分之几秒内发生。在肌肉细胞中,典型的动作电位持续时间约为五分之一秒。在其他类型的细胞和植物中,动作电位可能持续三秒或更长时间[3]。
细胞的电特性是由细胞周围的质膜的结构决定的。细胞膜由内嵌更大的蛋白质分子的脂双分子层组成。这种脂双分子层对带电离子的运动产生很强的阻力,因此产生绝缘作用。而质膜内嵌的大蛋白质可作离子的跨膜通道。驱动动作电位的通道蛋白随细胞内外电压差的变化,而在闭合和开放状态的构象之间转换。这些电压敏感蛋白被称为电压门控离子通道。
典型的神经元过程
动物身体组织中的细胞都是电极化的——换句话说,它们维持一个跨细胞质膜的电压差,即所谓的膜电位。这种电极化是嵌入在质膜的蛋白质结构(称为离子泵和离子通道)之间复杂的相互作用中产生的。神经元细胞膜上的离子通道在不同的细胞部位而类型不同,因而树突、轴突和胞体具有不同的电特性。因此,神经元质膜仅在某些部位是可兴奋的(能够产生动作电位)。近年的研究表明,神经元最易兴奋的部位是轴丘(axon hillock,轴突出离胞体的部位)后的部位,称为轴突始段(axonal initial segment),但在大多数情况下轴突和胞体也是可兴奋的[4]。
可兴奋的细胞膜片都有两个重要的膜电位:未受干扰时细胞维持的静息电位(resting potential),和更高值的阈电位。典型神经元的轴丘的静息电位约为 -70 mV,阈值电位约为 -55 mV。神经元的突触输入导致膜去极化或超极化,即它们使膜电位升高或降低。当去极化累积到足以使膜电位达到阈电位时,就会触发动作电位。动作电位被触发时,膜电位猝然上升,随后同样猝然下降,且常降到静息电位以下一段时间。动作电位的波形是固定不变的,这意味着在给定的细胞中,所有动作电位的升降幅度和时间过程大致相同(本文后面将讨论例外情况)。在大多数神经元中,整个过程发生在千分之一秒左右。很多类型的神经元不断地以每秒 10-100 次的速度发放动作电位。而有些类型更安静的细胞,可能持续几分钟或更长时间而不发生任何动作电位。
生物物理基础
动作电位因细胞膜上特殊类型的电压门控离子通道产生[5] 。电压门控离子通道是一种跨膜蛋白,有三关键性质:
- 它能够呈现多种构象。
- 至少一种构象能在膜上形成通道,以渗透特定种类的离子。
- 构象之间的转换受到膜电位的影响。
因此,电压门控离子通道在膜电位处于某些水平时倾向于打开,在其他水平时倾向于关闭。然而,膜电位和离子通道的状态之间在大多数情况下是一种概率关系,并且存在时间延迟。离子通道在不可预测的时间在不同构象之间切换:膜电位决定状态切换速率和单位时间每种切换类型的概率。
电压门控离子通道能够产生动作电位,是因为它们能够产生正反馈回路:膜电位控制离子通道的状态,而离子通道的状态控制膜电位。因此,在某些情况下,膜电位的上升会导致离子通道打开,又导致膜电位的进一步上升。当这种正反馈循环(Hodgkin 循环)爆发性地进行时,就会产生动作电位。电压门控离子通道的生物物理特性决定了动作电位的时间和幅度轨迹。存在几种能产生动作电位所必需的正反馈回路的离子通道。电压门控性钠通道负责神经传导的快速动作电位。肌细胞和某些类型的神经元的稍慢的动作电位是由电压门控钙通道产生的。每种类型都有多种变体,具有不同的电压灵敏度和不同的时间动力学。
研究最多的电压依赖型离子通道是快速神经传导中的钠通道。这些钠离子通道有时被称为 Hodgkin-Huxley 钠离子通道,因为它们是 Alan Hodgkin 和 Andrew Huxley 在他们获得诺贝尔奖的关于动作电位的生物物理研究中首先描述的,但更方便地被称为 NaV 通道(“ v”代表“电压”)。NaV 通道有三种可能的状态,即失活(deactivated)、激活(activated)和灭活(inactivated)。这些通道处于激活状态时,允许钠离子通过。当膜电位低时,通道大部分时间处于失活(关闭)状态。如果膜电位升高到某一水平以上,通道转换到激活(开放)状态的概率增加。膜电位越高,激活的可能性就越大。通道一旦被激活,最终会转换到灭火(关闭)状态,并倾向在一段时间内保持灭活状态;如果膜电位再次变低,通道最终会转换到失活状态。在动作电位发生过程中,大多数这种类型的通道经历失活→激活→灭活→失活的循环过程。然而这只是群体平均行为——理论上单个通道可在任何时刻发生任何转换。然而,通道从灭活状态直接转换到激活状态的概率极低:处于灭活状态的通道是不应的,直到它回到灭活状态。
这些的结果是,NaV 通道的动力学决定于状态转换矩阵,其中转换速率以一种复杂的方式依赖于电压。由于这些通道本身在决定电位中起着重要作用,系统的全局动力学可能很难计算出来。为了解决这个问题,Hodgkin 和 Huxley 为决定离子通道状态的参数建立了一组微分方程,称为 Hodgkin-Huxley 方程(Hodgkin-Huxley equations)。这些方程在后续的研究被修正了很多,但构成很多动作电位生物物理学的理论研究的起点。

随着膜电位的增加,钠离子通道打开,允许钠离子进入细胞。随后钾离子通道打开,允许钾离子流出细胞。钠离子内流增加了细胞中带正电荷的阳离子的浓度,导致去极化,这时细胞的电位高于细胞的静息电位。钠离子通道在动作电位峰值处关闭,而钾离子继续流出细胞。钾离子外流会降低细胞的膜电位或使细胞超极化。膜电位比静息电位高一点时,钾电流超过钠电流,而恢复到正常的静息值,通常为 -70 mV。然而,如果电位增加超过一个关键阈值,通常高于静息值 15 mV,钠电流将占主导地位。这就导致了一种失控的情况,即钠电流的正反馈激活了更多的钠通道。因此,细胞发放,产生动作电位。神经元诱发动作电位的频率通常被称为发放频率或神经放电频率。
在动作电位过程中,电压门控通道的开放所产生的电流通常明显大于起初的刺激电流。因此,动作电位的幅度、持续时间和波形在很大程度上取决于可兴奋膜的性质,而不是刺激的幅度或持续时间。动作电位的这种全或无的特性使它有别于受体电位(receptor potentials)、电紧张电位(electrotonic potentials)、阈下膜电位振荡(subthreshold membrane potential oscillations)和突触电位(synaptic potentials)等随刺激强度变化的级量电位(graded potential)。取决于电压门控通道的类型、漏电通道、通道分布、离子浓度、膜电容、温度等因素,许多细胞类型和细胞分区中存在多种动作电位类型。
与动作电位有关的主要离子是钠离子和钾离子;钠离子进入细胞,钾离子流出,恢复平衡。只需相对很少的离子跨膜就能引起膜电位剧烈的变化。因此,在动作电位期间交换的离子对内部和外部离子浓度的改变微不足道。少数跨膜的离子通过钠钾泵的连续作用再次泵出,钠钾泵与其他离子转运蛋白一起,维持了跨膜离子浓度的正常比例。钙离子和氯离子参与了几种类型的动作电位,比如分别参与心肌动作电位和单细胞的伞藻的动作电位。
虽然动作电位是在可兴奋的膜片上局部产生的,但由此产生的电流可以触发相邻膜片上的动作电位,促成多米诺骨牌般的传播。与被动传播的电位(电紧张电位)不同,动作电位沿着可兴奋的细胞膜重新产生,并且不衰减地传播[6]。轴突的有髓鞘区域不可兴奋,不产生动作电位,信号被动地以电紧张电位的形式传播。在郎飞节,即规律性间隔的无髓鞘膜片,产生动作电位来增强信号。这种类型的信号传播被称为跳跃式传导,是在信号传播速度和轴突直径之间的折衷。轴突末梢的去极化通常触发神经递质释放进入突触间隙。此外,在新皮层广泛存在的锥体神经元的树突中也记录到了反向传播的动作电位[lower-alpha 3]。这些都被认为脉冲时序依赖的突触可塑性(STDP, Spike-timing-dependent_plasticity)中起着重要作用。
在 Hodgkin-Huxley 膜电容模型中,动作电位的传输速度没有定义,而是假设附近区域受邻近通道释放的离子干扰而去极化。离子扩散和半径的测量表明这是不可能的。此外,对熵变和时序的测量中的矛盾,对电容模型是独立工作的产生质疑。另外,Gilbert Ling 的吸附假说认为活细胞的膜电位和动作电位是由于活动离子吸附在细胞的吸附位点上.[7]。
动作电位的电性质的成熟
神经元产生和传播动作电位的能力在发育过程中发生变化。神经元在电流脉冲作用下的膜电位变化量是膜输入电阻的函数。随着细胞的生长,膜上添加了更多的通道,导致输入电阻减小。一个成熟的神经元在突触电流的作用下,膜电位也会发生更短时间的变化。雪貂外侧膝状核的神经元在 P0 时比在 P30 时有更长的时间常数和更大的电压偏转[8] 。动作电位持续时间减少的一个后果是,可以保持高频刺激的反应信号的保真度。高频刺激后,未成熟神经元更容易发生突触抑制而非增强[8] 。
在许多生物体的早期发育过程中,动作电位实际上最初是由钙电流而不是钠电流携带的。发育过程中钙离子通道的开闭动力学比电压门控钠离子通道的开闭动力学要慢,而电压门控钠离子通道是成熟神经元的动作电位。钙离子通道的开放时间越长,动作电位的速度就会比成熟神经元慢得多[8] 。非洲爪蟾(Xenopus)神经元最初的动作电位需要 60-90 毫秒。在发育过程中,这个时间减少到 1 毫秒。这种急剧下降有两个原因。首先,向内的电流主要由钠离子通道输送 [9] 。其次,延迟整流器——一种钾离子通道电流——增加到最初强度的 3.5 倍 [8] 。
为了使钙离子依赖的动作电位转变为钠离子依赖的动作电位,膜上必须增加新的通道。如果非洲爪蟾神经元生长在有 RNA 合成抑制剂或蛋白质合成抑制剂的环境中,这种转变就被阻止了 [10]。甚至细胞本身的电活动也可能在通道的表达中发挥作用。如果阻断非洲爪蟾心肌细胞的动作电位,通常发生的钠和钾电流密度增加就会被阻止或延迟 [11]。
在不同物种中都可观察到这种电特性的成熟过程。非洲爪蟾的钠和钾电流在神经元进入有丝分裂的最后时相后急剧增加。大鼠大脑皮层神经元的钠电流密度在刚出生的 2 周内增加 600% [8]。
神经传递
神经元的解剖学
有几类细胞可以产生动作电位,比如植物细胞、肌肉细胞和心脏中的特化细胞(在这些细胞中发生心肌动作电位)。然而,最主要的兴奋性细胞是神经元,其亦具有最简单的动作电位机制。
神经元是电兴奋型细胞,一般包含一个或多个树突、一个胞体、一个轴突以及一个或多个轴突末梢。树突是细胞的突起,其主要功能是接收突触信号。突触上的突起被称为树突棘,用来捕获突触前神经元释放的神经递质。其上分布有高密度的配体门控离子通道。这些棘有一个细细的颈部,连接球状突起和树突。这确保树突棘内部发生的变化不太可能影响邻近的树突棘。树突棘除了极少数例外情况(见 LTP),可以作为一个独立的单位工作。树突从胞体延伸出来,胞体是细胞核和许多“正常”的真核细胞器的所在。与树突棘不同,胞体的表面布满了电压可激活的离子通道。这些通道帮助传输由树突产生的信号。从胞体延伸出来的是轴丘。这个区域的特征是有非常高浓度的电压激活钠离子通道。一般认为它是动作电位的起始区,或触发区。在树突棘处产生的多个信号,经胞体传输而汇聚于此。轴丘之后便是轴突。这是一个从胞体中延伸出来的细管状突起。轴突被髓鞘(myelin)绝缘。髓鞘由神经胶质细胞组成,在外周神经系统是施万细胞,在中央神经系统为少突胶质细胞。虽然神经胶质细胞不参与电信号的传递,但可以与神经元通讯和提供重要的生化支持。具体来说,髓鞘绕着轴突多重包裹,形成一层厚厚的脂肪层,阻止离子进入或逃离轴突。这种绝缘可以避免信号发生剧烈的衰减,并确保信号更快速地传播;但同时会限制轴突表面,使其没有离子通道。因此,在轴突上每隔一段就会有块不带绝缘层的膜片。这些郎飞结(nodes of Ranvier)可以被认为是“迷你轴丘”,因为其目的是增强信号,以避免明显的信号衰减。在最远端,轴突失去绝缘的髓鞘,并开始分支成几个轴突末梢。这些突触前末梢,或称突触扣结,是突触前细胞轴突内的一个特殊区域,其中包含神经递质,这些神经递质被包装在称为突触小泡的膜包裹的小球内。
动作电位的触发
动作电位沿轴突传播并终于突触扣结之前,要先在轴丘触发。触发的基本条件就是轴丘的膜电位提高到动作电位发放的域值以上。存在几种去极化的方式。
动作电位的动力学
动作电位多是由突触前神经元引起的兴奋性突触后电位(excitatory postsynaptic potentials)引起的。一般地,神经递质分子由突触前神经元释放后,与突触后细胞上的受体结合。这种结合打开了各种类型的离子通道,能够改变细胞膜的局部通透性,从而改变膜电位。如果这种结合提高膜电位(去极化),则突触是兴奋性的;而如果这种结合降低膜电位(使细胞膜超极化),它就是抑制性的。无论是升高还是降低,膜电位的变化都会被动传播到邻近区域的膜上(如电缆方程(cable equation )及其改进所刻画的),并且通常随着与突触的距离以及与神经递质结合后的时间呈现指数衰减。少量兴奋性电位可传至轴丘,并且(在极少情况下)使膜足够去极化以引发新的动作电位。更常见的是,从多个突触传来的兴奋性电位必须几乎同时作用才能引发一个新的动作电位。当然,这种共同作用也可能被反作用的抑制性突触后电位(inhibitory postsynaptic potentials)所阻。
神经传导也可通过电突触(electrical synapse)进行。兴奋性细胞之间以缝隙连接(gap junction)的形式直接相连,动作电位可以从一个细胞直接传递到下一个细胞。离子在细胞之间的自由流动使得非化学介导的快速传输成为可能。整流通道确保动作电位通过电突触单向移动。电突触存在于所有神经系统,包括人脑中,尽管它们只占很少部分。
“全或无”律
动作电位的幅度(amplitude)与引起动作电位的电流的大小无关。换句话说,更大的电流不会产生更大幅度的动作电位。因此,动作电位被称为全或无(all-or-none)信号,因为它们要么完全发生,要么根本不发生。[lower-alpha 4][lower-alpha 5][lower-alpha 6] 这与受体电位不同,受体电位的幅度取决于刺激的强度。这两种情况下,动作电位的频率都与刺激的强度相关。
感觉神经元
在感觉神经元(sensory neurons)中,压力、温度、光或声音等外部信号与离子通道的开关相耦联,进而改变细胞膜的离子通透性和电位。这些电位变化可以是兴奋性的(去极化)或抑制性(超极化)的,在某些感觉神经元中,不同突触电位的合力使轴丘足够去极化以引起动作电位。比如分别在人类嗅觉和触觉中至关重要的嗅觉感觉神经元和迈斯纳氏小体(Meissner's corpuscle)。然而,并不是所有的感觉神经元都将外部信号转换成动作电位,有些甚至没有轴突。而是将信号转换成一种神经递质的释放,或者转换成连续的级量电位,这两种都可以刺激后续的神经元发放动作电位。例如,人耳中的毛细胞将传入的声音转换成机械门控离子通道(mechanically gated ion channels)的开关,这可导致神经递质分子的释放。同样,在人类视网膜中,第一层光敏感的感光细胞以及第二层的双极细胞(bipolar cells)和水平细胞(horizontal cells)不产生动作电位;只有一些无长突细胞(amacrine cell)和第三层的神经节细胞(ganglion cells)产生动作电位,并沿视神经传递。
起搏电位
感觉神经元中,动作电位是由外部刺激引起的。然而,一些兴奋性细胞不需要这样的刺激就可以发放动作电位:它们自发地使轴丘去极化,以特定的速率发放动作电位,像内部时钟一样。这种细胞的电位变化称为起搏电位(pacemaker potentials)。心脏窦房结( sinoatrial node)的心肌起搏细胞(cardiac pacemaker cells)就是一个很好的例子。[lower-alpha 7] 虽然这种起搏电位有其自然节奏,但可以通过外部刺激进行调节;例如,药物以及交感神经和副交感神经发出的信号可以改变心率。外部刺激不是引起细胞动作电位的连续性发放,仅是改变其节奏。某些情况下,存在对发放频率更为复杂的调节,引起特定的动作电位模式,比如爆发(bursting)。
动作电位的相位
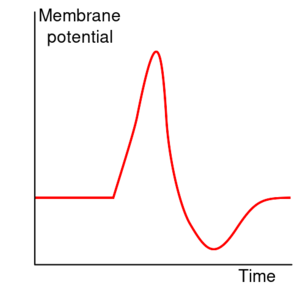
动作电位可分为五个阶段:上升相(the rising phase)、峰值相(the peak phase)、下降相(the falling phase)、下冲相(the undershoot phase)和不应期(the refractory period)。在上升相,膜电位去极化(正向变化)。去极化停止的点称为峰值相。在这个阶段,膜电位达到了最大值。在这之后就是下降相,膜电位负向变化,下降趋于静息电位。下冲(undershoot)或后超极化(afterhyperpolarization)相是膜电位短暂变得比静息时还负(超极化)的时期。最后,不能或很难继续发放动作电位的时期被称为不应期,可与其他阶段存在重叠。
动作电位的过程是由两个耦合的效应决定的。首先,膜电位的变化引起电压敏感离子通道的开关,进而改变了膜对这些离子的渗透性。其次,根据戈德曼方程(Goldman equation),这种渗透性的变化改变了平衡电位 Em,从而改变了膜电位。[lower-alpha 8] 因此,膜电位影响渗透性,其又进一步影响膜电位。这就为正反馈(positive feedback)创造了条件,而正反馈正是动作电位上升相的关键。更复杂的是,一个离子通道可能有多个内“门”,对 Vm 以相反的方式或不同速率做出反应。[lower-alpha 9] 例如,尽管提高 Vm 能打开电压敏感钠通道中的大多数门,但它也缓慢地关闭通道的“失活门(inactivation gate)”。因此,当 Vm 突然升高时,钠离子通道一开始打开,然后因较慢的失活而关闭。
Alan Lloyd Hodgkin 和 Andrew Huxley 在 1952 年建立了动作电位各个阶段的电压和电流的精确模型 [lower-alpha 9] 并因此获得 1963 年诺贝尔生理学或医学奖。[lower-Greek 1] 然而,他们的模型只考虑了两种类型的电压敏感性离子通道,并对齐提出几个假定条件,比如,通道内的各门的打开和关闭是相互独立的。实际上,离子通道有很多种类型,[12] 且并不总是独立打开和关闭的。[lower-alpha 10]
刺激和上升相
动作电位通常因刺激提高了 Vm 等因素使轴丘足够去极化而发生。这种去极化通常是由细胞注入额外的钠离子等阳离子引起的;这些阳离子有多种来源,如化学突触、感觉神经元或起搏电位。
对于处于静息状态的神经元来说,细胞外液的钠离子和氯离子浓度高于细胞内液中,而细胞内液的钾离子浓度高于细胞外液。使离子从高浓度向低浓度移动的浓度差,以及静电作用(相反电荷的吸引)决定离子流出或流入神经元。由于细胞的 K+ 外流,神经元内部相对于外部带负电。神经元的细胞膜对 K+ 的渗透性比其他离子更强,使得这种离子能够选择性地顺着浓度梯度流出细胞。这种浓度梯度以及神经元膜上的钾离子泄漏通道(potassium leak channel)导致钾离子外流,使静息电位接近 EK ≈ -75 mV。由于钠离子在细胞外的浓度较高,当钠离子通道打开时,浓度差和电位差都驱使其进入细胞。去极化打开了细胞膜上的钠通道和钾通道,允许离子分别流入和流出轴突。如果去极化很小(比方说,把 Vm 从 -70 mV 增加到 -60 mV),外向的钾电流大过内向的钠电流,膜复极化回到正常的静息电位 -70 mV 左右。然而,当去极化足够大时,内向钠电流的增加大于外向钾电流,出现了失控(正反馈)现象:内向钠电流越大, Vm 越是升高,其反过来又进一步增加内向钠电流。足够强的去极化( Vm 的增加)使电压敏感的钠通道开放,钠的渗透性增加使 Vm 趋向钠平衡电位 ENa ≈ +55 mV。电位增加进而导致更多的钠离子通道打开,这使得 Vm 更趋近 ENa。这种正反馈持续到钠离子通道完全打开,Vm 接近 ENa。Vm 和钠通透性的骤然上升与动作电位的上升相是对应的。
这种失控状态的临界阈值电位通常在 -45 mV 左右,但这取决于轴突最近的活动。刚发放过动作电位的细胞不能立即发放新的动作电位,因为 Na+ 通道还没有从失活状态恢复过来。不能发放新的动作电位的这段时间叫做绝对不应期(absolute refractory period)。在部分的离子通道恢复后,轴突可以被刺激产生新的动作电位,但需要更高的阈值电位,即需要更强的去极化,比如 -30 mV。很难触发动作电位的时期称为相对不应期(relative refractory period)。
峰值相
随着钠离子通道最大程度地开放,上升相的正反馈变慢并停止。在动作电位峰值,钠离子的渗透性最大,膜电位 Vm 几乎等于钠离子的平衡电压 ENa。然而,最初打开钠离子通道的膜电位上升也通过关闭通道孔而慢慢关闭通道;钠离子通道失活。这降低了细胞膜钠离子相对于钾离子的通透性,使膜电位重新回到静息值。同时,膜电位上升打开了电压敏感性钾离子通道,膜的钾离子通透性增加促使 Vm 向 EK 方向变化。这些钠离子与钾离子的通透性的变化使 Vm 迅速下降,使膜复极化,产生动作电位的“下降相”。
后超极化
去极化电位使额外的电压依赖性钾离子通道打开,但当膜恢复至正常的静息电位时,其中一些通道不会立即关闭。此外,在动作电位过程中,钙离子内流会引起更多的钾离子通道打开。细胞内钾离子浓度短暂地变得极低,使膜电位 Vm 更加接近钾离子平衡电位 EK,甚至低于静息膜电位。因此,存在一个下冲(undershoot)或超极化(hyperpolarization)称为后超极化,持续到膜的钾离子通透性恢复到正常值,恢复膜电位到静息状态。
不应期
每个动作电位后都接着一个不应期,这个不应期可以分绝对不应期和相对不应期。在绝对不应期,完全不能触发新的动作电位;在随后的相对的不应期,需要异常强的刺激才能引发动作电位。两个不应期是由钠离子和钾离子通道的分子状态变化造成的。在动作电位后关闭的钠通道进入“失活”状态,不管膜电位如何钠通道都不能被打开ーー这就产生了绝对不应期。即使有足够数量的钠离子通道已经过渡到其静息状态,但往往仍有部分的钾离子通道是开放的,这使得膜电位很难去极化,从而导致相对不应期。因为钾离子通道的密度和亚型在不同类型的神经元之间可能有很大的差异,相对的不应期的持续时间是高度可变的。
因为绝对不应期,动作电位沿轴突的传播是单向的。动作电位传播中的任一时刻,轴突上正在发放的位置后面是不应激的,而前方的膜片因为近期没有被激活,能够被动作电位的去极化刺激。
动作电位的传播
轴丘产生的动作电位像波一样沿轴突传播。动作电位的膜内向电流会沿着轴突扩散,并使邻近的细胞膜去极化。足够强的去极化则会引起邻近的膜片发放类似的动作电位。Alan Lloyd Hodgkin 在 1937 年证明了这种基本的机制。他发现挤压(crushing)或冷却(cooling)神经节段,从而阻断动作电位,而传至阻断部位一侧的动作电位可以引发另一侧的动作电位,只要阻断的节段足够短。[lower-alpha 11]
Once an action potential has occurred at a patch of membrane, the membrane patch needs time to recover before it can fire again. At the molecular level, this absolute refractory period corresponds to the time required for the voltage-activated sodium channels to recover from inactivation, i.e., to return to their closed state.模板:Sfn There are many types of voltage-activated potassium channels in neurons. Some of them inactivate fast (A-type currents) and some of them inactivate slowly or not inactivate at all; this variability guarantees that there will be always an available source of current for repolarization, even if some of the potassium channels are inactivated because of preceding depolarization. On the other hand, all neuronal voltage-activated sodium channels inactivate within several milliseconds during strong depolarization, thus making following depolarization impossible until a substantial fraction of sodium channels have returned to their closed state. Although it limits the frequency of firing,模板:Sfn the absolute refractory period ensures that the action potential moves in only one direction along an axon.模板:Sfn The currents flowing in due to an action potential spread out in both directions along the axon.模板:Sfn However, only the unfired part of the axon can respond with an action potential; the part that has just fired is unresponsive until the action potential is safely out of range and cannot restimulate that part. In the usual orthodromic conduction, the action potential propagates from the axon hillock towards the synaptic knobs(the axonal termini); propagation in the opposite direction—known as antidromic conduction—is very rare.模板:Sfn However, if a laboratory axon is stimulated in its middle, both halves of the axon are "fresh", i.e., unfired; then two action potentials will be generated, one traveling towards the axon hillock and the other traveling towards the synaptic knobs.
细胞膜片上一旦发生动作电位,膜片需要时间恢复才能再次激活。在分子水平上,这个绝对不应期对应于电压激活的钠离子通道从失活状态恢复到关闭状态所需的时间。神经元中存在多种类型的电压激活钾通道。其中一些迅速失活(A 型电流),一些缓慢失活或从不失活;这种变异性保证了,即使一些钾离子通道因去极化而失活,总有电流来源使膜复极化。另一方面,去极化较强时,神经元所有的电压激活钠通道在几毫秒内失活,从而使去极化不可能发生,直到相当一部分的钠通道恢复到关闭状态。绝对不应期虽然限制了发放频率,但确保了动作电位沿轴突单向传播。动作电位产生的电流会沿轴突双向扩布。然而,只有未发放的轴突部位才能作出动作电位的反应;刚刚发放过的部位是没有反应的,直到动作电位移到安全范围,不能再刺激该部位。在通常的正向传导(orthodromic conduction)中,动作电位从轴丘向突触扣结(轴突末梢)传导,向相反方向传导的反向传导(antidromic conduction)现象非常罕见。不过,如果实验中从中间刺激轴突,两边的轴突都是“新鲜的”,即未被刺激,那么就会产生两个动作电位,一个传向轴丘,另一个传向突触扣结。
髓鞘和跳跃式传导
为了在神经系统中快速高效地传递电信号,某些神经元的轴突上覆有髓鞘(myelin sheath)。髓鞘是多层膜,将轴突逐段包裹起来,段的间隔被称为郎飞结。它由专门的细胞产生:周围神经系统中是施万细胞(Schwann cells),中央神经系统中是少突胶质细胞(oligodendrocytes)。髓鞘减少了膜电容,并增加结间段的膜电阻,从而让动作电位在郎飞结之间快速、跳跃式的移动。[lower-alpha 12][lower-alpha 13][lower-alpha 14] 髓鞘形成(myelination)主要存在于脊椎动物,不过一些无脊椎动物也有类似的系统,比如某些种类的虾。[lower-alpha 15] 脊椎动物中并不是所有的神经元都有髓鞘;例如,组成自主神经系统的神经元的轴突一般都没有髓鞘。髓鞘阻止了离子从髓鞘包裹的轴突部位出入。一般地,髓鞘增加了动作电位的传导速度,使其能效更高。不管是否跳跃,动作电位的平均传导速度范围从 1 米每秒(m/s)到 100 m/s 以上,一般而言,随轴突直径的增大而增大。[lower-alpha 16]
动作电位不能在有髓鞘的轴突段的膜上传播。不过,电流经细胞质传输,足以使后面的一两个郎飞结去极化。就是说,一个郎飞结的动作电位产生的离子电流在下一个郎飞结引起另一个动作电位;动作电位的这种看似在郎飞结之间“跳跃”被称为跳跃式传导。跳跃式传导的机制在 1925 年就由 Ralph Lillie 提出,[lower-alpha 17] 但其首个实验证据来自 Ichiji Tasaki [lower-alpha 18] 和 Taiji Takeuchi [lower-alpha 19][13] 以及 Andrew Huxley 和 Robert Stämpflii。[lower-alpha 20] 而在无髓鞘的轴突,动作电位在紧邻的膜上引起另一个动作电位,并像波一样沿着轴突不断地移动。
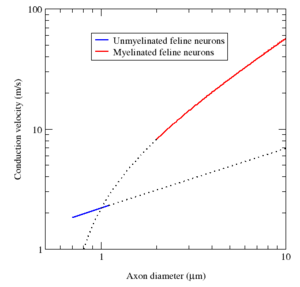
髓鞘具有两个重要的优势:传导速度快和能效高。粗于一个最小直径(大约 1 微米)的轴突,髓鞘通常能让动作电位的传导速度增加十倍。[lower-alpha 22] 反之,相同的传导速度,有髓鞘的神经纤维比无髓的更细。例如,有髓鞘的蛙轴突和无髓鞘的乌贼巨轴突(squid giant axon)的动作电位传导速度大致相同(25 米/秒),但是青蛙的轴突直径要小 30 倍,横截面积要小 1000 倍。此外,因为离子电流被局限于郎飞结,离子的跨膜“泄漏”要少得多,节省了新陈代谢能量。考虑到人类神经系统消耗大约 20% 的身体代谢能量,这种节省有显著的选择优势(selective advantage)。[lower-alpha 22]
髓鞘包裹的轴突节段的长度对跳跃式传导的成功至关重要。它们应尽可能长,以最大限度地提高传导速度,但不能太长,以至于传过去的信号太弱,无法在下一个郎飞结触发动作电位。在自然界中,有髓鞘节段通常足够长,使信号被动传播至少两个结点而仍有足够的强度在第二、三结点触发动作电位。因此,跳跃式传导的安全系数很高,可以绕过损伤的郎飞结继续传播。然而,动作电位可能在安全系数较低的某些位置过早终止,即使在无髓神经元中也是如此;一个常见的例子是轴突分支成两个轴突的分支点。
有些疾病会降解髓鞘,破坏跳跃式传导,降低动作电位的传导速度。[lower-alpha 23] 其中最被人所知的是多发性硬化症(multiple sclerosis),髓鞘的降解削弱协调运动。[14]
电缆学说
The flow of currents within an axon can be described quantitatively by cable theory[15] and its elaborations, such as the compartmental model.[16] Cable theory was developed in 1855 by Lord Kelvin to model the transatlantic telegraph cable[lower-alpha 24] and was shown to be relevant to neurons by Hodgkin and Rushton in 1946.[lower-alpha 25] In simple cable theory, the neuron is treated as an electrically passive, perfectly cylindrical transmission cable, which can be described by a partial differential equation[15]
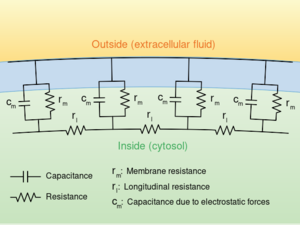
轴突内电流的流动可以用电缆理论(cable theory)[15] 及其细化模型,如房室模型(compartmental model)来定量描述。[16] 电缆理论是 Lord Kelvin 在 1855 年提出的,用来对跨大西洋电报电缆进行建模 [lower-alpha 24],并于 1946 年被 Hodgkin 和 Rushton 证明描述神经元也很有用。[lower-alpha 25] 简单的电缆理论中,神经元被看作是一个电被动的完美圆柱形的传输电缆,可用一个偏微分方程来描述[15]
- [math]\displaystyle{ \tau \frac{\partial V}{\partial t} = \lambda^2 \frac{\partial^2 V}{\partial x^2} - V }[/math]
where V(x, t) is the voltage across the membrane at a time t and a position x along the length of the neuron, and where λ and τ are the characteristic length and time scales on which those voltages decay in response to a stimulus. Referring to the circuit diagram on the right, these scales can be determined from the resistances and capacitances per unit length.模板:Sfn
其中 V(x, t) 是时间 t 和沿神经元长度的位置 x 的跨膜电压,其中 λ 和 τ 是特征长度和时间尺度,对刺激的反应电位以这些尺度发生衰减。参考右边的电路图,这些尺度可以通过单位长度的电阻和电容来确定。
- [math]\displaystyle{ \tau =\ r_m c_m \, }[/math]
- [math]\displaystyle{ \lambda = \sqrt \frac{r_m}{r_\ell} }[/math]
These time and length-scales can be used to understand the dependence of the conduction velocity on the diameter of the neuron in unmyelinated fibers. For example, the time-scale τ increases with both the membrane resistance rm and capacitance cm. As the capacitance increases, more charge must be transferred to produce a given transmembrane voltage (by the equation Q = CV); as the resistance increases, less charge is transferred per unit time, making the equilibration slower. In a similar manner, if the internal resistance per unit length ri is lower in one axon than in another (e.g., because the radius of the former is larger), the spatial decay length λ becomes longer and the conduction velocity of an action potential should increase. If the transmembrane resistance rm is increased, that lowers the average "leakage" current across the membrane, likewise causing λ to become longer, increasing the conduction velocity.
这些时间尺度和长度尺度可以用来理解无髓鞘纤维中传导速度依赖于神经元直径。比如,时间尺度 τ 随着膜电阻 rm 和膜电容 cm 的增大而增大。随着电容的增加,(根据公式 Q = CV)必须转移更多的电荷才能产生给定的跨膜电压;随着电阻的增加,每单位时间转移的电荷越少,越慢恢复平衡。同样,如果一个轴突的单位长度 ri 低于另一个轴突(比如,因为前者的半径较大),空间衰减长度 λ 变长,动作电位的传导速度应该增加。如果跨膜电阻 rm 增大,降低平均跨膜“泄漏”电流,同样导致 λ 变长,增加了传导速度。
动作电位的终止
化学突触
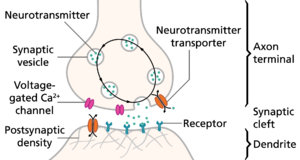
一般而言,到达突触扣结(synaptic knobs)的动作电位会使神经递质释放到突触间隙。[lower-alpha 26] 神经递质是可以打开突触后细胞离子通道的小分子;大多数轴突的所有末梢都有相同的神经递质。传来的动作电位打开了突触前膜上的电压敏感性钙通道,钙内流导致充满神经递质的突触囊泡(vesicle)迁移到细胞表面,并将其内容物释放到突触间隙(synaptic cleft)。[lower-alpha 27] 引起破伤风(tetanus)的破伤风痉挛毒素(tetanospasmin)和引起肉毒中毒( botulism)的肉毒杆菌毒素(botulinum toxin)等神经毒素会抑制这一复杂的过程。[lower-alpha 28]
电突触
有些突触不用“中间人”——神经递质,而将突触前细胞和突触后细胞连接起来。[lower-alpha 29] 当动作电位达到这样的突触时,流入突触前细胞的离子电流可以穿过两个细胞膜的屏障,通过称为连接子(connexon)的孔进入突触后细胞。[lower-alpha 30] 因此,突触前动作电位的离子电流可以直接刺激突触后细胞。电突触允许更快的传递,因为它们不需要神经递质在突触间隙中的缓慢扩散。因此,当快速反应和同步性协调非常重要的地方,就会使用电突触,例如在逃跑反射、脊椎动物的视网膜和心脏中。
神经肌肉接头
化学突触有个特例,就是运动神经元轴突末梢与肌纤维形成的神经肌肉接头(neuromuscular junction)。[lower-alpha 31] 运动神经元释放神经递质乙酰胆碱(acetylcholine),结合到肌膜(sarcolemma)上的内在膜蛋白乙酰胆碱受体(acetylcholine receptor)。[lower-alpha 32] 不过,乙酰胆碱结合后又很快解离并被位于突触中的乙酰胆碱酯酶(acetylcholinesterase)水解。这种酶能迅速减少对肌肉的刺激,从而使肌肉收缩的程度和时间受到精细的调控。一些毒药,例如神经毒剂沙林(sarin)和塔崩(tabun),[lower-alpha 33] 以及杀虫剂二嗪农(diazinon)和马拉硫磷(malathion),会使乙酰胆碱酯酶失活,从而阻断这种控制。[lower-alpha 34]
其他细胞类型
心肌动作电位
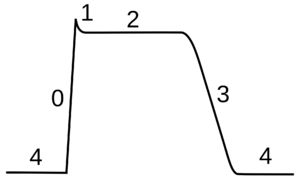
心肌动作电位与神经元动作电位的不同之处在于,心肌动作电位有一个延长的平台期,即膜会保持几百毫秒高电位之后,才被钾电流复极化。[lower-alpha 35] 这个平台是慢速钙通道打开的作用,使膜电位在钠通道失活之后,仍保持在其平衡电位附近。
心肌动作电位在协调心脏收缩中起着重要作用。窦房结的心肌细胞提供了同步心脏的起搏电位。[lower-alpha 35] 这些细胞的动作电位传导到并通过房室结(atrioventricular node)——心房和心室之间唯一的传导通路。房室结的动作电位通过希斯氏束(bundle of His)传递到浦肯野纤维(Purkinje fibers)。相对的,心肌动作电位的异常ーー无论是由于先天性基因突变还是损伤ーー都可能导致人类疾病,尤其是心律失常。[lower-alpha 35] 几种抗心律失常药物作用于心肌动作电位,如奎尼丁(quinidine)、利多卡因(lidocaine)、 β 受体阻滞剂(beta blockers)和维拉帕米(verapamil)。[lower-alpha 36]
肌肉动作电位
正常的骨骼肌细胞的动作电位与神经元的动作电位相似。动作电位是细胞膜(肌膜)去极化的结果,这种去极化开启了电压敏感的钠通道;这些电压敏感的钠通道失活,膜通过钾离子外向复极化。动作电位之前的静息电位通常是 -90mV,比典型的神经元稍微负。肌肉动作电位持续时间约为 2-4 ms,绝对不应期约为 1-3 ms,肌肉传导速率约为 5 m/s。动作电位释放钙离子,释放原肌球蛋白(tropomyosin),使肌肉收缩。肌肉动作电位是由突触前神经元动作电位传至神经肌肉接头引起的。神经肌肉接头是很多神经毒素的共同靶点。[lower-alpha 33]
植物动作电位
植物和真菌细胞[lower-alpha 37] 也是电兴奋性的。与动物动作电位的根本区别在于,植物细胞的去极化不是通过摄入带正电的钠离子,而是通过释放带负电的氯离子来完成的。[lower-alpha 38][lower-alpha 39] 1906 年,J. C. Bose 发表了对先前由 Burdon-Sanderson 和 Darwin 发现的植物动作电位 [17] 进行首次测量的结果。细胞质中钙离子的增加可能是阴离子释放进入细胞中的原因。因此,钙是离子移动的前体,比如大麦(barley)叶中负氯离子的内流和正钾离子的外流时。[18]
The initial influx of calcium ions also poses a small cellular depolarization, causing the voltage-gated ion channels to open and allowing full depolarization to be propagated by chloride ions.
钙离子的初始注入也使细胞些许去极化,导致电压门控离子通道打开并让氯离子流动产生完全的去极化。
一些植物(例如捕蝇草(Dionaea muscipula,也叫 Venus flytrap))使用钠门控的通道操作运动,本质上是“计数”。捕蝇草可以在北卡罗来纳州和南卡罗来纳州的亚热带湿地见到。[19] 当土壤养分不足时,捕蝇草依靠昆虫和动物为食。[20] 尽管对这种植物进行了研究,但对于捕蝇草以及一般的食肉植物的分子机制还缺乏了解。[21]
不过,已经有很多关于捕蝇草的动作电位及其对捕蝇草的运动和机械原理的作用研究。首先,捕蝇草的静息膜电位(-120 mV)低于动物细胞(通常为 -90 mV 至 -40 mV)。[21][22] 更低的静息电位使得动作电位更容易激发。因此,当一只昆虫落在植物的陷阱上时,它就会触发一个毛发样的机械感受器。[21] 这个受体激活一个持续约 1.5 毫秒的动作电位。[23] 最终,这会导致钙离子进入细胞,使细胞稍微去极化。
However, the flytrap doesn't close after one trigger. Instead, it requires the activation of 2 or more hairs.[20][21] If only one hair is triggered, it throws the activation as a false positive. Further, the second hair must be activated within a certain time interval (0.75 s - 40 s) for it to register with the first activation.[21] Thus, a buildup of calcium starts and slowly falls from the first trigger. When the second action potential is fired within the time interval, it reaches the Calcium threshold to depolarize the cell, closing the trap on the prey within a fraction of a second.[21]
然而,捕蝇草不会在一次触发后闭合,而是需要激活 2 根或更多的毛。[20][21] 如果只有一根毛被触发,这个激活会被视为假阳性。而且第二根毛必须在一定的时间间隔(0.75 s - 40 s)内被激活,才能将其与第一次激活一起记录。[21] 因此,钙的积累从第一次触发开始并且然后慢慢下降。当第二个动作电位在时间间隔内被激发时,它达到钙阈值使细胞去极化,在几分之一秒内关闭捕获物的陷阱。[21]
Together with the subsequent release of positive potassium ions the action potential in plants involves an osmotic loss of salt (KCl). Whereas, the animal action potential is osmotically neutral because equal amounts of entering sodium and leaving potassium cancel each other osmotically. The interaction of electrical and osmotic relations in plant cells[lower-alpha 40] appears to have arisen from an osmotic function of electrical excitability in a common unicellular ancestors of plants and animals under changing salinity conditions. Further, the present function of rapid signal transmission is seen as a newer accomplishment of metazoan cells in a more stable osmotic environment.[24] It is likely that the familiar signaling function of action potentials in some vascular plants (e.g. Mimosa pudica) arose independently from that in metazoan excitable cells.
随着随后释放的阳性钾离子,动作电位在植物中涉及盐(KCl)渗透损失。然而,动物的动作电位是渗透中性的,因为等量的钠进入和钾离开相互抵消渗透。植物细胞[lower-alpha 40]中电和渗透关系的相互作用似乎起源于盐度变化条件下动植物共同的单细胞祖先的电兴奋渗透作用。此外,目前的快速信号传递功能被认为是后生动物细胞在更稳定的渗透环境中更新的成就.[24] 。在一些维管植物中,动作电位的常见信号功能可能是。含羞草(Mimosa putica)是独立于后生动物兴奋细胞而产生的。
Unlike the rising phase and peak, the falling phase and after-hyperpolarization seem to depend primarily on cations that are not calcium. To initiate repolarization, the cell requires movement of potassium out of the cell through passive transportation on the membrane. This differs from neurons because the movement of potassium does not dominate the decrease in membrane potential; In fact, to fully repolarize, a plant cell requires energy in the form of ATP to assist in the release of hydrogen from the cell – utilizing a transporter commonly known as H+-ATPase.[25][21]
不同于上升相和峰值,下降相和后超极化似乎主要依赖于不是钙的阳离子。为了启动复极化,细胞需要钾离子通过细胞膜上的被动运输离开细胞。事实上,为了完全再极化,植物细胞需要能量以 ATP 的形式帮助细胞释放氢-利用一种通常被称为 H+-ATPase 酶的转运蛋白。[25][21]
分类学分布和进化优势
多细胞生物,包括植物、昆虫等无脊椎动物、爬行动物和哺乳动物等脊椎动物都存在动作电位。[lower-alpha 41] 海绵似乎是没有动作电位传递的主要多细胞真核生物门类,尽管一些研究表明这些生物也有一种电信号的形式。[lower-alpha 42] 尽管神经传导速率随轴突直径和髓鞘形成而发生显著变化,但静息电位、动作电位的大小和持续时间并没有随着进化而发生很大变化。
| 动物 | 细胞类型 | 静息电位(mV) | AP 增量(mV) | AP 持续时间 (ms) | 传导速率 (m/s) |
|---|---|---|---|---|---|
| 乌贼 | 巨大轴突 | −60 | 120 | 0.75 | 35 |
| 蚯蚓 | 中间大神经纤维 | −70 | 100 | 1.0 | 30 |
| 蟑螂 | 大神经纤维 | −70 | 80–104 | 0.4 | 10 |
| 蛙 | 坐骨神经轴突 | −60 to −80 | 110–130 | 1.0 | 7–30 |
| 猫 | 脊髓运动神经元 | −55 to −80 | 80–110 | 1–1.5 | 30–120 |
Given its conservation throughout evolution, the action potential seems to confer evolutionary advantages. One function of action potentials is rapid, long-range signaling within the organism; the conduction velocity can exceed 110 m/s, which is one-third the speed of sound. For comparison, a hormone molecule carried in the bloodstream moves at roughly 8 m/s in large arteries. Part of this function is the tight coordination of mechanical events, such as the contraction of the heart. A second function is the computation associated with its generation. Being an all-or-none signal that does not decay with transmission distance, the action potential has similar advantages to digital electronics. The integration of various dendritic signals at the axon hillock and its thresholding to form a complex train of action potentials is another form of computation, one that has been exploited biologically to form central pattern generators and mimicked in artificial neural networks.
鉴于动作电位在整个进化过程中的保守性,它似乎赋予生物某些进化优势。动作电位的一个功能是在生物体内快速的远距离信号传导,传导速率可逾 110 米/秒,即声速的三分之一。相比之下,血液携带的激素分子在大动脉中的运动速度约为 8 米/秒。一个功能是对力学活动,例如心脏的收缩,进行严格的协调。第二个功能是产生动作电位相关的计算。动作电位作为一种全或无信号,不随传输距离衰减,与数字电子技术具有相似的优点。轴丘上各种树突信号的整合及其阈值化形成一系列复杂的动作电位是另一种形式的计算方法,在生物中用来形成中央模式发生器,并在人工神经网络中进行模拟。
The common prokaryotic/eukaryotic ancestor, which lived perhaps four billion years ago, is believed to have had voltage-gated channels. This functionality was likely, at some later point, cross-purposed to provide a communication mechanism. Even modern single-celled bacteria can utilize action potentials to communicate with other bacteria in the same biofilm.[26]
生活在大约 40 亿年前的原核/真核生物的共同祖先,被认为具有电压门控通道。在以后的某个时候,这个功能可能会被用来提供一个通信机制。即使是现代的单细胞细菌也可以利用动作电位与生物膜(biofilm)中的其他细菌进行交流。[26]
实验方法

The study of action potentials has required the development of new experimental methods. The initial work, prior to 1955, was carried out primarily by Alan Lloyd Hodgkin and Andrew Fielding Huxley, who were, along John Carew Eccles, awarded the 1963 Nobel Prize in Physiology or Medicine for their contribution to the description of the ionic basis of nerve conduction. It focused on three goals: isolating signals from single neurons or axons, developing fast, sensitive electronics, and shrinking electrodes enough that the voltage inside a single cell could be recorded.
动作电位的研究一直以来需要开发新的实验方法。在 1955 年之前最初的工作主要是由 Alan Lloyd Hodgkin 和 Andrew Fielding Huxley 完成的,他们因为在描述神经传导的离子基础方面做出的贡献,和 John Carew Eccles 一起被授予 1963 年诺贝尔生理学或医学奖。它聚焦于三个目标:从单个神经元或轴突中分离出信号,发展快速、灵敏的电子设备,以及缩小电极,使单个细胞内的电压能够被记录下来。
The first problem was solved by studying the giant axons found in the neurons of the squid (Loligo forbesii and Doryteuthis pealeii, at the time classified as Loligo pealeii).[lower-alpha 43] These axons are so large in diameter (roughly 1 mm, or 100-fold larger than a typical neuron) that they can be seen with the naked eye, making them easy to extract and manipulate.[lower-alpha 9][lower-alpha 44] However, they are not representative of all excitable cells, and numerous other systems with action potentials have been studied.
第一个问题通过研究乌贼神经元中发现的巨大轴突(Loligo forbesii 和 Doryteuthis pealeii,当时被归类为 Loligo pealeii)得到了解决。[lower-alpha 43] 这些轴突直径很大(大约1毫米,比一个典型的神经元大100倍),可以用肉眼看到,因此很容易提取和操作。[lower-alpha 9][lower-alpha 44] 然而,它们并不代表所有可兴奋细胞,许多其他有动作电位的系统已被研究。
The second problem was addressed with the crucial development of the voltage clamp,[lower-alpha 45] which permitted experimenters to study the ionic currents underlying an action potential in isolation, and eliminated a key source of electronic noise, the current IC associated with the capacitance C of the membrane.模板:Sfn Since the current equals C times the rate of change of the transmembrane voltage Vm, the solution was to design a circuit that kept Vm fixed (zero rate of change) regardless of the currents flowing across the membrane. Thus, the current required to keep Vm at a fixed value is a direct reflection of the current flowing through the membrane. Other electronic advances included the use of Faraday cages and electronics with high input impedance, so that the measurement itself did not affect the voltage being measured.模板:Sfn
第二个问题由于电压钳[lower-alpha 45] 的重要发展解决,让实验人员可以研究单个实验者研究单独的动作电位的离子电流,并消除了电子噪声的主要根源——与膜电容 C 关联的电流 IC。由于电流等于C c 乘以跨膜电压 Vm 的变化率,所以解决方案是设计一个电路,使 Vm 保持固定(零变化率),而不管跨膜电流的变化。因此,使 Vm Vm 保持在一个固定值所需的电流是流过薄膜的电流的直接反射。其他电子方面的进步包括使用法拉第笼和具有高输入阻抗的电子器件,这样测量本身就不会影响被测量的电压。
The third problem, that of obtaining electrodes small enough to record voltages within a single axon without perturbing it, was solved in 1949 with the invention of the glass micropipette electrode,[lower-alpha 46] which was quickly adopted by other researchers.[lower-alpha 47][lower-alpha 48] Refinements of this method are able to produce electrode tips that are as fine as 100 Å (10 nm), which also confers high input impedance.[28] Action potentials may also be recorded with small metal electrodes placed just next to a neuron, with neurochips containing EOSFETs, or optically with dyes that are sensitive to Ca2+ or to voltage.[lower-alpha 49]
第三个问题是如何获得足够小的电极来记录单个轴突内的电压而不对其造成干扰,这个问题在1949年由于玻璃微电极[lower-alpha 46] 的发明而得到解决,并且很快被其他研究人员采用。[lower-alpha 47][lower-alpha 48] 这种方法的改进可以生产出 Å (10 nm)100 纳米的电极尖端,同时也提供了高的输入阻抗。[28] 动作电位也可以用放置在神经元旁的小金属电极记录下来,用含有 EOSFETs 的神经芯片,或者用对 Ca2+ 或电压敏感的染料记录下来。[lower-alpha 49]

玻璃微电极测量的是很多离子通道的总电流,在 1970 年代 Erwin Neher 和 Bert Sakmann 发明的膜片钳(patch clamp)使研究单个离子通道的电学性质成为可能。两位科学家因此被授予 1991 年诺贝尔生理学或医学奖科学奖。[lower-Greek 2] 膜片钳技术证实了离子通道具有分立的电导状态,如打开状态、关闭状态和失活状态。
近年来发展了光学成像(optical imaging)技术,通过同时多点记录或超空间分辨率来测量动作电位。利用电压敏感染料(voltage-sensitive dyes),可以光学记录小块心肌细胞(cardiomyocyte)膜的动作电位。[lower-alpha 50]
神经毒素
Several neurotoxins, both natural and synthetic, are designed to block the action potential. Tetrodotoxin from the pufferfish and saxitoxin from the Gonyaulax (the dinoflagellate genus responsible for "red tides") block action potentials by inhibiting the voltage-sensitive sodium channel;[lower-alpha 51] similarly, dendrotoxin from the black mamba snake inhibits the voltage-sensitive potassium channel. Such inhibitors of ion channels serve an important research purpose, by allowing scientists to "turn off" specific channels at will, thus isolating the other channels' contributions; they can also be useful in purifying ion channels by affinity chromatography or in assaying their concentration. However, such inhibitors also make effective neurotoxins, and have been considered for use as chemical weapons. Neurotoxins aimed at the ion channels of insects have been effective insecticides; one example is the synthetic permethrin, which prolongs the activation of the sodium channels involved in action potentials. The ion channels of insects are sufficiently different from their human counterparts that there are few side effects in humans.
一些天然和人造的神经毒素(neurotoxins)被设计用来阻断动作电位。来自河豚(pufferfish)的河豚毒素(tetrodotoxin)和来自沟鞭藻属(Gonyaulax)的石房蛤毒素(saxitoxin)通过抑制电压敏感性钠通道来阻断动作电位;同样地,黑曼巴(black mamba)蛇的树眼镜蛇毒素(dendrotoxin)也会抑制电压敏感性钾离子通道。这种离子通道的抑制剂有一个重要的研究目的,它可以让科学家随意关闭特定的通道,从而分离出其他通道的贡献;它们也可以用亲和色谱法(affinity chromatography)来纯化离子通道或测定它们的浓度。然而,这些抑制剂也能产生有效的神经毒素,并被认为是化学武器。针对昆虫离子通道的神经毒素一直是有效的杀虫剂,其中一个例子是合成氯菊酯(permethrin),它延长了与动作电位有关的钠通道的激活。昆虫的离子通道与人类的离子通道完全不同,因此对人类几乎没有副作用。
History历史
The role of electricity in the nervous systems of animals was first observed in dissected frogs by Luigi Galvani, who studied it from 1791 to 1797.[lower-alpha 52] Galvani's results stimulated Alessandro Volta to develop the Voltaic pile—the earliest-known electric battery—with which he studied animal electricity (such as electric eels) and the physiological responses to applied direct-current voltages.[lower-alpha 53]
电在动物神经系统中的作用最早是由 Luigi Galvani 在解剖的青蛙中观察到的,他从1791年到1797年研究了这一现象。伽伐尼的研究结果激励了Alessandro Volta 发明了伏打电堆(voltaic pile)ーー已知最早的电池ーー他用这种电池研究了动物电(如电鳗)以及对直流电压的生理反应。[lower-alpha 53]
Scientists of the 19th century studied the propagation of electrical signals in whole nerves (i.e., bundles of neurons) and demonstrated that nervous tissue was made up of cells, instead of an interconnected network of tubes (a reticulum).模板:Sfnm Carlo Matteucci followed up Galvani's studies and demonstrated that cell membranes had a voltage across them and could produce direct current. Matteucci's work inspired the German physiologist, Emil du Bois-Reymond, who discovered the action potential in 1843.[29] The conduction velocity of action potentials was first measured in 1850 by du Bois-Reymond's friend, Hermann von Helmholtz.[30] To establish that nervous tissue is made up of discrete cells, the Spanish physician Santiago Ramón y Cajal and his students used a stain developed by Camillo Golgi to reveal the myriad shapes of neurons, which they rendered painstakingly. For their discoveries, Golgi and Ramón y Cajal were awarded the 1906 Nobel Prize in Physiology.[lower-Greek 3] Their work resolved a long-standing controversy in the neuroanatomy of the 19th century; Golgi himself had argued for the network model of the nervous system.
19 世纪的科学家研究了电信号在整个神经(即神经元束)中的传播,并证明神经组织是由细胞组成的,而不是一个互相连接的管网(网状结构)。Carlo Matteucci 继续伽伐尼的研究,证明细胞膜上有一个电压,可以产生直流电。Carlo Matteucci 的工作启发了德国生理学家 Emil du Bois-Reymond,后者在1843 年发现了动作电位.[29] 。动作电位的传导速度最早是在1850年由du Bois-Reymond 杜波依斯-雷蒙德的朋友Hermann von Helmholtz赫尔曼·冯·亥姆霍兹 · 雷蒙德测量的.[30] 为了证明神经组织是由离散的细胞组成的,西班牙物理学家 Santiago Ramón y Cajal 和他的学生们使用了 Camillo Golgi 开发的染色剂来显示神经元的无数形状,他们煞费苦心地进行了渲染。由于他们的发现,Golgi 和 Ramón y Cajal 获得了1906年的诺贝尔生理学奖.[lower-Greek 3] 。他们的工作解决了19世纪神经解剖学中长期存在的争议;高尔基自己则主张神经系统的网络模型。
The 20th century was a significant era for electrophysiology. In 1902 and again in 1912, Julius Bernstein advanced the hypothesis that the action potential resulted from a change in the permeability of the axonal membrane to ions.[lower-alpha 54]模板:Sfn Bernstein's hypothesis was confirmed by Ken Cole and Howard Curtis, who showed that membrane conductance increases during an action potential.[lower-alpha 55] In 1907, Louis Lapicque suggested that the action potential was generated as a threshold was crossed,[lower-alpha 56] what would be later shown as a product of the dynamical systems of ionic conductances. In 1949, Alan Hodgkin and Bernard Katz refined Bernstein's hypothesis by considering that the axonal membrane might have different permeabilities to different ions; in particular, they demonstrated the crucial role of the sodium permeability for the action potential.[lower-alpha 57] They made the first actual recording of the electrical changes across the neuronal membrane that mediate the action potential.[lower-Greek 4] This line of research culminated in the five 1952 papers of Hodgkin, Katz and Andrew Huxley, in which they applied the voltage clamp technique to determine the dependence of the axonal membrane's permeabilities to sodium and potassium ions on voltage and time, from which they were able to reconstruct the action potential quantitatively.[lower-alpha 9] Hodgkin and Huxley correlated the properties of their mathematical model with discrete ion channels that could exist in several different states, including "open", "closed", and "inactivated". Their hypotheses were confirmed in the mid-1970s and 1980s by Erwin Neher and Bert Sakmann, who developed the technique of patch clamping to examine the conductance states of individual ion channels.[lower-alpha 58] In the 21st century, researchers are beginning to understand the structural basis for these conductance states and for the selectivity of channels for their species of ion,[lower-alpha 59] through the atomic-resolution crystal structures,[lower-alpha 60] fluorescence distance measurements[lower-alpha 61] and cryo-electron microscopy studies.[lower-alpha 62]
20 世纪是电生理的重要时期。1902 年和 1912 年,Julius Bernstein 提出了动作电位是由轴突膜对离子的渗透性改变引起的假说。[lower-alpha 54] Ken Cole 和 Howard Curtis 证实了 Bernstein 的假说,他们发现在动作电位期间膜电导增加。[lower-alpha 55] 1907年,Louis Lapicque 提出,动作电位产生的阈值被跨越,[lower-alpha 56] w,后来被证明为离子电导动力学系统的乘积。1949年,Alan Hodgkin 和 Bernard Katz 完善了 Bernstein 的假说,他们认为轴突膜对不同的离子可能有不同的通透性;特别是,他们证明了钠通透性对动作电位的关键作用。[lower-alpha 57] 。他们首次实际记录了神经元膜上的电变化,这些电变化介导了动作电位。[lower-Greek 4] 这一系列的研究在 Hodgkin,Katz 和 Andrew Huxley 的 5 篇 1952 年的论文中达到了顶峰,他们应用电压钳技术来确定轴突膜对钠离子和钾离子的通透性对电压和时间的依赖性,从而能够定量地重建动作电位。[lower-alpha 9] 。Hodgkin 和 Huxley 将其数学模型的性质与离散离子通道相关联,离散离子通道可以存在于几种不同的状态,包括“开放”、“封闭”和“失活”。他们的假设在20世纪70年代中期和80年代得到 Erwin Neher 和 Bert Sakmann 的证实,他们发明了膜片钳技术来检测单个离子通道的电导状态。[lower-alpha 58] 。在21世纪,通过原子分辨率晶体结构,[lower-alpha 60] 研究人员开始了解这些电导态的结构基础,以及离子种类的通道选择性,[lower-alpha 59] 荧光距离测量[lower-alpha 61] 和冷冻电子显微研究。[lower-alpha 62]
Julius Bernstein was also the first to introduce the Nernst equation for resting potential across the membrane; this was generalized by David E. Goldman to the eponymous Goldman equation in 1943.[lower-alpha 8] The sodium–potassium pump was identified in 1957[lower-alpha 63][lower-Greek 5] and its properties gradually elucidated,[lower-alpha 64][lower-alpha 65][lower-alpha 66] culminating in the determination of its atomic-resolution structure by X-ray crystallography.[lower-alpha 67] The crystal structures of related ionic pumps have also been solved, giving a broader view of how these molecular machines work.[lower-alpha 68]
Julius Bernstein 也是第一个将静息电位的能斯特方程引入到薄膜上的人;David E. Goldman 在1943年将这个方程推广到了以他的名字命名的戈德曼方程。[lower-alpha 8] 钠钾泵在1957年被鉴定出来 [lower-alpha 63][lower-Greek 5],它的性质逐渐被阐明,[lower-alpha 64][lower-alpha 65][lower-alpha 66],最终由 X光散射技术测定了它的原子分辨率结构。[lower-alpha 67] 相关的离子泵的晶体结构也已经被解决,从而为这些分子机器如何工作提供了更广阔的视野。[lower-alpha 68]
定量模型

Mathematical and computational models are essential for understanding the action potential, and offer predictions that may be tested against experimental data, providing a stringent test of a theory. The most important and accurate of the early neural models is the Hodgkin–Huxley model, which describes the action potential by a coupled set of four ordinary differential equations (ODEs).[lower-alpha 9] Although the Hodgkin–Huxley model may be a simplification with few limitations[31] compared to the realistic nervous membrane as it exists in nature, its complexity has inspired several even-more-simplified models,模板:Sfn[lower-alpha 69] such as the Morris–Lecar model[lower-alpha 70] and the FitzHugh–Nagumo model,[lower-alpha 71] both of which have only two coupled ODEs. The properties of the Hodgkin–Huxley and FitzHugh–Nagumo models and their relatives, such as the Bonhoeffer–Van der Pol model,[lower-alpha 72] have been well-studied within mathematics,[32][lower-alpha 73] computation[33] and electronics.[lower-alpha 74] However the simple models of generator potential and action potential fail to accurately reproduce the near threshold neural spike rate and spike shape, specifically for the mechanoreceptors like the Pacinian corpuscle.[34] More modern research has focused on larger and more integrated systems; by joining action-potential models with models of other parts of the nervous system (such as dendrites and synapses), researchers can study neural computation模板:Sfnm and simple reflexes, such as escape reflexes and others controlled by central pattern generators.[35][lower-alpha 75]
数学和计算模型对于理解动作电位是必不可少的,通过将模型产生的预测与实验数据进行比对,为理论提供严格的检验。早期神经模型中最重要和最准确的是 Hodgkin-Huxley 模型,它通过一组四个常微分方程(ODEs)来描述动作电位。[lower-alpha 9] 虽然 Hodgkin-Huxley 模型可能是一个带有限制的简化模型,[lower-alpha 69] 但与实际存在的神经膜相比,它的局限性很小 [31],其复杂性激发了几个更简化的模型,例如 Morris-Lecar 模型l[lower-alpha 70] a和 FitzHugh-Nagumo 模型,[lower-alpha 71] 这两个模型都只有两个耦合的常微分方程。Hodgkin-Huxley 模型和 FitzHugh-Nagumo 模型以及它们的近亲,如 Bonhoeffer-Van der Pol 模型,[lower-alpha 72] 已经在数学中得到了很好的研究,[32][lower-alpha 73] 计算,[33] 和电子学。[lower-alpha 74] 然而,简单的生成电位和动作电位模型并不能准确地再现近阈值神经元刺激速率和刺激形态,特别是对于机械性受体如帕西尼氏小体(Pacinian corpuscle)[34] 。更多的现代研究侧重于更大、更完整的系统;通过将动作电位模型与神经系统其他部分的模型(如树突和突触)结合起来,研究人员可以研究神经计算和简单反射,如逃逸反射和其他由中枢模式发生器控制的反射。[35][lower-alpha 75]
References
Footnotes
- ↑ Hodgkin AL, Huxley AF (August 1952). "A quantitative description of membrane current and its application to conduction and excitation in nerve". The Journal of Physiology. 117 (4): 500–44. doi:10.1113/jphysiol.1952.sp004764. PMC 1392413. PMID 12991237.
- ↑ "Cardiac Muscle Contraction". Retrieved 2021-05-28.
- ↑ Pickard B (June 1973). "Action Potentials in Higher Plants" (PDF). The Botanical Review. 39 (2): 188. doi:10.1007/BF02859299. S2CID 5026557.
- ↑ Leterrier C (February 2018). "The Axon Initial Segment: An Updated Viewpoint". The Journal of Neuroscience. 38 (9): 2135–2145. doi:10.1523/JNEUROSCI.1922-17.2018. PMC 6596274. PMID 29378864.
- ↑ "Voltage-Gated Ion Channels". Neuroscience (2nd ed.). Sunderland, MA: Sinauer Associates. 2001. https://www.ncbi.nlm.nih.gov/books/NBK10883/.
- ↑ Schmidt-Nielsen, p. 484.
- ↑ Tamagawa H, Funatani M, Ikeda K (January 2016). "Ling's Adsorption Theory as a Mechanism of Membrane Potential Generation Observed in Both Living and Nonliving Systems". Membranes. 6 (1): 11. doi:10.3390/membranes6010011. PMC 4812417. PMID 26821050.
- ↑ 8.0 8.1 8.2 8.3 8.4 Sanes, Dan H.; Reh, Thomas A (2012-01-01). Development of the nervous system (Third ed.). Elsevier Academic Press. pp. 211–214. ISBN 9780080923208. OCLC 762720374.
- ↑ Partridge, Donald (1991). Calcium Channels: Their Properties, Functions, Regulation, and Clinical relevance. CRC Press. pp. 138–142. ISBN 9780849388071.
- ↑ Black, Ira (1984) (in en). Cellular and Molecular Biology of Neuronal Development | Ira Black | Springer. Springer. pp. 103. ISBN 978-1-4613-2717-2. https://www.springer.com/us/book/9780306415500.
- ↑ Pedersen, Roger (1998). Current Topics in Developmental Biology, Volume 39. Elsevier Academic Press. ISBN 9780080584621. https://archive.org/details/currenttopicsind0000unse_x6e1.
- ↑ Goldin, AL in Waxman 2007, Neuronal Channels and Receptors, pp. 43–58.
- ↑ Tasaki, I in Field 1959, pp. 75–121
- ↑ Waxman, SG in Waxman 2007, Multiple Sclerosis as a Neurodegenerative Disease, pp. 333–346.
- ↑ 15.0 15.1 15.2 15.3 Rall, W in Koch & Segev 1989, Cable Theory for Dendritic Neurons, pp. 9–62.
- ↑ 16.0 16.1 "Compartmental Models of Complex Neurons". Methods in Neuronal Modeling: From Synapses to Networks.. Cambridge, Massachusetts: The MIT Press. 1989. pp. 63–96. ISBN 978-0-262-11133-1. LCCN 88008279. OCLC 18384545.
- ↑ Tandon, Prakash N (2019-07-01). "Jagdish Chandra Bose and Plant Neurobiology: Part I" (PDF). Indian Journal of History of Science. 54 (2). doi:10.16943/ijhs/2019/v54i2/49660. ISSN 0019-5235.
- ↑ Felle HH, Zimmermann MR (June 2007). "Systemic signalling in barley through action potentials". Planta. 226 (1): 203–14. doi:10.1007/s00425-006-0458-y. PMID 17226028. S2CID 5059716.
- ↑ Luken JO (December 2005). "Habitats of Dionaea muscipula (Venus' Fly Trap), Droseraceae, Associated with Carolina Bays". Southeastern Naturalist (in English). 4 (4): 573–584. doi:10.1656/1528-7092(2005)004[0573:HODMVF]2.0.CO;2. ISSN 1528-7092.
- ↑ 20.0 20.1 20.2 Böhm J, Scherzer S, Krol E, Kreuzer I, von Meyer K, Lorey C, et al. (February 2016). "The Venus Flytrap Dionaea muscipula Counts Prey-Induced Action Potentials to Induce Sodium Uptake". Current Biology. 26 (3): 286–95. doi:10.1016/j.cub.2015.11.057. PMC 4751343. PMID 26804557.
- ↑ 21.00 21.01 21.02 21.03 21.04 21.05 21.06 21.07 21.08 21.09 21.10 Hedrich R, Neher E (March 2018). "Venus Flytrap: How an Excitable, Carnivorous Plant Works". Trends in Plant Science. 23 (3): 220–234. doi:10.1016/j.tplants.2017.12.004. PMID 29336976.
- ↑ Purves D, Augustine GJ, Fitzpatrick D, et al., editors. Neuroscience. 2nd edition. Sunderland (MA): Sinauer Associates; 2001. Electrical Potentials Across Nerve Cell Membranes.Available from: https://www.ncbi.nlm.nih.gov/books/NBK11069/
- ↑ Volkov AG, Adesina T, Jovanov E (May 2007). "Closing of venus flytrap by electrical stimulation of motor cells". Plant Signaling & Behavior. 2 (3): 139–45. doi:10.4161/psb.2.3.4217. PMC 2634039. PMID 19516982.
- ↑ 24.0 24.1 Gradmann, D; Mummert, H in Spanswick, Lucas & Dainty 1980, Plant action potentials, pp. 333–344.
- ↑ 25.0 25.1 Opritov, V A, et al. “Direct Coupling of Action Potential Generation in Cells of a Higher Plant (Cucurbita Pepo) with the Operation of an Electrogenic Pump.” Russian Journal of Plant Physiology, vol. 49, no. 1, 2002, pp. 142–147.
- ↑ 26.0 26.1 Kristan WB (October 2016). "Early evolution of neurons". Current Biology. 26 (20): R949–R954. doi:10.1016/j.cub.2016.05.030. PMID 27780067.
- ↑ Hellier, Jennifer L. (2014). The Brain, the Nervous System, and Their Diseases. ABC-Clio. pp. 532. ISBN 9781610693387. https://books.google.com/books?id=SDi2BQAAQBAJ.
- ↑ 28.0 28.1 Snell, FM in Lavallée, Schanne & Hébert 1969, Some Electrical Properties of Fine-Tipped Pipette Microelectrodes.
- ↑ 29.0 29.1 Finkelstein, Gabriel Ward (2013). Emil du Bois-Reymond : neuroscience, self, and society in nineteenth-century Germany. Cambridge, Massachusetts. ISBN 9781461950325. OCLC 864592470.
- ↑ 30.0 30.1 Olesko, Kathryn M., and Frederic L. Holmes. "Experiment, Quantification and Discovery: Helmholtz's Early Physiological Researches, 1843-50". In Hermann von Helmholtz and the Foundations of Nineteenth Century Science, ed. David Cahan, 50-108. Berkeley; Los Angeles; London: University of California, 1994.
- ↑ 31.0 31.1 Baranauskas G, Martina M (January 2006). "Sodium currents activate without a Hodgkin-and-Huxley-type delay in central mammalian neurons". The Journal of Neuroscience. 26 (2): 671–84. doi:10.1523/jneurosci.2283-05.2006. PMC 6674426. PMID 16407565.
- ↑ 32.0 32.1 Sato, S; Fukai, H; Nomura, T; Doi, S in Reeke et al. 2005, Bifurcation Analysis of the Hodgkin-Huxley Equations, pp. 459–478.
* FitzHugh, R in Schwann 1969, Mathematical models of axcitation and propagation in nerve, pp. 12–16.
* Guckenheimer & Holmes 1986, pp. 12–16 - ↑ 33.0 33.1 Nelson, ME; Rinzel, J in Bower & Beeman 1995, The Hodgkin-Huxley Model, pp. 29–49.
* Rinzel, J & Ermentrout, GB; in Koch & Segev 1989, Analysis of Neural Excitability and Oscillations, pp. 135–169. - ↑ 34.0 34.1 Biswas A, Manivannan M, Srinivasan MA (2015). "Vibrotactile sensitivity threshold: nonlinear stochastic mechanotransduction model of the Pacinian Corpuscle". IEEE Transactions on Haptics. 8 (1): 102–13. doi:10.1109/TOH.2014.2369422. PMID 25398183. S2CID 15326972.
- ↑ 35.0 35.1 Getting, PA in Koch & Segev 1989, Reconstruction of Small Neural Networks, pp. 171–194.
Journal articles
- ↑ MacDonald PE, Rorsman P (February 2006). "Oscillations, intercellular coupling, and insulin secretion in pancreatic beta cells". PLOS Biology. 4 (2): e49. doi:10.1371/journal.pbio.0040049. PMC 1363709. PMID 16464129.

- ↑ 2.0 2.1 Barnett MW, Larkman PM (June 2007). "The action potential". Practical Neurology. 7 (3): 192–7. PMID 17515599. Archived from the original on 8 July 2011.
- ↑ Golding NL, Kath WL, Spruston N (December 2001). "Dichotomy of action-potential backpropagation in CA1 pyramidal neuron dendrites". Journal of Neurophysiology. 86 (6): 2998–3010. doi:10.1152/jn.2001.86.6.2998. PMID 11731556. S2CID 2915815.
- ↑ Sasaki, T., Matsuki, N., Ikegaya, Y. 2011 Action-potential modulation during axonal conduction Science 331 (6017), pp. 599–601
- ↑ Aur D, Connolly CI, Jog MS (November 2005). "Computing spike directivity with tetrodes". Journal of Neuroscience Methods. 149 (1): 57–63. doi:10.1016/j.jneumeth.2005.05.006. PMID 15978667. S2CID 34131910.
- ↑ Aur D., Jog, MS., 2010 Neuroelectrodynamics: Understanding the brain language, IOS Press, 2010. 脚本错误:没有“Vorlage:Handle”这个模块。
- ↑ Noble D (November 1960). "Cardiac action and pacemaker potentials based on the Hodgkin-Huxley equations". Nature. 188 (4749): 495–7. Bibcode:1960Natur.188..495N. doi:10.1038/188495b0. PMID 13729365. S2CID 4147174.
- ↑ 8.0 8.1 8.2 Goldman DE (September 1943). "Potential, Impedance, and Rectification in Membranes". The Journal of General Physiology. 27 (1): 37–60. doi:10.1085/jgp.27.1.37. PMC 2142582. PMID 19873371.
- ↑ 9.0 9.1 9.2 9.3 9.4 9.5 9.6 9.7 Hodgkin AL, Huxley AF, Katz B (April 1952). "Measurement of current-voltage relations in the membrane of the giant axon of Loligo". The Journal of Physiology. 116 (4): 424–48. doi:10.1113/jphysiol.1952.sp004716. PMC 1392219. PMID 14946712.
* Hodgkin AL, Huxley AF (April 1952). "Currents carried by sodium and potassium ions through the membrane of the giant axon of Loligo". The Journal of Physiology. 116 (4): 449–72. doi:10.1113/jphysiol.1952.sp004717. PMC 1392213. PMID 14946713.
* Hodgkin AL, Huxley AF (April 1952). "The components of membrane conductance in the giant axon of Loligo". The Journal of Physiology. 116 (4): 473–96. doi:10.1113/jphysiol.1952.sp004718. PMC 1392209. PMID 14946714.
* Hodgkin AL, Huxley AF (April 1952). "The dual effect of membrane potential on sodium conductance in the giant axon of Loligo". The Journal of Physiology. 116 (4): 497–506. doi:10.1113/jphysiol.1952.sp004719. PMC 1392212. PMID 14946715.
* Hodgkin AL, Huxley AF (August 1952). "A quantitative description of membrane current and its application to conduction and excitation in nerve". The Journal of Physiology. 117 (4): 500–44. doi:10.1113/jphysiol.1952.sp004764. PMC 1392413. PMID 12991237. - ↑ Naundorf B, Wolf F, Volgushev M (April 2006). "Unique features of action potential initiation in cortical neurons" (PDF). Nature. 440 (7087): 1060–3. Bibcode:2006Natur.440.1060N. doi:10.1038/nature04610. PMID 16625198. S2CID 1328840.
- ↑ Hodgkin AL (July 1937). "Evidence for electrical transmission in nerve: Part I". The Journal of Physiology. 90 (2): 183–210. doi:10.1113/jphysiol.1937.sp003507. PMC 1395060. PMID 16994885.
* Hodgkin AL (July 1937). "Evidence for electrical transmission in nerve: Part II". The Journal of Physiology. 90 (2): 211–32. doi:10.1113/jphysiol.1937.sp003508. PMC 1395062. PMID 16994886. - ↑ Zalc B (2006). "The acquisition of myelin: a success story". Novartis Foundation Symposium. Novartis Foundation Symposia. 276: 15–21, discussion 21–5, 54–7, 275–81. doi:10.1002/9780470032244.ch3. ISBN 978-0-470-03224-4. PMID 16805421.
- ↑ Poliak S, Peles E (December 2003). "The local differentiation of myelinated axons at nodes of Ranvier". Nature Reviews. Neuroscience. 4 (12): 968–80. doi:10.1038/nrn1253. PMID 14682359. S2CID 14720760.
- ↑ Simons M, Trotter J (October 2007). "Wrapping it up: the cell biology of myelination". Current Opinion in Neurobiology. 17 (5): 533–40. doi:10.1016/j.conb.2007.08.003. PMID 17923405. S2CID 45470194.
- ↑ Xu K, Terakawa S (August 1999). "Fenestration nodes and the wide submyelinic space form the basis for the unusually fast impulse conduction of shrimp myelinated axons". The Journal of Experimental Biology. 202 (Pt 15): 1979–89. doi:10.1242/jeb.202.15.1979. PMID 10395528.
- ↑ 16.0 16.1 Hursh JB (1939). "Conduction velocity and diameter of nerve fibers". American Journal of Physiology. 127: 131–39. doi:10.1152/ajplegacy.1939.127.1.131.
- ↑ Lillie RS (March 1925). "Factors Affecting Transmission and Recovery in the Passive Iron Nerve Model". The Journal of General Physiology. 7 (4): 473–507. doi:10.1085/jgp.7.4.473. PMC 2140733. PMID 19872151. See also Keynes & Aidley 1991, p. 78
- ↑ Tasaki I (1939). "Electro-saltatory transmission of nerve impulse and effect of narcosis upon nerve fiber". Am. J. Physiol. 127: 211–27. doi:10.1152/ajplegacy.1939.127.2.211.
- ↑ Tasaki I, Takeuchi T (1941). "Der am Ranvierschen Knoten entstehende Aktionsstrom und seine Bedeutung für die Erregungsleitung". Pflügers Archiv für die gesamte Physiologie. 244 (6): 696–711. doi:10.1007/BF01755414. S2CID 8628858.
* Tasaki I, Takeuchi T (1942). "Weitere Studien über den Aktionsstrom der markhaltigen Nervenfaser und über die elektrosaltatorische Übertragung des nervenimpulses". Pflügers Archiv für die gesamte Physiologie. 245 (5): 764–82. doi:10.1007/BF01755237. S2CID 44315437. - ↑ Huxley AF, Stämpfli R (May 1949). "Evidence for saltatory conduction in peripheral myelinated nerve fibres". The Journal of Physiology. 108 (3): 315–39. doi:10.1113/jphysiol.1949.sp004335. PMC 1392492. PMID 16991863.
* Huxley AF, Stampfli R (February 1951). "Direct determination of membrane resting potential and action potential in single myelinated nerve fibers". The Journal of Physiology. 112 (3–4): 476–95. doi:10.1113/jphysiol.1951.sp004545. PMC 1393015. PMID 14825228. - ↑ Rushton WA (September 1951). "A theory of the effects of fibre size in medullated nerve". The Journal of Physiology. 115 (1): 101–22. doi:10.1113/jphysiol.1951.sp004655. PMC 1392008. PMID 14889433.
- ↑ 22.0 22.1 Hartline DK, Colman DR (January 2007). "Rapid conduction and the evolution of giant axons and myelinated fibers". Current Biology. 17 (1): R29-35. doi:10.1016/j.cub.2006.11.042. PMID 17208176. S2CID 10033356.
- ↑ Miller RH, Mi S (November 2007). "Dissecting demyelination". Nature Neuroscience. 10 (11): 1351–4. doi:10.1038/nn1995. PMID 17965654. S2CID 12441377.
- ↑ 24.0 24.1 Kelvin WT (1855). "On the theory of the electric telegraph". Proceedings of the Royal Society. 7: 382–99. doi:10.1098/rspl.1854.0093. S2CID 178547827.
- ↑ 25.0 25.1 Hodgkin AL, Rushton WA (December 1946). "The electrical constants of a crustacean nerve fibre". Proceedings of the Royal Society of Medicine. 134 (873): 444–79. Bibcode:1946RSPSB.133..444H. doi:10.1098/rspb.1946.0024. PMID 20281590.
- ↑ "Neurotransmitter release". Pharmacology of Neurotransmitter Release. Handbook of Experimental Pharmacology. 184. 2008. pp. 1–21. doi:10.1007/978-3-540-74805-2_1. ISBN 978-3-540-74804-5. PMID 18064409.
- ↑ Rusakov DA (August 2006). "Ca2+-dependent mechanisms of presynaptic control at central synapses". The Neuroscientist. 12 (4): 317–26. doi:10.1177/1073858405284672. PMC 2684670. PMID 16840708.
- ↑ Humeau Y, Doussau F, Grant NJ, Poulain B (May 2000). "How botulinum and tetanus neurotoxins block neurotransmitter release". Biochimie. 82 (5): 427–46. doi:10.1016/S0300-9084(00)00216-9. PMID 10865130.
- ↑ Zoidl G, Dermietzel R (November 2002). "On the search for the electrical synapse: a glimpse at the future". Cell and Tissue Research. 310 (2): 137–42. doi:10.1007/s00441-002-0632-x. PMID 12397368. S2CID 22414506.
- ↑ Brink PR, Cronin K, Ramanan SV (August 1996). "Gap junctions in excitable cells". Journal of Bioenergetics and Biomembranes. 28 (4): 351–8. doi:10.1007/BF02110111. PMID 8844332. S2CID 46371790.
- ↑ Hirsch NP (July 2007). "Neuromuscular junction in health and disease". British Journal of Anaesthesia. 99 (1): 132–8. doi:10.1093/bja/aem144. PMID 17573397.
- ↑ Hughes BW, Kusner LL, Kaminski HJ (April 2006). "Molecular architecture of the neuromuscular junction". Muscle & Nerve. 33 (4): 445–61. doi:10.1002/mus.20440. PMID 16228970. S2CID 1888352.
- ↑ 33.0 33.1 Newmark J (January 2007). "Nerve agents". The Neurologist. 13 (1): 20–32. doi:10.1097/01.nrl.0000252923.04894.53. PMID 17215724. S2CID 211234081.
- ↑ Costa LG (April 2006). "Current issues in organophosphate toxicology". Clinica Chimica Acta; International Journal of Clinical Chemistry. 366 (1–2): 1–13. doi:10.1016/j.cca.2005.10.008. PMID 16337171.
- ↑ 35.0 35.1 35.2 Kléber AG, Rudy Y (April 2004). "Basic mechanisms of cardiac impulse propagation and associated arrhythmias". Physiological Reviews. 84 (2): 431–88. doi:10.1152/physrev.00025.2003. PMID 15044680. S2CID 21823003.
- ↑ Tamargo J, Caballero R, Delpón E (January 2004). "Pharmacological approaches in the treatment of atrial fibrillation". Current Medicinal Chemistry. 11 (1): 13–28. doi:10.2174/0929867043456241. PMID 14754423.
- ↑ Slayman CL, Long WS, Gradmann D (April 1976). ""Action potentials" in Neurospora crassa, a mycelial fungus". Biochimica et Biophysica Acta (BBA) - Biomembranes. 426 (4): 732–44. doi:10.1016/0005-2736(76)90138-3. PMID 130926.
- ↑ Mummert H, Gradmann D (December 1991). "Action potentials in Acetabularia: measurement and simulation of voltage-gated fluxes". The Journal of Membrane Biology. 124 (3): 265–73. doi:10.1007/BF01994359. PMID 1664861. S2CID 22063907.
- ↑ Gradmann D (2001). "Models for oscillations in plants". Aust. J. Plant Physiol. 28 (7): 577–590. doi:10.1071/pp01017.
- ↑ 40.0 40.1 Gradmann D, Hoffstadt J (November 1998). "Electrocoupling of ion transporters in plants: interaction with internal ion concentrations". The Journal of Membrane Biology. 166 (1): 51–9. doi:10.1007/s002329900446. PMID 9784585. S2CID 24190001.
- ↑ Fromm J, Lautner S (March 2007). "Electrical signals and their physiological significance in plants". Plant, Cell & Environment. 30 (3): 249–257. doi:10.1111/j.1365-3040.2006.01614.x. PMID 17263772.
- ↑ Leys SP, Mackie GO, Meech RW (May 1999). "Impulse conduction in a sponge". The Journal of Experimental Biology. 202 (Pt 9) (9): 1139–50. doi:10.1242/jeb.202.9.1139. PMID 10101111.
- ↑ 43.0 43.1 Keynes RD (1989). "The role of giant axons in studies of the nerve impulse". BioEssays. 10 (2–3): 90–3. doi:10.1002/bies.950100213. PMID 2541698.
- ↑ 44.0 44.1 Meunier C, Segev I (November 2002). "Playing the devil's advocate: is the Hodgkin-Huxley model useful?". Trends in Neurosciences. 25 (11): 558–63. doi:10.1016/S0166-2236(02)02278-6. PMID 12392930. S2CID 1355280.
- ↑ 45.0 45.1 Cole KS (1949). "Dynamic electrical characteristics of the squid axon membrane". Arch. Sci. Physiol. 3: 253–8.
- ↑ 46.0 46.1 Ling G, Gerard RW (December 1949). "The normal membrane potential of frog sartorius fibers". Journal of Cellular and Comparative Physiology. 34 (3): 383–96. doi:10.1002/jcp.1030340304. PMID 15410483.
- ↑ 47.0 47.1 Nastuk WL, Hodgkin A (1950). "The electrical activity of single muscle fibers". Journal of Cellular and Comparative Physiology. 35: 39–73. doi:10.1002/jcp.1030350105.
- ↑ 48.0 48.1 Brock LG, Coombs JS, Eccles JC (August 1952). "The recording of potentials from motoneurones with an intracellular electrode". The Journal of Physiology. 117 (4): 431–60. doi:10.1113/jphysiol.1952.sp004759. PMC 1392415. PMID 12991232.
- ↑ 49.0 49.1 Ross WN, Salzberg BM, Cohen LB, Davila HV (December 1974). "A large change in dye absorption during the action potential". Biophysical Journal. 14 (12): 983–6. Bibcode:1974BpJ....14..983R. doi:10.1016/S0006-3495(74)85963-1. PMC 1334592. PMID 4429774.
* Grynkiewicz G, Poenie M, Tsien RY (March 1985). "A new generation of Ca2+ indicators with greatly improved fluorescence properties". The Journal of Biological Chemistry. 260 (6): 3440–50. doi:10.1016/S0021-9258(19)83641-4. PMID 3838314. - ↑ Bu G, Adams H, Berbari EJ, Rubart M (March 2009). "Uniform action potential repolarization within the sarcolemma of in situ ventricular cardiomyocytes". Biophysical Journal. 96 (6): 2532–46. Bibcode:2009BpJ....96.2532B. doi:10.1016/j.bpj.2008.12.3896. PMC 2907679. PMID 19289075.
- ↑ Milligan JV, Edwards C (July 1965). "Some factors affecting the time course of the recovery of contracture ability following a potassium contracture in frog striated muscle". The Journal of General Physiology. 48 (6): 975–83. doi:10.1085/jgp.48.6.975. PMC 2195447. PMID 5855511.
* "The binding of saxitoxin and tetrodotoxin to excitable tissue". Reviews of Physiology, Biochemistry and Pharmacology, Volume 79. Reviews of Physiology, Biochemistry and Pharmacology. 79. 1977. pp. 1–50. doi:10.1007/BFb0037088. ISBN 0-387-08326-X. PMID 335473.
* Keynes RD, Ritchie JM (August 1984). "On the binding of labelled saxitoxin to the squid giant axon". Proceedings of the Royal Society of London. Series B, Biological Sciences. 222 (1227): 147–53. Bibcode:1984RSPSB.222..147K. doi:10.1098/rspb.1984.0055. PMID 6148754. S2CID 11465181. - ↑ Piccolino M (October 1997). "Luigi Galvani and animal electricity: two centuries after the foundation of electrophysiology". Trends in Neurosciences. 20 (10): 443–8. doi:10.1016/S0166-2236(97)01101-6. PMID 9347609. S2CID 23394494.
- ↑ 53.0 53.1 Piccolino M (April 2000). "The bicentennial of the Voltaic battery (1800-2000): the artificial electric organ". Trends in Neurosciences. 23 (4): 147–51. doi:10.1016/S0166-2236(99)01544-1. PMID 10717671. S2CID 393323.
- ↑ 54.0 54.1 Bernstein J (1902). "Untersuchungen zur Thermodynamik der bioelektrischen Ströme". Pflügers Archiv für die gesamte Physiologie. 92 (10–12): 521–562. doi:10.1007/BF01790181. S2CID 33229139.
- ↑ 55.0 55.1 Cole KS, Curtis HJ (May 1939). "Electric Impedance of the Squid Giant Axon During Activity". The Journal of General Physiology. 22 (5): 649–70. doi:10.1085/jgp.22.5.649. PMC 2142006. PMID 19873125.
- ↑ 56.0 56.1 Lapicque L (1907). "Recherches quantitatives sur l'excitationelectrique des nerfs traitee comme une polarisation". J. Physiol. Pathol. Gen. 9: 620–635.
- ↑ 57.0 57.1 Hodgkin AL, Katz B (March 1949). "The effect of sodium ions on the electrical activity of giant axon of the squid". The Journal of Physiology. 108 (1): 37–77. doi:10.1113/jphysiol.1949.sp004310. PMC 1392331. PMID 18128147.
- ↑ 58.0 58.1 Neher E, Sakmann B (April 1976). "Single-channel currents recorded from membrane of denervated frog muscle fibres". Nature. 260 (5554): 799–802. Bibcode:1976Natur.260..799N. doi:10.1038/260799a0. PMID 1083489. S2CID 4204985.
* Hamill OP, Marty A, Neher E, Sakmann B, Sigworth FJ (August 1981). "Improved patch-clamp techniques for high-resolution current recording from cells and cell-free membrane patches". Pflügers Archiv. 391 (2): 85–100. doi:10.1007/BF00656997. PMID 6270629. S2CID 12014433.
* Neher E, Sakmann B (March 1992). "The patch clamp technique". Scientific American. 266 (3): 44–51. Bibcode:1992SciAm.266c..44N. doi:10.1038/scientificamerican0392-44. PMID 1374932. - ↑ 59.0 59.1 Yellen G (September 2002). "The voltage-gated potassium channels and their relatives". Nature. 419 (6902): 35–42. Bibcode:2002Natur.419...35Y. doi:10.1038/nature00978. PMID 12214225. S2CID 4420877.
- ↑ 60.0 60.1 Doyle DA, Morais Cabral J, Pfuetzner RA, Kuo A, Gulbis JM, Cohen SL, et al. (April 1998). "The structure of the potassium channel: molecular basis of K+ conduction and selectivity". Science. 280 (5360): 69–77. Bibcode:1998Sci...280...69D. doi:10.1126/science.280.5360.69. PMID 9525859.
* Zhou Y, Morais-Cabral JH, Kaufman A, MacKinnon R (November 2001). "Chemistry of ion coordination and hydration revealed by a K+ channel-Fab complex at 2.0 A resolution". Nature. 414 (6859): 43–8. Bibcode:2001Natur.414...43Z. doi:10.1038/35102009. PMID 11689936. S2CID 205022645.
* Jiang Y, Lee A, Chen J, Ruta V, Cadene M, Chait BT, MacKinnon R (May 2003). "X-ray structure of a voltage-dependent K+ channel". Nature. 423 (6935): 33–41. Bibcode:2003Natur.423...33J. doi:10.1038/nature01580. PMID 12721618. S2CID 4347957. - ↑ 61.0 61.1 Cha A, Snyder GE, Selvin PR, Bezanilla F (December 1999). "Atomic scale movement of the voltage-sensing region in a potassium channel measured via spectroscopy". Nature. 402 (6763): 809–13. Bibcode:1999Natur.402..809C. doi:10.1038/45552. PMID 10617201. S2CID 4353978.
* Glauner KS, Mannuzzu LM, Gandhi CS, Isacoff EY (December 1999). "Spectroscopic mapping of voltage sensor movement in the Shaker potassium channel". Nature. 402 (6763): 813–7. Bibcode:1999Natur.402..813G. doi:10.1038/45561. PMID 10617202. S2CID 4417476.
* Bezanilla F (April 2000). "The voltage sensor in voltage-dependent ion channels". Physiological Reviews. 80 (2): 555–92. doi:10.1152/physrev.2000.80.2.555. PMID 10747201. - ↑ 62.0 62.1 Catterall WA (February 2001). "A 3D view of sodium channels". Nature. 409 (6823): 988–9, 991. Bibcode:2001Natur.409..988C. doi:10.1038/35059188. PMID 11234048. S2CID 4371677.
* Sato C, Ueno Y, Asai K, Takahashi K, Sato M, Engel A, Fujiyoshi Y (February 2001). "The voltage-sensitive sodium channel is a bell-shaped molecule with several cavities". Nature. 409 (6823): 1047–51. Bibcode:2001Natur.409.1047S. doi:10.1038/35059098. PMID 11234014. S2CID 4430165. - ↑ 63.0 63.1 Skou JC (February 1957). "The influence of some cations on an adenosine triphosphatase from peripheral nerves". Biochimica et Biophysica Acta. 23 (2): 394–401. doi:10.1016/0006-3002(57)90343-8. PMID 13412736.
- ↑ 64.0 64.1 Hodgkin AL, Keynes RD (April 1955). "Active transport of cations in giant axons from Sepia and Loligo". The Journal of Physiology. 128 (1): 28–60. doi:10.1113/jphysiol.1955.sp005290. PMC 1365754. PMID 14368574.
- ↑ 65.0 65.1 Caldwell PC, Hodgkin AL, Keynes RD, Shaw TL (July 1960). "The effects of injecting 'energy-rich' phosphate compounds on the active transport of ions in the giant axons of Loligo". The Journal of Physiology. 152 (3): 561–90. doi:10.1113/jphysiol.1960.sp006509. PMC 1363339. PMID 13806926.
- ↑ 66.0 66.1 Caldwell PC, Keynes RD (June 1957). "The utilization of phosphate bond energy for sodium extrusion from giant axons". The Journal of Physiology. 137 (1): 12–3P. doi:10.1113/jphysiol.1957.sp005830. PMID 13439598. S2CID 222188054.
- ↑ 67.0 67.1 Morth JP, Pedersen BP, Toustrup-Jensen MS, Sørensen TL, Petersen J, Andersen JP, et al. (December 2007). "Crystal structure of the sodium-potassium pump". Nature. 450 (7172): 1043–9. Bibcode:2007Natur.450.1043M. doi:10.1038/nature06419. PMID 18075585. S2CID 4344526.
- ↑ 68.0 68.1 Lee AG, East JM (June 2001). "What the structure of a calcium pump tells us about its mechanism". The Biochemical Journal. 356 (Pt 3): 665–83. doi:10.1042/0264-6021:3560665. PMC 1221895. PMID 11389676.
- ↑ 69.0 69.1 *Fitzhugh R (May 1960). "Thresholds and plateaus in the Hodgkin-Huxley nerve equations". The Journal of General Physiology. 43 (5): 867–96. doi:10.1085/jgp.43.5.867. PMC 2195039. PMID 13823315.
* Kepler TB, Abbott LF, Marder E (1992). "Reduction of conductance-based neuron models". Biological Cybernetics. 66 (5): 381–7. doi:10.1007/BF00197717. PMID 1562643. S2CID 6789007. - ↑ 70.0 70.1 Morris C, Lecar H (July 1981). "Voltage oscillations in the barnacle giant muscle fiber". Biophysical Journal. 35 (1): 193–213. Bibcode:1981BpJ....35..193M. doi:10.1016/S0006-3495(81)84782-0. PMC 1327511. PMID 7260316.
- ↑ 71.0 71.1 Fitzhugh R (July 1961). "Impulses and Physiological States in Theoretical Models of Nerve Membrane". Biophysical Journal. 1 (6): 445–66. Bibcode:1961BpJ.....1..445F. doi:10.1016/S0006-3495(61)86902-6. PMC 1366333. PMID 19431309.
* Nagumo J, Arimoto S, Yoshizawa S (1962). "An active pulse transmission line simulating nerve axon". Proceedings of the IRE. 50 (10): 2061–2070. doi:10.1109/JRPROC.1962.288235. S2CID 51648050. - ↑ 72.0 72.1 Bonhoeffer KF (September 1948). "Activation of passive iron as a model for the excitation of nerve". The Journal of General Physiology. 32 (1): 69–91. doi:10.1085/jgp.32.1.69. PMC 2213747. PMID 18885679.
* Bonhoeffer KF (1953). "Modelle der Nervenerregung". Naturwissenschaften. 40 (11): 301–311. Bibcode:1953NW.....40..301B. doi:10.1007/BF00632438. S2CID 19149460.
* Van der Pol B (1926). "On relaxation-oscillations". Philosophical Magazine. 2: 977–992.
* Van der Pol B, Van der Mark J (1928). "The heartbeat considered as a relaxation oscillation, and an electrical model of the heart". Philosophical Magazine. 6: 763–775. doi:10.1080/14786441108564652.
* Van der Pol B, van der Mark J (1929). "The heartbeat considered as a relaxation oscillation, and an electrical model of the heart". Arch. Neerl. Physiol. 14: 418–443. - ↑ 73.0 73.1 Evans JW (1972). "Nerve axon equations. I. Linear approximations". Indiana Univ. Math. J. 21 (9): 877–885. doi:10.1512/iumj.1972.21.21071.
* Evans JW, Feroe J (1977). "Local stability theory of the nerve impulse". Math. Biosci. 37: 23–50. doi:10.1016/0025-5564(77)90076-1. - ↑ 74.0 74.1 Keener JP (1983). "Analogue circuitry for the Van der Pol and FitzHugh-Nagumo equations". IEEE Transactions on Systems, Man and Cybernetics. 13 (5): 1010–1014. doi:10.1109/TSMC.1983.6313098. S2CID 20077648.
- ↑ 75.0 75.1 Hooper SL (March 2000). "Central pattern generators". Current Biology. 10 (5): R176–R179. CiteSeerX 10.1.1.133.3378. doi:10.1016/S0960-9822(00)00367-5. PMID 10713861. S2CID 11388348.
Books
- Neurocomputing: Foundations of Research. Cambridge, Massachusetts: The MIT Press. 1988. ISBN 978-0-262-01097-9. LCCN 87003022. OCLC 15860311. https://archive.org/details/neurocomputingfo0000unse.
- Elektrobiologie, die Lehre von den elektrischen Vorgängen im Organismus auf moderner Grundlage dargestellt. Braunschweig: Vieweg und Sohn. 1912. LCCN 12027986. OCLC 11358569.
- The Book of GENESIS: Exploring Realistic Neural Models with the GEneral NEural SImulation System. Santa Clara, Calif.: TELOS. 1995. ISBN 978-0-387-94019-9. LCCN 94017624. OCLC 30518469.
- A History of the Electrical Activity of the Brain. London: Pitman. 1961. LCCN 62001407. OCLC 556863.
- Structure and Function in the Nervous Systems of Invertebrates. A series of books in biology. San Francisco: W. H. Freeman. 1965. LCCN 65007965. OCLC 558128. https://archive.org/details/structurefunctio0000bull.
- Introduction to Nervous Systems. A series of books in biology. San Francisco: W. H. Freeman. 1977. ISBN 978-0-7167-0030-2. LCCN 76003735. OCLC 2048177. https://archive.org/details/introductiontone00theo.
- Handbook of Physiology: a Critical, Comprehensive Presentation of Physiological Knowledge and Concepts: Section 1: Neurophysiology. 1. Washington, DC: American Physiological Society. 1959. LCCN 60004587. OCLC 830755894.
- Ganong, WF (1991). Review of Medical Physiology (15th ed.). Norwalk, Conn.: Appleton and Lange. ISBN 978-0-8385-8418-7. ISSN 0892-1253. LCCN 87642343. OCLC 23761261.
- Nonlinear Oscillations, Dynamical Systems and Bifurcations of Vector Fields. Applied Mathematical Sciences. 42 (2nd ed.). New York: Springer Verlag. 1986. ISBN 978-0-387-90819-9. OCLC 751129941.
- An Introduction to the Mathematics of Neurons. Cambridge studies in mathematical biology. 6. Cambridge: Cambridge University Press. 1986. ISBN 978-0-521-31574-6. LCCN 85011013. OCLC 12052275.
- Nerve and Muscle Excitation (2nd ed.). Sunderland, Mass.: Sinauer Associates. 1981. ISBN 978-0-87893-410-2. LCCN 80018158. OCLC 6486925. https://archive.org/details/nervemuscleexcit00jung.
- Practical Electrophysiological Methods: A Guide for in Vitro Studies in Vertebrate Neurobiology. New York: Wiley. 1992. ISBN 978-0-471-56200-9. LCCN 92000179. OCLC 25204689.
- Nerve and Muscle (2nd ed.). Cambridge: Cambridge University Press. 1991. ISBN 978-0-521-41042-7. LCCN 90015167. OCLC 25204483.
- Methods in Neuronal Modeling: From Synapses to Networks. Cambridge, Massachusetts: The MIT Press. 1989. ISBN 978-0-262-11133-1. LCCN 88008279. OCLC 18384545.
- Glass Microelectrodes. New York: Wiley. 1969. ISBN 978-0-471-51885-3. LCCN 68009252. OCLC 686.
- Embodiments of Mind. Cambridge, Massachusetts: The MIT Press. 1988. ISBN 978-0-262-63114-3. LCCN 88002987. OCLC 237280.
- Garrison's History of Neurology. Springfield, Ill.: Charles C. Thomas. 1969. OCLC 429733931.
- Human Physiology: An Integrated Approach (5th ed.). San Francisco: Pearson. 2010. ISBN 978-0-321-55980-7. LCCN 2008050369. OCLC 268788623.
- Plant Membrane Transport: Current Conceptual Issues. Developments in Plant Biology. 4. Amsterdam: Elsevier Biomedical Press. 1980. ISBN 978-0-444-80192-0. LCCN 79025719. OCLC 5799924.
- "Release of Transmitters from Synaptic Vesicles". Neuroscience (2nd ed.). Sunderland, MA: Sinauer Associates. 2001. ISBN 978-0-87893-742-4. LCCN 00059496. OCLC 806472664. https://www.ncbi.nlm.nih.gov/books/bv.fcgi?rid=neurosci.section.326.
- Neuroscience (4th ed.). Sunderland, MA: Sinauer Associates. 2008. ISBN 978-0-87893-697-7. LCCN 2007024950. OCLC 144771764.
- Modeling in the Neurosciences: from Biological Systems to Neuromimetic Robotics. Boca Raton, Fla.: Taylor & Francis. 2005. ISBN 978-0-415-32868-5. LCCN 2005298022. OCLC 489024131.
- Animal Physiology: Adaptation and Environment (5th ed.). Cambridge: Cambridge University Press. 1997. ISBN 978-0-521-57098-5. LCCN 96039295. OCLC 35744403.
- Biological Engineering. Inter-University Electronics Series. 9. New York: McGraw-Hill. 1969. ISBN 978-0-07-055734-5. LCCN 68027513. OCLC 51993.
- Neurophysiology: A Primer. New York: John Wiley and Sons. 1966. ISBN 9780471824367. LCCN 66015872. OCLC 1175605. https://archive.org/details/neurophysiologyp0000stev.
- Molecular Neurology. Burlington, Mass.: Elsevier Academic Press. 2007. ISBN 978-0-12-369509-3. LCCN 2008357317. OCLC 154760295.
- The Neurosciences, Paths of Discovery. Cambridge, Massachusetts: The MIT Press. 1975. ISBN 978-0-262-23072-8. LCCN 75016379. OCLC 1500233. https://archive.org/details/TheNeurosc_00_Word.
Books
Web pages
- ↑ 模板:Cite press release
- ↑ 模板:Cite press release
- ↑ 3.0 3.1 模板:Cite press release
- ↑ 4.0 4.1 Warlow C (June 2007). "The Recent Evolution of a Symbiotic Ion Channel in the Legume Family Altered Ion Conductance and Improved Functionality in Calcium Signaling". Practical Neurology. BMJ Publishing Group. 7 (3): 192–197. Archived from the original on 14 March 2012. Retrieved 23 March 2013.
- ↑ 5.0 5.1 模板:Cite press release
Further reading
- Ion Channels: Molecules in Action. Cambridge: Cambridge University Press. 1996. ISBN 978-0-521-49882-1.
- Neuroscience: Exploring the Brain. Baltimore: Lippincott. 2001. ISBN 0-7817-3944-6.
- Clay JR (May 2005). "Axonal excitability revisited". Progress in Biophysics and Molecular Biology. 88 (1): 59–90. doi:10.1016/j.pbiomolbio.2003.12.004. PMID 15561301.
- Neuroelectric Systems. New York: New York University Press. 1987. ISBN 0-8147-1782-9.
- Ion Channels of Excitable Membranes (3rd ed.). Sunderland, MA: Sinauer Associates. 2001. ISBN 978-0-87893-321-1.
- Foundations of Cellular Neurophysiology. Cambridge, Massachusetts: Bradford Book, The MIT Press. 1995. ISBN 0-262-10053-3.
- Principles of Neural Science (4th ed.). New York: McGraw-Hill. 2000. ISBN 0-8385-7701-6.
- Miller C (1987). "How ion channel proteins work". Neuromodulation: The Biochemical Control of Neuronal Excitability. New York: Oxford University Press. pp. 39–63. ISBN 978-0-19-504097-5.
- Lehninger Principles of Biochemistry (5th ed.). New York: W. H. Freeman. 2008. ISBN 978-0-7167-7108-1. https://archive.org/details/lehningerprincip00lehn_1.
External links
- Ionic flow in action potentials at Blackwell Publishing
- Action potential propagation in myelinated and unmyelinated axons at Blackwell Publishing
- Generation of AP in cardiac cells and generation of AP in neuron cells
- Resting membrane potential from Life: The Science of Biology, by WK Purves, D Sadava, GH Orians, and HC Heller, 8th edition, New York: WH Freeman,
- Ionic motion and the Goldman voltage for arbitrary ionic concentrations at The University of Arizona
- A cartoon illustrating the action potential
- Action potential propagation
- Production of the action potential: voltage and current clamping simulationshttps://en.wikipedia.org/wiki/Defekte_Weblinks?dwl={{{url}}} Seite nicht mehr abrufbar], Suche in Webarchiven: Kategorie:Wikipedia:Weblink offline (andere Namensräume)[http://timetravel.mementoweb.org/list/2010/Kategorie:Wikipedia:Vorlagenfehler/Vorlage:Toter Link/URL_fehlt
- Open-source software to simulate neuronal and cardiac action potentials at SourceForge.net
- Introduction to the Action Potential, Neuroscience Online (electronic neuroscience textbook by UT Houston Medical School)
- Khan Academy: Electrotonic and action potential
- Ionic flow in action potentials at Blackwell Publishing
- Action potential propagation in myelinated and unmyelinated axons at Blackwell Publishing
- Generation of AP in cardiac cells and generation of AP in neuron cells
- Resting membrane potential from Life: The Science of Biology, by WK Purves, D Sadava, GH Orians, and HC Heller, 8th edition, New York: WH Freeman, .
- Ionic motion and the Goldman voltage for arbitrary ionic concentrations at The University of Arizona
- A cartoon illustrating the action potential
- Action potential propagation
- Production of the action potential: voltage and current clamping simulations
- Open-source software to simulate neuronal and cardiac action potentials at SourceForge.net
- Introduction to the Action Potential, Neuroscience Online (electronic neuroscience textbook by UT Houston Medical School)
- Khan Academy: Electrotonic and action potential
Category:Capacitors
Category:Neural coding
Category:Electrophysiology
Category:Electrochemistry
Category:Computational neuroscience
Category:Cellular neuroscience
Category:Cellular processes
Category:Membrane biology
Category:Plant cognition
Category:Action potentials
类别: 电容器类别: 神经编码类别: 电生理学类别: 电化学类别: 计算神经科学类别: 细胞神经科学类别: 细胞过程类别: 膜生物学类别: 植物认知类别: 动作电位
This page was moved from wikipedia:en:Action potential. Its edit history can be viewed at 动作电位/edithistory
- Pages containing cite templates with deprecated parameters
- CS1 English-language sources (en)
- 有脚本错误的页面
- CS1: long volume value
- Articles with short description
- Capacitors
- Neural coding
- Electrophysiology
- Electrochemistry
- Computational neuroscience
- Cellular neuroscience
- Cellular processes
- Membrane biology
- Plant cognition
- Action potentials
- 待整理页面