“主分层”的版本间的差异
| 第2行: | 第2行: | ||
|keywords=因果推断,统计技术 | |keywords=因果推断,统计技术 | ||
|description=是一种应用于因果推断的统计技术 | |description=是一种应用于因果推断的统计技术 | ||
| − | }} | + | }}本词条尚未编辑完毕 |
== 研究动机 == | == 研究动机 == | ||
| 第163行: | 第163行: | ||
== 主分层的关键假设 == | == 主分层的关键假设 == | ||
| + | 基于主要分层的分析分为三个阶段。第一阶段是确定我们前面描述的主要层次。总的来说,这个过程涉及到以一种相对高层次的方式思考实质性问题。下一阶段是将这些层次正式化,并编码进一步的实质性信息,以便日后进行估计。我们将在本节中讨论前两个阶段。最后一个阶段是估算,在第四部分中讨论。 | ||
| + | |||
| + | 首先,为了更好地界定地层,我们需要对随机试验的工作方式做一些假设。主要分层是基于潜在结果框架(Frangakis & Rubin,2002; Neyman,1923; Rubin,2005) ,它有效地考虑了每个研究个体具有个体的潜在结果和相关的潜在治疗效果。人 i,Yi (1)和 Yi (0)的潜在结果是我们可能看到的结果,如果我们治疗或不治疗的人,分别。 | ||
| + | |||
| + | 鉴于这些数值,一个关键的感兴趣的数量,整体平均治疗效果,是这些个别治疗效果的平均值。 | ||
| + | |||
| + | 因果影响是明确的,不依赖于任何分布或抽样假设: 人口由个人在实验中,而不是更多。挑战在于,虽然所有的潜在结果都已确定,但根据随机治疗分配,对于每个人来说,实际上只观察到一个潜在结果。 | ||
| + | |||
| + | 为了从这些基本定义出发,我们首先做出两个普遍接受的假设。首先,治疗实际上是随机的,我们将其表述为一个独立的假设,在个体是否接受治疗和个体的潜在结果是什么之间。第二个,通常被称为稳定单位治疗价值假设(SUTVA)(Rubin,1978,1980,1990) ,有效地说明治疗一个人不会影响另一个人(即,治疗一个学生没有溢出效应,不会帮助其他学生)。对于那些不熟悉潜在结果框架,我们建议 Angrist 等人的研究(1996年) ,其中讨论了这种情况下的不遵守。进一步的讨论,见 Imbens 和 Rubin (2015)或 Rosenbaum 的前三分之一(2010)。 | ||
| + | |||
| + | 上述假设为我们提供了明确的地层和明确的治理效果在每一个层。推理如下: 给定 SUTVA,个体对任何一种实验条件的反应本质上是个体的特征。这反过来又意味着,每个个体的成员阶层在本质上是个体的特征。鉴于治疗分配是随机的,它与阶层成员无关。因此,阶层内治疗效果是因果效应,就像其他亚组治疗效果一样。随着地层和地层水平处理效应的确定,我们进入下一阶段,我们增加了实质性的假设,对地层施加约束。这些限制非常重要,因为如果没有这些限制,通常很难在估计关键的利息数量方面取得进展。更重要的是,假设使我们能够正式地将我们对问题的实质性知识纳入我们的分析。这是主要分层框架的一个特别好处。在讨论前面提到的主体分层的其他设置之前,我们简要讨论了在标准不遵从性、单调性和排除限制的背景下最常见的两个假设 | ||
| + | |||
| + | === 二元不遵从语境中的单调性和排除限制 === | ||
| + | 人们实际上如何回应随机提出采取给定的干预措施。单调性是这样一种假设,即一个人至少有可能接受分配给治疗条件的治疗,就像分配给控制条件的治疗一样。回到图1,其中显示了在纽约市学校教育券实验的背景下为二元不遵守建立的主要分层,单调性假设排除了任何“违背者”的可能性,因为这个阶层的儿童会在没有教育券提供但没有教育券提供的情况下进入私立学校。 | ||
| + | |||
| + | |||
| + | 第二个主要假设是排除限制,它涉及到分配到治疗条件将如何影响那些实际上不接受治疗的个人,如果提供的话。同样,在图1所示的例子的上下文中,这些孩子的学校类型将被随机优惠券提供保持不变。总是接受教育的学生总是进入私立学校,有或没有教育券,而从不接受教育的学生总是进入公立学校。鉴于随机化不会改变这些亚组儿童的学校教育类型,我们假设随机化同样不会影响这些儿童的后续结果。同样地,我们假设,在这些地层中,治疗的效果为零 | ||
| + | |||
| + | |||
| + | 重要的是,这些假设本质上是实质性的,而非统计性的。因此,至关重要的是通过推理来判断这些假设在每个实质性应用的背景下是否合理。就代金券研究而言,单调性似乎完全合理,因为很难想象一个学生或家庭在没有代金券提供的财政援助的情况下更有可能接受私立学校教育。然而,对于总是接受者和从不接受者的排除限制值得进一步考虑。绝不接受的是那些不管有没有优惠券都会去上公立学校的孩子。由于这些儿童的学校环境和实际的学校建筑很可能没有改变,因此可以合理地假设,治疗方案不会影响随后与学校有关的结果。然而,对于总是接受教育的人来说,可以想象的是,教育券的提供可能导致家庭为子女选择不同的私立学校。如果优惠券允许一些家庭选择进入更高质量的私立学校,那么总是接受优惠券的学生的待遇效果可能不会为零。有鉴于此,研究必须严格考虑并捍卫排除限制对总是服药者的适用或不适用这一假设,而是估计对这一亚群的治疗效果。正如我们在下面的评估部分中所讨论的,这些假设在某些情况下可以被测试。 | ||
== 估计随机试验中的关键主要因果效应 == | == 估计随机试验中的关键主要因果效应 == | ||
| + | 正如上述讨论所表明的,主层的定义和实质性的假设,以限制这些地层的特点是没有参考或事先估计。在我们看来,这种分离是利用主要分层框架的一个有益的方面: 第一个表达兴趣的组和数量,第二个确定可能有助于进一步限制或通知这些数量的实质性知识(例如假设) ,然后才能评估估计是否可能以及如何可能。简而言之,估算过程是独立的,有别于阐明这些数量的估算过程。根据对问题施加的约束,可以采取不同的一般策略进行估计。这些策略可以分为基于矩的方法(非参数)和基于模型的方法。首先,我们纯粹依赖于我们最初的假设来表达目标数量(例如地层特定的平均处理效应)作为数据的直接可观察特征的函数。当这不可能实现时,可以削弱基于矩的方法,转而试图约束目标数量。第二种方法是直接对部分或全部数据建模。这通常需要对主要阶层的结果做出分布假设,并利用基线协变量来预测个人的阶层成员。 | ||
| + | |||
| + | 我们把第一种方法称为“基于时刻”,因为我们可以根据可估计的“时刻”或数量(如平均值和比例)来估计相关的特定层次的治疗效果。第二种方法是“基于模型的”,因为我们的评估过程涉及 | ||
| + | |||
| + | 从铰接模型估计参数(Imbens & Rubin,1997)。这两种方法之间的关键区别在于,基于矩的方法只使用样本级信息,而基于模型的方法使用个体级信息,正如我们下面所讨论的。在不遵从的情况下,第一种策略可能对应用的定量研究者更为熟悉,而与第二种策略相关的工具和程序对于在更复杂的主体分层应用中估计主要因果效应通常是必要的。关于比较这两种方法的教科书讨论,参见 Imbens 和 Rubin (2015)。还可以看到 Stuart,Perry,Le 和 Ialongo (2008)的介绍。这两种通用的方法有不同的优点和缺点。基于矩的非参数方法依赖于较弱的假设,并允许考虑的结果的非标准和未知的分布形式。然而,这种结构的缺乏使得解开许多地层变得更加困难。至少在原则上,基于模型的方法可以分离出多层,以便洞察治疗影响的复杂模式。然而,重要的是,基本的分析工作是分离混合物之一ーー这是一个出了名的困难问题ーー而且这样做可能有些微妙,因为治疗效果的估计可能对建模选择敏感 | ||
== 主分层框架的好处和局限性 == | == 主分层框架的好处和局限性 == | ||
| + | 主要分层框架为审议诸如前面例子中强调的那些重要的反事实问题提供了一些好处。首先,框架的使用需要非常清晰地阐明与特定研究问题相关的实验对象在治疗和控制下所采取的后随机化经验、决定或行动。这本身就很有用。其次,在确定了相关地层之后,该框架还突出了估计治疗效果所依赖的假设。例如,在上述应用中,单调性假设排除了某些地层的存在和排除限制,固定处理效应在某些地层为零。 | ||
| + | |||
| + | 主体分层框架有利于培养对利益关键数量界定的清晰思维。然而,估算的过程相对不那么简单。尽管如此,一些标准模型已经得到了很好的理解,例如处理二元不遵从性的应用程序,以及单调性和排除限制假设实质上是站得住脚的。在这里,基于矩的 IV 是一个经典的解决方案,基于模型的 IV 产生了非常相似的 ITTc 估计值(Imbens & Rubin,1997)。在样本量大、编制者比例高的情况下,这种等效性通常是正确的。在这种情况下,一个合理的问题是为什么 | ||
| + | |||
| + | 更复杂的基于模型的 IV?一个原因是,如果提出的参数模型近似正确(这里,最重要的是,阶层结果分布是正态分布) ,基于模型的方法可以导致更精确的估计(Imbens & Rubin,1997)。然而,更重要的是,基于模型的方法提供了一个灵活的框架,可以在其中处理额外的分析复杂性,例如缺少数据和放松某些建模假设的需要。例如,使用基于模型的方法,我们可以通过允许 ITTa 为非零来评估 ITTc 的估计对于从未接受者的排除限制的敏感性。回顾上文关于总是接受私立学校教育券的学生可能有机会进入更好的私立学校的讨论。正如预期的那样,模型的稳定性通常随着额外假设的施加而增加,但在许多情况下,这种类型的灵敏度检查可以用来说明 ITTc 的估计对这种排除限制并不特别敏感(Hirano,Imbens,Rubin,& Zhou,2000)。基于模型的方法的最后一个好处,也是对于上面讨论的主体分层的一些更复杂的应用来说特别重要的一个好处,就是它很容易扩展到利益层不再由二元变量定义的环境(如上面的开端和职业学院的例子) ,以及单调性和排除限制不是有效假设的环境(如上面的工作团队的例子)。这种分析策略有潜在的缺点。首先,基于模型的方法可以对模型的偏离敏感。第二,对于基于模型的 IV 估计没有一个封闭的解决方案,这会使估计过程看起来不透明,难以向从业人员解释,并且难以执行计算。最后,正如我们前面所描述的,基于模型的方法将结果纳入到地层成员的预测中。虽然从贝叶斯的角度来看是明智的,但这可能是一种强行推销。然而,我们指出,结果对建模选择的敏感性并不是像这里讨论的那些分析策略所特有的问题。然而,由于我们强调的许多原因,像前面描述的那些灵敏度检查是分析过程的一个关键组成部分。最后,必须指出,该领域尚未取得进展,以便为应用研究人员提供强有力的指导和统计软件,使他们能够在主体分层框架内广泛利用基于模型的估计战略。在我们自己的工作中,我们试图提供可用的教程和代码,使得复制我们自己的分析成为可能(例如,Feller 等,2014) ,但是认识到更广泛的采用将需要开发分析例程和用户友好的软件包。然而,对于有兴趣进一步了解主要分层的读者,我们推荐 Imbens 和 Rubin (2015) ,Mealli 和 Mattei (2012)以及 Schochet,Puma 和 Deke (2014)提供的概述作为下一组参考进行调查。 | ||
==另见== | ==另见== | ||
2022年8月14日 (日) 16:47的版本
本词条尚未编辑完毕
研究动机
社会科学研究的一个真理,一切都是变化的。虽然我们不能期望了解影响变化的所有因素,但我们经常可以了解在特定的亚种发生的变化。例如,我们可能会根据某些可观察到的个体特征(如性别、种族/民族或社会经济地位)来估计干预的效果是如何变化的。
在随机对照试验(RCT)的背景下,估计这些亚组处理效果通常是一个直接的分析练习,通常通过估计亚组特征定义的子样本内的处理-对照差异,或通过在线性模型中包括处理和亚组指标之间的交互项来完成。
这些方法给出了每个亚组的估计治疗效果,并通过似然比检验等测试程序确定亚组效应是否存在显著差异。本质上,这些方法将感兴趣的分组视为小型实验,并返回每个此类实验的处理影响的估计。
然而,越来越多的研究人员对部分观察到的甚至完全潜在的亚组的治疗效果变化感兴趣,这些亚组不是由标准的预处理特征(如性别或种族/民族)定义的,而是由随机化后的行为、行动或决定定义的。
例如
1.私立学校提供代金券对那些只在获得代金券后才会就读私立学校的孩子,而在其他情况下会就读公立学校的孩子有什么影响?
2. 对于那些无论是否有机会参加该计划都无法完成高中学业的学生来说,多层面预防辍学计划的影响是什么? 相比之下,该项目是否只改善了那些因有机会参加该项目而从高中毕业的学生的成绩?
3.对于那些有机会参加但没有机会接受家庭护理的儿童来说,参加幼儿计划会有什么影响?这与那些本可以参加其他中心护理的儿童的影响相比如何?
与标准的子组分析相比,在这些例子中,我们无法观察到相关子组中的个体成员,从而阻止了经典的子组方法。两个关键特征是值得强调的亚组的研究兴趣是由这些研究问题确定的。
首先,子组是由特定的随机化后行为定义的。其次,为了将研究参与者分成这些兴趣的亚组,我们需要能够在观察到的和未观察到的(即反事实)实验条件下观察个体水平的行为。
在前面提到的第一个问题中,我们感兴趣的是那些在对照条件下将被分配到公立学校,但在收到随机分配的代金券后将被分配到私立学校的孩子
在第二种情况下,我们感兴趣的是那些无论他们被分配到何种实验条件下都无法从高中毕业的学生。
第三,我们感兴趣的是那些接受早期儿童项目的孩子,如果这些孩子被分配到控制条件下,按照他们将经历的护理环境进行分组。
所有这些类型的问题都允许我们进一步解读整体的治疗意图(ITT)效应,以了解特定的干预措施对儿童和家庭的影响。答案可以帮助确定所观察到的ITT效应是否由一个特定的潜在亚组驱动,如果是,如何调整干预以更好地服务于所有预期参与者。
当然,在现实中,我们只能观察研究参与者在分配治疗或控制下的随机化后行为——但不能同时观察两者。处理这类研究问题的一个分析框架是主要分层(Frangakis & Rubin, 2002)。主要分层背后的思想是首先根据样本成员在随机化后的选择、行动或经验定义内生(或与规划相关)子组,简称为主分层。
在统计学上,“主要分层”一词源于医学试验中的并发症,并最终由Frangakis和Rubin(2002)正式确定。该框架的一个特殊贡献是,它提供了清晰的区分过程,确定治疗效果的兴趣,从分析策略用于估计这些数量,我们将在下面进一步说明。
概念定义
主分层 Principal stratification是指按照某处理后变量的潜在结果对总体分层,然后考察某一层内的因果作用,例如含有非依从性的试验中的依从者,含有死亡截断的试验中的永远幸存者。它是一种应用于因果推断的统计技术,它根据处置后协变量来调整因果效应。其基本思想是识别潜在的分层结构,然后只计算每一层的因果效应。这就是所谓的局部平均处理效应 local average treatment effect(LATE)。
在从在非依从现象时,我们能够识别的只是依从者——也就是人群中的某一“层”的平均因果作用。Frangakis和Rubin把这一观察总结为主分层(principal stratification)的概念,即按照某种处理后的潜在结果对总体进行分层,而真正关心的因果作用被局限在某一个主层内。
本文旨在作为主要分层的非技术入门。
在第二部分中,我们强调主要分层框架的几种不同应用,以说明它可以应用的实质性问题和方法问题的广度。
在第三部分中,我们将重点放在识别和估计地层特定处理效果的关键假设上。
在第四部分中,我们提出了两种不同的方法来估计随机试验中存在简单(即二元)不符合的关键主要因果效应。并强调某些估计程序如何可以扩展,以处理更复杂的应用的主要分层框架。
最后,我们将重点介绍主要分层框架的好处和局限性,以及该领域的分析工具的现状,这些分析工具将对应用定量研究人员产生兴趣和价值。
在整个过程中,我们强调了这种分析的反事实逻辑基础,以及支撑这种方法并使分析挑战更易于处理的假设。
示例1
主分层的一个例子是随机对照试验的退出偏移问题。使用处置后的二元协变量(例如:退出)和二元处置变量(例如:“处置”和“对照”) ,受试者可能有四种情形:
- 总是留在研究中的受试者,不管他们被分配了哪种治疗;
- 总是会退出研究的受试者,不管他们被分配了哪种治疗 ;
- 只有在分配到处置组时才退出的受试者;
- 只有在分配到对照组时才退出的受试者。
如果研究人员知道每个受试者属于哪种情形,那么研究人员只需比较第一种情况下的结果,并估计出对该群提有效的因果效应。然而,研究人员并不知道这些信息,因此这种方法需要模型假设。
使用主分层框架还允许为估计效应提供界限(在不同的界限假设下) ,这在退出偏移的情况下很常见。
在评价研究应用中,主成分层通常被称为内生 endogenous层或亚群体 subgroups,并涉及专门的分析方法,用来检查医学和社会科学中的干预或处置的效果。
示例2
考虑一项激励试验,医生随机地鼓励或不鼓励患者打疫苗。实际上,患者即使被鼓励打疫苗,他也有可能不打疫苗,而没有被鼓励的患者也可能自己去打疫苗。用Z表示医生是否鼓励患者打疫苗(Z=1表示鼓励,Z=0表示不鼓励),用A表示患者实际上是否打了疫苗(A=1表示打疫苗了,A=0表示没有打疫苗),用Y表示患者是否得了流感(Y=1表示得流感,Y=0表示没有得流感)。注意到A可以表示为Z的潜在结果,记为A(z);Y可以表示为Z和A的潜在结果,记为Y(z,a)。我们可以根据A(z)把人群分为四层:
a) A(0)=0, A(1)=0。即无论医生是否鼓励打疫苗,患者都不会打疫苗,称这些人为拒不服药者。
b) A(0)=1, A(1)=1。即无论医生是否鼓励打疫苗,患者都会打疫苗,称这些人为永远服药者。
c) A(1)=1, A(0)=0。即患者会按照医生的建议打疫苗,称这些人为依从者。
d) A(0)=1, A(1)=0。即患者会做出与医生建议相反的决策,称这些人为抵抗者。
假设排他性成立,即Y(0,a)=Y(1,a),一个人是否会得流感只依赖于他有没有打疫苗,与医生是否鼓励他并不直接相关。稍加观察我们就会发现,第a组人和第b组人对于估计打疫苗的真正作用是没有帮助的,因为他们得流感的潜在结果都相等,要么都是Y(0),要么都是Y(1)。只有第c组人和第d组人对于估计打疫苗的真正因故作用有帮助,因为对于这两组人来说,每一组内同时存在打疫苗的人和不打疫苗的人。
医学上常用意向治疗策略来描述激励试验,用E[Y|Z=1]-E[Y|Z=0]来描述鼓励患者打疫苗带来的作用。然而,这个量并没有因果解释,它并不能反映打疫苗的因果作用。利用主分层的框架,我们就能清楚地看到,只有在依从者或抵抗者这两个人群上才能定义因果作用。如果再假设单调性,认为抵抗者不存在,那么感兴趣的因果量就只能在依从者中定义了,这个量也就是前面提到的依从者平均因果作用了。
当然,主分层也能处理非依从以外的问题。假设我们想要知道某种治疗方案对于患者生活质量的改善情况,记Z为治疗方案(Z=1为积极治疗,Z=0为保守治疗),记Y为治疗两年后生活质量是否改善(Y=1为改善,Y=0为未改善),Y是Z的潜在结果,记为Y(z)。实际研究常遇到的一个问题是,患者可能再两年内死掉,导致收集不到结局变量。试想一下,如果一个人没有活着,那谈论他的生活质量还有意义吗?所以,只有对存活个体,才能定义结局变量,这一问题被叫作死亡截断问题。用S表示个体的存活状态(S=1表示存活,S=0表示死亡),S其实是Z的潜在结果,记为S(z)。按照S(z)可以把人群分为四层:
a) S(0)=0, S(1)=0。即无论采取何种治疗方案,患者都会死亡。
b) S(0)=1, S(1)=1。即无论采取何种治疗方案,患者都会存活。
c) S(1)=1, S(0)=0。即如果接受积极治疗会存活,如果接受保守治疗会死亡。
d) S(0)=1, S(1)=0。即如果接受积极治疗会死亡,如果接受保守治疗会存活。
对于第a、c、d这三组人群,至少有一个潜在结果Y(z)是无定义的,所以在这三层中我们无法给出良定义的因果参数。只有第b组人群的两个潜在结果Y(z)都有定义,我们可以在这一层内定义幸存者平均因果作用,即E[Y(1)-Y(0)|S(0)=1,S(1)=1]。
仅仅通过观察数据无法判断出一个个体属于哪个主层,所以需要为所定义的因果量找到合理的解释才有实际意义。值得一提的是,死亡截断的问题在其他领域中也会遇到。比如要研究给学生奖学金能否会提高学生成绩,学生成绩只有在其不辍学时才能定义;要研究疫苗对于病毒载量的影响,病毒载量只有当一个人感染了才能定义。
主分层的应用
不符合分配治疗的简单和复杂模式
在社会科学的实验研究中,研究参与者往往不遵守随机分配的积极干预。那些被分配到治疗条件可能会失败,接受治疗后,那些被分配到控制条件的人仍然可以获得治疗。
例如,Barnard, Frangakis, Hill和Rubin (2003)在分析纽约市学校选择奖学金项目时遇到了这个挑战。通过这种干预,符合条件的学生被随机挑选出来领取奖学金券,以帮助支付纽约私立(主要是教区)学校的入学费用。在这种情况下,学生对随机分配会有不同的反应。对于随机获得代金券的学生(治疗组),学生可以使用代金券进入私立学校,也可以拒绝代金券进入公立学校。对于那些没有获得代金券的学生(对照组),学生可以在被拒绝经济支持的情况下就读私立学校,也可以就读公立学校。
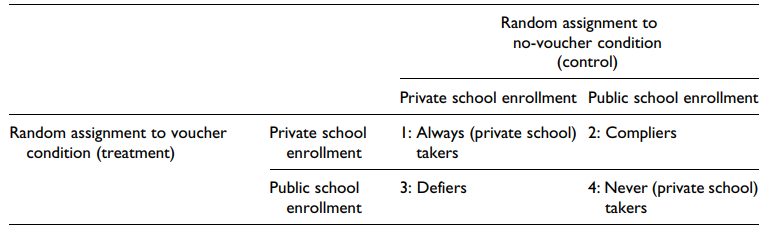
图1显示了对随机分配的这些可能的响应,最初由Angrist, Imbens和Rubin(1996)提出。在这个图中,行标题对应的是学生在分配到代金券(治疗)条件下的反应——他们要么注册私立学校,要么不注册。栏目标题同样表明了学生在没有凭证(控制)条件下的反应。在治疗和控制条件下,四对可能的潜在反应将个体分为四种反应“概况”之一,我们在此上下文中感兴趣的主要层次,如图1所示
干预的一个关键目标是了解私立学校对学生教育结果的影响。因此,从分析的角度来看,对于作为“合规者”的学生,也就是那些在获得代金券后才进入私立学校的学生来说,干预的影响是非常重要的。
作为参考,其他在定义上可能存在的群体是“总是索取者”,即不考虑分配代金券而就读私立学校的学生;“从不接受”的学生,无论他们的分配是什么,都不会进入私立学校;还有“对抗者”,指的是那些如果得到代金券就会去公立学校上学,但如果没有得到代金券就会去私立学校上学的学生。
在这种情况下,巴纳德和他的同事(2003年)发现,对于那些在研究之前就读于低于全市平均水平的学校的学生来说,教育券提供了更好的数学成绩。
因为不完美的依从性在社会科学实验中是典型的,这样的目标估计治疗效果的子集的个人参与实验的预期是相当普遍的。除了理解合规者之间的影响,这个框架还鼓励政策制定者考虑为什么某些个体没有按照实验设计的意图做出反应。事实上,以这种方式看待简单的不符合现在是标准的做法。
反事实条件下的变化
Feller, Grindal, Miratrix和Page最近转发的另一个主要分层的使用(2014)是在反事实条件下调查自然发生的变异。利用启智教育影响研究(HSIS)的数据,可以观察到,没有机会参加启智教育的儿童经历了不同形式的儿童护理,如替代的、非启智教育儿童护理中心,或由父母或其他亲属在家里提供的护理。
这种差异引发了这样一个问题:如果没有学前教育,孩子们所经历的护理环境不同,学前教育参与的影响是否会有差异。
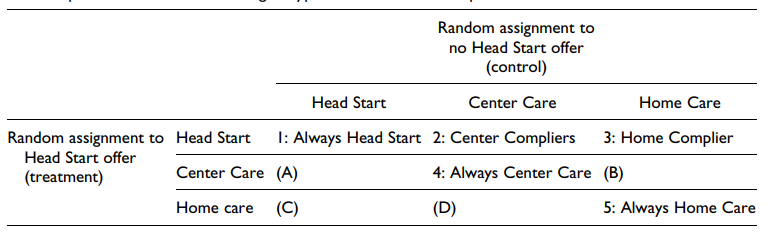
在这里,主要的兴趣层次是由儿童在分配治疗和分配控制时所经历的护理环境确定的,如图2所示。
图2中的这些主要层概括了图1所示的不符合情况。
在这个应用中,关键的亚组是两种类型的实验人群:一种是本应接受中心护理的人(图2中的单元2),另一种是本应接受家庭护理的人(单元3)。
重要的是,Feller和他的同事发现了启智式干预的主要实验效果很大程度上被那些被诱导进入的孩子所意识到,而作为随机注册的结果,启智计划和家庭护理设置,而注册启智计划的影响基本上为零,否则那些孩子会在另一个非启智计划中心的设置。这样的结果对决定项目的有效性和项目扩展的目标有影响
处理未观察到或未定义的结果
另一种情况下,当一个感兴趣的结果只对经历了另一个相关结果的个体子集可见时,主体分层是有用的。例如,考虑以劳动力发展为重点的干预措施,如就业团队(例如:Frumento等人,2012;Zhang, Rubin, & Mealli, 2008)。在评估这类项目的影响时,我们可能会特别关注项目分配对工资的影响。
复杂的是,工资只对被雇佣的个人可见和明确。一种朴素的方法是简单地比较所有观察到的在干预后被雇用的个人的工资。然而,这种方法的一个明显问题是,干预可能会诱导那些在就业时挣得特别低的人进入劳动力市场。如果是这样的话,我们可能会错误地得出这样的结论:干预对工资有负面影响。
另一种选择是为那些不工作的人的工资赋值为零。然而,这一决定将导致对该计划对就业和以就业为条件的工资的综合影响的估计。
主分层为这一常见的分析问题提供了一个有用的解决方案。Zhang, Rubin和Mealli(2008)使用了一个主要分层框架,并根据分配给处理和控制的就业状态来定义地层,如图3所示。在这里,个体可以属于四种可能的群体之一。一组无论干预与否都会被录用,一组无论干预与否都不会被录用,一组只有在接受干预时才会被录用,还有一组只有在接受控制条件时才会被录用。这个框架允许作者估计对理解项目影响特别有意义的影响。
首先,通过估计各阶层参与者的比例,作者估计了干预对就业的影响。他们通过比较两个阶层的人的比例来得出结论:那些只有在得到治疗后才会被雇用的人(即,该计划对就业有积极影响的个人)和那些只有在不被对待的情况下才会被雇用的人(即,该计划对就业有负面影响的个人)第二种和第一种的份额之间的差异是对就业的影响。
其次,对于那些在任何一种实验条件下被聘用的人,他们可以研究分配待遇对工资的影响。例如,在相关工作中,Lee(2009)发现,对于那些在两种实验条件下会被雇佣的人来说,工作团队确实会导致工资的增加,并基于这些结果得出结论,该项目通过增加人力资本(通过在这部分研究参与者中增加工资来衡量)和通过增加那些没有机会而不会被雇佣的人的就业率来影响劳动力市场结果。
替代结果和调解
主体分层的第三个应用涉及替代结果和调解问题。当追踪长期结果的成本过高或不可行时,替代结果就变得重要起来。调解问题对于理解干预行动的因果途径非常重要。
在这个领域最近的一个应用是Page(2012)对职业学院高中的研究。人力示范研究公司(MDRC)对这一高中模型的实验评估发现,随机录取进入职业学院对传统教育结果例如高中成绩,高中完成度,或者大学学历等没有影响。然而,高中毕业几年后,随机分配到职业学院的学生比对照组的学生收入要高得多。鉴于我们经常把这些传统教育里程碑视为未来劳动力市场成功的重要途径,这一组结果令人困惑。Page(2012)探索了一个假设,即通过项目提供的实习和工作见习等机会接触工作世界有助于这些积极的影响。为了探索这一假设,一个关键的分析步骤是根据学生如果有机会参加职业学院将会经历的劳动力市场暴露的变化程度来分层。
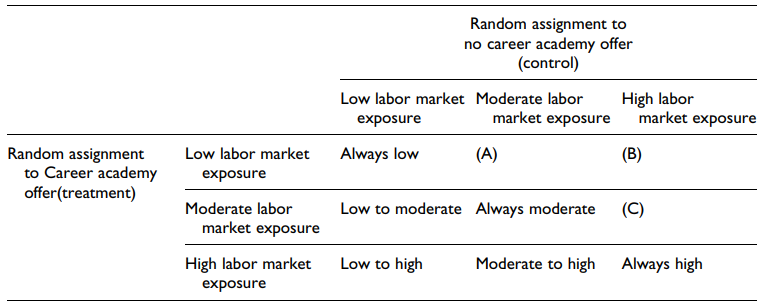
因此,这项分析的兴趣层次是由学生在实验和控制条件下所获得的工作环境接触程度来定义的。 根据学生报告的参与劳动力市场暴露活动的信息,Page将处理和控制条件下的学生分为低、中、高水平暴露。
图4说明了此应用程序中感兴趣的层次。通过估算各个阶层的待遇效应,Page发现,那些由于职业学院的提供而在工作领域经历了最大变化的学生,待遇对他们以后收入的影响最大。
这一发现是相关的,因为它与关于职业学院的关键项目组成部分的假设是一致的,这些部分导致了学生在劳动力市场的后续成功。然而,要得出替代结果是一个中介的结论,需要对机制作进一步的假设。目前,关于如何在主要分层框架内做到这一点存在一些争论。
主分层的关键假设
基于主要分层的分析分为三个阶段。第一阶段是确定我们前面描述的主要层次。总的来说,这个过程涉及到以一种相对高层次的方式思考实质性问题。下一阶段是将这些层次正式化,并编码进一步的实质性信息,以便日后进行估计。我们将在本节中讨论前两个阶段。最后一个阶段是估算,在第四部分中讨论。
首先,为了更好地界定地层,我们需要对随机试验的工作方式做一些假设。主要分层是基于潜在结果框架(Frangakis & Rubin,2002; Neyman,1923; Rubin,2005) ,它有效地考虑了每个研究个体具有个体的潜在结果和相关的潜在治疗效果。人 i,Yi (1)和 Yi (0)的潜在结果是我们可能看到的结果,如果我们治疗或不治疗的人,分别。
鉴于这些数值,一个关键的感兴趣的数量,整体平均治疗效果,是这些个别治疗效果的平均值。
因果影响是明确的,不依赖于任何分布或抽样假设: 人口由个人在实验中,而不是更多。挑战在于,虽然所有的潜在结果都已确定,但根据随机治疗分配,对于每个人来说,实际上只观察到一个潜在结果。
为了从这些基本定义出发,我们首先做出两个普遍接受的假设。首先,治疗实际上是随机的,我们将其表述为一个独立的假设,在个体是否接受治疗和个体的潜在结果是什么之间。第二个,通常被称为稳定单位治疗价值假设(SUTVA)(Rubin,1978,1980,1990) ,有效地说明治疗一个人不会影响另一个人(即,治疗一个学生没有溢出效应,不会帮助其他学生)。对于那些不熟悉潜在结果框架,我们建议 Angrist 等人的研究(1996年) ,其中讨论了这种情况下的不遵守。进一步的讨论,见 Imbens 和 Rubin (2015)或 Rosenbaum 的前三分之一(2010)。
上述假设为我们提供了明确的地层和明确的治理效果在每一个层。推理如下: 给定 SUTVA,个体对任何一种实验条件的反应本质上是个体的特征。这反过来又意味着,每个个体的成员阶层在本质上是个体的特征。鉴于治疗分配是随机的,它与阶层成员无关。因此,阶层内治疗效果是因果效应,就像其他亚组治疗效果一样。随着地层和地层水平处理效应的确定,我们进入下一阶段,我们增加了实质性的假设,对地层施加约束。这些限制非常重要,因为如果没有这些限制,通常很难在估计关键的利息数量方面取得进展。更重要的是,假设使我们能够正式地将我们对问题的实质性知识纳入我们的分析。这是主要分层框架的一个特别好处。在讨论前面提到的主体分层的其他设置之前,我们简要讨论了在标准不遵从性、单调性和排除限制的背景下最常见的两个假设
二元不遵从语境中的单调性和排除限制
人们实际上如何回应随机提出采取给定的干预措施。单调性是这样一种假设,即一个人至少有可能接受分配给治疗条件的治疗,就像分配给控制条件的治疗一样。回到图1,其中显示了在纽约市学校教育券实验的背景下为二元不遵守建立的主要分层,单调性假设排除了任何“违背者”的可能性,因为这个阶层的儿童会在没有教育券提供但没有教育券提供的情况下进入私立学校。
第二个主要假设是排除限制,它涉及到分配到治疗条件将如何影响那些实际上不接受治疗的个人,如果提供的话。同样,在图1所示的例子的上下文中,这些孩子的学校类型将被随机优惠券提供保持不变。总是接受教育的学生总是进入私立学校,有或没有教育券,而从不接受教育的学生总是进入公立学校。鉴于随机化不会改变这些亚组儿童的学校教育类型,我们假设随机化同样不会影响这些儿童的后续结果。同样地,我们假设,在这些地层中,治疗的效果为零
重要的是,这些假设本质上是实质性的,而非统计性的。因此,至关重要的是通过推理来判断这些假设在每个实质性应用的背景下是否合理。就代金券研究而言,单调性似乎完全合理,因为很难想象一个学生或家庭在没有代金券提供的财政援助的情况下更有可能接受私立学校教育。然而,对于总是接受者和从不接受者的排除限制值得进一步考虑。绝不接受的是那些不管有没有优惠券都会去上公立学校的孩子。由于这些儿童的学校环境和实际的学校建筑很可能没有改变,因此可以合理地假设,治疗方案不会影响随后与学校有关的结果。然而,对于总是接受教育的人来说,可以想象的是,教育券的提供可能导致家庭为子女选择不同的私立学校。如果优惠券允许一些家庭选择进入更高质量的私立学校,那么总是接受优惠券的学生的待遇效果可能不会为零。有鉴于此,研究必须严格考虑并捍卫排除限制对总是服药者的适用或不适用这一假设,而是估计对这一亚群的治疗效果。正如我们在下面的评估部分中所讨论的,这些假设在某些情况下可以被测试。
估计随机试验中的关键主要因果效应
正如上述讨论所表明的,主层的定义和实质性的假设,以限制这些地层的特点是没有参考或事先估计。在我们看来,这种分离是利用主要分层框架的一个有益的方面: 第一个表达兴趣的组和数量,第二个确定可能有助于进一步限制或通知这些数量的实质性知识(例如假设) ,然后才能评估估计是否可能以及如何可能。简而言之,估算过程是独立的,有别于阐明这些数量的估算过程。根据对问题施加的约束,可以采取不同的一般策略进行估计。这些策略可以分为基于矩的方法(非参数)和基于模型的方法。首先,我们纯粹依赖于我们最初的假设来表达目标数量(例如地层特定的平均处理效应)作为数据的直接可观察特征的函数。当这不可能实现时,可以削弱基于矩的方法,转而试图约束目标数量。第二种方法是直接对部分或全部数据建模。这通常需要对主要阶层的结果做出分布假设,并利用基线协变量来预测个人的阶层成员。
我们把第一种方法称为“基于时刻”,因为我们可以根据可估计的“时刻”或数量(如平均值和比例)来估计相关的特定层次的治疗效果。第二种方法是“基于模型的”,因为我们的评估过程涉及
从铰接模型估计参数(Imbens & Rubin,1997)。这两种方法之间的关键区别在于,基于矩的方法只使用样本级信息,而基于模型的方法使用个体级信息,正如我们下面所讨论的。在不遵从的情况下,第一种策略可能对应用的定量研究者更为熟悉,而与第二种策略相关的工具和程序对于在更复杂的主体分层应用中估计主要因果效应通常是必要的。关于比较这两种方法的教科书讨论,参见 Imbens 和 Rubin (2015)。还可以看到 Stuart,Perry,Le 和 Ialongo (2008)的介绍。这两种通用的方法有不同的优点和缺点。基于矩的非参数方法依赖于较弱的假设,并允许考虑的结果的非标准和未知的分布形式。然而,这种结构的缺乏使得解开许多地层变得更加困难。至少在原则上,基于模型的方法可以分离出多层,以便洞察治疗影响的复杂模式。然而,重要的是,基本的分析工作是分离混合物之一ーー这是一个出了名的困难问题ーー而且这样做可能有些微妙,因为治疗效果的估计可能对建模选择敏感
主分层框架的好处和局限性
主要分层框架为审议诸如前面例子中强调的那些重要的反事实问题提供了一些好处。首先,框架的使用需要非常清晰地阐明与特定研究问题相关的实验对象在治疗和控制下所采取的后随机化经验、决定或行动。这本身就很有用。其次,在确定了相关地层之后,该框架还突出了估计治疗效果所依赖的假设。例如,在上述应用中,单调性假设排除了某些地层的存在和排除限制,固定处理效应在某些地层为零。
主体分层框架有利于培养对利益关键数量界定的清晰思维。然而,估算的过程相对不那么简单。尽管如此,一些标准模型已经得到了很好的理解,例如处理二元不遵从性的应用程序,以及单调性和排除限制假设实质上是站得住脚的。在这里,基于矩的 IV 是一个经典的解决方案,基于模型的 IV 产生了非常相似的 ITTc 估计值(Imbens & Rubin,1997)。在样本量大、编制者比例高的情况下,这种等效性通常是正确的。在这种情况下,一个合理的问题是为什么
更复杂的基于模型的 IV?一个原因是,如果提出的参数模型近似正确(这里,最重要的是,阶层结果分布是正态分布) ,基于模型的方法可以导致更精确的估计(Imbens & Rubin,1997)。然而,更重要的是,基于模型的方法提供了一个灵活的框架,可以在其中处理额外的分析复杂性,例如缺少数据和放松某些建模假设的需要。例如,使用基于模型的方法,我们可以通过允许 ITTa 为非零来评估 ITTc 的估计对于从未接受者的排除限制的敏感性。回顾上文关于总是接受私立学校教育券的学生可能有机会进入更好的私立学校的讨论。正如预期的那样,模型的稳定性通常随着额外假设的施加而增加,但在许多情况下,这种类型的灵敏度检查可以用来说明 ITTc 的估计对这种排除限制并不特别敏感(Hirano,Imbens,Rubin,& Zhou,2000)。基于模型的方法的最后一个好处,也是对于上面讨论的主体分层的一些更复杂的应用来说特别重要的一个好处,就是它很容易扩展到利益层不再由二元变量定义的环境(如上面的开端和职业学院的例子) ,以及单调性和排除限制不是有效假设的环境(如上面的工作团队的例子)。这种分析策略有潜在的缺点。首先,基于模型的方法可以对模型的偏离敏感。第二,对于基于模型的 IV 估计没有一个封闭的解决方案,这会使估计过程看起来不透明,难以向从业人员解释,并且难以执行计算。最后,正如我们前面所描述的,基于模型的方法将结果纳入到地层成员的预测中。虽然从贝叶斯的角度来看是明智的,但这可能是一种强行推销。然而,我们指出,结果对建模选择的敏感性并不是像这里讨论的那些分析策略所特有的问题。然而,由于我们强调的许多原因,像前面描述的那些灵敏度检查是分析过程的一个关键组成部分。最后,必须指出,该领域尚未取得进展,以便为应用研究人员提供强有力的指导和统计软件,使他们能够在主体分层框架内广泛利用基于模型的估计战略。在我们自己的工作中,我们试图提供可用的教程和代码,使得复制我们自己的分析成为可能(例如,Feller 等,2014) ,但是认识到更广泛的采用将需要开发分析例程和用户友好的软件包。然而,对于有兴趣进一步了解主要分层的读者,我们推荐 Imbens 和 Rubin (2015) ,Mealli 和 Mattei (2012)以及 Schochet,Puma 和 Deke (2014)提供的概述作为下一组参考进行调查。
另见
参考文献
- Frangakis, Constantine E.; Rubin, Donald B. (March 2002). "Principal stratification in causal inference". Biometrics. 58 (1): 21–9. doi:10.1111/j.0006-341X.2002.00021.x. PMC 4137767. PMID 11890317. Preprint
- Zhang, Junni L.; Rubin, Donald B. (2003) "Estimation of Causal Effects via Principal Stratification When Some Outcomes are Truncated by "Death"", Journal of Educational and Behavioral Statistics, 28: 353–368 doi:10.3102/10769986028004353
- Barnard, John; Frangakis, Constantine E.; Hill, Jennifer L.; Rubin, Donald B. (2003) "Principal Stratification Approach to Broken Randomized Experiments", Journal of the American Statistical Association, 98, 299–323 doi:10.1198/016214503000071
- Roy, Jason; Hogan, Joseph W.; Marcus, Bess H. (2008) "Principal stratification with predictors of compliance for randomized trials with 2 active treatments", Biostatistics, 9 (2), 277–289. doi:10.1093/biostatistics/kxm027
- Egleston, Brian L.; Cropsey, Karen L.; Lazev, Amy B.; Heckman, Carolyn J.; (2010) "A tutorial on principal stratification-based sensitivity analysis: application to smoking cessation studies", Clinical Trials, 7 (3), 286–298. doi:10.1177/1740774510367811
- Peck, L. R.; (2013) "On estimating experimental impacts on endogenous subgroups: Part one of a methods note in three parts", American Journal of Evaluation, 34 (2), 225–236.
编者推荐
课程推荐
这个视频内容来自集智俱乐部读书会因果科学读书会第三季内容的分享, 主题是”因果推断在医学、药学、生物学中的应用“,由北京大学数学科学学院统计学2018级博士生邓宇昊分享。本
次分享关注因果推断框架在近二十年的两项重要进展:主分层(principal stratification)和再随机化(rerandomization)。
1.主分层。主分层的思路是根据处理后、结局前的潜在中间变量对总体进行分层,由于潜在中间变量(潜在结果)不受处理分配的影响,因此主层可被看作是处理前的基线协变量。主分层通常被
应用于两个场景中:非依从和死亡截断,尽管也存在其他场景。
2.再随机化。当面临不合适的随机分配时,Fisher建议进行再随机化。Morgan和Rubin首次对再随机化进行了正规的数学描述,其基本思路是:预先指定某种衡量协变量在不同处理组之间分布是
否平衡的准则,不采纳那些协变量不平衡的随机分配,而是一直进行随机化,直到获得协变量平衡的随机分配为止。Morgan和Rubin建议使用处理组和对照组协变量均值的平方马氏距离作为准
则,只接受平方马氏距离小于某个阈值的随机分配。他们还指出,通过再随机化,可以实现平均因果作用估计的方差下降。
文章总结
北京大学数学科学学院概率统计系的丁鹏老师在因果推断一文中第四章第一节详细介绍了主分层与工具变量
相关路径
- 因果科学与Casual AI读书会必读参考文献列表,这个是根据读书会中解读的论文,做的一个分类和筛选,方便大家梳理整个框架和内容。
- 因果推断方法概述,这个路径对因果在哲学方面的探讨,以及因果在机器学习方面应用的分析。
- 因果科学和 Causal AI入门路径,这条路径解释了因果科学是什么以及它的发展脉络。此路径将分为三个部分进行展开,第一部分是因果科学的基本定义及其哲学基础,第二部分是统计领域中的因果推断,第三个部分是机器学习中的因果(Causal AI)。
本中文词条由Jlyt007翻译,薄荷编辑,如有问题,欢迎在讨论页面留言。
本词条内容源自wikipedia及公开资料,遵守 CC3.0协议。