因果表征学习：问题，方法和应用

导语

这篇文章概括了张坤老师研究组在因果表征学习方面的最新工作，主要包含四个部分。第一部分是对因果发现传统工作的简介并且引入因果表征：何为因果表征学习，其与因果发现关系何在，以及为何需要新方法实现因果表征学习。第二部分着重于介绍因果表征学习的最新研究进展和方法， 包括在独立同分布情形、时间序列、分布迁移情形的情况下如何寻找因果隐变量和它们之间的因果关系。第三部分介绍了在迁移学习和适应性强化学习下的应用。因果表征学习为机器学习提供了更有解释性和更有效的方法。在第四部分，我们介绍了目前的分析工具causal-learn以及对未来研究工作和应用场景的展望。

研究领域：因果表征学习，机器学习，因果发现

简介

因果表征学习 Causal Representation Learning是连接因果科学与深度学习的桥梁。近十年来，深度学习成为了计算机视觉（CV）、自然语言处理（NLP）等人工智能（AI）基础领域的核心技术，同时为机器人，无人驾驶，人机交互系统，虚拟现实、生物制药、智慧城市等行业应用进行智慧赋能。深度学习是一种使用神经网络模型，通过梯度反传的信号反馈将非结构化数据，如图片、语言文字等，转化为可被机器处理的表征 representation，并使用这些表征解决识别、理解等下游任务的计算方法。2015年，在由Geoffrey Hinton, Yann LeCun 和 Yoshua Bengio（图灵奖获得者，深度学习著名人物）共同署名的Nature论文《Deep Learning》中，表征学习 Representation Learning被归为深度学习和现代AI技术取得巨大成功的主要原因。表征学习的目标是将高维的原始数据降维成低维特征，在保留信息的同时过滤掉原始数据中的噪声。

然而，通过扩大数据和模型的规模学得的表征往往只能对数据进行编码、压缩或记忆。这些表征不具有可供机器进行逻辑推理和规划的高阶语义因子（semantic concept），也不具备像人类一样在新环境下灵活解决问题的变通能力和鲁棒性。因此，如何使深度学习能像人类一样进行有意识的推理、思考与判断是下一代AI急需解决的问题。另一方面，因果（causal）模型，提供了一套系统性的、基于统计的因果推理和思考的计算方法。然而，因果模型往往只能处理结构化的数据，并不能处理生活中常见的高维的原始数据，比如图像。于是，将表征学习和因果模型进行融合，将图像这样的原始数据转化为可用于因果模型的结构化变量，赋予AI如同人类一样有意识的推理和思考的能力，成为了因果表征学习这一新兴学科的主要目标。如果我们能解决这个问题，我们就可以很好地将因果推断与机器学习结合起来，构建下一代灵活，可信的AI。

在因果表征学习中，我们通常假设数据是由因果相关的、满足一定条件的结构因果模型 Structural Causal Model（SCM）的因果隐变量，通过非线性的映射（神经网络）来产生。如果因果隐变量和它们之间的SCM能从原始数据中学习，我们就可以估计在干预了这些变量后的数据分布，或推断指定数据点的反事实结果，比如重新组合因果隐变量生成事实中不存在的数据，或者回答Why，What if等需要显式推理的问题。值得注意的是，因果表征学习与因果发现（Causal Discovery）有密不可分的关系。一方面，因果表征学习是在有很多混淆因子（confounder）下的因果发现问题的一个特例。另一方面，在没有领域知识的情况下，学习整个隐变量空间中的结构因果模型是极其困难的。因此，因果发现中常用的假设，比如Sparsity、Minimal Change Principle和Independent Causal Mechansim，通常可以成为因果表征学习的领域知识和使用的归纳偏置（Inductive Bias）。

因果发现传统工作简介

寻找因果关系的传统方法是通过随机对照实验。然而，随机对照实验通常需要耗费大量的时间和资源，有时甚至可能涉及伦理问题。例如，基因敲入是一种广泛用于创建疾病模型的技术。通常导致疾病的不是单个基因，而是由多个基因组成的网络。要找到这个网络可能需要太多的实验才能可行。因此，必须寻求替代方法——从观测数据中发现因果关系，称为因果发现，因为观测数据更容易获得。

经典的因果发现方法通常是寻找观测变量之间的因果关系，其大致分为两类。在 1980 年代末和 1990 年代初，人们注意到，在适当的假设下，可以根据变量之间的条件独立性关系恢复潜在因果结构的马尔可夫等价类 [Spirtes et al., 1993]。这产生了基于约束的方法（constraint-based method），该方法利用条件独立性测试（conditional independence tests）来进行因果发现。由此产生的等价类可能包含多个 有向无环图（DAG，或其他表示因果结构的图对象），这些DAG共享相同的条件独立性关系。所需的假设包括因果马尔可夫条件（causal Markov condition）和忠实度假设（faithfulness assumption），这两个假设建立了因果图中的d-分离属性与数据中的统计独立性属性之间的对应关系。相反，基于分数的方法 [Chickering, 2003, Heckerman et al., 1995] 不是使用统计测试，而是搜索在某些评分标准下给出最高分数的等价类，例如采用贝叶斯信息标准 [BIC, Schwartz, 1978]、给定数据的图的后验 [Heckerman et al., 1997] 和广义评分函数 [generalized score, Huang et al., 2018]。

另一组方法是基于函数因果模型 functional causal model（FCM），将效果表示为直接原因的函数以及独立的噪声项。研究表明，通过适当地约束模型类，因果方向是可识别的。具体来说，当在正确的因果方向上估计 FCM 时，估计的噪声项与假设原因独立，但在想反的方向上不成立。可识别的因果模型包括线性非高斯无环模型 [LiNGAM, Shimizu et al., 2006]、非线性加性噪声模型 [additive noise causal model, Hoyer et al., 2009, Zhang and Hyvärinen, 2009a] 和后非线性模型 [post-nonlinear causal model, Zhang and Chan, 2006, Zhang and Hyvärinen, 2009b]。但是需要注意的是，如果函数因果模型的函数空间没有约束，则无法识别因果方向，因为总是可以在反向上找到独立于预测变量的噪声项 [Zhang et al, 2015]。

上面介绍的方法已被扩展到更一般的场景。比如说LiNGAM已被扩展到有环的因果图 [Lacerda et al., 2008] 和存在潜在混杂因素的情况 [Hoyer et al., 2008] 。基于LiNGAM拓展的Specific and Shared Causal Relation Modeling [SSCM, Huang et al., 2019] 不仅可以提供整体的因果关系，还可以提供针对个体的个性化的因果知识， 以及基于因果关系来做聚类。同时，研究表明即使存在选择偏差的情况下，因果模型（包括因果方向）也是可能识别的 [Zhang et al., 2016]。

目前的因果发现方法集中在寻找观测变量之间的因果关系， 但是在现实世界的问题中，很多相关的特征可能没有被观察到，并且一些观测变量可能不是潜在的因果变量。例如，我们不能直接将图像像素视为因果变量。因此，正如在第一部分中所说的，我们想从测量的高维变量中学习潜在的因果表征（causal representation），以及它们之间的因果关系，它在通用人工智能和科学领域都是必不可少的。例如，在 AI 中，我们希望从高维视频序列中自动提取底层的低维因果变量或概念，这些变量或概念对于视频理解至关重要，从而促进下游预测或决策任务。在神经科学中，从 fMRI 记录中测量出数以万计的体素，一个关键问题是如何识别和分层聚类潜在的大脑功能区域并发现信息流。

在本篇推送中，我们将结合传统因果发现，从方法，应用和工具角度，详细探讨如何在独立同分布情形、时间序列和分布迁移情形下进行因果表征学习，寻找因果隐变量和它们之间的关系。我们总结了因果表征学习在迁移学习，适应性强化学习和视频动作识别中的应用。最后，我们对目前的可直接使用的分析工具做简要介绍和并对未来的研究和应用方向进行展望。

寻找因果隐变量和它们的关系

按所使用数据的不同性质，下面我们将把近几年提出的因果表征学习的方法分成三类进行讨论，它们分别适用于独立同分布数据、时间序列，以及有分布迁移性质的数据（比如非平稳或异构数据）。

独立同分布情形

解决含有隐变量(隐混淆因子)的一个经典方式是基于条件独立性测试，如FCI(Fast Causal Inference)算法[Spirtes et al., 1995]。该方法首先借助d-分离准则学习变量间的因果骨架图，然后通过 V-结构和一些定位准则进一步推断变量间的因果方向，最终得到因果祖先图。尽管这类方法在许多领域的到了应用，然而这类方法的输出是观测变量间的因果关系，而忽略了隐变量间的因果关系。近期，研究学者利用适用于隐变量下新的“d-分离准则”，包括Low-rank条件，Generalized Independent Noise (GIN)条件等，给出了线性系统下隐变量间因果结构的识别性条件和学习方法，接下来会在本节逐一介绍。

基于Low-rank的方法

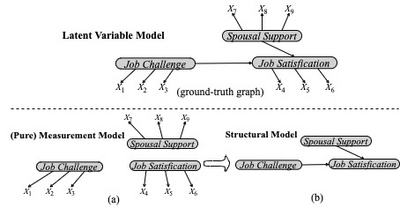
因子分析是解决隐变量间因果结构的经典方法，然而该方法输出的隐变量结构不能够保证是背后真实发生因果机制的结构[Spirtes et al., 2000; Silva et al., 2006]。Silva等人[Silva et al., 2006]开创性地利用Tetrad条件[Spearman,1928]，提出了一种两阶段学习隐变量结构的框架，即BPC（BulidPureClusters）算法+MIMBulid算法。具体来讲：以图1中上的子图为例。第一阶段利用Tetrad条件设计了三种判断测量变量间是否共享同一个父节点的规则从而去学习纯的测量模型（Pure Measurement Model，包含隐变量以及隐变量与测量变量之间的关系），即子图 (a)；第二阶段把每个隐变量所对应的测量变量为代理变量，进一步学习隐变量间的因果结构 （Structural Model，包含隐变量及其因果关系），即子图 (b)。

图1：两阶段学习隐变量间因果结构示例图。最上面为真实因果图；子图（a）第一阶段所学模型，即测量模型；子图（b）子图（a）第二阶段所学模型，即结构模型。

该研究证明了如果每一个隐变量至少有三个及其以上纯的测量变量（该变量有且只有一个隐变量作为其父节点），那么隐变量间的因果结构可通过测量变量去识别，输出结果达到Markov等价类。之后，为了高效地学习隐变量间的因果结构，Kummerfeld等人[Kummerfeld et al., 2016]基于更加宽泛的低秩条件[Sullivant et al., 2010]，提出了FOFC（FindOneFactorClusters）算法去估计隐变量间的因果结构。

基于GIN的方法

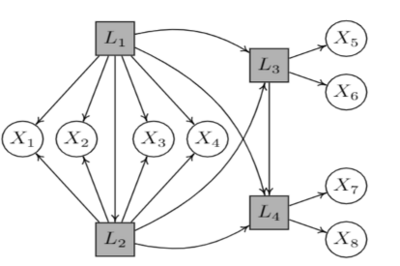
上一节中方法利用的是变量的协方差矩阵的秩的约束（second-order statistics），忽略了变量中隐含的非高斯性(High-order statistics)，导致部分因果信息被丢失。例如图2中的因果结构，包含4个隐变量和8个观察变量，上述的方法无法从这8个观察变量中去恢复隐变量间的因果结构。对于变量的非高斯而言，首先我们注意到非高斯性是可以根据观察数据轻松地检验此假设。此外，正如Cramér [1962]所述的Cramér分解定理，与高斯变量不同，非高斯分布的变量预计将无处不在，Spirtes和Zhang也同样在文献[Spirtes and Zhang 2016]中指出非高斯数据的普遍性。

图2：涉及4个隐变量的因果结构，其中X_i,i=1,…,8为观察变量。

为此，Xie等人[Xie et al., 2020 & Cai et al., 2019]根据观察数据的高阶统计量，设计了GIN (Generalized Independent Noise condition) 条件，以刻画潜在隐变量间的分离准则。直观上来说：泛化独立噪声（GIN） 条件是关于刻画观察变量的组合之间是否独立的性质，所以它可以被认为是经典的独立噪声 (independent noise (IN)) 条件的一种扩展。我们发现，通过检验一些GIN条件是否成立，能够帮助找出因果隐变量是否存在，所在位置，以及这些隐变量之间的因果关系。基于此，我们提出了一种两阶段的GIN发现算法，首先去定位隐变量及其个数，其次学习隐变量间的因果关系。

举例来说，如考虑图2中，GIN算法在第一阶段中定位到背后存在三组隐变量{L_1,L_2}，L_3和L_4，其中隐变量{L_1,L_2}包含的子节点（X_1,...,X_4）都相同。之后在第二阶段中学习{L_1,L_2}，L_3和L_4之间的因果关系。

与上一节方法相比，该方法明显的优势是：每一个隐变量所需的纯的测量变量更少，且隐变量间的因果方向都是可识别的。最近Chen等人[Chen et al., 2022]，考虑噪声是任意分布情况下，分析并给出了第二步中变量间因果方向识别的充分必要条件。

层级结构学习的方法（latent hierarchical structure）

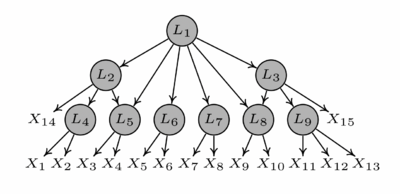
本小节继续考虑发现隐藏的因果变量及其它们之间的因果关系问题。相较于上述两个小节的模型，这里考虑更加宽泛的一种模型设定，允许一些隐藏的变量没有直接观察的变量作为其子节点，如图3中的隐变量L_1。为解决该问题，最近Xie等人[Xie et al., 2022]提出了一种最小层级结构的充分条件，并证明了在该条件下，线性非高斯的隐变量层级结构是可以通过部分观察变量完全识别的，包括隐变量的个数及其因果结构关系。

图3：一个涉及9个隐变量(L_i,i=1,…,9)和15个观察变量(X_i,i=1,…,15)的层级因果结构。

具体来讲，该研究首先定义了一种充分的最小隐变量层级结构条件（minimal latent hierarchical structure condition）：(1) 每一个隐变量至少有三个邻居节点; (2) 每一个隐变量至少有两个纯的子节点（该节点可以是隐的也可以是观察的）。研究证明：在线性非高斯系统下，如果最小隐变量层级结构条件成立，那么系统背后所有的隐变量及其因果关系可以仅有的观察变量去恢复。研究提出的LaHME算法包含以下两个步骤：步骤一：迭代地定位所有潜在隐变量的过程，包括(i) 从当前活动变量集中识别因果类 (共享共同父节点的集合)；(ii) 确定需要为这些因果类引入的新潜在变量的数量；(iii) 更新活动变量集三个子过程。步骤二：推断已识别潜在变量之间的因果结构，包括识别潜在变量之间的因果顺序和去除多余的边两个子过程。如考虑图3，在LaHME算法步骤一中，第一次迭代我们会发现结构中最下面一层的6个隐变量，即L_4,...,L_9。之后我们迭代地找出剩余的隐变量。LaHME算法的步骤二中，我们需要进一步确定隐变量间的因果关系，如L_2与L_5，L_3与L_8的关系。值得注意的是：如果背后的因果结构是一种经典的Tree-based结构，那么利用LaHME算法中的步骤一，我们就可以完全恢复背后的因果图，不需要进行步骤二的操作。

需要注意的是，本研究不需要提前已知系统背后隐变量的个数及其层级结构的层数。如果我们提前已知背后隐变量的个数，那么根据Adams等人[Adams et al., 2021]给出的充分的必要可识别性条件，我们可以通过部分观察变量，利用完备的ICA算法恢复其背后的隐变量层级结构。

我们知道因果关系对扰动具有鲁棒性，具有编码系统中的不变性，从而能够有效地推理其行为在环境中的影响。该研究对一些机器学习的任务，如图片识别问题，有重要的影响意义。这是因为往往产生因果关系的变量是一些的高级的隐的因果特征，而非直接观察的变量，如像素。因此问题就变成了找到背后真正发生因果关系的因果特征，从而推断这些特征间的因果关系，学习隐变量层级结构的问题。

小结

这一章节给出了如何从少量的观察数据中学习线性系统下的隐变量因果结构问题，给出了其结构可识别性的条件和估计算法。然而目前的研究仍然存在一些不足，如需要假定所有的观察变量不能够影响隐变量，即测量假设。第二个不足是结论是仅限于线性系统下的隐变量结构学习，如何估计非线性因果模型下的潜在隐结构并未给出。一个可行的方法是借鉴经典的非线性模型框架，如后非线性模型 [Zhang & Hyvärinen, 2009]去探索解决。

时间序列

传统因果发现: Granger causality, Granger causality with instantaneous relations

格兰杰因果关系检验（Granger causality test）是一种在无干扰因素的情况下，一种可以用来寻找时序变量之间的因果关系的方法。Granger causality test由2003年诺贝尔经济学奖得主Clive W. J. Granger所开创，常可用于分析经济变量之间的因果关系。格兰杰因果关系检验的基本观念在于：（1） 未来的事件不会对目前与过去产生因果影响，而过去的事件才可能对现在及未来产生影响。也就是说，如果我们试图探讨变量X是否对变量Y有因果影响，那么只需要估计x的落后期是否会影响y的现在值和（2）cause variable需要包含effect variable里独特非冗余的信息。假如在控制了Y变量的过去值以后，x 变量的过去值仍能对Y 变量有显著的解释能力，我们就可以称X能“Granger 影响”（Granger-cause) y。

在算法实现上，我们可通过非参数估计（Nonparametric）的方式，比如在PC algorithm上加上时序限制，即只允许因果方向从过去指向未来并在做独立检验时去除未来信息的方式来添加Granger temporal constraints。我们通常用线性自回归模型Vector autoregessive model进行简化。当X或者Y之间含有瞬时因果关系（Instantanous relations）的情形下，我们只需将现在值(Xt+1, Yt+1)也放入自回归模型的控制变量中，并保证瞬时因果关系满足有向无环图（DAG）假设即可。

值得注意的是，在使用Granger causality test寻找因果关系时，我们必须使用结构化数据，即数据中直接含有所有causal variable。当观测数据中的变量不存在直接因果关系，而是由因果隐变量或者干扰因素（counfounder）产成的，如视频数据，Granger causality test不能直接使用。

从静态时间序列中寻找因果隐变量和它们的关系

在上一章节，我们讨论了传统因果发现的方法的适用场景。然而，如果我们想从大多数实际时序信号数据，如视频数据，中寻找因果关系，Granger causality是不能直接使用的。这是在这种情形下，我们观测到的时序变量，即视频中每帧的像素，它们之间并不存在直接的因果关系。这些时序变量（像素）往往是由有具有时序因果关系的因果隐变量或干扰因素生成的。在这种情型下，我们需要做因果表征学习，从时间序列中寻找因果隐变量和它们之间的时序因果关系。在一般情况下，我们可以通过表征学习学得低维的数据表征，但我们无法保证能恢复因果隐变量。在本章节中，我们将探讨在[Yao et al., 2021 & 2022]中提出的两种从静态时间序列中寻找因果隐变量和因果关系的方法。

Linear Latent Causal Processes with Generalized Laplacian Noise

在传统因果发现中，Linear Non-Gaussian模型通常是我们期望的模型假设。在这种假设下，我们通常可以实现可识别，有保障的因果发现。我们首先将这种Inductive Bias加在Latent空间 [Yao et al., 2021]，假设实际的隐变量与其落后期之间满足线性假设（LNM）。观测到的数据Xt则是隐变量Zt的非线性（但可逆）的映射。另外，只要我们假设因果过程中的噪声（Process Noise）之间互相独立，且满足Genenralized Laplacian分布（一种Non-Gaussian模型假设）。通过理论推导，我们发现只要将这些假设转换为Variational Autoencoder （VAE）的参数化的方式，我们就可以有保证地恢复因果隐变量和它们之间的因果关系。

Figure: Linear Latent Causal Processes with Generalized Laplacian Noise模型假设

我们首先在KiTTiMask数据上验证我们的理论的模型。KiTTiMask是一个记录行人步行的视频数据集，其包含的三个因果隐变量，即行人在视频中的横向位置，纵向位置和行人在视频中的大小，它们之间满足独立线性时序关系并且噪声可近似成Laplacian Noise。下图中，实验结果验证了我们的模型能在独立线性时序关系的时序数据中恢复出因果隐变量。

Figure: KiTTiMask实验结果：（a）恢复的隐变量和真实因果隐变量之间的相关系数；（b）恢复的因变量和真实因果隐变量之间的散点图；（c）恢复出来的因果关系矩阵；（d）Latent traveral展示因果隐变量如何影响图像内容。

下一步，我们在二维质量弹簧系统视频数据上验证我们的理论和模型。质量弹簧系统满足线性假设。我们人为的在数据生成过程中在横向和纵向上加上独立的Laplacian Noise，使生成的数据满足我们的条件。下图中，实验结果验证了我们的模型能在线性时序关系的时序数据中恢复出因果隐变量和它们之间的因果关系。

Figure: 质量弹簧系统视频数据实验结果：（a）恢复的隐变量和真实因果隐变量之间的相关系数；（b）恢复出来的因果关系矩阵。

Nonparametric Latent Causal Processes

在上小节中，我们探讨了在时序因果隐变量和其落后期之间满足线性关系时，如何通过模型假设和添加归纳偏置的方式恢复因果隐变量和它们之间的关系。然而，线性假设是一种很强的函数形式假设，许多时序数据并不满足隐变量之间的线性假设。在这个小节，我们继续讨论在因果隐变量之间满足非线性，甚至非参数化（Nonparametric）的形式下，如何实现因果表征学习 。

Figure: Nonparametric Latent Causal Processes模型假设。

与上小节相同，我们仍假设数据Xt则是隐变量Zt的非线性（但可逆）的映射。不同的是，我们不再对时序因果隐变量之间的关系或噪声分布形式做任何参数化假设。然而，天下没有免费的午餐。非参数化（Nonparametric）的假设必然需要别的代价和条件来补偿。通过理论推导 [Yao et al., 2022]，我们发现在引入了因果关系指数导数之间的线性独立条件（Linear Independence Condition）后，除了Linear Gaussian Model之外的Latent Process，都有极大可能满足该线性独立条件。该条件可广泛使用于时序因果表征学习，在非参情况下寻找因果隐变量和它们的关系。

数据分布变化为时间序列因果表征学习带来的好处

在上一章节中，我们讨论了在静态时序环境下的因果表征学习。下一步，我们将继续探讨在数据分布发生变化的情况下，我们该如何恢复因果隐变量和它们的关系。值得注意的是，我们的分析是在能探测到分布变化的假设下进行的。即在恢复隐变量过程前，我们已知何时数据发生分布变化和哪种类别（class）的变化，比如域索引（domain Index）是已知的。我们的研究重是如何有效利用这些分布变化实现有效的因果表征学习，而不是检测分布变化。在LCD-NM [Yao er al., 2022]中，为了更简洁地描述不同domain之间分布的区别，我们分别引入在transition和observation function上的低维causal change factor 𝛉。即对于不同domain的数据，change factor 𝛉取不同的值。最后，我们扩展上节中探讨的Nonparametric Latent Causal Processes模型来描述数据分布变化下的数据生成过程。通过理论分析，我们发现在模型中引入变化，并在学习过程中估计数据的变化，因果隐变量的学习和识别效果可以得到显著的提升。

下面，我们分别以视频数据和动作捕捉数据为算例，验证我们的理论和模型。首先，我们在multi-domain cartpole数据上测试。在该数据集的不同domain之间，小车的质量和重力系数会发生变化，从而导致时序数据的分布发生变化。我们在该数据集上测试LCD-NM ，可以发现在数据分布发生变化的情况下，因果隐变量和它们之间的关系可以被识别。 同时，我们也在动作捕捉数据（CMU-Mocap）上验证算法。该组数据（Subject #8）记录11组不同类型行走（比如，小碎步、大跨步，快速行走等）试验数据。这些不同的行走方式导致了数据分布的不同。我们发现LCD-NM可以很好的在时序数据的分布发生变化的情况下恢复因果隐变量和它们的关系。同时，估计的因果因子change factor也能很好的描述分布的区别。

最后，值得注意的是，[Yao et. al., 2021]中提出的nonstationary noise非参数模型（LEAP）是LCD-NM的一个特例。相较而言，LCD-NM考虑了更普适的分布变化，比如因果关系的变化，同步也利用了nonstationary process中部分stationary process的特性学习来识别因果隐变量。

分布迁移情形

在许多情况下，记录的数据可能是非平稳的（non-stationary)，其数据分布随时间而变化，或者是异构的（heterogeneous），其数据分布随域（domain）变化。近来的研究表明，数据分布的变化反而可以给因果发现提供更多的信息，从而有助于因果发现。接下来着重介绍在分布发生变化的时候，不同情境下因果发现的几个工作。

Causal discovery from nonstationary/heterogeneous data [CD-NOD, Huang et al., 2020]:

CD-NOD 着力于解决在分布发生变化的情况下，如何找到观测变量之间的因果关系，主要包括以下三个问题：1. 检测哪些变量对应的因果机制发生了变化，以及如何学习因果骨架（causal skeleton）? 2. 如何充分利用数据分布变化携带的信息来判定因果方向？ 3. 找到了因果结构之后，如何进一步分析因果机制随着时间或条件具体是如何变化的？

观测变量分布的变化可以理解为存在一些未观测到的隐变量或隐藏的混杂变量（hidden confounders），其值可能随着时间或域变化，从而导致观测变量的概率分布发生变化。换句话说，一个变化的因果关系是因为背后存在影响这个因果过程的变量。例如，在 fMRI 数据中，数据分布可能会随着注意力或外部刺激而改变，而这种刺激可能会成为影响很多大脑区域的隐藏混杂因素。直接忽略这些隐藏的混杂因素可能会给我们带来误导性的结果，包括虚假的因果连接或错误的因果方向。

CD-NOD的基本思想如下：我们将隐藏的变化因素（hidden change factors）表示为C的函数，其中C可以是域索引（domain index），时间索引（ time index）， 或者条件索引（condition index）等。 C 充当表征潜在变化因素的代理变量（surrogate variable）。在前面的例子中，大脑区域之间的因果关系可能会被平滑变化的注意力或外部刺激所混淆，因此这里的C可以是表征注意力变化的时间指标。在处理包含来自不同受试者的数据时，因果关系可能会受到基因因素的混淆，而基因因素因受试者而异，因此在这种情况下，可以将C作为个体索引（subject index），以消除隐藏基因因素的影响。因此，我们将变量 C 纳入因果系统作为表征未观察到的变化因素的代理变量，然后在增广变量集（augmented variable set）上应用基于约束的因果发现算法来找因果结构。 其中，CD-NOD通过检测观测变量Vi和C之间的条件独立性，来检测哪些变量对应的因果机制发生了变化。这一步在异常检测和根本原因分析（root cause analysis）中非常有用，因为在一些实际问题中，虽然我们可能会观察到大量变量的联合分布的变化，但实际上只是由于与 C 有直接联系的少数根本原因。

Figure: 真实的因果关系图。其中g(C)和θ(C)表示未观测到的隐藏的变化因素，它们可以表示为随着C变化的函数。

进一步地，在学习了因果骨架之后，我们通过独立变化原理（independent change principle）来判定因果方向。 也就是说，原因的分布（P(cause)）和给定原因的结果的分布（P(effect|cause)）是独立变化的，但这种独立性通常在错误的方向上不成立。对于两个相邻变量，当其中只有一个与 C 直接连接，也就是invariance的情况，是一种特殊情况。

Figure: CD-NOD搜索过程示例。(a) 初始图。 （b）检测哪些变量对应的因果机制发生了变化。（c）恢复因果骨架。（d）识别因果方向。

从上述的分析我们很高兴地看到概率分布的变化其实有利于学习因果结构的。 回想下，在独立同分布的情况下，利用噪声项和原因之间的非对称独立性，只有在限定的函数空间下，因果方向才是唯一确定的。比如说，在线性高斯和在函数空间无任何限制的情况下，因果方向不能唯一确定。相反地，当有分布变化的时候，我们可以利用独立变化原理来确定因果方向，而不需要限制因果机制函数空间。

时变因果模型 (Time-varying causal model [Huang et al., 2019])：

在这个工作中，我们提出时变因果模型，来表示非平稳时间序列中的因果过程。特别地，我们把随时间变化的因果机制（causal mechanism) 看做隐变量，而不是参数，并且对因果机制的变化进行建模。特别地，假设变量之间的因果关系是线性的，并且其中的隐变量：因果系数和噪声项的方差，满足auto-regressive models来变化。并且，由于因果模型描述了概率分布是如何随着时间变化的，所以如果我们知道因果模型是如何随着时间变化的，就可以以此做出适应性预测。

Figure: 时变因果模型示意图。其中b和h是隐变量，他们分别用来表征满足auto-regressive model的因果系数和噪声项方差的对数。

之后的识别潜在的因果过程（identifying latent causal process）的工作，比如 [Yao et al., 2021，2022]，可以看做更进一步的扩展。其允许输入变量是图像，并且因果关系可以是非线性的。

Partial Disentanglement for Domain Adaption [Kong et. al., 2022]

图片识别的迁移学习（Domain Adaptation）任务通常会提供多组在不同source domain下图片x和标签y。其条件分布P(y|x)在不同domain下有一定变化。我们的目标是在使在source domain上训练的模型，通过迁移训练，能在未提供标签的target domain下具有良好表现。传统迁移学习着重于学习不同domain之间不变的部分，并使用这些不变的部分进行预测。与之不同的是，我们提出的iMSDA [Kong et. al., 2022]通过因果表征学习，识别出解释domain之间区别的因果隐变量，并使用这些隐变量对数据做translation，将其投射到同一domain进行训练，实现迁移学习。

如上图所示，我们假设图片x和标签y是由因果隐变量zc和zs通过非线性（但可逆）的映射生成。其中，zc包含图片content信息（domain之间不变的部分），zs包含图片style信息（domain之间变的部分）。值得注意的是，在不同domain下，生成函数是不变的，变化的部分仅有zs部分的分布。在这种情况下，我们学习生成函数其实是所有图片的共有的渲染程序。为了因果隐变量zs的可识别性，我们假设zs在给定domain index u的情况下的条件独立性（这是一种实现minimal change principle的方式）。通过学习并识别zs和其生成过程，我们可以multi-domain的图片，可识别地translate到target domain，如上图将所有颜色数据都投射到红色数字domain中，从而直接在target domain（红色数字）上解决迁移学习问题。

On the Identifiability of Nonlinear ICA: Sparsity and Beyond [Zheng et. al., 2022] Causal discovery with general non-linear relationships using non-linear ica. [Ricardo Pio et al. 2020]

最后，我们统一探讨独立成分分析（ICA）和因果学习之间的关系。简单来说，因果发现是ICA问题的一种特殊情况。ICA解决的问题是从（线性或非线性）混杂的信号中识别出相互独立的成分。而函数功能因果模型（FCM）的数据生成过程正是将相互独立的噪声，通过因果关系混杂成观测到数据。两者唯一的区别是，FCM在结构上需满足有向非环图（DAG），或在时序数据上满足Granger Causality假设等。线性ICA的可识别性只需满足non-Gaussian source就可达到，因此LiNGAM能将ICA直接应用到线性条件下的因果发现问题。然而，nonlinear ICA的可识别性是非常困难的问题。直到近两年，人们才发现在能找到多个domain的数据，并且因果隐变量在额外提供的surrogate variable下被条件独立时，我们才能恢复出这些因果隐变量。在[Ricardo Pio et al. 2022] 中，我们就是使用这种nonlinear ICA的可识别性，实现非线性的因果发现的。

因果表征学习则更是与ICA息息相关。例如，之前我们讨论的时序因果表征学习[Yao et al., 2021 & 2022]和迁移学习[Kong et. al., 2022]，都可视为这类情况下的nonlinear ICA在因果表征学习领域的拓展。然而，这类ICA方法的限制在于，训练数据必须含有足以解释domain区别的surrogate variable，而且这些surrogate variable可使因果隐变量独立。自然，我们会有疑问：在没有surrogate variable的情况下，nonlinear ICA是否也能达到的可识别性呢？在[Zheng et. al., 2022]中，我们使用structural sparsity assumption来回答这个问题。我们发现如果在生成过程中，对每个隐变量Si，我们都能找到一组变量{Xi}，使得Si是这组变量唯一的共有parent时，nonlinear ICA就可以达到可识别性。例如，在左图中，对于X1和X4，S1是它们之间唯一共有的parent。在这种结构稀疏性的条件下，我们可以在没有surrogate variable的情况下实现nonlinear ICA的可识别性。这类sparse nonlinear ICA在因果表征学习上的拓展会是一个很有意思的研究方向。

应用

在本章节中，我们将探讨因果表征学习在迁移学习、适应性强化学习、以及动作识别等机器学习任务上的应用。

迁移学习

Domain adaptation as a problem of inference on graphical models: causal view (2013 & 2016), data-driven (Petar’s work & particle disentanglement)

迁移学习是因果表征学习直接的应用之一。根据Minimal Change Principle [Huang et al., 2020]，在正确的因果表征下，不同domain之间的分布变化的通常可由在少数因果（隐）变量之间的causal edge/node上的干预来解释。因此，如果因果隐变量和它们之间的关系能被识别，迁移学习就只用发生在极少数的模型参数上。因果表征学习大大减少了迁移学习需要的数据量。这也是为什么人类在新环境在灵活变化、适应的根本原因。在[Zhang et al., 2020]中，我们首先使用上章节介绍的，在数据分布发生变化的情况下因果发现方法CD-NOD [Huang et. al., 2020]，寻找(X，Y)之间的因果图。如右图所示，在找出正确的causal factorization后，我们可对图里的每组独立因果模块，比如P(X3 | X2, Y, 𝛉3)，单独建模，通过因果变化因子𝛉捕捉不同source domain之间的分布区别。在做迁移时，我们只需使用少量target domain数据，推断或学习出发生变化的causal edge以及该edge上的变化因子，就可实现有效的迁移学习。当观测到的数据（比如图像像素）不是因果相关的变量而是由因果隐变量生成是，我们可使用上节探讨的iMSDA [Kong et. al., 2022]，通过因果表征学习，识别出解释domain之间变化的因果隐变量，并使用这些隐变量对图像数据做translation，将其投射到同一domain进行训练，从而实现图像迁移学习。

Image translation with minimal changes (include some nice pictures)

Xie, Shaoan, et al. "Unaligned image-to-image translation by learning to reweight." Proceedings of the IEEE/CVF International Conference on Computer Vision. 2021.

另外，基于Minimal Change Principle的因果表征学习也可应用于图片转换（Image Translation）任务。在训练数据集包含多个未匹配的图像domain情况下，我们提出的基于因果表征学习的模型IrwGAN [Xie et. al., 2021]可以有效地对不同domain的图片进行匹配同时学习图片转换函数，解决图片转换过程中content和style混杂的问题。

如上图所示，与其余现有方法相比，基于因果表征学习的图像转换方法IrwGAN保留了主要的图片内容信息，并且仅对图片的风格信息进行编辑和转换。

适应性强化学习

AdaRL: What, Where, and How to Adapt in Transfer Reinforcement Learning [Huang et al., 2022]:

强化学习是通过与外界环境互动来学习策略使得奖励最大化。强化学习的一个实际挑战是如何在面对新环境时对之前学习到的策略进行快速且有效的调整，因为现实世界总是在变化的。

AdaRL可以有效地适应跨领域最优策略的变化。其基本思想是：找到影响最优策略的最小充分因素集（a minimal sufficient set of factors），并理解这些因素在不同环境中是如何变化的。 例如，在Cartpole游戏中，当我们将系统从地球移动到火星时，如果agent可以刻画是重力改变了最优策略，并理解它如何影响策略，那么agent就可以通过仅用少量样本估计一维重力来快速适应策略。 与直接适应观察到的高维图像相比，它更有效，也更易于解释。

现在让我们详细看一下图表示(graphical representation)和模块化属性(modularity)是如何帮助迁移强化学习。

假设我们有来自多个领域的数据，包括高维图像序列、动作和奖励，并且不同的领域可能有不同的环境，比如重力和图像上所加噪声水平的变化。AdaRL的基本思想是我们利用简约的图表示（parsimonious graphical representation）来表征系统中变量之间的结构关系，包括不同维度的状态s、以及奖励变量r、动作变量a、以及感知图像o之间的结构。此外，与学习高维输入上的分布偏移的经典方法不同，由于图分解，我们引入了低维向量 θ 以紧凑的方式表征特定领域的信息。特别地，θo 用于表征观察函数的变化，θs 用于转换动态的变化，θr 用于奖励函数的变化。在这个例子中，域在重力和所加白噪声方面是不同的，因此我们可以使用一个二维向量来表征这些变化，其中一维用于重力，另一维用于不同的噪声水平。请注意，这里我们只观察图像序列 ot、奖励 rt 和动作 at，所有其他部分都是根据数据估计的，包括潜在状态 st、状态转移函数、变化因子 θ 以及变量之间的图结构。

我们可以看到，图表示提供了一种紧凑的方式来编码变化的内容和位置（what and where the changes ae)。具体来说，首先从图结构中，我们可以很直观地看出动作预测需要哪些维度的状态。在这个例子中，策略优化只需要 s1 和 s3，而不需要 s2，因为它不会影响未来的奖励。此外，我们从图表示里可以快速知道变化在哪里，并且知道哪些变化需要适应。在这个例子中，只有 θs 捕捉到的重力变化和 θr 捕捉到的可能的奖励变化需要适应，但我们不需要适应 θo 捕捉到的加在图像上的噪声的变化，因为它不会影响未来的奖励。另外，由于具有模块化（modularity）的特性，可以单独考虑各个因素，避免了维数灾难。 因此，通过明确地利用这种紧凑的表示来编码变化，在Cartpole这个例子中如何平衡pole的策略只随着重力而变化，所以在一个新的领域，只需要少量样本来估计低维变化因子，然后我们可以直接推导出新域中的最优策略。 我们可以看到图知识提供了更可解释和更有效的适应。此外，通过识别变化的位置和方式，我们不仅利用了不变部分，还利用了可变部分，因此可以更有效地适应。 值得一提的是，仅依靠不变部分可能会牺牲部分性能，因为一些关键信息会丢失。

目前的分析工具以及对对来的展望

Causal-learn

Causal-learn，由CMU张坤老师主导，多个团队（CMU-CLeaR因果研究团队、蔡瑞初老师团队、宫明明老师团队和Shohei Shimizu老师团队）联合开发出品的因果发现算法平台。 Causal-learn用Python实现了CMU开发的基于Java的Tetrad因果发现平台，并进一步加入新的算法和功能。其中包含了因果发现的经典算法与API，并且提供了模块化的代码，以方便研究者实现自己的算法。Causal-learn所有模块均基于Python实现，从而避免了传统因果发现库对R/Java的依赖，为Python开发者提供便利。 Causal-learn支持： Constrained-based causal discovery methods. Score-based causal discovery methods. Causal discovery methods based on constrained functional causal models. Hidden causal representation learning. Permutation-based causal discovery methods. Granger causal analysis. 多个独立的基础模块，比如独立性测试，评分函数，图操作，评测指标。 更多最新的因果发现算法，如gradient-based methods等

平台介绍

基于Python的统一算法框架

Causal-learn在设计上尽量的将代码模块化，简化了研究者的开发难度。同时通过提供简洁高效的代码接口，让不同领域的用户都能够轻松地应用因果发现算法。整体平台全部基于Python，用户无需再依赖于Java或R等环境，充分享受Python开发与使用的便利性。

同时，causal-learn提供了简单的安装方式，一行代码就能够将最经典、最全面的因果推荐算法部署在用户的项目中。

经典算法的官方实现

Causal-learn包含了许多经典算法及其扩展的官方实现，如PC，PNL, LiNGAM等。这些因果发现领域“里程碑式”的算法的主要作者，都在causal-learn的领导团队中为平台建设指引方向。因此，causal-learn提供了最“官方”的算法实现。用户通过熟悉相关代码，能够更快的掌握因果发现的经典算法，从而把握领域的整体发展，为相关研究提供启发。

持续更新，掌握领域前沿

Causal-learn有着一个稳定的开发与维护团队，其背后的科研团队也持续的在因果发现领域输出最新的工作。因此，用户通过关注causal-learn算法平台，能够时刻掌握领域最新进展，第一时间将最新工作应用在不同的科研与生产项目中。

简单上手

安装

Causal-learn提供Pip作为安装方式，同时支持Windows和Linux，用户可以通过简单的一行命令来进行安装使用:

pip install causal-learn

因果发现，只需一步

Causal-learn为所有模型都提供了简单易用的接口，用户可以通过一行代码在自己的数据上进行因果发现:

cg = pc(data)

可视化与评测

算法运行结束后，用户可以查看生成的因果图，并通过多种评测指标来与基准图进行对比

cg.draw_pydot_graph()

目前的难点和将来的重点

因果表征学习作为一个新兴领域，在其理论、方法和应用方面存在许多待解决的问题和难点。作为本文结尾，我们将列举目前的难点和将来的研究重点，以期能抛砖引玉，在结合因果模型和深度学习的路上与君共勉。我们认为，在理论方面，大多数现有工作都基于Independent Causal Mechanism，与Minimal Change Principle。那么，有没有别的归纳偏置可用于因果表征学习，来寻找并识别出因果隐变量和它们之间的关系？比如，在Conditional Indenpendence的假设不满足时，在时序因果表征学习中，能否在不使用干预信息的前提下，寻找具有瞬时因果关系的因果隐变量？如何在没有surrogate variable的情况下实现因果表征学习的可识别性？因果表征学习的理论分析可否推导出隐变量识别的收敛速度？

在方法方面，尽管现有的理论工作大多数都配有相应的模型和验证结果，到底哪种模型的构建方式能更有效地被深度学习的训练方式优化，从而在大样本数据下更好的识别因果隐变量和它们之间的关系？进一步思考，我们能否提出一个通用的大样本的基准数据集，来验证和比较各类因果表征学习方法？另一方面，现有因果表征学习大多数需要多domain数据并且我们需要假设模型知道分布何时会发生变化。将来的方法能否自动检测分布的变化，从来不需要对domain index进行人为的标注？在应用方面，我们能否判读出哪些AI任务的性能可以被因果表征学习显著提升，从而选定因果表征学习的最佳技术载体？比如，推荐系统作为AI与行业应用结合最紧密的方向，其用户/商品的表征和推荐准确度是否能受益于因果表征学习？

最后，我们认为，因果表征学习将来的研究重点须着重于与实际问题的结合，在因果模型理论的引导下，赋予AI如同人类一样有意识的推理和思考的能力。如果我们能解决这个问题，我们就可以很好地将因果推断与机器学习结合起来，构建下一代灵活，可信的AI。

参考文献

• LeCun, Yann, Yoshua Bengio, and Geoffrey Hinton. "Deep learning." nature 521.7553 (2015): 436-444.
• P. Spirtes, C. Glymour, and R. Scheines. Causation, Prediction, and Search. Spring-Verlag Lectures in Statistics, 1993.
• D. M. Chickering. Optimal structure identification with greedy search. Journal of Machine Learning Research, 3:507–554, 2003.
• D. Heckerman, D. Geiger, and D. M. Chickering. Learning bayesian networks: The combination of knowledge and statistical data. Machine Learning, 20:197–243, 1995.
• G. Schwartz. Estimating the dimension of a model. The Annals of Statistics, 5:461–464, 1978.
• D. Heckerman, C. Meek, and G. Cooper. Interventions and causal inference. In Innovations in Machine Learning, pages 1–28, 1997.
• B. Huang, K. Zhang, Y. Lin, B. Schölkopf, and C. Glymour. Generalized score functions for causal discovery. In KDD, pages 1551–1560, 2018.
• S. Shimizu, P.O. Hoyer, A. Hyvärinen, and A.J. Kerminen. A linear non-Gaussian acyclic model for causal discovery. Journal of Machine Learning Research, 7:2003–2030, 2006.
• P. O. Hoyer, D. Janzing, J. Mooji, J. Peters, and B. Schölkopf. Nonlinear causal discovery with additive noise models. In Advances in Neural Information Processing Systems 21, Vancouver, B.C., Canada, 2009.
• K. Zhang and A. Hyvärinen. Acyclic causality discovery with additive noise: An information- theoretical perspective. In Proc. European Conference on Machine Learning and Principles and Practice of Knowledge Discovery in Databases (ECML PKDD) 2009, Bled, Slovenia, 2009a.
• K. Zhang and L. Chan. Extensions of ICA for causality discovery in the hong kong stock market. In Proc. 13th International Conference on Neural Information Processing (ICONIP 2006), 2006.
• K. Zhang and A. Hyvärinen. On the identifiability of the post-nonlinear causal model. In Proceedings of the 25th Conference on Uncertainty in Artificial Intelligence, Montreal, Canada, 2009b.
• K. Zhang, Z. Wang, J. Zhang and B. Schölkopf. On estimation of functional causal models: general results and application to the post-nonlinear causal model. ACM Transactions on Intelligent Systems and Technology (TIST), 7(2), 1-22.
• G. Lacerda, P. Spirtes, J. Ramsey, and P. O. Hoyer. Discovering cyclic causal models by independent components analysis. In Proceedings of the 24th Conference on Uncertainty in Artificial Intelligence (UAI2008), Helsinki, Finland, 2008.
• P. O. Hoyer, S. Shimizu, A. J. Kerminen, and M. Palviainen. Estimation of causal effects using linear non-gaussian causal models with hidden variables. International Journal of Approximate Reasoning, 49:362–378, 2008.
• B. Huang, K. Zhang, P. Xie, M. Gong, E. Xing, and C. Glymour. Specific and shared causal relation modeling and mechanism-based clustering. In Advances in Neural Information Processing Systems (NeurIPS), 2019.
• K. Zhang, J. Zhang, B. Huang, B. Schölkopf, and C. Glymour. On the identifiability and estimation of functional causal models in the presence of outcome-dependent selection. UAI, 2016.
• Spirtes, P., Meek, C., and Richardson, T. Causal inference in the presence of latent variables and selection bias. In Proceedings of the Eleventh conference on Uncertainty in artificial intelligence (UAI 1995), pp. 499–506, 1995.
• Peter Spirtes, Clark Glymour, Richard Scheines. Causation, prediction, and search [M]. London: MIT press, 2000.

Charles Spearman. Pearson’s contribution to the theory of two factors [J]. British Journal of Psychology, 1928, 19(1):95–101.

• Ricardo Silva, Richard Scheines, Clark Glymour, and Peter Spirtes. Learning the structure of linear latent variable models [J]. Journal of Machine Learning Research, 2006, 7(Feb): 191-246.
• Ricardo Silva, Richard Scheines, Clark Glymour, and Peter Spirtes. Learning the structure of linear latent variable models [J]. Journal of Machine Learning Research, 2006, 7(Feb): 191-246.
• Erich Kummerfeld, and Joseph Ramsey. Causal clustering for 1-factor measurement models[C]. Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD 2016). New York: ACM, 2016: 1655-1664.
• H. Cramér. Random variables and probability distributions (2nd edition) [M]. Cambridge: Cambridge University Press, 1962.
• Peter Spirtes, and Kun Zhang. Causal discovery and inference: concepts and recent methodological advances [J]. Applied informatics, 2016, 3(1): 1-28.
• F. Xie, R. Cai, B. Huang, C. Glymour, Z. Hao, and K. Zhang. Generalized Independent Noise Condition for Estimating Latent Variable Causal Graphs. Advances in Neural Information Processing Systems 33 (NeurIPS 2020), Virtual Conference, 2020.
• R. Cai, F. Xie, C. Glymour, Z. Hao, and K. Zhang. Triad Constraints for Causal Discovery in the Presence of Latent Variables. Advances in Neural Information Processing Systems 32 (NeurIPS 2019), Vancouver, CANADA, 2019.
• Z. Chen, F. Xie, J. Qiao, Z. Hao, K. Zhang, and R. Cai. Identification of Linear Latent Variable Model with Arbitrary Distribution. Proceedings of the AAAI Conference on Artificial Intelligence (AAAI 2022), Vancouver, CANADA, 2022.
• F. Xie, B. Huang, Z. Chen, Y. He, Z. Geng, and K. Zhang. Identification of Linear Non-Gaussian Latent Hierarchical Structure. Thirty-ninth International Conference on Machine Learning (ICML 2022), Baltimore, Maryland USA, 2022.
• Adams, J., Hansen, N., and Zhang, K. Identification of partially observed linear causal models: Graphical conditions for the non-gaussian and heterogeneous cases. Advances in Neural Information Processing Systems (NeurIPS 2019), 34, 2021.
• Zhang, K. and Hyv¨arinen, A. On the identifiability of the post-nonlinear causal model. In Proceedings ofthe twenty-fifth conference on uncertainty in artificial intelli- gence, pp. 647–655. AUAI Press, 2009.
• Huang, Biwei, et al. "Causal Discovery from Heterogeneous/Nonstationary Data." J. Mach. Learn. Res. 21.89 (2020): 1-53.
• B. Huang, K. Zhang, M. Gong, and C. Glymour. Causal discovery and forecasting in nonstationary environments with state-space models. In ICML, 2019c.
• Zhang, Kun, et al. "Domain adaptation as a problem of inference on graphical models." Advances in Neural Information Processing Systems 33 (2020): 4965-4976.
• B. Huang, F. Feng, C. Lu, S. Magliacane, and K. Zhang. Adarl: What, where, and how to adapt in transfer reinforcement learning. ICLR, 2022.