“手写识别试验”的版本间的差异
| 第13行: | 第13行: | ||
</html> | </html> | ||
| − | + | <iframe width=350 height=400 frameborder=1 scrolling=no data-src="http://www.swarma.org"/> | |
=运行方法= | =运行方法= | ||
2024年5月8日 (三) 01:42的版本
- 名 称:手写识别试验
- 作 者:nay0648
- 源代码:pwriter.zip
运行方法
首先,在面板上写好字母点input键后,程序把面板上的图象信息转换为一个二进制向量,即按从左到右,从上到下的顺序检查面板,如果该位置被写过则对应1,如果没被写过则对应0。然后对该二进制向量进行单位化,单位化的目的是使得各种输入向量都有相等的长度,以便在第一层神经元中实现公平竞争。单位化了的向量送入神经网络进行计算。
运行原理
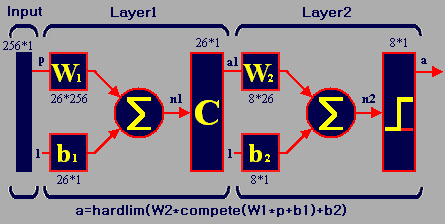
PWriter2所用的神经网络共两层,结构如图下图所示,注意图中大写粗体字母表示矩阵,小写粗体字母表示向量,小写细体字母表示标量。
网络的第一层有256个输入,26个神经元,每个输入都和各个神经元相连,即每个神经元都能接收这256个输入。每个神经元有256个权值,是字母的标准写法,即每个神经元都储存着一个标准模式,26个大写字母的标准写法分别由对应的这26个神经元储存。每个神经元的权值向量也是单位化的,同样是为了实现公平竞争。该层的传输函数为竞争函数。所谓竞争函数即每个神经元互相竞争,净输入最大者获胜,输出为1,其余净输入较小的神经元竞争失败,输出为0,以竞争函数为传输函数的神经元层每次只有净输入最大的那个神经元输出为1,其余都为0(不考虑净输入相等的情况)。
单神经元净输入的计算方法是输入向量的各个分量和权值向量的对应分量相乘,然后相加,再加上偏置值,即输入向量和权值向量的内积加上过竞争函数,该神经元输出1,其余输出0,这样一来就得到了一个26维向量,该向量进入第二层神经元继续计算。
第二层有26个输入,8个神经元,26个字母的ASCII码由这8个神经元的权值共同记录着,即每个神经元权值向量的第一个分量记录“A”的ASCII码,以二进制表示,第二个分量记录“B”……这层的传输函数为hardlim函数,该函数当净输入大于等于0时输出1,小于0时输出0。先前得到的向量进入该层后,由于只有一个分量为1,所以每个神经元只有该位置的数据为原来的数,其余分量位置上的数据都为0。再加上-0.5的偏置,使原来
为1的量为0.5,原来为0的量为-0.5,通过hardlim函数后所得的向量就为对应字母的ASCII码,再通过程序转换后就可输出该字母。
这个程序的问题还很多。由于第一层神经元记录的标准模式连字母在面板中的位置也记录了,所以即使当输入已经非常象一个标准模式,但位置偏了,所得的向量仍与标准向量差别较大,所以仍会认不准。而且,由于使用了竞争函数,所以即使人看来输入不象其中任何一个字母时,还是总会有一个标准向量与输入的内积最大,所以还是会认定一个错误的字母