预测物种的空间分布

数据准备

先引用一些包,从sklearn.datasets获得物种分布的数据。由S. J. Phillips等提供，论文参考见

   “Maximum entropy modeling of species geographic distributions” 
   S. J. Phillips, R. P. Anderson, R. E. Schapire - Ecological Modelling, 190:231-259, 2006.

这篇论文用了最大熵的方法来预测物种的分布，但我们完全可以使用其他方法例如logistic回归和SVM来进行预测。

    from sklearn.datasets.base import Bunch
    from sklearn.datasets import fetch_species_distributions
    from sklearn.datasets.species_distributions import construct_grids
    from sklearn import svm, metrics
    from mpl_toolkits.basemap import Basemap
    import matplotlib.pyplot as plt

    # Load the compressed data
    data = fetch_species_distributions()
    # Set up the data grid
    xgrid, ygrid = construct_grids(data)

data是一个字典（dictionary）,里面储存着Bradypus variegatus（一种树懒）和Microryzomys minutus（一种巢鼠）两个物种的地理分布数据，代号分别为"bradypus_variegatus_0",和"microryzomys_minutus_0"。对于每一个物种，储存着8个key-values对，如下所示：

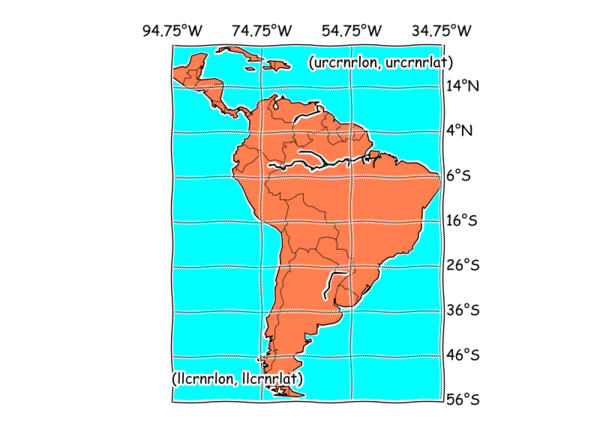
coverages是一个14 x 1592 x 1212的数组（array），它包含了整个南美洲的14个环境变量信息。每一个变量都由1592 x 1212的矩阵来表达。整个矩阵的覆盖范围是经度（longitude）94.8W 到 34.2W,维度（latitude）23.55N 到 56.05N。矩阵中的每一个点，也是图上的一个数据点，覆盖的实际地理面积是0.05 x 0.05度 （110km x 110km）, 大约是1.2万平方公里（北京市面积为1.6万平方公里）。矩阵中的缺失数据用-9999来表示。

这14个环境变量是：

1.年云覆盖天数（annual cloud cover）

2.年昼夜温差（annual diurnal temperature range）

3.年有雾天数 （annual frost frequency）

4.年均气压（annual vapor pressure）

5-9.一月、四月、七月、十月和年降水量（January, April, July, October and annual precipitation）

10-12. 全年每天温度的最低值、最高值和均值（minimum, maximum and mean annual temperature）

13. 海拔高度

14.植被覆盖率

我们的任务就是把这14个变量作为自变量，根据训练集中发现树懒的地点，去预测树懒可能的分布。为了验证预测的效力，我们将会观察我们预测存在树懒的地区是否覆盖了测试集的地区。

train是一个record array,它的shape 是 (1623,)。每一个数据点有三个fields: 物种名字：train['species'] is the species name 经度（单位：度）： train['dd long'] 维度（单位：度）： train['dd lat']

test也是一个record array,它的shape 是 (1623,)。每一个数据点有三个fields: 物种名字：train['species'] is the species name 经度（单位：度）： train['dd long'] 维度（单位：度）： train['dd lat']

Nx和Ny是两个整数，代表着地理数据矩阵的经纬度个数，其实就是1592和1212。

x_left_lower_corner和y_left_lower_corner是两个浮点数（floats），代表着地理数据矩阵的左下角（lower-left corner）的(x,y)位置。分别是-94.8和-56.05。

grid_size是一个浮点数（float），代表着矩阵中一个数据点的经纬跨度，其实就是0.05.

更详细的介绍参考原论文和fetch_species_distributions的定义

绘制地图背景

使用basemap包来画图（为了画出来的图更生动有趣，我们可以将matplotlib升级到1.3.1然后使用plt.xkcd()包）：

    # The grid in x,y coordinates
    # plt.xkcd()
    X, Y = np.meshgrid(xgrid, ygrid[::-1])
    m = Basemap(projection='cyl', llcrnrlat=Y.min(),
            urcrnrlat=Y.max(), llcrnrlon=X.min(),
            urcrnrlon=X.max(), resolution='c')
    m.drawcoastlines()
    m.drawcountries()
    #m.drawmapboundary(fill_color='aqua')
    #m.fillcontinents(color='coral',lake_color='aqua')
    parallels = np.arange(Y.min(),Y.max(),10.)
    # labels = [left,right,top,bottom]
    m.drawparallels(parallels,labels=[False,True,False,False])
    # labels = [left,right,top,bottom]
    meridians = np.arange(X.min(),X.max(),20.)
    m.drawmeridians(meridians,labels=[False,False,True,False])
    plt.text(X.min(),Y.min()+4,"(llcrnrlon, llcrnrlat)")
    plt.text(X.max()-30,Y.max()-5,"(urcrnrlon, urcrnrlat)")
    plt.text((X.max()-X.min())/2,Y.max()+20,"Basemap")

示例：提取树懒的数据

bradypus variegatus是一种树懒（slot），外貌如下图所示：

我们从data.train和data.test中提取出关于树懒的数据。

    speciesName="bradypus_variegatus_0"
    Name=' '.join(speciesName.split("_")[:2])
    bunch = Bunch(name=Name)
    points = dict(test=data.test, train=data.train)
    
    for label, pts in points.iteritems():
        # choose points associated with the desired species
        pts = pts[pts['species'] == speciesName]
        bunch['pts_%s' % label] = pts
        # determine coverage values for each of the training & testing points
        ix = np.searchsorted(xgrid, pts['dd long'])
        iy = np.searchsorted(ygrid, pts['dd lat'])
        bunch['cov_%s' % label] = data.coverages[:, -iy, ix].T

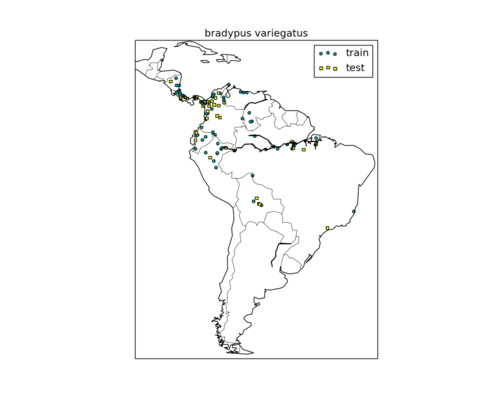
我们可以把数据中树懒的分布画出来，蓝色代表训练集，红色代表测试集

    m = Basemap(projection='cyl', llcrnrlat=Y.min(),
            urcrnrlat=Y.max(), llcrnrlon=X.min(),
            urcrnrlon=X.max(), resolution='c')
    m.drawcoastlines()
    m.drawcountries()
    plt.scatter(bunch.pts_train['dd long'], bunch.pts_train['dd lat'],
               s=4 ** 2, c='c', marker='o', label='train')
    plt.scatter(bunch.pts_test['dd long'], bunch.pts_test['dd lat'],
               s=4 ** 2, c='brown', marker='s', label='test')

训练SVM模型并进行预测树懒的生存范围

这里我们要考虑使用OneClassSVM，因为这是一个Outliers Detection的问题。关于Outliers Detection的更详细介绍参考这里。所谓Outliers Detection就是我们只有“是”的样本，而没有否的样本。因为我们并没有不适合树懒生存的地区的数据（除非我们很武断地认为只要没有发现树懒都是不适合树懒生存），所以现在的任务是，对于每一个新的需要判定的地点，我们根据当地的气候等变量判断这个地点与已有的训练集中的地点是否足够相似，是属于inlier还是属于outlier，如果是前者，我们猜测有树懒生存，否则，我们认为不太可能存在树懒。

那么，如果在这种情况下要应用logistic回归应该怎么办呢？因为logistic回归既需要response variable=1的数据，也需要response variable=0的数据，一个符合直觉的办法是，我们随机抽取一些没有观察到树懒的地点，设定为不适合树懒生存，然后通过这些地区和训练集中的地区之间的差异去训练一个logistic回归。显然，这种办法不如OneClassSVM更切题。

    # Standardize features
    mean = bunch.cov_train.mean(axis=0)
    std = bunch.cov_train.std(axis=0)
    train_cover_std = (bunch.cov_train - mean) / std
    # Fit OneClassSVM
    clf = svm.OneClassSVM(nu=0.1, kernel="rbf", gamma=0.5)
    clf.fit(train_cover_std)

如上所示训练完模型后，我们就可以对任意一个具备14个环境变量的地点进行预测。显然，我们只想预测陆地的部分，如下所示

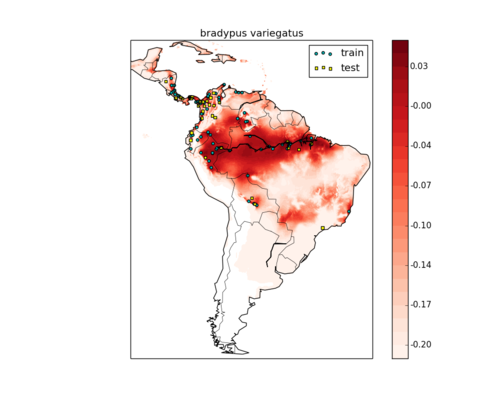
使用训练的模型预测南美洲树懒的活动范围并绘制地图

训练完模型，我们不仅可以对测试集中的地点进行判定，还可以对所有的地理数据点进行预测。下图中颜色越红代表存在树懒的概率越高。我们观察到大部分观察到的树懒的地区，包括测试集和训练集，都为深红色所覆盖，可见这个预测模型还是比较合理的：

    # Predict species distribution using the training data
    Z = np.ones((data.Ny, data.Nx), dtype=np.float64)
    # We'll predict only for the land points.
    land_reference = data.coverages[6]
    idx = np.where(land_reference > -9999)
    coverages_land = data.coverages[:, idx[0], idx[1]].T
    pred = clf.decision_function((coverages_land - mean) / std)[:, 0]
    Z *= pred.min()
    Z[idx[0], idx[1]] = pred
    levels = np.linspace(Z.min(), Z.max(), 25)
    Z[land_reference == -9999] = -9999
    # plot contours of the prediction
    figure(num=None, figsize=(10, 8), dpi=80, facecolor='w', edgecolor='k')    
    m.drawcoastlines()
    m.drawcountries()
    plt.contourf(X, Y, Z, levels=levels, cmap=plt.cm.Reds)
    plt.colorbar(format='%.2f')
    # scatter training/testing points
    plt.scatter(bunch.pts_train['dd long'], bunch.pts_train['dd lat'],
               s=4 ** 2, c='c', marker='o', label='train')
    plt.scatter(bunch.pts_test['dd long'], bunch.pts_test['dd lat'],
               s=4 ** 2, c='yellow', marker='s', label='test')
    plt.legend()
    plt.title(bunch.name)