“分形”的版本间的差异

来自集智百科 - 复杂系统|人工智能|复杂科学|复杂网络|自组织
跳到导航 跳到搜索
第17行： 第17行：
  
  
−
随着空间尺度不断变小，分形在某种结构或过程的特征却都是相似的。<ref name="Gouyet" />这样的现象我们称之为自相似，也称为扩展对称 Expanding Symmetry或展开对称  Unfolding Symmetry。如果这种信息的复制结果在每个纬度上都完全相同，就像'''门格海绵  Menger Sponge''' 一样，则其具有'''仿射自相似性  Affine Self-similar'''。 分形几何是拓扑学的一个数学分支。
+
随着空间尺度不断变小，分形在某种结构或过程的特征却都是相似的。<ref name="Gouyet" />这样的现象我们称之为'''自相似'''，也称为扩展对称 Expanding Symmetry或展开对称  Unfolding Symmetry。如果这种信息的复制结果在每个纬度上都完全相同，就像'''门格海绵  Menger Sponge''' 一样，则其具有'''仿射自相似性  Affine Self-similar'''。 分形几何是拓扑学的一个数学分支。
  
  

2020年4月18日 (六) 13:06的版本

曼德布洛特集
将曼德布洛特集放大
一个拓扑维数为1，豪斯多夫维数为1.893的谢尔宾斯基地毯（层级为6）的分形


分形是描述复杂几何形体结构的一种数学概念。它一般指维数取非整数的几何形体。在数学中，分形是欧几里德空间 Euclidean Space的一个子集，其分形维数的数值远远大于切赫-勒贝格维数 Topological Dimension（也称覆盖维数）。维数一般是指确定整个图形中点的位置所需要的坐标(或参数)的个数。


分形在不同的维度上看起来是相似的，就像曼德布洛特集 Mandelbrot set的连续放大一样，[1][2][3][4] 因此，分形在自然界中无处不在。


随着空间尺度不断变小，分形在某种结构或过程的特征却都是相似的。[5]这样的现象我们称之为自相似，也称为扩展对称 Expanding Symmetry或展开对称 Unfolding Symmetry。如果这种信息的复制结果在每个纬度上都完全相同，就像门格海绵 Menger Sponge 一样，则其具有仿射自相似性 Affine Self-similar。 分形几何是拓扑学的一个数学分支。


分形与有限几何图形 Geometric Figures 的不同之处在于它们的缩放方式。 对于有限几何图形而言：将一个多边形的边长增加一倍，其面积会变为原来的四倍，也就是 22倍。其中2为新边长与原边长之比，指数2为多边形所在空间的维数 。同样，如果一个球体的半径增加一倍，那么它的体积会变为原来的八倍，也就是23倍。其中2为新旧半径之比，指数3为球体所在空间的的维数。 然而，如果使分形的一维长度增加一倍，那么分形的空间尺度却不一定变为原来的整数倍。[1] 这是因为对于分形,如海岸线、科赫曲线、谢尔宾斯基海绵等的复杂性无法用维数等于 1、2、3 这样的数值来描述，由此产生了一个新的概念：分形维数，它通常比分形的拓扑维数 Topological Dimension还要大。[6]


分形维数是描述分形最主要的参量，它的计算公式为：


[math]\displaystyle{ d=\lim_{\varepsilon \rightarrow 0}[\log N(\varepsilon )/ \log(1/\varepsilon)] }[/math]


式中[math]\displaystyle{ \varepsilon }[/math]是小立方体一边的长度，[math]\displaystyle{ N(\varepsilon) }[/math]是用此小立方体覆盖被测形体所得的数目，分形维数是通过用边长为[math]\displaystyle{ \varepsilon }[/math]的小立方体覆盖被测形体来确定形体的维数来进行计算的。


分析学上，作为一个数学函数，分形通常是处处不可微的。[1][4][7] 无穷分形曲线可以理解为一条一维的曲线在空间中绕行，与普通的曲线不同，它的拓扑维数仍然是 1，但由于分形维数大于1，这使得它也有类似曲面的性质。[1][6]


我们可以从这些年来正式发表的文献中追踪关于分形概念的发展史。 从 17 世纪有了递归的概念开始，到 19 世纪伯纳德·波尔查诺 Bernard Bolzano、波恩哈德·黎曼 Bernhard Riemann和卡尔·魏尔斯特拉斯 Karl Weierstrass对连续不可微函数开创性的研究，[8] 这些严谨的数学概念推动着分形的发展。随着计算机建模技术的飞速发展和学界的研究兴趣日益浓厚，分形这个词在20世纪被创造出来。[9][10]


1975 年伯努·瓦曼德布洛特 Benoît B. Mandelbrot首次提出“分形 Fractal”这个术语。据曼德布洛特 教授自己说，Fractal一词是1975年夏天的一个寂静夜晚，他在冥思苦想之余偶翻他儿子的拉丁文字典时突然想到的。此词源于拉丁文形容词“Fractus”，对应的拉丁文动词是“Frangere”（“破碎”、“产生无规则碎片”）。此外与英文的“Fraction”（“碎片”、“分数”）及“Fragment”（“碎片”）具有相同的词根。在70年代中期以前，曼德布洛特 教授一直使用英文“Fractional”一词来表示他的分形思想。因此，取拉丁词之头，撷英文之尾的“Fractal”，本意是不规则的、破碎的、分数的。芒德布罗是想用此词来描述自然界中传统欧几里德几何学所不能描述的一大类复杂无规则的几何对象。例如，弯弯曲曲的海岸线、起伏不平的山脉、粗糙的断面，变幻无常的浮云、九曲回肠的河流、纵横交错的血管、令人眼花缭乱的满天繁星等。它们的特点都是极不规则或极不光滑。直观而粗略地说，这些对象都是分形。之后，曼德布洛特 教授将分形的概念从理论上的分形维数拓展到自然界中的几何图形。[1][11]


在数学中，分形的生成是基于一个不断迭代的方程，即一种基于递归的反馈系统。分形有几种类型，可以分别依据表现出的精确自相似性、半自相似性和统计自相似性来定义。如何良好的定义分形这一概念，权威学者之间仍有争论。曼德布洛特自己将分形总结为：“美丽、（研究起来）极其困难但又非常的有用，这就是分形”。[12] 1982 年曼德布洛特提出了更正式的定义：“分形是一种其豪斯多夫维数 Hausdorff–Besicovitch Dimension 严格大于拓扑维数的集合”。[13]后来他认为这种定义过于严格，于是简化并扩展了这个定义：“分形是由与整体在某些方面相似的部分构成的图形。”[14] 又过了一段时间，曼德布洛特决定使用以下方式来描述分形：“...在研究和使用分形 时，不需要迂腐的定义。用分形维数作为描述各种不同分型的通用术语”。 [15] 人们一致认为理论上的分形是无限迭代、自相似的、具有分形维数的精密数学结构，人们创造了许多分形图案并进行了充分的研究。[1][2][3] 分形并不限于几何图形，它也可以描述时间序列。 虽然分形是一种数学构造，它们同样可以在自然界中被找到，这使得它们被划入艺术作品的范畴。分形在医学、土力学、地震学和技术分析中都有应用。[5][4][16][17][18][19] 在自然[20][21][22][23][24]、技术[25][26][27][28]、艺术[29][30]、建筑[31] 和法律[32]等领域，人们对图形、结构和音频中[33] 不同程度自相似的分形图形进行了研究，并反过来利用分形理论去生成新的图形、结构和音频。此外，分形和混沌理论 Chaos Theory密切相关，因为混沌过程的图形大多数都是分形。[34]

引言

通过 javascript 创建一个简单的分形树

和数学家们相比，分形一词对大众来说含义不尽相同。相对于数学概念来说，大众可能更熟悉分形艺术 Fractal Art。即使是对数学家来说分形也很难进行一个准确的定义。但即使没有多少数学背景，也可以理解分形的核心特征。


自相似性 Self-Similarity的特征很容易理解，它类似于用镜头或其它装置放大图像，以便发现更精细的、以前看不见的新结构。 然而，如果放大一个分形的图像，就不会出现新的细节; 图像没有任何变化，相同的图案一遍遍地重复出现。或者对于某些分形来说，几乎相同的图案一遍遍地重复出现。 自相似性本身并不一定违反直觉。人们在生活中也能看到自我相似的现象，例如：两面平行的镜子间的无限重复、山上庙里老和尚的故事里的山......分形的不同之处在于重复的图案一定有着详尽的细节。[1][2][11]


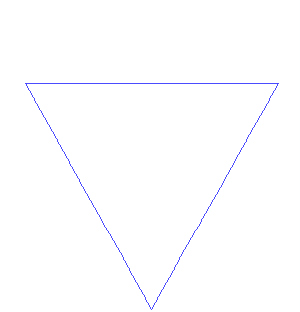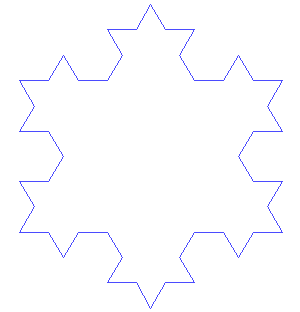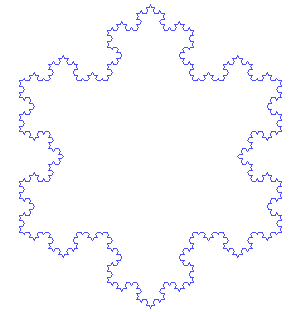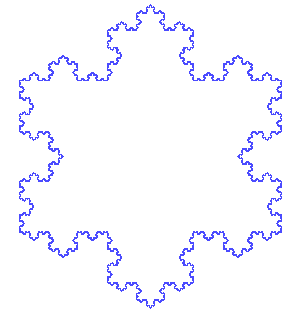
这种细节化的概念涉及到另一个不需要数学背景就可以理解的特征: 一个大于其拓扑维数的分形维数，通过将分形尺度与普通的几何形状相比较，我们便能感受到它们之间的差异。 例如，通常认为一条规则的曲线是一维的，如果将这样的曲线平铺成原曲线长度的1 / 3，那么总是有三个等长的曲线。 再比如：通常认为一个实心正方形是二维的，如果该图形代表一个碎片，将这个碎片在两个维度中都缩小了1 / 3，则会产生9个碎片。 而对于普通的自相似物体，其维数为n，将其重新平铺成一个个片段，每个片段按都缩小1 / r 倍，则会产生 rn个片段。 现在，考虑科赫曲线 Koch curve ， 它是形态似雪花的一种分形，它可以通过缩小为原来的1 / 3的方式进行平铺，从而形成四个子雪花曲线。因此，通过进行严格的类比，我们可以把科赫曲线的“维数”D计算出来，它满足3D=4。这说明，D决不是一个整数！ D其实就是数学家们所说的科赫曲线的分形维数。 由此，我们可以得出以下结论：由于科赫曲线具有非整数的分形维数，所以科赫曲线是一种分形。


这也引出了分形的第三个特征：分形在数学上是处处不可微的。具体来说，这意味着分形不能用传统的方法进行测量。[1][4][7]当测量波浪型非分形曲线的长度时，通过尽可能的放大，总能找到可测量的直线来拟合一小段曲线，从而就能用卷尺测量这段直线的长度，再将各段直线长度相加，就可以得出波浪的长度。这样做实质上是把曲线看作数学上的函数，在一小段范围内取一阶泰勒展开，近似为直线，然后求和总长度。但是在测量无限“扭动”的分形曲线时，譬如科赫雪花。（科赫雪花是以等边三角形三边生成的科赫曲线组成的）因为不论缩放到多小的尺度，锯齿状的图案总是会重复出现，因此，我们无法找到一条足够小的直线段来拟合曲线。当试图将卷尺越来越贴合曲线时，卷尺总会被拉长一些，这导致我们必须用无限长的卷尺才能完美的拟合整条科赫曲线。也就是说，科赫曲线的长度为无限大。同理，科赫雪花的周长也无限大。[1]


科赫雪花是一种分形，它以一个等边三角形开始，然后用一对构成等边凸点的线段去替换每个线段的三等分点


历史

一个科赫雪花是一个分形，它以一个等边三角形开始，然后用一对构成等边凸点的线段替换每个线段的中间三分之一
康托尔(三元)集
朱利娅集，一个与曼德尔布洛集相关的分形
利用分形树生成谢尔宾斯基垫片
一个具有多重分形维度的奇异吸引子
均匀质心三角形的分形图案
递归度

分形的历史可以从主要理论的研究追溯到现代计算机图形学中的应用，在这个过程中有几个著名的人物对典型的分形形式的研究做出了贡献。[9][10] 根据皮科弗 Pickover的说法：17 世纪时，数学家兼哲学家莱布尼茨 Gottfried Leibni思考过递归（可用于描述以自相似方法重复事物的过程），分形的数学从那时开始渐渐地成形（虽然他误认为只有直线会在递归的情况下有自相似的现象）。[35]


在他的著作中，Gottfried Leibniz使用了“分形指数”这个术语，但是遗憾的是在“几何”学上很多数学家未能接受或了解这一新概念。[1] 根据各种历史记载，在那之后，很少有数学家处理这些问题，即使有，处理这些问题的研究工作仍然含糊不清。这主要是因为当时的数学家们抵制这些陌生的新概念（这些概念有时被称为数学中的“怪物”）。[7][9][10] 因此，直到两个世纪之后，卡尔·魏尔斯特拉斯 Karl Weierstrass 才于1872年7月18日在皇家普鲁士科学院给出分形的第一个定义：分形是一种具有反直觉性质的函数图形。这种性质表现在它处处连续却又处处不可微。[9][10] 此外，其商差随着求和指数的增加而任意大。[36]不久之后，1883年，参加Karl Weierstrass 讲座[10]的康托尔 Georg Cantor也给出一个具有反直觉性质的例子：实直线上的子集——康托尔集，现在也被认为是分形。[9]在19世纪末，费利克斯 · 克莱因 Felix Klein 和亨利 · 庞加莱 Henri Poincaré也提出了“自逆”分形（分形的一种）。[1]


分形发展的一个里程碑在 1904 年，当时海里格·冯·科赫 Helge Von Koch不满意 Weierstrass的抽象又基于分析概念上的定义。他扩展了Poincaré的定义，给出了更加几何化的定义并附上了一个类似函数的手绘图形，也就是现在所说的科赫雪花。[9][10]


另一个里程碑在十一年之后，1915年，瓦茨瓦夫·谢尔宾斯基 Wacław Sierpiński构造出了谢尔宾斯基三角形；次年，又造出了谢尔宾斯基地毯。到1918年，两位法国数学家皮埃尔 · 法图 Pierre Fatou和加斯顿 · 朱利亚 Gaston Julia通过各自的独立工作，基本上同时得出相同的结论。该结论描述了复数映射以及函数迭代相关分形行为，并由此引出了关于奇异吸引子(即吸引或排斥其他点的点)的理论，该理论在分形研究中已变得非常重要。[4][9][10] 在关于奇异吸引子的结论提出后不久，到1918年3月，费利克斯 · 豪斯多夫 Felix Hausdorff扩展了“维数”的定义，这使得分形的定义更加明确，使集合具有非整数维数。[10] 1938年，保罗·皮埃尔·莱维 Paul Lévy在他的论文《平面、空间曲线和由与整体自相似部件组成的曲面 Plane or Space Curves and Surfaces Consisting of Parts Similar to the Whole》中进一步明确了自相似曲线的概念，还在文中描述了一个新的分形曲线——莱维C形曲线。


不同研究领域的学者都说：如果没有现代计算机图形学的帮助，仅凭早期的研究人员通过手工描绘图形，则不可能将美丽的图形进行可视化，也无法发现在图形中所蕴含的信息。(例如，朱利娅集只能通过几次迭代将图形可视化)。[1]:179[7][10] 然而，这种情况在20世纪60年代发生了改变，当时 Benoit Mandelbrot 开始研究自相似，在路易斯·弗莱·理查德森 Lewis Fry Richardson之前工作的基础上，写下了一篇论文《英国海岸有多长？ 统计自相似和分形维度》。[37][38]最终，在1975年[11]，曼德布洛特总结了数百年来关于分形的思想及数学上相关的结论，提出了"分形"一词，并用高超的计算机可视化构造来说明他的数学定义。包括他自己定义的曼德勃罗集在内的图像，激励大众展开了丰富的想象; 其中许多图像是基于递归的，从而使“分形”形成了现在的定义。[39][7][9][35]1980 年，洛伦·卡彭特 Loren Carpenter在计算机图形学顶级年会SIGGRAPH上发表了一次演讲，演讲中他介绍了他基于分形理论开发的用于产生景观的软件。[40]


而对于中国而言，最早把分形几何引进中国的可能是中科院沈阳金属研究所的龙期威研究员，他曾是中国科学技术大学教授并任中科院国际材料物理中心主任。他率先把分形理论应用于金属断裂研究，并培养了把分形方法引入到裂隙岩体非连续变形、强度和断裂破坏行为研究的一位优秀学生，也就是四川大学现任校长谢和平院士。

定义和相关特征

在曼德布洛特发表的一篇描述几何分形的文章中，对于分形的描述经常被引用：“一种粗糙或破碎的几何形状，可以被分割成几个部分，且每一个部分(至少大致上)都是整体的缩小版本”;[1] 这个定义有助于我们理解分形，但也有局限性。 作者不同意对分形进行确切定义，但经常阐述自相似的基本思想、具有反直觉性的分形以及他们所嵌入的空间。 [1][5][2][4][41]


有一点是可以确定的，分形图案具有分形维数的特性。这些维数量化了复杂性(例如，随着规模的变化而改变细节) ，它们没有特别的描述和详细说明如何构建特定的分形图案。 [42]1975年，当曼德布洛特 提出“分形”这个词时，是为了标记一个豪斯多夫-贝西科维奇维数 Hausdorff–Besicovitch dimension大于拓扑维数的对象。 [11]然而，像希尔伯特曲线这样的空间填充曲线并不能满足这一要求。


因为在为分形找到一个确切定义的过程中遇到了很多困难，有些人认为分形根本不应该被严格定义。 根据 福尔克纳 Falconer 的观点：分形除了处处不可微并且可以有分形维数之外，还应该具有以下可能的特征[2]：

  • 应该具有自相似性
  • 具有完全自相似性（即在所有尺度上都完全相同），譬如科赫雪花
  • 准自相似性：在不同尺度上拥有近似相同的形状; 可能包含扭曲和退化的完整分形的缩小副本;例如曼德勃罗集中的卫星集（也就是附属集）与整个集合是相似的，但它不是整个集合的精确副本
  • 统计自相似性:随机重复一个图案，以便在不同尺度上保留其数值或统计度量;例如，对于像英国海岸线一样随机生成的分图案来说，人们无法找到像科赫雪花中分段缩放且整齐重复的单元[4]
  • 定性自相似性: 如在时间序列中[16]
  • 多重分形缩放: 具有多个分形维数或多种缩放规则
  • 在任意小的尺度上都能有精细的结构； 这使得分形可能具有突现的性质（与这个列表中的下一个准则相关)[43]
  • 传统的欧几里德几何语言很难描述局部和全局的不规则性。 对于分形图案，可以用“光滑的堆积表面”和“漩涡中的漩涡”这来描述
  • 多数定义较为简单，且可能基于递归概念；（参见生成分形的常用方法)[6]
  • 一般地，其“分形维数”（通常为豪斯多夫维数）会大于拓扑维数（但在空间填充曲线如希尔伯特曲线例外）


按照这些标准，可以排除某些不确定其是不是分形的情况。比如那些可能自相似但没有其他典型的分形特征的情况。以一条直线举例，它是自相似的，但不是分形，因为它缺乏细节，而且可以用欧几里德语言进行简单描述，具有与拓扑维数相同的分形维数，并且完全不需要递归进行准确定义。[1][4]

生成分形的常用技术

用 L 系统原理在硅树脂中模拟自相似分支模式 [24]
交错链路有限细分法生成的分形

分形的图像可以通过分形生成软件生成。

  • 迭代函数系统(IFS)：使用固定的几何替换原则；可以是随机的或确定性的；[44] 例如，科赫雪花，康托集，哈弗曼地毯 Haferman Carpet，[45]，谢尔宾斯基地毯 Sierpinski Carpet，谢尔宾斯基垫片 Sierpinski Gasket，皮亚诺曲线 Peano Curve，哈特海威龙曲线 Harter-Heighway Dragon Curve，T-方形 T-Square，门格海绵 Menger Sponge。
  • 奇异吸引子 Strange Attractors——使用映射的迭代或表示出混沌的初值微分或差分方程系统的解(例如，参见多重分形图像或逻辑映射)。
  • L-系统：可能类似于植物、生物细胞(如神经元和免疫系统细胞[24])、血管、肺结构、等的分支模式，或海龟图形模式，如空间填充曲线和分割逃逸时间分形——在空间的每个点(如复平面)上使用公式或递推关系；通常是准自相似的 Quasi-Self-Similar；也被称为“轨道”分形；例如，曼德布洛特集 Mandelbrot set，朱利亚集 Julia set，燃烧船分形 Burning Ship Fractal，新星分形 Nova Fractal和李亚普诺夫分形 Lyapunov Fractal。
  • 由逃逸时间公式的一个或两个迭代产生的二维矢量场，当点(或像素数据)重复通过该场时，也会产生分形形式。
  • 随机分形-使用随机规则：例如:对莱维飞行 Levy Flight、渗透集群 Percolation Clusters，自回避行走 Self - Avoiding walks、分形景观、布朗运动轨迹和布朗树(即通过模拟扩散受限聚集或反应受限聚集簇生成的树枝状分形)。
  • 有限细分规则：使用递归拓扑算法来细化分割，它们类似于细胞分裂的过程。在创建康托尔集和谢尔宾斯基地毯的迭代过中程运用到该规则，具体例子如重心细分。[4]

模拟分形

由于物理时间和空间的实际限制，已有很多模拟分形的模型（尽管是在一定范围内而不是无限范围内）。具体来说，模型可以模拟具有分形特征的理论分形或自然现象。在建模过程中，我们可以得到高度艺术化的效果图、一些调查的结果、用于分形分析的基准。下面列出了分形在技术上的一些具体应用。图像和建模的一些结果通常被称为“分形”，即使它们没有严格的分形特征，此时可能是因为已经放大到一个不显示任何分形特性的分形图像区域，也可能是因为包含了计算或显示人工制品等特征（这些特征并不是真正的分形特征）。模拟的分形可以是声音、数字图像、电化学模式、昼夜节律等。分形图案已经在物理三维空间中重新进行构造（这通常被称为硅器件建模）。


分形模型通常是通过分形生成软件创建的，这些分形生成软件运用到上述所说的技术。譬如，利用递归算法和L系统 L-systems技术，[24] 可以在计算机上模拟树木、蕨类植物、神经系统细胞[24] 、血液和肺血管系统[46]及其他自然界的分支图形。某些图形的递归性质是很明显的——比如一棵树的树枝或蕨类植物的叶子是整个模式的微缩复制品:它们不完全相同，但在本质上是相似的。类似地，随机分形被用来描述/创造许多高度不规则的真实世界对象。但分形建模也有局限性：尽管分形模型生成的结果与自然现象有相似性，但并不能证明类似的建模算法可以自然生成我们人为建立的模型。

具有分形特征的自然现象

自然界中发现的近似分形在可扩展却有限的尺度范围内显示出自相似性。 例如，分形与树叶之间的联系，目前正被用来确定树木中含有多少碳。 已知具有分形特征的现象包括:[47]

  • 作用性细胞骨架[48]
  • 藻类
  • 动物的着色图案
  • 血管和肺血管[46]
  • 云层和雨量区[49]
  • 海岸线
  • 陨石坑
  • 水晶[50]
  • DNA
  • 地震[28][51]
  • 断层线
  • 几何光学[52]
  • 心率[20]
  • 心音[21]
  • 闪电
  • 山羊角
  • 山脉
  • 海浪[53]
  • 菠萝
  • 心理主观知觉[54]
  • 蛋白质[55]
  • 土星环[56][57]
  • 河网
  • 宝塔花菜
  • 雪花[58]
  • 土壤孔隙[59]
  • 湍流表面[60][61]
  • 树木
  • 布朗运动(由一维维纳过程产生)[62]

  • 冷玻璃上自然形成的霜晶呈现分形图案

  • 几何光学系统中的分形流域边界[56]

  • 拉开两个被胶水覆盖的丙烯酸片时产生的分形

  • 高压击穿4英寸(100毫米)的丙烯酸玻璃块创建一个电花分形图

  • 宝塔花菜，以自相似的形式构成了近似的自然分形

  • 极地火星的分形融霜模式,冷冻的二氧化碳升华形成了这些图案

  • 在木头上以分形方式生长的最大粘菌

由分形而诞生的创造性作品

自1999年以来，超过10个科学团队对杰克逊·波洛克 Jackson Pollock(1912-1956)的50多幅油画进行了分形分析，这些油画是直接将颜料倒在水平画布上创作出来的。[63][64][65][66][67][68][69][70][71][72][73][74][75]分形分析后来被用来区分 Jackson Pollock 的真品和赝品，辨认成功率达到了93% 。[76]认知神经科学家已经证实，Jackson Pollock的分形可以像计算机生成的分形和自然分形一样，减少观察者的识别难度。[77]


印花釉法 Decalcomania是马克斯•恩斯特 Max Ernst等艺术家使用的一种工艺技术，它可以产生分形样的图案。 该技术包括在两个表面之间压漆，然后把它们分开的步骤。[78]


控制论学者、民族数学家罗恩·埃格拉什 Ron Eglash认为分形几何和数学在非洲艺术、游戏、占卜、贸易和建筑中应用很普遍。如圆形房屋是一环套一环的，矩形房屋是一连串的矩形等等。 这种缩放图案也可以在非洲的纺织品、雕塑、甚至发型中找到。.[30][79]霍克基·西通基尔 Hokky Situngkir还建议在印度尼西亚传统艺术、蜡染和传统房屋的装饰品中运用分形的图案。[80][81]


控制论专家、民族数学家 Ron Eglash 还讨论了遍布贝宁的城市、村庄甚至房间的分形布局。 他评论说: “当欧洲人第一次来到非洲时，他们认为非洲的建筑非常混乱且原始。 他们从来没有想到非洲人可能使用了一种他们甚至还没有发现的数学形式来设计建筑。”[82]


在1996年对迈克尔 · 西尔弗布拉特 Michael Silverblatt的采访中，福斯特·华莱士 David Foster Wallace承认他给编辑迈克尔 · 皮奇 Michael Pietsch的《无尽的玩笑 Infinite Jest》第一稿的结构灵感来自于分形，特别是谢尔宾斯基三角形，但是经过修改后的小说“更像是一个侧面的谢尔宾斯基垫片”。[29]

  • 模拟山体表面的一种分形

  • 3D递归图像

  • 递归分形蝴蝶图像

  • 分形火焰

生理反应

人类似乎特别适合处理 D值（分形维数）在1.3到1.5之间的分形图案，[83] 这是因为当人们看到此类分形图案时，来自生理上的识别压力往往会降低。[84][85]

在科技上的应用

  • 分形晶体管[86]
  • 分形换热器[87]
  • 数码影像
  • 建筑[31]
  • 城市发展[88][89]
  • 组织病理学切片分类
  • 分形景观或海岸线复杂性
  • 用分形分析探测“我们不知道的生命”[90]
  • 酶(米氏方程)
  • 新型音乐的产生
  • 信号和图像压缩
  • 数码相片放大操作
  • 土力学中的分形
  • 电脑及电子游戏设计
  • 计算机图形学
  • 有机环境
  • 程序代
  • 断面分析和断裂力学分析
  • 分形粗糙系统的小角度散射理论
  • T 恤及其他流行事物
  • 生成迷彩图案，如 MARPAT
  • 数字日晷
  • 价格系列的技术分析
  • 网络中的分形
  • 医学[27]
  • 神经科学[22][23]
  • 影像诊断[26]
  • 病理学[91][92]
  • 地质学[93]
  • 地理位置[94]
  • 考古学[95][96]
  • 地震学[28]
  • 搜索和救援[97]
  • 技术分析[98]
  • 在纹理映射中GPU缓存一致性的Morton阶空间填充曲线[99][100][101] ，栅格化[102][103] 和湍流数据的索引[104][105]。

下面对于分形几何在电子技术方面的应用做一些说明：

分形天线

分形天线是一种无线通信用的新概念天线。和传统天线相比，它在同样面积或体积的条件下具有最大的有效长度或周长。这种天线具有极端紧凑和多宽频带等特性，非常适合于RFID和移动通讯方面的应用。由于现代通信工具种类越来越多，体积也越来越小，因而需要把天线做得很小很小，而且越小越好。为此目的，把天线的形状做成分形是个好主意，因为这可以在同样面积的限制条件下把天线做得很长，而且还能取代多条天线而同时工作在几个不同频率区间之中。[106]


把天线阵列设计成分形样子的做法早在1957年就出现了。它是由美国伊利诺伊大学电子工程系教授艾蒙德 · 杜哈梅尔 Raymond DuHamel 和学生 德怀特 · 伊斯贝尔 Dwight Isbell提出的对数周期阵列 Log Periodic Array 。分形天线阵列与传统天线阵列设计相比，具有多频和宽频特性，可用于快速计算方向图，可有效地利用狭小地域来布置庞大的平面阵列，可实现低副瓣设计策略，等等。两种典型的分形阵列天线是康托集阵列和维尔斯特拉斯 线性阵列，目前多用于电视天线。


基于分形结构来设计和优化单个天线的做法始于1988年，由波士顿大学教授内森·科恩 Nathan Cohen首先提出，但相关的学术论文到了1995年才第一次正式发表。 与传统天线相比，分形天线除了在缩小尺寸方面独具一格之外，还有其他优点，例如：可以利用其自相似性来增加工作频带数目和带宽，具有自加载特性而不需要额外的调谐线圈和电容等元器件或匹配电路来辅助其在宽带工作条件下达到阻抗匹配，还可以简化电路设计和降低系统造价，等等。据报道，基于分形设计的天线可以在UHF（862-928 MHz）频带的无线通信设备中GSM+DCS（900MHz和1800MHz）双频移动天线系统中得到较好的应用。目前的研究主要集中在GSM（900MHz）、PCS （1900MHz）、蓝牙无线通信系统（2.4GHz）等方面。它不仅可以在个人手提（如Cellular Phone，即蜂窝电话）和其他无线移动设备 （如无线局域网中的laptop，即笔记本电脑、车载天线系统）中得到应用，还可望用于卫星通信系统和相控阵雷达系统。目前看来，如果相关的一些技术障碍（如多频道信号之间的相互干涉）能够取得突破，则分形天线的前景还是颇为诱人的。 当然，从数学角度严格来讲，这些例子都只是利用了有限分形（或者伪分形），因而尚有潜力可以挖掘。事实上，目前一切还在尝试之中，期待新的进展。


据报道， 新近迅猛发展的纳米变形材料 Metamaterials 和用变形材料制造的天线都尽可能有效地利用分形几何结构。2011年还有报道说 ，用密封分形共振器合成的宽带变形材料可以制造出隐形外套，其原理是可以让光绕过这些材料而实现传播和折射.


分形电容

分形电容器的基本设计思想和分形天线一样。理论上，前者是在有限的面积内获得无限长的曲线以增加天线的有效长度，后者则是在有限的体积内获得无限宽的曲面以增加电容器的储电量。


研究发现，在传统的电容器中把部分纵向的相反电极分布改为横向可以有效提高其储电量。 分形电容器应用的一个成功试验性例子是由瑞士保罗·谢乐机构 Paul Scherrer Institute 公司研制的分形超级电容器 Supercapacitor /Ultracapacitor被安装在一辆名为 Hy. Power 的燃料驱动小汽车里，用作汽车爆发加速时的拖动功率补给。2002年1月16日，Hy. Power 成功地爬上了位于瑞士布里格 Brig与意大利多莫多索拉 Domodossola 之间海拔两千多米高的辛普伦 Simplon山口。这段山路极为陡峭，而当时山顶气候条件恶劣，同类型的小汽车只能望山兴叹 。 (摘自集智俱乐部 分形——故事之外)

离子推进

当二维空间的分形被多次迭代时，分形的周长增加到无穷大，但面积绝不会超过某一阈值。 三维空间的分形与此相似，这样的分形可能有无限的表面积，但体积绝不会超过某一阈值。[107]在选择电子发射体的结构和材料时，这样的特性可以用来最大限度地提高离子推进的效率。 如果操作正确，可使排放效率达到最高。[108]

著名学者简介

伯努·瓦曼德布洛特 Benoît B. Mandelbrot

伯努·瓦曼德布洛特 Benoît B. Mandelbrot是法国、美国数学家（双国籍），最大的成就是创立了分形几何。1967年，曼德布洛特在美国《Science》杂志上发表题目为《英国的海岸线有多长》的划时代论文，标志着其分形思想的萌芽。


朱尔·亨利·庞加莱 Jules Henri Poincaré

朱尔·亨利·庞加莱 Jules Henri Poincaré法国最伟大的数学家之一，理论科学家和科学哲学家。庞加莱被公认是19世纪后和20世纪初的领袖数学家，是继高斯之后对于数学及其应用具有全面知识的最后数学家。早在19世纪初，庞加莱在研究三体问题中，使用了新的几何方法。

格奥尔格·康托尔Georg Cantor

格奥尔格·康托尔 Georg Cantor是德国数学家，创立了现代集合论，是实数系以至整个微积分理论体系的基础，构造了三分康托尔集。

海里格·冯·科赫 Helge von Koch

海里格·冯·科赫 Helge Von Koch是瑞典数学家，在他1904年的一篇论文“关于一个可由基本几何方法构造出的，无切线的连续曲线”（原文的法文标题为：“Sur une courbe continue sans tangente, obtenue par une construction géométrique élémentaire”）中，他描述了科赫曲线的构造方法。


瓦茨瓦夫·谢尔宾斯基 Wacław Sierpiński

瓦茨瓦夫·谢尔宾斯基 Wacław Sierpiński 是波兰数学家，因对集合论、数论、函数的理论和拓扑学的出色贡献而闻名。两个著名的分形是根据他的名字命名：谢尔宾斯基三角形和谢尔宾斯基地毯；另外还有谢尔宾斯基数和谢尔宾斯基问题也是以他的名字命名。

费利克斯·豪斯多夫 Felix Hausdorff

费利克斯·豪斯多夫 Felix Hausdorff是德国数学家，他是拓扑学的创始人之一，他定义和研究偏序集、豪斯多夫空间和豪斯多夫维，证明Hausdorff maximality theorem。提出了豪斯多夫维数来计算分形维数。

进一步阅读


参考文献

  1. ↑ 1.00 1.01 1.02 1.03 1.04 1.05 1.06 1.07 1.08 1.09 1.10 1.11 1.12 1.13 1.14 Mandelbrot, Benoît B. (1983). The fractal geometry of nature. Macmillan. ISBN 978-0-7167-1186-5. https://books.google.com/books?id=0R2LkE3N7-oC. 
  2. ↑ 2.0 2.1 2.2 2.3 2.4 Falconer, Kenneth (2003). Fractal Geometry: Mathematical Foundations and Applications. John Wiley & Sons. xxv. ISBN 978-0-470-84862-3. 
  3. ↑ 3.0 3.1 Briggs, John (1992). Fractals:The Patterns of Chaos. London: Thames and Hudson. p. 148. ISBN 978-0-500-27693-8. 
  4. ↑ 4.0 4.1 4.2 4.3 4.4 4.5 4.6 4.7 4.8 Vicsek, Tamás (1992). Fractal growth phenomena. Singapore/New Jersey: World Scientific. pp. 31； 139–146. ISBN 978-981-02-0668-0. 
  5. ↑ 5.0 5.1 5.2 Gouyet, Jean-François (1996). Physics and fractal structures. Paris/New York: Masson Springer. ISBN 978-0-387-94153-0. 
  6. ↑ 6.0 6.1 6.2 Mandelbrot, Benoît B. (2004). Fractals and Chaos. Berlin: Springer. p. 38. ISBN 978-0-387-20158-0. "A fractal set is one for which the fractal (Hausdorff-Besicovitch) dimension strictly exceeds the topological dimension" 
  7. ↑ 7.0 7.1 7.2 7.3 7.4 Gordon, Nigel (2000). Introducing fractal geometry. Duxford: Icon. p. 71. ISBN 978-1-84046-123-7. https://archive.org/details/introducingfract0000lesm/page/71. 
  8. ↑ Segal, S. L. (June 1978). "Riemann's example of a continuous 'nondifferentiable' function continued". The Mathematical Intelligencer. 1 (2): 81–82. doi:10.1007/BF03023065.
  9. ↑ 9.0 9.1 9.2 9.3 9.4 9.5 9.6 9.7 Edgar, Gerald (2004). Classics on Fractals. Boulder, CO: Westview Press. ISBN 978-0-8133-4153-8. 
  10. ↑ 10.0 10.1 10.2 10.3 10.4 10.5 10.6 10.7 10.8 Trochet, Holly (2009). "A History of Fractal Geometry". MacTutor History of Mathematics. Archived from the original on March 12, 2012.
  11. ↑ 11.0 11.1 11.2 11.3 Albers, Donald J.; Alexanderson, Gerald L. (2008). "Benoît Mandelbrot: In his own words". Mathematical people : profiles and interviews. Wellesley, MA: AK Peters. p. 214. ISBN 978-1-56881-340-0. 
  12. ↑ Mandelbrot, Benoit. "24/7 Lecture on Fractals". 2006 Ig Nobel Awards. Improbable Research.
  13. ↑ Mandelbrot, B. B.: The Fractal Geometry of Nature. W. H. Freeman and Company, New York (1982); p. 15.
  14. ↑ Jens Feder (2013). Fractals. Springer Science & Business Media. p. 11. ISBN 978-1-4899-2124-6. https://books.google.com/books?id=mgvyBwAAQBAJ&pg=PA11. 
  15. ↑ Gerald Edgar (2007). Measure, Topology, and Fractal Geometry. Springer Science & Business Media. p. 7. ISBN 978-0-387-74749-1. https://books.google.com/books?id=dk2vruTv0_gC&pg=PR7. 
  16. ↑ 16.0 16.1 Peters, Edgar (1996). Chaos and order in the capital markets : a new view of cycles, prices, and market volatility. New York: Wiley. ISBN 978-0-471-13938-6. 
  17. ↑ Krapivsky, P. L.; Ben-Naim, E. (1994). "Multiscaling in Stochastic Fractals". Physics Letters A. 196 (3–4): 168. Bibcode:1994PhLA..196..168K. doi:10.1016/0375-9601(94)91220-3.
  18. ↑ Hassan, M. K.; Rodgers, G. J. (1995). "Models of fragmentation and stochastic fractals". Physics Letters A. 208 (1–2): 95. Bibcode:1995PhLA..208...95H. doi:10.1016/0375-9601(95)00727-k.
  19. ↑ Hassan, M. K.; Pavel, N. I.; Pandit, R. K.; Kurths, J. (2014). "Dyadic Cantor set and its kinetic and stochastic counterpart". Chaos, Solitons & Fractals. 60: 31–39. arXiv:1401.0249. Bibcode:2014CSF....60...31H. doi:10.1016/j.chaos.2013.12.010.
  20. ↑ 20.0 20.1 Tan, Can Ozan; Cohen, Michael A.; Eckberg, Dwain L.; Taylor, J. Andrew (2009). "Fractal properties of human heart period variability: Physiological and methodological implications". The Journal of Physiology. 587 (15): 3929. doi:10.1113/jphysiol.2009.169219. PMC 2746620. PMID 19528254.
  21. ↑ 21.0 21.1 Buldyrev, Sergey V.; Goldberger, Ary L.; Havlin, Shlomo; Peng, Chung-Kang; Stanley, H. Eugene (1995). "Fractals in Biology and Medicine: From DNA to the Heartbeat". In Bunde, Armin; Havlin, Shlomo. Fractals in Science. Springer. http://havlin.biu.ac.il/Shlomo%20Havlin%20books_f_in_s.php. 
  22. ↑ 22.0 22.1 Liu, Jing Z.; Zhang, Lu D.; Yue, Guang H. (2003). "Fractal Dimension in Human Cerebellum Measured by Magnetic Resonance Imaging". Biophysical Journal. 85 (6): 4041–4046. Bibcode:2003BpJ....85.4041L. doi:10.1016/S0006-3495(03)74817-6. PMC 1303704. PMID 14645092.
  23. ↑ 23.0 23.1 Karperien, Audrey L.; Jelinek, Herbert F.; Buchan, Alastair M. (2008). "Box-Counting Analysis of Microglia Form in Schizophrenia, Alzheimer's Disease and Affective Disorder". Fractals. 16 (2): 103. doi:10.1142/S0218348X08003880.
  24. ↑ 24.0 24.1 24.2 24.3 24.4 Jelinek, Herbert F.; Karperien, Audrey; Cornforth, David; Cesar, Roberto; Leandro, Jorge de Jesus Gomes (2002). "MicroMod-an L-systems approach to neural modelling". In Sarker, Ruhul. Workshop proceedings: the Sixth Australia-Japan Joint Workshop on Intelligent and Evolutionary Systems, University House, ANU. University of New South Wales. ISBN 9780731705054. OCLC 224846454. https://books.google.com/books?id=FFSUGQAACAAJ. Retrieved February 3, 2012. "Event location: Canberra, Australia" 
  25. ↑ Hu, Shougeng; Cheng, Qiuming; Wang, Le; Xie, Shuyun (2012). "Multifractal characterization of urban residential land price in space and time". Applied Geography. 34: 161–170. doi:10.1016/j.apgeog.2011.10.016.
  26. ↑ 26.0 26.1 Karperien, Audrey; Jelinek, Herbert F.; Leandro, Jorge de Jesus Gomes; Soares, João V. B.; Cesar Jr, Roberto M.; Luckie, Alan (2008). "Automated detection of proliferative retinopathy in clinical practice". Clinical Ophthalmology (Auckland, N.Z.). 2 (1): 109–122. doi:10.2147/OPTH.S1579. PMC 2698675. PMID 19668394.
  27. ↑ 27.0 27.1 Losa, Gabriele A.; Nonnenmacher, Theo F. (2005). Fractals in biology and medicine. Springer. ISBN 978-3-7643-7172-2. https://books.google.com/books?id=t9l9GdAt95gC. 
  28. ↑ 28.0 28.1 28.2 Vannucchi, Paola; Leoni, Lorenzo (2007). "Structural characterization of the Costa Rica décollement: Evidence for seismically-induced fluid pulsing". Earth and Planetary Science Letters. 262 (3–4): 413. Bibcode:2007E&PSL.262..413V. doi:10.1016/j.epsl.2007.07.056.
  29. ↑ 29.0 29.1 Wallace, David Foster (August 4, 2006). "Bookworm on KCRW". Kcrw.com. Retrieved 2010-10-17.
  30. ↑ 30.0 30.1 Eglash, Ron (1999). "African Fractals: Modern Computing and Indigenous Design". New Brunswick: Rutgers University Press. Archived from the original on January 3, 2018. Retrieved 2010-10-17.
  31. ↑ 31.0 31.1 Ostwald, Michael J., and Vaughan, Josephine (2016) The Fractal Dimension of Architecture. Birhauser, Basel. doi:10.1007/978-3-319-32426-5.
  32. ↑ Brothers, Harlan J. (2007). "Structural Scaling in Bach's Cello Suite No. 3". Fractals. 15 (1): 89–95. doi:10.1142/S0218348X0700337X.
  33. ↑ Baranger, Michael. "Chaos, Complexity, and Entropy: A physics talk for non-physicists" (PDF).
  34. ↑ 35.0 35.1 Pickover, Clifford A. (2009). The Math Book: From Pythagoras to the 57th Dimension, 250 Milestones in the History of Mathematics. Sterling. p. 310. ISBN 978-1-4027-5796-9. https://books.google.com/?id=JrslMKTgSZwC&pg=PA310&dq=fractal+koch+curve+book#v=onepage&q=fractal%20koch%20curve%20book. 
  35. ↑ "Fractal Geometry". www-history.mcs.st-and.ac.uk. Retrieved 2017-04-11.
  36. ↑ Mandelbrot, B. (1967). "How Long Is the Coast of Britain?". Science. 156 (3775): 636–638. Bibcode:1967Sci...156..636M. doi:10.1126/science.156.3775.636. PMID 17837158.
  37. ↑ Batty, Michael (April 4, 1985). "Fractals – Geometry Between Dimensions". New Scientist. 105 (1450): 31.
  38. ↑ Russ, John C. (1994). Fractal surfaces. 1. Springer. p. 1. ISBN 978-0-306-44702-0. https://books.google.com/?id=qDQjyuuDRxUC&pg=PA1. Retrieved 2011-02-05. 
  39. ↑ kottke.org. 2009. Vol Libre, an amazing CG film from 1980. [online] Available at: http://kottke.org/09/07/vol-libre-an-amazing-cg-film-from-1980
  40. ↑ Edgar, Gerald (2008). Measure, topology, and fractal geometry. New York: Springer-Verlag. p. 1. ISBN 978-0-387-74748-4. 
  41. ↑ Karperien, Audrey (2004). Defining microglial morphology: Form, Function, and Fractal Dimension. Charles Sturt University. doi:10.13140/2.1.2815.9048. 
  42. ↑ Spencer, John; Thomas, Michael S. C.; McClelland, James L. (2009). Toward a unified theory of development : connectionism and dynamic systems theory re-considered. Oxford/New York: Oxford University Press. ISBN 978-0-19-530059-8. 
  43. ↑ Frame, Angus (August 3, 1998). "Iterated Function Systems". In Pickover, Clifford A.. Chaos and fractals: a computer graphical journey : ten year compilation of advanced research. Elsevier. pp. 349–351. ISBN 978-0-444-50002-1. https://books.google.com/books?id=A51ARsapVuUC. Retrieved February 4, 2012. 
  44. ↑ "Haferman Carpet". WolframAlpha. Retrieved October 18, 2012.
  45. ↑ 46.0 46.1 Hahn, Horst K.; Georg, Manfred; Peitgen, Heinz-Otto (2005). "Fractal aspects of three-dimensional vascular constructive optimization". In Losa, Gabriele A.; Nonnenmacher, Theo F.. Fractals in biology and medicine. Springer. pp. 55–66. ISBN 978-3-7643-7172-2. https://books.google.com/books?id=t9l9GdAt95gC. 
  46. ↑ "Hunting the Hidden Dimensional". Nova. PBS. WPMB-Maryland. October 28, 2008.
  47. ↑ Sadegh, Sanaz (2017). "Plasma Membrane is Compartmentalized by a Self-Similar Cortical Actin Meshwork". Physical Review X. 7 (1): 011031. arXiv:1702.03997. Bibcode:2017PhRvX...7a1031S. doi:10.1103/PhysRevX.7.011031. PMC 5500227. PMID 28690919.
  48. ↑ Lovejoy, Shaun (1982). "Area-perimeter relation for rain and cloud areas". Science. 216 (4542): 185–187. Bibcode:1982Sci...216..185L. doi:10.1126/science.216.4542.185. PMID 17736252.
  49. ↑ Carbone, Alessandra; Gromov, Mikhael; Prusinkiewicz, Przemyslaw (2000). Pattern formation in biology, vision and dynamics. World Scientific. p. 78. ISBN 978-981-02-3792-9. https://books.google.com/?id=qZHyqUli9y8C&pg=PA78&dq=crystal+fractals+book#v=onepage&q=crystal%20fractals%20book. 
  50. ↑ Sornette, Didier (2004). Critical phenomena in natural sciences: chaos, fractals, selforganization, and disorder: concepts and tools. Springer. pp. 128–140. ISBN 978-3-540-40754-6. 
  51. ↑ Sweet, D.; Ott, E.; Yorke, J. A. (1999), "Complex topology in Chaotic scattering: A Laboratory Observation", Nature, 399 (6734): 315, Bibcode:1999Natur.399..315S, doi:10.1038/20573
  52. ↑ Addison, Paul S. (1997). Fractals and chaos: an illustrated course. CRC Press. pp. 44–46. ISBN 978-0-7503-0400-9. https://books.google.com/?id=l2E4ciBQ9qEC&pg=PA45&dq=lightning+fractals+book#v=onepage&q=lightning%20fractals%20book. Retrieved 2011-02-05. 
  53. ↑ Pincus, David (September 2009). "The Chaotic Life: Fractal Brains Fractal Thoughts". psychologytoday.com.
  54. ↑ Enright, Matthew B.; Leitner, David M. (January 27, 2005). "Mass fractal dimension and the compactness of proteins". Physical Review E. 71 (1): 011912. Bibcode:2005PhRvE..71a1912E. doi:10.1103/PhysRevE.71.011912. PMID 15697635.
  55. ↑ Takayasu, H. (1990). Fractals in the physical sciences. Manchester: Manchester University Press. p. 36. ISBN 9780719034343. https://archive.org/details/fractalsinphysic0000taka_s1f9/page/36. 
  56. ↑ Jun, Li; Ostoja-Starzewski, Martin (April 1, 2015). "Edges of Saturn's Rings are Fractal". SpringerPlus. 4, 158: 158. doi:10.1186/s40064-015-0926-6. PMC 4392038. PMID 25883885.
  57. ↑ Meyer, Yves; Roques, Sylvie (1993). Progress in wavelet analysis and applications: proceedings of the International Conference "Wavelets and Applications", Toulouse, France – June 1992. Atlantica Séguier Frontières. p. 25. ISBN 978-2-86332-130-0. https://books.google.com/?id=aHux78oQbbkC&pg=PA25&dq=snowflake+fractals+book#v=onepage&q=snowflake%20fractals%20book. Retrieved 2011-02-05. 
  58. ↑ Ozhovan M. I., Dmitriev I. E., Batyukhnova O. G. Fractal structure of pores of clay soil. Atomic Energy, 74, 241–243 (1993).
  59. ↑ Sreenivasan, K. R.; Meneveau, C. (1986). "The Fractal Facets of Turbulence". Journal of Fluid Mechanics. 173: 357–386. Bibcode:1986JFM...173..357S. doi:10.1017/S0022112086001209.
  60. ↑ de Silva, C. M.; Philip, J.; Chauhan, K.; Meneveau, C.; Marusic, I. (2013). "Multiscale Geometry and Scaling of the Turbulent–Nonturbulent Interface in High Reynolds Number Boundary Layers". Phys. Rev. Lett. 111 (6039): 192–196. Bibcode:2011Sci...333..192A. doi:10.1126/science.1203223. PMID 21737736.
  61. ↑ Falconer, Kenneth (2013). Fractals, A Very Short Introduction. Oxford University Press. 
  62. ↑ Taylor, R. P.; et al. (1999). "Fractal Analysis of Pollock's Drip Paintings". Nature. 399 (6735): 422. Bibcode:1999Natur.399..422T. doi:10.1038/20833.
  63. ↑ Mureika, J. R.; Dyer, C. C.; Cupchik, G. C. (2005). "Multifractal Structure in Nonrepresentational Art". Physical Review E. 72 (4): 046101–1–15. arXiv:physics/0506063. Bibcode:2005PhRvE..72d6101M. doi:10.1103/PhysRevE.72.046101. PMID 16383462.
  64. ↑ Redies, C.; Hasenstein, J.; Denzler, J. (2007). "Fractal-Like Image Statistics in Visual Art: Similarity to Natural Scenes". Spatial Vision. 21 (1): 137–148. doi:10.1163/156856807782753921. PMID 18073055.
  65. ↑ Lee, S.; Olsen, S.; Gooch, B. (2007). "Simulating and Analyzing Jackson Pollock's Paintings". Journal of Mathematics and the Arts. 1 (2): 73–83. CiteSeerX 10.1.1.141.7470. doi:10.1080/17513470701451253.
  66. ↑ Alvarez-Ramirez, J.; Ibarra-Valdez, C.; Rodriguez, E.; Dagdug, L. (2008). "1/f-Noise Structure in Pollock's Drip Paintings". Physica A. 387 (1): 281–295. Bibcode:2008PhyA..387..281A. doi:10.1016/j.physa.2007.08.047.
  67. ↑ Graham, D. J.; Field, D. J. (2008). "Variations in Intensity for Representative and Abstract Art, and for Art from Eastern and Western Hemispheres" (PDF). Perception. 37 (9): 1341–1352. CiteSeerX 10.1.1.193.4596. doi:10.1068/p5971. PMID 18986061.
  68. ↑ Alvarez-Ramirez, J.; Echeverria, J. C.; Rodriguez, E. (2008). "Performance of a high-dimensional R/S method for Hurst exponent estimation". Physica A. 387 (26): 6452–6462. Bibcode:2008PhyA..387.6452A. doi:10.1016/j.physa.2008.08.014.
  69. ↑ Coddington, J.; Elton, J.; Rockmore, D.; Wang, Y. (2008). "Multifractal Analysis and Authentication of Jackson Pollock Paintings". Proceedings of SPIE. 6810 (68100F): 1–12. Bibcode:2008SPIE.6810E..0FC. doi:10.1117/12.765015.
  70. ↑ Al-Ayyoub, M.; Irfan, M. T.; Stork, D. G. (2009). "Boosting Multi-Feature Visual Texture Classifiers for the Authentification of Jackson Pollock's Drip Paintings". SPIE Proceedings on Computer Vision and Image Analysis of Art II. Computer Vision and Image Analysis of Art II. 7869 (78690H): 78690H. Bibcode:2011SPIE.7869E..0HA. doi:10.1117/12.873142.
  71. ↑ Mureika, J. R.; Taylor, R. P. (2013). "The Abstract Expressionists and Les Automatistes: multi-fractal depth?". Signal Processing. 93 (3): 573. doi:10.1016/j.sigpro.2012.05.002.
  72. ↑ Taylor, R. P.; et al. (2005). "Authenticating Pollock Paintings Using Fractal Geometry". Pattern Recognition Letters. 28 (6): 695–702. doi:10.1016/j.patrec.2006.08.012.
  73. ↑ Jones-Smith, K.; et al. (2006). "Fractal Analysis: Revisiting Pollock's Paintings". Nature. 444 (7119): E9–10. Bibcode:2006Natur.444E...9J. doi:10.1038/nature05398. PMID 17136047.
  74. ↑ Taylor, R. P.; et al. (2006). "Fractal Analysis: Revisiting Pollock's Paintings (Reply)". Nature. 444 (7119): E10–11. Bibcode:2006Natur.444E..10T. doi:10.1038/nature05399.
  75. ↑ Shamar, L. (2015). "What Makes a Pollock Pollock: A Machine Vision Approach" (PDF). International Journal of Arts and Technology. 8: 1–10. CiteSeerX 10.1.1.647.365. doi:10.1504/IJART.2015.067389.
  76. ↑ Taylor, R. P.; Spehar, B.; Van Donkelaar, P.; Hagerhall, C. M. (2011). "Perceptual and Physiological Responses to Jackson Pollock's Fractals". Frontiers in Human Neuroscience. 5: 1–13. doi:10.3389/fnhum.2011.00060. PMC 3124832. PMID 21734876.
  77. ↑ Frame, Michael; and Mandelbrot, Benoît B.; A Panorama of Fractals and Their Uses
  78. ↑ Nelson, Bryn; Sophisticated Mathematics Behind African Village Designs Fractal patterns use repetition on large, small scale, San Francisco Chronicle, Wednesday, February 23, 2009
  79. ↑ Situngkir, Hokky; Dahlan, Rolan (2009). Fisika batik: implementasi kreatif melalui sifat fraktal pada batik secara komputasional. Jakarta: Gramedia Pustaka Utama.ISBN|978-979-22-4484-7
  80. ↑ Rulistia, Novia D. (October 6, 2015). "Application maps out nation's batik story". The Jakarta Post. Retrieved 2016-09-25.
  81. ↑ Koutonin, Mawuna (18 March 2016). "Story of cities #5: Benin City, the mighty medieval capital now lost without trace". Retrieved 2 April 2018.
  82. ↑ Taylor, Richard P. (2016). "Fractal Fluency: An Intimate Relationship Between the Brain and Processing of Fractal Stimuli". In Di Ieva, Antonio. The Fractal Geometry of the Brain. Springer Series in Computational Neuroscience. Springer. ISBN 978-1-4939-3995-4. 
  83. ↑ Taylor, Richard P. (2006). "Reduction of Physiological Stress Using Fractal Art and Architecture". Leonardo. 39 (3): 245–251. doi:10.1162/leon.2006.39.3.245.
  84. ↑ For further discussion of this effect, see Taylor, Richard P.; Spehar, Branka; Donkelaar, Paul Van; Hagerhall, Caroline M. (2011). "Perceptual and Physiological Responses to Jackson Pollock's Fractals". Frontiers in Human Neuroscience. 5: 60. doi:10.3389/fnhum.2011.00060. PMC 3124832. PMID 21734876.
  85. ↑ Reiner, Richard; Waltereit, Patrick; Benkhelifa, Fouad; Müller, Stefan; Walcher, Herbert; Wagner, Sandrine; Quay, Rüdiger; Schlechtweg, Michael; Ambacher, Oliver; Ambacher, O. (2012). "Fractal structures for low-resistance large area AlGaN/GaN power transistors". Proceedings of ISPSD: 341–344. doi:10.1109/ISPSD.2012.6229091. ISBN 978-1-4577-1596-9.
  86. ↑ Zhiwei Huang; Yunho Hwang; Vikrant Aute; Reinhard Radermacher (2016). "Review of Fractal Heat Exchangers" (PDF) International Refrigeration and Air Conditioning Conference. Paper 1725 {{cite journal}}: Cite journal requires |journal= (help)CS1 maint: postscript (link)
  87. ↑ Chen, Yanguang (2011). "Modeling Fractal Structure of City-Size Distributions Using Correlation Functions". PLOS ONE. 6 (9): e24791. arXiv:1104.4682. Bibcode:2011PLoSO...624791C. doi:10.1371/journal.pone.0024791. PMC 3176775. PMID 21949753.
  88. ↑ "Applications". Archived from the original on October 12, 2007. Retrieved 2007-10-21.
  89. ↑ "Detecting 'life as we don't know it' by fractal analysis"
  90. ↑ Smith, Robert F.; Mohr, David N.; Torres, Vicente E.; Offord, Kenneth P.; Melton III, L. Joseph (1989). "Renal insufficiency in community patients with mild asymptomatic microhematuria". Mayo Clinic Proceedings. 64 (4): 409–414. doi:10.1016/s0025-6196(12)65730-9. PMID 2716356.
  91. ↑ Landini, Gabriel (2011). "Fractals in microscopy". Journal of Microscopy. 241 (1): 1–8. doi:10.1111/j.1365-2818.2010.03454.x. PMID 21118245.
  92. ↑ Cheng, Qiuming (1997). "Multifractal Modeling and Lacunarity Analysis". Mathematical Geology. 29 (7): 919–932. doi:10.1023/A:1022355723781.
  93. ↑ Chen, Yanguang (2011). "Modeling Fractal Structure of City-Size Distributions Using Correlation Functions". PLOS ONE. 6 (9): e24791. arXiv:1104.4682. Bibcode:2011PLoSO...624791C. doi:10.1371/journal.pone.0024791. PMC 3176775. PMID 21949753.
  94. ↑ Burkle-Elizondo, Gerardo; Valdéz-Cepeda, Ricardo David (2006). "Fractal analysis of Mesoamerican pyramids". Nonlinear Dynamics, Psychology, and Life Sciences. 10 (1): 105–122. PMID 16393505.
  95. ↑ Brown, Clifford T.; Witschey, Walter R. T.; Liebovitch, Larry S. (2005). "The Broken Past: Fractals in Archaeology". Journal of Archaeological Method and Theory. 12: 37–78. doi:10.1007/s10816-005-2396-6.
  96. ↑ Saeedi, Panteha; Sorensen, Soren A. (2009). "An Algorithmic Approach to Generate After-disaster Test Fields for Search and Rescue Agents" (PDF). Proceedings of the World Congress on Engineering 2009: 93–98. ISBN 978-988-17-0125-1.
  97. ↑ Bunde, A.; Havlin, S. (2009). "Fractal Geometry, A Brief Introduction to". Encyclopedia of Complexity and Systems Science. pp. 3700. doi:10.1007/978-0-387-30440-3_218. ISBN 978-0-387-75888-6. 
  98. ↑ "GPU internals" (PDF).
  99. ↑ "sony patents".
  100. ↑ "description of swizzled and hybrid tiled swizzled textures".
  101. ↑ "US8773422B1 - System, method, and computer program product for grouping linearly ordered primitives". Google Patents. December 4, 2007. Retrieved December 28, 2019.
  102. ↑ "US20110227921A1 - Processing of 3D computer graphics data on multiple shading engines". Google Patents. December 15, 2010. Retrieved December 27, 2019.
  103. ↑ "Johns Hopkins Turbulence Databases".
  104. ↑ Li, Y.; Perlman, E.; Wang, M.; Yang, y.; Meneveau, C.; Burns, R.; Chen, S.; Szalay, A.; Eyink, G. (2008). "A Public Turbulence Database Cluster and Applications to Study Lagrangian Evolution of Velocity Increments in Turbulence". Journal of Turbulence. 9: N31. arXiv:0804.1703. Bibcode:2008JTurb...9...31L. doi:10.1080/14685240802376389.
  105. ↑ Hohlfeld, Robert G.; Cohen, Nathan (1999). "Self-similarity and the geometric requirements for frequency independence in Antennae". Fractals. 7 (1): 79–84. doi:10.1142/S0218348X99000098.
  106. ↑ "Introduction to Fractal Geometry". www.fractal.org. Retrieved 2017-04-11.
  107. ↑ DeFelice, David (August 18, 2015). "NASA – Ion Propulsion". NASA (in English). Retrieved 2017-04-11.

相关连接

编者推荐

系统科学简史与现代复杂系统科学,本课程主要探讨了现代复杂系统科学的研究主题，同时也介绍了系统科学的历史，生命游戏与分形结构等知识点

书籍推荐

分形对象：形、机遇和维数 Fractals:From,Chance,and Dimension

本书考察和研究出现在自然界中的若干典型分形对象，为我们提供了一个关于分形的内容，意义及方法的扼要介绍。尽管自该书第一版（法文版）问世以来，分形的理论及其应用发展极为迅速，并出现了大量的有关著作，但此书仍不失为分形理论最好的入门书之一


大自然的分形几何 The Fractal Geometry of Nature

这本书介绍了自然界中各种各样的分形理论，从海岸线、雪花，到河流、星系等自然现象，去阐述分形这一概念。作为多个学科的交叉，分形几何对以往欧氏几何不屑一顾（或说无能为力）的“病态”曲线（如科赫雪花曲线等）的全新解释，是人类认识客观世界不断开拓的必然结果。这说明欧氏几何只是对客观世界的近似反映，而分形几何则深化了这种认识，因此分形几何学是描述各种复杂自然曲线的大自然的几何学。


市场的（错误）行为：风险、破产与收益的分形观点The Misbehavior of Markets: A Fractal View of Financial Turbulence

《市场的（错误）行为》以分形视角观察金融市场的行为，推翻了作为当代金融分析基础的“随机游走”理论。通过分形模型，市场表现被重新阐释。本书是现代金融理论标准工具和模型的一次革命性重估，书中的观点颠覆了成千上万投资者的既有观念。


网站资源

分形艺术网作品

分形艺术网

分形艺术网是一个展示分形艺术之美，学习交流分形艺术创作的平台，其中包含了很多分形艺术作品及分形资源推荐。


分形的世界

在此堂课程，主要介绍了关于分形的思想与脉络，分形现象、分形维数、利用分形规律的计算方法以及混沌。主讲人为北京师范大学系统学院狄增如教授。狄增如教授主要从事复杂网络和经济（金融）物理学等方面的研究，是国内最早从事经济物理学研究的学者之一。


视频资源

TED分享视频：伯努·瓦曼德布洛特: 分形和粗糙的艺术 Benoit Mandelbrot: Fractals and the Art of Roughness

Benoit Mandelbrot的研究使世界对分形有了更深刻的理解，分形是研究粗糙的广泛而有力的工具，在自然界和人类的作品中都是如此。该视频概述了分形的研究，以及它们为许多领域带来的颠覆性见解。

寻找隐藏的维 Hunting the Hidden Dimension

什么是电影特效，股票市场，和心脏病的共同点？它们连接了一个革命性的新的数学分支，改变了我们看世界，开辟了广阔的新领域，以科学的分析和理解。数学家们开发不规则碎片形是从单纯的好奇心到接触几乎每一个分科的理解，包括我们宇宙的命运。

课程推荐

分形与奇异吸引子的几何学

本课程对非线性动力学和混沌进行了详细的讲解，强调分析方法、具体实例和几何直觉。主讲人为Steven Strogatz。


集智百科文章

分形几何：寻找隐藏的维度 | 集智百科

与树共舞：分形舞蹈可视化

城市为何遵循规模法则？分形几何揭开幂律成因

混沌、分形理论及其在信息科学中的应用 | IWCFTA2018


本中文词条由趣木木参与编译，薄荷编辑，欢迎在讨论页面留言。

本词条内容源自wikipedia及公开资料，遵守 CC3.0协议。

取自“https://wiki.swarma.org/index.php?title=分形&oldid=3676”