“信号处理”的版本间的差异

2020年4月18日 (六) 16:20的版本

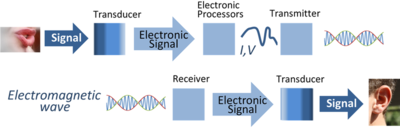
电信号的传输过程。传感器将信号从其他物理波形转换成电流或电压波形，然后对这些波形进行处理，以电磁波的形式传输，再由另一个传感器接收和转换成最需要的信号形式。

信号处理(Signal processing)是电子工程领域的一个分支，致力于分析、加工和合成诸如声音、图像和生物测量等信号。信号处理技术可用于提高传输和存储效率以及信号主观质量，也研究如何提取和检测可测信号中的有效成分。

发展历史

按照奥本海姆 Alan V. Oppenheim和谢弗 Ronald w. Schafer的观点，信号处理的原理可以追溯到17世纪的经典数值分析技术。奥本海姆和谢弗进一步指出，这些数字信号领域的技术改进可以在1940-1950年代的数字控制系统领域中找到。

1948年克劳德香农Claude Shannon在Bell System Technical Journal期刊上发表了非常具有影响力的论文《A Mathematical Theory of Communication》。这篇论文为之后的信息通信系统奠定了基础。与此同时，随着信号处理的出现，信息传输技术也开始飞速发展。

电子信号处理由于MOSFET(金属氧化物半导体场效应管，一般称之为MOS晶体管)的出现而发生了革命性的改变。该晶体管由Mohamed M. Atalla和Dawon Kahng在1959年发明。MOS集成电路技术是20世纪70年代初第一个单片机微处理器和微控制器出现的基础，随之第一个单片信号处理器(DSP)在1979年出现。

分类

模拟信号 Analog Signal

模拟信号处理面向的是那些没有被数字化的信号（包括线性和非线性的电子电路信号），比如传统的无线电、电话、雷达和电视系统（编者注：现在绝大多数电视机均采用数字信号，很多年前的天线采用模拟信号，如今配置机顶盒的电视机基本上都是数字信号）。线性电子电路包括无源滤波器、有源滤波器、附加混频器、积分器和延迟线等。非线性电路包括压控电路、倍增器（频率混合器和压控放大器）、压控滤波器、压控振荡器和锁相环电路。

连续信号 Continuous-time signal

连续时间信号处理（一般也称为连续信号处理）面向随连续域变化而变化的信号（忽略某些单个中断点）。

信号处理一般会从时域、频域和复频域三个角度对信号进行分析。该技术主要讨论线性时不变连续系统的建模、系统零状态响应的积分、系统函数的建立以及确定性信号的连续时间滤波。

离散信号 Discrete time signal

离散时间信号处理（一般也称为离散信号处理）是面向采样信号的，即定义在时间离散点上的信号，因此该信号仅在时间上是量化的，而不对幅度进行量化。

模拟离散时间信号处理是面向持续采样电路、模拟时分复用器、模拟延迟线和模拟反馈移位寄存器等电子器件的技术。这项技术是数字信号处理的前身（见下一部分数字信号），目前仍应用于千兆赫兹信号的高级处理。

离散信号处理的概念也是一门理论学科，它为数字信号处理建立了数学基础，不过没有考虑量化噪声。

数字信号 Digital Signal

数字信号处理是面向数字化离散时间采样信号的技术。处理过程需要通用计算机或者数字电路，如ASICs(专用集成电路)、FPGA（现场可编程门阵列）或者专门的数字信号处理器(DSP芯片)。典型的算术运算包括不动点和浮点、实值和复值、乘法和加法。需要硬件支持的一些典型操作包括循环缓冲区和查找表。数字信号处理算法包括FFT(快速傅立叶变换)、FIR(有限脉冲响应滤波器)、IIR(无限脉冲响应滤波器)以及自适应滤波器（比如维纳滤波器和卡尔曼滤波器）。

非线性信号 Nonlinear Signal

非线性信号处理适用于非线性系统产生信号，可以在时间、频率或时空域内进行。非线性系统可以产生高度复杂的行为，包括分岔、混沌、谐波和分谐波，这些行为无法用线性方法产生和分析。

统计信号 Statistical Signal

统计信号处理是将信号视为随机过程，利用其统计特征来完成信号处理任务的一种方法。统计技术广泛应用于信号处理领域。例如，我们可以为拍摄图像时产生的噪声建立概率分布模型，并基于该模型构造相关的信号处理技术来降低图像中的噪声。

应用领域

地震波信号处理

音频信号处理——用来表示声音的电信号，如语音或者音乐
图像处理——应用于数码相机，计算机和各种成像系统中
视频信号处理——用于处理电子影像
无线通信——波形的形成、调制解调、滤波、均衡
数组处理——处理来自传感器列阵的信号
过程控制——使用多源信号，包括行业标准等
金融数据处理——使用信号处理技术分析财务数据，尤其是用于预测
特征提出——用于提取信号特征，主要应用于图像的理解和语音识别。在很多人工智能领域中，这是必不可少的一环。
编码——包括音频压缩、图像压缩和视频压缩

典型设备

滤波器 ——例如模拟（无源和有源）或数字（FIR、IIR、频域和随机滤波器等）
用于信号采集和重建的采样器和模数转换器，包括测量物理信号，将其存储或传输为数字信号，之后再还原为原始信号或其近似值。
信号压缩器
数字信号处理器（DSP）

@@ 第31行： / 第31行： @@
 离散信号处理的概念也是一门理论学科，它为数字信号处理建立了数学基础，不过没有考虑量化噪声。
-===数字信号(Digital Signal)===
+===数字信号 Digital Signal===
 数字信号处理是面向数字化离散时间采样信号的技术。处理过程需要通用计算机或者数字电路，如ASICs(专用集成电路)、FPGA（现场可编程门阵列）或者专门的数字信号处理器(DSP芯片)。典型的算术运算包括不动点和浮点、实值和复值、乘法和加法。需要硬件支持的一些典型操作包括循环缓冲区和查找表。数字信号处理算法包括FFT(快速傅立叶变换)、FIR(有限脉冲响应滤波器)、IIR(无限脉冲响应滤波器)以及自适应滤波器（比如维纳滤波器和卡尔曼滤波器）。