“信号处理”的版本间的差异

来自集智百科 - 复杂系统|人工智能|复杂科学|复杂网络|自组织
跳到导航 跳到搜索
第1行： 第1行：
  
−
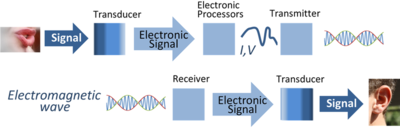
[[File:Signal processing system.png|thumb|400px|电信号的传输过程。 传感器将信号从其他物理波形转换成电流或电压波形，然后对这些波形进行处理，以电磁波的形式传输，再由另一个传感器接收和转换成最需要的信号形式。]]
+
[[File:Signal processing system.png|thumb|400px|电信号的传输过程。 传感器将信号从其他物理波形转换成电流或电压波形，然后对这些波形进行处理，以电磁波的形式传输，再由另一个传感器接收和转换成最需要的信号形式。]]<ref>{{cite book|title=Discrete-Time Signal Processing|author=Alan V. Oppenheim and Ronald W. Schafer|publisher=Prentice Hall|year=1989|isbn=0-13-216771-9|page=1}}</ref>
  
−
'''信号处理 Signal processing'''是电子工程领域的一个分支，致力于分析、加工和合成诸如声音、图像和生物测量等信号。信号处理技术可用于提高传输和存储效率以及信号主观质量，也研究如何提取和检测可测信号中的有效成分。
+
'''信号处理 Signal processing'''是电子工程领域的一个分支，致力于分析、加工和合成诸如声音、图像和生物测量等信号。<ref>{{cite journal|last=Sengupta|first=Nandini|author2=Sahidullah, Md|author3=Saha, Goutam|date=August 2016|title=Lung sound classification using cepstral-based statistical features|url=|journal=Computers in Biology and Medicine|volume=75|issue=1|pages=118–129|doi=10.1016/j.compbiomed.2016.05.013|pmid=27286184}}</ref>信号处理技术可用于提高传输和存储效率以及信号主观质量，也研究如何提取和检测可测信号中的有效成分。
  
 
==发展历史==
 
==发展历史==
−
按照'''奥本海姆 Alan V. Oppenheim'''和'''谢弗 Ronald w. Schafer'''的观点，信号处理的原理可以追溯到17世纪的经典数值分析技术。奥本海姆和谢弗进一步指出，这些数字信号领域的技术改进可以在1940-1950年代的数字控制系统领域中找到。
+
按照'''奥本海姆 Alan V. Oppenheim'''和'''谢弗 Ronald w. Schafer'''的观点，信号处理的原理可以追溯到17世纪的经典数值分析技术。奥本海姆和谢弗进一步指出，这些数字信号领域的技术改进可以在1940-1950年代的数字控制系统领域中找到。<ref>{{cite book |title=Digital Signal Processing |year=1975 |publisher=[[Prentice Hall]] |isbn=0-13-214635-5 |author=Oppenheim, Alan V. |author2=Schafer, Ronald W. |page= 5}}</ref>
  
  
−
1948年'''[[克劳德香农Claude Shannon]]'''在Bell System Technical Journal期刊上发表了非常具有影响力的论文《A Mathematical Theory of Communication》。这篇论文为之后的信息通信系统奠定了基础。与此同时，随着信号处理的出现，信息传输技术也开始飞速发展。
+
1948年'''[[克劳德香农Claude Shannon]]'''在Bell System Technical Journal期刊上发表了非常具有影响力的论文《A Mathematical Theory of Communication》。<ref>{{cite web |url=https://www.computerhistory.org/revolution/digital-logic/12/269/1331 |title=A Mathematical Theory of Communication – CHM Revolution |website=Computer History |access-date=2019-05-13}}</ref> 这篇论文为之后的信息通信系统奠定了基础。与此同时，随着信号处理的出现，信息传输技术也开始飞速发展。<ref name=fifty>{{cite book |title=Fifty Years of Signal Processing: The IEEE Signal Processing Society and its Technologies, 1948–1998 |publisher=The IEEE Signal Processing Society |year=1998}}</ref>
  
  
第42行： 第42行：
 
===非线性信号 Nonlinear Signal===
 
===非线性信号 Nonlinear Signal===
  
−
非线性信号处理适用于非线性系统产生信号，可以在时间、频率或时空域内进行。非线性系统可以产生高度复杂的行为，包括分岔、混沌、谐波和分谐波，这些行为无法用线性方法产生和分析。
+
非线性信号处理适用于非线性系统产生信号，可以在时间、频率或时空域内进行。<ref name="Billings">{{cite book |last=Billings |first=S. A. |title=Nonlinear System Identification: NARMAX Methods in the Time, Frequency, and Spatio-Temporal Domains |publisher=Wiley |year=2013 |isbn=978-1119943594 }}</ref><ref name="VSA">{{cite book |authors=Slawinska, J., Ourmazd, A., and Giannakis, D. |title=2018 IEEE Statistical Signal Processing Workshop (SSP) |chapter=A New Approach to Signal Processing of Spatiotemporal Data |pages=338–342 |publisher=IEEE Xplore |year=2018 |doi=10.1109/SSP.2018.8450704|isbn=978-1-5386-1571-3 }}</ref>非线性系统可以产生高度复杂的行为，包括分岔、混沌、谐波和分谐波，这些行为无法用线性方法产生和分析。
  
  
 
===统计信号 Statistical Signal===
 
===统计信号 Statistical Signal===
  
−
统计信号处理是将信号视为随机过程，利用其统计特征来完成信号处理任务的一种方法。统计技术广泛应用于信号处理领域。例如，我们可以为拍摄图像时产生的噪声建立概率分布模型，并基于该模型构造相关的信号处理技术来降低图像中的噪声。
+
统计信号处理是将信号视为随机过程，利用其统计特征来完成信号处理任务的一种方法。<ref name ="Scharf">{{cite book |first=Louis L. |last=Scharf |title=Statistical signal processing: detection, estimation, and time series analysis |publisher=[[Addison–Wesley]] |location=[[Boston]] |year=1991 |pages= |isbn=0-201-19038-9 |oclc=61160161}}</ref>统计技术广泛应用于信号处理领域。例如，我们可以为拍摄图像时产生的噪声建立概率分布模型，并基于该模型构造相关的信号处理技术来降低图像中的噪声。
  
  
第63行： 第63行：
 
* 特征提出——用于提取信号特征，主要应用于图像的理解和语音识别。在很多人工智能领域中，这是必不可少的一环。
 
* 特征提出——用于提取信号特征，主要应用于图像的理解和语音识别。在很多人工智能领域中，这是必不可少的一环。
 
* 编码——包括音频压缩、图像压缩和视频压缩
 
* 编码——包括音频压缩、图像压缩和视频压缩
 +
 +
 
==典型设备==
 
==典型设备==
 
* 滤波器  ——例如模拟（无源和有源）或数字（FIR、IIR、频域和随机滤波器等）
 
* 滤波器  ——例如模拟（无源和有源）或数字（FIR、IIR、频域和随机滤波器等）
第68行： 第70行：
 
* 信号压缩器
 
* 信号压缩器
 
* 数字信号处理器（DSP）
 
* 数字信号处理器（DSP）
 +
 +
 
==相关数学方法==
 
==相关数学方法==
−
* 微分方程
+
* 微分方程<ref name="Gaydecki2004">{{cite book|author=Patrick Gaydecki|title=Foundations of Digital Signal Processing: Theory, Algorithms and Hardware Design|url=https://books.google.com/?id=6Qo7NvX3vz4C&pg=PA40&dq=%22differential+equations%22+%22signal+processing%22#v=snippet&q=%22differential%20equation%22%20OR%20%22differential%20equations%22&f=false|year=2004|publisher=IET|isbn=978-0-85296-431-6|pages=40–}}</ref>
−
* 递归关系
+
* 递归关系<ref name="Engelberg2008">{{cite book|author=Shlomo Engelberg|title=Digital Signal Processing: An Experimental Approach|url=https://books.google.com/books?id=z3CpcCHbtgIC|date=8 January 2008|publisher=Springer Science & Business Media|isbn=978-1-84800-119-0}}</ref>
 
* 变换理论
 
* 变换理论
−
* 时频分析  –用于处理非平稳信号
+
* 时频分析  –用于处理非平稳信号<ref>{{cite book|title=Time frequency signal analysis and processing a comprehensive reference|year=2003|publisher=Elsevier|location=Amsterdam|isbn=0-08-044335-4|edition=1|editor=Boashash, Boualem}}</ref>
−
* 频谱估计  –用于确定时间序列的频谱内容（即功率在频率上的分布）
+
* 频谱估计  –用于确定时间序列的频谱内容（即功率在频率上的分布）<ref>{{cite book|first1=Petre|last1=Stoica|first2=Randolph|last2=Moses|title=Spectral Analysis of Signals|year=2005|publisher=Prentice Hall|location=NJ|url=http://user.it.uu.se/%7Eps/SAS-new.pdf}}</ref>
 
* 统计信号处理  –根据信号和噪声的随机特性分析和提取信息
 
* 统计信号处理  –根据信号和噪声的随机特性分析和提取信息
 
* 线性时不变系统理论和变换理论
 
* 线性时不变系统理论和变换理论
第79行： 第83行：
 
* 系统识别和分类
 
* 系统识别和分类
 
* 微积分
 
* 微积分
−
* 复杂分析
+
* 复杂分析<ref name="SchreierScharf2010">{{cite book|author1=Peter J. Schreier|author2=Louis L. Scharf|title=Statistical Signal Processing of Complex-Valued Data: The Theory of Improper and Noncircular Signals|url=https://books.google.com/books?id=HBaxLfDsAHoC&printsec=frontcover#v=onepage&q=%22complex%20analysis%22&f=false|date=4 February 2010|publisher=Cambridge University Press|isbn=978-1-139-48762-7}}</ref>
−
* 向量空间和线性代数
+
* 向量空间和线性代数<ref name="Little2019">{{cite book|author=Max A. Little|title=Machine Learning for Signal Processing: Data Science, Algorithms, and Computational Statistics|url=https://books.google.com/books?id=ejGoDwAAQBAJ&printsec=frontcover#v=onepage&q=%22vector%20space%22&f=false|date=13 August 2019|publisher=OUP Oxford|isbn=978-0-19-102431-3}}</ref>
−
* 功能分析
+
* 功能分析<ref name="DamelinJr2012">{{cite book|author1=Steven B. Damelin|author2=Willard Miller, Jr|title=The Mathematics of Signal Processing|url=https://books.google.com/books?id=MtPLYXQ9d9MC&printsec=frontcover#v=onepage&q=%22functional%20analysis%22&f=false|year=2012|publisher=Cambridge University Press|isbn=978-1-107-01322-3}}</ref>
−
* 概率论和随机过程
+
* 概率论和随机过程<ref name="Scharf"/>
 
* 信号检测
 
* 信号检测
 
* 参数估计
 
* 参数估计
−
* 优化方法
+
* 优化方法<ref name="PalomarEldar2010">{{cite book|author1=Daniel P. Palomar|author2=Yonina C. Eldar|title=Convex Optimization in Signal Processing and Communications|url=https://books.google.com/books?id=UOpnvPJ151gC|year=2010|publisher=Cambridge University Press|isbn=978-0-521-76222-9}}</ref>
 
* 数值方法
 
* 数值方法
 
* 时间序列
 
* 时间序列
 
* 数据挖掘  –用于统计分析大量变量之间的关系(代表许多物理信号），以提取未知的有用信息
 
* 数据挖掘  –用于统计分析大量变量之间的关系(代表许多物理信号），以提取未知的有用信息
 +
 +
 +
==进一步阅读==
 +
* {{cite book|last=P Stoica|first=R Moses|title=Spectral Analysis of Signals|year=2005|publisher=Prentice Hall|location=NJ|url=http://user.it.uu.se/%7Eps/SAS-new.pdf}}
 +
* {{cite book |first=Steven M. |last=Kay |title=Fundamentals of Statistical Signal Processing |publisher=[[Prentice Hall]] |location=[[Upper Saddle River, New Jersey]] |year=1993 |pages= |isbn=0-13-345711-7 |oclc=26504848}}
 +
* {{cite book |first=Athanasios |last=Papoulis |title=Probability, Random Variables, and Stochastic Processes |year=1991 |edition=third |publisher=McGraw-Hill |isbn=0-07-100870-5}}
 +
* Kainam Thomas Wong [http://www.eie.polyu.edu.hk/~enktwong/]: Statistical Signal Processing lecture notes at the University of Waterloo, Canada.
 +
* [[Ali H. Sayed]], Adaptive Filters, Wiley, NJ, 2008, {{isbn|978-0-470-25388-5}}.
 +
* [[Thomas Kailath]], [[Ali H. Sayed]], and [[Babak Hassibi]], Linear Estimation, Prentice-Hall, NJ, 2000, {{isbn|978-0-13-022464-4}}.
 +
 +
 +
==相关链接==
 +
* [http://www.sp4comm.org/ 通信的信号处理] – Paolo Prandoni和Martin Vetterli撰写的免费在线教科书（2008）
 +
* [http://www.dspguide.com 科学家和工程师数字信号处理指南] – Stephen Smith提供的免费在线教科书
 +
* [http://www.usbr.gov/research/projects/detail.cfm?id=9962 确定发电厂特性的信号处理技术]
 +
* [http://www.signalprocessingsociety.org/ IEEE信号处理学会]
 +
* [http://siliconmentor.blogspot.in/2015/03/bio-medical-signal-processing-at-glance.html 生物医学信号处理概览]
 +
* [https://github.com/unpingco/Python-for-Signal-Processing 用于信号处理的Python的IPython笔记本]
  
 
==参考文献==
 
==参考文献==

2020年4月18日 (六) 16:46的版本

电信号的传输过程。 传感器将信号从其他物理波形转换成电流或电压波形，然后对这些波形进行处理，以电磁波的形式传输，再由另一个传感器接收和转换成最需要的信号形式。

[1]

信号处理 Signal processing是电子工程领域的一个分支，致力于分析、加工和合成诸如声音、图像和生物测量等信号。[2]信号处理技术可用于提高传输和存储效率以及信号主观质量，也研究如何提取和检测可测信号中的有效成分。

发展历史

按照奥本海姆 Alan V. Oppenheim和谢弗 Ronald w. Schafer的观点，信号处理的原理可以追溯到17世纪的经典数值分析技术。奥本海姆和谢弗进一步指出，这些数字信号领域的技术改进可以在1940-1950年代的数字控制系统领域中找到。[3]


1948年克劳德香农Claude Shannon在Bell System Technical Journal期刊上发表了非常具有影响力的论文《A Mathematical Theory of Communication》。[4] 这篇论文为之后的信息通信系统奠定了基础。与此同时，随着信号处理的出现，信息传输技术也开始飞速发展。[5]


电子信号处理由于MOSFET(金属氧化物半导体场效应管，一般称之为MOS晶体管)的出现而发生了革命性的改变。该晶体管由Mohamed M. Atalla和Dawon Kahng在1959年发明。MOS集成电路技术是20世纪70年代初第一个单片机微处理器和微控制器出现的基础，随之第一个单片信号处理器(DSP)在1979年出现。

分类

模拟信号 Analog Signal

模拟信号处理面向的是那些没有被数字化的信号（包括线性和非线性的电子电路信号），比如传统的无线电、电话、雷达和电视系统（编者注：现在绝大多数电视机均采用数字信号，很多年前的天线采用模拟信号，如今配置机顶盒的电视机基本上都是数字信号）。线性电子电路包括无源滤波器、有源滤波器、附加混频器、积分器和延迟线等。非线性电路包括压控电路、倍增器（频率混合器和压控放大器）、压控滤波器、压控振荡器和锁相环电路。

连续信号 Continuous-time signal

连续时间信号处理（一般也称为连续信号处理）面向随连续域变化而变化的信号（忽略某些单个中断点）。

信号处理一般会从时域、频域和复频域三个角度对信号进行分析。该技术主要讨论线性时不变连续系统的建模、系统零状态响应的积分、系统函数的建立以及确定性信号的连续时间滤波。


离散信号 Discrete time signal

离散时间信号处理（一般也称为离散信号处理）是面向采样信号的，即定义在时间离散点上的信号，因此该信号仅在时间上是量化的，而不对幅度进行量化。

模拟离散时间信号处理是面向持续采样电路、模拟时分复用器、模拟延迟线和模拟反馈移位寄存器等电子器件的技术。这项技术是数字信号处理的前身（见下一部分数字信号），目前仍应用于千兆赫兹信号的高级处理。

离散信号处理的概念也是一门理论学科，它为数字信号处理建立了数学基础，不过没有考虑量化噪声。


数字信号 Digital Signal

数字信号处理是面向数字化离散时间采样信号的技术。处理过程需要通用计算机或者数字电路，如ASICs(专用集成电路)、FPGA（现场可编程门阵列）或者专门的数字信号处理器(DSP芯片)。典型的算术运算包括不动点和浮点、实值和复值、乘法和加法。需要硬件支持的一些典型操作包括循环缓冲区和查找表。数字信号处理算法包括FFT(快速傅立叶变换)、FIR(有限脉冲响应滤波器)、IIR(无限脉冲响应滤波器)以及自适应滤波器（比如维纳滤波器和卡尔曼滤波器）。


非线性信号 Nonlinear Signal

非线性信号处理适用于非线性系统产生信号，可以在时间、频率或时空域内进行。[6][7]非线性系统可以产生高度复杂的行为，包括分岔、混沌、谐波和分谐波，这些行为无法用线性方法产生和分析。


统计信号 Statistical Signal

统计信号处理是将信号视为随机过程，利用其统计特征来完成信号处理任务的一种方法。[8]统计技术广泛应用于信号处理领域。例如，我们可以为拍摄图像时产生的噪声建立概率分布模型，并基于该模型构造相关的信号处理技术来降低图像中的噪声。


应用领域

地震波信号处理
  • 音频信号处理——用来表示声音的电信号，如语音或者音乐
  • 图像处理——应用于数码相机，计算机和各种成像系统中
  • 视频信号处理——用于处理电子影像
  • 无线通信——波形的形成、调制解调、滤波、均衡
  • 数组处理——处理来自传感器列阵的信号
  • 过程控制——使用多源信号，包括行业标准等
  • 金融数据处理——使用信号处理技术分析财务数据，尤其是用于预测
  • 特征提出——用于提取信号特征，主要应用于图像的理解和语音识别。在很多人工智能领域中，这是必不可少的一环。
  • 编码——包括音频压缩、图像压缩和视频压缩


典型设备

  • 滤波器 ——例如模拟（无源和有源）或数字（FIR、IIR、频域和随机滤波器等）
  • 用于信号采集和重建的采样器和模数转换器，包括测量物理信号，将其存储或传输为数字信号，之后再还原为原始信号或其近似值。
  • 信号压缩器
  • 数字信号处理器（DSP）


相关数学方法

  • 微分方程[9]
  • 递归关系[10]
  • 变换理论
  • 时频分析 –用于处理非平稳信号[11]
  • 频谱估计 –用于确定时间序列的频谱内容（即功率在频率上的分布）[12]
  • 统计信号处理 –根据信号和噪声的随机特性分析和提取信息
  • 线性时不变系统理论和变换理论
  • 多项式信号处理 –使用多项式分析与输入和输出相关的系统
  • 系统识别和分类
  • 微积分
  • 复杂分析[13]
  • 向量空间和线性代数[14]
  • 功能分析[15]
  • 概率论和随机过程[8]
  • 信号检测
  • 参数估计
  • 优化方法[16]
  • 数值方法
  • 时间序列
  • 数据挖掘 –用于统计分析大量变量之间的关系(代表许多物理信号），以提取未知的有用信息


进一步阅读

取自“https://wiki.swarma.org/index.php?title=信号处理&oldid=3736”