“NIS+”的版本间的差异
(→NIS的缺陷) |
(→概述) |
||
| 第143行: | 第143行: | ||
[[文件:NIS+odd.png|替代=|无框|800x800像素]] | [[文件:NIS+odd.png|替代=|无框|800x800像素]] | ||
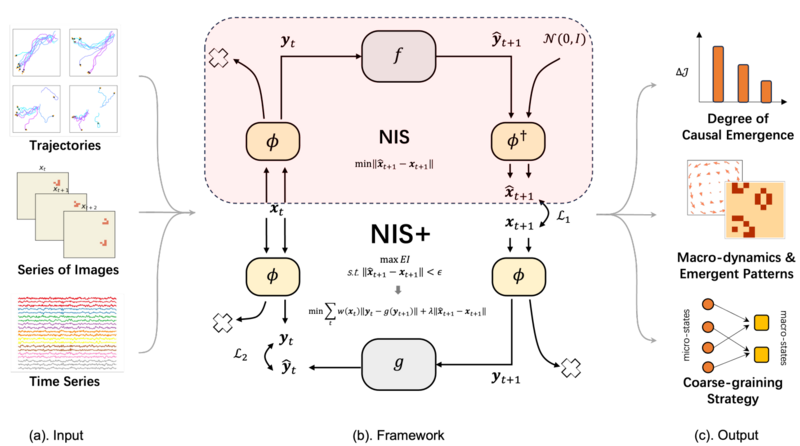
| − | 为了最大化式{{EquationNote|1}} | + | 为了最大化式{{EquationNote|1}}中定义的EI,作者将NIS的框架扩展为NIS+。在NIS+中,我们首先使用互信息和变分不等式的公式将互信息的最大化问题转化为机器学习问题,其次,使用<math>y_{t+1}=\phi(x_{t+1})</math>来预测<math>y_{t}</math>,从而保证[[互信息]]最大化。这里,[math]\phi[/math]是反向动力学学习器神经网络。最后,利用样本重加权技术来解决均匀分布干预的挑战,从而优化EI。所有这些技术组成了增强版神经信息压缩机(NIS+)<ref>Mingzhe Yang, Zhipeng Wang, Kaiwei Liu, et al. Finding emergence in data by maximizing effective information. National Science Review, 2024, nwae279</ref>。在此框架中,输入可观测的数据,输出是因果涌现的程度、宏观动力学、涌现斑图以及粗粒化策略。 |
== 数学推导 == | == 数学推导 == | ||
2024年9月4日 (三) 11:53的版本
NIS+(Neural Information Squeezer Plus)是一个机器学习框架,可学习宏观动力学,并识别因果涌现。该框架通过最大化有效信息,得到一个宏观动态模型。作者通过在模拟数据和实际数据上的实验,证明了该框架的有效性。且该框架在不同测试环境里表现出更强的泛化能力。
问题与背景
在自然界和人类社会中,存在着许多由无数相互作用的元素构成的复杂系统,如气候系统、生态系统、鸟群、蚁群、细胞和大脑等。这些系统展现出丰富的非线性动力学行为,如果我们仅关注微观的尺度,会发现它们的行为非常复杂且难以预测。当我们从更宏观的尺度观察这些系统时,可以用更加简洁的规律来解释和预测这些系统,这便是复杂系统独有的涌现现象。
涌现现象与因果关系紧密相连。一方面,涌现现象是系统内部各元素间复杂非线性相互作用的结果;另一方面,这些涌现的特性又会对系统中的个体产生影响。因果涌现这个概念最早由Erik Hoel正式提出并定义,即因果涌现描述了宏观层面相对于微观层面在因果效应上的可能会增强这一现象,这揭示了同一个系统在宏观与微观两种尺度之间的差异和联系。
因果涌现的概念不仅将因果推理与复杂系统的涌现特性相结合,而且为解决一系列哲学问题提供了一个定量化的视角。
目前,关于如何定义因果涌现,有四个主要代表,分别是:①Hoel等基于有效信息的因果涌现理论[1][2]、②Rosas等基于整合信息分解的因果涌现理论[3]、③张江等人基于奇异值分解的因果涌现理论[4]、④Barnett等的基于动力学解耦的涌现理论[5]。
具体内容可以参考词条因果涌现。
因果涌现识别
现实中,当我们要应用涌现的量化框架时,会出现微观状态的数据难以获取、粗粒化策略不好确定的问题,所以,我们需要找到从可观测数据中直接识别因果涌现的方法。
识别出复杂系统中的因果涌现,一方面可以节约预测成本,增强预测效果,尤其是泛化效果;一方面也可以诱导或者预防涌现的发生。在实际应用中,一些微观数据难以捕捉,我们往往只能收集到观测数据,并且,无法得到系统的真实动力学。因此,从可观测数据中识别系统中因果涌现的发生是一个关键的问题。近年来,基于神经网络的机器学习方法取得了突破性进展,借助此方法,以数据驱动的方式自主发现复杂系统的因果关系甚至动力学成为可能。此外,机器学习和神经网络还可以帮助我们找到更好的粗粒化策略、从数据中发现宏观层面的因果关系。
下面介绍两种因果涌现的识别方法:①基于信息分解的因果涌现识别近似方法、②神经信息压缩器方法系列(Neural Information Squeezer,简称NIS)。
基于信息分解的因果涌现识别
Rosas等学者[3][6]通过信息分解框架给出了和Hoel等人不同的对因果涌现的新定义,并基于此识别量化因果涌现。但是信息分解框架中定义的信息原子难以计算,所以作者推导出只需要计算互信息的近似公式,提出了判定因果涌现发生的充分条件,即[math]\displaystyle{ \Psi_{t, t+1}(V) }[/math],具体公式如下:
[math]\displaystyle{ \Psi_{t, t+1}(V):=I\left(V_t ; V_{t+1}\right)-\sum_j I\left(X_t^j ; V_{t+1}\right) }[/math]
式中,[math]\displaystyle{ V }[/math]是给定的宏观状态,[math]\displaystyle{ V_t ; V_{t+1} }[/math]代表两个连续时间的宏观状态变量,[math]\displaystyle{ X_t^j }[/math]表示第 j 维t时刻的微观变量。
当[math]\displaystyle{ \Psi_{t, t+1}(V) \gt 0 }[/math],系统发生因果涌现。但当[math]\displaystyle{ \mathrm{\Psi}\lt 0 }[/math],我们不能确定系统是否发生因果涌现。
需要指出的是,Hoel的定义和识别方法基于Judea Pearl因果,而此方法是基于格兰杰因果,计算互信息的组合,没有引入do干预。
该方法因为是格兰杰因果,所以计算比较方便,不需要找到底层的动力学机制。且对系统的动力学没有马尔可夫性的假设和要求。但是也存在一些缺点:
1)该方法只是基于互信息计算,且得到的仅仅是发生因果涌现的近似的充分条件;
2)该方法需要手动给定粗粒化策略和宏观变量,而不同的选择会对结果造成显著影响;
3)高维系统中,[math]\displaystyle{ \Psi }[/math]作为近似条件,误差非常大,很容易得到负值,从而无法判断是否有因果涌现发生。
为了能够自动找到最佳的粗粒化策略,这套理论框架也发展出了相应的机器学习方法[7]。Kaplanis等人基于机器学习的方法学习宏观态[math]\displaystyle{ V }[/math]以及最大化[math]\displaystyle{ \mathrm{\Psi} }[/math]:使用神经网络来学习将微观输入粗粒化成宏观输出,同时使用两个神经网络来分别学习互信息的计算,最后通过最大化两者之间的差(即[math]\displaystyle{ \mathrm{\Psi} }[/math])来优化学习。
NIS系列
张江等[8]学者尝试基于神经网络和数据驱动提出了一种方法,能从时间序列数据中识别系统中的因果涌现,并且自动提取有效的粗粒化策略和宏观动力学,即神经信息压缩器(Neural Information Squeezer,简称NIS)。
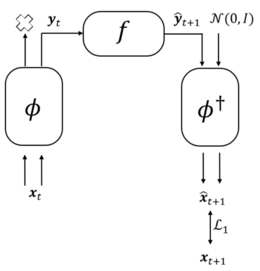
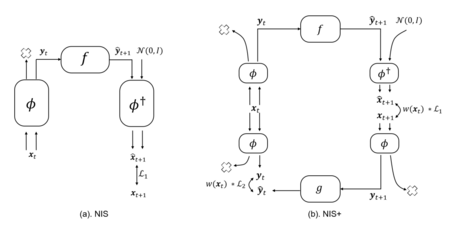
模型由编码器(encoder)、动力学学习器([math]\displaystyle{ f }[/math])以及解码器(decoder)三个部分构成,编码器和解码器主要由可逆神经网络(Invertible Neural Network,简称INN)[9]构建,动力学学习器由多层感知机(Multilayer Perceptron,简称MLP)构建。此模型框架可以看成是一个神经信息压缩器,将包含噪音的微观态压缩成宏观态,丢弃无用的信息,从而使得宏观动力学的因果性更强。NIS方法的模型框架如左图所示。
图中,模型输入是微观状态[math]\displaystyle{ X_t\ (X_t^1,X_t^2,…,X_t^p ) }[/math],[math]\displaystyle{ p }[/math]表示输入数据的维数。[math]\displaystyle{ ϕ }[/math]是粗粒化函数(编码器),将输入的[math]\displaystyle{ p }[/math]维数据映射到[math]\displaystyle{ q }[/math]维数据上,得到宏观变量[math]\displaystyle{ Y_t }[/math],此步还包括了通过投影算子抛弃[math]\displaystyle{ p-q }[/math]维信息的操作。[math]\displaystyle{ f }[/math]是动力学学习器,在宏观层面上学习有效的马尔可夫动力学。[math]\displaystyle{ \hat{y}_{t+1} }[/math]是通过[math]f[/math]预测的t+1时刻的宏观状态。由于此时数据是[math]\displaystyle{ q }[/math]维的,为了使用反粗粒化函数[math]\displaystyle{ ϕ^† }[/math](解码器),需要用[math]\displaystyle{ p-q }[/math]维高斯随机向量填充维度不足的数据。宏观变量经过反粗粒化函数之后可以得到预测的微观变量[math]\displaystyle{ \hat{x}_{t+1} }[/math]。而[math]\displaystyle{ x_t+1 }[/math]和[math]\displaystyle{ \hat{x}_{t+1} }[/math]之间的差值即为预测损失评估值,可以用来训练整个网络架构。
该方法的目标函数是希望在保证微观状态预测误差很小的条件下最大化有效信息,保证预测误差约束足够小是为了避免平凡解(粗粒化丢失太多信息,以致宏观动力学无效)的出现。NIS最终希望得到有效的粗粒化维度[math]\displaystyle{ q }[/math]、粗粒化策略[math]\displaystyle{ \mathrm{\phi}_q }[/math]和宏观动力学[math]\displaystyle{ {\hat{f}}_{\mathrm{\phi}_q} }[/math]。
然而,NIS框架并没有实现真正的有效信息最大化。具体内容请参考NIS。
机器学习领域的分布外泛化问题
目前,机器学习任务需要建立在训练数据和测试数据是独立同分布(Independent and Identically Distributed,简称IID)的基础之上,这是一种理想化的假设。现实应用中,几乎不能满足IID假设,所以模型的性能都会有不同程度的下降[10]。
以一个狗识别的图像判别任务为例。训练图像的背景一般是在草地上,可以看见整个狗。经过大量数据训练后,若给模型一个在草地上的狗的图像,那模型的正确率可以在95%以上;若给一张在水泥地上,且遮挡了狗部分身体的图像,那么模型的正确率可能是一半。
机器学习经过训练学习得到的很大程度上是变量之间的相关关系,这种相关关系可能来自样本选择偏差(Sample Selection Bias)。当考虑了其他变量后,原本看似有相关性的变量可能实际上并无关联,是一种虚假的相关关系。在上面的狗识别的例子中,机器学习学到的可能是根据草地和狗鼻子这两个因素来判断是不是狗,但是有因果关系的是狗鼻子,草地只是由于样本的分布不均匀,这就导致了模型不能有效识别出在水里、沙漠里的狗。简单来说,草地和标签之间是强相关、弱因果的,狗鼻子和标签之间是强相关、强因果的。
而在动力学系统中,模型可能对初始条件非常敏感,即使是微小的初始条件变化也可能导致系统行为的显著差异。如果训练数据的初始条件分布与测试数据不同,模型可能无法准确预测测试数据下的系统行为。我们希望的是,模型可以透过初始条件的差异,抓住系统动力学的本质。甚至有时候,我们期待模型可以泛化到某些动力学参数不同的系统测试数据上,依旧有不错的表现。在实际应用中,我们希望学习到的是因果关系(Causation)[11],只有这样才能使得结果更加稳定且具有可解释性。
分布外泛化(Out-of-Distribution Generalization,简称OOD Generalization)是指模型在面对与训练数据分布不同的新数据时,仍然能够保持较好的性能,涉及到模型对未知或未见情况的适应能力,以及是否能削弱样本选择偏差的情况。此问题通常表现为模型在训练集上运行良好,但在面对分布外的各种数据时,模型性能有所下降。造成这个问题的原因可能是过度拟合训练数据,导致模型泛化能力差;也可能是由于训练数据无法覆盖所有可能的输入情况,特别是对于罕见或极端的情况。
为了增强分布外泛化能力,学者可以生成多样化的数据,模拟不同的测试环境,还可以通过域适应技术(Domain Adaptation),使模型可以适应不同的测试数据分布,还有不变性学习(Invariant Learning)、元学习(Meta Learning)等方法。
神经信息压缩机(NIS)介绍
概述
假设复杂动态系统的行为数据是时间序列 [math]\displaystyle{ \{x_t\} }[/math],时间步长[math]\displaystyle{ t = 1,2,…, T }[/math],维数是p,它们构成了可观测的微观状态,我们假设不存在未观测变量。一个粗粒化策略(编码器) [math]\displaystyle{ ϕ: R_p → R_q }[/math] ,其中 [math]\displaystyle{ q ≤ p }[/math], [math]\displaystyle{ q }[/math]是宏观状态的维度,作为超参数给定;一个相应的反粗粒化策略(解码器)[math]\displaystyle{ ϕ^\dagger: R_q → R_p }[/math],以及一个宏观层面的马尔可夫动力学(动力学学习器)[math]\displaystyle{ f_q }[/math] ,使得[math]\displaystyle{ f_q }[/math]的有效信息([math]\displaystyle{ \mathcal{J} }[/math])值在通过[math]\displaystyle{ ϕ }[/math]、[math]\displaystyle{ f_q }[/math]和[math]\displaystyle{ ϕ^\dagger }[/math]预测出的[math]\displaystyle{ x_{t+1} }[/math]与[math]\displaystyle{ x_{t+1} }[/math]的实际数据的差距最小的约束下最大化。[math]\displaystyle{ \epsilon }[/math]是给定的常数。它们的关系用方程表示为:
-
[math]\displaystyle{ \begin{aligned}&\max_{\phi,f_{q},\phi^{+}}\mathcal{J}(f_{q}),\\&s.t.\begin{cases}\parallel\hat{x}_{t+1}-x_{t+1}\parallel\lt \epsilon,\\\hat{x}_{t+1}=\phi^{\dagger}\left(f_{q}(\phi(x_{t})\bigr)\right).\end{cases}\end{aligned} }[/math]
(1)
为了数学性质和可解释性,以及降低模型参数量,采用了可逆神经网络。作者将编码过程分解为了两个步骤:
①双射映射,[math]\displaystyle{ ψ: R_p → R_p }[/math],此步无信息丢失,由可逆神经网络实现。
②投影运算,[math]\displaystyle{ \chi_q }[/math],此步将输入的[math]\displaystyle{ p }[/math]维数据映射到[math]\displaystyle{ q }[/math]维数据上,得到宏观变量[math]\displaystyle{ Y_t }[/math],此步丢失[math]\displaystyle{ p-q }[/math]维信息。
[math]\displaystyle{ y = \phi(x) = \chi_q (\psi(x)) }[/math]
解码器也分为两个步骤:
①用[math]\displaystyle{ p-q }[/math]维高斯随机向量填充数据得到[math]\displaystyle{ p }[/math]维数据。式中,ξ为p−q维的标准高斯随机向量,⊕表示向量拼接操作。
②使用反粗粒化函数得到预测的微观变量[math]\displaystyle{ \hat{x}_{t+1} }[/math]。由于使用可逆神经网络,此步和编码器中的双射映射共享参数。
[math]\displaystyle{ \phi^{\dagger}(x)=\psi_{\omega}^{-1}(x\oplus\xi) }[/math]
在编码器一步,虽然有丢失信息,但是通过数学证明可以得知,当神经网络训练收敛时,数据中相邻宏观状态之间的互信息倾向于接近两个相邻时间步的微观态互信息,丢失的信息与预测几乎无关,所有有效信息都汇聚到动力学学习器的信息瓶颈之中。且在此框架下,信息瓶颈的应用更加明显、更具可解释性。
然而由于该目标函数是一个泛函优化问题,往往很难优化。为了解决这个问题,作者将优化过程分为两个阶段。
第一个阶段:在给定宏观尺度[math]\displaystyle{ q }[/math]的情况下,最小化预测误差[math]\displaystyle{ \left\|\phi_q^{\dagger}(Y(t+1))-X_{t+1}\right\| }[/math]。可以采用随机梯度下降技术,通过训练神经网络解决。在此步,我们可以得到依赖于q的有效粗粒化策略和宏观动力学。
第二个阶段:由于参数 [math]\displaystyle{ q }[/math] 是一维的,且 [math]\displaystyle{ 0 \lt q \lt p }[/math],简单迭代找到有效信息最大的宏观尺度。此步将复杂的泛函问题转化成一维空间中线性搜索问题。
具体请阅读词条NIS。
神经网络上的EI计算
如果神经网络的输入[math]\displaystyle{ X=(x_1,x_2,\cdot\cdot\cdot,x_n)\in [-L,L]^n }[/math],则表示X定义在一个大小为L的超立方体上,其中L是一个非常大的整数。输出为[math]\displaystyle{ Y=(y_1,y_2,\cdot\cdot\cdot,y_m) }[/math], [math]\displaystyle{ Y=\mu(X) }[/math]。这里µ是神经网络实现的确定性映射:[math]\displaystyle{ \mu: \mathcal{R}^n\rightarrow \mathcal{R}^m }[/math],它在X处的雅可比矩阵是[math]\displaystyle{ \partial_{X'} \mu(X)\equiv \left\{\frac{\partial \mu_i(X')}{\partial X'_j}\left|_{X'=X}\right.\right\}_{nm} }[/math]。如果神经网络可以看作是给定X条件下的高斯分布,则神经网络的有效信息(EI)可以用以下方法计算:
-
[math]\displaystyle{ EI_L(μ)=I(do(X\sim U([-L,L]^{n};Y) ≈ -\frac{m+m\ln(2\pi)+\sum_{i=1}^m\sigma_i^2/m}{2}+n\ln(2L)+\mathbf{E}_{X\sim U([-L,L]^n} \left(\ln |\det(\partial_{X'} f(X))|\right) }[/math]
(2)
式中,[math]\displaystyle{ \Sigma=diag(\sigma_1^2,\sigma_2^2,\cdot\cdot\cdot,\sigma_m^2) }[/math] 是协方差矩阵, [math]\displaystyle{ \sigma_i }[/math]是输出[math]\displaystyle{ y_i }[/math]的标准差,可由[math]\displaystyle{ y_i }[/math]的均方误差估计得到,[math]\displaystyle{ U([-L,L]^n) }[/math]为[math]\displaystyle{ [-L,L]^n }[/math]上的均匀分布,[math]\displaystyle{ | · | }[/math]为绝对值,det为行列式。如果[math]\displaystyle{ \det(\partial_{X'} \mu(X))\equiv 0 }[/math]对于所有X,则令EI≈0。
但是,此公式不能直接应用于实际情况,因为它会随着输入n或输出m的维数增加而增加。解决这一问题的方法是通过除以输入维数来定义维度平均有效信息(dEI),记为:
[math]\displaystyle{ \mathcal{J}_L = \frac{EI_L(\mu)}{n} }[/math]
当输入输出数相同时(m = n),则:
[math]\displaystyle{ \mathcal{J}_L(\mu)=-\frac{1+\ln(2\pi)+\sum_{i=1}^n\sigma_i^2/n}{2}+\ln(2L)+\frac{1}{n}\mathbf{E}_{X\sim U([-L,L]^n} \left(\ln |\det(\partial_{X'} f(X))|\right) }[/math]
不过,此式子依赖于参数L,输入数据的域范围。为了消除L的影响,作者计算维度平均CE。对于维度q的宏观动力学[math]\displaystyle{ f_M }[/math]和维度p的微观动力学[math]\displaystyle{ f_m }[/math],我们将维度平均CE定义为:
[math]\displaystyle{ \Delta\mathcal{J}_L(f_M,f_m)=\mathcal{J}_L(f_M)-\mathcal{J}_L(f_m)=\frac{EI_L(f_M)}{q}-\frac{EI_L(f_m)}{p} }[/math]
如果[math]\displaystyle{ f_M }[/math]和[math]\displaystyle{ f_m }[/math]由q维的[math]\displaystyle{ µ_M }[/math]和p维的[math]\displaystyle{ µ_m }[/math]的神经网络参数化,则:
[math]\displaystyle{ \Delta\mathcal{J}=\left(\frac{1}{q}\mathbf{E}_{X_M}\ln|\det \partial_{X_M}\mu_M|-\frac{1}{p}\mathbf{E}_{X_m}\ln|\det \partial_{X_m}\mu_m|\right)-\left(\frac{1}{q}\sum_{i=1}^{q}\ln\sigma_{i,M}^2-\frac{1}{p}\sum_{i=1}^{p}\ln\sigma_{i,m}^2\right) }[/math]
式中,其中[math]\displaystyle{ \sigma_{i,M} }[/math]和[math]\displaystyle{ \sigma_{i,m} }[/math]分别是[math]\displaystyle{ \mu_M }[/math]和[math]\displaystyle{ \mu_m }[/math]在第i维上的标准差。
此时,完全消除了输入或输出维度以及参数L的影响,使其成为一个更可靠的指标。从数据中识别因果涌现的结果只受到雅可比矩阵的方差的相对值和行列式的对数值的影响。
NIS的缺陷
此模型在弹簧振子、马尔科夫链、布尔网络上都进行了实验,实验效果理想,表明此模型的正确性、有效性。
但是此模型还有一些缺点和尚未改进的地方:
1)此框架目前只能在小数据集上使用,难以拓展到更大规模的复杂系统上。
2)此方法的数学形式是一个泛函问题,无法直接进行优化,虽然可以通过两个阶段得到结果,但是NIS没有真正地最大化有效信息。在NIS+中,作者将通过计算变分下界解决泛函问题。
具体请阅读词条NIS。
强化版神经信息压缩机(NIS+)
概述
为了最大化式1中定义的EI,作者将NIS的框架扩展为NIS+。在NIS+中,我们首先使用互信息和变分不等式的公式将互信息的最大化问题转化为机器学习问题,其次,使用[math]\displaystyle{ y_{t+1}=\phi(x_{t+1}) }[/math]来预测[math]\displaystyle{ y_{t} }[/math],从而保证互信息最大化。这里,[math]\phi[/math]是反向动力学学习器神经网络。最后,利用样本重加权技术来解决均匀分布干预的挑战,从而优化EI。所有这些技术组成了增强版神经信息压缩机(NIS+)[12]。在此框架中,输入可观测的数据,输出是因果涌现的程度、宏观动力学、涌现斑图以及粗粒化策略。
数学推导
式1中,数学形式是一个泛函问题,无法直接进行优化,作者将通过计算并优化变分下界来解决泛函优化问题。同时,在NIS+框架中,作者使用了编码器将p维的输入数据进行粗粒化,得到q维的宏观数据,下面编码器的通用逼近定理将证明编码器的可以近似任意复杂的粗粒化函数。
在此章节,作者将使用大写字母来表示相应的随机变量。
例如,[math]\displaystyle{ X_{t} }[/math]表示时间t的微观状态[math]\displaystyle{ x_{t} }[/math]的随机变量,[math]\displaystyle{ Y_t+1 }[/math]表示时间t+1的宏观状态[math]\displaystyle{ y_t+1 }[/math]对应的随机变量。对于任意随机变量X, [math]\displaystyle{ \tilde{X} }[/math]表示干预后的同一随机变量X。[math]\displaystyle{ \hat{X} }[/math]表示神经网络对X的预测。
宏观EI的变分下界
原始的有约束的目标优化公式如式1所示。
在此方程中[math]\displaystyle{ \hat{X}_{t+1}=\psi_{\omega}^{-1}(\hat{Y}_{t+1}\bigoplus \xi) }[/math],其中[math]\displaystyle{ \psi_{\omega}^{-1} }[/math]是可逆映射,根据引理1和引理2以及互信息的性质,我们可以得到:
[math]\displaystyle{ I(Y_t,\hat{Y}_{t+1})=I(Y_t,\hat{X}_{t+1})=H(Y_t)-H(Y_t|\hat{X}_{t+1}) }[/math]
令[math]\displaystyle{ U_q }[/math]为宏观变量的均匀分布,那么[math]\displaystyle{ H(\tilde{Y}_t)=H(U_q) }[/math]。故:
[math]\displaystyle{ \mathcal{J}(f_{\theta,q})=I(\tilde{Y}_{t},\hat{X}_{t+1})=H(U_q)-H(\tilde{Y}_t|\tilde{X}_{t+1}) }[/math]
由于[math]\displaystyle{ H(U_q) }[/math]为常数,所以[math]\displaystyle{ \mathcal{J}(f_{q}) }[/math]的优化可以转化为条件熵[math]\displaystyle{ H(\tilde{Y}_t|\tilde{X}_{t+1}) }[/math]的最小化优化问题。根据引理3可以得知:
[math]\displaystyle{ H(\tilde{Y}_t|\tilde{X}_{t+1}) \le -\iint \tilde{p}(\boldsymbol{y}_t, \boldsymbol{x}_{t+1})\ln g(\boldsymbol{y}_t|\boldsymbol{x}_{t+1}) \mathrm{d}\boldsymbol{y}_t \mathrm{d}\boldsymbol{x}_{t+1} = -\iint \tilde{p}(\boldsymbol{y}_{t})\tilde{p}(\boldsymbol{x}_{t+1}|\boldsymbol{y}_t)\ln g(\boldsymbol{y}_t|\boldsymbol{x}_{t+1}) \mathrm{d}\boldsymbol{y}_t \mathrm{d}\boldsymbol{x}_{t+1} }[/math]
式中,[math]\displaystyle{ \tilde{p} }[/math]表示随机变量[math]\displaystyle{ Y_t }[/math]被干预情况下的概率分布函数。
作者使用神经网络来拟合分布[math]\displaystyle{ g(y_t|x_t+1) }[/math],根据引理3,[math]\displaystyle{ g(y_t|x_t+1) }[/math]可以是任何分布,在这里,假设[math]\displaystyle{ g(y_t|x_t+1) }[/math]为正态分布,即[math]\displaystyle{ g(\boldsymbol{y}_t|\boldsymbol{x}_{t+1})\sim N(\mu,\Sigma) }[/math],其中[math]\displaystyle{ \mu =g_{\theta'}(\phi(\boldsymbol{x}_{t+1})) }[/math],[math]\displaystyle{ \Sigma=diag(\sigma_1, \sigma_2,\cdot\cdot\cdot,\sigma_q) }[/math]是常数对角矩阵,进一步,假设[math]\displaystyle{ \sigma_i }[/math]是有界的,则[math]\displaystyle{ \sigma_i\in[\sigma_m,\sigma_M] }[/math],其中[math]\displaystyle{ \sigma_m }[/math]和[math]\displaystyle{ \sigma_M }[/math]分别是MSE的最小值和最大值。则[math]\displaystyle{ g(y_t|x_t+1) }[/math]的对数概率密度函数为:
[math]\displaystyle{ \ln g(\boldsymbol{y}_t|\boldsymbol{x}_{t+1})\approx \ln \frac{1}{(2\pi)^{\frac{m}{2}}|\Sigma|^\frac{1}{2}} e^{-\frac{(\boldsymbol{y}_t-g_{\theta'}(\phi(\boldsymbol{x}_{t+1})))^2}{2|\Sigma|}} = -\frac{(\boldsymbol{y}_t-g_{\theta'}(\phi(\boldsymbol{x}_{t+1})))^2}{2|\Sigma|}+\ln \frac{1}{(2\pi)^{\frac{m}{2}}|\Sigma|^\frac{1}{2}} ≥ -\frac{(\boldsymbol{y}_t-g_{\theta'}(\phi(\boldsymbol{x}_{t+1})))^2}{2|\Sigma|}+\ln \frac{1}{(2\pi)^{\frac{m}{2}}|\Sigma|_{max}^\frac{1}{2}} }[/math]
如果训练足够充分,那么[math]\displaystyle{ \tilde{p}(\boldsymbol{x}_{t+1}|\boldsymbol{y}_t)\approx p(\boldsymbol{x}_{t+1}|\boldsymbol{y}_t) }[/math],故:
[math]\displaystyle{ H(\tilde{Y}_t|\tilde{X}_{t+1}) \le \iint \tilde{p}(\boldsymbol{y}_{t})p(\boldsymbol{x}_{t+1}|\boldsymbol{y}_t)\left[\frac{(\phi (\boldsymbol{x}_t)-g_{\theta'}(\phi(\boldsymbol{x}_{t+1})))^2}{2|\Sigma|_{min}}-\ln \frac{1}{(2\pi)^{\frac{m}{2}}|\Sigma|_{max}^\frac{1}{2}}\right] \mathrm{d}\boldsymbol{y}_t \mathrm{d}\boldsymbol{x}_{t+1} }[/math]
式中,[math]\displaystyle{ |\Sigma|_{min}=\sigma_{min}^q }[/math],[math]\displaystyle{ |\Sigma|_{max}=\sigma_{max}^q }[/math]。
由于[math]\displaystyle{ \tilde{p}(\boldsymbol{y}_{t})p(\boldsymbol{x}_{t+1}|\boldsymbol{y}_t)=\frac{\tilde{p}(\boldsymbol{y}_{t})}{p(\boldsymbol{y}_{t})}p(\boldsymbol{x}_{t+1},\boldsymbol{y}_t) }[/math],其中[math]\displaystyle{ \tilde{p}(\boldsymbol{y}_{t}) }[/math]是目标分布,[math]\displaystyle{ p(\boldsymbol{y}_{t}) }[/math]是数据的原始分布。我们定义逆概率权重[math]\displaystyle{ w(\boldsymbol{x}_t) \equiv \frac{\tilde{p}(\boldsymbol{y}_{t})}{p(\boldsymbol{y}_{t})} }[/math],[math]\displaystyle{ z=\frac{(\phi (\boldsymbol{x}_t)-g_{\theta'}(\phi(\boldsymbol{x}_{t+1})))^2}{2|\Sigma|_{min}}-\ln \frac{1}{(2\pi)^{\frac{m}{2}}|\Sigma|_{max}^\frac{1}{2}} }[/math]。且由于我们使用离散样本[math]\displaystyle{ {x_t} }[/math]来训练神经网络,所以我们可以使用样本均值作为期望的近似估计。因此,[math]\displaystyle{ H(\tilde{Y}_t|\tilde{X}_{t+1}) }[/math]的变分上界可写成:
[math]\displaystyle{ H(\tilde{Y}_t|\tilde{X}_{t+1}) \le \iint w(\boldsymbol{x}_t)p(\boldsymbol{x}_{t+1},\boldsymbol{y}_t)z \mathrm{d}\boldsymbol{y}_t \mathrm{d}\boldsymbol{x}_{t+1} \approx \frac{1}{T}\sum_{i=0}^{T-1}w(\boldsymbol{x}_t)z }[/math]
进而,我们可以得到原目标函数的变分下界:
[math]\displaystyle{ \mathcal{J}(f_{\theta,q}) \ge H(U_q)-\frac{1}{T}\sum_{i=0}^{T-1}w(\boldsymbol{x}_t)z }[/math]
原优化问题(式1)便转换成:
[math]\displaystyle{ \min_{\omega,\theta,\theta'} \sum_{i=0}^{T-1}w(\boldsymbol{x}_t)|\phi(\boldsymbol{x}_t)-g_{\theta'}(\phi(\boldsymbol{x}_{t+1}))|^2 }[/math]
[math]\displaystyle{ s.t. || \hat{\boldsymbol{x}}_{t+1}-\boldsymbol{x}_{t+1} || \lt \epsilon }[/math]
式中,[math]\displaystyle{ \omega }[/math],[math]\displaystyle{ \theta }[/math], [math]\displaystyle{ \theta' }[/math]分别表示NIS+框架中三个神经网络[math]\displaystyle{ \psi }[/math], [math]\displaystyle{ f_{\theta} }[/math], [math]\displaystyle{ g_{\theta'} }[/math]的参数。
然后构造拉格朗日函数:
[math]\displaystyle{ L(\omega,\theta,\theta',\lambda)=\sum_{i=0}^{T-1}w(\boldsymbol{x}_t)|\phi(\boldsymbol{x}_t)-g_{\theta'}(\phi(\boldsymbol{x}_{t+1}))|^2+\lambda|| \phi^\dagger(\boldsymbol{y}_{t+1})-\boldsymbol{x}_{t+1} || }[/math]
优化目标(式1)便转化为:
-
[math]\displaystyle{ \begin{aligned}&\min_{f,g,\phi,\phi\dagger}\sum_{t=1}^{T-1}w(\boldsymbol{x}_t)\parallel\boldsymbol{y}_t-g(\boldsymbol{y}_{t+1})\parallel+\lambda\parallel\hat{x}_{t+1}-\boldsymbol{x}_{t+1}\parallel,\\&s.t.\begin{cases}y_{t}=\phi(x_{t}),\\\hat{y}_{t+1}=f(y_t),\\\hat{x}_{t+1}=\phi^{\dagger}\left(f_{q}(\phi(x_{t})\bigr)\right),\\y_{t+1}=\phi(x_{t+1}).\end{cases}\end{aligned} }[/math]
(3)
式中,[math]\displaystyle{ x_{t} }[/math]、[math]\displaystyle{ x_{t+1} }[/math]表示可观测的微观数据,[math]\displaystyle{ y_{t} }[/math]、[math]\displaystyle{ y_{t+1} }[/math]表示经过粗粒化函数[math]\displaystyle{ \phi }[/math]得到的宏观数据,[math]\displaystyle{
\hat{y}_{t+1}
}[/math]表示[math]\displaystyle{
y_{t}
}[/math]经过宏观动力学[math]\displaystyle{ f: R_q → R_q }[/math]得到的预测[math]\displaystyle{
t+1
}[/math]时刻宏观变量值,[math]\displaystyle{
\hat{x}_{t+1}
}[/math]表示[math]\displaystyle{ \hat{y}_{t+1} }[/math]经过反粗粒化函数[math]\displaystyle{
\phi^{\dagger}
}[/math]得到的预测的[math]\displaystyle{
t+1
}[/math]时刻微观变量值,[math]\displaystyle{ g: R_q → R_q }[/math]表示反宏观动力学函数,可以根据[math]\displaystyle{
t+1
}[/math]时刻宏观变量值[math]\displaystyle{ y_{t+1} }[/math]推出预测的[math]\displaystyle{
t
}[/math]时刻的宏观变量值[math]\displaystyle{
\hat{y}_{t}
}[/math],[math]\displaystyle{ λ }[/math]作为拉格朗日乘子,在实验框架内被认为是一个可调的超参数。
引理1——双射映射不影响互信息[8]:
对于任意给定的连续随机变量X和Z,如果存在一个双射(一对一)映射f与另一个随机变量Y,使得对于任意[math]\displaystyle{ x\in Dom (X) }[/math]存在一个[math]\displaystyle{ y=f (x)\in Dom (Y) }[/math],反之亦然,其中[math]\displaystyle{ Dom (X) }[/math]表示变量X的域,则X与Z之间的互信息等于Y与Z之间的互信息,即:
[math]\displaystyle{ I (X;Z)=I (Y;Z) }[/math]
引理2——连续自变量不影响互信息[8]:
若[math]\displaystyle{ X\in Dom (X) }[/math]与[math]\displaystyle{ Y\in Dom (Y) }[/math]构成一条马尔可夫链[math]\displaystyle{ X\rightarrow Y }[/math],且[math]\displaystyle{ Z\in Dom (Z) }[/math]是一个与X、Y均无关的随机变量,则:
[math]\displaystyle{ I (X;Y)=I (X;Y\bigoplus Z) }[/math]
引理3——条件熵的变分上界:
给定一个条件熵[math]\displaystyle{ H(\boldsymbol{y}|\boldsymbol{x}) }[/math],其中[math]\displaystyle{ \boldsymbol{x}\in \mathcal{R}^s }[/math],[math]\displaystyle{ \boldsymbol{y}\in \mathcal{R}^q }[/math],则该条件熵存在一个变分上界:
[math]\displaystyle{ H(Y|X)\le -\iint p(\boldsymbol{y}, \boldsymbol{x})\ln g(\boldsymbol{y}|\boldsymbol{x}) \mathrm{d}\boldsymbol{y} \mathrm{d}\boldsymbol{x} }[/math]
其中[math]\displaystyle{ H(Y|X) \in R^q × R^s }[/math]是任意分布。
编码器的通用逼近定理
首先,我们扩展基本编码器的定义,引入一个新的运算[math]\displaystyle{ \eta_{p,s}: \mathcal{R}^p\rightarrow \mathcal{R}^s }[/math],它表示原始变量的自复制。
[math]\displaystyle{ \eta_{p,s}(\boldsymbol{x})=\boldsymbol{x}\bigoplus \boldsymbol{x}_{s-p} }[/math]
向量[math]\displaystyle{ \boldsymbol{x}_{s-p} }[/math]是[math]\displaystyle{ s-p }[/math]维,其中每个维都是x中特定维的重复。例如,若[math]\displaystyle{ \boldsymbol{x}=(0.1,0.2,0.3) }[/math],则[math]\displaystyle{ \eta_{2,5}(\boldsymbol{x})=(0.1,0.2,0.3,0.1,0.2) }[/math]。
学者们曾提出一般前馈神经网络[13][14]和可逆神经网络[15][16]的通用逼近定理,将其作为桥梁,可以证明任何前馈神经网络都可以用一系列双射映射(ψ)、投影(χ)和向量扩展(η)过程来模拟。对向量展开进行扩展后的基本编码器可表示为:
[math]\displaystyle{ \phi= Proj_q \circ\psi_{s} \circ \eta_{p,s}\circ \psi_{p} }[/math]
式中,函数[math]\displaystyle{ \psi_s: \mathcal{R}^s\rightarrow \mathcal{R}^s }[/math]和[math]\displaystyle{ \psi_p: \mathcal{R}^p\rightarrow \mathcal{R}^p }[/math]表示两个可逆映射。保留的最终维数q可能大于初始维数p。φ为降维算子。
根据通用逼近定理[13][14],对于定义在[math]\displaystyle{ K\times \mathcal{R}^p }[/math]上的任意函数[math]\displaystyle{ f }[/math],其中[math]\displaystyle{ K\in \mathcal{R}^p }[/math]是紧集,且[math]\displaystyle{ p\gt q\in \mathcal{Z^+} }[/math],则存在整数[math]\displaystyle{ s }[/math]和[math]\displaystyle{ W\in\mathcal{R}^{s\times p}, W'\in\mathcal{R}^{q\times s}, b\in\mathcal{R}^{s} }[/math],使得:
[math]\displaystyle{ W'\cdot \sigma(W+b)\simeq f }[/math]
式中,[math]\displaystyle{ \sigma(\boldsymbol{x})=1/(1+\exp(-\boldsymbol{x})) }[/math]是向量上的sigmoid函数。
根据引理4,[math]\displaystyle{ +b }[/math]和[math]\displaystyle{ \sigma(\cdot) }[/math]都是可逆算子,因此,存在可逆神经网络[math]\displaystyle{ \psi_{q},\psi_{s}',\psi_{s},\psi_{p} }[/math]和两个整数[math]\displaystyle{ s_1,s_2 }[/math](矩阵[math]\displaystyle{ W' }[/math]和[math]\displaystyle{ W }[/math]的秩),使得:
[math]\displaystyle{ (\psi_{q}\circ\eta_{s_2,q}\circ\chi_{s,s_2}\circ\psi_{s}')\circ(\psi_{s}\circ\eta_{s_1,s}\circ\chi_{p,s_1}\circ\psi_{p})\simeq W'\cdot\sigma(W\cdot+b) }[/math]
式中,[math]\displaystyle{ \psi_{s}\circ\eta_{s_1,s}\circ\chi_{p,s_1}\circ\psi_{p} }[/math]近似(模拟)函数[math]\displaystyle{ \sigma(W\cdot+b) }[/math],[math]\displaystyle{ \psi_{q}\circ\eta_{s_2,q}\circ\chi_{s,s_2}\circ\psi_{s}' }[/math]近似(模拟)函数[math]\displaystyle{ W'\cdot }[/math]。
因此,如果令[math]\displaystyle{ \phi_{p,s,q}=(\psi_{q}\circ\eta_{s_2,q}\circ\chi_{s,s_2}\circ\psi_{s}')\circ(\psi_{s}\circ\eta_{s_1,s}\circ\chi_{p,s_1}\circ\psi_{p}) }[/math],那么[math]\displaystyle{ \phi_{p,s,q}\simeq f }[/math]。
在实际应用中,虽然基本编码器和扩展版本不包括展开运算符,但我们总是在输入向量为编码器输入之前展开它。因此,有理由相信此定理仍然适用于堆叠编码器。
综上可知,编码器通用逼近定理:
对于任何连续函数[math]\displaystyle{ f }[/math],定义在[math]\displaystyle{ K\times \mathcal{R}^p }[/math],[math]\displaystyle{ K\in \mathcal{R}^p }[/math]是一个紧集,[math]\displaystyle{ p\gt q\in \mathcal{Z^+} }[/math],存在整数[math]\displaystyle{ s }[/math]和扩展堆编码器[math]\displaystyle{ \phi_{p,s,q}: \mathcal{R}^p\rightarrow \mathcal{R}^q }[/math](有[math]\displaystyle{ s }[/math]隐藏层)和扩展操作[math]\displaystyle{ \eta_{p,s} }[/math],使得:
[math]\displaystyle{ \phi_{p,s,q}\simeq f }[/math]
此后,扩展堆叠编码器具有通用逼近性质,这意味着它可以近似(模拟)任何定义在[math]\displaystyle{ \mathcal{R}^p\times \mathcal{R}^q }[/math]粗粒化函数。
引理4——编码器的信息瓶颈:
对于任意向量[math]\displaystyle{ X\in \mathcal{R}^p }[/math]和矩阵[math]\displaystyle{ W\in \mathcal{R}^{s\times p} }[/math],其中[math]\displaystyle{ s,p\in \mathcal{N} }[/math],存在一个整数[math]\displaystyle{ s_1\leq \min(s,p) }[/math]和两个编码器的基本单位:[math]\displaystyle{ \psi_{s}\circ\eta_{s_1,s} }[/math]和[math]\displaystyle{ \chi_{p,s_1}\circ \psi_{p} }[/math]使得:
[math]\displaystyle{ W\cdot X\simeq(\psi_{s}\circ\eta_{s_1,s})\circ(\chi_{p,s_1}\circ \psi_{p})(X) }[/math]
式中,[math]\displaystyle{ \simeq }[/math]表示近似或模拟。
机器学习算法
样本重加权
输入数据的分布会对结果产生一定的影响,为了减少此影响,作者需要对样本进行重加权,也就是通过为数据中的每个单元分配适当的权重来改变输入数据的分布,解决选择偏差问题。在因果机器学习、因果推断领域、因果特征学习(Causal feature learning)和稳定学习(Stable learning)中发挥着重要作用。可以使结果减少偏见的影响,提高模型在未知环境下的泛化能力[10]。
为了使用逆概率加权技术,我们需要估计样本的概率分布。KDE(Kernel Density Estimation)是一种常用的估计方法,它可以有效地消除离群值对整体概率分布估计的影响。
对于一个样本[math]\displaystyle{ (x_1, x_2, ..., x_n) }[/math],我们有如下的核密度估计:
[math]\displaystyle{ \hat{f}_h(x)=\frac{1}{nh}\sum_{i=1}^n K(\frac{x-x_i}{h}) }[/math]
式中,n表示样本数,超参数h表示带宽(根据数据的粗略范围确定),文章中,作者一般设为0.05。K是核函数,具体来说是标准正态密度函数。
得到估计函数后,对每个样本点单独求值,得到每个样本点对应的概率值[math]\displaystyle{ p(y_t) }[/math]。将目标分布(均匀分布)的概率[math]\displaystyle{ \tilde{p}(y_t) }[/math]除以我们估计的概率值,得到每个样本点对应的逆概率权值[math]\displaystyle{ w(\boldsymbol{x}_t) }[/math]。为了覆盖所有的样本点,需要用参数L来限制均匀分布的范围,以保证边长为2L的正方形可以覆盖所有维度的所有样本点。
此时获得的权重与样本量有关,因此需要对它们进行归一化。然而,这将导致与样本对应的权重值非常小。因此,有必要将它们乘以样本数量以将权重值放大回其正常范围。然后,将该权值乘以每个样本的训练损失,增强稀疏区域的训练,达到逆概率加权的目的。由于每次迭代时编码器参数都会发生变化,导致[math]\displaystyle{ y_t }[/math]的分布发生变化,因此作者将每1000次迭代使用KDE重新估计整个样本的概率分布。
反向动力学
正向动力学[math]\displaystyle{ f }[/math]训练是最小化预测误差[math]\displaystyle{ L_1 }[/math],即[math]\displaystyle{ \left\|\phi_q^{\dagger}(Y(t+1))-X_{t+1}\right\| }[/math],保证动力学预测未来的准确性,但是EI作为一种特殊的互信息,不仅与确定性有关,还与简并性有关。我们需要在提高动力学学习器的确定性的同时,提高它的非简并性。因此,作者在NIS的框架基础之上,加入了反向动力学[math]\displaystyle{ g }[/math],用以反向预测。即输入[math]\displaystyle{ y_{t+1} }[/math],通过动力学学习器[math]\displaystyle{ g }[/math]之后,得到宏观量的反向预测值[math]\displaystyle{ \hat{y}_{t} }[/math],使[math]\displaystyle{ y_{t+1} }[/math]和[math]\displaystyle{ \hat{y}_{t} }[/math]之间的误差值[math]\displaystyle{ L_2 }[/math]最小化。通过训练反向动力学学习器[math]\displaystyle{ g }[/math],我们可以影响编码器,进而影响隐空间中的数据分布,从而使得动力学学习器[math]\displaystyle{ f }[/math]可以学到一个简并性低的动力学。
分阶段训练
在实践中,为了减轻机器学习的压力,作者先让模型学到比较靠谱的编码策略,然后通过反向动力学将编码策略调整至最优解。NIS+的训练过程分为两个阶段。
第一阶段:只训练前向神经网络,最小化预测误差[math]\displaystyle{ w(\boldsymbol{x}_t)\parallel\boldsymbol{y}_t-g(\boldsymbol{y}_{t+1})\parallel }[/math]。
第二阶段,训练反向神经网络和前向神经网络,本质上是用于训练[math]\displaystyle{ \phi_{ω} }[/math]。在此过程中,用[math]\displaystyle{ λ }[/math]来平衡前向神经网络预测误差[math]\displaystyle{ w(\boldsymbol{x}_t)\parallel\boldsymbol{y}_t-g(\boldsymbol{y}_{t+1})\parallel }[/math]和反向神经网络预测误差[math]\displaystyle{ \parallel\hat{x}_{t+1}-\boldsymbol{x}_{t+1}\parallel }[/math]。在不同的实验中,根据超参数搜索法,[math]\displaystyle{ λ }[/math]取不同的值。
在整个模型的训练过程中,总的目标如式3。
面对大规模复杂系统的拓展
在实际应用中,如果系统不是小规模系统,而是类似元胞自动机的大规模的复杂系统,我们需要对此框架进行拓展,将编码器(解码器)进行组合,从而减轻模型训练的压力和难度。
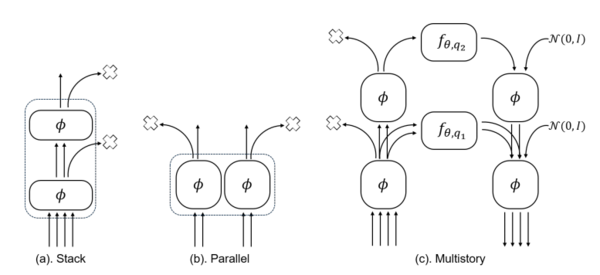
首先,在处理高维复杂系统时,一次丢弃多个维度会给训练神经网络带来很大的挑战。我们可以将一系列基本编码器堆叠(串联)在一起并逐渐丢弃维度,降低训练难度。如右图a所示。
此外,一些大规模复杂系统具有先验知识,我们可以根据先验知识对微观维度进行分组,分组之后,对每一组都用编码器进行编码,相当于把编码器进行了并联。并行编码器之间共享参数,故神经网络依然可以高效、准确地获得粗粒化规则。最后,将从所有编码器获得的宏观变量连接成一个向量,以导出总体的宏观变量。这种并行结构也可以与卷积神经网络等架构结合起来。如右图b所示。
为了提高搜索最优尺度的效率,我们可以利用堆叠编码器获得隐藏空间的多个尺度,同时训练多个不同尺度的动力学学习器(相当于搜索不同q的宏观动力学),从而避免重新训练编码器,提高模型效率。如右图c所示。
将NIS+的编码器替换为堆叠编码器与并行编码器的任意组合时,式3的最优化函数依然适用(引理5、引理6)。
引理5——堆叠编码器不影响互信息:
若[math]\displaystyle{ X\in Dom(X) }[/math]和[math]\displaystyle{ Y\in Dom(Y) }[/math]形成一个马尔可夫链[math]\displaystyle{ X\rightarrow Y }[/math], [math]\displaystyle{ \phi_L }[/math]和[math]\displaystyle{ \phi^\dagger_L }[/math]分别表示L层堆叠的编码器和解码器,则:
[math]\displaystyle{ I(X;Y)=I(X;\Phi^\dagger_L(Y)) }[/math]
引理6——并行编码器不影响互信息:
若[math]\displaystyle{ X\in Dom(X) }[/math]和[math]\displaystyle{ Y\in Dom(Y) }[/math]形成一个马尔可夫链[math]\displaystyle{ X\rightarrow Y }[/math], [math]\displaystyle{ \phi_T }[/math]和[math]\displaystyle{ \phi^\dagger_T }[/math]分别表示由T个普通编码器或解码器组成的并行编码器和解码器,则:
[math]\displaystyle{ I(X;Y)=I(X;\Phi^\dagger_T(Y)) }[/math]
NIS+ 框架有效性的验证(数值实验)
在此部分中,作者通过四个实验验证NIS+框架有效性:SIR模型实验、Boids模型实验、生命游戏模型实验、大脑fMRI实验。实验数据包括人脑的核磁共振成像数据和不同的人工模型(动态系统、多主体系统和元胞自动机)生成的数据。每个实验中,作者评估了NIS+的因果涌现识别能力和泛化能力。
SIR模型实验
在本实验中,SIR(Susceptible[math]\displaystyle{ \rightarrow }[/math]Infected[math]\displaystyle{ \rightarrow }[/math]Recovered Model)模型是一个简单的宏观动态系统,而微观变量是通过在宏观变量中引入噪声来产生的。这是一个已知宏观机制的玩具模型,可以验证NIS+是否真的做到了宏观有效信息最大化。
SIR宏观动力学可以描述为:
[math]\displaystyle{ \begin{cases} \frac{\mathrm{d}S}{\mathrm{d}t}=-\beta SI, \\ \frac{\mathrm{d}I}{\mathrm{d}t}=\beta SI - \gamma I, \\ \frac{\mathrm{d}R}{\mathrm{d}t}= \gamma I, \end{cases} }[/math]
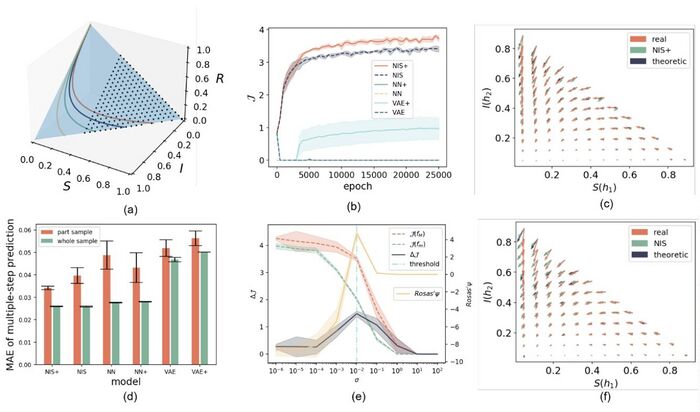
其中[math]\displaystyle{ S,I,R\in[0,1] }[/math]表示种群中健康,感染和康复或死亡个体的比例,[math]\displaystyle{ \beta=1 }[/math]是感染率,即健康人感染成感染者的概率,[math]\displaystyle{ \gamma=0.5 }[/math]是恢复率,即感染者康复或者死亡的概率。图(a)显示了SIR动力学的相空间(S, I, R)。由于SIR模型只有两个自由度([math]\displaystyle{ S + I + R = 1 }[/math]),所以所有的宏观状态都分布在三维的三角形平面上,故作者仅用S和I构成宏观状态变量[math]\displaystyle{ \boldsymbol{y}=(S,I) }[/math]。
同时,作者通过引入高斯噪声将[math]\displaystyle{ \boldsymbol{y}=(S,I) }[/math]展开为一个四维变量,并将其看做微观状态。
[math]\displaystyle{ \begin{cases}\boldsymbol{S}'=(S,S)+\boldsymbol{\xi}_1, \\\boldsymbol{I}'=(I,I)+\boldsymbol{\xi}_2\end{cases} }[/math]
其中,[math]\displaystyle{ \boldsymbol{\xi}_1,\boldsymbol{\xi}_2 \sim \scriptsize{N}(0,\Sigma) }[/math]为相互独立的二维高斯噪声,[math]\displaystyle{ \Sigma }[/math]为相关矩阵。微观状态序列[math]\displaystyle{ \boldsymbol{x}_t = (\boldsymbol{S}'_t,\boldsymbol{I}'_t) }[/math]作为实验中的训练样本。作者在图(a)的三角形区域内采样,以此来随机选择初始条件,并使用上述过程生成时间序列数据,用以训练模型。
一、NIS+识别CE的能力。
首先,为了确保EI被NIS+最大化,作者绘制相应图形,观察EI(维平均)J在训练时期的演变。
实验结果表明(图(b)),NIS+(红色实线)、NIS(黑色虚线)和VAE+(绿色实线)的曲线呈上升趋势,但NIS+的增长速度更快。这表明NIS+比其他模型更能有效地最大化J。值得注意的是,NIS也表现出EI的自然增长,因为它逐渐使预测误差最小化。
其次,为了检验NIS+检测和识别CE的能力,作者计算随着噪音的增大,[math]\displaystyle{ \Delta{J} }[/math]的变化,并将其与[math]\displaystyle{ \Psi }[/math]指标进行比较。比较过程中,作者利用从NIS+中学习到的宏观状态来计算[math]\displaystyle{ \Psi }[/math]。结果用图(e)中的黑色和黄色实线表示。
实验结果表明(图(e)),当[math]\displaystyle{ σ <0.01 }[/math]时,[math]\displaystyle{ \Delta{J}\gt 0 }[/math]始终保持不变,但[math]\displaystyle{ \sigma=10^{-3} }[/math]后,[math]\displaystyle{ \Psi\gt 0 }[/math]。NIS+表明在低噪声水平因果涌现始终发生,而信息分解的方法则并非如此。NIS+的结果更合理,因为它可以从有噪声的数据中提取出类似于真实宏观机制的宏观动力学,并且这种确定性动力学应该比有噪声的微观动力学具有更大的EI。作者还分别绘制了宏观和微观动力学曲线[math]\displaystyle{ J(f_M) }[/math](红色虚线)和[math]\displaystyle{ J(f_m) }[/math](绿色虚线)。这些曲线随着σ的增大而减小,但[math]\displaystyle{ J(f_m) }[/math]的减小速度更快,导致观测到CE的发生。但是,当[math]\displaystyle{ \Psi\lt 0 }[/math]时,因为Ψ只能为CE提供充分条件,作者不能做出明确的判断。这两个指标在[math]\displaystyle{ \sigma=10^{-2} }[/math]处达到峰值,这与作者模拟中使用的时间步长([math]\displaystyle{ dt=0.01 }[/math])的大小相对应,反映了微观状态的变化水平。另一方面,如果噪声过大,有限的观测数据将使NIS+难以从数据中准确识别正确的宏观动力学。因此,CE的程度降至零。虽然NIS+判定[math]\displaystyle{ σ > 10 }[/math]时不存在CE,但这一结果并不可靠,因为[math]\displaystyle{ \sigma=10^{-2} }[/math]后的归一化预测误差已经超过了所选阈值0.3(垂直虚线和虚线)。
二、NIS+与其他模型比较预测和泛化能力。
比较的模型包括NIS模型、前馈神经网络(NN)、变分自编码器(VAE)。为了进行公平比较,作者确保所有模型具有大致相同数量的参数,且将样本重加权技术和反向动力学技术应用于前馈神经网络(NN)和变分自编码器(VAE),构建出NN+和VAE+。
在单独的测试数据集上预测多个时间步(10步)的未来状态,以比较NIS+与其他模型的预测未来状态的能力。之后,以图(a)中带点区域为训练数据集,即[math]\displaystyle{ \frac{1}{3} ≤ S ≤ 1 }[/math]的部分。以图(a)中整个蓝色三角形为测试数据集,即[math]\displaystyle{ 0 ≤ S ≤ 1 }[/math]的部分。这样训练NIS+的时候不会用到[math]\displaystyle{ 0 ≤ S ≤ \frac{1}{3} }[/math]的数据,但是测试NIS+的时候会用到[math]\displaystyle{ 0 ≤ S ≤ \frac{1}{3} }[/math]的数据,可以通过测试[math]\displaystyle{ 0 ≤ S ≤ \frac{1}{3} }[/math]的数据的误差大小来比较各个模型的泛化能力。
实验结果表明(图(d)),NIS+和NIS在整体数据集上(绿色条)表现优于其他模型(NN、NN+、VAE、VAE+)。这说明在编码器和解码器中使用可逆神经网络会更好。
实验结果表明(图(d)),NIS+的分布外泛化能力优于其他模型,在部分数据集上,不同模型之间的差异较大。
三、NIS+能否发现真正的宏观动态。
将真实的SIR动力学的向量场([math]\displaystyle{ d\boldsymbol{y}/dt }[/math])(红色)、基于编码器的雅可比矩阵得到的理论向量(蓝色)与通过模型学习到的宏观动态的向量([math]\displaystyle{ d(h_1,h_2)/dt }[/math])(绿色)进行比较。
实验结果表明(图(c)表示NIS+,图(f)表示NIS),学习到的向量与真实向量对齐和理论向量对齐。NIS+明显优于NIS,尤其是在没有训练样本的外围区域。
综上可知,通过最大化EI和学习独立的因果机制,NIS+可以有效地忽略数据中的噪声,准确地学习真实宏观动态,并有良好的泛化能力。此外,NIS+在识别CE方面表现出优越的性能。
Boids 模型实验
Boids模型,是一个著名的多主体模型,用于模拟鸟类的集体行为[17]。此实验有四个基本目标:①NIS+识别CE的能力;②提高NIS+训练粗粒化策略的可解释性;③NIS+的泛化能力;④内在噪音和外部噪音对NIS+识别CE的影响。
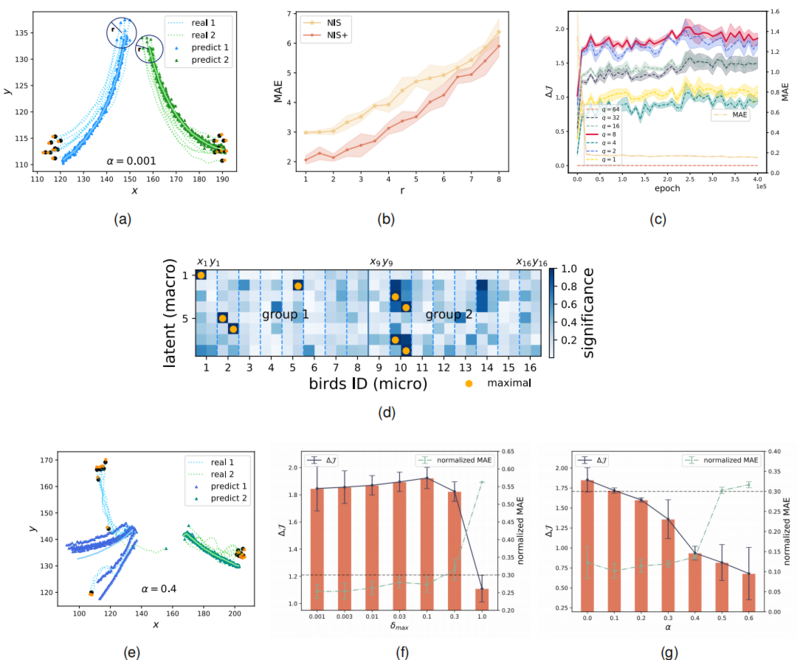
作者根据Reynolds(1987)[17]的方法模拟Boids模型,在300 × 300的画布上用N = 16个鸟生成训练数据。为了评估NIS+发现有意义的宏观状态的能力,作者将鸟群分为两组,并为每组引入不同的恒定转向力。这一修改确保了两组分别沿着不同转弯角度的轨迹运动,如图(a)所示。作者通过模拟生成训练和测试数据。在每个时间步长t上,微状态生成为4N维向量:
[math]\displaystyle{ X_t=(x_1^t,y_1^t,v_{x,1}^t,v_{y,1}^t, \dots, x_N^t,y_N^t,v_{x,N}^t,v_{y,N}^t) }[/math]
其中[math]\displaystyle{ (x_i^t,y_i^t) }[/math]是位置,[math]\displaystyle{ (v_{x,i}^t,v_{y,i}^t) }[/math]是时刻t的速度,[math]\displaystyle{ i=1,2,\dots,16 }[/math]。
一、NIS+识别CE的能力。
实验结果表明(图(a)),预测的涌现集体飞行行为(50步)与两组的真实轨迹密切相关,特别是在初始阶段。这些预测轨迹是通过将预测的宏观状态解码为相应的微观状态来生成的,两条实线表示它们的平均值。
对于宏观状态,一群鸟需要两个坐标相关的维度和两个速度相关的维度来描述它们的运动状态。所以两组鸟需要八个维度。作者推测有一只鸟作为这群鸟的代表,观察这只鸟的情况可以预测这群鸟的整体运动趋势。然后作者利用两个位置维度来进行预测。除了表示位置的两个维度外,速度还可以由两个连续时刻之间的位置差导出。然而,一次只能输入来自单个时刻的信息,这就需要额外的自由度来表示速度。因此,作者仍然需要八个自由度来描述两组鸟的宏观状态。
根据观察,CE在q = 8时达到最大值,如图(c)所示,这与本实验选择超参数q = 8(宏观变量的维度)相符。
二、NIS+粗粒化策略的可解释性。
作者利用积分梯度(IG)[18]来识别每个学到的涌现宏观状态维度中最重要的微观状态,将计算的IG归一化,并在每个宏观状态中提高微观状态的最大梯度,并且忽略每只鸟的速度维度(与宏观状态的相关性较低)。最后,作者将归一化的IG绘制成矩阵图,用以描述每个宏观维度(纵轴)和每只鸟空间坐标(横轴)之间的关系,并用橙色点表示每个宏观状态中最重要的微观状态。
实验结果表明(图(d)),宏观状态的第1、2、5、6维分别对应第一组中的ID(ID<8)(图(d)中group 1 的橙色点在第1行、第2行、第5行、第6行),第3、4、7、8维对应第二组中的ID(ID>=8)(图(d)中group 2 的橙色点在第3行、第4行、第7行、第8行)。因此,学习到的粗粒化策略使用两个位置坐标来表示所有其他信息,形成一个维度的宏观状态。
三、NIS+的泛化能力。
在生成训练数据的仿真过程中,所有鸟的位置被约束在一个半径为r的圆内,如图(a)所示。作者评估当初始位置位于较大的圆上时两种模型的预测能力。
实验结果表明(图(b)),NIS+和NIS的MAE值随半径r的增加而增加,而预测误差MAE越小,泛化能力越好。结果清楚地表明,与NIS相比,NIS+在所有测试半径r上具有优越的泛化能力。
四、内在噪音和外部噪音对NIS+识别CE的影响。
通过在每个时间步长为每只鸟增加随机转角,引入内在噪声。这些角度均匀分布在区间[math]\displaystyle{ \alpha\cdot [-\pi,\pi] }[/math]内,其中[math]\displaystyle{ \alpha\in[0,1] }[/math]是控制内在噪声大小的参数。另一方面,假定外部噪声会影响观测的微观状态。在这种情况下,作者假设不能直接观察到每个物体的微观状态,而是获得有噪声的数据。将外部或观测噪声[math]\displaystyle{ \delta\sim \mathcal{N}(0,\delta_{max}) }[/math]添加到微观状态中,[math]\displaystyle{ \delta_{max} }[/math]是决定该噪声水平的参数。
实验结果表明(图(f)和图(g)),在这两种情况下,归一化MAE都增加了,这表明随着内在和外在噪声的增加,预测任务更具挑战性。然而,这两种类型的噪声之间的差异可以通过检查CE([math]\displaystyle{ \Delta{J}\gt 0 }[/math])的程度来观察。从图(f)可以看出,[math]\displaystyle{ \Delta{J}\gt 0 }[/math]随外部噪声([math]\displaystyle{ \delta_{max} }[/math])的增大而增大,说明粗粒化策略可以在一定范围内减轻噪声,增强因果效应。[math]\displaystyle{ \delta_{max}\lt 0.1 }[/math]时,归一化MAE小于0.3(黑色虚线),满足式1的约束。在这种情况下,CE的程度随着[math]\displaystyle{ \delta_{max} }[/math]的增大而增大。然而,当超过0.3的阈值时,即使[math]\displaystyle{ \Delta{J}\gt 0 }[/math]减小,作者也无法得出有意义的结论(违反了式1中的约束),结果的可靠性就会降低。从图(g)可以看出,[math]\displaystyle{ \Delta{J}\gt 0 }[/math]随着内部噪声(α)水平的增加而减小。这是由于宏观层面的动态学习器试图在这一阶段捕捉每个群体的群体行为。然而,随着内部噪声的增加,群体行为逐渐减弱,导致CE降低。因为归一化MAE超过0.3的阈值时违反了式1中的约束,作者没有计算[math]\displaystyle{ \alpha\gt 0.6 }[/math]的情况。图(e)显示了随机偏转角噪声[math]\displaystyle{ \alpha=0.4 }[/math]时候的真实轨迹和预测。可以观察到,在早期可以预测直线趋势,但随着噪声引起的偏差逐渐增大,误差也随之增大,CE降低。
综上可知,NIS+具有识别涌现集体行为和噪声对涌现集体行为的影响程度的能力。
NIS+可以学习最优宏观动态和粗粒度策略,具有良好的泛化能力。学习到的宏观状态有效地识别了平均群体行为,并且可以使用IG方法将其归因于个体位置。此外,CE的程度随外在噪声的增加而增加,随内在噪声的增大而减少。这一观察结果表明,通过粗粒化可以消除外在噪声,而不能消除内在噪声。
生命游戏模型实验
康威的生命游戏是一个著名的二维元胞自动机模型,在这个模型上出现了滑翔机、正方形、花朵、信号灯、蜂窝、交通灯等各种有趣的动态模式。与SIR模型和Boids模型不同的是,在规则网格上,生命游戏模型在每个时间步长的微观状态是离散的(0或1)。此外,微观动力学不能用微分方程或差分方程来表示,而是用规则表来表示。
一、NIS+的拓展。
为了进行此实验,作者在空间和时间维度上对元胞自动机的微观状态进行粗粒化处理。为此,作者引入了时空卷积的概念。
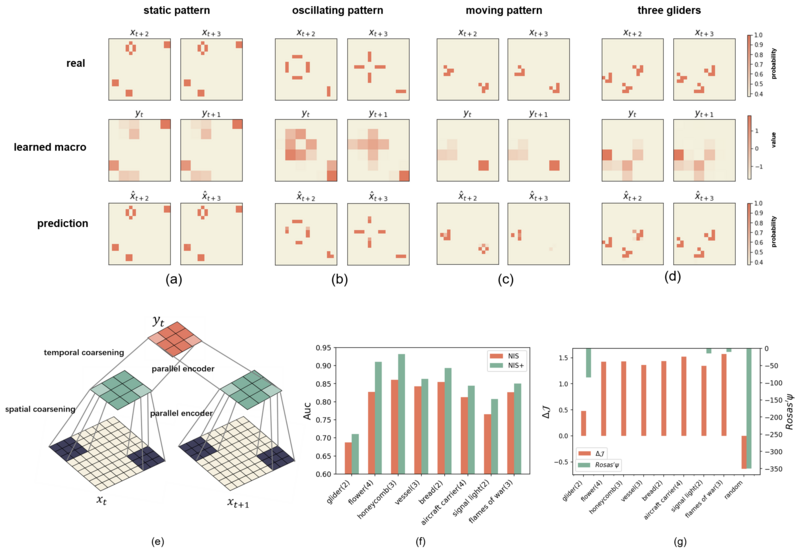
本实验中使用的体系结构如图10(e)所示。整个粗粒化过程可分为两个步骤:①在固定大小的窗口(本文为3x3窗口)内聚合信息,获得空间粗粒化结果;②将这些结果在多个连续的时间步长上聚合,形成一个时空粗粒化的宏观状态。所有这些过程都是通过NIS+中的并行编码器实现的。
二、NIS+捕获模式的能力。
作者使用随机初始条件下模拟生成的数据来训练NIS+,并提取从第100步到第120步的状态时间序列。图(a)、(b)和(c)显示了由真实宏观机制模拟(第一行)和NIS+预测(第三行)生成的动态模式,以及可以进行这些预测的涌现宏观状态(第二行)。作者将两个连续时间步长的图像输入到NIS+中,再用两个连续时间步长得到另一个图像对。把上面的图片和下面的图片比较一下,图案是相似的。然而,由于在随机初始条件下具有某些模式的训练样本出现有限,第三列的学习和预测模式有些(特别是“滑翔机”模式)显得模糊。为了提高预测的质量,作者生成一组包含两个“滑翔机”初始条件的新训练样本。结果如图(d)所示,尽管这个测试环境中的滑翔机数量是3个,预测也更加清晰。这意味着,NIS+可以捕获包括移动、静态和振荡结构在内的模式。
三、NIS+的泛化能力。
作者比较了在不同于初始随机模式下,NIS和NIS+对8种不同模式类型的多步预测性能。
实验结果表明(图(f)),对于所有模式类型,NIS+始终比NIS具有更高的AUC(曲线下面积)。其中,在x坐标的刻度标签中,作者采用“模式名称(数量)”的格式来表示各种初始条件。例如,“滑翔机(2)”表示包含两个滑翔机的初始配置。实验表明,NIS+在捕获这些模式方面具有优越的泛化能力。
四、NIS+识别CE的能力。
在比较过程中,作者使用相同的模式作为初始条件。
实验结果表明(图(g)),除“随机”情况外,其余8例均发生CE。由于出现“滑翔机”的训练样本有限,NIS+在此部分训练不充分,故“滑翔机”型预测不良,CE程度最低(见图(c))。其余7种模式的[math]\displaystyle{ \Delta{J} }[/math]值相似。这些结果表明,[math]\displaystyle{ \Delta{J} }[/math]提供了CE发生的更合理的指示。但是,对于Ψ,所有情况产生的值都小于或等于0,这可能是因为此系统是一个高维的复杂系统,冗余信息更多,而Ψ的近似忽略了许多冗余信息,使得Ψ无法确定CE是否发生。因此,本文提出的[math]\displaystyle{ \Delta{J} }[/math]是一种较好的鉴别CE的方法。
大脑fMRI 实验
作者在830名受试者(AOMIC ID1000)的大脑fMRI真实时间序列数据上测试了NIS+[19]。fMRI扫描数据是在受试者观看同一段电影时收集的,这对应于具有不同初始条件的相同动力学的时间序列。采样率(重复时间)为:ID1000为2.2s,PIOP2为2s。作者通过Schaefer atlas方法对原始数据进行预处理[20],将每个受试者的时间序列维数从大约140,000(不同受试者的维数不同)降至100,使NIS+能够运行并获得更清晰的结果。然后,选取前800个时间序列数据进行训练,剩下的30个时间序列进行测试。作者还将结果与另一个fMRI数据集AOMIC PIOP2[19]进行了比较,其中50名受试者处于静息状态。
一、对微观状态的预测能力。
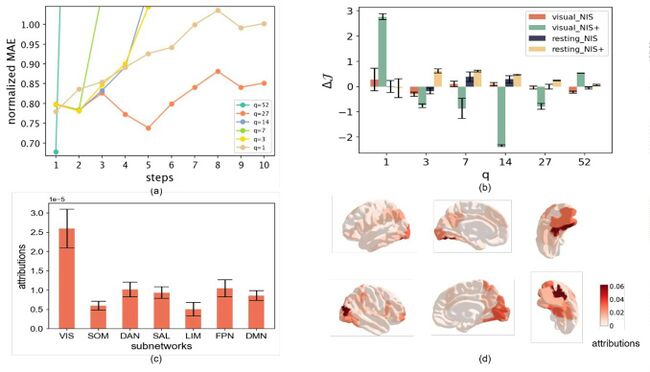
实验结果表明(图(a)),当q = 27和q = 1时,NIS+的预测效果更好。具体来说,随着预测步骤的增加,与q = 1的曲线相比,q = 27的曲线显示出较慢的增长率。这表明选择超参数q为27可能比1更合适。
然而,图(b)显示了不同的结果。图(b)中绿色柱子就是NIS+应用于第一组实验数据(非静息数据)所计算出不同维度q下的因果涌现数值。可以看出q=1的时候[math]\displaystyle{ \Delta{J} }[/math]数值最高。为了比对,作者也用NIS框架分析了同样的数据,如图(b)中的红色柱子所示,可以看出它在不同维度上的分布与绿色柱子近似相同,但是因果涌现度量都比较小。这说明,q=1 维能够展现因果涌现是一个稳定客观的结果,其次,NIS+由于最大化了EI,因而会让这一结果更加突出。反之,当q = 27时,[math]\displaystyle{ \Delta{J} }[/math]值为负。这表明,当q = 27时,预测结果的改善可能是由于过拟合。综合来看,当被试在看同一组视频的时候,它们的fMRI数据用一个维度的宏观动力学就可以很好地概括大脑的活动了。
此外,作者还将NIS+模型和NIS模型应用于静息数据,观察到NIS(深蓝色条)和NIS+(黄色条)在q = 3或q = 7处达到峰值,此时,大脑的动态表现无法简化为一个一维的宏观动力学,而至少需要3~7个维度才能对大脑的活动进行概括。
二、尝试研究粗粒化如何将输入数据转化为一维宏观状态。
作者利用归因分析技术,追踪这一个维度的宏观态数据到底和哪些原始数据维度有关,并把归因分析的强度值分配到这100个原始微观态维度所对应的脑区。结果如(d)所示,可以看出,颜色较深的区域大多都是负责视觉信号加工的脑区。
综上,NIS+是可以直接从fMRI时间序列数据揭示出大脑在不同尺度的动力学,并发现因果涌现主要发生在哪个尺度;当被试集中看视频的时候,大脑活动可以被一个维度的宏观信号所概括,这一维度主要代表的是视觉区域的活动状态,大脑发生了非常明显的因果涌现现象;而在静息态下,被试大脑虽然也发生了因果涌现现象,但强度明显低于前者。大脑的主要活动则相对第一组更复杂,因为它不能简单地被一个维度的宏观态所概括,而是集中在一个3~7维的介观尺度上。
总结与展望
总结
受因果涌现理论的启发,作者构建了一种新的机器学习框架Neural Information Squeezer Plus (NIS+)来学习涌现宏观动力学,并直接从数据中找到合适的粗粒化策略、量化各种条件下CE的程度。
与其他机器学习框架相比,NIS+专注于在保持有效性约束的同时最大化宏观动力学的有效信息(EI)。这使得学习到的涌现宏观动力学能够捕获尽可能独立于输入数据分布的不变因果机制。这个特性不仅使NIS+能够识别不同环境中的数据CE,而且还增强了它对不同于训练数据的环境进行泛化的能力。通过将误差约束纳入式1,作者增强了EI最大化框架的鲁棒性,解决了[21]中提出的重整化和时间演化算子的交换性问题。作者的框架确保微观动力学演化与编码的宏观动力学相匹配。由于编码器和解码器所使用的神经网络互为可逆函数且参数共享,这种微观状态和编码成的宏观状态之间的一致性证实了学习宏观的动力学和粗粒化策略是可交换的。因此,NIS+扩展了Hoel[1]的CE理论,使其既适用于离散和连续动力系统,也适用于实际数据。
实验表明,①通过最大化EI,NIS+的多步预测能力、泛化能力、模式捕获能力优于其他机器学习模型,可以在隐空间中获得更稳健的宏观动力学。②NIS+可以比Ψ指标更合理地识别CE。NIS+可以有效地学习复杂系统的粗粒度化过程,并使用积分梯度(IG)方法可以将宏观状态和微观状态之间的关系可视化,从而可以识别微观状态中最重要的变量。③外在噪声会增加CE,而内在噪声会降低CE。这表明,由观测不确定性引起的外部噪声可以通过学到的粗粒化策略减轻。另一方面,由于动态规则的内在不确定性而产生的固有噪声无法消除。
此外,NIS+还调和了关于涌现是一个客观概念还是一个依赖于观察者的认知概念的争论。通过设计一个最大化EI的机器,我们可以提取出客观的涌现特征和动态。这台机器充当了一个观察者,但却是一个客观的观察者。如果机器观察者在数据中检测到有趣的模式,就会认为出现涌现。
展望
NIS+也存在一些局限性。
①NIS+需要大量的训练数据来学习宏观动态和粗粒化策略,这在很多现实情况下可能是不可行的。如果训练不充分,可能导致CE的错误识别。因此,有必要结合其他数值方法,如ΦID[3],以作出准确的判断。NIS+的一个优点是它能够识别粗粒化的宏观状态,然后可以将其用作ΦID[3]的输入。
②神经网络的可解释性。增强学习模型的可解释性可以提供对潜在机制的有价值的见解,并提高结果的可信度。
③作者的工作是对[1][2]中提出的研究的延伸,这些研究假设动力学是马尔可夫的。然而,当动态表现出强烈的非马尔可夫特征时,其他量化涌现的框架,如[3][5]中提出的框架,可能具有更大的优势。
参考文献
- ↑ 1.0 1.1 1.2 Hoel E P, Albantakis L, Tononi G. Quantifying causal emergence shows that macro can beat micro[J]. Proceedings of the National Academy of Sciences, 2013, 110(49): 19790-19795.
- ↑ 2.0 2.1 Hoel E P. When the map is better than the territory[J]. Entropy, 2017, 19(5): 188.
- ↑ 3.0 3.1 3.2 3.3 3.4 Rosas F E, Mediano P A, Jensen H J, et al. Reconciling emergences: An information-theoretic approach to identify causal emergence in multivariate data[J]. PLoS computational biology, 2020, 16(12): e1008289.
- ↑ Zhang J, Tao R, Yuan B. Dynamical Reversibility and A New Theory of Causal Emergence. arXiv preprint arXiv:2402.15054. 2024 Feb 23.
- ↑ 5.0 5.1 Barnett L, Seth AK. Dynamical independence: discovering emergent macroscopic processes in complex dynamical systems. Physical Review E. 2023 Jul;108(1):014304.
- ↑ P. A. Mediano, F. Rosas, R. L. Carhart-Harris, A. K. Seth, A. B. Barrett, Beyond integrated information: A taxonomy of information dynamics phenomena, arXiv preprint arXiv:1909.02297 (2019).
- ↑ Kaplanis Christos, Mediano Pedro, Rosas Fernando. Learning Causally Emergent Representations. NeurIPS 2023 workshop: Information-Theoretic Principles in Cognitive Systems
- ↑ 8.0 8.1 8.2 Zhang J, Liu K. Neural information squeezer for causal emergence[J]. Entropy, 2022, 25(1): 26.
- ↑ Dinh, L.; Sohl-Dickstein, J.; Bengio, S. Density estimation using real nvp. arXiv 2016, arXiv:1605.08803.
- ↑ 10.0 10.1 Cui, Peng, Athey, et al. Stable learning establishes some common ground between causal inference and machine learning. nature machine intelligence, 2022, 4(2): 110-115
- ↑ Arjovsky, M.; Bottou, L.; Gulrajani, I.; Lopez-Paz, D. Invariant risk minimization. arXiv 2019, arXiv:1907.02893
- ↑ Mingzhe Yang, Zhipeng Wang, Kaiwei Liu, et al. Finding emergence in data by maximizing effective information. National Science Review, 2024, nwae279
- ↑ 13.0 13.1 Shalizi C and Moore C. What is a macrostate? subjective observations and objective dynamics. arXiv: cond-mat/0303625.
- ↑ 14.0 14.1 Fisch D, Jänicke M and Sick B et al. Quantitative emergence–a refined approach based on divergence measures. Fourth IEEE International Conference on Self-Adaptive and Self-Organizing Systems, 2010.
- ↑ Mnif M and Müller-Schloer C. Quantitative emergence. In: Müller-Schloer C, Schmeck H and Ungerer T(ed.). Organic Computing—A Paradigm Shift for Complex Systems. Berlin: Springer, 2011, 39-52.
- ↑ Fisch D, Jänicke M and Müller-Schloer C et al. Divergence measures as a generalised approach to quantitative emergence. In: Müller-Schloer C, Schmeck H and Ungerer T(ed.). Organic Computing—A Paradigm Shift for Complex Systems. Berlin: Springer, 2011, 53-66.
- ↑ 17.0 17.1 Reynolds C-W. Flocks, herds and schools: A distributed behavioral model. Proceedings of the 14th annual conference on Computer graphics and interactive techniques, Denver, 27 July - 1 August 1987.
- ↑ Sundararajan M, Taly A and Yan Q. Axiomatic attribution for deep networks. Proceedings of the 34th International Conference on Machine Learning, Sydney, 6-11 August 2017.
- ↑ 19.0 19.1 Snoek L, Miesen M and Beemsterboer T et al. The amsterdam open mri collection, a set of multimodal mri datasets for individual difference analyses. Sci Data 2021; 8: 03.
- ↑ Schaefer A, Kong R and Gordon E-M et al. Local-Global Parcellation of the Human Cerebral Cortex from Intrinsic Functional Connectivity MRI. Cereb Cortex 2017; 28:3095–3114.
- ↑ Eberhardt F and Lee L-L. Causal emergence: When distortions in a map obscure the territory. Philosophies 2022; 7: 30.