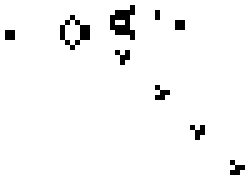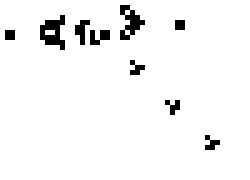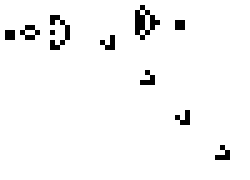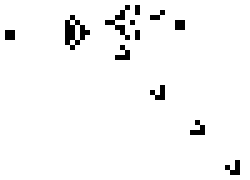“康威的生命游戏 Conway's Game of Life”的版本间的差异
(→编者推荐) |
(→模式示例) |
||
| 第41行: | 第41行: | ||
==模式示例== | ==模式示例== | ||
| − | + | 在生命游戏中会出现许多不同类型的模式,可根据行为特点对这些模式进行分类。常见的模式类型包括: | |
| + | |||
| + | 1.静态,从一代到下一代都不会改变; | ||
| + | |||
| + | 2.振荡态,经过有限的迭代后返回其初始状态; | ||
| + | |||
| + | 3.太空船态,可在网格中进行自我变换。 | ||
| + | |||
| + | 4.穿梭机态,蜂王可以在两个静态块之间往复移动。 | ||
| + | |||
| + | 5.滑翔机枪,它由两个块稳定的蜂王穿梭机组成,可以向外发射滑翔机。 | ||
| + | |||
| + | 6.图灵机,它是一种能够进行图灵完备计算的模式,可以执行任意计算。 | ||
生命游戏最早的比较有趣的模式是在不使用计算机的情况下就被发现的。最简单的静态和振荡态是在使用方格纸、黑板和物理游戏板记录一些运行实例时发现的。在早期研究中,Conway发现“R-pentomino”在次数较少的迭代中无法稳定。实际上,它需要1103次迭代才能稳定下来,到那时它已拥有116个种群,并已产生了6个移动的“滑翔机”。<ref>{{cite web|url=http://www.conwaylife.com/wiki/index.php?title=R-pentomino|title=R-pentomino|publisher=LifeWiki|accessdate=July 12, 2009}}</ref>这是有史以来发现的第一批“太空船”模式。<ref>{{cite web|url=http://www.conwaylife.com/ref/lexicon/lex_g.htm#glider|author=Stephen A. Silver|title=Glider|publisher=The Life Lexicon|accessdate=March 4, 2019}} | 生命游戏最早的比较有趣的模式是在不使用计算机的情况下就被发现的。最简单的静态和振荡态是在使用方格纸、黑板和物理游戏板记录一些运行实例时发现的。在早期研究中,Conway发现“R-pentomino”在次数较少的迭代中无法稳定。实际上,它需要1103次迭代才能稳定下来,到那时它已拥有116个种群,并已产生了6个移动的“滑翔机”。<ref>{{cite web|url=http://www.conwaylife.com/wiki/index.php?title=R-pentomino|title=R-pentomino|publisher=LifeWiki|accessdate=July 12, 2009}}</ref>这是有史以来发现的第一批“太空船”模式。<ref>{{cite web|url=http://www.conwaylife.com/ref/lexicon/lex_g.htm#glider|author=Stephen A. Silver|title=Glider|publisher=The Life Lexicon|accessdate=March 4, 2019}} | ||
</ref> | </ref> | ||
| − | + | 下面显示了上述六种模式类型的常见<ref>{{cite web|url=http://www.conwaylife.com/soup/census.asp?rule=B3/S23&sl=1&os=1&ss=1|archiveurl=https://web.archive.org/web/20090910010855/http://conwaylife.com/soup/census.asp?rule=B3%2FS23&sl=1&os=1&ss=1|archivedate=2009-09-10|title=Census Results in Conway's Game of Life|publisher=The Online Life-Like CA Soup Search|accessdate=July 12, 2009|url-status=dead}} | |
</ref><ref>{{cite web|url=http://wwwhomes.uni-bielefeld.de/achim/moving.html|title=Spontaneous appeared Spaceships out of Random Dust|publisher=Achim Flammenkamp (1995-12-09)|accessdate=July 10, 2012}}</ref>示例(因为它们经常从随机的细胞初始配置中出现),活细胞显示为黑色,死细胞显示为白色。周期指的是模式返回初始配置之前必须迭代的周期数。 | </ref><ref>{{cite web|url=http://wwwhomes.uni-bielefeld.de/achim/moving.html|title=Spontaneous appeared Spaceships out of Random Dust|publisher=Achim Flammenkamp (1995-12-09)|accessdate=July 10, 2012}}</ref>示例(因为它们经常从随机的细胞初始配置中出现),活细胞显示为黑色,死细胞显示为白色。周期指的是模式返回初始配置之前必须迭代的周期数。 | ||
2024年11月14日 (四) 09:55的版本
康威生命游戏 (Conway's Game of Life),又称康威生命棋,是英国数学家约翰·何顿·康威 John Horton Conway在1970年发明的元胞自动机。[1]
该游戏是零玩家游戏,这意味着它的发展由其初始状态决定,不需要进一步的输入。通过创建初始配置并观察其演变,它可以与生命游戏互动。它是具有图灵完备性的,可以模拟通用构造器或任何其他图灵机。
规则
我们所说的生命游戏是一个无限的,二维正方形的栅格单元网格,每一个单元格有2种状态可能性:活或死的(或者黑和白)。每个单元格都与其八个相邻的单元交互,这八个单元格是水平、垂直或对角线相邻的单元格。在每个时间步上,都会发生以下转换:
- 当前细胞为存活状态时,当周围的存活细胞低于2个时(不包含2个),该细胞变成死亡状态。(模拟生命数量稀少)
- 当前细胞为存活状态时,当周围有2个或3个存活细胞时,该细胞保持原样。
- 当前细胞为存活状态时,当周围有超过3个存活细胞时,该细胞变成死亡状态。(模拟生命数量过多)
- 当前细胞为死亡状态时,当周围有3个存活细胞时,该细胞变成存活状态。(模拟繁殖)
这些将自动机的行为与现实生活进行比较的规则可以归纳为以下内容:
- 任何有两个或三个邻居的活细胞都可以存活。
- 具有三个活动邻居的任何死细胞都将成为活细胞。
- 所有其他活细胞将在下一代死亡。同样,所有其他死细胞仍保持死亡状态。
可以把最初的细胞结构定义为种子,当所有在种子中的细胞同时被以上规则处理后,可以得到第一代细胞图。按规则继续处理当前的细胞图,可以得到下一代的细胞图,周而复始。
起源
1940年末,约翰·冯·诺依曼 John von Neumann将生命定义为可以自我复制且可模拟图灵机的存在。冯·诺依曼考虑使用随机漂浮在液体或气体中的电磁成分来模拟生命。[2]然而受当时技术所限,他的方案并未成为现实。后来,乌兰姆 Stanislaw Ulam发明了元胞自动机,旨在模拟冯·诺依曼的理论电磁构造。乌兰姆在他的几篇论文中讨论了用计算器在二维晶格中模拟元胞自动机。与此同时,约翰·冯·诺依曼 John von Neumann也在尝试构建乌兰姆的元胞自动机。虽然进展顺利,但他同时忙于其他项目,有一些细节未完成。他构造的机器很复杂,因为加入了一些他自己的工程设计。随着时间推移,有其他研究人员提供了更简单的构造,并发表在论文和书籍中。
受数学逻辑问题以及乌兰姆等学者在模拟游戏方面工作的启发,约翰·康威 John Conway于1968年开始使用各种不同的2D元胞自动机规则进行实验。[3]Conway的最初目标是定义一种有趣且不可预测的元胞自动机。因此,他希望一些运行实例可以能持续很长时间后终止,而另一些运行实例则在不出现循环的情况下永久运行下去。这是一个巨大的挑战。也是多年以来一个悬而未决的问题。后来元胞自动机专家们终于证明Conway的生命游戏满足Von Neumann提出的两个基本要求。在Conway之前,生命游戏以证明为导向,而Conway以构造简单的生命游戏模型为导向,并没有先验地证明自动机可以持续存活。
经过大量实验后,Conway仔细选择了自己的规则,使得符合以下条件:
- 不应出现爆炸性增长。
- 应该存在小的初始模式,这些模式会导致混沌,不可预测的结果。
- 冯·诺依曼通用构造机(universal constructor)应该有潜力。
- 在遵守上述约束的同时,规则应尽可能简单。[4]
自从发明以来,Conway的生命游戏就吸引了很多人,因为它可以使初始模式以令人惊讶的方式进行演变。生命游戏是系统涌现和自组织的一个例子。计算机科学,物理学,生物学,生物化学,经济学,数学,哲学和生成科学等各个领域的学者都可从这种“通过执行简单规则即可产生复杂模式”的方式汲取营养。生命游戏也可以用作教学分析,用于展现一些反直觉的观念,即设计和组织可以在没有设计师的情况下自发出现。例如,认知科学家丹尼尔·丹内特 Daniel Dennett广泛使用了Conway生命游戏中的 “宇宙” ,来说明复杂的哲学构造(如意识和自由意志)可能从相对简单的确定性物理定律集演化而来,而这些简单的物理定律可以控制我们的宇宙。[5][6][7]
Conway的生命游戏之所以受欢迎,是因为它的问世刚好赶上新一代的廉价计算机进入市场的时机。生命游戏可以在这些机器上运行数小时。对一些来说,生命游戏仅仅是编程挑战:一种有趣的方式来占用CPU使用率,反正不用也会浪费。对另一些人来说,生命戏则具有哲学内涵。当前的发展已经达到在生命游戏的范畴内创建计算机系统的理论仿真的程度。[8][9]
模式示例
在生命游戏中会出现许多不同类型的模式,可根据行为特点对这些模式进行分类。常见的模式类型包括:
1.静态,从一代到下一代都不会改变;
2.振荡态,经过有限的迭代后返回其初始状态;
3.太空船态,可在网格中进行自我变换。
4.穿梭机态,蜂王可以在两个静态块之间往复移动。
5.滑翔机枪,它由两个块稳定的蜂王穿梭机组成,可以向外发射滑翔机。
6.图灵机,它是一种能够进行图灵完备计算的模式,可以执行任意计算。
生命游戏最早的比较有趣的模式是在不使用计算机的情况下就被发现的。最简单的静态和振荡态是在使用方格纸、黑板和物理游戏板记录一些运行实例时发现的。在早期研究中,Conway发现“R-pentomino”在次数较少的迭代中无法稳定。实际上,它需要1103次迭代才能稳定下来,到那时它已拥有116个种群,并已产生了6个移动的“滑翔机”。[10]这是有史以来发现的第一批“太空船”模式。[11]
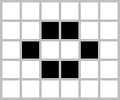
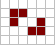
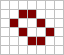
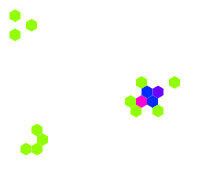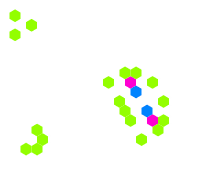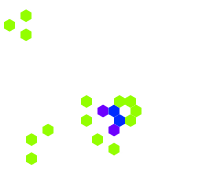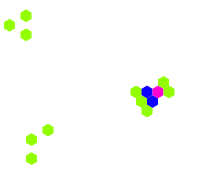
下面显示了上述六种模式类型的常见[12][13]示例(因为它们经常从随机的细胞初始配置中出现),活细胞显示为黑色,死细胞显示为白色。周期指的是模式返回初始配置之前必须迭代的周期数。
静态示例
震荡态示例
太空船示例
不可判定性
生命游戏中的许多模式最终成为静止态、振荡态和太空船态的组合; 其他模式可以被称为混沌。 一个模式可能会在很长一段时间内保持混乱,直到它最终稳定为这样一个组合。生命是无法判定的,这意味着给定一个初始模式和一个后来的模式,没有算法能够判断后来的模式是否会出现。 这是不确定问题的必然结果: 从一个最初的输入开始,在给定参数的情况下,模型是会一直运行下去还是结束运行。[14]事实上,由于生命游戏包含一个相当于通用图灵机的模式,这个决策算法,如果它存在的话,可以用来解决停机问题,方法是将初始模式作为对应于一个通用图灵机加上一个输入的模式,将后面的模式作为对应于一个通用图灵机的停机状态的模式。 同时,一些模式永远保持着混乱的状态。 如果不是这样的话,你可以按顺序进行游戏,直到一个非混乱的模式出现,然后计算是否会出现一个后来的模式。
自我复制
2010年5月18日,安德鲁·约翰·韦德 Andrew John Wade宣布了一个自我构建的模式,被称为“双子座” ,在摧毁母体的同时创建一个自我复制品。[15][16] 这种模式经过3400万代的复制,使用由滑翔机制成的指令带在两个由查普曼-格林结构臂构成的稳定结构之间来回摆动。 这些,反过来,会创建新的副本的模式,并销毁以前的副本。 双子座也是太空船态,是生命游戏中建造的第一艘倾斜的太空船,它既不是正交的也不是纯对角的。[17] [18]2015年12月,斜对角线版的双子座建成了。 [19] 2013年11月23日,Dave Greene 在 Conway 的《生命游戏》中制造了第一个复制因子,这个复制因子可以创建一个完整的自我拷贝,包括指令带。[20] 2018年10月,Adam p. Goucher 完成了0E0P metacell 的建造工作,这是一个可以存储自我复制的 metacell。 这与之前的元细胞不同,比如 Brice Due 的 OTCA metapixel,它只能处理附近已经构建好的副本。[21] 0E0P 元细胞的工作原理是使用构造臂来创建模拟编程规则的副本。 对 Conway’ s Life 或其他 Moore 邻居规则的实际模拟是通过使用具有更多状态的冯诺依曼邻域来模拟一个等价规则来完成的。[22]0E0P 是“ Zero Encoded by Zero Population”的缩写,这意味着0E0P 元胞不是处于“关闭”状态,而是在细胞进入“关闭”状态时自行移动,留下空白空间。[23]
迭代
从网格上最随机的细胞初始模式中,观察者会发现人口随着时代的推移而不断变化。 从简单规则中产生的模式可以被认为是数学美的一种形式。 没有初始对称性的孤立的小亚模式趋向于对称。 一旦这种情况发生,对称性可能会增加丰富性,但它不会丢失,除非附近的子模式接近到足以干扰它。 在极少数情况下,社会最终会消亡,所有的活细胞都会消失,尽管这种情况可能不会发生很多代。 大多数最初的模式最终会结束,产生稳定的数字或模式,永远在两个或两个以上的状态之间振荡; [24][25]许多还产生一架或多架滑翔机或太空飞船,它们可以无限期地远离最初的位置。 由于基于最近邻的规则,没有任何信息能够以大于每单位时间一个单元的速率通过网格,所以这个速度被称为光的细胞自动机速度,并用 c 表示。
算法
在具有未知前景的早期模式,如 R-pentomino,使世界各地的计算机程序员编写程序来跟踪生命模式的演变。 大多数早期的算法是相似的: 它们将生命模式表示为计算机内存中的二维数组。 通常使用两个数组: 一个用于保存当前生成,另一个用于计算其后续数组。 通常0和1分别代表死细胞和活细胞。 嵌套的 for 循环依次考虑当前数组的每个元素,计算每个单元格的活动邻居,以决定后续数组的相应元素是0还是1。对于下一次迭代,数组交换角色,以便上一次迭代中的后继数组成为下一次迭代中的当前数组。
对这个基本方案进行各种小的改进是可能的,并且有许多方法可以节省不必要的计算。 如果一个单元格在上一个时间步骤中没有发生更改,而且其邻居也没有发生更改,则保证该单元格在当前时间步骤中也不发生更改。 因此,跟踪哪些区域处于活动状态的程序可以通过不更新非活动区域来节省时间。[26]
为了避免计数循环中的决定和分支,规则可以以自我为中心的方法从内域对其邻域的重新设定,科学观察者的观点: 如果一个给定邻域的所有九个场之和为3,下一代的内域状态将是生存; 如果全场和为4,内域保持其当前状态; 其他的和,则内域状态是死亡。
如果希望节省内存,可以将存储量减少到一个数组加两个行缓冲区。 一个行缓冲区用于计算一行的继承状态,然后第二个行缓冲区用于计算下一行的继承状态。 然后将第一个缓冲区写入其行,并释放以保存第三行的继承者状态。 如果使用环形数组,则需要第三个缓冲区,以便保存数组中第一行的原始状态,直到计算最后一行。
原则上,生命域是无限的,但计算机的内存是有限的。 当活动区域侵入阵列的边界时,这就会导致问题。 程序员使用了几种策略来解决这些问题。 最简单的策略是简单地假设阵列外的每个单元格都已死亡。 这是很容易编程,但会导致不准确的结果,使得活动区跨越边界。 一个更复杂的技巧是考虑将场的左右边缘结合在一起,以及顶部和底部边缘,生成一个环形阵列。 其结果是,跨越场边缘的活动区域在相反的边缘重新出现。还可以使用动态存储分配技术,创建越来越大的数组来保存生长模式。 有时对有限域上的生命进行明确的研究; 有些实现,例如 Golly,支持在标准无限域、一维无限域或有限域中进行选择,并可选择柱面、环面或Möbius strip。
或者,程序员可以放弃用二维数组表示 Life 字段的概念,而使用不同的数据结构,例如用坐标对表示活细胞的向量。 这种方法允许模式在场中不受阻碍地移动,只要人口不超过活动坐标阵列的大小。 缺点是计算生存的邻居变成了散列表查找或搜索操作,降低了模拟速度。 使用更复杂的数据结构,这个问题也可以基本上得到解决。
对于在非常长的时间深度探索大型模式,像 Hashlife 这样的复杂算法可能是有用的。 还有一种方法,也适用于其他细胞自动机,用任意的异步更新来实现生命游戏,同时仍然完全模仿同步游戏的行为。[27] 在 Rosetta Code 中可以找到用各种编程语言(包括 c、 c + + 、 Java 和 Python)实现基本生命游戏场景的源代码示例。[28]
代码实现
Netlogo代码实现
代码整体分为两部分,setup和go部分。其中setup进行环境的初始化,go进行持续运行。Netlogo源代码
setup部分
setup的核心代码如下:
patches-own[living]
to setup
clear-all
reset-ticks
ask patches[
if random-float 1 < 0.5 [ #以0.5的概率设置白格,黑白格比例为1:1,可以在实际中将0.5改为其他值,来模拟不同黑白格比例
set pcolor white
]
set living 0
]
end
to go
ask patches[
set living count neighbors with [pcolor = black]
]
ask patches[
ifelse pcolor = black[
if living > 3 or living < 2[
set pcolor white
]
][
if living = 3[
set pcolor black
]
]
]
tick
end
运行效果如下所示:
go部分
go按钮在创建之时就设定了持续执行,因此程序会一直进行下去。在每一轮中,程序都会遍历每个格,来判断每个格周围的存活数量。如果黑格周围存活数不等于3,其将死亡,表现为由黑格转为白格。若一个白格周围存活数正好是3,会变为黑色,即为存活状态。在棋盘上所有格子均判断完一轮后,由于设定了持续执行,程序会再次进行遍历,不断循环下去。随着迭代次数的增加,整个环境也会趋于较稳定状态。go部分的核心代码如下:
ask patches[
ifelse pcolor = black[
if living > 3 or living < 2[
set pcolor white
]
][
if living = 3[
set pcolor black
]
]
]
运行结果:
Python代码实现
以下代码在安装相应的库后复制粘贴便可运行。
import numpy as np
import matplotlib.pyplot as plt
class GameOfLife(object):
def __init__(self, cells_shape):
"""
Parameters
----------
cells_shape : 一个元组,表示画布的大小。
Examples
--------
建立一个高20,宽30的画布
game = GameOfLife((20, 30))
"""
# 矩阵的四周不参与运算
self.cells = np.zeros(cells_shape)
real_width = cells_shape[0] - 2
real_height = cells_shape[1] - 2
self.cells[1:-1, 1:-1] = np.random.randint(2, size=(real_width, real_height))
self.timer = 0
self.mask = np.ones(9)
self.mask[4] = 0
def update_state(self):
"""更新一次状态"""
buf = np.zeros(self.cells.shape)
cells = self.cells
for i in range(1, cells.shape[0] - 1):
for j in range(1, cells.shape[0] - 1):
# 计算该细胞周围的存活细胞数
neighbor = cells[i-1:i+2, j-1:j+2].reshape((-1, ))
neighbor_num = np.convolve(self.mask, neighbor, 'valid')[0]
if neighbor_num == 3:
buf[i, j] = 1
elif neighbor_num == 2:
buf[i, j] = cells[i, j]
else:
buf[i, j] = 0
self.cells = buf
self.timer += 1
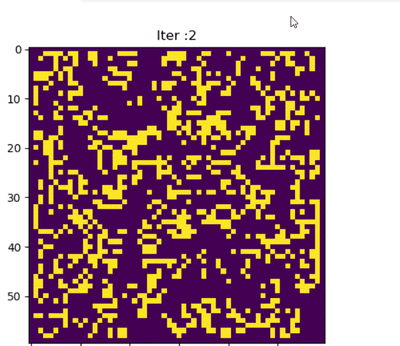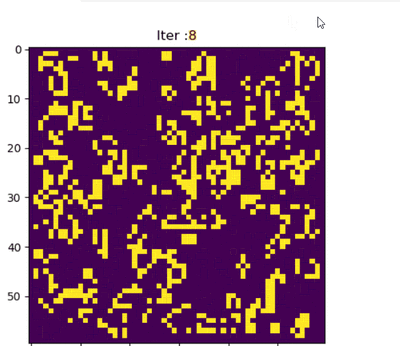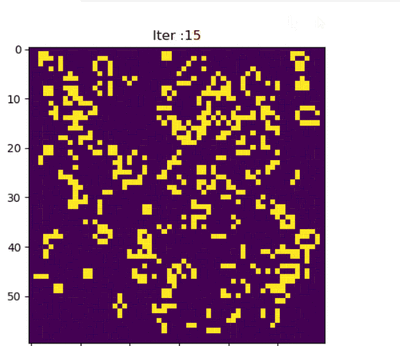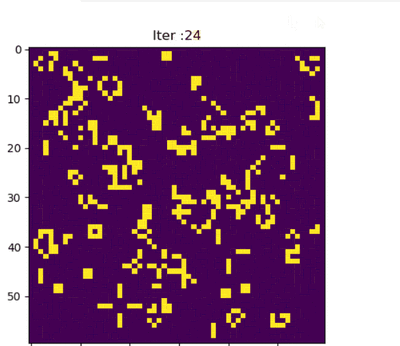
def plot_state(self):
"""画出当前的状态"""
plt.title('Iter :{}'.format(self.timer))
plt.imshow(self.cells)
plt.show()
def update_and_plot(self, n_iter):
"""更新状态并画图
Parameters
----------
n_iter : 更新的轮数
"""
plt.ion()
for _ in range(n_iter):
plt.title('Iter :{}'.format(self.timer))
plt.imshow(self.cells)
self.update_state()
plt.pause(0.2)
plt.ioff()
if __name__ == '__main__':
game = GameOfLife(cells_shape=(60, 60))
game.update_and_plot(200)
运行效果:
总结:相比较Netlogo与Python实现,可以看出,python实现首先需要构建运行环境,再实现功能,最终实现的功能也并没有NetLogo丰富,建议从NetLogo实现开始。
音乐
各种音乐创作技术都会使用康威的生命游戏。[29]特别是在 MIDI旋律中,有各种各样的程序可以从生命游戏中产生的模式中发出声音。[30][31][32]
游戏试玩
下面是康威生命游戏的玩法演示。您可以选择不同的初始模式,点击开始按钮▷来观察元胞的演化过程,点击'更新为初始状态'按钮来重置游戏,选择Empty模式可以自定义游戏的初始状态。 此游戏的源代码来自github:https://github.com/rowett/lifeviewer
参见
参考文献
- ↑ Gardner, Martin (October 1970). "Mathematical Games - The Fantastic Combinations of John Conway's New Solitaire Game 'Life'" (PDF). Scientific American (223): 120–123. doi:10.1038/scientificamerican1070-120.
- ↑ Wolfram, Stephen (2002). A New Kind of Science. Wolfram Media, Inc.. p. 1179. ISBN 978-1-57955-008-0. https://archive.org/details/newkindofscience00wolf/page/1179.
- ↑ Wolfram, Stephen (2002). A New Kind of Science. Wolfram Media, Inc.. p. 877. ISBN 978-1-57955-008-0. https://archive.org/details/newkindofscience00wolf/page/877.
- ↑ Conway, private communication to the 'Life list', 14 April 1999.
- ↑ Dennett, D. C. (1991). Consciousness Explained. Boston: Back Bay Books. ISBN 978-0-316-18066-5. https://archive.org/details/consciousnessexp00denn.
- ↑ Dennett, D. C. (1995). Darwin's Dangerous Idea: Evolution and the Meanings of Life. New York: Simon & Schuster. ISBN 978-0-684-82471-0. https://archive.org/details/darwinsdangerous0000denn.
- ↑ Dennett, D. C. (2003). Freedom Evolves. New York: Penguin Books. ISBN 978-0-14-200384-8.
- ↑ Paul Rendell (January 12, 2005). "A Turing Machine in Conway's Game of Life". Retrieved July 12, 2009.
- ↑ Adam P. Goucher. "Spartan universal computer-constructor". LifeWiki. Retrieved July 12, 2009.
- ↑ "R-pentomino". LifeWiki. Retrieved July 12, 2009.
- ↑ Stephen A. Silver. "Glider". The Life Lexicon. Retrieved March 4, 2019.
- ↑ "Census Results in Conway's Game of Life". The Online Life-Like CA Soup Search. Archived from the original on 2009-09-10. Retrieved July 12, 2009.
- ↑ "Spontaneous appeared Spaceships out of Random Dust". Achim Flammenkamp (1995-12-09). Retrieved July 10, 2012.
- ↑ Elwyn R. Berlekamp, John H. Conway, and Richard K. Guy, Winning Ways for your Mathematical Plays. Academic Press, 1982
- ↑ "Universal Constructor Based Spaceship". Conwaylife.com. Retrieved 2012-06-24.
- ↑ "Gemini – LifeWiki". Conwaylife.com. Retrieved 2012-06-24.
- ↑ Aron, Jacob (16 June 2010). "First replicating creature spawned in life simulator" [1]. New Scientist. Retrieved 12 October 2013.
- ↑ "Gemini – LifeWiki" [2].Conwaylife.com. Retrieved 2013-10-16.
- ↑ "Demonoid". LifeWiki. Retrieved 18 June 2016.
- ↑ "Geminoid Challenge". Conwaylife.com. Retrieved 2015-06-25.
- ↑ Passe-Science (2019-05-29), Automate Cellulaire - Passe-science #27, retrieved 2019-06-25
- ↑ apgoucher (2018-11-12). "Fully self-directed replication". Complex Projective 4-Space (in English). Retrieved 2019-06-25.
- ↑ "0E0P metacell - LifeWiki". www.conwaylife.com. Retrieved 2019-06-24.
- ↑ Andrzej Okrasinski. "Game of Life Object Statistics". Archived from the original on 2009-07-27. Retrieved July 12, 2009.
- ↑ Nathaniel Johnston. "The Online Life-Like CA Soup Search". Archived from the original on 2009-09-10. Retrieved July 12, 2009.
- ↑ Alan Hensel. "About my Conway's Game of Life Applet". Retrieved July 12, 2009.
- ↑ Nehaniv, Chrystopher L. (15–18 July 2002). Self-Reproduction in Asynchronous Cellular Automata. 2002 NASA/DoD Conference on Evolvable Hardware. Alexandria, Virginia, USA: IEEE Computer Society Press. pp. 201–209. doi:10.1109/EH.2002.1029886. ISBN 0-7695-1718-8.
- ↑ "Conway's Game of Life".
- ↑ Burraston, Dave; Edmonds, Ernest; Livingstone, Dan; Miranda, Eduardo Reck (2004). "CellularAutomata in MIDI based Computer usic" [3]. Proceedings of the 2004 International Computer Music Conference.CiteSeerX 10.1.1.6.3882 httpps://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.6.3882].hdl:10453/1425 [4].
- ↑ "glitchDS – Cellular Automaton Sequencer For The Nintendo DS" [5].Synthtopia.com. 2008-05-29. Retrieved 2012-06-24.
- ↑ "Game Of Life Music Sequencer" [6]. Synthtopia.com. 2009-04-29. Retrieved 2012-06-24.
- ↑ "Game Of Life Music Sequencer For iOS, Runxt Life" [7]. Synthtopia.com. 2011-01-12. Retrieved 2012-06-24.
编者推荐
人工生命入门路径
该文章整理自Lana Sinapayen为人工智能研究者们提供的一份人工生命入门指南,主要介绍了人工生命的研究目标、简史以及与人工智能之间的关系。
生命游戏
该网站是一个在线的生命游戏网站,可实际体验生命游戏过程。
相关课程
用“生命游戏”认识Patch
该课程利用NetLogo搭建出“生命游戏”这个虚拟宇宙。并在该过程中了解NetLogo中的Patch(即方格)对象,以及if,ifelse,随机数发生器random-float等最基本的语法。
课程视频:探索元胞自动机
该课程可以帮助初学者将更加深入地探索元胞自动机的其它方面,并进行有趣的现实创造,比如元胞自动机创造的音乐。
课程视频:认识元胞自动机
该课程带领初学者将进入到元胞自动机的学习中,并运用Netlogo完成计算机模拟。
集智相关文章
算法描绘的“人造生命”,运动流畅自然,如同显微镜下的实景
本中文词条由11795用户参与编译,Ilseyao1980审校,薄荷编辑,欢迎在讨论页面留言。
本词条内容源自wikipedia及公开资料,遵守 CC3.0协议。