“博弈论”的版本间的差异

来自集智百科 - 复杂系统|人工智能|复杂科学|复杂网络|自组织
跳到导航 跳到搜索
第214行： 第214行：
 
</math>起作用，就像两个个体在玩一个普通的游戏一样。C的均衡收益是一个基本函数。虽然有不同的例子有助于在共同游戏中确定收益数额，但并不是所有的博弈在其功能形式可以进行这样的推导。
 
</math>起作用，就像两个个体在玩一个普通的游戏一样。C的均衡收益是一个基本函数。虽然有不同的例子有助于在共同游戏中确定收益数额，但并不是所有的博弈在其功能形式可以进行这样的推导。
 
从形式上看，一个特征函数是''(N,v)''，其中''N''表示一组人员（也可视为一组集合），<math>v:2^N \to \mathbf{R}</math>则是一个常用的应用推导。
 
从形式上看，一个特征函数是''(N,v)''，其中''N''表示一组人员（也可视为一组集合），<math>v:2^N \to \mathbf{R}</math>则是一个常用的应用推导。
−
这些特征函数已经扩展到描述没有可移动工具的游戏。（比如围棋）
+
这些特征函数已经扩展到描述没有可移动工具的游戏（比如围棋）。
  
 
===替代形式===
 
===替代形式===

2020年4月19日 (日) 23:23的版本


博弈论：研究具有斗争或竞争性质现象的理论和方法

博弈论 Game Theory（ 亦称对策论或赛局理论） 是研究理性决策者之间战略互动的数学模型 Mathematical models ，[1]是研究具有斗争或竞争性质现象的理论和方法。博弈论既是现代数学的一个新分支，也是运筹学的一个重要学科，在社会科学 Social science 、逻辑学 Logic、系统科学 Systems science和计算机科学 Computer science 中也有应用。 博弈论最初产生于零和游戏 Zero-sum game（也称零和博弈），在这种游戏中，赢家的利润来自于输家的亏损，每个参与者的收益或损失由其他参与者的损失或收益来平衡，各方损益总和永远为“零”。 今天，博弈论适用于广泛的行为关系，已成为人类、动物和计算机逻辑决策科学的总称。


现代博弈理论始于双人零和游戏 Zero-sum games 中的混合策略 mixed strategy 均衡思想以及约翰·冯·诺依曼 John von Neumann 对该思想的论证。John von Neumann使用连续映射到紧凸集 Convex set 的布劳威尔不动点定理 Brouwer fixed-point theorem ，建立了博弈论和数学经济学 Mathemastical economics 的标准方法。 他的论文发表之后，又于1944年与奥斯卡·摩根斯腾 Oskar Morgenstern 合著了《博弈论与经济行为 Theory of Games and Economic Behavior》 一书，该书考虑了多人博弈。 这本书的第二版提供了一个公理系统的预期效用，它允许数学统计学家和经济学家处理在不确定情况下的决策。


20世纪50年代，众多学者将博弈论发扬光大；到了70年代，博弈论在生物学 Biology 中崭露头角 ，类似的发展历程至少可以追溯到30年代。 博弈论作为一种重要的工具在许多领域得到了广泛的认同。1999年， 约翰·梅纳德·史密斯 John Maynard Smith 因将博弈论应用于生物学而被授予克雷福德生物科学奖 Crafoord Prize 。在他一生的学术研究中，其最突出的贡献在于将博弈论的分析方法引入到生物演化过程中的竞争行为和选择问题，并对群体行为变化的动力学机制进行相关分析。 2014年，诺贝尔经济学奖 Nobel Memorial Prize in Economic Sciences 授予博弈论学家让·梯若尔 Jean Tirole 。其后又有11位博弈论学家获得了诺贝尔经济学奖。

历史背景

John von Neumann
John nash

早在现代数学博弈论兴起之前，关于二人博弈的讨论就开始了。 已知的对于博弈论的第一次讨论，源于一封1973年被认为是活跃的雅各宾派成员查尔斯•瓦德格拉夫 Charles Waldegrave 写的信。他是英国外交官詹姆斯•瓦德格拉夫 James Waldegrave 的叔叔。[2] 鉴于现有的细节和证据有限且对原作者的介绍较为模糊，原作者的真实身份尚难确认。


有一种理论认为 James Waldegrave 才是真正的作者，但这还有待证实。[3]在这封信中， James Waldegrave 为法国的一种纸牌游戏 le Her提供了一个极小极大的混合策略解决方案，这个方案现在被称为瓦德格拉夫问题 Waldegrave problem 。1838年，安东尼·奥古斯汀·库尔诺 Antoine Augustin Cournot 在《财富理论的数学原理 Principes de la Théorie des Richesses 》 一书中考虑了双寡头垄断，并提出了一个解决方案，即博弈论中的纳什平衡 Nash equilibrium 。


1913年，恩斯特·泽梅罗 Ernst Zermelo 发表了《关于集合论在国际象棋博弈理论中的应用 On a Application of Set Theory to the Theory of the Game of the Chess》 ，证明了最优的国际象棋策略是严格确定的。这为定理的一般化铺平了道路。[4]


1938年，丹麦数学经济学家弗雷德里克·祖恩 Frederik Zeuthen 利用布劳威尔不动点定理 Brouwer's fixed point theorem ，[5]证明了数学模型具有获胜策略。在波莱尔 Emile Borel 1938年的著作《哈萨德的应用 Applications aux Jeux de Hasard》 和更早的笔记中，Borel 证明了当收益矩阵是对称时， 二人零和矩阵对策的极大极小定理，并提供了一个非平凡无限对策的解（在英语中称为Blotto博弈）。Borel推测有限二人零和博弈中不存在混合策略均衡，这一猜想被约翰·冯·诺依曼 John von Neumann 证明是错误的。


直到1928年约翰·冯·诺依曼 John von Neumann 发表了关于战略博弈论的论文，博弈论才真正成为一个独立的研究领域。[6][7] 约翰·冯·诺依曼 John von Neumann的原始证明采用了布劳威尔关于连续映射到紧凸集的布劳威尔不动点定理 Brouwer fixed-point theorem。该种方法成为研究博弈论和数理经济学的标准方法。随后，他在1944年与奥斯卡•摩根斯坦 Oskar Morgenstern 合著了《博弈论与经济行为 Theory of Games and Economic Behavior》 一书。[8] 这本书的第二版提供了一个不言自明的效用理论，它将丹尼尔·伯努利 Daniel Bernoulli 的旧的效用理论（与金钱相关）转变为一个独立的学科。约翰·冯·诺依曼 John von Neumann在博弈论方面的工作突出反映在这本1944年出版的书中。这项基础工作包含了为二人零和博弈找到相互一致解的方法。 随后的工作主要集中在合作博弈 cooperative game 理论上：假设群体中的每个个体能够执行他们之间关于适当策略的协议，这个理论将分析个体的最佳策略。[9]


1950年，关于囚徒困境 prisoner's dilemma 的第一次数学讨论出现了。作为兰德公司 RAND Corporation研究博弈论的一部分，著名数学家梅里尔M.弗拉德 Merrill M. Flood 和梅尔文德雷舍尔 Melvin Dresher 进行了一项实验。兰德之所以进行这些研究，是因为它们可能应用于全球核战略。

由John Forbes Nash故事翻拍而来的电影《美丽心灵》

大约在同一时间，小约翰·福布斯·纳什 John Forbes Nash 提出了一种球员策略相互一致性的标准，称为纳什均衡，适用于比约翰·冯·诺依曼 John von Neumann 和 Morgenstern提出的标准更广泛的博弈。[10] John Forbes Nash 是美国数学家，前马萨诸塞理工学院摩尔荣誉讲师，主要研究博弈论、微分几何学和偏微分方程。晚年成为普林斯顿大学的资深研究数学家。1950年， John Forbes Nash 获得美国普林斯顿大学的博士学位，他在仅仅28页的博士论文中提出了一个重要概念，这成为博弈论中一项重要突破。这个概念就是前文提到的“纳什均衡”。它被广泛运用在经济学、计算机科学、演化生物学、人工智能、会计学、政策和军事理论等方面。John Forbes Nash 最突出的数学成就是在微分几何和偏微分方程领域，特别是将黎曼流形等距嵌入到欧氏空间的一系列结果巩固了Nash在数学界的重要地位。因为在非线性偏微分方程上的贡献，他与路易·尼伦伯格 Louis nierenberg 共同获得了2015年阿贝尔奖 Abel Prize。著名几何学家米哈伊尔·格罗默夫 Mikhail Gromov 这样评价 John Forbes Nash 的工作：“他有巨大的数学分析能力和几何洞察力……他的几何工作，不论是他的结果、技术、使用的想法，都与任何人原先预期的相反……他在几何学所做的，从我看来，比起他在经济学所做的无可比拟地伟大得多,相差很多个数量级。”在1959年之后，由于出现精神上的症状，他的研究生涯曾经中断，在1959年及1961年两度进入医院疗养，被诊断为思觉失调症。John Forbes Nash 拒绝接受精神药物治疗。在1970年后，症状逐渐好转，因此再度回到学术研究工作。他这段时间的经历，由西尔维娅·娜萨 Sylvia Nasar 写成传记，并翻拍为电影《美丽心灵》，使得他的事迹广为人知。 John Forbes Nash 证明了纳什均衡在n人有限博弈中的普遍存在性，从而开创了与约翰·冯·诺依曼 John von Neumann和Morgenstern 框架路线均完全不同的“非合作博弈 Non-cooperative Game”理论。由此推出非合作博弈都存在一个混合策略的纳什均衡点。


博弈论在20世纪50年代经历了一场运动，广义形式游戏 The extensive form game、虚拟行动 Fictitious play 、重复博弈 Repeated games 、Shapley值 Shapley value等核心概念在此期间得到发展。

20世纪50年代，博弈论首次应用于哲学和政治学。

1979年，罗伯特•阿克塞尔罗德 Robert Axelrod 试图以玩家身份设置电脑程序，结果在他们之间的锦标赛中，他发现获胜者往往是一个简单的“以牙还牙”程序，在第一步中进行合作，然后在接下来的步骤中，按照对手在上一步中的动作进行自己下一步的动作。这一事实被广泛用来解释进化生物学和社会科学中的合作现象。[11]


相关成果

1965年，泽尔腾 Reinhard Selten 引入了子博弈完美均衡 Subgame perfect equilibria 的解决方案，进一步完善了纳什平衡。 后来，他还介绍了颤抖手完美均衡 Trembling hand perfection 。 1994年，John Nash 和其他两位博弈论学家约翰·C·海萨尼 John C. Harsany 和莱因哈德·泽尔腾 Reinhard Selten 由于对经济博弈论的贡献共同获得了诺贝尔经济学奖。其中，John nash 21岁时关于“纳什均衡”的博士毕业论文为他获得诺贝尔学奖奠定了基础；Harsanyi 因为他对不完全信息博弈（即所谓的贝叶斯博弈）进行了高度创新的分析而为人们所熟知。他还为博弈论和经济推理在政治和道德哲学（特别是功利主义道德）中的使用以及为均衡选择的研究做出了重要贡献；Reinhard Selten因在“非合作博弈理论中开创性的均衡分析”方面的杰出贡献而荣获诺贝尔经济学奖。


20世纪70年代，博弈论在生物学中得到了广泛的应用。这在很大程度上归功于约翰·梅纳德·史密斯 John Maynard Smith 在进化稳定策略方面的工作。此外，他还介绍并分析了相关均衡 Correlated equilibrium 、颤抖手完美 Trembling hand perfection 、和共同知识 Common konwledge 的概念。


2005年，博弈论学家托马斯·谢林 Thomas Schelling 和罗伯特·奥曼 Robert Aumann 紧随 John Forbes Nash 、塞尔滕 Selten 和哈萨尼 Harsanyi 之后，获得了诺贝尔奖。Schelling 研究的是动态模型，即演化博弈理论 Evolutionary game theory的早期例子。Aumann对均衡学派的贡献更大，他引入了均衡粗化和相关均衡，并对共同知识的假设及其结果进行了广义形式上的分析。


2007年，莱昂尼德•赫维奇 Leonid Hurwicz 、埃里克•马斯金 Eric Maskin 和罗杰•迈尔森 Roger Myerson 由于为机制设计理论奠定了基础而被授予诺贝尔经济学奖。其中，Myerson的贡献包括提出适度均衡的概念以及一篇重要的毕业论文《博弈论，冲突分析》； Hurwicz介绍并正式提出了激励相容 Incentive compatibility 的概念。


2012年，阿尔文• E •罗斯 Alvin E. Roth 和劳埃德•沙普利 Lloyd S. Shapley 因“稳定配置理论和市场设计实践”而获得诺贝尔经济学奖。 2014年，让•梯若尔Jean Tirole 因其在市场力量和监管的分析取得重大发现而荣获诺贝尔经济学奖 。

博弈类型

合作/非合作

如果玩家能够形成具有约束力的外部强制承诺（如通过合同法 contract law ），那么游戏就是合作性的。如果玩家不能结成联盟，或者所有协议都需要自我实施 self-enforcing （如通过可置信威胁 Credible threats ），那么游戏就是非合作的。[12]


合作博弈通常是通过合作博弈理论的框架来分析的。该理论侧重于预测哪些联盟将会形成，群体采取的联合行动以及由此产生的集体收益。它与传统的非合作博弈论不同。（传统的非合作博弈论侧重于预测个体的行为和结果，以及分析纳什平衡）。[13][14]合作博弈论提供了一种高层次的方法，因为它只描述联盟的结构、战略和收益，而非合作博弈论还研究议价过程影响联盟内收益分配的因素。由于非合作博弈论具有更广泛的适用性，合作博弈可以通过非合作博弈论(逆向不成立)的方法进行分析。前提是作出充分的假设，以涵盖由于合作外部实施的可能性而可能存在的所有策略。 因此，尽管在一个非合作框架下表达所有博弈是最佳做法，但在许多情况下，会由于没有足够的信息准确地模拟战略谈判的过程，或由此产生的模型过于复杂，而无法为运用在现实世界中提供较为实用的工具。 在这种情况下，合作博弈理论提供了一种简化的方法，该方法允许对整个游戏进行分析，而不必对议价能力做出任何假设。

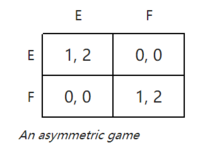
对称/非对称博弈

非对称博弈

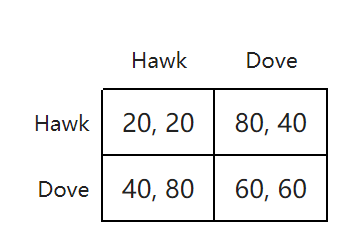
对称博弈是指博弈的收益只依赖于选手所选择的策略而不依赖于进行博弈的选手的一种博弈。也就是说，如果玩家的身份可以改变而策略的收益不能改变，那么游戏就是对称的。许多常用的2×2对策是对称的。例如：斗鸡博弈 Chicken game 、囚徒困境 Prisoner's dilemma 和猎鹿博弈 Stag hunt 都是对称博弈。一些学者们也会考虑某些非对称博弈的例子。不过，最常见的还是对称博弈。


非对称博弈是研究最多的是两个博弈者的策略不相同的博弈。 例如，最后通牒游戏 Ultimatum game和类似的独裁者游戏 Dictator game 对每个玩家都有不同的策略。 然而，对于一个游戏，两个玩家的策略可能是相同的，但是不对称。 例如，上图所示的游戏尽管两名玩家的策略设置相同，但是收益是不对称的。

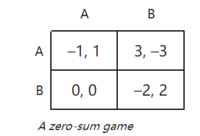
零和/非零和博弈

零和博弈

零和博弈是一种特殊的常和博弈。在这种博弈下，博弈者的选择既不能增加也不能减少可用资源。在零和游戏中，对于每一种策略组合，游戏中所有玩家的总收益总是为零（更通俗地说，玩家只会以牺牲他人利益为代价获得收益）。[15]扑克游戏是零和游戏的典型(忽略了庄家分牌的可能性)，因为一个人赢得的金额恰好与对手输掉的金额相等。其他的零和游戏包括匹配硬币 Matching pennies 和大多数包括围棋和国际象棋在内的经典棋盘游戏，


博弈论学者研究的许多博弈（包括著名的囚徒困境 Prisoner's dilemma ）都是非零和博弈，因为结果的净结果要么大于零，要么小于零。不太正式的说法为：在非零和游戏中，一方的收益不一定对应另一方的损失。


常和博弈对应的是盗窃和赌博等活动，而不是从贸易中获得潜在利益的基本经济形势。 通过添加一个虚拟玩家来补偿玩家的净赢利，可以将任何博弈转化为（可能是不对称的）零和博弈。

同时/序贯博弈

同时行动：石头剪刀布游戏

同时博弈 Simultaneous games （或静态博弈）是指两个玩家同时行动的游戏，或者如果他们不同时行动，后面的玩家并不知道前面的玩家的行动（使得他们实际上同时行动）。同时游戏用正规形式表示，并用纳什均衡的概念求解。最简单的例子就是石头剪刀布.


序贯博弈 Sequential games （或动态游戏）是后期玩家对早期动作有一定了解的游戏。这不需要早期玩家每一个动作的完全信息 Perfect information ;它可能是非常少的知识。例如，一个玩家可能知道前面的玩家没有执行某个特定的动作，但他/她不知道第一个玩家实际上执行了哪些其他可用的动作。序贯博弈就像一棵大树生根发芽一样从初始点向前推进，最终形成的博弈树就是用来分析均衡策略的工具，从终点结沿着树枝向前逆推，最终的得出最优策略，就是逆推均衡。很知名的例子大概是IBM开发的计算机“深蓝”打败了国际象棋大师的故事。但这方法未必总行得通，因为博弈的前提是假设每个参与人都是理性人，终极价值追求就是个人的最大收益，而现实中人的行为模式可要复杂多变得多。


同时博弈和序贯博弈之间的区别体现在上面讨论的不同表现形式中。通常，标准形式用于表示同时博弈，而扩展形式用于表示序贯博弈。泛化向范式的转换是同一种方式，即多种泛化形式的博弈对应于同一范式。 因此，同时博弈的均衡概念不足以推出序贯博弈。


简而言之，同时博弈和序贯博弈的区别如下:

序贯博弈 同时博弈
表示形式 决策树 支付矩阵 Payoff matrix
对手先前
的行动
 Yes No
时间先后 Yes No
其他
扩展式赛局
Extensive game
策略游戏
Strategic game

完美信息与非完美信息博弈

不完美博弈（虚线为玩家2所不知道的信息 正式的说为信息集合）

完美信息博弈是序贯博弈中特别重要的一种。 如果所有玩家都知道其他玩家之前所做的动作，那么游戏就是一个完美信息。博弈论中研究的大多数博弈都是不完美信息博弈。 完美信息博弈的例子包括井字游戏 Tic-tac-toe 、跳棋 Checkers 、无限象棋 Infinite chess 和围棋 Go 。[16][17][18][19]


许多纸牌游戏是不完美信息博弈，如扑克和桥牌。 [20] 完美信息博弈经常与完全信息博弈相混淆。完全博弈要求每个玩家都知道其他玩家可以使用的策略和收益，但不一定知道所采取的行动。而完美信息博弈指一个参与人对其他参与人（包括自然）的行动选择有准确了解的情况，即每个信息集里只包含一个值。不完美信息博弈可以通过引入自然波动 Moves by nature 的概念来进行简化。

组合博弈

西洋双陆棋 Backgammon：你必须在对方完成之前，把所有的十五个棋子送到你的领地去

组合博弈是由可移动的多样变化决定寻找最优策略的难度的一种博弈。例如国际象棋和围棋。包含不完美信息的游戏也可能有很强的组合特征，例如西洋双陆棋 Backgammon 。虽然没有统一的理论来处理游戏中的组合元素。然而，有些数学工具可以解决特定的问题并回答一般的问题。


完美信息博弈已经在组合博弈论 Combinatorial game theory 中得到研究，发展出新颖的表示法，例如超现实数字 Surreal numbers ，以及利用组合和代数（有时是非构造性的）的证明方法来解决特定类型的博弈，包括可能导致无限长移动序列的“环形”博弈。 [21][22]比起传统意义上的博弈理论，该方法解决的博弈问题具有更高的组合复杂性，一个典型例子就是“十六进制博弈”。博弈复杂性是借鉴计算复杂性理论来估计计算困难程度，从而寻找最佳策略的一个相关研究领域。 [23]


人工智能的研究已经解决了完美和不完美信息博弈。这些博弈具有非常复杂的组合结构(如国际象棋、围棋或西洋双陆棋) ，但尚未找到（可证明的）最优策略。 实际的解决方案包括计算启发式算法，如 阿尔法贝塔剪枝 Alpha–beta pruning 或使用由强化学习训练 Reinforcement learning 的人工神经网络 Artificial neural networks ，这使得博弈在计算实践中更易于处理。[24][25]

无限长博弈

经济学家和现实世界的游戏玩家往往研究有限步数的步数。而纯数学家就不那么受约束了，其中集合论理论家尤其喜欢研究那些无穷多步的博弈，直到所有这些步都完成后才能知道赢家（或收益）。


在无限长博弈中，人们的注意力通常不是集中在玩这种游戏的最佳方式上，而是集中在一个玩家是否有制胜的策略上。(根据选择公理，我们可以证明，有些游戏，即使信息完美，结局只有“赢”或“输”，但双方都没有获胜的策略。)对于设计巧妙的博弈而言，这种策略在描述集理论中有着重要的影响。

离散和连续博弈

许多博弈论都与有限且离散的博弈有关。这些博弈具有有限数量的玩家、步数、事件、结果等。但是，可以扩展许多概念。连续游戏 Continuous games允许玩家从连续策略集中选择策略。例如，古诺竞争 Cournot competition 通常以玩家的策略为任何非负数量（包括小数）来建模。


差分博弈 Differential games 适用于在真实世界中经常遇到环境、状态、行为都处于连续空间的情况。这时一般选择用差分方程来表达连续空间。在此类博弈中，终止时间是具有给定概率分布函数的随机变量。因此，参与者最大化了成本函数的数学期望。结果表明，改进的优化问题可以转化为无穷时间区间上的一个折现差分博弈。


连续追逐和逃避等差分博弈是一类状态变量的演化受差分方程控制的连续博弈。差分博弈中最优策略的求解问题与最优控制理论密切相关。特别地，有两种类型的策略:使用Pontryagin极大值原理 The Pontryagin maximum principle 发现开环策略，而使用Bellman动态规划方法 Bellman's Dynamic Programming 发现闭环策略。

演化博弈理论

与传统博弈理论不同，演化博弈理论并不要求参与人是完全理性，也不要求具备完全信息的条件。它主要研究根据并不那么有远见的规则随时间调整政策的有限理性玩家。一般来说，在这种博弈中，策略随时间的演化会被建模为一个状态变量(如当前策略配置文件或最近的游戏玩法)的马尔科夫链 Markov chain 。这些规则的特征是：可能模仿、优化或适者生存。


在生物学中，这样的模型可以代表(生物)进化，在这种进化中，后代采用父母的策略，而采用更成功策略的父母(即与更高的回报相对应)有更多的后代。在社会科学中，这样的模型通常代表了玩家在一生中多次玩游戏，并偶尔有意或无意地调整策略。

随机博弈（以及与其他领域的关系）

《黑天鹅效应:你身边无处不在的风险与恐惧》作者丹·加德纳：黑天鹅事件（英文："Black swan" incidents)指非常难以预测，且不寻常的事件，通常会引起市场连锁负面反应甚至颠覆。

具有随机博弈的个人决策问题有时被认为是“单人博弈”。 有些作者并不认为这些情况是博弈论讨论的范畴。 它们可以在决策理论、运筹学和人工智能领域的相关学科中使用类似的工具进行建模，尤其是人工智能规划(具有不确定性)和多智能体系统。 虽然这些领域可能有不同的激发因素，但所涉及的数学基本上是相同的，例如使用马尔可夫决策过程 Markov decision processes（MDPs） 。 [26]


随机博弈也能以添加一个随机行动的玩家进行随机移动（“自然移动”）的方式根据博弈理论进行建模。 在双人游戏中，这个玩家通常不被认为是第三人，而只是作为在游戏需要的地方掷骰子的“人”。


对于某些问题，不同的随机博弈建模方法可能导致不同的解决方案。 例如，马尔可夫决策过程MDPs 和最大最小解Minimax solution解决方案之间的区别在于后者考虑的是一系列对抗性动作的最坏情况，而不是在给定一个固定概率分布的情况下对这些动作作一个预判。 在不确定性的随机模型不可用的情况下，最大最小解解决方案可能是有利的，但也可能高估极不可能(但代价高昂)发生事件的可能性，如果假设对手可以强行让这样的事件发生，则会极大地影响了战略。[27] 关于这类模型问题，特别是与预测和限制投资银行业的损失有关的问题，请参阅黑天鹅效应的更多讨论。


一般模型也研究了随机博弈的所有元素、对手、和局部或噪声可观察性(其他参与者的行动)。 “金标准”被认为是部分可观测的随机对策 Partial Observable Stochastic Game（POSG） ，但很多能在 POSG 中表示的现实问题却无法在计算上实现。[27]

元游戏

元游戏的玩法是在目标游戏或主题游戏中，它要求最大化所开发规则集的实用价值。元模型理论是与机构设计理论相联系的。


亚对策分析 metagame analysis 这个术语也用来指奈杰尔 · 霍华德 Nigel Howar 开发的一种实用方法。 在这种分析方法中，将一种情况框定为一种战略游戏，然后在游戏中，利益相关者试图通过他们可作出的选择来实现他们的目标。 后来在逐步发展中使对抗分析 Confrontation analysis 得以提出。

台球博弈论

在经验路径上，台球博弈论 Pooling games 一般是指在一条经验路径上有着不断变化的回报表的重复博弈（都是盛行于各种社会形式的博弈），其均衡策略通常采用进化的社会惯例和经济惯例的形式。 台球博弈理论的出现真正使人认识到在一个游戏中的最优选择和即将到来的收益表更新路径之间的相互作用，识别不变性的存在性和鲁棒性（它是在异常和危险情况下系统生存的关键），并可随着时间的变化做出预测。 该理论基于收益表随时间变化的拓扑变换分类来预测收益表的方差和不变性，同时也在有序系统中可达最优性计算规律的约束范围内。[28]

平均场博弈论

平均场博弈论 Mean field game theory 研究的是在非常大的小型互动主体群体中的战略决策。 这类问题在博伊扬·乔万诺维奇 Boyan Jovanovic 和罗伯特·W·罗森塔尔 Robert W. Rosenthal 、彼得·凯恩斯 Peter E. Caines 的经济学文献中 、数学家皮埃尔-路易·利翁 Pierre-Louis Lions 和 让·米歇尔·拉斯里 Jean-Michel Lasry 的工程文献中所提及。

博弈表示形式

博弈论中研究的博弈是定义良好的数学对象。 为了得到充分的定义，一个游戏必须指定以下元素: 游戏的玩家 player，每个玩家在每个决定点可以获得的信息 information 和行动 action，以及每个结果的收益 payoffs。埃里克·拉斯穆森 Eric Rasmusen 用缩写词“ PAPI”来指这四个“基本要素”。博弈论学者通常使用这些元素，以及他们自己选择的解决方案，为每个参与者推导出一套均衡策略。这样，当这些策略被使用时，没有一个博弈者能够通过单方面偏离策略而获利。 这些均衡策略决定了博弈的均衡状态，在这种状态下，要么出现一个结果，要么出现一系列已知概率的结果。


合作博弈多以特征函数形式出现，而非合作博弈则以广义形式和标准形式出现。

广义形式

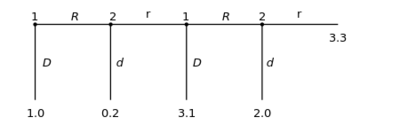
广义形式

广义形式 Extensive form 可用于按时间顺序对游戏进行形式化。利用广义形式表示的博弈为树状（如图所示）。在这里，每个节点代表玩家的一个选择点，每个玩家由节点列出的数字指定，顶点外的线表示该玩家可能采取的行动。收益在树的底部指定。广义形式可以看作是决策树的多层泛化。要解决任何广义形式的博弈，必须使用逆向归纳法。它涉及到向上工作的博弈树，以确定有理性的玩家将在树的最后一个节点处执行的操作、在考虑到最后采取行动的玩家移动合理的情况下确定采取前一行动的玩家会做什么，依此类推，直到玩家到达树的顶点。[29]


图中的博弈由两名玩家组成。这种特定游戏的结构方式（即具有序贯决策和完全信息），玩家1首先通过选择F 或U（公平或不公平）来“移动”。接下来，已经见过玩家1的行动的玩家2，选择A或R 。一旦玩家2做了选择，便认为该游戏已经结束，每个玩家都将获得各自的收益。假设玩家1选择U，然后玩家2 选择A：玩家1然后得到“八”的收益（在现实世界中，可以用多种方式来解释，其中最简单的方法是在金钱方面，但是可能意味着诸如八天的假期或八个国家被侵占，甚至八次机会与其他玩家进行同一场的游戏），而玩家2 获得“二”的收益。


广义形式还可以捕捉到同时博弈和不完美信息博弈。为了表示它，要么用虚线连接不同的顶点以将它们表示为同一信息集合的一部分（即参与者不知道它们在哪一点），要么在它们周围绘制一条闭合线。

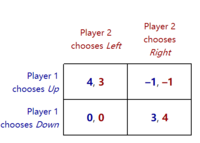
标准形式

二人策略游戏的标准形式或收益矩阵

标准形式（战略形式）表示的博弈通常由矩阵表示，该矩阵显示玩家，策略和收益（请参见右侧的示例）。更一般而言，它可以用任何一个函数来表示，这个函数将每个玩家的回报与每个可能的动作组合联系起来。在随附的示例中，有两个玩家：一个选择行，另一个选择列。每个玩家都有两种策略，分别由行数和列数指定。收益在内部提供。第一个数字是选择行的玩家收到的收益（在我们的示例中为玩家1）；第二个是选择列的玩家收到的收益（在我们的示例中为玩家2）。假设玩家1选择向上和玩家2选择左，则玩家1的回报为“4”，而玩家2的回报为“3”。


假定每个玩家同时行动，或者至少在不了解对方行动的情况下行动，此时会以标准形式呈现博弈；如果玩家对其他玩家的选择有一些了解，此时会以广义形式呈现博弈。 每个扩展形式的博弈都有一个等效的规范博弈，但是，转换为标准形式可能会导致表示形式的大小呈指数级膨胀，从而不能进行计算。

特征函数形式

在具有可移动特点的博弈中，不提供单独的奖励，而是由特征函数决定了每个集合的收益。这就是说，如果该集合为空集，则没有任何报酬。


这种形式的起源可以在约翰·冯·诺依曼 John von Neumann和 Oskar Morgenstern的书中找到;当查看这些实例时，他们猜测当一个集合[math]\displaystyle{ C }[/math]出现时，它将对分数[math]\displaystyle{ \left(\frac{\mathbf{N}}{\mathbf{C}}\right) }[/math]起作用，就像两个个体在玩一个普通的游戏一样。C的均衡收益是一个基本函数。虽然有不同的例子有助于在共同游戏中确定收益数额，但并不是所有的博弈在其功能形式可以进行这样的推导。 从形式上看，一个特征函数是(N,v)，其中N表示一组人员（也可视为一组集合），[math]\displaystyle{ v:2^N \to \mathbf{R} }[/math]则是一个常用的应用推导。 这些特征函数已经扩展到描述没有可移动工具的游戏（比如围棋）。

替代形式

替代形式被用于表示博弈的某些子类或调整一些跨学科研究的需求。除了经典游戏表示法以外，一些替代表示法还应用于编码与时间相关的方面。[30]

应用领域

博弈论作为一种应用数学方法，已被广泛应用于研究人类和动物的各种行为。 它最初是在经济学中发展起来的，旨在理解大量的经济行为（包括企业，市场和消费者的行为）。博弈论分析的首次使用是安托万·奥古斯丁·古诺 Antoine Augustin Cournot 在1838年提出的古诺双寡头 Cournot duopoly的解决方法中。博弈论已经扩展应用到社会科学中，也已应用于政治，社会学和心理行为等领域。


尽管二十世纪以前的博物学家，如查尔斯·达尔文 Charles Darwin 提出了各种博弈论的论述，但是博弈论分析在生物学中的应用始于20世纪30年代罗纳德·费舍尔 Ronald Fisher 对动物行为的研究。这项工作早于“博弈论”正式提出的时间，但该工作运用到了很多关于博弈论的相关特征。后来约翰•梅纳德•史密斯 John Maynard Smith 在他的“ 进化与游戏理论”一书中将博弈论在经济学的发展运用于生物学。[31]


除了用于描述，预测和解释行为外，博弈论还被用于发展道德或规范行为的理论以规范人们的行为。在经济学和哲学中，学者们运用博弈论来帮助理解良好或适当的行为。这种类型的博弈论论证可以追溯到柏拉图 Plato 。博弈论中的化学博弈论 Chemical game theory ，它将玩家的选择比作称为“知识分子”的化学反应分子，将博弈结果计算为化学反应系统的平衡解。


描述和建模

蜈蚣博弈

博弈论的主要用途是描述和建模人类的行为。一些学者认为，通过找到博弈的平衡点，他们就可以预测实际人口在面对与所研究博弈相似的情况时的行为方式。 这种特殊的博弈论观点存在争议。有人认为，在应用于现实情况时，博弈论者所做的假设经常被推翻。游戏理论家通常认为玩家的行为是理性的，但是在实践中，人类的行为却常常偏离这种模式。博弈论者通过将其假设与物理假设相比较来进行预测。因此，尽管他们的假设并不总是成立，但他们可以将博弈论视为一种合理的科学理想，类似于物理学家所使用的模型。[32]


然而，经验工作表明，在一些经典游戏中，例如蜈蚣博弈 Centipede game ，“猜均值的2/3”游戏 Guess 2/3 of the average game 和独裁者游戏 Dictator game ，人们通常不会完全按照纳什均衡的模式进行游戏。目前正在对这些实验的重要性以及对实验的分析是否能充分反映出相关情况的各个方面进行相关讨论。


在约翰·梅纳德·史密斯 John Maynard Smith 和乔治·R·普莱斯 George R. Price 的工作之后，一些博弈论者转向演化博弈理论以解决这些问题。这些模型假定参与者没有理性或有限理性。尽管称为演化博弈理论，但演化博弈理论并不一定假定生物学意义上的自然选择。演化博弈理论既包括生物进化也包括文化进化，还包括个体学习的模型（例如，虚拟游戏 Fictitious play）。

规范性与规范性分析

囚徒困境

有些学者认为博弈论并不是预测人类行为的工具，而是对人们应该如何行为的一种建议。因为与博弈中的纳什均衡 Nash equilibrium 相对应的策略构成了一个人对其他参与者行为的最佳反应——假设他们处于(相同的)纳什均衡中，那么选择作为纳什均衡相对应的策略作为一定依据似乎是合适的。这种对博弈论的规范性运用也存在着争议。

经济与商业

博弈论是数理经济学 Mathematical economics 和商学中对相互作用的主体的竞争行为进行建模的主要方法。应用包括一系列广泛的经济现象和方法：如拍卖 Auctions, 议价 Bargaining , 收购定价 Mergers & acquisitions pricing ，公平划分 Fair division ,双寡头垄断 Duopolies ,寡头垄断 Oligopolies ,社会网络 Social network formation , 基于主体的计算经济学 Agent-based computational economics ,一般均衡 General equilibrium ,机制设计 Mechanism design 和投票系统Voting systems 。博弈论在实验经济学 Experimental economics ,行为经济学 Behavioral economics ,信息经济学 Information economics,工业组织 Industrial organization 以及政治经济 Political economy 等领域也有着广泛应用。


这种研究通常集中在被称为“解概念”或“均衡”的特定策略集上。一个常见的假设是参与者的行为是理性的。在非合作博弈中，最著名的就是纳什均衡。在一个博弈过程中，无论对方的策略选择如何，当事人一方都会选择某个确定的策略，则该策略被称作支配性策略。如果两个博弈的当事人的策略组合分别构成各自的支配性策略，那么这个策略组合就被定义为纳什均衡。如果所有的参与者都按照纳什均衡进行决策，他们就不会有单方面的偏离动机，因为他们的策略保证他们获得最佳收益。


一篇关于经济学中的博弈论的原型论文首先展示了一个抽象的特定经济形势下的博弈。选择一个或多个解概念，并证明所提出的对策集是适当类型的均衡。人们自然会想，这些信息应该有什么用呢?经济学家和商业教授提出了两种主要用途(如上所述):描述性和规范性。

项目管理

明智的决策对于项目的成功至关重要。在项目管理中，博弈论用于对参与者（例如投资者，项目经理，承包商，分包商，政府和客户）的决策过程进行建模。这些参与者经常需要相互竞争来获取利益，有时他们的利益会直接损害其他参与者的利益，这使得项目管理方案非常适合用博弈论进行建模。[33]

皮拉韦南 Piraveenan （2019）在他的综述中提供了几个用博弈论建模项目管理场景的例子。 例如，一个投资者通常有几个投资选择，每个选择对应着不同的项目，因此，在制定项目章程之前必须进行选择。类似地，任何涉及分包商的大型项目，例如建筑项目，在主承包商（项目经理）和分包商之间，或者在分包商之间，都有复杂的相互影响，通常具有多个决策点。例如，如果承包商和分包商之间的合同含糊不清，则每个人都必须决定在不损害整个项目的情况下如何艰难地推进自己的计划，并可能会因此损害自己的利益。同样，当启动来自竞争组织的项目时，营销人员必须决定何时营销最终产品或服务，以及采用哪种最佳策略，目的是以便在竞争中获得最大的吸引力。在每种情况下，所需的决策都取决于其他参与者的决策，这些参与者在某种程度上都拥有与决策者的利益竞争的利益，因此可以理想地使用博弈论进行建模。


Piraveenan总结说[34]，二人博弈主要用于对项目管理场景进行建模，根据这些玩家的身份，在项目管理中使用了五种不同类型的博弈。

  1. 政府部门-私营部门的博弈（模拟公私合营的博弈）
  2. 承包商-承包商博弈
  3. 承包商-分包商博弈
  4. 分包商-分包商博弈
  5. 涉及其他玩家的博弈

就游戏的类型而言，合作和非合作游戏，标准形式和广义形式的游戏以及零和以及非零和博弈都可以用来对各种项目管理方案进行建模。

政治学

博弈论在政治学中的应用集中在公平分配 Fair division,政治经济学 Political economy , 公共选择 Public choice , 战争谈判 War bargaining , 积极政治理论 Positive political theory 和社会选择理论 Social choice theory 等交叉领域。在上述每个领域，研究人员都开发了博弈论模型，其中的参与者通常是选民，州，特殊利益集团和政客。


安东尼.唐斯 Anthony Downs 将博弈论应用于组织科学。在他的《民主的经济理论》 An Economic Theory of Democracy 一书中，他将霍特林的公司选址模型应用到政治上。在唐斯模型中，以投票选举为例，若收益大于成本，那就收集信息、投票，反之就不投票。唐斯首先展示了如果选民充分了解某位候选人的信息，（对于投票人而言，投谁的票主要依据自己所掌握的有关候选人的信息，至于是否收集信息、投票，那就取决于预期从这些活动中能获取的收益与付出的代价。），选民就更偏好于选择该候选人；但当选民数量和候选人数量增加时，可能出现收益很低而投票成本很高的情况，此时理性的选民就会选择不去投任何候选人的票。博弈论在1962年在约翰·肯尼迪 John F. Kennedy 总统任期内应用于古巴导弹危机 Cuban missile crisis 。[35]


也有人提出，博弈论可以解释任何形式的政治政府的稳定性。以最简单的君主制为例，就拿君主政体最简单的例子来说，国王只有一个人，他不能也不可能通过亲自对所有甚至任何数量的臣民进行实际控制来维持他的权威。相反，而主权控制则是通过让每个公民都认识到，所有公民都希望彼此将国王(或其他已建立的政府)视为服从其命令的人。为了取代国王而进行的公民之间的商量交流实际上是被禁止的，而因为策划阴谋以夺取君主的王位的行为通常会被视为犯罪而受到惩罚。因此，在一个可以通过囚徒困境变体建模的过程中，我们得出该结论：在稳定时期，即使所有公民都知道如果所有人都集体行动会更好，也不会有公民去取代主权（国王/已建立的政府）。[36]


对于民主制，博弈论的解释是：民主国家会向其他国家传递关于其意图清晰且可信任的信息。相反，对于非民主国家来说，我们很难知道非民主领导人的意图，也不知道如果让步将会有什么后果以及是否能够兑现诺言。因此，如果争端中至少有一个当事方是非民主国家，就会有不信任和不愿意让步。


另一方面，博弈论预测，即使两国领导人意识到战争的代价，它们仍然可能会发动战争。战争可能源于信息不对称；两国可能错误估计他们所拥有的军事资源的数量，从而使它们无法在不诉诸战斗的情况下达成和解。而且，战争可能是由于承诺问题而引起的：如果两个国家希望通过和平手段解决争端，但每个国家都希望对方满足自己之前所提出的条件，那么他们别无选择，只能诉诸战争。最后，因为不可调和的争端也可能导致战争。[37]


当有新的政策或法律要在国家实行时，博弈论也可以帮助预测政策/法律实行后的情况。一个例子就是彼得·约翰·伍德 Peter John Wood（2013）的研究，当时他研究了国家可以采取哪些措施来减少气候变化，提出可以通过与其他国家达成减少温室气体排放的条约来实现。但是，他总结说，这个想法行不通，因为这将给各国带来类似像囚徒困境的困扰。[38]

生物学

与经济学中的博弈不同，生物学中博弈的收益与适应性相对应。 此外，人们对与理性概念相对应的均衡的关注较少，而更多地关注由进化力量维持的均衡。 生物学中最著名的平衡称为 ESS 平衡 Evolutional stable strategy ，于1973年(Smith & Price 1973)首次引入。 虽然它最初并没有与纳什均衡相联系，但每一个 ESS 都是一个纳什均衡点。


在生物学中，博弈论被用作一种模型来理解许多不同的现象。它首先被用来解释约1:1的性别比例的稳定性。费希尔 Fisher(1930）认为1:1的性别比是进化力量作用于个体的结果，因为这保证了他们的后代数量的最大化。


鹰鸽博弈

此外，生物学家已经使用演化博弈理论和ESS来解释动物交流的出现。对信号游戏和其他交流游戏的分析也为动物间交流的进化提供了思路。例如，许多物种的群居行为 The mobbing behavior ，即大量的被捕食动物攻击更大的捕食者的现象似乎是自发涌现组织的一个例子。蚂蚁也表现出类似的前馈行为(参见保罗•奥默罗德 Paul Ormerod的蝴蝶经济学)。生物学家利用斗鸡博弈来分析争斗行为和领地意识。


梅纳德•史密斯 Maynard Smith 在《进化论与博弈论 Evolution and the Theory of Games》一书的序言中表示，“矛盾的是，事实证明，博弈论更容易应用于生物学，而不是它最初所涉及的经济行为领域”。 演化博弈理论已经被用来解释自然界中许多看起来不协调的现象。


其中一种现象被称为生物利他主义。 在这种情况下，一种生物体的行为方式似乎有利于其他生物体，但有害于自己。 这不同于传统的利他主义观念，因为这种行为是无意识的，似乎是为提高整体适应性而产生的一种进化。 这样的例子可以在以下物种中找到: 吸血蝙蝠将它们从夜间狩猎中获得的血液回流给未进食的群体成员; 工蜂照顾蜂王一辈子，从不交配; 黑长尾猴警告猴群有捕食者靠近，即使这样做会危及到个体生存。 所有这些行动都增加了一个群体的整体适应性，但是个体却付出了代价。[39]


演化博弈理论用亲缘选择的观点来解释这种利他主义。 利他主义者区别对待他们所帮助的人和亲戚。 汉密尔顿定律 Hamilton's rule 用方程式[math]\displaystyle{ {c \lt b \times r} }[/math],解释了这种选择背后的进化原理，即利他主义者的成本 c 必须小于利他主义者的收益 b 乘以关联系数 r。 两种有机体的亲缘关系越密切，利他主义的发生率就越高，因为它们有许多相同的等位基因。 这意味着利他的个体，通过确保其近亲的等位基因能够通过其后代的存活而进行传递时，就会放弃拥有后代的选择。例如，帮助兄弟姐妹(在二倍体动物中)的概率为1 / 2，因为(平均而言)每个个体在其兄弟姐妹的后代中分享1 / 2的等位基因。在确保兄弟姐妹的后代很大概率能够存活并且繁衍后，就排除了利他主义个体繁衍后代的必要性。 该系数值很大程度上取决于竞争环境的范围：例如，如果选择的对象包括了所有的遗传生物，那么我们就假设所有生物之间的差异只占了生态环境多样性的1%，那么对于更小的生存空间，关联系数就会由0.5变成了0.995。同样地，如果认为非遗传性质的信息(如表观遗传学、宗教、科学等)会随着时间的推移而持续存在，那么竞争环境就会变得更大，差异也会更小。

计算机科学与逻辑

博弈论在逻辑学和计算机科学中发挥着越来越重要的作用，有几种逻辑理论是建立在游戏语义学基础上的。此外，计算机科学家已经使用游戏来模拟交互计算。博弈论也为多智能体系统的研究提供了理论基础。[40]


另外，博弈论在线算法中也扮演了重要角色，尤其是 k -服务器问题，这在过去被称为具有移动成本和请求回答游戏的博弈。 姚期智所提出的的原理是一种博弈论技术，用于证明随机算法，尤其是在线算法的计算复杂度的下界。


互联网的出现推动了在游戏、市场、计算机拍卖、点对点系统、安全和信息市场中寻找均衡的算法的发展。算法博弈论和算法机制设计将复杂系统的计算算法设计和分析与经济理论相结合。

哲学

博弈论在哲学中有几种用途。看完W.V.O.奎恩(1960、1967)的两篇论文后，刘易斯(1969)运用博弈论发展了一种对惯例的哲学解释。在此过程中，他首次对共同知识进行了分析，并将其用于协调博弈中的博弈分析。此外，他首先提出信号博弈的概念。之后，许多哲学家都在研究这信号博弈。继 Lewis(1969)对共同知识的博弈论进行解释之后，艾德娜 Edna Ullmann-Margalit(1977)和比基耶里 Bicchieri(2006)提出了社会规范理论，将其定义为将混合动机博弈转化为协调博弈的纳什均衡。[41][42]


博弈论也要求哲学家们从交互认识论的角度思考:集体拥有共同的信念或知识意味着什么，以及这些知识对主体之间相互作用所产生的社会结果有什么影响。在这一领域工作过的哲学家包括Bicchieri(1989,1993)、布莱恩·斯吉尔姆斯 Brian Skyrms(1990)、以及斯托纳克 Stalnaker(1999)。在伦理学上，有些人试图追寻托马斯·霍布斯 Thomas Hobbes 从自身利益出发推导道德的理论。既然像囚徒困境这样的游戏在道德和私利之间存在明显的冲突，那么解释为什么为了私利需要合作就是这个项目的一个重要组成部分。这一总体战略是政治哲学中一般社会契约观的组成部分(例如，参见戴维·哥梯尔 David Gauthier(1986)和卡夫卡 Kavka(1986))。其他作者试图用演化博弈理论来解释人类对道德的态度和相应的动物行为的出现。他们考察了包括囚徒困境 The prisoner's dilemma 、猎鹿博弈 Stag hunt , 和纳什讨价还价理论 The Nash bargaining game 在内的几种博弈，为人们对道德的看法进行分析解释(参见，如Brian Skyrms(1996, 2004)的《清醒与威尔逊》(1999))。

零售与消费品定价

黑色星期五：美国最受欢迎的购物假期

博弈论在零售和消费市场的定价策略中大量被应用，尤其是在无弹性商品 Inelastic goods 的销售中。随着零售商不断争夺消费者市场份额，为了增加实体店的客流量（电子商务零售商的网站访问量）或增加辅助或赠送产品的销售量，零售商间歇性地对某些商品打折已经成为一种常态，黑色星期五 Black Friday ,是美国最受欢迎的购物假期，许多零售商都在寻找最佳定价策略以占领购物市场。在黑色星期五时，零售商会运用博弈论来预测“主要竞争对手对自己的影响是什么？” [43] 在这种情况下，游戏有两个参与者：零售商和消费者。零售商专注于最优定价策略，而消费者则专注于最佳交易；在这种封闭式系统中，通常没有主导策略，因为双方都有替代选择权，即零售商可以找到不同的顾客，而消费者可以在不同的商店购物。

但是，考虑到当今的市场竞争，零售商的主要策略是超越竞争对手。开放系统假定有多个零售商出售相似的商品，并且有有限数量的消费者以最优价格购买商品。一位康奈尔大学 Cornell University 教授的博客提供了这样一个策略的例子:亚马逊 Amazon 将三星电视 Samsung TV 的定价定在比零售价低100美元的水平，实际上是在打压竞争对手。亚马逊通过提高HDMI电缆的价格弥补了部分差异，因为人们发现，在购买二手商品时，标价之间的差异并不是很大。


在涉及到消费品定价时，零售市场继续发展博弈论的策略和应用。在分析受控环境中的仿真与现实世界中的零售经验之间时，我们发现，这种策略的应用更加复杂，因为每个零售商都必须在定价，供应商关系，品牌形象以及蚕食利润更高的产品销售潜力之间找到最佳平衡。[44]

流行文化

奇爱博士：该片获得了第37届奥斯卡金像奖四项提名，与《2001太空漫游》、《发条橙》并称为“未来三部曲”
  • 基于Sylvia Nasar的关于Nahs的著作诞生了电影《美丽心灵 A Beautiful Mind》(1998)。[45]
  • 1959年由[罗伯特·海莱因 Robert A. Heinlein]创作的[军事科幻小说]《小说星河战队 Starship Troopers》提到“博弈论”和“博弈论”。 在1997年的同名电影中，角色 Carl Jenkins 把他的军事情报任务称为“游戏和理论”。
  • 1964年的电影《奇爱博士 Dr. Strangelove》讽刺了关于[威慑理论 deterrence theory]的游戏理论观点。 例如，核威慑取决于是否一旦发现核攻击就威胁要进行灾难性的报复。 博弈论者可能会争辩说，这种威胁可能是“不可信的” ，因为它们可能导致子博弈不完美的均衡 subgame imperfect equilibria。 这部电影把这个想法又推进了一步，苏联不可逆转地做出了灾难性的核反应，而没有将这一威胁公之于众。[46]
  • 20世纪80年代[强力流行 power pop]乐队“博弈论(乐队)” 由创作歌手Scott Miller (流行音乐人)创立，他将乐队的名字形容为暗指“研究如何在对手面前计算出最适当的行动... ... 让自己失败的次数最少” 。[47]
  • 2005年的日本电视剧《骗子游戏 Liar Game 》和2007年的电视剧《骗子游戏 Liar Game 》中，每一集的主要角色都有一个从博弈论中抽取出来的游戏或问题，从游戏中的角色运用的策略就证明了这一点。
  • Len Deighton，1974年的小说《间谍故事 Spy Story》探讨了关于冷战军队演习的博弈论元素。




另请参阅

参考文献

  1. ↑ Roger B. Myerson (1991). Game Theory: Analysis of Conflict, Harvard University Press, p. 1. Chapter-preview links, pp. vii–xi.
  2. ↑ Bellhouse, David R. (2007), "The Problem of Waldegrave" (PDF), Journal Électronique d'Histoire des Probabilités et de la Statistique [Electronic Journal of Probability History and Statistics], 3 (2)
  3. ↑ Bellhouse, David R. (2015). "Le Her and Other Problems in Probability Discussed by Bernoulli, Montmort and Waldegrave". Statistical Science. Institute of Mathematical Statistics. 30 (1): 26–39. arXiv:1504.01950. Bibcode:2015arXiv150401950B.
  4. ↑ Zermelo, Ernst (1913). Hobson, E. W.; Love, A. E. H. (eds.). Über eine Anwendung der Mengenlehre auf die Theorie des Schachspiels [On an Application of Set Theory to the Theory of the Game of Chess] (PDF). Proceedings of the Fifth International Congress of Mathematicians (1912) (in Deutsch). Cambridge: Cambridge University Press. pp. 501–504. Archived from the original (PDF) on October 23, 2015. Retrieved August 29, 2019.
  5. ↑ Kim, Sungwook, ed. (2014). Game theory applications in network design. IGI Global. p. 3. ISBN 9781466660519. https://books.google.com/books?id=phOXBQAAQBAJ&pg=PA3. 
  6. ↑ Neumann, John von (1928). "Zur Theorie der Gesellschaftsspiele" [On the Theory of Games of Strategy]. Mathematische Annalen [Mathematical Annals] (in Deutsch). 100 (1): 295–320. doi:10.1007/BF01448847.
  7. ↑ Neumann, John von (1959). "On the Theory of Games of Strategy". In Tucker, A. W.; Luce, R. D.. Contributions to the Theory of Games. 4. pp. 13–42. https://books.google.com/books?id=9lSVFzsTGWsC&pg=PA13. 
  8. ↑ Mirowski, Philip (1992). "What Were von Neumann and Morgenstern Trying to Accomplish?". In Weintraub, E. Roy. Toward a History of Game Theory. Durham: Duke University Press. pp. 113–147. ISBN 978-0-8223-1253-6. https://books.google.com/books?id=9CHY2Gozh1MC&pg=PA113. 
  9. ↑ Leonard, Robert (2010), Von Neumann, Morgenstern, and the Creation of Game Theory, New York: Cambridge University Press, doi:10.1017/CBO9780511778278, ISBN 9780521562669
  10. ↑ Kuhn, Steven (September 4, 1997). Zalta, Edward N. (ed.). "Prisoner's Dilemma". Stanford Encyclopedia of Philosophy. Stanford University. Retrieved January 3, 2013.
  11. ↑ Wolfram, Stephen (2002). A New Kind of Science. Wolfram Media. p. 1104. ISBN 978-1-57955-008-0. https://archive.org/details/newkindofscience00wolf. 
  12. ↑ Shor, Mike. "Non-Cooperative Game". GameTheory.net. Retrieved September 15, 2016.
  13. ↑ Chandrasekaran, Ramaswamy. "Cooperative Game Theory" (PDF). University of Texas at Dallas.
  14. ↑ Brandenburger, Adam. "Cooperative Game Theory: Characteristic Functions, Allocations, Marginal Contribution" (PDF). Archived from the original (PDF) on May 27, 2016.
  15. ↑ Owen, Guillermo (1995). Game Theory: Third Edition. Bingley: Emerald Group Publishing. p. 11. ISBN 978-0-12-531151-9. 
  16. ↑ Ferguson, Thomas S. "Game Theory" (PDF). UCLA Department of Mathematics. pp. 56–57.
  17. ↑ "Complete vs Perfect information in Combinatorial Game Theory". June 24, 2014.
  18. ↑ Mycielski, Jan (1992). "Games with Perfect Information". Handbook of Game Theory with Economic Applications. Volume 1. pp. 41–70. ISBN 9780444880987. 
  19. ↑ {{cite web |url=https://www.youtube.com/watch?v=PN-I6u-AxMg&t=0m25s |title=Infinite Chess |work=PBS Infinite Series |date=March 2, 2017 }
  20. ↑ Owen, Guillermo (1995). Game Theory: Third Edition. Bingley: Emerald Group Publishing. p. 4. ISBN 978-0-12-531151-9. 
  21. ↑ Albert, Michael H.; Nowakowski, Richard J.; Wolfe, David (2007), Lessons in Play: In Introduction to Combinatorial Game Theory, A K Peters Ltd, pp. 3–4, ISBN 978-1-56881-277-9
  22. ↑ Beck, József (2008). Combinatorial Games: Tic-Tac-Toe Theory. Cambridge University Press. pp. 1–3. ISBN 978-0-521-46100-9. 
  23. ↑ Hearn, Robert A.; Demaine, Erik D. (2009), Games, Puzzles, and Computation, A K Peters, Ltd., ISBN 978-1-56881-322-6
  24. ↑ Jörg Bewersdorff (2005). "31". Luck, logic, and white lies: the mathematics of games. A K Peters, Ltd.. pp. ix–xii. ISBN 978-1-56881-210-6. 
  25. ↑ Jones, M. Tim (2008). Artificial Intelligence: A Systems Approach. Jones & Bartlett Learning. pp. 106–118. ISBN 978-0-7637-7337-3. 
  26. ↑ Lozovanu, D; Pickl, S (2015). A Game-Theoretical Approach to Markov Decision Processes, Stochastic Positional Games and Multicriteria Control Models. Springer, Cham. ISBN 978-3-319-11832-1. 
  27. ↑ 27.0 27.1 McMahan, Hugh Brendan (2006). "Robust Planning in Domains with Stochastic Outcomes, Adversaries, and Partial Observability" (PDF). CMU-CS-06-166: 3–4.
  28. ↑ Wang, Wenliang (2015). Pooling Game Theory and Public Pension Plan. ISBN 978-1507658246. 
  29. ↑ Williams, Paul D. (2013). Security Studies: an Introduction (second ed.). Abingdon: Routledge. pp. 55–56. 
  30. ↑ Tagiew, Rustam (May 3, 2011). "If more than Analytical Modeling is Needed to Predict Real Agents' Strategic Interaction". arXiv:1105.0558 [cs.GT].
  31. ↑ Friedman, Daniel (1998). "On economic applications of evolutionary game theory" (PDF). Journal of Evolutionary Economics. 8: 14–53.
  32. ↑ Camerer, Colin F. (2003). "1.1 What Is Game Theory Good For?". Behavioral Game Theory: Experiments in Strategic Interaction. pp. 5–7. Archived from the original on 14 May 2011. https://web.archive.org/web/20110514201411/http://press.princeton.edu/chapters/i7517.html. 
  33. ↑ Aumann, Robert J. (2008). "game theory". The New Palgrave Dictionary of Economics (2nd ed.). http://www.dictionaryofeconomics.com/article?id=pde2008_G000007&edition=current&q=game%20theory&topicid=&result_number=4. 
  34. ↑ Piraveenan, Mahendra (2019). "Applications of Game Theory in Project Management: A Structured Review and Analysis". Mathematics. 7 (9): 858.Creative Commons Attribution 4.0 International License.
  35. ↑ Brams, Steven J. (January 1, 2001). "Game theory and the Cuban missile crisis". Plus Magazine. Retrieved January 31, 2016.
  36. ↑ Morrison, Andrew Stumpff (January 2013). "Yes, Law is the Command of the Sovereign". SSRN. doi:10.2139/ssrn.2371076.{{cite journal}}: CS1 maint: date and year (link)
  37. ↑ Fearon, James D. (January 1, 1995). "Rationalist Explanations for War". International Organization. 49 (3): 379–414. doi:10.1017/s0020818300033324. JSTOR 2706903.
  38. ↑ Wood, Peter John (2011). "Climate change and game theory" (PDF). Ecological Economics Review. 1219 (1): 153–70. Bibcode:2011NYASA1219..153W. hdl:1885/67270. PMID 21332497.
  39. ↑ Alexander, J. McKenzie (July 19, 2009). Zalta, Edward N. (ed.). "Evolutionary Game Theory". Stanford Encyclopedia of Philosophy. Stanford University. Retrieved January 3, 2013.
  40. ↑ Shoham, Yoav; Leyton-Brown, Kevin (15 December 2008). Multiagent Systems: Algorithmic, Game-Theoretic, and Logical Foundations. Cambridge University Press. ISBN 978-1-139-47524-2. https://books.google.com/books?id=bMR_qScakukC&printsec=frontcover#v=onepage&q=%22game%20theory%22&f=false. 
  41. ↑ Ullmann-Margalit, E. (1977), The Emergence of Norms, Oxford University Press
  42. ↑ Bicchieri, Cristina (2006), The Grammar of Society: the Nature and Dynamics of Social Norms, Cambridge University Press, ISBN 978-0521573726
  43. ↑ "How e-Commerce Uses Game Theory to Capture Consumer Dollars : Networks Course blog for INFO 2040/CS 2850/Econ 2040/SOC 2090". Retrieved 2020-01-11.
  44. ↑ "Black Friday Games: Concurrent pricing wars for a competitive advantage". SFK Inc. | SKK Marine | SFK SecCon (in English). 2018-11-27. Retrieved 2020-01-11.
  45. ↑ Singh, Simon (14 June 1998) "Between Genius and Madness", New York Times.
  46. ↑ "Dr. Strangelove Or How I Learned to Stop Worrying and Love the Bomb" (in English). 1964-01-29. 51 minutes in. ... is that the whole point of the doomsday machine is lost, if you keep it a secret!
  47. ↑ Guzman, Rafer (6 March 1996). "Star on hold: Faithful following, meager sales". Pacific Sun (newspaper). Archived from the original on 6 November 2013. Retrieved 25 July 2018.

编者推荐

行为博弈视角中的群体协调课程 本课程重点关注了不同信息反馈方式下的群体协调行为，并对结果从心理学角度进行解读，以期为社会预期管理问题的解决提供一定的参考

下为一些链接(源于集智俱乐部公众号)能够更好的了解博弈论的相关信息： 来自YouTube上面的Complexity Labs（Complexity Labs是一个专门介绍复杂系统领域知识的在线学习网站）

来自集智学园关于博弈论的相关课程

此外，还有根据纳什的传记改编的电源

本书在对风险领域研究的开创性意义方面值得关注。丹·加德纳作为一位资深的媒体记者，能够静下心来系统探讨关乎人们身心健康的风险与恐惧问题，着实不易，而丹·加德纳却令人信服地做到了。



本中文词条由李欣儒参与编译，刘佩佩、陈关荣审校，Meng莫和费米子编辑，欢迎在讨论页面留言。


本词条内容源自wikipedia及公开资料，遵守 CC3.0协议。

取自“https://wiki.swarma.org/index.php?title=博弈论&oldid=4034”