“伯努利图灵机”的版本间的差异
| 第15行: | 第15行: | ||
<math> | <math> | ||
C_{\mu}(x) | C_{\mu}(x) | ||
| − | </math> | + | </math>是统计复杂度,表示时间序列<math> |
x | x | ||
</math>的复杂性度量。它反映了在给定精度<math> | </math>的复杂性度量。它反映了在给定精度<math> | ||
| 第29行: | 第29行: | ||
</math>的最简单形式,且在该模型中尽量减少其复杂性。<math> | </math>的最简单形式,且在该模型中尽量减少其复杂性。<math> | ||
\left\|⋅\right\| | \left\|⋅\right\| | ||
| − | </math> | + | </math>这个符号表示对模型复杂度的量化。由于内部模型作为一种图灵机,本身也是用字符串(因果态)来描述,所以可以用长度、香农熵等指标来度量内部模型的复杂度。当我们使用香农熵来刻画内部模型的复杂度时,我们可以给出对于观测序列来说,伯努利图灵机定义下的统计复杂度通常是不可计算的,但它有一个等价的关于香农熵的可计算定义为: |
<math>C_\mu(\mathcal{x})\equiv H[\mathcal{S}] </math>,其中<math>\mathcal{S} </math>为观测数据<math>\mathcal{x} </math>的因果态集合。 | <math>C_\mu(\mathcal{x})\equiv H[\mathcal{S}] </math>,其中<math>\mathcal{S} </math>为观测数据<math>\mathcal{x} </math>的因果态集合。 | ||
2024年12月24日 (二) 10:12的版本
伯努利图灵机(BTM)是一种对基本图灵机模型进行概率性推广的计算模型,在计算理论中具有重要意义,它通过与信息源(如热浴)的连接,引入了随机性,从而为研究计算和信息处理提供了更广泛的视角。
定义与公式
伯努利图灵机是一种确定性图灵机的扩展,它包含输入磁带、输出磁带、有限状态控制单元和工作磁带。输入(输出)磁带单元只能按顺序读取(写入)一次,中间处理和存储由工作磁带提供,工作磁带允许双向访问其内容。
伯努利图灵机的公式为
[math]\displaystyle{ C_{\mu}(x)=\left\|M_{\min }(x \mid \mathrm{BTM})\right\| }[/math]
[math]\displaystyle{ C_{\mu}(x) }[/math]是统计复杂度,表示时间序列[math]\displaystyle{ x }[/math]的复杂性度量。它反映了在给定精度[math]\displaystyle{ \mu }[/math]下,最小模型的复杂度,伯努利图灵机(Bernoulli-Turing machine,简称BTM)是确定性通用图灵机的一种扩展,通过引入随机数发生器,可以计算离散随机序列。它包含输入磁带、输出磁带、有限状态控制单元和工作磁带。输入(输出)磁带单元只能按顺序读取(写入)一次,中间处理和存储由工作磁带提供,工作磁带允许双向访问其内容。在运行过程中,伯努利图灵机按照常规图灵机的方式读取纸带上的符号和自身的当前状态,并依据内置的规则表进行操作。与普通图灵机不同的是,当遇到与随机相关的规则时,它会根据随机数发生器的采样结果来决定具体的执行路径。例如,在某个状态下,图灵机可能有两种可选的操作,普通图灵机根据确定的规则选择其中一种,而伯努利图灵机则通过随机源以一定的概率来决定执行哪一种操作。[math]\displaystyle{ M_{\min }(x \mid \mathrm{BTM}) }[/math]这是在给定伯努利图灵机背景下的最小化模型[1],用于捕捉序列[math]\displaystyle{ x }[/math]的模式。这个模型是能够有效预测[math]\displaystyle{ x }[/math]的最简单形式,且在该模型中尽量减少其复杂性。[math]\displaystyle{ \left\|⋅\right\| }[/math]这个符号表示对模型复杂度的量化。由于内部模型作为一种图灵机,本身也是用字符串(因果态)来描述,所以可以用长度、香农熵等指标来度量内部模型的复杂度。当我们使用香农熵来刻画内部模型的复杂度时,我们可以给出对于观测序列来说,伯努利图灵机定义下的统计复杂度通常是不可计算的,但它有一个等价的关于香农熵的可计算定义为:
[math]\displaystyle{ C_\mu(\mathcal{x})\equiv H[\mathcal{S}] }[/math],其中[math]\displaystyle{ \mathcal{S} }[/math]为观测数据[math]\displaystyle{ \mathcal{x} }[/math]的因果态集合。
相比之下,统计复杂度[math]\displaystyle{ C_μ(x) }[/math]剔除了通用图灵机在模拟随机比特时所花费的计算努力。统计复杂度的一个特征是,对于完全随机对象,有[math]\displaystyle{ C_μ(x)=0 }[/math],如抛硬币产生的序列。同时对于简单的周期性过程,如[math]\displaystyle{ x=00000000…0 }[/math]时,也有[math]\displaystyle{ C_μ(x)=0 }[/math]。因此,统计复杂度的值对于(简单的)周期性过程和完全随机过程都很小。
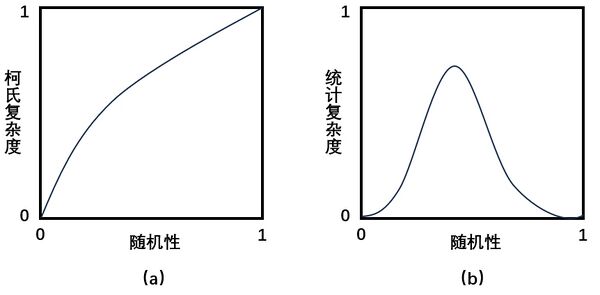
下图展示了柯式复杂度和统计复杂度随着序列从简单周期性到完全随机的过程中的差异。如图(a)所示,柯式复杂度是过程中随机性的单调递增函数。相反,统计复杂度在两个极端点上均为零,并在中间达到最大值(见图(b))。它基于这样的观点:随机性在统计上是简单的,一个完全随机的过程具有零统计复杂度。周期性在统计上也是简单的,一个完全周期性过程具有较低的统计复杂度。复杂过程在这两个极端之间产生,并且是可预测机制和随机机制的混合,有中等程度随机性的数据具有最大的统计复杂度。
- ↑ C. H. Bennett. Dissipation, information, computational complexity, and the definition of organization. In D. Pines, editor, Emerging Syntheses in the Sciences. Addison-Wesley, Redwood City, 1988.