“超图 Hypergraph”的版本间的差异
Liushikang1992(讨论 | 贡献) |
|||
| 第377行: | 第377行: | ||
Hypergraphs have been extensively used in [[machine learning]] tasks as the data model and classifier [[regularization (mathematics)]].<ref>{{citation| last1 = Zhou | first1 = Dengyong| last2 = Huang | first2 = Jiayuan | last3=Scholkopf | first3=Bernhard| issue = 2| journal = Advances in Neural Information Processing Systems| pages = 1601–1608| title = Learning with hypergraphs: clustering, classification, and embedding| year = 2006}}</ref> The applications include [[recommender system]] (communities as hyperedges),<ref>{{citation|last1=Tan | first1=Shulong | last2=Bu | first2=Jiajun | last3=Chen | first3=Chun | last4=Xu | first4=Bin | last5=Wang | first5=Can | last6=He | first6=Xiaofei|issue = 1| journal = ACM Transactions on Multimedia Computing, Communications, and Applications| title = Using rich social media information for music recommendation via hypergraph model| year = 2013|url=https://www.researchgate.net/publication/226075153| bibcode=2011smma.book..213T }}</ref> [[image retrieval]] (correlations as hyperedges),<ref>{{citation|last1=Liu | first1=Qingshan | last2=Huang | first2=Yuchi | last3=Metaxas | first3=Dimitris N. |issue = 10–11| journal = Pattern Recognition| title = Hypergraph with sampling for image retrieval| pages=2255–2262| year = 2013| doi=10.1016/j.patcog.2010.07.014 | volume=44}}</ref> and [[bioinformatics]] (biochemical interactions as hyperedges).<ref>{{citation|last1=Patro |first1=Rob | last2=Kingsoford | first2=Carl| issue = 10–11| journal = Bioinformatics| title = Predicting protein interactions via parsimonious network history inference| year = 2013| pages=237–246|doi=10.1093/bioinformatics/btt224 |pmid=23812989 |pmc=3694678 | volume=29}}</ref> Representative hypergraph learning techniques include hypergraph [[spectral clustering]] that extends the [[spectral graph theory]] with hypergraph Laplacian,<ref>{{citation|last1=Gao | first1=Tue | last2=Wang | first2=Meng | last3=Zha|first3=Zheng-Jun|last4=Shen|first4=Jialie|last5=Li|first5=Xuelong|last6=Wu|first6=Xindong|issue = 1| journal = IEEE Transactions on Image Processing| volume=22 | title = Visual-textual joint relevance learning for tag-based social image search| year = 2013| pages=363–376|url=http://ink.library.smu.edu.sg/cgi/viewcontent.cgi?article=2510&context=sis_research | doi=10.1109/tip.2012.2202676| pmid=22692911 | bibcode=2013ITIP...22..363Y }}</ref> and hypergraph [[semi-supervised learning]] that introduces extra hypergraph structural cost to restrict the learning results.<ref>{{citation|last1=Tian|first1=Ze|last2=Hwang|first2=TaeHyun|last3=Kuang|first3=Rui|issue = 21| journal = Bioinformatics| title = A hypergraph-based learning algorithm for classifying gene expression and arrayCGH data with prior knowledge| year = 2009| pages=2831–2838|doi=10.1093/bioinformatics/btp467|pmid=19648139| volume=25|doi-access=free}}</ref> For large scale hypergraphs, a distributed framework<ref name=hyperx /> built using [[Apache Spark]] is also available. | Hypergraphs have been extensively used in [[machine learning]] tasks as the data model and classifier [[regularization (mathematics)]].<ref>{{citation| last1 = Zhou | first1 = Dengyong| last2 = Huang | first2 = Jiayuan | last3=Scholkopf | first3=Bernhard| issue = 2| journal = Advances in Neural Information Processing Systems| pages = 1601–1608| title = Learning with hypergraphs: clustering, classification, and embedding| year = 2006}}</ref> The applications include [[recommender system]] (communities as hyperedges),<ref>{{citation|last1=Tan | first1=Shulong | last2=Bu | first2=Jiajun | last3=Chen | first3=Chun | last4=Xu | first4=Bin | last5=Wang | first5=Can | last6=He | first6=Xiaofei|issue = 1| journal = ACM Transactions on Multimedia Computing, Communications, and Applications| title = Using rich social media information for music recommendation via hypergraph model| year = 2013|url=https://www.researchgate.net/publication/226075153| bibcode=2011smma.book..213T }}</ref> [[image retrieval]] (correlations as hyperedges),<ref>{{citation|last1=Liu | first1=Qingshan | last2=Huang | first2=Yuchi | last3=Metaxas | first3=Dimitris N. |issue = 10–11| journal = Pattern Recognition| title = Hypergraph with sampling for image retrieval| pages=2255–2262| year = 2013| doi=10.1016/j.patcog.2010.07.014 | volume=44}}</ref> and [[bioinformatics]] (biochemical interactions as hyperedges).<ref>{{citation|last1=Patro |first1=Rob | last2=Kingsoford | first2=Carl| issue = 10–11| journal = Bioinformatics| title = Predicting protein interactions via parsimonious network history inference| year = 2013| pages=237–246|doi=10.1093/bioinformatics/btt224 |pmid=23812989 |pmc=3694678 | volume=29}}</ref> Representative hypergraph learning techniques include hypergraph [[spectral clustering]] that extends the [[spectral graph theory]] with hypergraph Laplacian,<ref>{{citation|last1=Gao | first1=Tue | last2=Wang | first2=Meng | last3=Zha|first3=Zheng-Jun|last4=Shen|first4=Jialie|last5=Li|first5=Xuelong|last6=Wu|first6=Xindong|issue = 1| journal = IEEE Transactions on Image Processing| volume=22 | title = Visual-textual joint relevance learning for tag-based social image search| year = 2013| pages=363–376|url=http://ink.library.smu.edu.sg/cgi/viewcontent.cgi?article=2510&context=sis_research | doi=10.1109/tip.2012.2202676| pmid=22692911 | bibcode=2013ITIP...22..363Y }}</ref> and hypergraph [[semi-supervised learning]] that introduces extra hypergraph structural cost to restrict the learning results.<ref>{{citation|last1=Tian|first1=Ze|last2=Hwang|first2=TaeHyun|last3=Kuang|first3=Rui|issue = 21| journal = Bioinformatics| title = A hypergraph-based learning algorithm for classifying gene expression and arrayCGH data with prior knowledge| year = 2009| pages=2831–2838|doi=10.1093/bioinformatics/btp467|pmid=19648139| volume=25|doi-access=free}}</ref> For large scale hypergraphs, a distributed framework<ref name=hyperx /> built using [[Apache Spark]] is also available. | ||
| + | |||
| + | |||
| + | ==超图与机器学习== | ||
| + | |||
| + | 超图已被广泛用于机器学习中,常作为一种数据结构或一种正则化的方式[25]。这些应用包括推荐系统(社团作为超边)[26]、图像检索(相关性作为超边)[27]、和生物信息学(生物、化学分子间相互作用作为超边)[28]。比较典型的超图机器学习方法包括:超图谱聚类法(用超图Laplacian扩展光谱图理论)[29]和超图半监督学习(通过引入超图结构来对结果进行限定)。对于大尺寸的超图,可以使用Apache Spark构建的分布式框架[15]。 | ||
==See also== | ==See also== | ||
2020年4月22日 (三) 17:03的版本
我们在组织翻译超图这个词条,这个词条是之前Wolfram发的那篇长文中一个非常重要的概念,我们希望可以整理好这个词条,帮助大家更好的理解那篇文章。
现在招募6个小伙伴一起翻译超图这个词条 https://wiki.swarma.org/index.php?title=超图_Hypergraph
- 开头正文部分+术语定义(Terminology)——十三维
- 二分图模型+不对称性+同构与平等——淑慧
- 对称超图+横截面——瑾晗
- 关联矩阵+超图着色+分区---厚朴
- 定理+超图绘制+超图语法——十三维
- 概括+超图学习——世康
截止时间:北京时间18:00之前。
In mathematics, a hypergraph is a generalization of a graph in which an edge can join any number of vertices. In contrast, in an ordinary graph, an edge connects exactly two vertices. Formally, a hypergraph [math]\displaystyle{ H }[/math] is a pair [math]\displaystyle{ H = (X,E) }[/math] where [math]\displaystyle{ X }[/math] is a set of elements called nodes or vertices, and [math]\displaystyle{ E }[/math] is a set of non-empty subsets of [math]\displaystyle{ X }[/math] called hyperedges or edges. Therefore, [math]\displaystyle{ E }[/math] is a subset of [math]\displaystyle{ \mathcal{P}(X) \setminus\{\emptyset\} }[/math], where [math]\displaystyle{ \mathcal{P}(X) }[/math] is the power set of [math]\displaystyle{ X }[/math]. The size of the vertex set is called the order of the hypergraph, and the size of edges set is the size of the hypergraph.
While graph edges are 2-element subsets of nodes, hyperedges are arbitrary sets of nodes, and can therefore contain an arbitrary number of nodes. However, it is often desirable to study hypergraphs where all hyperedges have the same cardinality; a k-uniform hypergraph is a hypergraph such that all its hyperedges have size k. (In other words, one such hypergraph is a collection of sets, each such set a hyperedge connecting k nodes.) So a 2-uniform hypergraph is a graph, a 3-uniform hypergraph is a collection of unordered triples, and so on. A hypergraph is also called a set system or a family of sets drawn from the universal set.
Hypergraphs can be viewed as incidence structures. In particular, there is a bipartite "incidence graph" or "Levi graph" corresponding to every hypergraph, and conversely, most, but not all, bipartite graphs can be regarded as incidence graphs of hypergraphs.
Hypergraphs have many other names. In computational geometry, a hypergraph may sometimes be called a range space and then the hyperedges are called ranges.[1] In cooperative game theory, hypergraphs are called simple games (voting games); this notion is applied to solve problems in social choice theory. In some literature edges are referred to as hyperlinks or connectors.[2]
Special kinds of hypergraphs include: k-uniform ones, as discussed briefly above; clutters, where no edge appears as a subset of another edge; and abstract simplicial complexes, which contain all subsets of every edge.
The collection of hypergraphs is a category with hypergraph homomorphisms as morphisms.
Terminology
Definitions
There are different types of hypergraphs such as:
- Empty hypergraph: a hypergraph with no edges.
- Non-simple (or multiple) hypergraph: a hypergraph allowing loops (hyperedges with a single vertex) or repeated edges, which means there can be two or more edges containing the same set of vertices.
- Simple hypergraph: a hypergraph that contains no loops and no repeated edges.
- [math]\displaystyle{ k }[/math]-uniform hypergraph: a hypergraph where each edge contains precisely [math]\displaystyle{ k }[/math] vertices.
- [math]\displaystyle{ d }[/math]-regular hypergraph: a hypergraph where every vertex has degree [math]\displaystyle{ d }[/math].
- Acyclic hypergraph: a hypergraph that does not contain any cycles.
Because hypergraph links can have any cardinality, there are several notions of the concept of a subgraph, called subhypergraphs, partial hypergraphs and section hypergraphs.
Let [math]\displaystyle{ H=(X,E) }[/math] be the hypergraph consisting of vertices
- [math]\displaystyle{ X = \lbrace x_i | i \in I_v \rbrace, }[/math]
and having edge set
- [math]\displaystyle{ E = \lbrace e_i | i\in I_e \land e_i \subseteq X \land e_i \neq \emptyset \rbrace, }[/math]
where [math]\displaystyle{ I_v }[/math] and [math]\displaystyle{ I_e }[/math] are the index sets of the vertices and edges respectively.
A subhypergraph is a hypergraph with some vertices removed. Formally, the subhypergraph [math]\displaystyle{ H_A }[/math] induced by [math]\displaystyle{ A \subseteq X }[/math] is defined as
- [math]\displaystyle{ H_A=\left(A, \lbrace e \cap A | e \in E \land e \cap A \neq \emptyset \rbrace \right). }[/math]
An extension of a subhypergraph is a hypergraph where each hyperedge of [math]\displaystyle{ H }[/math] which is partially contained in the subhypergraph [math]\displaystyle{ H_A }[/math] and is fully contained in the extension [math]\displaystyle{ Ex(H_A) }[/math]. Formally
- [math]\displaystyle{ Ex(H_A) = (A \cup A', E' ) }[/math] with [math]\displaystyle{ A' = \bigcup_{e \in E} e \setminus A }[/math] and [math]\displaystyle{ E' = \lbrace e \in E | e \subseteq (A \cup A') \rbrace }[/math].
The partial hypergraph is a hypergraph with some edges removed. Given a subset [math]\displaystyle{ J \subset I_e }[/math] of the edge index set, the partial hypergraph generated by [math]\displaystyle{ J }[/math] is the hypergraph
- [math]\displaystyle{ \left(X, \lbrace e_i | i\in J \rbrace \right). }[/math]
Given a subset [math]\displaystyle{ A\subseteq X }[/math], the section hypergraph is the partial hypergraph
- [math]\displaystyle{ H \times A = \left(A, \lbrace e_i | i\in I_e \land e_i \subseteq A \rbrace \right). }[/math]
The dual [math]\displaystyle{ H^* }[/math] of [math]\displaystyle{ H }[/math] is a hypergraph whose vertices and edges are interchanged, so that the vertices are given by [math]\displaystyle{ \lbrace e_i \rbrace }[/math] and whose edges are given by [math]\displaystyle{ \lbrace X_m \rbrace }[/math] where
- [math]\displaystyle{ X_m = \lbrace e_i | x_m \in e_i \rbrace. }[/math]
When a notion of equality is properly defined, as done below, the operation of taking the dual of a hypergraph is an involution, i.e.,
- [math]\displaystyle{ \left(H^*\right)^* = H. }[/math]
A connected graph G with the same vertex set as a connected hypergraph H is a host graph for H if every hyperedge of H induces a connected subgraph in G. For a disconnected hypergraph H, G is a host graph if there is a bijection between the connected components of G and of H, such that each connected component G' of G is a host of the corresponding H'.
A hypergraph is bipartite if and only if its vertices can be partitioned into two classes U and V in such a way that each hyperedge with cardinality at least 2 contains at least one vertex from both classes. Alternatively, such a hypergraph is said to have Property B.
The 2-section (or clique graph, representing graph, primal graph, Gaifman graph) of a hypergraph is the graph with the same vertices of the hypergraph, and edges between all pairs of vertices contained in the same hyperedge.
二部图模型 Bipartite graph model
A hypergraph H may be represented by a bipartite graph BG as follows: the sets X and E are the partitions of BG, and (x1, e1) are connected with an edge if and only if vertex x1 is contained in edge e1 in H. Conversely, any bipartite graph with fixed parts and no unconnected nodes in the second part represents some hypergraph in the manner described above. This bipartite graph is also called incidence graph.
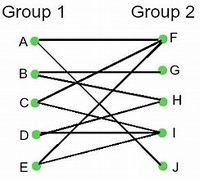
一个超图“ [math]\displaystyle{ {H} }[/math]”可以用二部图“[math]\displaystyle{ {BG} }[/math]”表示,其构成如下: 集合"X"和" E"是"BG"的分割,而且 ("x1", "e1") 与边连通当且仅当顶点"x1"包含在" [math]\displaystyle{ H }[/math]"的边" e1"中。 反之,任何具有固定的部分 part且在第二部分中没有不连通节点的二部图也代表具有上述性质的部分超图。 这个二部图也称为关联图。
Acyclicity
In contrast with ordinary undirected graphs for which there is a single natural notion of cycles and acyclic graphs, there are multiple natural non-equivalent definitions of acyclicity for hypergraphs which collapse to ordinary graph acyclicity for the special case of ordinary graphs.
与只有圈 cycle和森林 forest的普通无向图相比,对于超图的特殊情形,那些坍缩为平凡图的非循环性超图有多种自然不等价的非循环性 acyclicity 定义。
A first definition of acyclicity for hypergraphs was given by Claude Berge:[3] a hypergraph is Berge-acyclic if its incidence graph (the bipartite graph defined above) is acyclic. This definition is very restrictive: for instance, if a hypergraph has some pair [math]\displaystyle{ v \neq v' }[/math] of vertices and some pair [math]\displaystyle{ f \neq f' }[/math] of hyperedges such that [math]\displaystyle{ v, v' \in f }[/math] and [math]\displaystyle{ v, v' \in f' }[/math], then it is Berge-cyclic. Berge-cyclicity can obviously be tested in linear time by an exploration of the incidence graph. 由Claude Berge 给出了超图非循环性的首个定义: [4] 如果它的关联图(上面定义的二部图)是非循环的,则称这个超图是 Berge 不循环的。 这个定义是非常严格的:例如,假设一个超图有一些顶点[math]\displaystyle{ v \neq v' }[/math]和一些超边[math]\displaystyle{ f \neq f' }[/math] ,例如 math>v, v' \in f</math> 和[math]\displaystyle{ v, v' \in f' }[/math],那么它就是 Berge循环的 Berge-cyclic。 通过对关联图的探讨,Berge循环 berge-cyclity可以在线性时间 linear time内得到有效验证 。
We can define a weaker notion of hypergraph acyclicity,[5] later termed α-acyclicity. This notion of acyclicity is equivalent to the hypergraph being conformal (every clique of the primal graph is covered by some hyperedge) and its primal graph being chordal; it is also equivalent to reducibility to the empty graph through the GYO algorithm[6][7] (also known as Graham's algorithm), a confluent iterative process which removes hyperedges using a generalized definition of ears. In the domain of database theory, it is known that a database schema enjoys certain desirable properties if its underlying hypergraph is α-acyclic.[8] Besides, α-acyclicity is also related to the expressiveness of the guarded fragment of first-order logic.
We can test in linear time if a hypergraph is α-acyclic.[9]
Note that α-acyclicity has the counter-intuitive property that adding hyperedges to an α-cyclic hypergraph may make it α-acyclic (for instance, adding a hyperedge containing all vertices of the hypergraph will always make it α-acyclic). Motivated in part by this perceived shortcoming, Ronald Fagin[10] defined the stronger notions of β-acyclicity and γ-acyclicity. We can state β-acyclicity as the requirement that all subhypergraphs of the hypergraph are α-acyclic, which is equivalent[10] to an earlier definition by Graham.[7] The notion of γ-acyclicity is a more restrictive condition which is equivalent to several desirable properties of database schemas and is related to Bachman diagrams. Both β-acyclicity and γ-acyclicity can be tested in polynomial time.
Those four notions of acyclicity are comparable: Berge-acyclicity implies γ-acyclicity which implies β-acyclicity which implies α-acyclicity. However, none of the reverse implications hold, so those four notions are different.[10]
Isomorphism and equality
A hypergraph homomorphism is a map from the vertex set of one hypergraph to another such that each edge maps to one other edge.
A hypergraph [math]\displaystyle{ H=(X,E) }[/math] is isomorphic to a hypergraph [math]\displaystyle{ G=(Y,F) }[/math], written as [math]\displaystyle{ H \simeq G }[/math] if there exists a bijection
- [math]\displaystyle{ \phi:X \to Y }[/math]
and a permutation [math]\displaystyle{ \pi }[/math] of [math]\displaystyle{ I }[/math] such that
- [math]\displaystyle{ \phi(e_i) = f_{\pi(i)} }[/math]
The bijection [math]\displaystyle{ \phi }[/math] is then called the isomorphism of the graphs. Note that
- [math]\displaystyle{ H \simeq G }[/math] if and only if [math]\displaystyle{ H^* \simeq G^* }[/math].
When the edges of a hypergraph are explicitly labeled, one has the additional notion of strong isomorphism. One says that [math]\displaystyle{ H }[/math] is strongly isomorphic to [math]\displaystyle{ G }[/math] if the permutation is the identity. One then writes [math]\displaystyle{ H \cong G }[/math]. Note that all strongly isomorphic graphs are isomorphic, but not vice versa.
When the vertices of a hypergraph are explicitly labeled, one has the notions of equivalence, and also of equality. One says that [math]\displaystyle{ H }[/math] is equivalent to [math]\displaystyle{ G }[/math], and writes [math]\displaystyle{ H\equiv G }[/math] if the isomorphism [math]\displaystyle{ \phi }[/math] has
- [math]\displaystyle{ \phi(x_n) = y_n }[/math]
and
- [math]\displaystyle{ \phi(e_i) = f_{\pi(i)} }[/math]
Note that
- [math]\displaystyle{ H\equiv G }[/math] if and only if [math]\displaystyle{ H^* \cong G^* }[/math]
If, in addition, the permutation [math]\displaystyle{ \pi }[/math] is the identity, one says that [math]\displaystyle{ H }[/math] equals [math]\displaystyle{ G }[/math], and writes [math]\displaystyle{ H=G }[/math]. Note that, with this definition of equality, graphs are self-dual:
- [math]\displaystyle{ \left(H^*\right) ^* = H }[/math]
A hypergraph automorphism is an isomorphism from a vertex set into itself, that is a relabeling of vertices. The set of automorphisms of a hypergraph H (= (X, E)) is a group under composition, called the automorphism group of the hypergraph and written Aut(H).
Examples
Consider the hypergraph [math]\displaystyle{ H }[/math] with edges
- [math]\displaystyle{ H = \lbrace e_1 = \lbrace a,b \rbrace, e_2 = \lbrace b,c \rbrace, e_3 = \lbrace c,d \rbrace, e_4 = \lbrace d,a \rbrace, e_5 = \lbrace b,d \rbrace, e_6 = \lbrace a,c \rbrace \rbrace }[/math]
and
- [math]\displaystyle{ G = \lbrace f_1 = \lbrace \alpha,\beta \rbrace, f_2 = \lbrace \beta,\gamma \rbrace, f_3 = \lbrace \gamma,\delta \rbrace, f_4 = \lbrace \delta,\alpha \rbrace, f_5 = \lbrace \alpha,\gamma \rbrace, f_6 = \lbrace \beta,\delta \rbrace \rbrace }[/math]
Then clearly [math]\displaystyle{ H }[/math] and [math]\displaystyle{ G }[/math] are isomorphic (with [math]\displaystyle{ \phi(a)=\alpha }[/math], etc.), but they are not strongly isomorphic. So, for example, in [math]\displaystyle{ H }[/math], vertex [math]\displaystyle{ a }[/math] meets edges 1, 4 and 6, so that,
- [math]\displaystyle{ e_1 \cap e_4 \cap e_6 = \lbrace a\rbrace }[/math]
In graph [math]\displaystyle{ G }[/math], there does not exist any vertex that meets edges 1, 4 and 6:
- [math]\displaystyle{ f_1 \cap f_4 \cap f_6 = \varnothing }[/math]
In this example, [math]\displaystyle{ H }[/math] and [math]\displaystyle{ G }[/math] are equivalent, [math]\displaystyle{ H\equiv G }[/math], and the duals are strongly isomorphic: [math]\displaystyle{ H^*\cong G^* }[/math].
Symmetric hypergraphs
The[math]\displaystyle{ r(H) }[/math] of a hypergraph [math]\displaystyle{ H }[/math] is the maximum cardinality of any of the edges in the hypergraph. If all edges have the same cardinality k, the hypergraph is said to be uniform or k-uniform, or is called a k-hypergraph. A graph is just a 2-uniform hypergraph.
The degree d(v) of a vertex v is the number of edges that contain it. H is k-regular if every vertex has degree k.
The dual of a uniform hypergraph is regular and vice versa.
Two vertices x and y of H are called symmetric if there exists an automorphism such that [math]\displaystyle{ \phi(x)=y }[/math]. Two edges [math]\displaystyle{ e_i }[/math] and [math]\displaystyle{ e_j }[/math] are said to be symmetric if there exists an automorphism such that [math]\displaystyle{ \phi(e_i)=e_j }[/math].
A hypergraph is said to be vertex-transitive (or vertex-symmetric) if all of its vertices are symmetric. Similarly, a hypergraph is edge-transitive if all edges are symmetric. If a hypergraph is both edge- and vertex-symmetric, then the hypergraph is simply transitive.
Because of hypergraph duality, the study of edge-transitivity is identical to the study of vertex-transitivity.
Transversals
A transversal (or "hitting set") of a hypergraph H = (X, E) is a set [math]\displaystyle{ T\subseteq X }[/math] that has nonempty intersection with every edge. A transversal T is called minimal if no proper subset of T is a transversal. The transversal hypergraph of H is the hypergraph (X, F) whose edge set F consists of all minimal transversals of H.
Computing the transversal hypergraph has applications in combinatorial optimization, in game theory, and in several fields of computer science such as machine learning, indexing of databases, the satisfiability problem, data mining, and computer program optimization.
Incidence matrix
Let [math]\displaystyle{ V = \{v_1, v_2, ~\ldots, ~ v_n\} }[/math] and [math]\displaystyle{ E = \{e_1, e_2, ~ \ldots ~ e_m\} }[/math]. Every hypergraph has an [math]\displaystyle{ n \times m }[/math] incidence matrix [math]\displaystyle{ A = (a_{ij}) }[/math] where
- [math]\displaystyle{ a_{ij} = \left\{ \begin{matrix} 1 & \mathrm{if} ~ v_i \in e_j \\ 0 & \mathrm{otherwise}. \end{matrix} \right. }[/math]
The transpose [math]\displaystyle{ A^t }[/math] of the incidence matrix defines a hypergraph [math]\displaystyle{ H^* = (V^*,\ E^*) }[/math] called the dual of [math]\displaystyle{ H }[/math], where [math]\displaystyle{ V^* }[/math] is an m-element set and [math]\displaystyle{ E^* }[/math] is an n-element set of subsets of [math]\displaystyle{ V^* }[/math]. For [math]\displaystyle{ v^*_j \in V^* }[/math] and [math]\displaystyle{ e^*_i \in E^*, ~ v^*_j \in e^*_i }[/math] if and only if [math]\displaystyle{ a_{ij} = 1 }[/math].
分别设 [math]\displaystyle{ V = \{v_1, v_2, ~\ldots, ~ v_n\} }[/math], [math]\displaystyle{ E = \{e_1, e_2, ~ \ldots ~ e_m\} }[/math]。
每一个超图都有一个 [math]\displaystyle{ n \times m }[/math]关联矩阵[math]\displaystyle{ A = (a_{ij}) }[/math]其为:[math]\displaystyle{ a_{ij} = \left\{ \begin{matrix} 1 & \mathrm{if} ~ v_i \in e_j \\ 0 & \mathrm{otherwise}. \end{matrix} \right. }[/math]
其关联矩阵的转设 [math]\displaystyle{ A^t }[/math]定义了 [math]\displaystyle{ H^* = (V^*,\ E^*) }[/math]称为[math]\displaystyle{ H }[/math]的对偶,其中[math]\displaystyle{ V^* }[/math]是一个m元集合 [math]\displaystyle{ E^* }[/math]是一个[math]\displaystyle{ V^* }[/math]子集的n元集合。
对于[math]\displaystyle{ v^*_j \in V^* }[/math] 和 [math]\displaystyle{ e^*_i \in E^*, ~ v^*_j \in e^*_i }[/math] 当且仅当 [math]\displaystyle{ a_{ij} = 1 }[/math]。
Hypergraph coloring
Classic hypergraph coloring is assigning one of the colors from set [math]\displaystyle{ \{1,2,3,...\lambda\} }[/math] to every vertex of a hypergraph in such a way that each hyperedge contains at least two vertices of distinct colors. In other words, there must be no monochromatic hyperedge with cardinality at least 2. In this sense it is a direct generalization of graph coloring. Minimum number of used distinct colors over all colorings is called the chromatic number of a hypergraph.
经典超图着色是将集合[math]\displaystyle{ \{1,2,3,...\lambda\} }[/math]中的其中一种颜色赋予给超图的每个顶点,使每个超边至少包含两个不同颜色的顶点。换句话说,不能存在基数至少为2的单色深边。从此意义上出发,它是通常图着色的直接推广。在所有着色行为中使用到最小的不同颜色数称为超图的色数。
Hypergraphs for which there exists a coloring using up to k colors are referred to as k-colorable. The 2-colorable hypergraphs are exactly the bipartite ones. 存在着使用多达k 种颜色着色的超图称为k- 可着色图。2-可染超图就是二分图。
There are many generalizations of classic hypergraph coloring. One of them is the so-called mixed hypergraph coloring, when monochromatic edges are allowed. Some mixed hypergraphs are uncolorable for any number of colors. A general criterion for uncolorability is unknown. When a mixed hypergraph is colorable, then the minimum and maximum number of used colors are called the lower and upper chromatic numbers respectively. See http://spectrum.troy.edu/voloshin/mh.html for details.
经典超图着色有许多推广。在允许单色边情况下,混合超图着色是其中之一。一些混合超图对于任意数量的颜色都是不可着色的。同时不可着色性的内在标准是未知的。当一个混合超图是可着色时,其所使用的最小和最大颜色数分别称为下色数和上色数。详情请参阅 http://spectrum.troy.edu/voloshin/mh.html
Partitions
A partition theorem due to E. Dauber[11] states that, for an edge-transitive hypergraph [math]\displaystyle{ H=(X,E) }[/math], there exists a partition
- [math]\displaystyle{ (X_1, X_2,\cdots,X_K) }[/math]
of the vertex set [math]\displaystyle{ X }[/math] such that the subhypergraph [math]\displaystyle{ H_{X_k} }[/math] generated by [math]\displaystyle{ X_k }[/math] is transitive for each [math]\displaystyle{ 1\le k \le K }[/math], and such that
- [math]\displaystyle{ \sum_{k=1}^K r\left(H_{X_k} \right) = r(H) }[/math]
where [math]\displaystyle{ r(H) }[/math] is the rank of H.
As a corollary, an edge-transitive hypergraph that is not vertex-transitive is bicolorable.
由E. Dauber[12]所提出的一个分区定理表明,对于边传递超图 [math]\displaystyle{ H=(X,E) }[/math]存在一个分区:[math]\displaystyle{ (X_1, X_2,\cdots,X_K) }[/math]对于顶点集 [math]\displaystyle{ X }[/math]使得由[math]\displaystyle{ X_k }[/math]生成的子超图[math]\displaystyle{ H_{X_k} }[/math]在[math]\displaystyle{ 1\le k \le K }[/math]时是可传递的,并且使得[math]\displaystyle{ \sum_{k=1}^K r\left(H_{X_k} \right) = r(H) }[/math],其中[math]\displaystyle{ r(H) }[/math]是 H的秩。
作为推论,不是点传递的边传递超图则是双色的。
Graph partitioning (and in particular, hypergraph partitioning) has many applications to IC design[13] and parallel computing.[14][15][16] Efficient and Scalable hypergraph partitioning algorithms are also important for processing large scale hypergraphs in machine learning tasks.[17]
图分区(特别是超图分区)在集成电路设计[18] 和并行计算[19][20][21]中有很多应用。在机器学习任务中,高效、可扩展的超图分区算法对于处理大规模超图也很重要。[17]
Theorems
Many theorems and concepts involving graphs also hold for hypergraphs. Ramsey's theorem and Line graph of a hypergraph are typical examples. Some methods for studying symmetries of graphs extend to hypergraphs.
Two prominent theorems are the Erdős–Ko–Rado theorem and the Kruskal–Katona theorem on uniform hypergraphs.
Hypergraph drawing
Although hypergraphs are more difficult to draw on paper than graphs, several researchers have studied methods for the visualization of hypergraphs.
In one possible visual representation for hypergraphs, similar to the standard graph drawing style in which curves in the plane are used to depict graph edges, a hypergraph's vertices are depicted as points, disks, or boxes, and its hyperedges are depicted as trees that have the vertices as their leaves.[22][23] If the vertices are represented as points, the hyperedges may also be shown as smooth curves that connect sets of points, or as simple closed curves that enclose sets of points.[24][25][26]
In another style of hypergraph visualization, the subdivision model of hypergraph drawing,[27] the plane is subdivided into regions, each of which represents a single vertex of the hypergraph. The hyperedges of the hypergraph are represented by contiguous subsets of these regions, which may be indicated by coloring, by drawing outlines around them, or both. An order-n Venn diagram, for instance, may be viewed as a subdivision drawing of a hypergraph with n hyperedges (the curves defining the diagram) and 2n − 1 vertices (represented by the regions into which these curves subdivide the plane). In contrast with the polynomial-time recognition of planar graphs, it is NP-complete to determine whether a hypergraph has a planar subdivision drawing,[28] but the existence of a drawing of this type may be tested efficiently when the adjacency pattern of the regions is constrained to be a path, cycle, or tree.[29]
An alternative representation of the hypergraph called PAOH[30] is shown in the figure on top of this article. Edges are vertical lines connecting vertices. Vertices are aligned on the left. The legend on the right shows the names of the edges. It has been designed for dynamic hypergraphs but can be used for simple hypergraphs as well.
Hypergraph grammars
By augmenting a class of hypergraphs with replacement rules, graph grammars can be generalised to allow hyperedges.
Generalizations
One possible generalization of a hypergraph is to allow edges to point at other edges. There are two variations of this generalization. In one, the edges consist not only of a set of vertices, but may also contain subsets of vertices, subsets of subsets of vertices and so on ad infinitum. In essence, every edge is just an internal node of a tree or directed acyclic graph, and vertices are the leaf nodes. A hypergraph is then just a collection of trees with common, shared nodes (that is, a given internal node or leaf may occur in several different trees). Conversely, every collection of trees can be understood as this generalized hypergraph. Since trees are widely used throughout computer science and many other branches of mathematics, one could say that hypergraphs appear naturally as well. So, for example, this generalization arises naturally as a model of term algebra; edges correspond to terms and vertices correspond to constants or variables.
For such a hypergraph, set membership then provides an ordering, but the ordering is neither a partial order nor a preorder, since it is not transitive. The graph corresponding to the Levi graph of this generalization is a directed acyclic graph. Consider, for example, the generalized hypergraph whose vertex set is [math]\displaystyle{ V= \{a,b\} }[/math] and whose edges are [math]\displaystyle{ e_1=\{a,b\} }[/math] and [math]\displaystyle{ e_2=\{a,e_1\} }[/math]. Then, although [math]\displaystyle{ b\in e_1 }[/math] and [math]\displaystyle{ e_1\in e_2 }[/math], it is not true that [math]\displaystyle{ b\in e_2 }[/math]. However, the transitive closure of set membership for such hypergraphs does induce a partial order, and "flattens" the hypergraph into a partially ordered set.
Alternately, edges can be allowed to point at other edges, irrespective of the requirement that the edges be ordered as directed, acyclic graphs. This allows graphs with edge-loops, which need not contain vertices at all. For example, consider the generalized hypergraph consisting of two edges [math]\displaystyle{ e_1 }[/math] and [math]\displaystyle{ e_2 }[/math], and zero vertices, so that [math]\displaystyle{ e_1 = \{e_2\} }[/math] and [math]\displaystyle{ e_2 = \{e_1\} }[/math]. As this loop is infinitely recursive, sets that are the edges violate the axiom of foundation. In particular, there is no transitive closure of set membership for such hypergraphs. Although such structures may seem strange at first, they can be readily understood by noting that the equivalent generalization of their Levi graph is no longer bipartite, but is rather just some general directed graph.
The generalized incidence matrix for such hypergraphs is, by definition, a square matrix, of a rank equal to the total number of vertices plus edges. Thus, for the above example, the incidence matrix is simply
- [math]\displaystyle{ \left[ \begin{matrix} 0 & 1 \\ 1 & 0 \end{matrix} \right]. }[/math]
Hypergraph learning
Hypergraphs have been extensively used in machine learning tasks as the data model and classifier regularization (mathematics).[31] The applications include recommender system (communities as hyperedges),[32] image retrieval (correlations as hyperedges),[33] and bioinformatics (biochemical interactions as hyperedges).[34] Representative hypergraph learning techniques include hypergraph spectral clustering that extends the spectral graph theory with hypergraph Laplacian,[35] and hypergraph semi-supervised learning that introduces extra hypergraph structural cost to restrict the learning results.[36] For large scale hypergraphs, a distributed framework[17] built using Apache Spark is also available.
超图与机器学习
超图已被广泛用于机器学习中,常作为一种数据结构或一种正则化的方式[25]。这些应用包括推荐系统(社团作为超边)[26]、图像检索(相关性作为超边)[27]、和生物信息学(生物、化学分子间相互作用作为超边)[28]。比较典型的超图机器学习方法包括:超图谱聚类法(用超图Laplacian扩展光谱图理论)[29]和超图半监督学习(通过引入超图结构来对结果进行限定)。对于大尺寸的超图,可以使用Apache Spark构建的分布式框架[15]。
See also
- Combinatorial design
- Factor graph
- Greedoid
- Incidence structure
- Matroid
- Multigraph
- P system
- Sparse matrix-vector multiplication
- Matching in hypergraphs
Notes
- ↑ Haussler, David; Welzl, Emo (1987), "ε-nets and simplex range queries", Discrete and Computational Geometry, 2 (2): 127–151, doi:10.1007/BF02187876, MR 0884223.
- ↑ Judea Pearl, in HEURISTICS Intelligent Search Strategies for Computer Problem Solving, Addison Wesley (1984), p. 25.
- ↑ Claude Berge, Graphs and Hypergraphs
- ↑ Claude Berge,Graphs and Hypergraphs
- ↑ C. Beeri, R. Fagin, D. Maier, M. Yannakakis, On the Desirability of Acyclic Database Schemes
- ↑ C. T. Yu and M. Z. Özsoyoğlu. An algorithm for tree-query membership of a distributed query. In Proc. IEEE COMPSAC, pages 306-312, 1979
- ↑ 7.0 7.1 M. H. Graham. On the universal relation. Technical Report, University of Toronto, Toronto, Ontario, Canada, 1979
- ↑ S. Abiteboul, R. B. Hull, V. Vianu, Foundations of Databases
- ↑ R. E. Tarjan, M. Yannakakis. Simple linear-time algorithms to test chordality of graphs, test acyclicity of hypergraphs, and selectively reduce acyclic hypergraphs. SIAM J. on Computing, 13(3):566-579, 1984.
- ↑ 10.0 10.1 10.2 Ronald Fagin, Degrees of Acyclicity for Hypergraphs and Relational Database Schemes
- ↑ E. Dauber, in Graph theory, ed. F. Harary, Addison Wesley, (1969) p. 172.
- ↑ E. Dauber, in Graph theory, ed. F. Harary, Addison Wesley, (1969) p. 172.
- ↑ Karypis, G., Aggarwal, R., Kumar, V., and Shekhar, S. (March 1999), "Multilevel hypergraph partitioning: applications in VLSI domain", IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 7 (1): 69–79, CiteSeerX 10.1.1.553.2367, doi:10.1109/92.748202.
{{citation}}: CS1 maint: multiple names: authors list (link) - ↑ Hendrickson, B., Kolda, T.G. (2000), "Graph partitioning models for parallel computing", Parallel Computing (Submitted manuscript), 26 (12): 1519–1545, doi:10.1016/S0167-8191(00)00048-X.
{{citation}}: CS1 maint: multiple names: authors list (link) - ↑ Catalyurek, U.V.; Aykanat, C. (1995). A Hypergraph Model for Mapping Repeated Sparse Matrix-Vector Product Computations onto Multicomputers. Proc. International Conference on Hi Performance Computing (HiPC'95).
- ↑ Catalyurek, U.V.; Aykanat, C. (1999), "Hypergraph-Partitioning Based Decomposition for Parallel Sparse-Matrix Vector Multiplication", IEEE Transactions on Parallel and Distributed Systems, 10 (7): 673–693, CiteSeerX 10.1.1.67.2498, doi:10.1109/71.780863.
- ↑ 17.0 17.1 17.2 Huang, Jin; Zhang, Rui; Yu, Jeffrey Xu (2015), "Scalable Hypergraph Learning and Processing", Proceedings of the IEEE International Conference on Data Mining
- ↑ Karypis, G., Aggarwal, R., Kumar, V., and Shekhar, S. (March 1999), "Multilevel hypergraph partitioning: applications in VLSI domain", IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 7 (1): 69–79, CiteSeerX 10.1.1.553.2367, doi:10.1109/92.748202.
{{citation}}: CS1 maint: multiple names: authors list (link) - ↑ Hendrickson, B., Kolda, T.G. (2000), "Graph partitioning models for parallel computing", Parallel Computing (Submitted manuscript), 26 (12): 1519–1545, doi:10.1016/S0167-8191(00)00048-X.
{{citation}}: CS1 maint: multiple names: authors list (link) - ↑ Catalyurek, U.V.; Aykanat, C. (1995). A Hypergraph Model for Mapping Repeated Sparse Matrix-Vector Product Computations onto Multicomputers. Proc. International Conference on Hi Performance Computing (HiPC'95).
- ↑ Catalyurek, U.V.; Aykanat, C. (1999), "Hypergraph-Partitioning Based Decomposition for Parallel Sparse-Matrix Vector Multiplication", IEEE Transactions on Parallel and Distributed Systems, 10 (7): 673–693, CiteSeerX 10.1.1.67.2498, doi:10.1109/71.780863.
- ↑ Sander, G. (2003), "Layout of directed hypergraphs with orthogonal hyperedges", Proc. 11th International Symposium on Graph Drawing (GD 2003), Lecture Notes in Computer Science, vol. 2912, Springer-Verlag, pp. 381–386.
- ↑ Eschbach, Thomas; Günther, Wolfgang; Becker, Bernd (2006), "Orthogonal hypergraph drawing for improved visibility" (PDF), Journal of Graph Algorithms and Applications, 10 (2): 141–157, doi:10.7155/jgaa.00122.
- ↑ Mäkinen, Erkki (1990), "How to draw a hypergraph", International Journal of Computer Mathematics, 34 (3): 177–185, doi:10.1080/00207169008803875.
- ↑ Bertault, François; Eades, Peter (2001), "Drawing hypergraphs in the subset standard", Proc. 8th International Symposium on Graph Drawing (GD 2000), Lecture Notes in Computer Science, vol. 1984, Springer-Verlag, pp. 45–76, doi:10.1007/3-540-44541-2_15, ISBN 978-3-540-41554-1.
- ↑ Naheed Anjum, Arafat; Bressan, Stéphane (2017), "Hypergraph Drawing by Force-Directed Placement", 28th International Conference on Database and Expert Systems Applications (DEXA 2017), Lecture Notes in Computer Science, vol. 10439, Springer International Publishing, pp. 387–394, doi:10.1007/978-3-319-64471-4_31, ISBN 978-3-319-64470-7.
- ↑ Kaufmann, Michael; van Kreveld, Marc; Speckmann, Bettina (2009), "Subdivision drawings of hypergraphs", Proc. 16th International Symposium on Graph Drawing (GD 2008), Lecture Notes in Computer Science, vol. 5417, Springer-Verlag, pp. 396–407, doi:10.1007/978-3-642-00219-9_39, ISBN 978-3-642-00218-2.
- ↑ Johnson, David S.; Pollak, H. O. (2006), "Hypergraph planarity and the complexity of drawing Venn diagrams", Journal of Graph Theory, 11 (3): 309–325, doi:10.1002/jgt.3190110306.
- ↑ Buchin, Kevin; van Kreveld, Marc; Meijer, Henk; Speckmann, Bettina; Verbeek, Kevin (2010), "On planar supports for hypergraphs", Proc. 17th International Symposium on Graph Drawing (GD 2009), Lecture Notes in Computer Science, vol. 5849, Springer-Verlag, pp. 345–356, doi:10.1007/978-3-642-11805-0_33, ISBN 978-3-642-11804-3.
- ↑ 引用错误:无效
<ref>标签;未给name属性为paoh的引用提供文字 - ↑ Zhou, Dengyong; Huang, Jiayuan; Scholkopf, Bernhard (2006), "Learning with hypergraphs: clustering, classification, and embedding", Advances in Neural Information Processing Systems (2): 1601–1608
- ↑ Tan, Shulong; Bu, Jiajun; Chen, Chun; Xu, Bin; Wang, Can; He, Xiaofei (2013), "Using rich social media information for music recommendation via hypergraph model", ACM Transactions on Multimedia Computing, Communications, and Applications (1), Bibcode:2011smma.book..213T
- ↑ Liu, Qingshan; Huang, Yuchi; Metaxas, Dimitris N. (2013), "Hypergraph with sampling for image retrieval", Pattern Recognition, 44 (10–11): 2255–2262, doi:10.1016/j.patcog.2010.07.014
- ↑ Patro, Rob; Kingsoford, Carl (2013), "Predicting protein interactions via parsimonious network history inference", Bioinformatics, 29 (10–11): 237–246, doi:10.1093/bioinformatics/btt224, PMC 3694678, PMID 23812989
- ↑ Gao, Tue; Wang, Meng; Zha, Zheng-Jun; Shen, Jialie; Li, Xuelong; Wu, Xindong (2013), "Visual-textual joint relevance learning for tag-based social image search", IEEE Transactions on Image Processing, 22 (1): 363–376, Bibcode:2013ITIP...22..363Y, doi:10.1109/tip.2012.2202676, PMID 22692911
- ↑ Tian, Ze; Hwang, TaeHyun; Kuang, Rui (2009), "A hypergraph-based learning algorithm for classifying gene expression and arrayCGH data with prior knowledge", Bioinformatics, 25 (21): 2831–2838, doi:10.1093/bioinformatics/btp467, PMID 19648139
References
- Claude Berge, "Hypergraphs: Combinatorics of finite sets". North-Holland, 1989.
- Claude Berge, Dijen Ray-Chaudhuri, "Hypergraph Seminar, Ohio State University 1972", Lecture Notes in Mathematics 411 Springer-Verlag
- Hazewinkel, Michiel, ed. (2001) [1994], "Hypergraph", Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4
- Alain Bretto, "Hypergraph Theory: an Introduction", Springer, 2013.
- Vitaly I. Voloshin. "Coloring Mixed Hypergraphs: Theory, Algorithms and Applications". Fields Institute Monographs, American Mathematical Society, 2002.
- Vitaly I. Voloshin. "Introduction to Graph and Hypergraph Theory". Nova Science Publishers, Inc., 2009.
- This article incorporates material from hypergraph on PlanetMath, which is licensed under theCreative Commons Attribution/Share-Alike License.
External links
- PAOHVis: open-source PAOHVis system for visualizing dynamic hypergraphs.
de:Graph (Graphentheorie)#Hypergraph
编者推荐
- 《超图-限集的组合学》by [法]Claude Berge
超图的第一本专著,作者是近代图论之父法国数学家Claude Berge,将图里的普通边拓展为超边,小小的一步拓展却引发了一个大的领域。