“超图 Hypergraph”的版本间的差异
| 第47行: | 第47行: | ||
超图还有许多其它名称。在'''计算几何学 family of sets'''中,超图有时可以被称为'''范围空间 range space''',将超图的边称为''范围 ranges''.<ref>{{citation | 超图还有许多其它名称。在'''计算几何学 family of sets'''中,超图有时可以被称为'''范围空间 range space''',将超图的边称为''范围 ranges''.<ref>{{citation | ||
| − | | last1 = Haussler | first1 = David | David Haussler | + | | last1 = Haussler | first1 = David | author1-link = David Haussler |
| last2 = Welzl | first2 = Emo | | last2 = Welzl | first2 = Emo | ||
| doi = 10.1007/BF02187876 | | doi = 10.1007/BF02187876 | ||
2020年4月23日 (四) 00:06的版本
我们在组织翻译超图这个词条,这个词条是之前Wolfram发的那篇长文中一个非常重要的概念,我们希望可以整理好这个词条,帮助大家更好的理解那篇文章。
现在招募6个小伙伴一起翻译超图这个词条 https://wiki.swarma.org/index.php?title=超图_Hypergraph
- 开头正文部分+术语定义(Terminology)——十三维
- 二分图模型+不对称性+同构与平等——淑慧
- 对称超图+横截面——瑾晗
- 关联矩阵+超图着色+分区---厚朴
- 定理+超图绘制+超图语法——十三维
- 概括+超图学习——世康
截止时间:北京时间18:00之前。
In mathematics, a hypergraph is a generalization of a graph in which an edge can join any number of vertices. In contrast, in an ordinary graph, an edge connects exactly two vertices. Formally, a hypergraph [math]\displaystyle{ H }[/math] is a pair [math]\displaystyle{ H = (X,E) }[/math] where [math]\displaystyle{ X }[/math] is a set of elements called nodes or vertices, and [math]\displaystyle{ E }[/math] is a set of non-empty subsets of [math]\displaystyle{ X }[/math] called hyperedges or edges. Therefore, [math]\displaystyle{ E }[/math] is a subset of [math]\displaystyle{ \mathcal{P}(X) \setminus\{\emptyset\} }[/math], where [math]\displaystyle{ \mathcal{P}(X) }[/math] is the power set of [math]\displaystyle{ X }[/math]. The size of the vertex set is called the order of the hypergraph, and the size of edges set is the size of the hypergraph.
在数学中, 超图 hypergraph是一种广义上的图,是有限集合中最一般的离散结构,在信息科学、生命科学等领域有着广泛的应用。它的一条边 edge可以连接任意数量的顶点 vertices。相对而言,在普通图中,一条边只能连接两个顶点。形式上,超图 [math]\displaystyle{ H }[/math] 是一个有序二元组 [math]\displaystyle{ H = (X,E) }[/math] 其中[math]\displaystyle{ X }[/math] 是一个以节点 nodes或顶点为元素的非空集合,即顶点集,而 [math]\displaystyle{ E }[/math] 是[math]\displaystyle{ X }[/math] 的一组非空子集簇,[math]\displaystyle{ E }[/math]的元素被称为边或超边 hyperedges。 没有相同边的超图称为单超图。
因此,若[math]\displaystyle{ \mathcal{P}(X) }[/math]是 [math]\displaystyle{ E }[/math]的幂集 power set,则[math]\displaystyle{ X }[/math]是 [math]\displaystyle{ \mathcal{P}(X) \setminus\{\emptyset\} }[/math] 的一个子集。在[math]\displaystyle{ H }[/math]中,顶点集的大小被称为超图的阶数 order of the hypergraph,边集的大小被称为超图的大小 size of the hypergraph。
While graph edges are 2-element subsets of nodes, hyperedges are arbitrary sets of nodes, and can therefore contain an arbitrary number of nodes. However, it is often desirable to study hypergraphs where all hyperedges have the same cardinality; a k-uniform hypergraph is a hypergraph such that all its hyperedges have size k. (In other words, one such hypergraph is a collection of sets, each such set a hyperedge connecting k nodes.) So a 2-uniform hypergraph is a graph, a 3-uniform hypergraph is a collection of unordered triples, and so on. A hypergraph is also called a set system or a family of sets drawn from the universal set.
普通图的边是节点的二元子集,超边则是节点的任意集合,所以可以包含任意数量的节点。但我们总先需要研究具有相同基数超边的超图,即一个k-一致超图 k-uniform hypergraph(所有超边的大小都为 k,也译作k-均匀超图)。因此一个2-一致超图就是普通图,一个3-一致
超图就是无序三元组 unordered triples 的集合,依此类推。超图也被称为从泛集 universal set 中抽取的一个集系统 set system 或集族 family of sets。
Hypergraphs can be viewed as incidence structures. In particular, there is a bipartite "incidence graph" or "Levi graph" corresponding to every hypergraph, and conversely, most, but not all, bipartite graphs can be regarded as incidence graphs of hypergraphs.
超图可以看做是关联结构 incidence structure。特别的,每个超图都有一个与超图相对应的二分 "关联图 incidence graph"或 "列维图 Levi graph",反之,大多数(但不是全部)二分图 bipartite graph都可以看作是超图的关联图。
Hypergraphs have many other names. In computational geometry, a hypergraph may sometimes be called a range space and then the hyperedges are called ranges.[1] In cooperative game theory, hypergraphs are called simple games (voting games); this notion is applied to solve problems in social choice theory. In some literature edges are referred to as hyperlinks or connectors.[2]
超图还有许多其它名称。在计算几何学 family of sets中,超图有时可以被称为范围空间 range space,将超图的边称为范围 ranges.[3] 在合作博弈论 cooperative game中,超图被称为简单博弈 simple games(投票博弈 voting games);这个概念被应用于解决社会选择理论 social choice theory 中的问题。在一些文献中,超边被称为超连接或连接器。[4]
Special kinds of hypergraphs include: k-uniform ones, as discussed briefly above; clutters, where no edge appears as a subset of another edge; and abstract simplicial complexes, which contain all subsets of every edge. The collection of hypergraphs is a category with hypergraph homomorphisms as morphisms.
特殊类型的超图包括:上文简单讨论过的k-一致超图;散簇 clutter,也即没有一条边作是另一条边的子集;以及抽象单纯复形 abstract simplicial complexes,这里面包含每条边的所有子集。
超图是一个以超图同态 homomorphism 为态射 morphism 的范畴。
术语 Terminology
定义 Definitions
There are different types of hypergraphs such as:
- Empty hypergraph: a hypergraph with no edges.
- Non-simple (or multiple) hypergraph: a hypergraph allowing loops (hyperedges with a single vertex) or repeated edges, which means there can be two or more edges containing the same set of vertices.
- Simple hypergraph: a hypergraph that contains no loops and no repeated edges.
- [math]\displaystyle{ k }[/math]-uniform hypergraph: a hypergraph where each edge contains precisely [math]\displaystyle{ k }[/math] vertices.
- [math]\displaystyle{ d }[/math]-regular hypergraph: a hypergraph where every vertex has degree [math]\displaystyle{ d }[/math].
- Acyclic hypergraph: a hypergraph that does not contain any cycles.
超图有不同的类型,如:
- 空超图 Empty hypergraph:没有边的超图
- 非简单(或多重)超图 Non-simple (or multiple) hypergraph :允许有环 loops(有单个顶点的超边)或重复边的超图,也就是说可以有两个或两个以上的边包含同一组顶点。
- 简单超图 Simple hypergraph :不包含循环和重复边的超图。
- [math]\displaystyle{ k }[/math]-一致超图 [math]\displaystyle{ k }[/math]-uniform hypergraph:每条超边都正好包含 k 个顶点的超图。
- [math]\displaystyle{ d }[/math]-正则超图 [math]\displaystyle{ d }[/math]-regular hypergraph:每个顶点的度数都是 𝑑 的超图。
- 无环超图 Acyclic hypergraph:不包含任何环的超图。
Because hypergraph links can have any cardinality, there are several notions of the concept of a subgraph, called subhypergraphs, partial hypergraphs and section hypergraphs.
因为超图中的连接可以有任意基数,所以有好几种关于子图的概念,分别是子超图 subhypergraphs、部分超图 partial hypergraphs和分段超图 section hypergraphs。
Let [math]\displaystyle{ H=(X,E) }[/math] be the hypergraph consisting of vertices
- [math]\displaystyle{ X = \lbrace x_i | i \in I_v \rbrace, }[/math]
and having edge set
- [math]\displaystyle{ E = \lbrace e_i | i\in I_e \land e_i \subseteq X \land e_i \neq \emptyset \rbrace, }[/math]
where [math]\displaystyle{ I_v }[/math] and [math]\displaystyle{ I_e }[/math] are the index sets of the vertices and edges respectively.
假定 [math]\displaystyle{ H=(X,E) }[/math] 是一个超图,包含顶点集:
[math]\displaystyle{ X = \lbrace x_i | i \in I_v \rbrace, }[/math]
和 “边集”:
[math]\displaystyle{ E = \lbrace e_i | i\in I_e \land e_i \subseteq X \land e_i \neq \emptyset \rbrace, }[/math]
其中 [math]\displaystyle{ I_v }[/math] 和 [math]\displaystyle{ I_e }[/math] 分别是顶点和边集的索引集 index set
A subhypergraph is a hypergraph with some vertices removed. Formally, the subhypergraph [math]\displaystyle{ H_A }[/math] induced by [math]\displaystyle{ A \subseteq X }[/math] is defined as
- [math]\displaystyle{ H_A=\left(A, \lbrace e \cap A | e \in E \land e \cap A \neq \emptyset \rbrace \right). }[/math]
- 子超图 subhypergraph 是去掉某些顶点的超图。在形式上,若 [math]\displaystyle{ A \subseteq X }[/math] 是顶点子集,则子超图 [math]\displaystyle{ H_A }[/math] 被定义为:
[math]\displaystyle{ H_A=\left(A, \lbrace e \cap A | e \in E \land e \cap A \neq \emptyset \rbrace \right). }[/math]
An extension of a subhypergraph is a hypergraph where each hyperedge of [math]\displaystyle{ H }[/math] which is partially contained in the subhypergraph [math]\displaystyle{ H_A }[/math] and is fully contained in the extension [math]\displaystyle{ Ex(H_A) }[/math]. Formally
- 一个子超图的扩展 extension是一个超图,其中每个属于 [math]\displaystyle{ H }[/math] 的超边都部分包含在子超图的 [math]\displaystyle{ H_A }[/math]中,并且完全包含在扩展的 [math]\displaystyle{ Ex(H_A) }[/math] 中。即在形式上:
- [math]\displaystyle{ Ex(H_A) = (A \cup A', E' ) }[/math]和 [math]\displaystyle{ A' = \bigcup_{e \in E} e \setminus A }[/math] 和[math]\displaystyle{ E' = \lbrace e \in E | e \subseteq (A \cup A') \rbrace }[/math]。
The partial hypergraph is a hypergraph with some edges removed. Given a subset [math]\displaystyle{ J \subset I_e }[/math] of the edge index set, the partial hypergraph generated by [math]\displaystyle{ J }[/math] is the hypergraph
- 部分超图 partial hypergraph是去掉一些边的超图。给定一个边索引集的子集 [math]\displaystyle{ J \subset I_e }[/math] ,由 [math]\displaystyle{ J }[/math] 生成的部分超图就是
[math]\displaystyle{ \left(X, \lbrace e_i | i\in J \rbrace \right). }[/math]
Given a subset [math]\displaystyle{ A\subseteq X }[/math], the section hypergraph is the partial hypergraph
- 而给定一个子集 [math]\displaystyle{ A\subseteq X }[/math],则section hypergraph是部分超图:
[math]\displaystyle{ H \times A = \left(A, \lbrace e_i | i\in I_e \land e_i \subseteq A \rbrace \right). }[/math]
The dual [math]\displaystyle{ H^* }[/math] of [math]\displaystyle{ H }[/math] is a hypergraph whose vertices and edges are interchanged, so that the vertices are given by [math]\displaystyle{ \lbrace e_i \rbrace }[/math] and whose edges are given by [math]\displaystyle{ \lbrace X_m \rbrace }[/math] where
[math]\displaystyle{ H }[/math] 的对偶 [math]\displaystyle{ H^* }[/math] 则是一个顶点和边互换的超图,因此顶点由 [math]\displaystyle{ \lbrace e_i \rbrace }[/math] 给出,边由 [math]\displaystyle{ \lbrace X_m \rbrace }[/math] 给出,其中:
[math]\displaystyle{ X_m = \lbrace e_i | x_m \in e_i \rbrace. }[/math]
When a notion of equality is properly defined, as done below, the operation of taking the dual of a hypergraph is an involution, i.e.,
当等式的记号被合理定义时,如下所示,对一个超图采取两次乘方 involution运算是就可得到[math]\displaystyle{ H }[/math] 的对偶: [math]\displaystyle{ \left(H^*\right)^* = H. }[/math]
A connected graph G with the same vertex set as a connected hypergraph H is a host graph for H if every hyperedge of H induces a connected subgraph in G. For a disconnected hypergraph H, G is a host graph if there is a bijection between the connected components of G and of H, such that each connected component G' of G is a host of the corresponding H'.
对于连通的超图 G 和具有相同顶点连通的超图 H,如果 H 的每个超边都由 G 中一个子图导出 induce,则 G 是一个主图 host graph; 对于不连通的超图 H,如果 G 和 H 的连通部分之间存在一个双射,使得 G 的每个连通部分 G 都是对应的 H 的主图,则 G 是一个主图。
A hypergraph is bipartite if and only if its vertices can be partitioned into two classes U and V in such a way that each hyperedge with cardinality at least 2 contains at least one vertex from both classes. Alternatively, such a hypergraph is said to have Property B.
一个超图是二分(bipartite)的,当且仅当它的顶点能被分成两类U 和 V :每个基数至少为 2 超边包含两类中的至少一个顶点。换而言之,超图则被称为具有 B 属性 Property B。
The 2-section (or clique graph, representing graph, primal graph, Gaifman graph) of a hypergraph is the graph with the same vertices of the hypergraph, and edges between all pairs of vertices contained in the same hyperedge.
2-段 2-section 超图(或团图 clique graph,表示图 representing graph,原始图 primal graph、盖夫曼图 Gaifman graph)是具有相同顶点的图,并且所有顶点对之间的边包含在相同的超边中。
二分图模型 Bipartite graph model
A hypergraph H may be represented by a bipartite graph BG as follows: the sets X and E are the partitions of BG, and (x1, e1) are connected with an edge if and only if vertex x1 is contained in edge e1 in H. Conversely, any bipartite graph with fixed parts and no unconnected nodes in the second part represents some hypergraph in the manner described above. This bipartite graph is also called incidence graph.
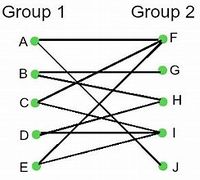
一个超图“ [math]\displaystyle{ {H} }[/math]”可以用二部图“[math]\displaystyle{ {BG} }[/math]”表示,其构成如下: 集合"X"和" E"是"BG"的分割,而且 ("x1", "e1") 与边连通当且仅当顶点"x1"包含在" [math]\displaystyle{ H }[/math]"的边" e1"中。 反之,任何具有固定的部分 part且在第二部分中没有不连通节点的二部图也代表具有上述性质的部分超图。 这个二部图也称为关联图。
无环性 Acyclicity
In contrast with ordinary undirected graphs for which there is a single natural notion of cycles and acyclic graphs, there are multiple natural non-equivalent definitions of acyclicity for hypergraphs which collapse to ordinary graph acyclicity for the special case of ordinary graphs.
与只有圈 cycle和森林 forest的普通无向图相比,对于超图的特殊情形,那些坍缩为普通图的无环性超图天然地有多种不等价的无环性 acyclicity 定义。
A first definition of acyclicity for hypergraphs was given by Claude Berge:[5] a hypergraph is Berge-acyclic if its incidence graph (the bipartite graph defined above) is acyclic. This definition is very restrictive: for instance, if a hypergraph has some pair [math]\displaystyle{ v \neq v' }[/math] of vertices and some pair [math]\displaystyle{ f \neq f' }[/math] of hyperedges such that [math]\displaystyle{ v, v' \in f }[/math] and [math]\displaystyle{ v, v' \in f' }[/math], then it is Berge-cyclic. Berge-cyclicity can obviously be tested in linear time by an exploration of the incidence graph.
由Claude Berge 给出了超图无环性的首个定义: [6] 如果它的关联图(上面定义的二部图)是无环的,则称这个超图是 Berge 无环的 Berge-acyclic。 这个定义是非常严格的:例如,假设一个超图有一些顶点[math]\displaystyle{ v \neq v' }[/math]和一些超边[math]\displaystyle{ f \neq f' }[/math] ,例如 [math]\displaystyle{ v, v' \in f }[/math] 和[math]\displaystyle{ v, v' \in f' }[/math],那么它就是 Berge成环的 Berge-cyclic。 通过对关联图的探讨,Berge成环性 berge-cyclity可以在线性时间 linear time内得到有效验证 。
We can define a weaker notion of hypergraph acyclicity,[7] later termed α-acyclicity. This notion of acyclicity is equivalent to the hypergraph being conformal (every clique of the primal graph is covered by some hyperedge) and its primal graph being chordal; it is also equivalent to reducibility to the empty graph through the GYO algorithm[8][9] (also known as Graham's algorithm), a confluent iterative process which removes hyperedges using a generalized definition of ears. In the domain of database theory, it is known that a database schema enjoys certain desirable properties if its underlying hypergraph is α-acyclic.[10] Besides, α-acyclicity is also related to the expressiveness of the guarded fragment of first-order logic.
此处,我们可以定义一个减弱的超图无环性的概念[11],后来被称为 [math]\displaystyle{ {\alpha} }[/math]-无环性 [math]\displaystyle{ {\alpha} }[/math] acyclicity。 这个无环性的概念等价于超图是同构的(原图的每个团都被某个超边所覆盖) ,它的原图称为弦图 chordal graph ; 它也等价于通过 GYO 算法 Graham-Yu-Ozsoyoglu Algorithm (也称为格雷厄姆算法 Graham's algorithm) 得到具有可约性的空图[12][9]。GYO 算法是一个合流 confluence(抽象重写 abstract rewriting)迭代过程,该算法中使用耳朵 ear的广义定义去除超边 (图论中的耳朵就定义为一条路径,其中除了端点外的点的度数均为 2(端点可以重合),而且删去后不破坏图的连通性)。众所周知, 在数据库理论 database theory 的领域中,如果一个数据库模式 database schema的底层超图是[math]\displaystyle{ {\alpha} }[/math]无环的,那么它就具有某些理想的性质。 [13] 除此之外,[math]\displaystyle{ {\alpha} }[/math]无环性也与一阶逻辑 first-order logic 保护的片段 guarded fragment 的表达能力有关。
We can test in linear time if a hypergraph is α-acyclic.[14]
我们可以在线性时间 linear time内检验超图是否是-无环的。 [15]
Note that α-acyclicity has the counter-intuitive property that adding hyperedges to an α-cyclic hypergraph may make it α-acyclic (for instance, adding a hyperedge containing all vertices of the hypergraph will always make it α-acyclic). Motivated in part by this perceived shortcoming, Ronald Fagin[16] defined the stronger notions of β-acyclicity and γ-acyclicity. We can state β-acyclicity as the requirement that all subhypergraphs of the hypergraph are α-acyclic, which is equivalent[16] to an earlier definition by Graham.[9] The notion of γ-acyclicity is a more restrictive condition which is equivalent to several desirable properties of database schemas and is related to Bachman diagrams. Both β-acyclicity and γ-acyclicity can be tested in polynomial time.
注意到[math]\displaystyle{ {\alpha} }[/math]-无环性似乎与直觉不相符,即[math]\displaystyle{ {\alpha} }[/math]-成环超图添加超边可能使其成为[math]\displaystyle{ {\alpha} }[/math]-无环的(例如,添加一条包含超图所有顶点的超边总能其成为[math]\displaystyle{ {\alpha} }[/math]-无环的)。 为了克服这个缺点,Ronald Fagin[16] 定义了更强的 [math]\displaystyle{ {\beta} }[/math]-无环性 [math]\displaystyle{ {\beta} }[/math]-acylicity 和 [math]\displaystyle{ {\gamma} }[/math]无环性 [math]\displaystyle{ {\gamma} }[/math]-acylicity 概念。 应当指出:[math]\displaystyle{ {\gamma} }[/math]无环超图是推出其所有子超图都是[math]\displaystyle{ {\alpha} }[/math]无环的必要条件,这与 Graham 的早期定义[9] 等价。 [math]\displaystyle{ {\gamma} }[/math]无环性的概念是一个更加严苛的条件,它等价于数据库模式的几个理想性质,并且与Bachman 图 Bachman diagrams有关. [math]\displaystyle{ {\beta} }[/math]-无环性 和 [math]\displaystyle{ {\gamma} }[/math]无环性 都可以在多项式时间 polynomial time(PTIME)内完成检测。
Those four notions of acyclicity are comparable: Berge-acyclicity implies γ-acyclicity which implies β-acyclicity which implies α-acyclicity. However, none of the reverse implications hold, so those four notions are different.[16]
无环性的四个概念具有可比性: berge-无环性意味着 [math]\displaystyle{ {\gamma} }[/math]- 无环性, [math]\displaystyle{ {\gamma} }[/math]- 无环性又意味着 [math]\displaystyle{ {\beta} }[/math]- 无环性, [math]\displaystyle{ {\beta} }[/math]- 无环性又可以推出 [math]\displaystyle{ {\alpha} }[/math] 无环性。 然而,反之均不成立。[16]
同构和相等 Isomorphism and equality
A hypergraph homomorphism is a map from the vertex set of one hypergraph to another such that each edge maps to one other edge.
超图同态 homomorphism是指从一个超图的顶点集到另一个超图的顶点集的映射,如此使得每条边映射到另一条边。
A hypergraph [math]\displaystyle{ H=(X,E) }[/math] is isomorphic to a hypergraph [math]\displaystyle{ G=(Y,F) }[/math], written as [math]\displaystyle{ H \simeq G }[/math] if there exists a bijection
- [math]\displaystyle{ \phi:X \to Y }[/math]
and a permutation [math]\displaystyle{ \pi }[/math] of [math]\displaystyle{ I }[/math] such that
- [math]\displaystyle{ \phi(e_i) = f_{\pi(i)} }[/math]
The bijection [math]\displaystyle{ \phi }[/math] is then called the isomorphism of the graphs. Note that
- [math]\displaystyle{ H \simeq G }[/math] if and only if [math]\displaystyle{ H^* \simeq G^* }[/math].
如果一个超图 [math]\displaystyle{ H=(X,E) }[/math]同构 isomorphic 与另外一个超图[math]\displaystyle{ G=(Y,F) }[/math],则存在一个双射:[math]\displaystyle{ H \simeq G }[/math] :[math]\displaystyle{ \phi:X \to Y }[/math]
和 关于[math]\displaystyle{ I }[/math]的置换 permutation 使得: :[math]\displaystyle{ \phi(e_i) = f_{\pi(i)} }[/math]
那么这个双射被称为图的同构 isomorphism,记作:[math]\displaystyle{ H \simeq G }[/math]但且仅当[math]\displaystyle{ H^* \simeq G^* }[/math]。
When the edges of a hypergraph are explicitly labeled, one has the additional notion of strong isomorphism. One says that [math]\displaystyle{ H }[/math] is strongly isomorphic to [math]\displaystyle{ G }[/math] if the permutation is the identity. One then writes [math]\displaystyle{ H \cong G }[/math]. Note that all strongly isomorphic graphs are isomorphic, but not vice versa.
When the vertices of a hypergraph are explicitly labeled, one has the notions of equivalence, and also of equality. One says that [math]\displaystyle{ H }[/math] is equivalent to [math]\displaystyle{ G }[/math], and writes [math]\displaystyle{ H\equiv G }[/math] if the isomorphism [math]\displaystyle{ \phi }[/math] has
- [math]\displaystyle{ \phi(x_n) = y_n }[/math]
and
- [math]\displaystyle{ \phi(e_i) = f_{\pi(i)} }[/math]
Note that
- [math]\displaystyle{ H\equiv G }[/math] if and only if [math]\displaystyle{ H^* \cong G^* }[/math]
If, in addition, the permutation [math]\displaystyle{ \pi }[/math] is the identity, one says that [math]\displaystyle{ H }[/math] equals [math]\displaystyle{ G }[/math], and writes [math]\displaystyle{ H=G }[/math]. Note that, with this definition of equality, graphs are self-dual:
- [math]\displaystyle{ \left(H^*\right) ^* = H }[/math]
A hypergraph automorphism is an isomorphism from a vertex set into itself, that is a relabeling of vertices. The set of automorphisms of a hypergraph H (= (X, E)) is a group under composition, called the automorphism group of the hypergraph and written Aut(H).
当超图的边被明确标记时,就有了“强同构 strong isomorphism ”这个新的概念。 当前面提及的置换是唯一的,则称[math]\displaystyle{ H }[/math] 强同构于 [math]\displaystyle{ G }[/math] 。 记作[math]\displaystyle{ H \cong G }[/math]。 注意,所有强同构图都是同构的,但反过来就不成立。
当超图的顶点被明确标记时,就有了“等价 equivalence”和“相等 equality”的概念。 我们称[math]\displaystyle{ H }[/math]和[math]\displaystyle{ G }[/math]等价记作:[math]\displaystyle{ H\equiv G }[/math] 如果同构[math]\displaystyle{ \phi }[/math] 满足:
[math]\displaystyle{ \phi(x_n) = y_n }[/math]
而且:
[math]\displaystyle{ \phi(e_i) = f_{\pi(i)} }[/math]
记作: [math]\displaystyle{ H\equiv G }[/math] 当且仅当 [math]\displaystyle{ H^* \cong G^* }[/math]
超图自同构 automorphism是从顶点集到自身的同构,也就是顶点的重标号。 超图“ [math]\displaystyle{ {H } }[/math]”(= (X, E))的自同构集合是超图的群 group,称为超图的自同构群 automorphism group,并写成 [math]\displaystyle{ {Aut(''H'')} }[/math]。
例子 Examples
Consider the hypergraph [math]\displaystyle{ H }[/math] with edges
- [math]\displaystyle{ H = \lbrace e_1 = \lbrace a,b \rbrace, e_2 = \lbrace b,c \rbrace, e_3 = \lbrace c,d \rbrace, e_4 = \lbrace d,a \rbrace, e_5 = \lbrace b,d \rbrace, e_6 = \lbrace a,c \rbrace \rbrace }[/math]
and
- [math]\displaystyle{ G = \lbrace f_1 = \lbrace \alpha,\beta \rbrace, f_2 = \lbrace \beta,\gamma \rbrace, f_3 = \lbrace \gamma,\delta \rbrace, f_4 = \lbrace \delta,\alpha \rbrace, f_5 = \lbrace \alpha,\gamma \rbrace, f_6 = \lbrace \beta,\delta \rbrace \rbrace }[/math]
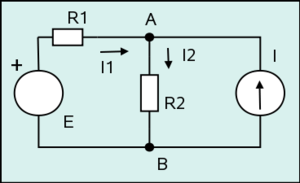
Then clearly [math]\displaystyle{ H }[/math] and [math]\displaystyle{ G }[/math] are isomorphic (with [math]\displaystyle{ \phi(a)=\alpha }[/math], etc.), but they are not strongly isomorphic. So, for example, in [math]\displaystyle{ H }[/math], vertex [math]\displaystyle{ a }[/math] meets edges 1, 4 and 6, so that,
- [math]\displaystyle{ e_1 \cap e_4 \cap e_6 = \lbrace a\rbrace }[/math]
In graph [math]\displaystyle{ G }[/math], there does not exist any vertex that meets edges 1, 4 and 6:
- [math]\displaystyle{ f_1 \cap f_4 \cap f_6 = \varnothing }[/math]
In this example, [math]\displaystyle{ H }[/math] and [math]\displaystyle{ G }[/math] are equivalent, [math]\displaystyle{ H\equiv G }[/math], and the duals are strongly isomorphic: [math]\displaystyle{ H^*\cong G^* }[/math].
考虑超图[math]\displaystyle{ H }[/math],他的边为:
[math]\displaystyle{ H = \lbrace e_1 = \lbrace a,b \rbrace, e_2 = \lbrace b,c \rbrace, e_3 = \lbrace c,d \rbrace, e_4 = \lbrace d,a \rbrace, e_5 = \lbrace b,d \rbrace, e_6 = \lbrace a,c \rbrace \rbrace }[/math]
和超图[math]\displaystyle{ G }[/math]:
[math]\displaystyle{ G = \lbrace f_1 = \lbrace \alpha,\beta \rbrace, f_2 = \lbrace \beta,\gamma \rbrace, f_3 = \lbrace \gamma,\delta \rbrace, f_4 = \lbrace \delta,\alpha \rbrace, f_5 = \lbrace \alpha,\gamma \rbrace, f_6 = \lbrace \beta,\delta \rbrace \rbrace }[/math]
很明显 [math]\displaystyle{ H }[/math] 和 [math]\displaystyle{ G }[/math] 同构(有[math]\displaystyle{ \phi(a)=\alpha }[/math]等),但是他们不是强同构,因为比如在超图[math]\displaystyle{ H }[/math]中,[math]\displaystyle{ a }[/math] 顶点连接1,4,6三条边,所以:
[math]\displaystyle{ e_1 \cap e_4 \cap e_6 = \lbrace a\rbrace }[/math]
在图[math]\displaystyle{ G }[/math],不存在连接边1,4,6的顶点:
[math]\displaystyle{ f_1 \cap f_4 \cap f_6 = \varnothing }[/math]
在这个例子,[math]\displaystyle{ H }[/math] 和 [math]\displaystyle{ G }[/math]是等价的, [math]\displaystyle{ H\equiv G }[/math],而且两者的对偶图是强同构的:[math]\displaystyle{ H^*\cong G^* }[/math]。
对称超图 Symmetric hypergraphs
The[math]\displaystyle{ r(H) }[/math] of a hypergraph [math]\displaystyle{ H }[/math] is the maximum cardinality of any of the edges in the hypergraph. If all edges have the same cardinality k, the hypergraph is said to be uniform or k-uniform, or is called a k-hypergraph. A graph is just a 2-uniform hypergraph.
超图[math]\displaystyle{ H }[/math]的[math]\displaystyle{ r(H) }[/math]表示该超图中任何一条边的最大基数。如果所有边具有相同的基数k,则称该超图为一致的或k-一致的,或称之为k-超图。普通图只是一个2-一致的超图。
The degree d(v) of a vertex v is the number of edges that contain it. H is k-regular if every vertex has degree k.
顶点[math]\displaystyle{ v }[/math]的度[math]\displaystyle{ d(v) }[/math]表示包含该顶点的边的数量。如果每个顶点的度都为k,则超图H是k-正则的。
The dual of a uniform hypergraph is regular and vice versa.
一致超图的对偶是正则的,反之亦然。
Two vertices x and y of H are called symmetric if there exists an automorphism such that [math]\displaystyle{ \phi(x)=y }[/math]. Two edges [math]\displaystyle{ e_i }[/math] and [math]\displaystyle{ e_j }[/math] are said to be symmetric if there exists an automorphism such that [math]\displaystyle{ \phi(e_i)=e_j }[/math].
如果存在一个形如[math]\displaystyle{ \phi(x)=y }[/math]的自同构,则超图H的两个顶点x和y对称 symmetric。如果存在一个自同构使得[math]\displaystyle{ \phi(e_i)=e_j }[/math],则称两个边[math]\displaystyle{ e_i }[/math]和[math]\displaystyle{ e_j }[/math]对称。
A hypergraph is said to be vertex-transitive (or vertex-symmetric) if all of its vertices are symmetric. Similarly, a hypergraph is edge-transitive if all edges are symmetric. If a hypergraph is both edge- and vertex-symmetric, then the hypergraph is simply transitive.
如果超图的所有顶点都是对称的,则称其为顶点可传递的 vertex-transitive (或顶点对称的 vertex-symmetric)。类似地,如果超图的所有边都是对称的,则该超图是边传递的 edge-transitive。 如果一个超图既是边对称的又是顶点对称的,则该超图是简单传递的 simply transitive。
Because of hypergraph duality, the study of edge-transitivity is identical to the study of vertex-transitivity.
由于超图的对偶性,边传递性的研究与顶点传递性的研究是相似的。
横截面 Transversals
A transversal (or "hitting set") of a hypergraph H = (X, E) is a set [math]\displaystyle{ T\subseteq X }[/math] that has nonempty intersection with every edge. A transversal T is called minimal if no proper subset of T is a transversal. The transversal hypergraph of H is the hypergraph (X, F) whose edge set F consists of all minimal transversals of H.
超图[math]\displaystyle{ ''H'' = (''X'', ''E'') }[/math]的横截集 transversal(或命中集 hitting set)是一个[math]\displaystyle{ T\subseteq X }[/math]集合,该集合与每条边都有非空的交集。如果[math]\displaystyle{ ''T'' }[/math]的真子集不是横截集,则称[math]\displaystyle{ ''T'' }[/math]为极小截集。[math]\displaystyle{ ''H'' }[/math]的横截超图是超图[math]\displaystyle{ (''X'', ''F'') }[/math],其边集F包含H的所有最小横截集。
Computing the transversal hypergraph has applications in combinatorial optimization, in game theory, and in several fields of computer science such as machine learning, indexing of databases, the satisfiability problem, data mining, and computer program optimization.
计算横截面超图在组合优化 Combinatorial Optimization、博弈论 Game Theory和计算机科学 Computer Science的一些领域(例如机器学习 Machine Learning、数据库索引 Indexing of Databases、可满足性问题the Satisfiability Problem、数据挖掘Data Mining和计算机程序优化 Program Optimization)都有应用。
Incidence matrix
Let [math]\displaystyle{ V = \{v_1, v_2, ~\ldots, ~ v_n\} }[/math] and [math]\displaystyle{ E = \{e_1, e_2, ~ \ldots ~ e_m\} }[/math]. Every hypergraph has an [math]\displaystyle{ n \times m }[/math] incidence matrix [math]\displaystyle{ A = (a_{ij}) }[/math] where
- [math]\displaystyle{ a_{ij} = \left\{ \begin{matrix} 1 & \mathrm{if} ~ v_i \in e_j \\ 0 & \mathrm{otherwise}. \end{matrix} \right. }[/math]
The transpose [math]\displaystyle{ A^t }[/math] of the incidence matrix defines a hypergraph [math]\displaystyle{ H^* = (V^*,\ E^*) }[/math] called the dual of [math]\displaystyle{ H }[/math], where [math]\displaystyle{ V^* }[/math] is an m-element set and [math]\displaystyle{ E^* }[/math] is an n-element set of subsets of [math]\displaystyle{ V^* }[/math]. For [math]\displaystyle{ v^*_j \in V^* }[/math] and [math]\displaystyle{ e^*_i \in E^*, ~ v^*_j \in e^*_i }[/math] if and only if [math]\displaystyle{ a_{ij} = 1 }[/math].
分别设 [math]\displaystyle{ V = \{v_1, v_2, ~\ldots, ~ v_n\} }[/math], [math]\displaystyle{ E = \{e_1, e_2, ~ \ldots ~ e_m\} }[/math]。
每一个超图都有一个 [math]\displaystyle{ n \times m }[/math] 关联矩阵 incidence matrix[math]\displaystyle{ A = (a_{ij}) }[/math],其为:[math]\displaystyle{ a_{ij} = \left\{ \begin{matrix} 1 & \mathrm{if} ~ v_i \in e_j \\ 0 & \mathrm{otherwise}. \end{matrix} \right. }[/math]。
其关联矩阵的转置 transpose [math]\displaystyle{ A^t }[/math]定义了 [math]\displaystyle{ H^* = (V^*,\ E^*) }[/math]称为[math]\displaystyle{ H }[/math]的对偶,其中[math]\displaystyle{ V^* }[/math]是一个m元集合, [math]\displaystyle{ E^* }[/math]是[math]\displaystyle{ V^* }[/math]的一个n元子集。
对于[math]\displaystyle{ v^*_j \in V^* }[/math] 和 [math]\displaystyle{ e^*_i \in E^*, ~ v^*_j \in e^*_i }[/math] 当且仅当 [math]\displaystyle{ a_{ij} = 1 }[/math]。
Hypergraph coloring
Classic hypergraph coloring is assigning one of the colors from set [math]\displaystyle{ \{1,2,3,...\lambda\} }[/math] to every vertex of a hypergraph in such a way that each hyperedge contains at least two vertices of distinct colors. In other words, there must be no monochromatic hyperedge with cardinality at least 2. In this sense it is a direct generalization of graph coloring. Minimum number of used distinct colors over all colorings is called the chromatic number of a hypergraph.
经典超图着色是将集合[math]\displaystyle{ \{1,2,3,...\lambda\} }[/math]中的其中一种颜色赋予给超图的每个顶点,使每个超边至少包含两个不同颜色的顶点。换句话说,不能存在基数至少为2的单色深边。从此意义上出发,它是通常图着色的直接推广。在所有着色行为中使用到最小的不同颜色数称为超图的色数。
Hypergraphs for which there exists a coloring using up to k colors are referred to as k-colorable. The 2-colorable hypergraphs are exactly the bipartite ones. 存在着使用多达k 种颜色着色的超图称为k- 可着色图。2-可染超图就是二分图。
There are many generalizations of classic hypergraph coloring. One of them is the so-called mixed hypergraph coloring, when monochromatic edges are allowed. Some mixed hypergraphs are uncolorable for any number of colors. A general criterion for uncolorability is unknown. When a mixed hypergraph is colorable, then the minimum and maximum number of used colors are called the lower and upper chromatic numbers respectively. See http://spectrum.troy.edu/voloshin/mh.html for details.
经典超图着色有许多推广。在允许单色边情况下,混合超图着色是其中之一。一些混合超图对于任意数量的颜色都是不可着色的。同时不可着色性的内在标准是未知的。当一个混合超图是可着色时,其所使用的最小和最大颜色数分别称为下色数和上色数。详情请参阅 http://spectrum.troy.edu/voloshin/mh.html
Partitions
A partition theorem due to E. Dauber[17] states that, for an edge-transitive hypergraph [math]\displaystyle{ H=(X,E) }[/math], there exists a partition
- [math]\displaystyle{ (X_1, X_2,\cdots,X_K) }[/math]
of the vertex set [math]\displaystyle{ X }[/math] such that the subhypergraph [math]\displaystyle{ H_{X_k} }[/math] generated by [math]\displaystyle{ X_k }[/math] is transitive for each [math]\displaystyle{ 1\le k \le K }[/math], and such that
- [math]\displaystyle{ \sum_{k=1}^K r\left(H_{X_k} \right) = r(H) }[/math]
where [math]\displaystyle{ r(H) }[/math] is the rank of H.
As a corollary, an edge-transitive hypergraph that is not vertex-transitive is bicolorable.
由E. Dauber[18]所提出的一个分区定理表明,对于边传递超图 [math]\displaystyle{ H=(X,E) }[/math]存在一个分区:[math]\displaystyle{ (X_1, X_2,\cdots,X_K) }[/math]对于顶点集 [math]\displaystyle{ X }[/math]使得由[math]\displaystyle{ X_k }[/math]生成的子超图[math]\displaystyle{ H_{X_k} }[/math]在[math]\displaystyle{ 1\le k \le K }[/math]时是可传递的,并且使得[math]\displaystyle{ \sum_{k=1}^K r\left(H_{X_k} \right) = r(H) }[/math],其中[math]\displaystyle{ r(H) }[/math]是 H的秩。
作为推论,不是点传递的边传递超图则是双色的。
Graph partitioning (and in particular, hypergraph partitioning) has many applications to IC design[19] and parallel computing.[20][21][22] Efficient and Scalable hypergraph partitioning algorithms are also important for processing large scale hypergraphs in machine learning tasks.[23]
图分区(特别是超图分区)在集成电路设计[24] 和并行计算[25][26][27]中有很多应用。在机器学习任务中,高效、可扩展的超图分区算法对于处理大规模超图也很重要。[23]
Theorems
Many theorems and concepts involving graphs also hold for hypergraphs. Ramsey's theorem and Line graph of a hypergraph are typical examples. Some methods for studying symmetries of graphs extend to hypergraphs.
Two prominent theorems are the Erdős–Ko–Rado theorem and the Kruskal–Katona theorem on uniform hypergraphs.
许多涉及图的定理和概念也适用于超图,典型的例子有拉姆西定理(Ramsey's theorem)和超图的线图。研究图的对称性的一些方法也被扩展到超图。 一致超图上有Erdős-Ko-Rado theorem和Kruskal-Katona theorem两个著名定理。
Hypergraph drawing
Although hypergraphs are more difficult to draw on paper than graphs, several researchers have studied methods for the visualization of hypergraphs. 尽管超图比图更难画在纸上,但一些研究者已经研究了超图可视化方法。
In one possible visual representation for hypergraphs, similar to the standard graph drawing style in which curves in the plane are used to depict graph edges, a hypergraph's vertices are depicted as points, disks, or boxes, and its hyperedges are depicted as trees that have the vertices as their leaves.[28][29] If the vertices are represented as points, the hyperedges may also be shown as smooth curves that connect sets of points, or as simple closed curves that enclose sets of points.[30][31][32]
其中一种超图的可视化表示法,类似于标准的图的画法:用平面内的曲线来描绘图边,将超图的顶点画成点状、圆盘或盒子,超边则被描绘成以顶点为叶子的树。[33][34] 。如果顶点表示为点,超边也可以被描绘成连接点集的平滑曲线,或显示为封闭点集的简单闭合曲线[35][36][37]
In another style of hypergraph visualization, the subdivision model of hypergraph drawing,[38] the plane is subdivided into regions, each of which represents a single vertex of the hypergraph. The hyperedges of the hypergraph are represented by contiguous subsets of these regions, which may be indicated by coloring, by drawing outlines around them, or both. An order-n Venn diagram, for instance, may be viewed as a subdivision drawing of a hypergraph with n hyperedges (the curves defining the diagram) and 2n − 1 vertices (represented by the regions into which these curves subdivide the plane). In contrast with the polynomial-time recognition of planar graphs, it is NP-complete to determine whether a hypergraph has a planar subdivision drawing,[39] but the existence of a drawing of this type may be tested efficiently when the adjacency pattern of the regions is constrained to be a path, cycle, or tree.[40]
超图可视化的另一种样式,是绘制超图的细分模型[41] ,平面被细分为区域,每个区域代表超图的一个顶点。超图的超边用这些区域的相邻子集来表示,这些子集可以通过着色、或在它们周围画轮廓来表示,或者兼而有之。[42] but the existence of a drawing of this type may be tested efficiently when the adjacency pattern of the regions is constrained to be a path, cycle, or tree.[43]
An alternative representation of the hypergraph called PAOH[44] is shown in the figure on top of this article. Edges are vertical lines connecting vertices. Vertices are aligned on the left. The legend on the right shows the names of the edges. It has been designed for dynamic hypergraphs but can be used for simple hypergraphs as well.
超图的另一种表示法被称做 PAOH[44],如上图所示,边是连接顶点的垂线,顶点在左边是对齐的。右边的图例显示了边的名称。它是为动态超图设计的,但也可以用于简单的超图。
Hypergraph grammars
By augmenting a class of hypergraphs with replacement rules, graph grammars can be generalised to allow hyperedges.
通过扩充一组替换规则于超图,图语法可以被推广超边上。
Generalizations
One possible generalization of a hypergraph is to allow edges to point at other edges. There are two variations of this generalization. In one, the edges consist not only of a set of vertices, but may also contain subsets of vertices, subsets of subsets of vertices and so on ad infinitum. In essence, every edge is just an internal node of a tree or directed acyclic graph, and vertices are the leaf nodes. A hypergraph is then just a collection of trees with common, shared nodes (that is, a given internal node or leaf may occur in several different trees). Conversely, every collection of trees can be understood as this generalized hypergraph. Since trees are widely used throughout computer science and many other branches of mathematics, one could say that hypergraphs appear naturally as well. So, for example, this generalization arises naturally as a model of term algebra; edges correspond to terms and vertices correspond to constants or variables.
For such a hypergraph, set membership then provides an ordering, but the ordering is neither a partial order nor a preorder, since it is not transitive. The graph corresponding to the Levi graph of this generalization is a directed acyclic graph. Consider, for example, the generalized hypergraph whose vertex set is [math]\displaystyle{ V= \{a,b\} }[/math] and whose edges are [math]\displaystyle{ e_1=\{a,b\} }[/math] and [math]\displaystyle{ e_2=\{a,e_1\} }[/math]. Then, although [math]\displaystyle{ b\in e_1 }[/math] and [math]\displaystyle{ e_1\in e_2 }[/math], it is not true that [math]\displaystyle{ b\in e_2 }[/math]. However, the transitive closure of set membership for such hypergraphs does induce a partial order, and "flattens" the hypergraph into a partially ordered set.
Alternately, edges can be allowed to point at other edges, irrespective of the requirement that the edges be ordered as directed, acyclic graphs. This allows graphs with edge-loops, which need not contain vertices at all. For example, consider the generalized hypergraph consisting of two edges [math]\displaystyle{ e_1 }[/math] and [math]\displaystyle{ e_2 }[/math], and zero vertices, so that [math]\displaystyle{ e_1 = \{e_2\} }[/math] and [math]\displaystyle{ e_2 = \{e_1\} }[/math]. As this loop is infinitely recursive, sets that are the edges violate the axiom of foundation. In particular, there is no transitive closure of set membership for such hypergraphs. Although such structures may seem strange at first, they can be readily understood by noting that the equivalent generalization of their Levi graph is no longer bipartite, but is rather just some general directed graph.
The generalized incidence matrix for such hypergraphs is, by definition, a square matrix, of a rank equal to the total number of vertices plus edges. Thus, for the above example, the incidence matrix is simply
- [math]\displaystyle{ \left[ \begin{matrix} 0 & 1 \\ 1 & 0 \end{matrix} \right]. }[/math]
超图概念的延伸
超图的相关概念可以进行进一步的延伸,如超图中的一些边可以指向另一些边。这种延伸有两种变体。在第一种变体中,超图的边不仅包含一组节点,而且还可以包含这组节点的子集、子集的子集等等。本质上,超图的每条边只是树结构或有向无环图的一个内部节点,而节点就是叶子。从这个意义上来说,超图就是具有共享节点的树的集合(即内部节点或叶子可能出现在不同的树结构中),反过来说,每个树的集合又可以理解为一个超图。因为树结构在计算机科学和许多数学分支中被广泛使用,所以超图的出现也是自然而然的。比如这种延伸是作为项代数的模型而自然产生的:边对应项,节点对应常量或变量。
对于上述的超图,节点集提供了一种排序。但是该排序既不是偏序也不是预序,因为它是不可传递的。与这一延伸方式的Levi图相对应的图是有向无环图。例如,一个超图的节点集为[math]\displaystyle{ V= \{a,b\} }[/math],边为[math]\displaystyle{ e_1=\{a,b\} }[/math]和[math]\displaystyle{ e_2=\{a,e_1\} }[/math]。那么,虽然[math]\displaystyle{ b\in e_1 }[/math]且[math]\displaystyle{ e_1\in e_2 }[/math],但[math]\displaystyle{ b\in e_2 }[/math]却不是真的。然而,这类超图节点集的封闭传递确实诱导了偏序,并将超图“展平”为一个偏序集。
第二种变体中,超图中的边可以指向其他边,同时不用考虑必须形成有向非循环图的要求。这允许超图具有边的循环,而不需要有任何节点。例如,考虑由两条边e1和e2组成的,节点个数为零的广义超图,使得[math]\displaystyle{ e_1 = \{e_2\} }[/math]且[math]\displaystyle{ e_2 = \{e_1\} }[/math]。因为这个循环是无限递归的,所以边的集合违反了基础公理。具体来说,对于这样的超图,不存在节点集的封闭传递。虽然这样的结构乍看起来可能很奇怪,但只要注意到它的Levi图的等价延伸不再是二分图,而是一般的有向图,就可以很容易地去理解。
根据定义,这种超图的广义关联矩阵是一个方阵,其秩等于节点和边的总数。因此,对于上面的示例,关联矩阵为: [math]\displaystyle{ \left[ \begin{matrix} 0 & 1 \\ 1 & 0 \end{matrix} \right] }[/math]。
Hypergraph learning
Hypergraphs have been extensively used in machine learning tasks as the data model and classifier regularization (mathematics).[45] The applications include recommender system (communities as hyperedges),[46] image retrieval (correlations as hyperedges),[47] and bioinformatics (biochemical interactions as hyperedges).[48] Representative hypergraph learning techniques include hypergraph spectral clustering that extends the spectral graph theory with hypergraph Laplacian,[49] and hypergraph semi-supervised learning that introduces extra hypergraph structural cost to restrict the learning results.[50] For large scale hypergraphs, a distributed framework[23] built using Apache Spark is also available.
超图与机器学习
超图已被广泛用于机器学习中,常作为一种数据结构或一种正则化的方式[25]。这些应用包括推荐系统(社团作为超边)[26]、图像检索(相关性作为超边)[27]、和生物信息学(生物、化学分子间相互作用作为超边)[28]。比较典型的超图机器学习方法包括:超图谱聚类法(用超图Laplacian扩展光谱图理论)[29]和超图半监督学习(通过引入超图结构来对结果进行限定)。对于大尺寸的超图,可以使用Apache Spark构建的分布式框架[15]。
See also
- Combinatorial design
- Factor graph
- Greedoid
- Incidence structure
- Matroid
- Multigraph
- P system
- Sparse matrix-vector multiplication
- Matching in hypergraphs
Notes
- ↑ Haussler, David; Welzl, Emo (1987), "ε-nets and simplex range queries", Discrete and Computational Geometry, 2 (2): 127–151, doi:10.1007/BF02187876, MR 0884223.
- ↑ Judea Pearl, in HEURISTICS Intelligent Search Strategies for Computer Problem Solving, Addison Wesley (1984), p. 25.
- ↑ Haussler, David; Welzl, Emo (1987), "ε-nets and simplex range queries", Discrete and Computational Geometry, 2 (2): 127–151, doi:10.1007/BF02187876, MR 0884223.
- ↑ Judea Pearl, in HEURISTICS Intelligent Search Strategies for Computer Problem Solving, Addison Wesley (1984), p. 25.
- ↑ Claude Berge, Graphs and Hypergraphs
- ↑ Claude Berge,Graphs and Hypergraphs
- ↑ C. Beeri, R. Fagin, D. Maier, M. Yannakakis, On the Desirability of Acyclic Database Schemes
- ↑ C. T. Yu and M. Z. Özsoyoğlu. An algorithm for tree-query membership of a distributed query. In Proc. IEEE COMPSAC, pages 306-312, 1979
- ↑ 9.0 9.1 9.2 9.3 M. H. Graham. On the universal relation. Technical Report, University of Toronto, Toronto, Ontario, Canada, 1979
- ↑ S. Abiteboul, R. B. Hull, V. Vianu, Foundations of Databases
- ↑ C. Beeri, R. Fagin, D. Maier, M. Yannakakis, On the Desirability of Acyclic Database Schemes
- ↑ C. T. Yu and M. Z. Özsoyoğlu. An algorithm for tree-query membership of a distributed query. In Proc. IEEE COMPSAC, pages 306-312, 1979
- ↑ Serge Abiteboul, Richard B. Hull, Victor Vianu|V. Vianu, Foundations of Databases
- ↑ R. E. Tarjan, M. Yannakakis. Simple linear-time algorithms to test chordality of graphs, test acyclicity of hypergraphs, and selectively reduce acyclic hypergraphs. SIAM J. on Computing, 13(3):566-579, 1984.
- ↑ Robert Tarjan|R. E. Tarjan, Mihalis Yannakakis|M. Yannakakis. Simple linear-time algorithms to test chordality of graphs, test acyclicity of hypergraphs, and selectively reduce acyclic hypergraphs. SIAM J. on Computing, 13(3):566-579, 1984.
- ↑ 16.0 16.1 16.2 16.3 16.4 Ronald Fagin, Degrees of Acyclicity for Hypergraphs and Relational Database Schemes
- ↑ E. Dauber, in Graph theory, ed. F. Harary, Addison Wesley, (1969) p. 172.
- ↑ E. Dauber, in Graph theory, ed. F. Harary, Addison Wesley, (1969) p. 172.
- ↑ Karypis, G., Aggarwal, R., Kumar, V., and Shekhar, S. (March 1999), "Multilevel hypergraph partitioning: applications in VLSI domain", IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 7 (1): 69–79, CiteSeerX 10.1.1.553.2367, doi:10.1109/92.748202.
{{citation}}: CS1 maint: multiple names: authors list (link) - ↑ Hendrickson, B., Kolda, T.G. (2000), "Graph partitioning models for parallel computing", Parallel Computing (Submitted manuscript), 26 (12): 1519–1545, doi:10.1016/S0167-8191(00)00048-X.
{{citation}}: CS1 maint: multiple names: authors list (link) - ↑ Catalyurek, U.V.; Aykanat, C. (1995). A Hypergraph Model for Mapping Repeated Sparse Matrix-Vector Product Computations onto Multicomputers. Proc. International Conference on Hi Performance Computing (HiPC'95).
- ↑ Catalyurek, U.V.; Aykanat, C. (1999), "Hypergraph-Partitioning Based Decomposition for Parallel Sparse-Matrix Vector Multiplication", IEEE Transactions on Parallel and Distributed Systems, 10 (7): 673–693, CiteSeerX 10.1.1.67.2498, doi:10.1109/71.780863.
- ↑ 23.0 23.1 23.2 Huang, Jin; Zhang, Rui; Yu, Jeffrey Xu (2015), "Scalable Hypergraph Learning and Processing", Proceedings of the IEEE International Conference on Data Mining
- ↑ Karypis, G., Aggarwal, R., Kumar, V., and Shekhar, S. (March 1999), "Multilevel hypergraph partitioning: applications in VLSI domain", IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 7 (1): 69–79, CiteSeerX 10.1.1.553.2367, doi:10.1109/92.748202.
{{citation}}: CS1 maint: multiple names: authors list (link) - ↑ Hendrickson, B., Kolda, T.G. (2000), "Graph partitioning models for parallel computing", Parallel Computing (Submitted manuscript), 26 (12): 1519–1545, doi:10.1016/S0167-8191(00)00048-X.
{{citation}}: CS1 maint: multiple names: authors list (link) - ↑ Catalyurek, U.V.; Aykanat, C. (1995). A Hypergraph Model for Mapping Repeated Sparse Matrix-Vector Product Computations onto Multicomputers. Proc. International Conference on Hi Performance Computing (HiPC'95).
- ↑ Catalyurek, U.V.; Aykanat, C. (1999), "Hypergraph-Partitioning Based Decomposition for Parallel Sparse-Matrix Vector Multiplication", IEEE Transactions on Parallel and Distributed Systems, 10 (7): 673–693, CiteSeerX 10.1.1.67.2498, doi:10.1109/71.780863.
- ↑ Sander, G. (2003), "Layout of directed hypergraphs with orthogonal hyperedges", Proc. 11th International Symposium on Graph Drawing (GD 2003), Lecture Notes in Computer Science, vol. 2912, Springer-Verlag, pp. 381–386.
- ↑ Eschbach, Thomas; Günther, Wolfgang; Becker, Bernd (2006), "Orthogonal hypergraph drawing for improved visibility" (PDF), Journal of Graph Algorithms and Applications, 10 (2): 141–157, doi:10.7155/jgaa.00122.
- ↑ Mäkinen, Erkki (1990), "How to draw a hypergraph", International Journal of Computer Mathematics, 34 (3): 177–185, doi:10.1080/00207169008803875.
- ↑ Bertault, François; Eades, Peter (2001), "Drawing hypergraphs in the subset standard", Proc. 8th International Symposium on Graph Drawing (GD 2000), Lecture Notes in Computer Science, vol. 1984, Springer-Verlag, pp. 45–76, doi:10.1007/3-540-44541-2_15.
- ↑ Naheed Anjum, Arafat; Bressan, Stéphane (2017), "Hypergraph Drawing by Force-Directed Placement", 28th International Conference on Database and Expert Systems Applications (DEXA 2017), Lecture Notes in Computer Science, vol. 10439, Springer International Publishing, pp. 387–394, doi:10.1007/_31.
- ↑ Sander, G. (2003), "Layout of directed hypergraphs with orthogonal hyperedges", Proc. 11th International Symposium on Graph Drawing (GD 2003), Lecture Notes in Computer Science, vol. 2912, Springer-Verlag, pp. 381–386.
- ↑ Eschbach, Thomas; Günther, Wolfgang; Becker, Bernd (2006), "Orthogonal hypergraph drawing for improved visibility" (PDF), Journal of Graph Algorithms and Applications, 10 (2): 141–157, doi:10.7155/jgaa.00122.
- ↑ Mäkinen, Erkki (1990), "How to draw a hypergraph", International Journal of Computer Mathematics, 34 (3): 177–185, doi:10.1080/00207169008803875.
- ↑ Bertault, François; Eades, Peter (2001), "Drawing hypergraphs in the subset standard", Proc. 8th International Symposium on Graph Drawing (GD 2000), Lecture Notes in Computer Science, vol. 1984, Springer-Verlag, pp. 45–76, doi:10.1007/3-540-44541-2_15.
- ↑ Naheed Anjum, Arafat; Bressan, Stéphane (2017), "Hypergraph Drawing by Force-Directed Placement", 28th International Conference on Database and Expert Systems Applications (DEXA 2017), Lecture Notes in Computer Science, vol. 10439, Springer International Publishing, pp. 387–394, doi:10.1007/_31.
- ↑ Kaufmann, Michael; van Kreveld, Marc; Speckmann, Bettina (2009), "Subdivision drawings of hypergraphs", Proc. 16th International Symposium on Graph Drawing (GD 2008), Lecture Notes in Computer Science, vol. 5417, Springer-Verlag, pp. 396–407, doi:10.1007/_39.
- ↑ Johnson, David S.; Pollak, H. O. (2006), "Hypergraph planarity and the complexity of drawing Venn diagrams", Journal of Graph Theory, 11 (3): 309–325, doi:10.1002/jgt.3190110306.
- ↑ Buchin, Kevin; van Kreveld, Marc; Meijer, Henk; Speckmann, Bettina; Verbeek, Kevin (2010), "On planar supports for hypergraphs", Proc. 17th International Symposium on Graph Drawing (GD 2009), Lecture Notes in Computer Science, vol. 5849, Springer-Verlag, pp. 345–356, doi:10.1007/_33.
- ↑ Kaufmann, Michael; van Kreveld, Marc; Speckmann, Bettina (2009), "Subdivision drawings of hypergraphs", Proc. 16th International Symposium on Graph Drawing (GD 2008), Lecture Notes in Computer Science, vol. 5417, Springer-Verlag, pp. 396–407, doi:10.1007/_39.
- ↑ Johnson, David S.; Pollak, H. O. (2006), "Hypergraph planarity and the complexity of drawing Venn diagrams", Journal of Graph Theory, 11 (3): 309–325, doi:10.1002/jgt.3190110306.
- ↑ Buchin, Kevin; van Kreveld, Marc; Meijer, Henk; Speckmann, Bettina; Verbeek, Kevin (2010), "On planar supports for hypergraphs", Proc. 17th International Symposium on Graph Drawing (GD 2009), Lecture Notes in Computer Science, vol. 5849, Springer-Verlag, pp. 345–356, doi:10.1007/_33.
- ↑ 44.0 44.1 引用错误:无效
<ref>标签;未给name属性为paoh的引用提供文字 - ↑ Zhou, Dengyong; Huang, Jiayuan; Scholkopf, Bernhard (2006), "Learning with hypergraphs: clustering, classification, and embedding", Advances in Neural Information Processing Systems (2): 1601–1608
- ↑ Tan, Shulong; Bu, Jiajun; Chen, Chun; Xu, Bin; Wang, Can; He, Xiaofei (2013), "Using rich social media information for music recommendation via hypergraph model", ACM Transactions on Multimedia Computing, Communications, and Applications (1), Bibcode:2011smma.book..213T
- ↑ Liu, Qingshan; Huang, Yuchi; Metaxas, Dimitris N. (2013), "Hypergraph with sampling for image retrieval", Pattern Recognition, 44 (10–11): 2255–2262, doi:10.1016/j.patcog.2010.07.014
- ↑ Patro, Rob; Kingsoford, Carl (2013), "Predicting protein interactions via parsimonious network history inference", Bioinformatics, 29 (10–11): 237–246, doi:10.1093/bioinformatics/btt224, PMC 3694678, PMID 23812989
- ↑ Gao, Tue; Wang, Meng; Zha, Zheng-Jun; Shen, Jialie; Li, Xuelong; Wu, Xindong (2013), "Visual-textual joint relevance learning for tag-based social image search", IEEE Transactions on Image Processing, 22 (1): 363–376, Bibcode:2013ITIP...22..363Y, doi:10.1109/tip.2012.2202676, PMID 22692911
- ↑ Tian, Ze; Hwang, TaeHyun; Kuang, Rui (2009), "A hypergraph-based learning algorithm for classifying gene expression and arrayCGH data with prior knowledge", Bioinformatics, 25 (21): 2831–2838, doi:10.1093/bioinformatics/btp467, PMID 19648139
References
- Claude Berge, "Hypergraphs: Combinatorics of finite sets". North-Holland, 1989.
- Claude Berge, Dijen Ray-Chaudhuri, "Hypergraph Seminar, Ohio State University 1972", Lecture Notes in Mathematics 411 Springer-Verlag
- Hazewinkel, Michiel, ed. (2001) [1994], "Hypergraph", Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN
- Alain Bretto, "Hypergraph Theory: an Introduction", Springer, 2013.
- Vitaly I. Voloshin. "Coloring Mixed Hypergraphs: Theory, Algorithms and Applications". Fields Institute Monographs, American Mathematical Society, 2002.
- Vitaly I. Voloshin. "Introduction to Graph and Hypergraph Theory". Nova Science Publishers, Inc., 2009.
- This article incorporates material from hypergraph on PlanetMath, which is licensed under theCreative Commons Attribution/Share-Alike License.
编者推荐
- 《超图-限集的组合学》by [法]Claude Berge
超图的第一本专著,作者是近代图论之父法国数学家Claude Berge,将图里的普通边拓展为超边,小小的一步拓展却引发了一个大的领域。