联合熵

此词条暂由彩云小译翻译，未经人工整理和审校，带来阅读不便，请见谅。

A misleading Venn diagram showing additive, and subtractive relationships between various information measures associated with correlated variables X and Y. The area contained by both circles is the joint entropy H(X,Y). The circle on the left (red and violet) is the individual entropy H(X), with the red being the conditional entropy H(X|Y). The circle on the right (blue and violet) is H(Y), with the blue being H(Y|X). The violet is the mutual information I(X;Y).

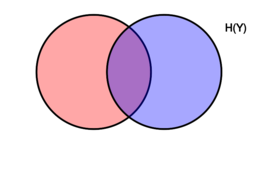
A misleading [[Venn diagram showing additive, and subtractive relationships between various information measures associated with correlated variables X and Y. The area contained by both circles is the joint entropy H(X,Y). The circle on the left (red and violet) is the individual entropy H(X), with the red being the conditional entropy H(X|Y). The circle on the right (blue and violet) is H(Y), with the blue being H(Y|X). The violet is the mutual information I(X;Y).]]

一种误导性的[显示与相关变量 x 和 y 相关的各种信息测度之间的加减关系的维恩图。两个圆所包含的面积为联合熵 h (x，y)。左边的圆圈(红色和紫色)是单个熵 h (x) ，红色是条件熵 h (x & # x7c; y)。右边的圆(蓝色和紫色)是 h (y) ，蓝色是 h (y & # x7c; x)。紫色是互信息 i (x; y)]

In information theory, joint entropy is a measure of the uncertainty associated with a set of variables.

In information theory, joint entropy is a measure of the uncertainty associated with a set of variables.

在信息论中，联合熵是对与一组变量相关的不确定性的度量。

Definition

定义

The joint Shannon entropy (in bits) of two discrete random variables [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] with images [math]\displaystyle{ \mathcal X }[/math] and [math]\displaystyle{ \mathcal Y }[/math] is defined as

The joint Shannon entropy (in bits) of two discrete random variables [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] with images [math]\displaystyle{ \mathcal X }[/math] and [math]\displaystyle{ \mathcal Y }[/math] is defined as

将两个离散随机变量的数学 x / math 和数学 y / math 与图像数学 x / math 和数学 y / math 的联合 Shannon 熵定义为

{{Equation box 1

{{Equation box 1

{方程式方框1

|indent =

|indent =

不会有事的

|title=

|title=

标题

|equation =

[math]\displaystyle{ \Eta(X,Y) = -\sum_{x\in\mathcal X} \sum_{y\in\mathcal Y} P(x,y) \log_2[P(x,y)] }[/math]

(Eq.1)

|equation = }}

会公式开始

|cellpadding= 6

|cellpadding= 6

6号手术室

|border

|border

边界

|border colour = #0073CF

|border colour = #0073CF

0073CF

|background colour=#F5FFFA}}

|background colour=#F5FFFA}}

5 / fffa }

where [math]\displaystyle{ x }[/math] and [math]\displaystyle{ y }[/math] are particular values of [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math], respectively, [math]\displaystyle{ P(x,y) }[/math] is the joint probability of these values occurring together, and [math]\displaystyle{ P(x,y) \log_2[P(x,y)] }[/math] is defined to be 0 if [math]\displaystyle{ P(x,y)=0 }[/math].

where [math]\displaystyle{ x }[/math] and [math]\displaystyle{ y }[/math] are particular values of [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math], respectively, [math]\displaystyle{ P(x,y) }[/math] is the joint probability of these values occurring together, and [math]\displaystyle{ P(x,y) \log_2[P(x,y)] }[/math] is defined to be 0 if [math]\displaystyle{ P(x,y)=0 }[/math].

其中 math x / math 和 math y / math 是数学 x / math 和 math y / math 的特定值，math p (x，y) / math 是这些值共同出现的联合概率，math p (x，y) log 2[ p (x，y)] / math 被定义为0，如果 math p (x，y)0 / math。

For more than two random variables [math]\displaystyle{ X_1, ..., X_n }[/math] this expands to

For more than two random variables [math]\displaystyle{ X_1, ..., X_n }[/math] this expands to

对于两个以上的随机变量，数学 x1，... ，xn / math，这个扩展为

{{Equation box 1

{{Equation box 1

{方程式方框1

|indent =

|indent =

不会有事的

|title=

|title=

标题

|equation =

[math]\displaystyle{ \Eta(X_1, ..., X_n) = |equation = {{NumBlk||\lt math\gt \Eta(X_1, ..., X_n) = | 方程{ NumBlk | math Eta (x1，... ，xn) -\sum_{x_1 \in\mathcal X_1} ... \sum_{x_n \in\mathcal X_n} P(x_1, ..., x_n) \log_2[P(x_1, ..., x_n)] }[/math]

(Eq.2)

-\sum_{x_1 \in\mathcal X_1} ... \sum_{x_n \in\mathcal X_n} P(x_1, ..., x_n) \log_2[P(x_1, ..., x_n)]</math>|}}

- sum { x1} ... sum { xn in mathcal xn } p (x1，... ，xn) log 2[ p (x1，... ，xn)] / math | }

|cellpadding= 6

|cellpadding= 6

6号手术室

|border

|border

边界

|border colour = #0073CF

|border colour = #0073CF

0073CF

|background colour=#F5FFFA}}

|background colour=#F5FFFA}}

5 / fffa }

where [math]\displaystyle{ x_1,...,x_n }[/math] are particular values of [math]\displaystyle{ X_1,...,X_n }[/math], respectively, [math]\displaystyle{ P(x_1, ..., x_n) }[/math] is the probability of these values occurring together, and [math]\displaystyle{ P(x_1, ..., x_n) \log_2[P(x_1, ..., x_n)] }[/math] is defined to be 0 if [math]\displaystyle{ P(x_1, ..., x_n)=0 }[/math].

where [math]\displaystyle{ x_1,...,x_n }[/math] are particular values of [math]\displaystyle{ X_1,...,X_n }[/math], respectively, [math]\displaystyle{ P(x_1, ..., x_n) }[/math] is the probability of these values occurring together, and [math]\displaystyle{ P(x_1, ..., x_n) \log_2[P(x_1, ..., x_n)] }[/math] is defined to be 0 if [math]\displaystyle{ P(x_1, ..., x_n)=0 }[/math].

其中 math x1，... ，xn / math 是数学 x1，... ，xn / math 的特定值，math p (x1，... ，xn) / math 是这些值一起发生的概率，math p (x1，... ，xn) log 2[ p (x1，... ，xn)] / math 被定义为0 if math p (x1，... ，xn)0 / math。

Properties

属性

Nonnegativity

非消极性

The joint entropy of a set of random variables is a nonnegative number.

The joint entropy of a set of random variables is a nonnegative number.

一组随机变量的联合熵是一个非负数。

[math]\displaystyle{ \Eta(X,Y) \geq 0 }[/math]

[math]\displaystyle{ \Eta(X,Y) \geq 0 }[/math]

Math Eta (x，y) geq 0 / math

[math]\displaystyle{ \Eta(X_1,\ldots, X_n) \geq 0 }[/math]

[math]\displaystyle{ \Eta(X_1,\ldots, X_n) \geq 0 }[/math]

Math Eta (x1， ldots，xn) geq 0 / math

Greater than individual entropies

大于个体的熵

The joint entropy of a set of variables is greater than or equal to the maximum of all of the individual entropies of the variables in the set.

The joint entropy of a set of variables is greater than or equal to the maximum of all of the individual entropies of the variables in the set.

一组变量的联合熵大于或等于集合中所有变量个体熵的最大值。

[math]\displaystyle{ \Eta(X,Y) \geq \max \left[\Eta(X),\Eta(Y) \right] }[/math]

[math]\displaystyle{ \Eta(X,Y) \geq \max \left[\Eta(X),\Eta(Y) \right] }[/math]

Math Eta (x，y) geq max 左[ Eta (x) ， Eta (y)右] / math

[math]\displaystyle{ \Eta \bigl(X_1,\ldots, X_n \bigr) \geq \max_{1 \le i \le n} \lt math\gt \Eta \bigl(X_1,\ldots, X_n \bigr) \geq \max_{1 \le i \le n} Math Eta bigl (x1，ldots，xn bigr) geq max {1} \Bigl\{ \Eta\bigl(X_i\bigr) \Bigr\} }[/math]

   \Bigl\{ \Eta\bigl(X_i\bigr) \Bigr\}</math>

[1][2][2][3][3][3][3][4][4][4][4][4][4][4][4][4][4][4][4][4][4][5][5][5][5][5][5][5][5][5][5][5][5][5][5][5][5][5][

Less than or equal to the sum of individual entropies

小于或等于个体熵的总和

The joint entropy of a set of variables is less than or equal to the sum of the individual entropies of the variables in the set. This is an example of subadditivity. This inequality is an equality if and only if [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] are statistically independent.

The joint entropy of a set of variables is less than or equal to the sum of the individual entropies of the variables in the set. This is an example of subadditivity. This inequality is an equality if and only if [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] are statistically independent.

一组变量的联合熵小于或等于这组变量中各个变量的熵之和。这是次加性的一个例子。这个不等式是平等的，当且仅当数学 x / 数学和数学 y / 数学是统计独立的。

[math]\displaystyle{ \Eta(X,Y) \leq \Eta(X) + \Eta(Y) }[/math]

[math]\displaystyle{ \Eta(X,Y) \leq \Eta(X) + \Eta(Y) }[/math]

Math Eta (x，y) leq Eta (x) + Eta (y) / math

[math]\displaystyle{ \Eta(X_1,\ldots, X_n) \leq \Eta(X_1) + \ldots + \Eta(X_n) }[/math]

[math]\displaystyle{ \Eta(X_1,\ldots, X_n) \leq \Eta(X_1) + \ldots + \Eta(X_n) }[/math]

Math Eta (x1， ldots，xn) leq Eta (x1) + ldots + Eta (xn) / math

Relations to other entropy measures

与其他熵测度的关系

Joint entropy is used in the definition of conditional entropy

Joint entropy is used in the definition of conditional entropy

联合熵被用来定义条件熵

[math]\displaystyle{ \Eta(X|Y) = \Eta(Y,X) - \Eta(Y)\, }[/math],

[math]\displaystyle{ \Eta(X|Y) = \Eta(Y,X) - \Eta(Y)\, }[/math],

数学 Eta (x | y) Eta (y，x)- Eta (y) ，/ math,

and [math]\displaystyle{ \Eta(X_1,\dots,X_n) = \sum_{k=1}^n \Eta(X_k|X_{k-1},\dots, X_1) }[/math]It is also used in the definition of mutual information

and [math]\displaystyle{ \Eta(X_1,\dots,X_n) = \sum_{k=1}^n \Eta(X_k|X_{k-1},\dots, X_1) }[/math]It is also used in the definition of mutual information

数学显示“ block” Eta (x1， dots，xn) sum { k1} ^ n Eta (xk | xk-1} ， dots，x1) / math 它也用于互信息的定义

[math]\displaystyle{ \operatorname{I}(X;Y) = \Eta(X) + \Eta(Y) - \Eta(X,Y)\, }[/math]

[math]\displaystyle{ \operatorname{I}(X;Y) = \Eta(X) + \Eta(Y) - \Eta(X,Y)\, }[/math]

{ i }(x; y) Eta (x) + Eta (y)- Eta (x，y) ，/ math

In quantum information theory, the joint entropy is generalized into the joint quantum entropy.

In quantum information theory, the joint entropy is generalized into the joint quantum entropy.

在量子信息论中，联合熵被推广到联合量子熵。

Joint differential entropy

联合微分熵

Definition

定义

The above definition is for discrete random variables and no more valid in the case of continuous random variables. The continuous version of discrete joint entropy is called joint differential (or continuous) entropy. Let [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] be a continuous random variables with a joint probability density function [math]\displaystyle{ f(x,y) }[/math]. The differential joint entropy [math]\displaystyle{ h(X,Y) }[/math] is defined as

The above definition is for discrete random variables and no more valid in the case of continuous random variables. The continuous version of discrete joint entropy is called joint differential (or continuous) entropy. Let [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] be a continuous random variables with a joint probability density function [math]\displaystyle{ f(x,y) }[/math]. The differential joint entropy [math]\displaystyle{ h(X,Y) }[/math] is defined as

上述定义是离散型随机变量，在连续型随机变量情况下不再有效。离散联合熵的连续形式称为联合微分(或连续)熵。让数学 x / math 和数学 y / math 是一个连续的随机变量和一个概率密度函数 / 数学 f (x，y) / math。微分联合熵数学 h (x，y) / math 定义为

{{Equation box 1

{{Equation box 1

{方程式方框1

|indent =

|indent =

不会有事的

|title=

|title=

标题

|equation =

[math]\displaystyle{ h(X,Y) = -\int_{\mathcal X , \mathcal Y} f(x,y)\log f(x,y)\,dx dy }[/math]

(Eq.3)

|equation = }}

会公式开始

|cellpadding= 6

|cellpadding= 6

6号手术室

|border

|border

边界

|border colour = #0073CF

|border colour = #0073CF

0073CF

|background colour=#F5FFFA}}

|background colour=#F5FFFA}}

5 / fffa }

For more than two continuous random variables [math]\displaystyle{ X_1, ..., X_n }[/math] the definition is generalized to:

For more than two continuous random variables [math]\displaystyle{ X_1, ..., X_n }[/math] the definition is generalized to:

对于两个以上的连续随机变量，数学 x1，... ，xn / math，定义被推广到:

{{Equation box 1

{{Equation box 1

{方程式方框1

|indent =

|indent =

不会有事的

|title=

|title=

标题

|equation =

[math]\displaystyle{ h(X_1, \ldots,X_n) = -\int f(x_1, \ldots,x_n)\log f(x_1, \ldots,x_n)\,dx_1 \ldots dx_n }[/math]

(Eq.4)

|equation = }}

会公式开始

|cellpadding= 6

|cellpadding= 6

6号手术室

|border

|border

边界

|border colour = #0073CF

|border colour = #0073CF

0073CF

|background colour=#F5FFFA}}

|background colour=#F5FFFA}}

5 / fffa }

The integral is taken over the support of [math]\displaystyle{ f }[/math]. It is possible that the integral does not exist in which case we say that the differential entropy is not defined.

The integral is taken over the support of [math]\displaystyle{ f }[/math]. It is possible that the integral does not exist in which case we say that the differential entropy is not defined.

这个积分是用数学 f / 数学来支持的。有可能积分不存在，在这种情况下，我们说微分熵是没有定义的。

Properties

属性

As in the discrete case the joint differential entropy of a set of random variables is smaller or equal than the sum of the entropies of the individual random variables:

As in the discrete case the joint differential entropy of a set of random variables is smaller or equal than the sum of the entropies of the individual random variables:

在离散情况下，一组随机变量的联合微分熵小于或等于各个随机变量的熵之和:

[math]\displaystyle{ h(X_1,X_2, \ldots,X_n) \le \sum_{i=1}^n h(X_i) }[/math]

[math]\displaystyle{ h(X_1,X_2, \ldots,X_n) \le \sum_{i=1}^n h(X_i) }[/math]

数学 h (x1，x2， ldots，xn) le sum { i 1} ^ n h (xi) / math

The following chain rule holds for two random variables:

The following chain rule holds for two random variables:

下面的链式规则适用于两个随机变量:

[math]\displaystyle{ h(X,Y) = h(X|Y) + h(Y) }[/math]

[math]\displaystyle{ h(X,Y) = h(X|Y) + h(Y) }[/math]

H (x，y) h (x | y) + h (y) / math

In the case of more than two random variables this generalizes to:

In the case of more than two random variables this generalizes to:

对于两个以上的随机变量，这种情况可以推广到:

[math]\displaystyle{ h(X_1,X_2, \ldots,X_n) = \sum_{i=1}^n h(X_i|X_1,X_2, \ldots,X_{i-1}) }[/math]

[math]\displaystyle{ h(X_1,X_2, \ldots,X_n) = \sum_{i=1}^n h(X_i|X_1,X_2, \ldots,X_{i-1}) }[/math]

数学 h (x1，x2， ldots，xn) sum { i } ^ n h (xi | x1，x2， ldots，x { i-1}) / math

Joint differential entropy is also used in the definition of the mutual information between continuous random variables:

Joint differential entropy is also used in the definition of the mutual information between continuous random variables:

联合微分熵也用于连续随机变量之间互信息的定义:

[math]\displaystyle{ \operatorname{I}(X,Y)=h(X)+h(Y)-h(X,Y) }[/math]

[math]\displaystyle{ \operatorname{I}(X,Y)=h(X)+h(Y)-h(X,Y) }[/math]

Math operatorname { i }(x，y) h (x) + h (y)-h (x，y) / math

References

参考资料

Category:Entropy and information

类别: 熵和信息

de:Bedingte Entropie#Blockentropie

1. blockentropie

This page was moved from wikipedia:en:Joint entropy. Its edit history can be viewed at 联合熵/edithistory