“雷卡·阿尔伯特 Réka Albert”的版本间的差异
(→集智论文) |
(→集智视频) |
||
| 第175行: | 第175行: | ||
<br> | <br> | ||
| − | ==集智视频== | + | ===集智视频=== |
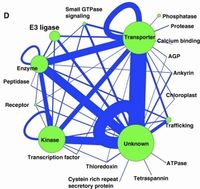
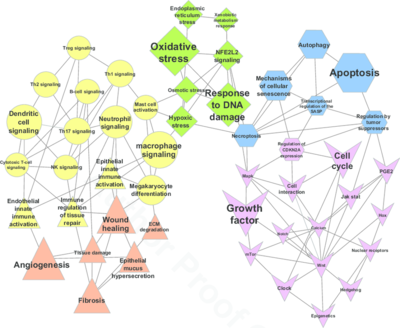
[[File:Biological-networks-included-in-CausalBioNet-each-node-is-labeled-with-the-network-name.png|right|400px|缩略图|[https://www.youtube.com/watch?v=2WkfJbY4wTU 生物网络]]] | [[File:Biological-networks-included-in-CausalBioNet-each-node-is-labeled-with-the-network-name.png|right|400px|缩略图|[https://www.youtube.com/watch?v=2WkfJbY4wTU 生物网络]]] | ||
====[https://campus.swarma.org/course/1110 重访经典:无标度网络]==== | ====[https://campus.swarma.org/course/1110 重访经典:无标度网络]==== | ||
2020年5月17日 (日) 18:03的版本
基本信息
| 类别 | 信息 |
|---|---|
| 姓名: | Réka Albert(雷卡·阿尔伯特) |
| 出生日期: | 1972年3月2日 |
| 出生地: | 罗马尼亚雷京 |
| 国籍: | 罗马尼亚,匈牙利 |
| 母校: | 巴比什-博雅依大学(理学学士、硕士学位),圣母大学(博士学位) |
| 曾属机构: | 应用与计算数学,普林斯顿大学 |
| 成就: | BA模型,无标度网络 Scale-free network |
| 主要研究方向: | 优先连接 |
雷卡·阿尔伯特 Réka Albert是匈牙利科学家,出生于罗马尼亚,是宾夕法尼亚州立大学的物理学和生物学教授。 她以Barabási-Albert模型及其在无标度网络 Scale-free network上的工作而闻名。
研究领域
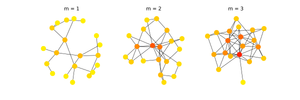
Albert与Albert-László Barabási共同创建了Barabási–Albert算法,该算法通过优先连接生成无标度随机图。
其工作从广义上讲涉及网络,例如对万维网的容错能力的研究和对北美电网脆弱性的研究。
其目前的研究重点是生物网络和系统生物学的动态建模。
就职企业、机构或院校
- 美国物理学会研究员
- 网络科学学会研究员
- 匈牙利科学院外部成员
- 《npj系统生物学与应用 npj Systems Biology and Applications》,《IET系统生物学 IET Systems Biology》,《数学生物学简报 Bulletin of Mathematical Biology》编辑委员会成员
主要文章及著作
- 《通过控制细胞内网络动态进行细胞命运重编程 Cell fate reprogramming by control of intracellular network dynamics》,JGT Zañudo, R Albert(2015), PLoS Computational Biology 11 (4), e1004193.(被引用99次)
- 《生物调控网络的布尔建模:方法学教程 Boolean modeling of biological regulatory networks: A methodology tutorial》,A. Saadatpour, R. Albert, (2013), Methods 62, 3-12 .(被引用116次)
- 《植物-授粉媒介群落装配的网络模型 A network model for plant–pollinator community assembly》.C. Campell, S. Yang, R. Albert and K. Shea.(2011), Proceedings of the National Academy of Sciences 108 (1), 197-202.(被引用79次)
- 《复杂网络的统计力学 Statistical mechanics of complex networks》,Albert R., Barabási A.-L.(2002), Reviews of Modern Physics, Vol. 74, Nr. 1, pp. 47–97. (被引用23023次)
- 复杂网络描述了自然界和社会中各种各样的系统,被广泛引用的例子包括细胞、通过化学反应连接起来的化学物质网络,或者互联网、通过物理链接连接起来的路由器和计算机网络。 虽然传统上这些系统被建模为随机图,但人们越来越认识到,真实网络的拓扑结构和演化是由鲁棒的组织原则支配的。 在本篇文章中,作者回顾了复杂网络领域的最新进展,重点介绍了统计力学网络拓扑和动力学。 在回顾了近年来引起人们对网络研究兴趣的经验数据之后,讨论了网络的主要模型和分析工具,包括随机图、小世界和无标度网络 Scale-free network,以及拓扑结构和网络对失效和攻击的鲁棒性之间的相互作用。
- 《代谢网络的大标度组织 The large-scale organization of metabolic networks》,Jeong H., Tombor B., Albert R., Oltvai Z.N., Barabási A.-L.(2000), Nature 407, pp. 651–654.(被引用5867次)
- 《复杂网络的错误和攻击容忍度 Error and attack tolerance of complex networks》, Albert R., Jeong H., Barabási A.-L.(2000), Nature 406, pp. 378–382.(被引用9084次)
- 《随机网络中标度的出现 Emergence of scaling in random networks》,Barabási A.-L., Albert R.(1999), Science, Vol. 286, Nr. 5439, pp. 509–12.(被引用36517次)
- 随机网络中标度的出现:各种各样的系统,如遗传网络或万维网,最适合描述为具有复杂拓扑结构的网络。 许多大型网络的一个共同特性是顶点连接性服从无标度幂律分布 power law。 这个特征被发现是两个通用机制的结果,网络通过增加新的顶点不断扩大,新的顶点优先附加到已经良好连接的网站。 基于这两个因素的模型再现了观测到的稳态无标度分布,表明大型网络的发展受到超越个体系统特性的稳健自组织现象的支配。
研究课题及合作者
肝癌上皮向间质转化的模型
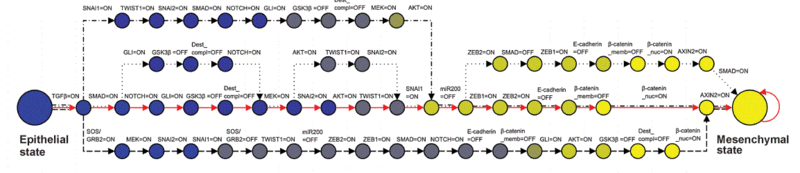
上皮-间质转化(EMT)是癌细胞离开原发肿瘤部位、侵袭周围组织并建立远处转移的发展过程。通过整合发展性EMT和浸润性肝癌中已知失调的信号通路,其研究人员构建了一个由70个节点和135条边组成的EMT网络。然后通过离散动态建模来了解由TGFβ驱动的EMT网络的动力学。研究使用该模型来识别抑制EMT的组合干预措施,并通过siRNA实验对其进行了验证。研究还发现许多明显成功的单一干预措施可能导致上皮状态和间充质状态之间的稳定状态。
合作者:弗吉尼亚大学医学院博士Thomas P. Loughran
生态社区建模
掠食者与猎物之间的关系,或植物与昆虫授粉媒介之间的共生相互作用,将生态群落的物种连接成一个相互依存的复杂网络。这意味着一个物种的灭绝会产生连锁反应,这种连锁反应很难预测,有时甚至是灾难性的。
合作者:宾夕法尼亚州立大学生物学教授Katriona Shea
植物保卫细胞中的信号转导
植物已经进化出能响应不断变化的环境条件的复杂信号转导机制,其一是受光打开气孔、干旱条件将其关闭。研究者已整合有关光和干旱信号的实验信息,以重建保卫细胞的信号转导网络并建模。其工作发现了知识空白,并产生了新的预测和假设。
合作者:宾夕法尼亚州立大学生物学系教授Sarah Assmann和Waller
研究团队
- Dr. Jorge G. T. Zanudo
- Dr. David Wooten
- Xiao Gan
- Parul Maheshwari
- Jordan Rozum
- Fatemeh Sadat Fatemi
学生
毕业博士(2013-2018)
- Dr. Gang Yang
- Dr. Steven Steinway, MD, PhD
- Dr. Zhongyao Sun
- Dr. Assieh Saadatpour
- Dr. Ranran Zhang
- Dr. Usha Nandini Raghavan
- Dr. Hari Thadakamalla
- Dr. Claire Christensen
- Dr. Song Li
博士后(2013-2018)
- Dr. Jorge G. T. Zanudo
- Dr. Colin Campbell
- Dr. Anshuman Gupta
- Dr. Jaewook Joo
- Dr. Juilee Thakar
- Dr. Suann Yang
- Dr. Rui-Sheng Wang
研究报道
- 一些依赖少数物种的社群,《物理学》
- Reka Albert正在用基于复杂网络的模型帮助生物学家解决迫切问题,《宾夕法尼亚州概况》
- 沉默蛋白质可能杀死T细胞,逆转白血病,《宾夕法尼亚州新闻》
- 基本科学指标,《科学观察》
获得荣誉
- 2019年,被选为美国科学进步协会学会会员 Fellow of the American Association for the Advancement of Science [1]。
- 2018年,雷卡 · 阿尔伯特当选为网络科学 Network Science Society 学会会员 [2]。
- 2016年,她成为匈牙利科学院 Hungarian Academy of Sciences 的外聘成员 [3]。
- 2010年,她被任命为美国物理学会 American Physical Society 会员 [4] 。 一年后,她获得了玛丽亚·格佩特-梅耶奖 Maria Goeppert-Mayer Award。[5] 玛丽亚·格佩特-梅耶奖(英语:Maria Goeppert-Mayer Award)是由美国物理协会颁发的年度奖项,授予对物理学做出杰出贡献的女性科学家。该奖项于1986年首次颁发,以1963年诺贝尔物理学奖得主玛丽亚·格佩特-梅耶的名字命名。格佩特-梅耶是继居里夫人之后,第二位获得诺贝尔物理学奖的女性。
- 2007年,被授予国家科学基金会 National Science Foundation 职业奖 CAREER Award 。
- 2004年,被选为斯隆研究员 Sloan Research Fellow。斯隆研究奖自1955年设立每年颁发一次,以表彰那些在其研究领域内被认为最有前途的早期职业学者(2020 年斯隆研究奖的完整获奖名单详见)。
联系方式
- 地址:152E Davey Laboratory, Pennsylvania State University, University Park, PA 16802
- 电话:814-865-1141
- 电子邮件:rza1@psu.edu
相关链接
参考文献
- ↑ https://www.aaas.org/page/2019-fellows
- ↑ https://netscisociety.net/award-prizes/society-fellows
- ↑ https://mta.hu/koztestuleti_tagok?PersonId=10048437
- ↑ https://science.psu.edu/news-and-events/2010-news/Albert2-2010
- ↑ "2011 Maria Goeppert Mayer Award Recipient". American Physical Society. Retrieved 18 February 2013.
编者推荐
集智论文
Barabasi-Albert 网络的配置模型 The configuration model for Barabasi-Albert networks
- 本论文介绍了重新布线方法(最初由纽曼提出) ,允许建立随机网络具有预先指定的度分布和两点相关性。
Barabasi-Albert 网络的扩散传染过程 The Diffusive Epidemic Process on Barabasi-Albert Networks
- 本文给出了无标度图上具有有限阈值的扩散传染病过程。 传染病的扩散过程描述了传染病在一个非定居人群中传播的过程,它是一个反应扩散过程。 在扩散阶段,根据感染者和易感者不同的扩散率,个体可以在连通节点之间跳跃。 在反应阶段,如果有一个被感染的个体共享同一个节点,并且被感染的个体可以自发恢复,那么就可能发生传染。 主要创新点是通过使用带有反应时间的 Gillespie 算法,使个体相互作用的数量与种群大小无关。
基因型自旋Barabási-Albert网络的修正 Ising 模型 A Modified Ising Model of Barabási-Albert Network with Gene-type Spins
- 由于生物状态之间的明显不对称性,本文提出了一个对称Ising模型的改进,以适应生命系统的非对称性,这里称为基因型自旋的修正Ising模型。 利用蒙特卡罗方法对相变进行了模拟分析,提出了一种与实际网络非常相似的网络类型的修正Ising模型的均场解,即无标度网络的Barabási-Albert模型。
集智视频
重访经典:无标度网络
本课程来自集智第 47 期图网络论文解读活动。
是对论文Emergence of scaling in random networks的解读
这篇文章是艾伯特-拉斯洛·巴拉巴西 Albert-László Barabási的大作,也是复杂网络领域的经典文献,它总结了存在于许多实际网络中的幂律分布特性,首次命名了无标度 网络这一重要概念,并研究了其背后的生成机制——偏好连接 preferential attachment。在当时学界主要研究网络的静态性质时, 它引入了对网络增长机制的研究,并且紧扣复杂系统的相关特性,至今仍然相当具有启发性,值得我们细读。
解读幂律分布与无标度网络
认真学习本课程,你能够做到:
- 熟悉幂律分布的概念与原理,了解分布在自然界的各种有趣幂律分布
- 了解无标度网络的相关原理与研究方法
其他
油管视频:Barabasi-Albert算法实现
视频中介绍Barabasi-Albert算法实现richer getting richer 现象。
油管视频:Reka Albert公开课(1)
本课程介绍了:网络结构和逻辑决定了生物网络的动态库 Network Structure and Logic Determines the Dynamic Repertoire of Biological Networks。
油管视频:Reka Albert公开课(2)
本课程介绍了:基于网络的生物系统动态建模 Network-based dynamic modeling of biological systems。
本中文词条由费米子编辑,欢迎在讨论页面留言。
本词条内容源自wikipedia及公开资料,遵守 CC3.0协议。