Banavar的推理运算
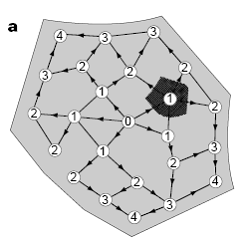
在该网络中每条有向边[math]\displaystyle{ e }[/math]就表示资源的流向,并且边的权重表示资源流量的大小[math]\displaystyle{ f_e }[/math]。
整个网络是由节点填充的一个D维空间中的区域,因此,网络的节点数与这个填充空间所占的体积成正比。例如,在2维空间中[math]\displaystyle{ N \sim r^2 }[/math],假设整个网络镶嵌在一个圆形区域里面,那么整个网络的节点数 。因此,D维空间中就是[math]\displaystyle{ N \sim r^D }[/math] ,其中[math]\displaystyle{ r }[/math]可以理解为整个系统的某种特征尺度。
接下来,假设每个网络节点在每个时刻都要消耗固定数量的能量资源C。那么每个时刻系统消耗的总的资源也就是系统的新陈代谢率就是:
同时,流入该节点的流量减去流出该节点的流量需等于常数值即对任意的节点[math]\displaystyle{ k }[/math]都应该有:
另一方面,我们可以统计整个网络中各个边的总流量,并认为这个流量即构成了整个生物体的重量(与生物体的尺寸成正比)。因此,有:
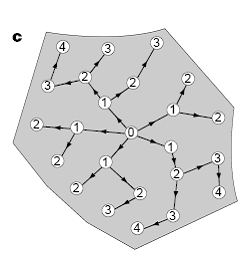
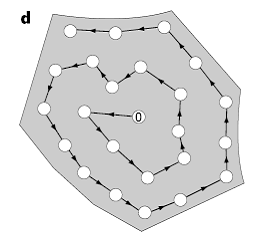
这样不同的网络拓扑结构在满足上述条件的情况下就会得到不同的[math]\displaystyle{ M }[/math]值。有定理保证,[math]\displaystyle{ M }[/math]值在图c所示的生成树网络中有最小值,而在d所示的螺旋形状的网络中有最大值。
并且可以计算出,c图所示的生成树对应的[math]\displaystyle{ M }[/math]满足:
所以:
当[math]\displaystyle{ D=3 }[/math]维空间的时候,它刚好是3/4律。
我们知道,[math]\displaystyle{ M }[/math]值最小意味着在保证能够供给网络上所有节点足够能量的前提下需要的消耗在运输网络中的能量最小,也就是说这样的网络是一种最有效的结构。这种最有效的结构恰恰是一个从源出发不断分叉构成的分形树状网络。因此该理论从最优原理的角度出发,不仅得到了3/4律,而且自发得到了分形网络结构。