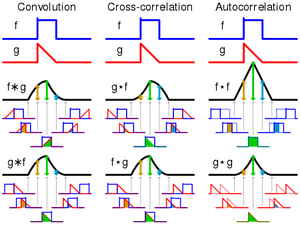
相关函数

卷积、互相关性和自相关性的视觉比较。

相关函数(量子场论)是一个给出随机变量之间的统计相关性的函数，其统计相关性取决于这些变量之间的空间或时间距离。如果我们认为随机变量之间的相关函数(量子场论) 代表在两个不同点测量的相同数量，那么这通常指的是由自相关组成的自相关函数。不同随机变量的相关函数有时被称为互相关函数，因为它们是由互相关组成的，该种函数主要强调由互相关组成的不同变量。

相关函数作为在时间或空间距离上的函数，是一种有效用的依赖性指标，可以用来评估样本点之间所需的距离，以使值有效地不相关。此外，在没有观测值的点上，它们进行了插值处理，提供了相关计算基础。

天文学、金融分析、计量经济学和统计力学中所使用到的相关函数的区别仅在于它们所应用的特定随机过程的不同。在量子场论中，量子分布上存在相关函数。

定义

对于在某些空间上不同点s和t的可能的不同随机变量 X(s)和 Y(t)，其相关函数(量子场论)为：

[math]\displaystyle{ C(s,t) = \operatorname{corr} ( X(s), Y(t) ) , }[/math]

其中,[math]\displaystyle{ \operatorname{corr} }[/math] 在相关性的文章中有描述。在这个定义中，我们假设随机变量是标量。如果不是，则可以定义更复杂的相关函数。例如，若 X(s) 是一个 n 维元素的随机向量， Y(t) 是一个q 维元素的向量，则用 [math]\displaystyle{ i,j }[/math] 元素定义相关函数的 n×q 矩阵：

[math]\displaystyle{ C_{ij}(s,t) = \operatorname{corr}( X_i(s) ，Y_j(t) ) 。 }[/math]

When n=q, sometimes the trace of this matrix is focused on. If the probability distributions have any target space symmetries, i.e. symmetries in the value space of the stochastic variable (also called internal symmetries), then the correlation matrix will have induced symmetries. Similarly, if there are symmetries of the space (or time) domain in which the random variables exist (also called spacetime symmetries), then the correlation function will have corresponding space or time symmetries. Examples of important spacetime symmetries are —

When n=q, sometimes the trace of this matrix is focused on. If the probability distributions have any target space symmetries, i.e. symmetries in the value space of the stochastic variable (also called internal symmetries), then the correlation matrix will have induced symmetries. Similarly, if there are symmetries of the space (or time) domain in which the random variables exist (also called spacetime symmetries), then the correlation function will have corresponding space or time symmetries. Examples of important spacetime symmetries are —

当 n=q 时，有时该矩阵的迹会集聚。如果概率分布具有目标空间对称性，即在随机变量的值空间中存在对称性(也称为内对称性) ，则相关矩阵将具有诱导对称性。类似地，如果随机变量所存在的空间(或时间)域具有对称性(也称为时空对称性) ，则相关函数(量子场论)将具有相应的空间或时间对称性。重要的时空对称的例子有:

平移对称 场域中C(s,s') = C(s − s')，其中s和 s' 被解释为给出点的坐标的向量

旋转对称 除上面提到的以外，还给出了C(s,s') = C(s − s')，其中|x|表示向量“ x”的标准值(对于实际的旋转，这是欧几里得或2-范数)。

高阶相关函数经常被定义。一个典型的n阶相关函数(量子场论)为：

[math]\displaystyle{ C_{i_1i_2\cdots i_n}(s_1,s_2,\cdots,s_n) = \langle X_{i_1}(s_1) X_{i_2}(s_2) \cdots X_{i_n}(s_n)\rangle。 }[/math]模板:Clarification needed

如果随机向量只有一个分量变量，那么指数[math]\displaystyle{ i,j }[/math]是冗余的。如果存在对称性，那么相关函数(量子场论)可以被分解成对称性的不可约表示,包括内对称性和时空对称性。

概率分布的性质

在这些定义下，相关函数的研究类似于概率分布的研究。许多随机过程可以用它们自有的相关函数完全表征；其中最著名的例子就是一类高斯过程。

在有限个点上定义的概率分布总是可以规范化的，但是当它们定义在连续空间上时，则需要格外注意。对这种分布的研究始于对随机游动的研究，并引出了Itō 演算的概念。

欧几里德空间中的 Feynman 路径积分将这个问题推广到了统计力学所着眼的其他问题中。任何满足被称为反射正性的相关函数条件的概率分布，在威克转动到闵可夫斯基时空之后，就引导出了局域量子场论（见Osterwalder-Schrader公理）。重整化运算是从概率分布空间到其本身的一组特定的映射。如果一个量子场论的映射有一个可以给出量子场论的不动点，则这个量子场论是可重整化的。