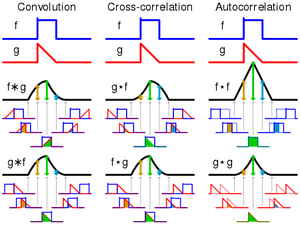
相关函数
相关函数是一个给出随机变量之间的统计相关性的函数,其统计相关性取决于这些变量之间的空间或时间距离。如果我们认为随机变量之间的相关函数代表在两个不同点测量的相同数量,那么这通常指的是由自相关组成的自相关函数。不同随机变量的相关函数有时被称为互相关函数,因为它们是由互相关组成的,该种函数主要强调由互相关组成的不同变量。
相关函数作为在时间或空间距离上的函数,是一种有效用的依赖性指标,可以用来评估样本点之间所需的距离,以使值有效地不相关。此外,在没有观测值的点上,它们进行了插值处理,提供了相关计算基础。
天文学、金融分析、计量经济学和统计力学中所使用到的相关函数的区别仅在于它们所应用的特定随机过程的不同。在量子场论中,量子分布上存在相关函数。
定义
对于在某些空间上不同点s和t的可能的不同随机变量 X(s)和 Y(t),其相关函数(量子场论)为:
- [math]\displaystyle{ C(s,t) = \operatorname{corr} ( X(s), Y(t) ) , }[/math]
其中,[math]\displaystyle{ \operatorname{corr} }[/math] 在相关性的文章中有描述。在这个定义中,我们假设随机变量是标量。如果不是,则可以定义更复杂的相关函数。例如,若 X(s) 是一个 n 维元素的随机向量, Y(t) 是一个q 维元素的向量,则用 [math]\displaystyle{ i,j }[/math] 元素定义相关函数的 n×q 矩阵:
- [math]\displaystyle{ C_{ij}(s,t) = \operatorname{corr}( X_i(s) ,Y_j(t) ) 。 }[/math]
当 n=q 时,有时该矩阵的迹会集聚。如果概率分布具有目标空间对称性,即在随机变量的值空间中存在对称性(也称为内对称性) ,则相关矩阵将具有诱导对称性。类似地,如果随机变量所存在的空间(或时间)域具有对称性(也称为时空对称性) ,则相关函数(量子场论)将具有相应的空间或时间对称性。重要的时空对称的例子有:
- 平移对称 场域中C(s,s') = C(s − s'),其中s和 s' 被解释为给出点的坐标的向量
- 旋转对称 除上面提到的以外,还给出了C(s,s') = C(s − s'),其中|x|表示向量“ x”的标准值(对于实际的旋转,这是欧几里得或2-范数)。
高阶相关函数经常被定义。一个典型的n阶相关函数(量子场论)为:
- [math]\displaystyle{ C_{i_1i_2\cdots i_n}(s_1,s_2,\cdots,s_n) = \langle X_{i_1}(s_1) X_{i_2}(s_2) \cdots X_{i_n}(s_n)\rangle。 }[/math]
如果随机向量只有一个分量变量,那么指数[math]\displaystyle{ i,j }[/math]是冗余的。如果存在对称性,那么相关函数(量子场论)可以被分解成对称性的不可约表示,包括内对称性和时空对称性。
概率分布的性质
在这些定义下,相关函数的研究类似于概率分布的研究。许多随机过程可以用它们自有的相关函数完全表征;其中最著名的例子就是一类高斯过程。
在有限个点上定义的概率分布总是可以规范化的,但是当它们定义在连续空间上时,则需要格外注意。对这种分布的研究始于对随机游动的研究,并引出了Itō 演算的概念。
欧几里德空间中的 Feynman 路径积分将这个问题推广到了统计力学所着眼的其他问题中。任何满足被称为反射正性的相关函数条件的概率分布,在威克转动到闵可夫斯基时空之后,就引导出了局域量子场论(见Osterwalder-Schrader公理)。重整化运算是从概率分布空间到其本身的一组特定的映射。如果一个量子场论的映射有一个可以给出量子场论的不动点,则这个量子场论是可重整化的。
参见
在天文学中,相关函数(量子场论)描述了宇宙中星系的分布。默认状态下,“相关函数(量子场论)”是指两点自相关函数。两点相关函数是一个变量(距离)的函数; 它描述了发现两个距离相隔的星系的所代表的超额概率(超过在假定情况下星系单独分散并且概率一致,所产生的概率)。它可以被认为是一个lumpy因子——某个距离尺度的值越高,在这个距离尺度上的宇宙就越接近lumpy宇宙
在统计力学中,相关函数(量子场论)是一个系统中秩序的度量,以数学相关函数(量子场论)为特征表现。相关函数描述了如自旋和密度的微观变量,在不同的位置是如何达到相关的。更具体地说,相关函数量化了微观变量之间在空间和时间上的平均相互变化。这种空间关联的一个典型例子是在铁和反铁磁材料中,自旋更愿分别与其最近邻居平行和反平行排列。(求证)
在量子场论中,(实空间) n 点相关函数(量子场论)被定义为{显式 n }场算子在不同位置的乘积的函数平均(函数期望值) [math]\displaystyle{ C_n\left(x_1, x_2, \ldots, x_n\right) := \left\langle\phi(x_1)\phi(x_2)\cdots\phi(x_n)\right\rangle = \frac{\int \mathcal{D}\phi\; e^{-S[\phi]}\phi(x_1)\cdots\phi(x_n)}{\int \mathcal{D}\phi\; e^{-S[\phi]}} }[/math] 对于依赖时间的相关函数,包括时间排序运算符[math]\displaystyle{ T }[/math]。相关函数也称为简单的相关因子,相关函数(量子场论)可以从物理上解释为粒子在 y 和 x 之间传播或激发的振幅。
相关资料
- wolfram官网中讲解了相关函数实践方法
- 自相关函数与互相关函数]相关概念、性质及意义。
- 以期望更长远的学习可以看一下这篇论文 [论文地址]
- 教材上也主要是应用讲解,尤其是信号分析、时间序列分析、随机过程上,推荐这本《信号与系统分析和应用》教材
编者推荐
集智相关课程
相关分析(一)(二)
该系列课程由研究复杂性理论的樊瑛老师讲授,主要讲解了定类与定类、数值型变量之间的相关性变量方法、定序与定序变量相关的变量方法以及偏相关和典型相关分析。
本中文词条由厚朴编译,小头盔审校,薄荷编辑,欢迎在讨论页面留言。
本词条内容翻译自 wikipedia.org,遵守 CC3.0协议。