经济复杂性指
理解经济复杂性指数需要在理解产品空间为基础。以里卡多·豪斯曼 Ricardo Hausmann 的话来说:产品空间要解决的是“鸡生蛋,蛋生鸡”的问题。试想,一个地区本来以种植玉米为主要经济来源,如果这时当地的人们想去改种植高粱似乎并不是一件困难的事情,但如果说,当地人想改行去做钟表这就是一件困难的事情了。 “没有钟表匠,你就做不出来钟表;但是钟表匠也不可能存在于一个不生产钟表的地方。”
因为有工程诀窍,管理经验等隐性知识的存在,所以即便当地的庄稼汉们获得了制作钟表的图纸也无法立刻投入生产。研究者把这种“隐性知识”称之为:Know-how。正是这样的隐形知识使得不同的产品生产之间存在了距离的差异。农夫不会在获得图纸后立刻变成钟表匠;流水线工人也不会在买到电脑后立刻变成程序员。在上面的例子中,“玉米-高粱”这两个产品之间的距离比“玉米-钟表”要更近一些。
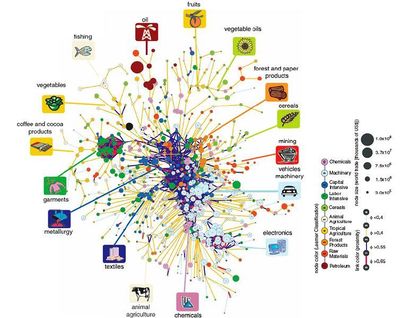
产品空间 Product Space 就是用来刻画不同产品间距离的图网络。两样产品共同出口的可能性决定了这二者在产品空间中的距离远近。
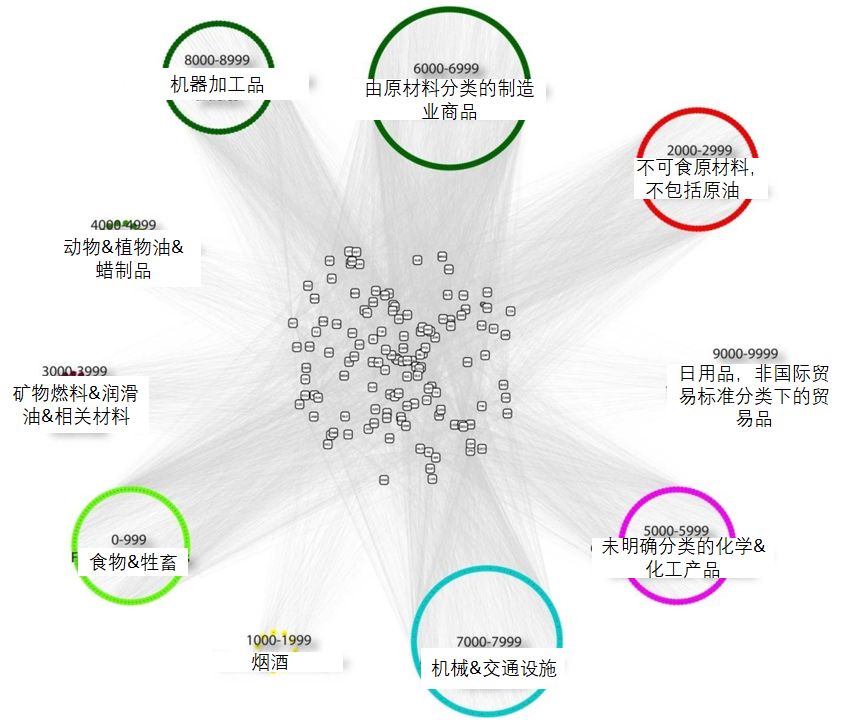
研究者设定了一个显示性比较优势指数 Revealed Comparative Advantage Index,RCA阈值,借用相关国家的进出口数据以及产品名录,当某一国家出口的产品超过该阈值时,即可在国家-产品网络中为这两个节点链接对应的边。由此研究者刻画出的2000年国家-产品网络图像(部分)如下:
该图像中包含了 129 个国家(中间小方框)、772 个各类产品(外围的各色实心点,已按照产品名录分类)和 13470 条连边。(图片来源:Hidalgo et al., 2009)
在得到这样的网络图像后,就可以进一步通过反射方法 Method of Reflections 来计算一个国家生产产品的多样性和普遍性——即经济复杂性。这一过程类似于计算机领域的PageRank 算法,在多次迭代后,能得到一个稳定的结果。经济复杂性指数 Economic Complexity Index,ECI 则是计算过程中相关矩阵的特征值。采用同样的方法 Hidalgo 等人也定义了产品领域的产品复杂性指数 Product Complexity Index,PCI。但是,经济复杂性指数和产品复杂性指数的解释在近些年的研究中缺存在一些争议。
按照上述定义,经济复杂性指数被描述为一个与国家出口商品多样性相关的指数,但是在后续的研究中,经济复杂性指数被斯德哥尔摩环境研究所的 Eric Kemp-Benedict 证明是和多样性正交的量,证明它在解释多样性上的能力有限,但尽管经济复杂性指数和产品多样性的关系被证明是正交的,但是这也并不能意味着完全无关,在电子科技大学研究员高见的研究中,就表明中国城市的经济复杂性和多样性呈现正相关。
在 Penny Mealy 等人最新的研究中对经济复杂性指数给出了另外一种新的解释:谱聚类 Spectral Clustering是一种聚类算法,对非线性可分的数据具有较强的区分能力。Penny Mealy 的研究工作中证明经济复杂性指数在数学上等价于谱聚类。经济复杂性指数是由节点间的距离(相似程度)来定义的。
尽管存在解释上的争执。不过,研究者普遍认为一个经济体的经济复杂性指数和GDP数据呈现正相关性。
维基百科上对于经济复杂性指数的定义为:经济复杂性指数 ECI 是衡量大型经济系统(通常是城市、地区或国家)生产能力的整体指标。特别是经济复杂性指数可以用来解释在人口中通过城市、国家或地区的经济活动来表现的累计知识。
为了实现这一目标,经济复杂性指数将一个地点的可用知识定义为该地点开展的所有活动的平均知识,将一项活动的平均知识定义为开展该经济活动的地点的平均知识。与经济复杂性指数等价的概念是产品复杂性指数或 PCI。
[[File:Index of economic complexity - Iran.svg|thumb|经济复杂性指数,伊朗(1964-2014)
背景
经济复杂性指数是由麻省理工学院媒体实验室的凯撒·伊达尔戈César A. Hidalgo和哈佛大学肯尼迪政府学院的里卡多·豪斯曼 Ricardo Hausmann 共同开发的。César Hidalgo 是麻省理工学院媒体实验室的科学家,也是集体学习研究组 Collective Learning Group 的负责人。2008-2010年于哈佛大学国际发展中心从事博士后研究工作,期间,Hidalgo和他的同事Ricardo Hausmann合作发表了一系列论文,探讨如何利用经济复杂性去刻画一个国家和地区的经济水平与生产能力。并在 2009 年发表的论文 The building blocks of economic complexity 中提出了经济复杂性指数 Economic Complexity Index,ECI。经济复杂性指数的数据可在经济复杂性观测站获得。其原始公式于2009年发表在美国国家科学院院刊上。[1]
基础
在其严格的数学定义中,经济复杂性指数是连接国家与国家之间的矩阵的特征向量来定义的,是连接国家与其出口产品的矩阵投影。由于经济复杂性指数涉及到国家的多样性和产品的普遍性的相关信息,因此它能够得出一种衡量经济复杂性的方法,其中包含了一个国家出口的多样性和其复杂性的信息。例如,经济复杂性指数较高的日本或德国出口的许多商品普遍性较低,且这些产品是由高度多样化的国家生产的,这表明这些国家是多样化且复杂的经济体。 而经济复杂性指数较低的国家,如安哥拉和赞比亚,仅出口少数产品,这些产品的普遍性相对较高,而生产的国家则普遍低多样化,这表明这些国家几乎不存在多样性,其出口的产品也不是很复杂。
应用
凯撒·伊达尔戈 César A. Hidalgo 和里卡多·豪斯曼 Ricardo Hausmann所提出的经济复杂性指数概念不仅是一种描述性指标,而且也是经济增长和收入不平等的预测工具。根据他们在《经济复杂性地图集》(2011)一书中提出的统计模型,[2]与传统的治理、竞争力(世界经济论坛的全球竞争力指数)和人力资本(按教育程度衡量)指标相比,经济复杂性指数能够更准确地预测人均GDP增长。经济复杂性还显示出与收入不平等的强烈负相关性,表明知识密集型的生产结构在收入分配方面更具包容性,并对收入不平等的跨国差异提供了一个从统计上讲比库兹涅茨曲线更强有力的解释。[3]
参见
References
<references>
编者推荐
集智文章
经济复杂性指数:利用网络科学判断国家经济实力
广为熟知的宏观经济指标 GDP(国民生产总值)、CPI(消费者价格指数);刻量贫富差距的基尼系数等指标具有一定的局限,不能完整体现经济实力的全貌,因此提出利用经济复杂性去刻画一个国家和地区的经济水平与生产能力。该文章简要介绍了经济复杂性指数及相关概念。
集智课程
经济金融系统复杂性研究
本课程主要介绍经济系统复杂性(复杂性经济学)的基本思想以及复杂系统研究的多主体建模(计算实验)方法。在此基础上,作为案例介绍我们所做的两个具体工作。
李红刚:经济金融系统复杂性
李红刚:经济金融系统复杂性 主要介绍经济金融系统复杂性的独特表现以及经济金融系统复杂性研究的基本思想和主要方法,并简要介绍本科研小组在金融市场演化行为以及金融机构系统性风险研究方面的典型工作。
应对社会经济系统复杂性的系统思维与系统方法
本课程中,将会介绍如何利用系统思维和系统动力学、多主体模型模拟、复杂网络等系统方法,帮助我们更好理解和应对复杂的社会经济系统。
本中文词条由[[用户:]]参与编译,薄荷编辑,欢迎在讨论页面留言。
本词条内容源自wikipedia及公开资料,遵守 CC3.0协议。
- ↑ Cesar A. Hidalgo, Ricardo Hausmann (2009). "The Building Blocks of Economic Complexity". Proceedings of the National Academy of Sciences. PNAS. 106 (26): 10570–10575. arXiv:0909.3890. Bibcode:2009PNAS..10610570H. doi:10.1073/pnas.0900943106. PMC 2705545. PMID 19549871.
- ↑ Ricardo Hausmann, Cesar Hidalgo; et al. "The Atlas of Economic Complexity". Puritan Press, Cambridge MA. Archived from the original on 18 May 2012. Retrieved 26 April 2012.
- ↑ Dominik Hartmann, Miguel Guevara, Cristian Jara-Figueroa, Manuel Aristaran, Cesar Hidalgo (2018), "Linking Economic Complexity, Institutions, and Income Inequality", World Development, 93: 75–93, arXiv:1505.07907, doi:10.1016/j.worlddev.2016.12.020
{{citation}}: CS1 maint: multiple names: authors list (link)