复杂系统生物学

来自集智百科 - 复杂系统|人工智能|复杂科学|复杂网络|自组织
Moonscar（讨论 | 贡献）2020年7月14日 (二) 21:32的版本 （Moved page from wikipedia:en:Complex systems biology (history)）
(差异) ←上一版本 | 最后版本 (差异) | 下一版本→ (差异)
跳到导航 跳到搜索

此词条暂由彩云小译翻译，未经人工整理和审校，带来阅读不便，请见谅。

模板:Multiple issues

}}

Complex systems biology (CSB) is a branch or subfield of mathematical and theoretical biology concerned with complexity of both structure and function in biological organisms, as well as the emergence and evolution of organisms and species, with emphasis being placed on the complex interactions of, and within, bionetworks,[1] and on the fundamental relations and relational patterns that are essential to life.[2][3][4][5][6] CSB is thus a field of theoretical sciences aimed at discovering and modeling the relational patterns essential to life that has only a partial overlap with complex systems theory,[7] and also with the systems approach to biology called systems biology; this is because the latter is restricted primarily to simplified models of biological organization and organisms, as well as to only a general consideration of philosophical or semantic questions related to complexity in biology.[citation needed] Moreover, a wide range of abstract theoretical complex systems are studied as a field of applied mathematics, with or without relevance to biology, chemistry or physics.

Complex systems biology (CSB) is a branch or subfield of mathematical and theoretical biology concerned with complexity of both structure and function in biological organisms, as well as the emergence and evolution of organisms and species, with emphasis being placed on the complex interactions of, and within, bionetworks, and on the fundamental relations and relational patterns that are essential to life. CSB is thus a field of theoretical sciences aimed at discovering and modeling the relational patterns essential to life that has only a partial overlap with complex systems theory, and also with the systems approach to biology called systems biology; this is because the latter is restricted primarily to simplified models of biological organization and organisms, as well as to only a general consideration of philosophical or semantic questions related to complexity in biology. Moreover, a wide range of abstract theoretical complex systems are studied as a field of applied mathematics, with or without relevance to biology, chemistry or physics.

复杂系统生物学(Complex systems biology，CSB)是数学和理论生物学的一个分支或分支，研究生物有机体的结构和功能的复杂性，以及生物体和物种的出现和进化，重点研究生物网络内部和生物网络之间的复杂相互作用，以及对生命至关重要的基本关系和关系模式。因此，CSB 是一个理论科学领域，旨在发现和建模的关系模式的基本生命，只有一部分重叠的复杂系统理论，也与生物学的系统方法称为系统生物学; 这是因为后者主要限于简化模型的生物组织和有机体，以及只有一个哲学或语义问题的复杂性在生物学的一般考虑。此外，广泛的抽象理论复杂系统作为应用数学领域的研究，与生物学，化学或物理学有关或无关。

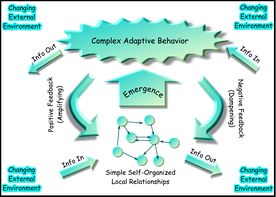
Network Representation of a Complex Adaptive System

Network Representation of a Complex Adaptive System

复杂适应性系统的网络表示


Complexity of organisms and biosphere

A complete definition of complexity for individual organisms, species, ecosystems, biological evolution and the biosphere has eluded researchers, and still is an ongoing issue.[3][8]

Seawifs global biosphere.jpg

A complete definition of complexity for individual organisms, species, ecosystems, biological evolution and the biosphere has eluded researchers, and still is an ongoing issue.right

对于单个生物体、物种、生态系统、生物进化和生物圈的复杂性的完整定义一直困扰着研究人员，而且仍然是一个持续的问题


Most complex system models are often formulated in terms of concepts drawn from statistical physics, information theory and non-linear dynamics; however, such approaches are not focused on, or do not include, the conceptual part of complexity related to organization and topological attributes or algebraic topology, such as network connectivity of genomes, interactomes and biological organisms that are very important.[6][9][10] Recently, the two complementary approaches based both on information theory, network topology/abstract graph theory concepts are being combined for example in the fields of neuroscience and human cognition.[7][11] It is generally agreed that there is a hierarchy of complexity levels of organization that should be considered as distinct from that of the levels of reality in ontology.[7][12][13] The hierarchy of complexity levels of organization in the biosphere is also recognized in modern classifications

Most complex system models are often formulated in terms of concepts drawn from statistical physics, information theory and non-linear dynamics; however, such approaches are not focused on, or do not include, the conceptual part of complexity related to organization and topological attributes or algebraic topology, such as network connectivity of genomes, interactomes and biological organisms that are very important. Recently, the two complementary approaches based both on information theory, network topology/abstract graph theory concepts are being combined for example in the fields of neuroscience and human cognition. It is generally agreed that there is a hierarchy of complexity levels of organization that should be considered as distinct from that of the levels of reality in ontology. The hierarchy of complexity levels of organization in the biosphere is also recognized in modern classifications

大多数复杂系统模型通常是根据从统计物理学、信息论和非线性动力学中提取的概念来建立的; 然而，这些方法并不关注或不包括与组织和拓扑属性或代数拓扑相关的复杂性的概念部分，例如基因组的网络连接、交叉点和非常重要的生物有机体。近年来，以信息论为基础的网络拓扑/抽象图论两种互补的研究方法在神经科学和人类认知领域得到了广泛的应用。人们普遍认为，组织的复杂性层次有一个层次，应该被视为不同于本体论中的实在层次。在现代分类中，生物圈内组织的复杂程度等级也得到承认

of taxonomic ranks, such as: biological domain and biosphere, biological kingdom, Phylum, biological class, order, family, genus and species. Because of their dynamic and composition variability, intrinsic "fuzziness", autopoietic attributes, ability to self-reproduce, and so on, organisms do not fit into the 'standard' definition of general systems, and they are therefore 'super-complex' in both their function and structure; organisms can be thus be defined in CSB only as 'meta-systems' of simpler dynamic systems[7][14] Such a meta-system definition of organisms, species, 'ecosystems', and so on, is not equivalent to the definition of a system of systems as in Autopoietic Systems Theory,;[15] it also differs from the definition proposed for example by K.D. Palmer in meta-system engineering,[16] organisms being quite different from machines and automata with fixed input-output transition functions, or a continuous dynamical system with fixed phase space,引用错误：没有找到与</ref>对应的<ref>标签 contrary to the Cartesian philosophical thinking; thus, organisms cannot be defined merely in terms of a quintuple A of (states, startup state, input and output sets/alphabet, transition function),[17] although 'non-deterministic automata', as well as 'fuzzy automata' have also been defined. Tessellation or cellular automata provide however an intuitive, visual/computational insight into the lower levels of complexity, and have therefore become an increasingly popular, discrete model studied in computability theory, applied mathematics, physics, computer science, theoretical biology/systems biology, cancer simulations and microstructure modeling. Evolving cellular automata using genetic algorithms[18][19] contrary to the Cartesian philosophical thinking; thus, organisms cannot be defined merely in terms of a quintuple A of (states, startup state, input and output sets/alphabet, transition function), although 'non-deterministic automata', as well as 'fuzzy automata' have also been defined. Tessellation or cellular automata provide however an intuitive, visual/computational insight into the lower levels of complexity, and have therefore become an increasingly popular, discrete model studied in computability theory, applied mathematics, physics, computer science, theoretical biology/systems biology, cancer simulations and microstructure modeling. Evolving cellular automata using genetic algorithms[20] 与笛卡尔哲学思想相反; 因此，生物体不能仅仅被定义为五个 a (状态，启动状态，输入和输出集/字母表，转换函数) ，虽然“非确定性自动机” ，以及“模糊自动机”也已经被定义。镶嵌或细胞自动机提供了一个直观的，可视的/可计算的洞察力的复杂性较低的水平，因此已成为一个越来越流行的，离散模型研究在可计算性理论，应用数学，物理，计算机科学，理论生物学/系统生物学，癌症模拟和微观结构建模。使用遗传算法进化细胞自动机

Evolving Cellular Automata with Genetic Algorithms: A Review of Recent Work, Melanie Mitchell, James P. Crutchfeld, Rajarshi Das (In Proceedings of the First International Conference on Evolutionary Computation and Its Applications (EvCA'96). Moscow, Russia: Russian Academy of Sciences, 1996.)</ref>[21] is also an emerging field attempting to bridge the gap between the tessellation automata and the higher level complexity approaches in CSB.

Evolving Cellular Automata with Genetic Algorithms: A Review of Recent Work, Melanie Mitchell, James P. Crutchfeld, Rajarshi Das (In Proceedings of the First International Conference on Evolutionary Computation and Its Applications (EvCA'96). Moscow, Russia: Russian Academy of Sciences, 1996.)</ref> is also an emerging field attempting to bridge the gap between the tessellation automata and the higher level complexity approaches in CSB.

基于遗传算法的细胞自动机的演化: 最新研究回顾，Melanie Mitchell，James p. Crutchfeld，Rajarshi Das (In Proceedings of the First International Conference o n n x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x。俄罗斯，莫斯科: 俄罗斯科学院，1996年。) </ref > 也是一个新兴的领域，它试图弥合分块自动机和 CSB 中更高层次复杂性方法之间的差距。


Topics in complex systems biology

Animated Molecular Model of a DNA double helix

Animated Molecular Model of a DNA double helix

DNA 的动态分子模型双螺旋

Telomerase structure and function

Telomerase structure and function

端粒酶的结构与功能

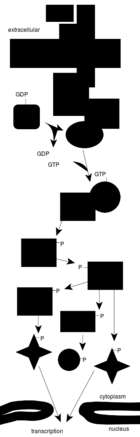
A Complex Signal Transduction Pathway

A Complex Signal Transduction Pathway

一条复杂的信号转导

The following is only a partial list of topics covered in complex systems biology:

The following is only a partial list of topics covered in complex systems biology:

以下只是复杂系统生物学所涉及的部分主题清单:

{{cite journal

{{cite journal

{引用期刊 

|author1=Hayete, B |author2=Gardner, TS |author3=Collins, JJ | year = 2007

|author1=Hayete, B |author2=Gardner, TS |author3=Collins, JJ | year = 2007

1 = Hayete，b | author2 = Gardner，TS | author3 = Collins，JJ | year = 2007 

| title = Size matters: network inference tackles the genome scale

| title = Size matters: network inference tackles the genome scale

| title = 规模问题: 网络推理解决了基因组规模 

| journal = Molecular Systems Biology

| journal = Molecular Systems Biology

分子系统生物学 

| volume = 3 |issue = 1| pages = 77

| volume = 3 |issue = 1| pages = 77

3 | issue = 1 | pages = 77 

| doi = 10.1038/msb4100118

| doi = 10.1038/msb4100118

| doi = 10.1038/msb4100118 

| pmid = 17299414

| pmid = 17299414

17299414 

| pmc = 1828748

| pmc = 1828748

1828748

}}</ref>

}}</ref>

} </ref >

  • Immune system


See also

模板:Portal

模板:Biological classification

模板:Colbegin


Biographies

模板:Colbegin


Notes

  1. ↑ Sprites, P; Glymour, C; Scheines, R (2000). Causation, Prediction, and Search: Adaptive Computation and Machine Learning (2nd ed.). MIT Press. 
  2. ↑ Donald Snooks, Graeme, "A general theory of complex living systems: Exploring the demand side of dynamics", Complexity, vol. 13, no. 6, July/August 2008.
  3. ↑ 3.0 3.1 Bonner, J. T. 1988. The Evolution of Complexity by Means of Natural Selection. Princeton: Princeton University Press.
  4. ↑ 4.0 4.1 Rosen, R. (1958a). "A Relational Theory of Biological Systems". Bulletin of Mathematical Biophysics. 20 (3): 245–260. doi:10.1007/bf02478302.
  5. ↑ Baianu, I. C. (2006). "Robert Rosen's Work and Complex Systems Biology". Axiomathes. 16 (1–2): 25–34. doi:10.1007/s10516-005-4204-z.
  6. ↑ 6.0 6.1 Rosen, R. (1958b). "The Representation of Biological Systems from the Standpoint of the Theory of Categories". Bulletin of Mathematical Biophysics. 20 (4): 317–341. doi:10.1007/bf02477890.
  7. ↑ Heylighen, Francis (2008). "Complexity and Self-Organization". In Bates, Marcia J.; Maack, Mary Niles. Encyclopedia of Library and Information Sciences. CRC.
  8. ↑ ^ Heylighen, Francis (2008). "Complexity and Self-Organization". In Bates, Marcia J.; Maack, Mary Niles. Encyclopedia of Library and Information Sciences. CRC.
  9. ↑ "abstract relational biology (ARB)". PlanetPhysics. Retrieved 2010-03-17.
  10. ↑ http://hdl.handle.net/10101/npre.2011.6115.1 Wallace, Rodrick. When Spandrels Become Arches: Neural crosstalk and the evolution of consciousness. Available from Nature Precedings (2011)
  11. ↑ Poli R (2001a). "The Basic Problem of the Theory of Levels of Reality". Axiomathes. 12 (3–4): 261–283. doi:10.1023/A:1015845217681.
  12. ↑ Poli R (1998). "Levels". Axiomathes. 9 (1–2): 197–211. doi:10.1007/bf02681712. PMID 8053082.
  13. ↑ Metasystem Transition Theory, Valentin Turchin, Cliff Joslyn, 1993-1997
  14. ↑ Reflexive Autopoietic Systems Theory
  15. ↑ Meta-system Engineering, Kent D. Palmer, 1996
  16. ↑ John E. Hopcroft, Rajeev Motwani, Jeffrey D. Ullman.2000. Introduction to Automata Theory, Languages, and Computation (2nd Edition)Pearson Education.
  17. ↑ The Evolutionary Design of Collective Computation in Cellular Automata, James P. Crutchfeld, Melanie Mitchell, Rajarshi Das (In J. P. Crutchfield and P. K. Schuster (editors), Evolutionary Dynamics|Exploring the Interplay of Selection, Neutrality, Accident, and Function. New York: Oxford University Press, 2002.)
  18. ↑ Framework for Systems with Dynamic Topology. International Journal of Computing Anticipatory System's 14:259–270
  19. ↑ 动态拓扑系统框架。国际计算期刊预期系统的14:259-270 </ref
  20. ↑ Peak, West; Messinger, Mott; Messinger, SM; Mott, KA (2004). "Evidence for complex, collective dynamics and emergent, distributed computation in plants". Proceedings of the National Academy of Sciences of the USA. 101 (4): 918–922. Bibcode:2004PNAS..101..918P. doi:10.1073/pnas.0307811100. PMC 327117. PMID 14732685.
  21. ↑ Rosen, R. 1960. (1960). "A quantum-theoretic approach to genetic problems". Bulletin of Mathematical Biophysics. 22 (3): 227–255. doi:10.1007/BF02478347.
  22. ↑ Baianu, I. C.: 2006 (2006). "Robert Rosen's Work and Complex Systems Biology". Axiomathes. 16 (1–2): 25–34. doi:10.1007/s10516-005-4204-z.
  23. ↑ Rosen, R.: 1958b (1958). "The Representation of Biological Systems from the Standpoint of the Theory of Categories". Bulletin of Mathematical Biophysics. 20 (4): 317–341. doi:10.1007/BF02477890.
  24. ↑ PlanetMath
  25. ↑ "PlanetMath". PlanetMath. Retrieved 2010-03-17.
  26. ↑ 27.0 27.1 {{cite journal {{cite journal {引用期刊 | author = Faith, JJ | author = Faith, JJ 作者 = Faith，JJ | year = 2007 | year = 2007 2007年 | title = Large-Scale Mapping and Validation of Escherichia coli Transcriptional Regulation from a Compendium of Expression Profiles | title = Large-Scale Mapping and Validation of Escherichia coli Transcriptional Regulation from a Compendium of Expression Profiles | title = 大比例绘制和验证表达式概要中的大肠桿菌转录调控 | journal = PLOS Biology | journal = PLOS Biology | journal = PLOS Biology | volume = 5 | issue = 1 | pages = 54–66 | volume = 5 | issue = 1 | pages = 54–66 5 | issue = 1 | pages = 54-66 | doi = 10.1371/journal.pbio.0050008 | doi = 10.1371/journal.pbio.0050008 10.1371/journal.pbio. 0050008 | pmid = 17214507 | pmid = 17214507 17214507 | pmc = 1764438 | pmc = 1764438 1764438 | display-authors = 1 | display-authors = 1 | display-authors = 1 | last2 = Hayete | last2 = Hayete 2 = Hayete | first2 = Boris | first2 = Boris 2 = Boris | last3 = Thaden | last3 = Thaden 3 = Thaden | first3 = Joshua T. | first3 = Joshua T. 3 = Joshua t. | last4 = Mogno | last4 = Mogno 4 = Mogno | first4 = Ilaria | first4 = Ilaria 4 = Ilaria | last5 = Wierzbowski | last5 = Wierzbowski 5 = Wierzbowski | first5 = Jamey | first5 = Jamey 5 = Jamey | last6 = Cottarel | last6 = Cottarel 6 = Cottarel | first6 = Guillaume | first6 = Guillaume 6 = Guillaume | last7 = Kasif | last7 = Kasif 7 = Kasif | first7 = Simon | first7 = Simon 7 = Simon | last8 = Collins | last8 = Collins 8 = Collins | first8 = James J. | first8 = James J. 8 = James j. | last9 = Gardner | last9 = Gardner 9 = Gardner | first9 = Timothy S. | first9 = Timothy S. 9 = Timothy s. }}
  27. ↑ 28.0 28.1 28.2 }} 引用错误：无效<ref>标签；name属性“Hayete2007”使用不同内容定义了多次


References cited

取自“https://wiki.swarma.org/index.php?title=复杂系统生物学&oldid=10288”