热力学第二定律

此词条暂由彩云小译翻译，未经人工整理和审校，带来阅读不便，请见谅。

The second law of thermodynamics states that the total entropy of an isolated system can never decrease over time, and is constant if and only if all processes are reversible.^[1] Isolated systems spontaneously evolve towards thermodynamic equilibrium, the state with maximum entropy.

The second law of thermodynamics states that the total entropy of an isolated system can never decrease over time, and is constant if and only if all processes are reversible. Isolated systems spontaneously evolve towards thermodynamic equilibrium, the state with maximum entropy.

热力学第二定律指出，孤立系统的总熵永远不会随着时间而减少，而且只有当且仅当所有过程都是可逆的时，总熵才是恒定的。孤立的系统自发地进化到热力学平衡状态，即熵最大的状态。

The total entropy of a system and its surroundings can remain constant in ideal cases where the system is in thermodynamic equilibrium, or is undergoing a (fictive) reversible process. In all processes that occur, including spontaneous processes,^[2] the total entropy of the system and its surroundings increases and the process is irreversible in the thermodynamic sense. The increase in entropy accounts for the irreversibility of natural processes, and the asymmetry between future and past.^[3]

The total entropy of a system and its surroundings can remain constant in ideal cases where the system is in thermodynamic equilibrium, or is undergoing a (fictive) reversible process. In all processes that occur, including spontaneous processes, the total entropy of the system and its surroundings increases and the process is irreversible in the thermodynamic sense. The increase in entropy accounts for the irreversibility of natural processes, and the asymmetry between future and past.

系统及其周围环境的总熵在理想情况下可以保持不变，在这种情况下，系统处于热力学平衡期，或者正在经历一个(虚拟的)可逆过程期。在所有发生的过程中，包括自发过程，系统及其周围环境的总熵增加，这一过程在热力学意义上是不可逆的。熵的增加解释了自然过程的不可逆性，以及未来和过去之间的不对称性。

Historically, the second law was an empirical finding that was accepted as an axiom of thermodynamic theory. Statistical mechanics, classical or quantum, explains the microscopic origin of the law.

从历史上看，第二定律是一个经验性的发现，被公认为热力学理论的公理。统计力学，无论是经典的还是量子的，都可以解释这个定律的微观起源。

The second law has been expressed in many ways. Its first formulation is credited to the French scientist Sadi Carnot, who in 1824 showed that there is an upper limit to the efficiency of conversion of heat to work in a heat engine. This aspect of the second law is also known as Carnot's rule or limit.^[4]

The second law has been expressed in many ways. Its first formulation is credited to the French scientist Sadi Carnot, who in 1824 showed that there is an upper limit to the efficiency of conversion of heat to work in a heat engine. This aspect of the second law is also known as Carnot's rule or limit.

第二定律已经用许多方式表达过了。法国科学家萨迪 · 卡诺在1824年证明了热能在热机中转化为功的效率是有上限的。这方面的第二定律也被称为卡诺的规则或限制。

Introduction

引言

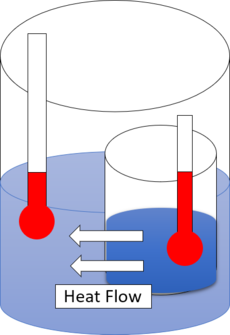
Heat flow from hot water to cold water.

热量从热水流向冷水。

The first law of thermodynamics provides the definition of the internal energy of a thermodynamic system, and expresses the law of conservation of energy.^[5]^[6] The second law is concerned with the direction of natural processes.^[7] It asserts that a natural process runs only in one sense, and is not reversible. For example, when a path for conduction and radiation is made available, heat always flows spontaneously from a hotter to a colder body. Such phenomena are accounted for in terms of entropy.^[8]^[9] If an isolated system is held initially in internal thermodynamic equilibrium by internal partitioning impermeable walls, and then some operation makes the walls more permeable, then the system spontaneously evolves to reach a final new internal thermodynamic equilibrium, and its total entropy, $S$ , increases.

The first law of thermodynamics provides the definition of the internal energy of a thermodynamic system, and expresses the law of conservation of energy. The second law is concerned with the direction of natural processes. It asserts that a natural process runs only in one sense, and is not reversible. For example, when a path for conduction and radiation is made available, heat always flows spontaneously from a hotter to a colder body. Such phenomena are accounted for in terms of entropy. If an isolated system is held initially in internal thermodynamic equilibrium by internal partitioning impermeable walls, and then some operation makes the walls more permeable, then the system spontaneously evolves to reach a final new internal thermodynamic equilibrium, and its total entropy, , increases.

能量守恒定律提供了热力学系统内能的定义，并表达了能量守恒定律。第二定律与自然过程的方向有关。它断言自然过程只在一种意义上运行，而且是不可逆的。例如，当有了传导和辐射的路径时，热总是自发地从一个较热的物体流向一个较冷的物体。这种现象可以用熵来解释。如果一个孤立的系统最初是通过内部分隔不可渗透的墙来保持在内部热力学平衡，然后一些操作使墙更具渗透性，那么系统自发地进化到最终达到一个新的内部热力学平衡，其总熵增加。

In a fictive reversible process, an infinitesimal increment in the entropy ( $d S$ ) of a system is defined to result from an infinitesimal transfer of heat ( $δ Q$ ) to a closed system (which allows the entry or exit of energy – but not transfer of matter) divided by the common temperature ( $T$ ) of the system in equilibrium and the surroundings which supply the heat:^[10]

In a fictive reversible process, an infinitesimal increment in the entropy () of a system is defined to result from an infinitesimal transfer of heat () to a closed system (which allows the entry or exit of energy – but not transfer of matter) divided by the common temperature () of the system in equilibrium and the surroundings which supply the heat:

在虚构的可逆过程中，系统熵的无穷小增量被定义为由无穷小的热量传递()到一个封闭系统(允许能量进入或出去，但不允许物质传递)除以平衡系统和提供热量的环境的共同温度() :

[math]\displaystyle{ \mathrm dS = \frac{\delta Q}{T} \,\, \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \text {(closed system, idealized fictive reversible process)}. }[/math]

[math]\displaystyle{ \mathrm dS = \frac{\delta Q}{T} \,\, \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \text {(closed system, idealized fictive reversible process)}. }[/math]

(闭合系统，理想化的可逆过程) / math

Different notations are used for infinitesimal amounts of heat ( $δ$ ) and infinitesimal amounts of entropy ( $d$ ) because entropy is a function of state, while heat, like work, is not. For an actually possible infinitesimal process without exchange of mass with the surroundings, the second law requires that the increment in system entropy fulfills the inequality ^[11]^[12]

Different notations are used for infinitesimal amounts of heat () and infinitesimal amounts of entropy () because entropy is a function of state, while heat, like work, is not. For an actually possible infinitesimal process without exchange of mass with the surroundings, the second law requires that the increment in system entropy fulfills the inequality

用不同的符号表示无穷小量的热量()和无穷小量的熵() ，因为熵是状态的函数，而热量和功一样不是。第二定律要求系统熵的增量满足不等式，对于实际上可能存在的不与环境发生质量交换的无穷小过程，系统熵增量满足不等式

[math]\displaystyle{ \mathrm dS \gt \frac{\delta Q}{T_{surr}} \,\, \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \text {(closed system, actually possible, irreversible process).} }[/math]

[math]\displaystyle{ \mathrm dS \gt  \frac{\delta Q}{T_{surr}} \,\, \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \text {(closed system, actually possible, irreversible process).} }[/math]

(实际上可能是封闭系统，不可逆性)。数学

This is because a general process for this case may include work being done on the system by its surroundings, which can have frictional or viscous effects inside the system, because a chemical reaction may be in progress, or because heat transfer actually occurs only irreversibly, driven by a finite difference between the system temperature ( $T$ ) and the temperature of the surroundings ( $T$ _surr).^[13]^[14] Note that the equality still applies for pure heat flow,^[15]

This is because a general process for this case may include work being done on the system by its surroundings, which can have frictional or viscous effects inside the system, because a chemical reaction may be in progress, or because heat transfer actually occurs only irreversibly, driven by a finite difference between the system temperature () and the temperature of the surroundings (_surr).

这是因为这种情况下的一般过程可能包括周围环境对系统所做的功，这可能在系统内部产生摩擦或粘滞效应，因为一个化学反应可能正在进行，或者因为热传递实际上只是不可逆地发生，由系统温度()和周围环境温度(sub surr / sub)之间的差分驱动。

[math]\displaystyle{ \mathrm dS = \frac{\delta Q}{T} \,\, \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \text {(actually possible quasistatic irreversible process without composition change).} }[/math]

[math]\displaystyle{ \mathrm dS = \frac{\delta Q}{T} \,\, \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \text {(actually possible quasistatic irreversible process without composition change).} }[/math]

(实际上可能是不改变成分的准静态不可逆性)。数学

which is the basis of the accurate determination of the absolute entropy of pure substances from measured heat capacity curves and entropy changes at phase transitions, i.e. by calorimetry.^[16] ^[11] Introducing a set of internal variables [math]\displaystyle{ \xi }[/math] to describe the deviation of a thermodynamic system in physical equilibrium (with the required well-defined uniform pressure P and temperature T)^[15] from the chemical equilibrium state, one can record the equality

which is the basis of the accurate determination of the absolute entropy of pure substances from measured heat capacity curves and entropy changes at phase transitions, i.e. by calorimetry. from the chemical equilibrium state, one can record the equality

这是根据测得的热容曲线和相变时的熵变精确确定纯物质的绝对熵的基础。用量热法。从化学平衡来看，人们可以记录平等

[math]\displaystyle{ \mathrm dS = \frac{\delta Q}{T} - \frac{1}{T} \sum_{j} \, \Xi_{j} \,\delta \xi_j \,\, \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \text {(closed system, actually possible quasistatic irreversible process).} }[/math]

[math]\displaystyle{ \mathrm dS = \frac{\delta Q}{T} - \frac{1}{T} \sum_{j} \, \Xi_{j} \,\delta \xi_j \,\, \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \text {(closed system, actually possible quasistatic irreversible process).} }[/math]

- frac { t }-frac {1}{ j } ， Xi { j } ， delta Xi j，，，，，，，，，，，，，，，，，，，，，，，， ,.数学

The second term represents work of internal variables that can be perturbed by external influences, but the system cannot perform any positive work via internal variables. This statement introduces the impossibility of the reversion of evolution of the thermodynamic system in time and can be considered as a formulation of the second principle of thermodynamics – the formulation, which is, of course, equivalent to the formulation of the principle in terms of entropy.^[17]^[18]

The second term represents work of internal variables that can be perturbed by external influences, but the system cannot perform any positive work via internal variables. This statement introduces the impossibility of the reversion of evolution of the thermodynamic system in time and can be considered as a formulation of the second principle of thermodynamics – the formulation, which is, of course, equivalent to the formulation of the principle in terms of entropy.

第二项代表内部变量的工作，这些内部变量可以受到外部影响的干扰，但是系统不能通过内部变量执行任何正功。这种说法介绍了热力学系统在时间上不可能逆转演化的事实，并且可以被认为是热力学第二原理的表述---- 这个表述，当然，相当于熵原理的表述。

The zeroth law of thermodynamics in its usual short statement allows recognition that two bodies in a relation of thermal equilibrium have the same temperature, especially that a test body has the same temperature as a reference thermometric body.^[19] For a body in thermal equilibrium with another, there are indefinitely many empirical temperature scales, in general respectively depending on the properties of a particular reference thermometric body. The second law allows模板:How? a distinguished temperature scale, which defines an absolute, thermodynamic temperature, independent of the properties of any particular reference thermometric body.^[20]^[21]

The zeroth law of thermodynamics in its usual short statement allows recognition that two bodies in a relation of thermal equilibrium have the same temperature, especially that a test body has the same temperature as a reference thermometric body. For a body in thermal equilibrium with another, there are indefinitely many empirical temperature scales, in general respectively depending on the properties of a particular reference thermometric body. The second law allows a distinguished temperature scale, which defines an absolute, thermodynamic temperature, independent of the properties of any particular reference thermometric body.

美国热力学第零定律协会在其通常的简短声明中允许承认，相对于热平衡的两个物体具有相同的温度，特别是测试物体具有与参考温度测量物体相同的温度。对于一个物体和另一个物体之间的热平衡，存在着无限多的经验温度标度，通常分别取决于特定参考温度标度的性质。第二定律允许区分温度标度，它定义了一个绝对的热力学温度，与任何特定的参考温度体的性质无关。

Various statements of the law

各种各样的法律陈述

The second law of thermodynamics may be expressed in many specific ways,^[22] the most prominent classical statements模板:Sfnp being the statement by Rudolf Clausius (1854), the statement by Lord Kelvin (1851), and the statement in axiomatic thermodynamics by Constantin Carathéodory (1909). These statements cast the law in general physical terms citing the impossibility of certain processes. The Clausius and the Kelvin statements have been shown to be equivalent.模板:Sfnp

The second law of thermodynamics may be expressed in many specific ways, the most prominent classical statements being the statement by Rudolf Clausius (1854), the statement by Lord Kelvin (1851), and the statement in axiomatic thermodynamics by Constantin Carathéodory (1909). These statements cast the law in general physical terms citing the impossibility of certain processes. The Clausius and the Kelvin statements have been shown to be equivalent.

热力学第二定律可以用许多特定的方式来表达，最突出的经典陈述是 Rudolf Clausius (1854)的陈述，Kelvin 勋爵(1851)的陈述，以及康斯坦丁·卡拉西奥多里(1909)在公理化热力学中的陈述。这些陈述用一般的物理术语描述法律，引用某些过程的不可能性。克劳修斯和开尔文陈述被证明是等价的。

Carnot's principle

卡诺原理

The historical origin^[23] of the second law of thermodynamics was in Carnot's principle. It refers to a cycle of a Carnot heat engine, fictively operated in the limiting mode of extreme slowness known as quasi-static, so that the heat and work transfers are between subsystems that are always in their own internal states of thermodynamic equilibrium. The Carnot engine is an idealized device of special interest to engineers who are concerned with the efficiency of heat engines. Carnot's principle was recognized by Carnot at a time when the caloric theory of heat was seriously considered, before the recognition of the first law of thermodynamics, and before the mathematical expression of the concept of entropy. Interpreted in the light of the first law, it is physically equivalent to the second law of thermodynamics, and remains valid today. Carnot's original arguments were made from the viewpoint of the caloric theory, before the discovery of the first law of thermodynamics. Some samples from his book are:

The historical origin of the second law of thermodynamics was in Carnot's principle. It refers to a cycle of a Carnot heat engine, fictively operated in the limiting mode of extreme slowness known as quasi-static, so that the heat and work transfers are between subsystems that are always in their own internal states of thermodynamic equilibrium. The Carnot engine is an idealized device of special interest to engineers who are concerned with the efficiency of heat engines. Carnot's principle was recognized by Carnot at a time when the caloric theory of heat was seriously considered, before the recognition of the first law of thermodynamics, and before the mathematical expression of the concept of entropy. Interpreted in the light of the first law, it is physically equivalent to the second law of thermodynamics, and remains valid today. Carnot's original arguments were made from the viewpoint of the caloric theory, before the discovery of the first law of thermodynamics. Some samples from his book are:

热力学第二定律的历史起源源于卡诺的原则。它指的是一个卡诺热机周期，虚拟地以被称为准静态的极慢极限模式运行，因此热量和功量在子系统之间传递，这些子系统始终处于它们自己的内部热力学平衡状态。卡诺发动机是热机效率工程师特别感兴趣的理想设备。卡诺认识到卡诺原理的时候，正是热量热理论被认真考虑的时候，正是能量守恒定律理论被认识之前，正是熵概念的数学表达之前。根据第一定律的解释，它在物理上等同于热力学第二定律，并且在今天仍然有效。卡诺最初的论点是从卡路里理论的观点提出的，直到能量守恒定律的发现。以下是他书中的一些例子:

...wherever there exists a difference of temperature, motive power can be produced.^[24]

...wherever there exists a difference of temperature, motive power can be produced.

只要有温差，就能产生动力。

The production of motive power is then due in steam engines not to an actual consumption of caloric, but to its transportation from a warm body to a cold body ...^[25]

The production of motive power is then due in steam engines not to an actual consumption of caloric, but to its transportation from a warm body to a cold body ...

动力的产生不是由于蒸汽机实际消耗的热量，而是由于它从一个温暖的物体运输到一个寒冷的物体..。

The motive power of heat is independent of the agents employed to realize it; its quantity is fixed solely by the temperatures of the bodies between which is effected, finally, the transfer of caloric.^[26]

The motive power of heat is independent of the agents employed to realize it; its quantity is fixed solely by the temperatures of the bodies between which is effected, finally, the transfer of caloric.

热的动力与实现热的媒介无关，热的数量完全取决于两个物体之间的温度，最后是热量的传递。

In modern terms, Carnot's principle may be stated more precisely:

用现代术语来说，卡诺的原则可能更为准确:

The efficiency of a quasi-static or reversible Carnot cycle depends only on the temperatures of the two heat reservoirs, and is the same, whatever the working substance. A Carnot engine operated in this way is the most efficient possible heat engine using those two temperatures.^[27]^[28]^[29]^[30]^[31]^[32]

The efficiency of a quasi-static or reversible Carnot cycle depends only on the temperatures of the two heat reservoirs, and is the same, whatever the working substance. A Carnot engine operated in this way is the most efficient possible heat engine using those two temperatures.

准静态或可逆卡诺循环的效率只取决于两个热源的温度，而且无论工作物质是什么，效率是相同的。以这种方式运行的卡诺发动机是使用这两种温度的最有效的热机。

Clausius statement

克劳修斯声明

The German scientist Rudolf Clausius laid the foundation for the second law of thermodynamics in 1850 by examining the relation between heat transfer and work.模板:Sfnp His formulation of the second law, which was published in German in 1854, is known as the Clausius statement:

The German scientist Rudolf Clausius laid the foundation for the second law of thermodynamics in 1850 by examining the relation between heat transfer and work. His formulation of the second law, which was published in German in 1854, is known as the Clausius statement:

1850年，德国科学家 Rudolf Clausius 通过研究热传递和功之间的关系，为热力学第二定律实验室奠定了基础。他在1854年用德语发表的第二定律的提法被称为克劳修斯声明:

Heat can never pass from a colder to a warmer body without some other change, connected therewith, occurring at the same time.模板:Sfnp

Heat can never pass from a colder to a warmer body without some other change, connected therewith, occurring at the same time.

热量不可能从一个较冷的物体传递到一个较热的物体，除非同时发生一些其他的变化。 / blockquote

The statement by Clausius uses the concept of 'passage of heat'. As is usual in thermodynamic discussions, this means 'net transfer of energy as heat', and does not refer to contributory transfers one way and the other.

克劳修斯的陈述使用了“热量通道”的概念。正如通常在热力学的讨论，这意味着“能量作为热量的净转移” ，并没有提到促成转移的一种方式和其他。

Heat cannot spontaneously flow from cold regions to hot regions without external work being performed on the system, which is evident from ordinary experience of refrigeration, for example. In a refrigerator, heat flows from cold to hot, but only when forced by an external agent, the refrigeration system.

如果不对系统进行外部功，热就不能自发地从冷区流向热区，这一点从制冷的普通经验中可以看出。在冰箱中，热量从冷到热，但只有在外部介质——制冷系统的强制作用下才会发生变化。

Kelvin statements

开尔文陈述

Lord Kelvin expressed the second law in several wordings.

开尔文勋爵用几个字表达了第二定律。

It is impossible for a self-acting machine, unaided by any external agency, to convey heat from one body to another at a higher temperature.

没有任何外部机构的帮助，自动机器是不可能把热量从一个物体传递到另一个物体的较高温度。

It is impossible, by means of inanimate material agency, to derive mechanical effect from any portion of matter by cooling it below the temperature of the coldest of the surrounding objects.模板:Sfnp

It is impossible, by means of inanimate material agency, to derive mechanical effect from any portion of matter by cooling it below the temperature of the coldest of the surrounding objects.

通过无生命物质的作用，把物质冷却到周围最冷的物体的温度以下，从物质的任何部分获得机械效应是不可能的。

Equivalence of the Clausius and the Kelvin statements

克劳修斯和开尔文陈述的等价性

Derive Kelvin Statement from Clausius Statement

从克劳修斯陈述推导出开尔文陈述

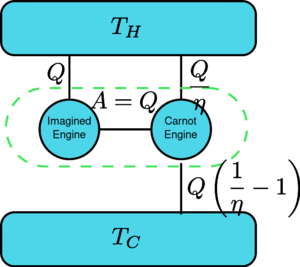
Suppose there is an engine violating the Kelvin statement: i.e., one that drains heat and converts it completely into work in a cyclic fashion without any other result. Now pair it with a reversed Carnot engine as shown by the figure. The efficiency of a normal heat engine is η and so the efficiency of the reversed heat engine is 1/η. The net and sole effect of the combined pair of engines is to transfer heat [math]\displaystyle{ \Delta Q=Q\left(\frac{1}{\eta}-1\right) }[/math] from the cooler reservoir to the hotter one, which violates the Clausius statement. (This is a consequence of the first law of thermodynamics, as for the total system's energy to remain the same, [math]\displaystyle{ \text{Input}+\text{Output}=0 \implies Q-\frac{Q}{\eta} = -Q_c }[/math], so therefore [math]\displaystyle{ Q_c=Q\left( \frac{1}{\eta}-1\right) }[/math] ). Thus a violation of the Kelvin statement implies a violation of the Clausius statement, i.e. the Clausius statement implies the Kelvin statement. We can prove in a similar manner that the Kelvin statement implies the Clausius statement, and hence the two are equivalent.

假设有一个引擎违反了开尔文定理: 也就是说，这个引擎以循环的方式吸收热量并将其转化为功，没有任何其他结果。现在配对与反向卡诺发动机如图所示。普通热机的效率为，反向热机的效率为1 / 。这对组合发动机的净效应和唯一效应是将热量从较冷的贮存器转移到较热的贮存器，这违反了克劳修斯的说法。(这是能量守恒定律的结果，因为系统的总能量保持不变，数学文本{输入} + 文本{输出}0暗示 q-frac { eta }-qc / math，所以数学 qc 向左(frac { eta-1 right) / math)。因此，违反开尔文陈述意味着违反克劳修斯陈述，即。克劳修斯的说法暗示了凯尔文的说法。我们可以用类似的方式证明开尔文陈述暗示了克劳修斯陈述，因此两者是等价的。

Planck's proposition

普朗克的命题

Planck offered the following proposition as derived directly from experience. This is sometimes regarded as his statement of the second law, but he regarded it as a starting point for the derivation of the second law.

普朗克提出了直接来自经验的如下命题。这有时被认为是他对第二定律的陈述，但他认为这是第二定律推导的起点。

It is impossible to construct an engine which will work in a complete cycle, and produce no effect except the raising of a weight and cooling of a heat reservoir.^[33]^[34]

It is impossible to construct an engine which will work in a complete cycle, and produce no effect except the raising of a weight and cooling of a heat reservoir.

建造一台发动机是不可能的，这台发动机将在一个完整的循环中工作，并且除了提高重量和冷却热储以外不会产生任何效果。

Relation between Kelvin's statement and Planck's proposition

开尔文命题与普朗克命题的关系

It is almost customary in textbooks to speak of the "Kelvin-Planck statement" of the law, as for example in the text by ter Haar and Wergeland.^[35]

It is almost customary in textbooks to speak of the "Kelvin-Planck statement" of the law, as for example in the text by ter Haar and Wergeland.

在教科书中几乎习惯性地提到该定律的“开尔文-普朗克说明” ，例如在 ter Haar 和 Wergeland 的文本中。

The Kelvin–Planck statement (or the heat engine statement) of the second law of thermodynamics states that

The Kelvin–Planck statement (or the heat engine statement) of the second law of thermodynamics states that

开尔文-普朗克声明(或者说热机声明)指出，热力学第二定律的研究表明

It is impossible to devise a cyclically operating device, the sole effect of which is to absorb energy in the form of heat from a single thermal reservoir and to deliver an equivalent amount of work.^[36]

It is impossible to devise a cyclically operating device, the sole effect of which is to absorb energy in the form of heat from a single thermal reservoir and to deliver an equivalent amount of work.

设计一种循环运行的装置是不可能的，这种装置的唯一作用是从单个热源吸收热量形式的能量，并提供等量的功。

Planck's statement

普朗克的声明

Planck stated the second law as follows.

普朗克提出的第二定律如下。

Every process occurring in nature proceeds in the sense in which the sum of the entropies of all bodies taking part in the process is increased. In the limit, i.e. for reversible processes, the sum of the entropies remains unchanged.^[37]^[38]^[39]

Every process occurring in nature proceeds in the sense in which the sum of the entropies of all bodies taking part in the process is increased. In the limit, i.e. for reversible processes, the sum of the entropies remains unchanged.

自然界中发生的每一个过程都是在所有参与这一过程的物体的熵的总和增加的意义下进行的。在极限内，即。对于可逆过程，熵的总和保持不变。

Rather like Planck's statement is that of Uhlenbeck and Ford for irreversible phenomena.

Rather like Planck's statement is that of Uhlenbeck and Ford for irreversible phenomena.

就像普朗克关于不可逆现象的论断一样，Uhlenbeck 和福特也是如此。

... in an irreversible or spontaneous change from one equilibrium state to another (as for example the equalization of temperature of two bodies A and B, when brought in contact) the entropy always increases.^[40]

... in an irreversible or spontaneous change from one equilibrium state to another (as for example the equalization of temperature of two bodies A and B, when brought in contact) the entropy always increases.

在从一个平衡态到另一个平衡态的不可逆或自发的变化中(例如，当两个物体 a 和 b 接触时，温度平衡) ，熵总是增加。

Principle of Carathéodory

卡拉斯定律原理

—— caratheodory 的原理在这里重新定向——

Constantin Carathéodory formulated thermodynamics on a purely mathematical axiomatic foundation. His statement of the second law is known as the Principle of Carathéodory, which may be formulated as follows:^[41]

Constantin Carathéodory formulated thermodynamics on a purely mathematical axiomatic foundation. His statement of the second law is known as the Principle of Carathéodory, which may be formulated as follows:

康斯坦丁·卡拉西奥多里在纯数学公理的基础上制定了热力学公式。他对第二定律的陈述被称为 carath odory 原理，可以这样表述:

In every neighborhood of any state S of an adiabatically enclosed system there are states inaccessible from S.^[42]

In every neighborhood of any state S of an adiabatically enclosed system there are states inaccessible from S.

在绝热封闭系统的任何状态 s 的每个邻域中，都有从 s / blockquote 不可达的状态

With this formulation, he described the concept of adiabatic accessibility for the first time and provided the foundation for a new subfield of classical thermodynamics, often called geometrical thermodynamics. It follows from Carathéodory's principle that quantity of energy quasi-statically transferred as heat is a holonomic process function, in other words, [math]\displaystyle{ \delta Q=TdS }[/math].^[43] 模板:Clarify

With this formulation, he described the concept of adiabatic accessibility for the first time and provided the foundation for a new subfield of classical thermodynamics, often called geometrical thermodynamics. It follows from Carathéodory's principle that quantity of energy quasi-statically transferred as heat is a holonomic process function, in other words, [math]\displaystyle{ \delta Q=TdS }[/math].

利用这个公式，他第一次描述了绝热可达性的概念，并为经典热力学的一个新的子领域，即通常所说的几何热力学，提供了基础。它遵循 carath odory 的原理，能量的准静态转移作为热量是一个完整过程函数，换句话说，数学△ q TdS / math。

Though it is almost customary in textbooks to say that Carathéodory's principle expresses the second law and to treat it as equivalent to the Clausius or to the Kelvin-Planck statements, such is not the case. To get all the content of the second law, Carathéodory's principle needs to be supplemented by Planck's principle, that isochoric work always increases the internal energy of a closed system that was initially in its own internal thermodynamic equilibrium.^[14]模板:Sfnp^[44]^[45] 模板:Clarify

Though it is almost customary in textbooks to say that Carathéodory's principle expresses the second law and to treat it as equivalent to the Clausius or to the Kelvin-Planck statements, such is not the case. To get all the content of the second law, Carathéodory's principle needs to be supplemented by Planck's principle, that isochoric work always increases the internal energy of a closed system that was initially in its own internal thermodynamic equilibrium.

尽管在教科书中几乎习惯性地说，卡拉斯 · 奥多里原则表达了第二定律，并将其视为克劳修斯原则或 Kelvin-Planck 原则的等价物，但事实并非如此。为了得到第二定律的所有内容，卡拉斯 · 奥多里原理需要补充普朗克原理，即等量功总是增加一个封闭系统的内部能量，这个封闭系统最初处于自己的内部热力学平衡。

Planck's principle

普朗克定律

In 1926, Max Planck wrote an important paper on the basics of thermodynamics.^[44]^[46] He indicated the principle

In 1926, Max Planck wrote an important paper on the basics of thermodynamics. He indicated the principle

1926年，马克斯 · 普朗克写了一篇关于热力学基础的重要论文。他指出了这个原则

The internal energy of a closed system is increased by an adiabatic process, throughout the duration of which, the volume of the system remains constant.^[14]模板:Sfnp

The internal energy of a closed system is increased by an adiabatic process, throughout the duration of which, the volume of the system remains constant.

一个封闭系统的内部能量增加了一个绝热过程，在整个过程中，系统的体积保持不变。

This formulation does not mention heat and does not mention temperature, nor even entropy, and does not necessarily implicitly rely on those concepts, but it implies the content of the second law. A closely related statement is that "Frictional pressure never does positive work."^[47] Planck wrote: "The production of heat by friction is irreversible."^[48]^[49]

This formulation does not mention heat and does not mention temperature, nor even entropy, and does not necessarily implicitly rely on those concepts, but it implies the content of the second law. A closely related statement is that "Frictional pressure never does positive work." Planck wrote: "The production of heat by friction is irreversible."

这个公式没有提到热，没有提到温度，甚至没有提到熵，也不一定隐含地依赖于这些概念，但它暗示了第二定律的内容。一个密切相关的陈述是，“摩擦压力从来不起正作用。”普朗克写道: “摩擦产生热是不可逆的。”

Not mentioning entropy, this principle of Planck is stated in physical terms. It is very closely related to the Kelvin statement given just above.^[50] It is relevant that for a system at constant volume and mole numbers, the entropy is a monotonic function of the internal energy. Nevertheless, this principle of Planck is not actually Planck's preferred statement of the second law, which is quoted above, in a previous sub-section of the present section of this present article, and relies on the concept of entropy.

Not mentioning entropy, this principle of Planck is stated in physical terms. It is very closely related to the Kelvin statement given just above. It is relevant that for a system at constant volume and mole numbers, the entropy is a monotonic function of the internal energy. Nevertheless, this principle of Planck is not actually Planck's preferred statement of the second law, which is quoted above, in a previous sub-section of the present section of this present article, and relies on the concept of entropy.

更不用说熵了，这个普朗克定律是用物理术语来表述的。它与上面给出的开尔文陈述非常密切相关。相关的是，对于恒定体积和摩尔数的系统，熵是内能的单调函数。然而，普朗克的这个原理实际上并不是普朗克对第二定律的首选陈述，而是依赖于熵的概念。

A statement that in a sense is complementary to Planck's principle is made by Borgnakke and Sonntag. They do not offer it as a full statement of the second law:

在某种意义上说，这是对普朗克原理的补充，这是由 Borgnakke 和 Sonntag 提出的。他们没有将其作为第二定律的完整陈述:

... there is only one way in which the entropy of a [closed] system can be decreased, and that is to transfer heat from the system.^[51]

... there is only one way in which the entropy of a [closed] system can be decreased, and that is to transfer heat from the system.

只有一种方法可以减少[闭合]系统的熵，那就是从系统中传递热量。

Differing from Planck's just foregoing principle, this one is explicitly in terms of entropy change. Removal of matter from a system can also decrease its entropy.

与普朗克刚才提出的原理不同，这一原理明确地以熵的变化为基础。从系统中去除物质也可以减少系统的熵。

Statement for a system that has a known expression of its internal energy as a function of its extensive state variables

一个系统的内能作为其扩展状态变量的函数的已知表达式的陈述

The second law has been shown to be equivalent to the internal energy U being a weakly convex function, when written as a function of extensive properties (mass, volume, entropy, ...).^[52]^[53] 模板:Clarify

The second law has been shown to be equivalent to the internal energy U being a weakly convex function, when written as a function of extensive properties (mass, volume, entropy, ...).

第二定律被证明等价于内能 u 是一个弱凸函数，当它被写成具有广泛性质(质量，体积，熵，...)的函数时。

Corollaries

推论

Perpetual motion of the second kind

第二种永动机

模板:Main article

Before the establishment of the second law, many people who were interested in inventing a perpetual motion machine had tried to circumvent the restrictions of first law of thermodynamics by extracting the massive internal energy of the environment as the power of the machine. Such a machine is called a "perpetual motion machine of the second kind". The second law declared the impossibility of such machines.

在第二定律建立之前，许多有兴趣发明永动机的人试图通过提取环境的巨大内部能量作为机器的动力来绕过能量守恒定律的限制。这种机器被称为“第二种永动机”。第二定律宣布这种机器是不可能的。

Carnot theorem

卡诺定理

Carnot's theorem (1824) is a principle that limits the maximum efficiency for any possible engine. The efficiency solely depends on the temperature difference between the hot and cold thermal reservoirs. Carnot's theorem states:

卡诺定理(1824)是一个限制任何可能的发动机的最大效率的原则。效率完全取决于热库和冷库之间的温差。卡诺定理指出:

All irreversible heat engines between two heat reservoirs are less efficient than a Carnot engine operating between the same reservoirs.

All reversible heat engines between two heat reservoirs are equally efficient with a Carnot engine operating between the same reservoirs.

In his ideal model, the heat of caloric converted into work could be reinstated by reversing the motion of the cycle, a concept subsequently known as thermodynamic reversibility. Carnot, however, further postulated that some caloric is lost, not being converted to mechanical work. Hence, no real heat engine could realise the Carnot cycle's reversibility and was condemned to be less efficient.

在他的理想模型中，热量转换成功的热量可以通过反转循环的运动而恢复，这个概念后来被称为热力学可逆性。然而，卡诺进一步假定，一些热量损失了，并没有转化为机械功。因此，没有一个真正的热机能够实现卡诺循环的可逆性，并且被认为效率较低。

Though formulated in terms of caloric (see the obsolete caloric theory), rather than entropy, this was an early insight into the second law.

虽然是用热量表述的(见过时的热量理论) ，而不是熵，这是对第二定律的早期见解。

Clausius inequality

克劳修斯不等式

The Clausius theorem (1854) states that in a cyclic process

克劳修斯定理》(1854)指出，在一个循环的过程中

[math]\displaystyle{ \oint \frac{\delta Q}{T} \leq 0. }[/math]

[math]\displaystyle{ \oint \frac{\delta Q}{T} \leq 0. }[/math]

0. / math oint frac { delta q } leq 0. / math

The equality holds in the reversible case^[54] and the strict inequality holds in the irreversible case. The reversible case is used to introduce the state function entropy. This is because in cyclic processes the variation of a state function is zero from state functionality.

The equality holds in the reversible case and the strict inequality holds in the irreversible case. The reversible case is used to introduce the state function entropy. This is because in cyclic processes the variation of a state function is zero from state functionality.

等式在可逆情况下成立，严格不等式在不可逆情况下成立。利用可逆情形引入状态函数熵。这是因为在循环过程中，状态函数的变化从状态函数变化为零。

Thermodynamic temperature

热力学温度

模板:Main article

For an arbitrary heat engine, the efficiency is:

对于任意的热机，效率是:

[math]\displaystyle{ \eta = \frac {W_n}{q_H} = \frac{q_H-q_C}{q_H} = 1 - \frac{q_C}{q_H} \qquad (1) }[/math]

[math]\displaystyle{ \eta = \frac {W_n}{q_H} = \frac{q_H-q_C}{q_H} = 1 - \frac{q_C}{q_H} \qquad (1) }[/math]

数学{ q h } frac { q h }{ q h }1-frac { q h } qquad (1) / math

where W_n is for the net work done per cycle. Thus the efficiency depends only on q_C/q_H.

其中 w 子 n / sub 表示每个循环所做的净功。因此效率只取决于 q 子 c / sub / q 子 h / sub。

Carnot's theorem states that all reversible engines operating between the same heat reservoirs are equally efficient.

卡诺定理指出，所有在相同热源间运行的可逆发动机的效率是相同的。

Thus, any reversible heat engine operating between temperatures T₁ and T₂ must have the same efficiency, that is to say, the efficiency is the function of temperatures only:

因此，任何在温度 t 小于1 / sub 和 t 小于2 / sub 之间运行的可逆热机必须具有相同的效率，也就是说，效率只是温度的函数:

[math]\displaystyle{ \frac{q_C}{q_H} = f(T_H,T_C)\qquad (2). }[/math]

Math frac { q }{ q h } f (t h，t c) qquad (2) . / math

In addition, a reversible heat engine operating between temperatures T₁ and T₃ must have the same efficiency as one consisting of two cycles, one between T₁ and another (intermediate) temperature T₂, and the second between T₂ andT₃. This can only be the case if

另外，在 t1 / sub 和 t3 / sub 之间工作的可逆热机必须具有与由两个循环组成的循环相同的效率，一个循环在 t1 / sub 和另一个(中间)温度 t2 / sub 之间，第二个循环在 t2 / sub 和 t3 / sub 之间。只有在下列情况下才会出现这种情况:

[math]\displaystyle{ \lt math\gt 数学 f(T_1,T_3) = \frac{q_3}{q_1} = \frac{q_2 q_3} {q_1 q_2} = f(T_1,T_2)f(T_2,T_3). f(T_1,T_3) = \frac{q_3}{q_1} = \frac{q_2 q_3} {q_1 q_2} = f(T_1,T_2)f(T_2,T_3). F (t1，t3) frac { q1} frac { q2 q3}{ q1 q2} f (t1，t2) f (t2，t3). }[/math]

</math>

数学

Now consider the case where [math]\displaystyle{ T_1 }[/math] is a fixed reference temperature: the temperature of the triple point of water. Then for any T₂ and T₃,

现在考虑这样一个例子，数学 t1 / math 是一个固定的参考温度: 水的三相点的温度。然后对于任意 t 小于2 / sub 和 t 小于3 / sub,

[math]\displaystyle{ f(T_2,T_3) = \frac{f(T_1,T_3)}{f(T_1,T_2)} = \frac{273.16 \cdot f(T_1,T_3)}{273.16 \cdot f(T_1,T_2)}. }[/math]

[math]\displaystyle{ f(T_2,T_3) = \frac{f(T_1,T_3)}{f(T_1,T_2)} = \frac{273.16 \cdot f(T_1,T_3)}{273.16 \cdot f(T_1,T_2)}. }[/math]

数学 f (t2，t3) frac { f (t1，t3)}{ f (t1，t2)} frac {273.16 ctf (t1，t3)}{273.16 ctf (t1，t2)} / math

Therefore, if thermodynamic temperature is defined by

因此，如果热力学温度被定义为

[math]\displaystyle{ T = 273.16 \cdot f(T_1,T) \, }[/math]

[math]\displaystyle{ T = 273.16 \cdot f(T_1,T) \, }[/math]

数学 t273.16 cdot f (t1，t) ，/ math

then the function f, viewed as a function of thermodynamic temperature, is simply

那么函数 f 作为热力学温度的函数

[math]\displaystyle{ f(T_2,T_3) = \frac{T_3}{T_2}, }[/math]

[math]\displaystyle{ f(T_2,T_3) = \frac{T_3}{T_2}, }[/math]

数学 f (t2，t3) frac { t3}{ t2} ，/ math

and the reference temperature T₁ will have the value 273.16. (Any reference temperature and any positive numerical value could be used模板:Sndthe choice here corresponds to the Kelvin scale.)

and the reference temperature T₁ will have the value 273.16. (Any reference temperature and any positive numerical value could be usedthe choice here corresponds to the Kelvin scale.)

参考温度 t 小于1 / sub 的值为273.16。(任何参考温度和任何正数值都可以用这里的选择对应开尔文标度。)

Entropy

熵

模板:Main article

According to the Clausius equality, for a reversible process

根据克劳修斯的平等原则，可逆过程

[math]\displaystyle{ \oint \frac{\delta Q}{T}=0 }[/math]

[math]\displaystyle{ \oint \frac{\delta Q}{T}=0 }[/math]

0 / math oint frac { delta q }{ t }0

That means the line integral [math]\displaystyle{ \int_L \frac{\delta Q}{T} }[/math] is path independent for reversible processes.

这意味着线积分 math int l frac { delta q }{ t } / math 对于可逆过程是路径无关的。

So we can define a state function S called entropy, which for a reversible process or for pure heat transfer^[15] satisfies

So we can define a state function S called entropy, which for a reversible process or for pure heat transfer satisfies

所以我们可以定义一个叫做熵的状态函数，对于可逆过程或者纯热传递，它满足

[math]\displaystyle{ dS = \frac{\delta Q}{T} \! }[/math]

[math]\displaystyle{ dS = \frac{\delta Q}{T} \! }[/math]

数学 dS frac delta q }{ t } ! / math

With this we can only obtain the difference of entropy by integrating the above formula. To obtain the absolute value, we need the third law of thermodynamics, which states that S = 0 at absolute zero for perfect crystals.

只有对上述公式进行积分，才能得到熵的差值。为了获得绝对值，我们需要热力学第三定律，它指出完美晶体的 s 0处于绝对零度。

For any irreversible process, since entropy is a state function, we can always connect the initial and terminal states with an imaginary reversible process and integrating on that path to calculate the difference in entropy.

对于任何不可逆性，由于熵是一个状态函数，我们总是可以将初始状态和终端状态与一个虚拟的可逆过程联系起来，并在这条路径上积分以计算熵的差值。

Now reverse the reversible process and combine it with the said irreversible process. Applying the Clausius inequality on this loop,

现在把可逆过程倒过来，把它和上述的不可逆性结合起来。把克劳修斯不等式应用到这个环上,

[math]\displaystyle{ -\Delta S+\int\frac{\delta Q}{T}=\oint\frac{\delta Q}{T}\lt 0 }[/math]

[math]\displaystyle{ -\Delta S+\int\frac{\delta Q}{T}=\oint\frac{\delta Q}{T}\lt  0 }[/math]

数学- Delta s + int frac { t } Delta q } oint frac { t }0 / math

Thus,

因此,

[math]\displaystyle{ \Delta S \ge \int \frac{\delta Q}{T} \,\! }[/math]

[math]\displaystyle{ \Delta S \ge \int \frac{\delta Q}{T} \,\! }[/math]

数学 | Delta | s | ge | int | frac | Delta | q | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | |

where the equality holds if the transformation is reversible.

如果变换是可逆的，等式就成立。

Notice that if the process is an adiabatic process, then [math]\displaystyle{ \delta Q=0 }[/math], so [math]\displaystyle{ \Delta S\ge 0 }[/math].

注意，如果这个过程是一个绝热过程，那么数学 Delta q 0 / math，所以数学 Delta s ge 0 / math。

Energy, available useful work

能量，有用的工作

An important and revealing idealized special case is to consider applying the Second Law to the scenario of an isolated system (called the total system or universe), made up of two parts: a sub-system of interest, and the sub-system's surroundings. These surroundings are imagined to be so large that they can be considered as an unlimited heat reservoir at temperature T_R and pressure P_R 模板:Sndso that no matter how much heat is transferred to (or from) the sub-system, the temperature of the surroundings will remain T_R; and no matter how much the volume of the sub-system expands (or contracts), the pressure of the surroundings will remain P_R.

An important and revealing idealized special case is to consider applying the Second Law to the scenario of an isolated system (called the total system or universe), made up of two parts: a sub-system of interest, and the sub-system's surroundings. These surroundings are imagined to be so large that they can be considered as an unlimited heat reservoir at temperature T_R and pressure P_R so that no matter how much heat is transferred to (or from) the sub-system, the temperature of the surroundings will remain T_R; and no matter how much the volume of the sub-system expands (or contracts), the pressure of the surroundings will remain P_R.

考虑将第二定律应用于孤立系统(称为整体系统或宇宙)的情形，是一个重要的、具有启发性的理想情形。孤立系统由两部分组成: 感兴趣的子系统和子系统的环境。这些环境被想象为如此之大，以至于它们可以被认为是一个温度为 t 子 r / sub 和压力为 p 子 r / sub 的无限热源，因此无论有多少热量被转移到(或来自)子系统，周围环境的温度将保持 t 子 r / sub; 无论子系统的体积扩大(或收缩)多少，周围环境的压力将保持 p 子 r / sub。

Whatever changes to dS and dS_R occur in the entropies of the sub-system and the surroundings individually, according to the Second Law the entropy S_tot of the isolated total system must not decrease:

Whatever changes to dS and dS_R occur in the entropies of the sub-system and the surroundings individually, according to the Second Law the entropy S_tot of the isolated total system must not decrease:

根据第二定律，孤立总体系统的熵 s 子系统 / 子系统的熵不能减小，无论子系统和周围环境的熵对 dS 和 dS 子系统 r / 子系统发生什么变化:

[math]\displaystyle{ dS_{\mathrm{tot}}= dS + dS_R \ge 0 }[/math]

[math]\displaystyle{  dS_{\mathrm{tot}}= dS + dS_R \ge 0  }[/math]

数学 dS + dS r ge 0 / math

According to the first law of thermodynamics, the change dU in the internal energy of the sub-system is the sum of the heat δq added to the sub-system, less any work δw done by the sub-system, plus any net chemical energy entering the sub-system d ∑μ_iRN_i, so that:

According to the first law of thermodynamics, the change dU in the internal energy of the sub-system is the sum of the heat δq added to the sub-system, less any work δw done by the sub-system, plus any net chemical energy entering the sub-system d ∑μ_iRN_i, so that:

根据能量守恒定律，子系统内部能量的变化 dU 是子系统内部能量 q 的总和，减去子系统所做的任何功，再加上进入子系统 d ∑ sub iR / sub n sub i / sub 的任何净化学能，因此:

[math]\displaystyle{ dU = \delta q - \delta w + d(\sum \mu_{iR}N_i) \, }[/math]

[math]\displaystyle{  dU = \delta q - \delta w + d(\sum \mu_{iR}N_i) \, }[/math]

数学 dU delta q- delta w + d ( sum mu iR } n i) ，/ math

where μ_iR are the chemical potentials of chemical species in the external surroundings.

其中亚 iR / 亚是外部环境中化学物种的化学势。

Now the heat leaving the reservoir and entering the sub-system is

现在热量离开储存器进入子系统是

[math]\displaystyle{ \delta q = T_R (-dS_R) \le T_R dS }[/math]

[math]\displaystyle{  \delta q = T_R (-dS_R) \le T_R dS  }[/math]

数学△ qtr (- dS r) le tr dS / math

where we have first used the definition of entropy in classical thermodynamics (alternatively, in statistical thermodynamics, the relation between entropy change, temperature and absorbed heat can be derived); and then the Second Law inequality from above.

其中我们首先使用了经典热力学中熵的定义(在统计热力学中，熵变、温度和吸收热量之间的关系可以推导出来) ，然后从上面推导出第二定律的不等式。

It therefore follows that any net work δw done by the sub-system must obey

因此，子系统所做的任何净功都必须服从

[math]\displaystyle{ \delta w \le - dU + T_R dS + \sum \mu_{iR} dN_i \, }[/math]

[math]\displaystyle{  \delta w \le - dU + T_R dS + \sum \mu_{iR} dN_i \, }[/math]

数学增量 w le-dU + tds + sum mu { iR } dN i，/ math

It is useful to separate the work δw done by the subsystem into the useful work δw_u that can be done by the sub-system, over and beyond the work p_R dV done merely by the sub-system expanding against the surrounding external pressure, giving the following relation for the useful work (exergy) that can be done:

It is useful to separate the work δw done by the subsystem into the useful work δw_u that can be done by the sub-system, over and beyond the work p_R dV done merely by the sub-system expanding against the surrounding external pressure, giving the following relation for the useful work (exergy) that can be done:

将子系统所做的功与子系统所能做的功分离为子系统所能做的有用功，超过了子系统对外界压力所做的功，给出了子系统所能做的有用功(火用)的下列关系式:

[math]\displaystyle{ \delta w_u \le -d (U - T_R S + p_R V - \sum \mu_{iR} N_i )\, }[/math]

[math]\displaystyle{  \delta w_u \le -d (U - T_R S + p_R V - \sum \mu_{iR} N_i )\, }[/math]

D (u-t r s + p r v-sum { iR } n i) ，/ math

It is convenient to define the right-hand-side as the exact derivative of a thermodynamic potential, called the availability or exergy E of the subsystem,

It is convenient to define the right-hand-side as the exact derivative of a thermodynamic potential, called the availability or exergy E of the subsystem,

可以很方便地将子系统的右侧定义为热动力位能的精确衍生物，称为子系统的可用性或火用 e,

[math]\displaystyle{ E = U - T_R S + p_R V - \sum \mu_{iR} N_i }[/math]

[math]\displaystyle{  E = U - T_R S + p_R V - \sum \mu_{iR} N_i  }[/math]

数学 e u-t r s + p r v- sum { iR } n i / math

The Second Law therefore implies that for any process which can be considered as divided simply into a subsystem, and an unlimited temperature and pressure reservoir with which it is in contact,

因此，第二定律意味着，对于任何可以简单地被视为分为一个子系统和一个与之接触的无限温度和压力储存器的过程,

[math]\displaystyle{ dE + \delta w_u \le 0 \, }[/math]

[math]\displaystyle{  dE + \delta w_u \le 0 \,  }[/math]

数学德 delta u le 0，/ math

i.e. the change in the subsystem's exergy plus the useful work done by the subsystem (or, the change in the subsystem's exergy less any work, additional to that done by the pressure reservoir, done on the system) must be less than or equal to zero.

也就是。子系统(火用)的变化加上子系统所做的有用功(或者，子系统(火用)的变化不包括任何功，除了压力贮存器所做的功之外，在系统中所做的功)必须小于或等于零。

In sum, if a proper infinite-reservoir-like reference state is chosen as the system surroundings in the real world, then the Second Law predicts a decrease in E for an irreversible process and no change for a reversible process.

In sum, if a proper infinite-reservoir-like reference state is chosen as the system surroundings in the real world, then the Second Law predicts a decrease in E for an irreversible process and no change for a reversible process.

总之，如果选择一个合适的类似于无限库的参考状态作为现实世界中的系统环境，那么第二定律预测一个不可逆性的 e 值会减少，而一个可逆过程的 e 值不会变化。

[math]\displaystyle{ dS_{tot} \ge 0 }[/math] Is equivalent to [math]\displaystyle{ dE + \delta w_u \le 0 }[/math]

[math]\displaystyle{ dS_{tot} \ge 0  }[/math] Is equivalent to [math]\displaystyle{  dE + \delta w_u \le 0  }[/math]

数学 d = 0 = 0 = 0 = 0 = 0

This expression together with the associated reference state permits a design engineer working at the macroscopic scale (above the thermodynamic limit) to utilize the Second Law without directly measuring or considering entropy change in a total isolated system. (Also, see process engineer). Those changes have already been considered by the assumption that the system under consideration can reach equilibrium with the reference state without altering the reference state. An efficiency for a process or collection of processes that compares it to the reversible ideal may also be found (See second law efficiency.)

This expression together with the associated reference state permits a design engineer working at the macroscopic scale (above the thermodynamic limit) to utilize the Second Law without directly measuring or considering entropy change in a total isolated system. (Also, see process engineer). Those changes have already been considered by the assumption that the system under consideration can reach equilibrium with the reference state without altering the reference state. An efficiency for a process or collection of processes that compares it to the reversible ideal may also be found (See second law efficiency.)

这个表达式连同相关的参考状态允许在宏观的设计工程师利用第二定律，而不需要直接测量或考虑整个孤立系统的熵变。(另外，请参阅流程工程师)。这些变化已经被考虑，假设被考虑的系统可以达到平衡的参考状态而不改变参考状态。还可以找到一个过程或过程集合的效率，将其与可逆的理想状态相比较

This approach to the Second Law is widely utilized in engineering practice, environmental accounting, systems ecology, and other disciplines.

第二定律的这种方法被广泛应用于工程实践、环境会计、系统生态学和其他学科。

The second law in chemical thermodynamics

化学热力学的第二定律

For a spontaneous chemical process in a closed system at constant temperature and pressure without non-PV work, the Clausius inequality ΔS > Q/T_surr transforms into a condition for the change in Gibbs free energy

For a spontaneous chemical process in a closed system at constant temperature and pressure without non-PV work, the Clausius inequality ΔS > Q/T_surr transforms into a condition for the change in Gibbs free energy

对于一个封闭系统中的自发化学过程，在没有非 pv 功的情况下，在恒定温度和压力下，将克劳修斯不等式 s q / t sub surr / sub 转化为吉布斯自由能变化的条件

[math]\displaystyle{ \Delta G \lt 0 }[/math]

[math]\displaystyle{ \Delta G \lt  0  }[/math]

数学 Delta g 0 / 数学

or dG < 0. For a similar process at constant temperature and volume, the change in Helmholtz free energy must be negative, [math]\displaystyle{ \Delta A \lt 0 }[/math]. Thus, a negative value of the change in free energy (G or A) is a necessary condition for a process to be spontaneous. This is the most useful form of the second law of thermodynamics in chemistry, where free-energy changes can be calculated from tabulated enthalpies of formation and standard molar entropies of reactants and products.^[16] ^[11] The chemical equilibrium condition at constant T and p without electrical work is dG = 0.

or dG < 0. For a similar process at constant temperature and volume, the change in Helmholtz free energy must be negative, [math]\displaystyle{ \Delta A \lt 0 }[/math]. Thus, a negative value of the change in free energy (G or A) is a necessary condition for a process to be spontaneous. This is the most useful form of the second law of thermodynamics in chemistry, where free-energy changes can be calculated from tabulated enthalpies of formation and standard molar entropies of reactants and products. The chemical equilibrium condition at constant T and p without electrical work is dG = 0.

或者 dG 0。对于一个相似的过程，在恒定的温度和体积下，亥姆霍兹自由能的变化一定是负的，这是 Delta a 0 / math。因此，自由能(g 或 a)变化的负值是过程自发的必要条件。这是热力学第二定律在化学中最有用的形式，其中自由能的变化可以通过列表的生成焓和反应物和产物的标准摩尔熵来计算。在 t 和 p 不变的情况下，化学平衡条件是 dG 0。

History

历史

Nicolas Léonard Sadi Carnot in the traditional uniform of a student of the École Polytechnique.

尼古拉·莱昂纳尔·萨迪·卡诺穿着传统的巴黎综合理工学院制服

The first theory of the conversion of heat into mechanical work is due to Nicolas Léonard Sadi Carnot in 1824. He was the first to realize correctly that the efficiency of this conversion depends on the difference of temperature between an engine and its environment.

第一个把热转化为机械功的理论是在1824年由尼古拉·莱昂纳尔·萨迪·卡诺提出的。他是第一个正确认识到这种转换的效率取决于发动机和环境之间的温差。

Recognizing the significance of James Prescott Joule's work on the conservation of energy, Rudolf Clausius was the first to formulate the second law during 1850, in this form: heat does not flow spontaneously from cold to hot bodies. While common knowledge now, this was contrary to the caloric theory of heat popular at the time, which considered heat as a fluid. From there he was able to infer the principle of Sadi Carnot and the definition of entropy (1865).

Recognizing the significance of James Prescott Joule's work on the conservation of energy, Rudolf Clausius was the first to formulate the second law during 1850, in this form: heat does not flow spontaneously from cold to hot bodies. While common knowledge now, this was contrary to the caloric theory of heat popular at the time, which considered heat as a fluid. From there he was able to infer the principle of Sadi Carnot and the definition of entropy (1865).

认识到詹姆斯·普雷斯科特·焦耳在能量守恒方面工作的重要性，Rudolf Clausius 在1850年第一个提出了第二定律: 热不会自发地从冷物体流向热物体。虽然现在的常识是，这与当时流行的热量理论相反，热量理论认为热量是一种流体。从那里他能够推断出萨迪卡诺定律和熵的定义(1865年)。

Established during the 19th century, the Kelvin-Planck statement of the Second Law says, "It is impossible for any device that operates on a cycle to receive heat from a single reservoir and produce a net amount of work." This was shown to be equivalent to the statement of Clausius.

建立于19世纪的开尔文-普朗克第二定律(Kelvin-Planck)说，“任何循环运行的设备都不可能从单个蓄热体接收热量，并产生净功。”这被证明相当于克劳修斯的陈述。

The ergodic hypothesis is also important for the Boltzmann approach. It says that, over long periods of time, the time spent in some region of the phase space of microstates with the same energy is proportional to the volume of this region, i.e. that all accessible microstates are equally probable over a long period of time. Equivalently, it says that time average and average over the statistical ensemble are the same.

遍历假设对玻尔兹曼方法也很重要。它说，在很长一段时间内，在具有相同能量的微观态的相空间的某些区域所花费的时间与这个区域的体积成正比，即。在很长一段时间内，所有可访问的微观状态的可能性都是一样的。同样的，它表明时间平均值和系综平均值是相同的。

There is a traditional doctrine, starting with Clausius, that entropy can be understood in terms of molecular 'disorder' within a macroscopic system. This doctrine is obsolescent.^[55]^[56]^[57]

There is a traditional doctrine, starting with Clausius, that entropy can be understood in terms of molecular 'disorder' within a macroscopic system. This doctrine is obsolescent.

有一种传统的学说，从克劳修斯开始，认为熵可以被理解为宏观系统中的分子“无序”。这种学说已经过时了。

Account given by Clausius

作者: 克劳修斯

Rudolf Clausius

鲁道夫 · 克劳修斯

In 1856, the German physicist Rudolf Clausius stated what he called the "second fundamental theorem in the mechanical theory of heat" in the following form:模板:Sfnp

In 1856, the German physicist Rudolf Clausius stated what he called the "second fundamental theorem in the mechanical theory of heat" in the following form:

1856年，德国物理学家鲁道夫 · 克劳修斯阐述了他所谓的“热力学理论中的第二个基本定理” ，其形式如下:

[math]\displaystyle{ \int \frac{\delta Q}{T} = -N }[/math]

[math]\displaystyle{ \int \frac{\delta Q}{T} = -N }[/math]

- n / math

where Q is heat, T is temperature and N is the "equivalence-value" of all uncompensated transformations involved in a cyclical process. Later, in 1865, Clausius would come to define "equivalence-value" as entropy. On the heels of this definition, that same year, the most famous version of the second law was read in a presentation at the Philosophical Society of Zurich on April 24, in which, in the end of his presentation, Clausius concludes:

其中 q 是热，t 是温度，n 是一个循环过程中所有未补偿的相变的“等价值”。后来，在1865年，克劳修斯将“等价值”定义为熵。紧接着这个定义，也就是在同一年，第二定律最著名的版本在4月24日苏黎世哲学学会的一次演讲中被宣读，在演讲的最后，克劳修斯总结道:

The entropy of the universe tends to a maximum.

宇宙的熵趋于最大

This statement is the best-known phrasing of the second law. Because of the looseness of its language, e.g. universe, as well as lack of specific conditions, e.g. open, closed, or isolated, many people take this simple statement to mean that the second law of thermodynamics applies virtually to every subject imaginable. This is not true; this statement is only a simplified version of a more extended and precise description.

这句话是第二定律中最广为人知的措辞。由于其语言的松散性，例如:。这个问题的答案是肯定的，因为这个问题的答案是肯定的。开放，封闭，或孤立，许多人认为这个简单的陈述意味着热力学第二定律适用于几乎所有可以想象的主题。这是不正确的; 这个陈述只是一个更加扩展和精确描述的简化版本。

In terms of time variation, the mathematical statement of the second law for an isolated system undergoing an arbitrary transformation is:

就时间变化而言，经历任意变换的孤立系统第二定律的数学表述是:

[math]\displaystyle{ \frac{dS}{dt} \ge 0 }[/math]

[math]\displaystyle{ \frac{dS}{dt} \ge 0 }[/math]

0 / math

where

在哪里

S is the entropy of the system and

S is the entropy of the system and

S 是系统的熵

t is time.

t is time.

时间到了。

!-- 可逆过程需要与周围环境保持平衡。这对于一个孤立的系统是不可能的。因此，关于可逆过程的讨论已经转移到对封闭系统的分析----

The equality sign applies after equilibration. An alternative way of formulating of the second law for isolated systems is:

平衡后应用等式符号。建立孤立系统第二定律的另一种方法是:

[math]\displaystyle{ \frac{dS}{dt} = \dot S_{i} }[/math] with [math]\displaystyle{ \dot S_{i} \ge 0 }[/math]

[math]\displaystyle{ \frac{dS}{dt} = \dot S_{i} }[/math] with [math]\displaystyle{  \dot S_{i} \ge 0 }[/math]

用数学点 s { i } ge 0 / math

with [math]\displaystyle{ \dot S_{i} }[/math] the sum of the rate of entropy production by all processes inside the system. The advantage of this formulation is that it shows the effect of the entropy production. The rate of entropy production is a very important concept since it determines (limits) the efficiency of thermal machines. Multiplied with ambient temperature [math]\displaystyle{ T_{a} }[/math] it gives the so-called dissipated energy [math]\displaystyle{ P_{diss}=T_{a}\dot S_{i} }[/math].

用数学 s { i } / 数学表示系统内所有进程的产生熵之和。这种配方的优点是它显示了产生熵的效果。产生熵是一个非常重要的概念，因为它决定(限制)热机器的效率。与环境温度数学 t { a } / math 相乘，得到所谓的耗散能量数学 p { diss } t { a } dot s { i } / math。

The expression of the second law for closed systems (so, allowing heat exchange and moving boundaries, but not exchange of matter) is:

封闭系统的第二定律(允许热量交换和移动边界，但不允许物质交换)的表达式是:

[math]\displaystyle{ \frac{dS}{dt} = \frac{\dot Q}{T}+\dot S_{i} }[/math] with [math]\displaystyle{ \dot S_{i} \ge 0 }[/math]

[math]\displaystyle{ \frac{dS}{dt} = \frac{\dot Q}{T}+\dot S_{i} }[/math] with [math]\displaystyle{  \dot S_{i} \ge 0 }[/math]

用数学点 s { i } ge 0 / math 来计算数学点 q } + 点 s { i } / math

Here

给你

[math]\displaystyle{ \dot Q }[/math] is the heat flow into the system

[math]\displaystyle{ \dot Q }[/math] is the heat flow into the system

数学 q / math 是进入系统的热流

[math]\displaystyle{ T }[/math] is the temperature at the point where the heat enters the system.

[math]\displaystyle{ T }[/math] is the temperature at the point where the heat enters the system.

Math 是热量进入系统时的温度。

The equality sign holds in the case that only reversible processes take place inside the system. If irreversible processes take place (which is the case in real systems in operation) the >-sign holds. If heat is supplied to the system at several places we have to take the algebraic sum of the corresponding terms.

等式符号在只有可逆过程在系统内发生的情况下成立。如果发生不可逆过程(在实际操作系统中就是这种情况) ,-符号保持不变。如果系统有多处供热，我们必须求相应项的代数和。

For open systems (also allowing exchange of matter):

对于开放系统(也允许物质交换) :

[math]\displaystyle{ \frac{dS}{dt} = \frac{\dot Q}{T}+\dot S+\dot S_{i} }[/math] with [math]\displaystyle{ \dot S_{i} \ge 0 }[/math]

[math]\displaystyle{ \frac{dS}{dt} = \frac{\dot Q}{T}+\dot S+\dot S_{i} }[/math] with [math]\displaystyle{  \dot S_{i} \ge 0 }[/math]

用数学点 s { i } ge 0 / math 表示数学点 q } + 点 s + 点 s { i } / math

Here [math]\displaystyle{ \dot S }[/math] is the flow of entropy into the system associated with the flow of matter entering the system. It should not be confused with the time derivative of the entropy. If matter is supplied at several places we have to take the algebraic sum of these contributions.

这里的数学 s / math 是熵流进入系统，与物质流进入系统有关。它不应该与熵的时间导数混淆。如果物质在几个地方提供，我们必须取这些贡献的代数和。

Statistical mechanics

统计力学

Statistical mechanics gives an explanation for the second law by postulating that a material is composed of atoms and molecules which are in constant motion. A particular set of positions and velocities for each particle in the system is called a microstate of the system and because of the constant motion, the system is constantly changing its microstate. Statistical mechanics postulates that, in equilibrium, each microstate that the system might be in is equally likely to occur, and when this assumption is made, it leads directly to the conclusion that the second law must hold in a statistical sense. That is, the second law will hold on average, with a statistical variation on the order of 1/模板:Radic where N is the number of particles in the system. For everyday (macroscopic) situations, the probability that the second law will be violated is practically zero. However, for systems with a small number of particles, thermodynamic parameters, including the entropy, may show significant statistical deviations from that predicted by the second law. Classical thermodynamic theory does not deal with these statistical variations.

Statistical mechanics gives an explanation for the second law by postulating that a material is composed of atoms and molecules which are in constant motion. A particular set of positions and velocities for each particle in the system is called a microstate of the system and because of the constant motion, the system is constantly changing its microstate. Statistical mechanics postulates that, in equilibrium, each microstate that the system might be in is equally likely to occur, and when this assumption is made, it leads directly to the conclusion that the second law must hold in a statistical sense. That is, the second law will hold on average, with a statistical variation on the order of 1/ where N is the number of particles in the system. For everyday (macroscopic) situations, the probability that the second law will be violated is practically zero. However, for systems with a small number of particles, thermodynamic parameters, including the entropy, may show significant statistical deviations from that predicted by the second law. Classical thermodynamic theory does not deal with these statistical variations.

通过假设物质是由不断运动的原子和分子组成的，统计力学对第二定律给出了解释。系统中每个粒子的一组特定的位置和速度称为系统的微观状态，由于系统的不断运动，系统不断地改变其微观状态。统计力学假设，在平衡状态下，系统可能处于的每个微观状态发生的可能性是相等的，当这个假设被提出时，它直接导致了第二定律必须在统计意义上成立的结论。也就是说，第二定律平均成立，其中 n 是系统中粒子数的1 / 数量级的统计变化。在日常(宏观)情况下，违反第二定律的概率几乎为零。然而，对于粒子数量很少的系统，热力学参数，包括熵，可能显示出与第二定律预测的显著的统计偏差。经典热力学理论没有处理这些统计变量。

（by Jie XIANG) 在通过假定一种物质由不断运动的原子和分子组成的前提下，统计力学对热力学第二定律进行了解释。系统中每个粒子其特定的位置和速度组成为系统的微观状态，由于（原子和分子的）不断运动，系统也持续改变其微观状态。统计力学假设，在系统力平衡的情况下，其微观状态其实是等可能发生的，进而能够得出结论：热力学第二定律必须在统计学意义上成立。也就是说，第二定律将保持均值不变，其统计变化为1 /√N，N为系统中的粒子数。在日常(宏观)情况下，违反热力学第二定律的概率几乎为零，但是，对于粒子数量非常少的系统，其热力学参数（包括熵）可能会显示出与第二定律所预测的明显统计偏差。然而经典热力学理论并不处理这些统计变量。

Derivation from statistical mechanics

从统计力学导出

模板:Further information

The first mechanical argument of the Kinetic theory of gases that molecular collisions entail an equalization of temperatures and hence a tendency towards equilibrium was due to James Clerk Maxwell in 1860;^[58] Ludwig Boltzmann with his H-theorem of 1872 also argued that due to collisions gases should over time tend toward the Maxwell–Boltzmann distribution.

The first mechanical argument of the Kinetic theory of gases that molecular collisions entail an equalization of temperatures and hence a tendency towards equilibrium was due to James Clerk Maxwell in 1860; Ludwig Boltzmann with his H-theorem of 1872 also argued that due to collisions gases should over time tend toward the Maxwell–Boltzmann distribution.

气体动力学理论的第一个力学论证由詹姆斯·克拉克·麦克斯韦在1860年给出，指出分子碰撞引起温度均衡，因此整体趋向于平衡；路德维希·玻尔兹曼在1872年提出的 H 定理也认为，气体由于碰撞应该随着时间的推移趋向于麦克斯韦-波兹曼分布。

Due to Loschmidt's paradox, derivations of the Second Law have to make an assumption regarding the past, namely that the system is uncorrelated at some time in the past; this allows for simple probabilistic treatment. This assumption is usually thought as a boundary condition, and thus the second Law is ultimately a consequence of the initial conditions somewhere in the past, probably at the beginning of the universe (the Big Bang), though other scenarios have also been suggested.^[59]^[60]^[61]

Due to Loschmidt's paradox, derivations of the Second Law have to make an assumption regarding the past, namely that the system is uncorrelated at some time in the past; this allows for simple probabilistic treatment. This assumption is usually thought as a boundary condition, and thus the second Law is ultimately a consequence of the initial conditions somewhere in the past, probably at the beginning of the universe (the Big Bang), though other scenarios have also been suggested.

由于洛施密特悖论，第二定律的导出必须对过去做出一个假设，即系统在过去的某个时刻是不相关的；这样的假设允许进行简单的概率处理。这个假设通常被认为是一个边界条件，因此热力学第二定律最终是过去某个地方的初始条件的结果，可能是在宇宙的开始(大爆炸) 。也有人提出了其他假设。

Given these assumptions, in statistical mechanics, the Second Law is not a postulate, rather it is a consequence of the fundamental postulate, also known as the equal prior probability postulate, so long as one is clear that simple probability arguments are applied only to the future, while for the past there are auxiliary sources of information which tell us that it was low entropy.^{[citation needed]} The first part of the second law, which states that the entropy of a thermally isolated system can only increase, is a trivial consequence of the equal prior probability postulate, if we restrict the notion of the entropy to systems in thermal equilibrium. The entropy of an isolated system in thermal equilibrium containing an amount of energy of [math]\displaystyle{ E }[/math] is:

Given these assumptions, in statistical mechanics, the Second Law is not a postulate, rather it is a consequence of the fundamental postulate, also known as the equal prior probability postulate, so long as one is clear that simple probability arguments are applied only to the future, while for the past there are auxiliary sources of information which tell us that it was low entropy. The first part of the second law, which states that the entropy of a thermally isolated system can only increase, is a trivial consequence of the equal prior probability postulate, if we restrict the notion of the entropy to systems in thermal equilibrium. The entropy of an isolated system in thermal equilibrium containing an amount of energy of [math]\displaystyle{ E }[/math] is:

考虑到这些假设，在统计力学中，第二定律不是一个假设，而是统计力学基本假设的一个结果，也被称为等先验概率假设。这个基本假设表明，只要一个人清楚地知道，简单的概率论证只适用于未来，而对于过去，有辅助的信息来源告诉我们，它是低熵的。热力学第二定律的第一部分指出，热孤立系统的熵只能增加。如果我们把熵的概念限制在热平衡系统中，那么热力学第二定律的第一部分是等先验概率假设的一个显然结果。在热平衡，一个孤立系统的熵包含数学 e / math 的能量是:

[math]\displaystyle{ S = k_{\mathrm B} \ln\left[\Omega\left(E\right)\right]\, }[/math]

[math]\displaystyle{ S = k_{\mathrm B} \ln\left[\Omega\left(E\right)\right]\, }[/math]

左[ Omega 左(e 右)右] / math

where [math]\displaystyle{ \Omega\left(E\right) }[/math] is the number of quantum states in a small interval between [math]\displaystyle{ E }[/math] and [math]\displaystyle{ E +\delta E }[/math]. Here [math]\displaystyle{ \delta E }[/math] is a macroscopically small energy interval that is kept fixed. Strictly speaking this means that the entropy depends on the choice of [math]\displaystyle{ \delta E }[/math]. However, in the thermodynamic limit (i.e. in the limit of infinitely large system size), the specific entropy (entropy per unit volume or per unit mass) does not depend on [math]\displaystyle{ \delta E }[/math].

其中 math Omega left (e right) / math 是 math e / math 和 math e + delta e / math 之间一个小区间内的量子状态数。这里的 math delta e / math 是一个宏观上很小的能量区间，并且保持不变。严格地说，这意味着熵取决于对 math delta e / math 的选择。然而，在香港特别行政区热力学极限。在无穷大系统的极限条件下，特定熵(单位体积或单位质量的熵)不依赖于数学上的增量 e / math。

Suppose we have an isolated system whose macroscopic state is specified by a number of variables. These macroscopic variables can, e.g., refer to the total volume, the positions of pistons in the system, etc. Then [math]\displaystyle{ \Omega }[/math] will depend on the values of these variables. If a variable is not fixed, (e.g. we do not clamp a piston in a certain position), then because all the accessible states are equally likely in equilibrium, the free variable in equilibrium will be such that [math]\displaystyle{ \Omega }[/math] is maximized as that is the most probable situation in equilibrium.

假设我们有一个孤立系统，其宏观状态由许多变量指定。这些宏观变量可以，例如，参考总体积，活塞在系统中的位置等。然后 math Omega / math 将取决于这些变量的值。如果一个变量不是固定的，例如。我们不会在某个位置夹住活塞) ，那么因为所有可达状态在平衡状态下的可能性是相等的，平衡状态下的自由变量是这样的，因为这是平衡状态下最可能的情况。

If the variable was initially fixed to some value then upon release and when the new equilibrium has been reached, the fact the variable will adjust itself so that [math]\displaystyle{ \Omega }[/math] is maximized, implies that the entropy will have increased or it will have stayed the same (if the value at which the variable was fixed happened to be the equilibrium value).

如果变量最初固定到某个值，然后在释放时，当达到新的平衡时，变量将自我调整，使 math Omega / math 最大化，这意味着熵将增加或保持不变(如果变量固定的值恰好是平衡值)。

Suppose we start from an equilibrium situation and we suddenly remove a constraint on a variable. Then right after we do this, there are a number [math]\displaystyle{ \Omega }[/math] of accessible microstates, but equilibrium has not yet been reached, so the actual probabilities of the system being in some accessible state are not yet equal to the prior probability of [math]\displaystyle{ 1/\Omega }[/math]. We have already seen that in the final equilibrium state, the entropy will have increased or have stayed the same relative to the previous equilibrium state. Boltzmann's H-theorem, however, proves that the quantity $H$ increases monotonically as a function of time during the intermediate out of equilibrium state.

Suppose we start from an equilibrium situation and we suddenly remove a constraint on a variable. Then right after we do this, there are a number [math]\displaystyle{ \Omega }[/math] of accessible microstates, but equilibrium has not yet been reached, so the actual probabilities of the system being in some accessible state are not yet equal to the prior probability of [math]\displaystyle{ 1/\Omega }[/math]. We have already seen that in the final equilibrium state, the entropy will have increased or have stayed the same relative to the previous equilibrium state. Boltzmann's H-theorem, however, proves that the quantity increases monotonically as a function of time during the intermediate out of equilibrium state.

假设我们从一个平衡状态出发，突然移除了对一个变量的约束。然后在我们做完这个之后，有一些关于可达到的微观状态的数学 / Omega / math，但是还没有达到平衡，所以系统处于可达到的状态的实际概率还不等于 math 1 / Omega / math 的先验概率。我们已经看到，在最终的平衡状态，相对于之前的平衡状态，熵会增加，或者保持不变。然而，玻耳兹曼的 h 定理证明了在中间离开平衡态时，量作为时间的函数单调增加。

Derivation of the entropy change for reversible processes

可逆过程熵变的推导

The second part of the Second Law states that the entropy change of a system undergoing a reversible process is given by:

第二定律的第二部分指出，经历可逆过程的系统的熵变是由以下因素给出的:

[math]\displaystyle{ dS =\frac{\delta Q}{T} }[/math]

[math]\displaystyle{ dS =\frac{\delta Q}{T} }[/math]

数学 dS frac delta q }{ t } / math

where the temperature is defined as:

其中温度定义为:

[math]\displaystyle{ \frac{1}{k_{\mathrm B} T}\equiv\beta\equiv\frac{d\ln\left[\Omega\left(E\right)\right]}{dE} }[/math]

[数学][[欧米茄][左(右)][右][数学][数学]

See here for the justification for this definition. Suppose that the system has some external parameter, x, that can be changed. In general, the energy eigenstates of the system will depend on x. According to the adiabatic theorem of quantum mechanics, in the limit of an infinitely slow change of the system's Hamiltonian, the system will stay in the same energy eigenstate and thus change its energy according to the change in energy of the energy eigenstate it is in.

请参阅此处对此定义的正当理由。假设系统有一些可以改变的外部参数 x。一般来说，系统的能量本征态将依赖于 x。根据量子力学的绝热定理，在系统哈密顿量无限缓慢变化的极限下，系统将保持在相同的定态，因此系统的能量会随着其所在定态的能量变化而变化。

The generalized force, X, corresponding to the external variable x is defined such that [math]\displaystyle{ X dx }[/math] is the work performed by the system if x is increased by an amount dx. E.g., if x is the volume, then X is the pressure. The generalized force for a system known to be in energy eigenstate [math]\displaystyle{ E_{r} }[/math] is given by:

广义力，x，对应于外部变量 x 的定义是，如果 x 增加一个量 dx，那么 math x dx / math 就是系统所做的功。例如，如果 x 是体积，那么 x 是压强。一个已知的系统的广义力在定态数学 e { r } / math 中给出:

[math]\displaystyle{ X = -\frac{dE_{r}}{dx} }[/math]

[math]\displaystyle{ X = -\frac{dE_{r}}{dx} }[/math]

数学 x- frac { dE { r }{ dx } / math

Since the system can be in any energy eigenstate within an interval of [math]\displaystyle{ \delta E }[/math], we define the generalized force for the system as the expectation value of the above expression:

由于系统可以在一个数学△ e / math 区间内的任意定态内，我们将系统的广义力定义为上述表达式的期望值:

[math]\displaystyle{ X = -\left\langle\frac{dE_{r}}{dx}\right\rangle\, }[/math]

[math]\displaystyle{ X = -\left\langle\frac{dE_{r}}{dx}\right\rangle\, }[/math]

数学 x- 左 langle frac { dE { dx }右 rangle，/ math

To evaluate the average, we partition the [math]\displaystyle{ \Omega\left(E\right) }[/math] energy eigenstates by counting how many of them have a value for [math]\displaystyle{ \frac{dE_{r}}{dx} }[/math] within a range between [math]\displaystyle{ Y }[/math] and [math]\displaystyle{ Y + \delta Y }[/math]. Calling this number [math]\displaystyle{ \Omega_{Y}\left(E\right) }[/math], we have:

为了计算平均值，我们通过计算在数学 y / math 和数学 y + delta y / math 之间的范围内，其中有多少数学 y / math 能量本征态有一个值来划分 ω 左(e 右) / math 能量本征态。把这个数字命名为 math Omega { y } left (e right) / math，我们有:

[math]\displaystyle{ \Omega\left(E\right)=\sum_{Y}\Omega_{Y}\left(E\right)\, }[/math]

[math]\displaystyle{ \Omega\left(E\right)=\sum_{Y}\Omega_{Y}\left(E\right)\, }[/math]

Math Omega left (e right) sum { y } Omega { y } left (e right) ，/ math

The average defining the generalized force can now be written:

定义广义力的平均值现在可以写成:

[math]\displaystyle{ X = -\frac{1}{\Omega\left(E\right)}\sum_{Y} Y\Omega_{Y}\left(E\right)\, }[/math]

[math]\displaystyle{ X = -\frac{1}{\Omega\left(E\right)}\sum_{Y} Y\Omega_{Y}\left(E\right)\, }[/math]

数学 x frac {1} Omega 左(e 右) sum { y Omega { y }左(e 右) ，/ math

We can relate this to the derivative of the entropy with respect to x at constant energy E as follows. Suppose we change x to x + dx. Then [math]\displaystyle{ \Omega\left(E\right) }[/math] will change because the energy eigenstates depend on x, causing energy eigenstates to move into or out of the range between [math]\displaystyle{ E }[/math] and [math]\displaystyle{ E+\delta E }[/math]. Let's focus again on the energy eigenstates for which [math]\displaystyle{ \frac{dE_{r}}{dx} }[/math] lies within the range between [math]\displaystyle{ Y }[/math] and [math]\displaystyle{ Y + \delta Y }[/math]. Since these energy eigenstates increase in energy by Y dx, all such energy eigenstates that are in the interval ranging from E – Y dx to E move from below E to above E. There are

我们可以把它和熵对 x 在恒定能量 e 下的导数联系起来，如下所示。假设我们把 x 改成 x + dx。然后 math Omega left (e right) / math 将会改变，因为能量本征态依赖于 x，导致能量本征态进入或超出数学 e / math 和数学 e + delta e / math 之间的范围。让我们再次关注数学 y / math 和数学 y + delta y / math 之间的能量本征态。由于这些能量本征态的能量增加了 y dx，所有这些能量本征态在 e-y dx 到 e 之间的区间内从 e 以下移动到 e 以上。有

[math]\displaystyle{ N_{Y}\left(E\right)=\frac{\Omega_{Y}\left(E\right)}{\delta E} Y dx\, }[/math]

[math]\displaystyle{ N_{Y}\left(E\right)=\frac{\Omega_{Y}\left(E\right)}{\delta E} Y dx\, }[/math]

数学 n { y }左(e 右) frac { y }左(e 右)}{ delta e } y dx ，/ math

such energy eigenstates. If [math]\displaystyle{ Y dx\leq\delta E }[/math], all these energy eigenstates will move into the range between [math]\displaystyle{ E }[/math] and [math]\displaystyle{ E+\delta E }[/math] and contribute to an increase in [math]\displaystyle{ \Omega }[/math]. The number of energy eigenstates that move from below [math]\displaystyle{ E+\delta E }[/math] to above [math]\displaystyle{ E+\delta E }[/math] is given by [math]\displaystyle{ N_{Y}\left(E+\delta E\right) }[/math]. The difference

这样的能量本征态。如果数学 y dx leq delta e / math，所有这些能量本征态将移动到数学 e / math 和数学 e + delta e / math 之间的范围内，有助于数学 ω / math 的增加。从数学 e + △ e / math 下移到数学 e + △ e / math 上的能量本征态的个数是由数学 n { y }左(e + △ e 右) / math 给出的。区别在于

[math]\displaystyle{ N_{Y}\left(E\right) - N_{Y}\left(E+\delta E\right)\, }[/math]

[math]\displaystyle{ N_{Y}\left(E\right) - N_{Y}\left(E+\delta E\right)\, }[/math]

数学 n { y }左(e 右)-n { y }左(e + delta e 右) ，/ math

is thus the net contribution to the increase in [math]\displaystyle{ \Omega }[/math]. Note that if Y dx is larger than [math]\displaystyle{ \delta E }[/math] there will be the energy eigenstates that move from below E to above [math]\displaystyle{ E+\delta E }[/math]. They are counted in both [math]\displaystyle{ N_{Y}\left(E\right) }[/math] and [math]\displaystyle{ N_{Y}\left(E+\delta E\right) }[/math], therefore the above expression is also valid in that case.

因此是数学增长的净贡献欧米茄 / 数学。请注意，如果 y dx 大于 math delta e / math，那么将会有能量本征态从 e 下面移动到 e + delta e / math 上面。它们在数学 n { y } left (e right) / math 和数学 n { y } left (e + delta e right) / math 中都有计算，因此上述表达式在这种情况下也是有效的。

Expressing the above expression as a derivative with respect to E and summing over Y yields the expression:

将上面的表达式表示为对 e 的导数，对 y 的求和得到表达式:

[math]\displaystyle{ \left(\frac{\partial\Omega}{\partial x}\right)_{E} = -\sum_{Y}Y\left(\frac{\partial\Omega_{Y}}{\partial E}\right)_{x}= \left(\frac{\partial\left(\Omega X\right)}{\partial E}\right)_{x}\, }[/math]

[math]\displaystyle{ \left(\frac{\partial\Omega}{\partial x}\right)_{E} = -\sum_{Y}Y\left(\frac{\partial\Omega_{Y}}{\partial E}\right)_{x}= \left(\frac{\partial\left(\Omega X\right)}{\partial E}\right)_{x}\, }[/math]

数学左(部分欧米茄左(部分欧米茄右){ e }-和 y 左(部分欧米茄右){ x 左(部分欧米茄左(部分欧米茄右)}{ x 右) ，/ 数学

The logarithmic derivative of [math]\displaystyle{ \Omega }[/math] with respect to x is thus given by:

关于 x 的欧米茄 / 数学对数导数由以下方式给出:

[math]\displaystyle{ \left(\frac{\partial\ln\left(\Omega\right)}{\partial x}\right)_{E} = \beta X +\left(\frac{\partial X}{\partial E}\right)_{x}\, }[/math]

[math]\displaystyle{ \left(\frac{\partial\ln\left(\Omega\right)}{\partial x}\right)_{E} = \beta X +\left(\frac{\partial X}{\partial E}\right)_{x}\, }[/math]

Math 左( frac { partial ln 左( Omega 右)}{部分 x 右){ e } beta x + 左( frac { partial x 右){ x } ，/ math

The first term is intensive, i.e. it does not scale with system size. In contrast, the last term scales as the inverse system size and will thus vanishes in the thermodynamic limit. We have thus found that:

第一个术语是密集型的，即。它不能根据系统大小进行缩放。相比之下，最后一项的规模与逆系统的规模一样，因此将在热力学极限中消失。因此，我们发现:

[math]\displaystyle{ \left(\frac{\partial S}{\partial x}\right)_{E} = \frac{X}{T}\, }[/math]

[math]\displaystyle{ \left(\frac{\partial S}{\partial x}\right)_{E} = \frac{X}{T}\, }[/math]

数学左(部分 s }右){ e } frac { x }{ t } ，/ math

Combining this with

结合这一点

[math]\displaystyle{ \left(\frac{\partial S}{\partial E}\right)_{x} = \frac{1}{T}\, }[/math]

[math]\displaystyle{ \left(\frac{\partial S}{\partial E}\right)_{x} = \frac{1}{T}\, }[/math]

数学左(部分 s }右){ x } frac {1}{ t } ，/ math

Gives:

给予:

[math]\displaystyle{ dS = \left(\frac{\partial S}{\partial E}\right)_{x}dE+\left(\frac{\partial S}{\partial x}\right)_{E}dx = \frac{dE}{T} + \frac{X}{T} dx=\frac{\delta Q}{T}\, }[/math]

[math]\displaystyle{ dS = \left(\frac{\partial S}{\partial E}\right)_{x}dE+\left(\frac{\partial S}{\partial x}\right)_{E}dx = \frac{dE}{T} + \frac{X}{T} dx=\frac{\delta Q}{T}\, }[/math]

数学 dS 左(部分 s }部分 e }右){ x } dE + 左(部分 s }右){ e } dx frac { t } + frac { t }{ delta q }{ t } ，/ math

Derivation for systems described by the canonical ensemble

正则系综描述的系统的推导

If a system is in thermal contact with a heat bath at some temperature T then, in equilibrium, the probability distribution over the energy eigenvalues are given by the canonical ensemble:

如果一个系统在某个温度 t 下与热浴热接触，那么，在平衡状态下，概率分布的能量本征值由正则系综给出:

[math]\displaystyle{ P_{j}=\frac{\exp\left(-\frac{E_{j}}{k_{\mathrm B} T}\right)}{Z} }[/math]

[math]\displaystyle{ P_{j}=\frac{\exp\left(-\frac{E_{j}}{k_{\mathrm B} T}\right)}{Z} }[/math]

数学 p { j } frac { exp left (- frac { j }{ k { mathrm b }{右)}{ z } / math

Here Z is a factor that normalizes the sum of all the probabilities to 1, this function is known as the partition function. We now consider an infinitesimal reversible change in the temperature and in the external parameters on which the energy levels depend. It follows from the general formula for the entropy:

这里 z 是一个因子，它使所有概率之和正态化为1，这个函数被称为配分函数。我们现在考虑温度和能级所依赖的外部参数的无限小的可逆变化。它遵循熵的一般公式:

[math]\displaystyle{ S = -k_{\mathrm B}\sum_{j}P_{j}\ln\left(P_{j}\right) }[/math]

[math]\displaystyle{ S = -k_{\mathrm B}\sum_{j}P_{j}\ln\left(P_{j}\right) }[/math]

数学 s-k { m b } sum { j } p { j } ln 左(p { j }右) / 数学

that

那个

[math]\displaystyle{ dS = -k_{\mathrm B}\sum_{j}\ln\left(P_{j}\right)dP_{j} }[/math]

[math]\displaystyle{ dS = -k_{\mathrm B}\sum_{j}\ln\left(P_{j}\right)dP_{j} }[/math]

数学 dS-k mathrm b } sum { j } ln 左(p { j }右) dP { j } / 数学

Inserting the formula for [math]\displaystyle{ P_{j} }[/math] for the canonical ensemble in here gives:

在这里插入正则系综的数学公式 p { j } / math 给出:

[math]\displaystyle{ dS = \frac{1}{T}\sum_{j}E_{j}dP_{j}=\frac{1}{T}\sum_{j}d\left(E_{j}P_{j}\right) - \frac{1}{T}\sum_{j}P_{j}dE_{j}= \frac{dE + \delta W}{T}=\frac{\delta Q}{T} }[/math]

[math]\displaystyle{ dS = \frac{1}{T}\sum_{j}E_{j}dP_{j}=\frac{1}{T}\sum_{j}d\left(E_{j}P_{j}\right) - \frac{1}{T}\sum_{j}P_{j}dE_{j}= \frac{dE + \delta W}{T}=\frac{\delta Q}{T} }[/math]

数学 dS frac {1}{ t } sum { j } e { j } dP { j } frac {1}{ t }{ j }{ j }向左(e { j } p { j }右)-frac {1}{ t }{ j }和{ j }向右(t }{ j }向右)-frac {1}{ j }向右(t }{ j }向左)-frac { j }向右(t }{ j }向右(t }向右)-f rc { j }{ j }向右(t }向右(t)向右(t }向右)-f rc { j }向右(t }向右) -

Living organisms

生命体

There are two principal ways of formulating thermodynamics, (a) through passages from one state of thermodynamic equilibrium to another, and (b) through cyclic processes, by which the system is left unchanged, while the total entropy of the surroundings is increased. These two ways help to understand the processes of life. This topic is mostly beyond the scope of this present article, but has been considered by several authors, such as Erwin Schrödinger, Léon Brillouin^[62] and Isaac Asimov. It is also the topic of current模板:When research.^{[citation needed]}

There are two principal ways of formulating thermodynamics, (a) through passages from one state of thermodynamic equilibrium to another, and (b) through cyclic processes, by which the system is left unchanged, while the total entropy of the surroundings is increased. These two ways help to understand the processes of life. This topic is mostly beyond the scope of this present article, but has been considered by several authors, such as Erwin Schrödinger, Léon Brillouin and Isaac Asimov. It is also the topic of current research.

表述热力学主要有两种方式：(a)描述从一种热力学平衡状态到另一种状态的路径，(b)通过使系统保持不变，同时增加周围环境的总熵的循环过程。这两种方法有助于理解生命过程。这个话题大大超出了本文的范围，但是已经有一些研究者考虑过这个问题，比如埃尔温·薛定谔、莱昂·布里渊和艾萨克.阿西莫夫。这也是当前研究的主题。

To a fair approximation, living organisms may be considered as examples of (b). Approximately, an animal's physical state cycles by the day, leaving the animal nearly unchanged. Animals take in food, water, and oxygen, and, as a result of metabolism, give out breakdown products and heat. Plants take in radiative energy from the sun, which may be regarded as heat, and carbon dioxide and water. They give out oxygen. In this way they grow. Eventually they die, and their remains rot away, turning mostly back into carbon dioxide and water. This can be regarded as a cyclic process. Overall, the sunlight is from a high temperature source, the sun, and its energy is passed to a lower temperature sink, i.e. radiated into space. This is an increase of entropy of the surroundings of the plant. Thus animals and plants obey the second law of thermodynamics, considered in terms of cyclic processes. Simple concepts of efficiency of heat engines are hardly applicable to this problem because they assume closed systems.

从近似的角度来看，生命体可以被认为是(b)的一个例子。近似地，一只动物的身体状态每天循环，使得它几乎没有什么变化。动物吸收食物、水和氧气，经过新陈代谢，输出分解的产物和热量。植物吸收来自太阳的辐射能量，这可以认为是热量，以及二氧化碳和水，然后它们释放氧气。它们就是这样生长的，最终会死亡，尸体腐烂，大部分重新变成二氧化碳和水。这可以看作是一个循环过程。总的来说，阳光来自一个高温的源——太阳，它的能量被传递到一个较低的温度汇，例如向太空辐射。这个过程使得植物周围环境的熵增加。因此从循环过程的角度来看，动物和植物服从热力学第二定律。简单的热机效率概念很难适用于这个问题，因为它们假定系统是封闭的。

From the thermodynamic viewpoint that considers (a), passages from one equilibrium state to another, only a roughly approximate picture appears, because living organisms are never in states of thermodynamic equilibrium. Living organisms must often be considered as open systems, because they take in nutrients and give out waste products. Thermodynamics of open systems is currently often considered in terms of passages from one state of thermodynamic equilibrium to another, or in terms of flows in the approximation of local thermodynamic equilibrium. The problem for living organisms may be further simplified by the approximation of assuming a steady state with unchanging flows. General principles of entropy production for such approximations are subject to unsettled current debate or research. Nevertheless, ideas derived from this viewpoint on the second law of thermodynamics are enlightening about living creatures.

从(a)的热力学观点考虑，即考虑从一个平衡状态到另一个平衡状态的路径，只会产生一个粗略近似的图像，因为生命体从来不会处于热力学平衡状态。生物体经常必须被认为是开放的系统，因为它们吸收营养物质并排出废弃物。开放系统热力学目前通常从一个热力学平衡状态到另一个状态的路径的角度来考虑，或者是考虑局部热力学平衡近似下的流。生命体的问题可以通过假定一个流不变的稳态来进一步简化。对于这样的近似，熵产生的一般原理在目前有争论和研究的不确定性。尽管如此，从热力学第二定律的这个角度出发衍生出来的想法对生物是有启发意义的。

Gravitational systems

重力系统

In systems that do not require for their descriptions the general theory of relativity, bodies always have positive heat capacity, meaning that the temperature rises with energy. Therefore, when energy flows from a high-temperature object to a low-temperature object, the source temperature is decreased while the sink temperature is increased; hence temperature differences tend to diminish over time. This is not always the case for systems in which the gravitational force is important and the general theory of relativity is required. Such systems can spontaneously change towards uneven spread of mass and energy. This applies to the universe in large scale, and consequently it may be difficult or impossible to apply the second law to it.^[63] Beyond this, the thermodynamics of systems described by the general theory of relativity is beyond the scope of the present article.

In systems that do not require for their descriptions the general theory of relativity, bodies always have positive heat capacity, meaning that the temperature rises with energy. Therefore, when energy flows from a high-temperature object to a low-temperature object, the source temperature is decreased while the sink temperature is increased; hence temperature differences tend to diminish over time. This is not always the case for systems in which the gravitational force is important and the general theory of relativity is required. Such systems can spontaneously change towards uneven spread of mass and energy. This applies to the universe in large scale, and consequently it may be difficult or impossible to apply the second law to it. Beyond this, the thermodynamics of systems described by the general theory of relativity is beyond the scope of the present article.

在不需要描述广义相对论的系统中，物体总是具有正的热容，这意味着温度随着能量的增加而升高。因此，当能量从高温物体流向低温物体时，源温度降低，而汇温度升高; 因此温差随时间而减小。这种情况并不总是发生在那些需要引力和广义相对论的系统中。这样的系统可以自发地朝着质量和能量不均匀分布的方向变化。这在大尺度上适用于宇宙，因此可能很难或不可能将第二定律应用于宇宙。除此之外，广义相对论所描述的系统热力学超出了本文的范围。

Non-equilibrium states

模板:Main article

The theory of classical or equilibrium thermodynamics is idealized. A main postulate or assumption, often not even explicitly stated, is the existence of systems in their own internal states of thermodynamic equilibrium. In general, a region of space containing a physical system at a given time, that may be found in nature, is not in thermodynamic equilibrium, read in the most stringent terms. In looser terms, nothing in the entire universe is or has ever been truly in exact thermodynamic equilibrium.^[63]^[64]

The theory of classical or equilibrium thermodynamics is idealized. A main postulate or assumption, often not even explicitly stated, is the existence of systems in their own internal states of thermodynamic equilibrium. In general, a region of space containing a physical system at a given time, that may be found in nature, is not in thermodynamic equilibrium, read in the most stringent terms. In looser terms, nothing in the entire universe is or has ever been truly in exact thermodynamic equilibrium.

经典热力学或平衡热力学的理想化。一个主要的假设或假设，往往甚至没有明确说明，是系统的存在，在他们自己的内部状态的热力学平衡。一般来说，在给定时间内包含一个物理系统的空间区域---- 可能在自然界中找到---- 不是在热力学平衡中，用最严格的术语来解释。从更宽松的角度来说，整个宇宙中没有任何东西是或者曾经是完全精确的热力学平衡。

For purposes of physical analysis, it is often enough convenient to make an assumption of thermodynamic equilibrium. Such an assumption may rely on trial and error for its justification. If the assumption is justified, it can often be very valuable and useful because it makes available the theory of thermodynamics. Elements of the equilibrium assumption are that a system is observed to be unchanging over an indefinitely long time, and that there are so many particles in a system, that its particulate nature can be entirely ignored. Under such an equilibrium assumption, in general, there are no macroscopically detectable fluctuations. There is an exception, the case of critical states, which exhibit to the naked eye the phenomenon of critical opalescence. For laboratory studies of critical states, exceptionally long observation times are needed.

为了物理分析的目的，假设热力学平衡是非常方便的。这种假设可能依赖于试错来证明其正当性。如果这个假设是正确的，它通常是非常有价值和有用的，因为它提供了热力学理论。平衡假设的要素是，一个系统被观察到在无限长的时间内是不变的，而且一个系统中有如此多的粒子，以至于它的微粒性质可以被完全忽略。在这样的平衡假设下，一般来说，没有宏观上可以探测到的波动。有一个例外，即临界状态的例子，它们用肉眼就可以看到临界乳光现象。对于临界状态的实验室研究，需要非常长的观察时间。

In all cases, the assumption of thermodynamic equilibrium, once made, implies as a consequence that no putative candidate "fluctuation" alters the entropy of the system.

在所有情况下，热力学平衡的假设，一旦做出，就意味着没有假定的候选者“涨落”改变系统的熵。

It can easily happen that a physical system exhibits internal macroscopic changes that are fast enough to invalidate the assumption of the constancy of the entropy. Or that a physical system has so few particles that the particulate nature is manifest in observable fluctuations. Then the assumption of thermodynamic equilibrium is to be abandoned. There is no unqualified general definition of entropy for non-equilibrium states.^[65]

It can easily happen that a physical system exhibits internal macroscopic changes that are fast enough to invalidate the assumption of the constancy of the entropy. Or that a physical system has so few particles that the particulate nature is manifest in observable fluctuations. Then the assumption of thermodynamic equilibrium is to be abandoned. There is no unqualified general definition of entropy for non-equilibrium states.

一个物理系统很容易发生内部的宏观变化，其速度之快足以使熵的恒定性假设失效。或者一个物理系统的粒子太少，以至于微粒的本质在可观测的波动中是显而易见的。那么热力学平衡的假设就会被放弃。对于非平衡态，熵没有绝对的一般定义。

There are intermediate cases, in which the assumption of local thermodynamic equilibrium is a very good approximation,^[66]^[67]^[68]^[69] but strictly speaking it is still an approximation, not theoretically ideal.

There are intermediate cases, in which the assumption of local thermodynamic equilibrium is a very good approximation, but strictly speaking it is still an approximation, not theoretically ideal.

还有一些中间情况，其中局部热力学平衡的假设是一个非常好的近似值，但严格地说它仍然是一个近似值，不是理论上的理想值。

For non-equilibrium situations in general, it may be useful to consider statistical mechanical definitions of other quantities that may be conveniently called 'entropy', but they should not be confused or conflated with thermodynamic entropy properly defined for the second law. These other quantities indeed belong to statistical mechanics, not to thermodynamics, the primary realm of the second law.

对于一般的非平衡状态，考虑其他量的统计力学定义可能是有用的，这些量可以方便地称为‘熵’ ，但是它们不应该与第二定律正确定义的熵混淆或混淆。这些其他的量确实属于统计力学，而不是热力学---- 第二定律的主要领域。

The physics of macroscopically observable fluctuations is beyond the scope of this article.

宏观观测波动的物理学超出了本文的范围。

Arrow of time

时间之箭

模板:Further informationThermodynamic Asymmetry in Time

Thermodynamic Asymmetry in Time

时间中的热力学不对称性

The second law of thermodynamics is a physical law that is not symmetric to reversal of the time direction. This does not conflict with notions that have been observed of the fundamental laws of physics, namely CPT symmetry, since the second law applies statistically, it is hypothesized, on time-asymmetric boundary conditions.^[70]

The second law of thermodynamics is a physical law that is not symmetric to reversal of the time direction. This does not conflict with notions that have been observed of the fundamental laws of physics, namely CPT symmetry, since the second law applies statistically, it is hypothesized, on time-asymmetric boundary conditions.

热力学第二定律是一个物理定律，它不对称于时间方向的反转。这与已经观察到的物理学基本定律，即 CPT 对称性的概念并不冲突，因为第二定律在统计上适用，它是假设的，是关于时间非对称的边界条件。

The second law has been proposed to supply a partial explanation of the difference between moving forward and backwards in time, such as why the cause precedes the effect (the causal arrow of time).^[71]

The second law has been proposed to supply a partial explanation of the difference between moving forward and backwards in time, such as why the cause precedes the effect (the causal arrow of time).

第二定律被提出来部分解释时间向前和向后移动的区别，例如为什么原因先于结果(因果关系的时间箭头)。

Irreversibility

不可逆性

Irreversibility in thermodynamic processes is a consequence of the asymmetric character of thermodynamic operations, and not of any internally irreversible microscopic properties of the bodies. Thermodynamic operations are macroscopic external interventions imposed on the participating bodies, not derived from their internal properties. There are reputed "paradoxes" that arise from failure to recognize this.

热力学过程的不可逆性是热力学作用不对称性的结果，而不是物体内部不可逆的微观性质的结果。热力学操作是施加在参与机构上的宏观外部干预，而不是从它们的内部性质中得到的。由于没有认识到这一点，产生了被称为“悖论”的说法。

Loschmidt's paradox

洛斯密特悖论

模板:Main article

Loschmidt's paradox, also known as the reversibility paradox, is the objection that it should not be possible to deduce an irreversible process from the time-symmetric dynamics that describe the microscopic evolution of a macroscopic system.

洛斯密特悖论，也被称为可逆性悖论，其目的在于不可能从描述宏观系统微观演化的时间对称动力学推导出不可逆性。

In the opinion of Schrödinger, "It is now quite obvious in what manner you have to reformulate the law of entropy模板:Sndor for that matter, all other irreversible statements模板:Sndso that they be capable of being derived from reversible models. You must not speak of one isolated system but at least of two, which you may for the moment consider isolated from the rest of the world, but not always from each other."^[72] The two systems are isolated from each other by the wall, until it is removed by the thermodynamic operation, as envisaged by the law. The thermodynamic operation is externally imposed, not subject to the reversible microscopic dynamical laws that govern the constituents of the systems. It is the cause of the irreversibility. The statement of the law in this present article complies with Schrödinger's advice. The cause–effect relation is logically prior to the second law, not derived from it.

In the opinion of Schrödinger, "It is now quite obvious in what manner you have to reformulate the law of entropyor for that matter, all other irreversible statementsso that they be capable of being derived from reversible models. You must not speak of one isolated system but at least of two, which you may for the moment consider isolated from the rest of the world, but not always from each other." The two systems are isolated from each other by the wall, until it is removed by the thermodynamic operation, as envisaged by the law. The thermodynamic operation is externally imposed, not subject to the reversible microscopic dynamical laws that govern the constituents of the systems. It is the cause of the irreversibility. The statement of the law in this present article complies with Schrödinger's advice. The cause–effect relation is logically prior to the second law, not derived from it.

根据薛定谔的观点，“现在很明显，你必须用什么方式来重新定义该物质的熵定律，所有其他不可逆的状态，这样它们才能从可逆模型中导出。你不能只谈论一个孤立的系统，而应该至少谈论两个，你可以暂时认为它们与世界其它地方是孤立的，但并不总是相互孤立的。”这两个系统被隔离墙隔离开来，直到按照法律的设想被热力学操作拆除。热力学操作是外部强加的，不受支配系统组成部分的可逆微观动力学定律的制约。它是不可逆转性的原因。本文中的法律陈述符合薛定谔的建议。因果关系在逻辑上优先于第二定律，而不是从第二定律派生出来的。

Poincaré recurrence theorem

庞加莱始态复现定理

模板:Main article

The Poincaré recurrence theorem considers a theoretical microscopic description of an isolated physical system. This may be considered as a model of a thermodynamic system after a thermodynamic operation has removed an internal wall. The system will, after a sufficiently long time, return to a microscopically defined state very close to the initial one. The Poincaré recurrence time is the length of time elapsed until the return. It is exceedingly long, likely longer than the life of the universe, and depends sensitively on the geometry of the wall that was removed by the thermodynamic operation. The recurrence theorem may be perceived as apparently contradicting the second law of thermodynamics. More obviously, however, it is simply a microscopic model of thermodynamic equilibrium in an isolated system formed by removal of a wall between two systems. For a typical thermodynamical system, the recurrence time is so large (many many times longer than the lifetime of the universe) that, for all practical purposes, one cannot observe the recurrence. One might wish, nevertheless, to imagine that one could wait for the Poincaré recurrence, and then re-insert the wall that was removed by the thermodynamic operation. It is then evident that the appearance of irreversibility is due to the utter unpredictability of the Poincaré recurrence given only that the initial state was one of thermodynamic equilibrium, as is the case in macroscopic thermodynamics. Even if one could wait for it, one has no practical possibility of picking the right instant at which to re-insert the wall. The Poincaré recurrence theorem provides a solution to Loschmidt's paradox. If an isolated thermodynamic system could be monitored over increasingly many multiples of the average Poincaré recurrence time, the thermodynamic behavior of the system would become invariant under time reversal.

庞加莱始态复现定理认为这是一个孤立的物理系统的理论微观描述。这可以被认为是一个热力学系统的模型后，一个热力学操作已经移除了一个内墙。在足够长的时间之后，系统将返回到一个非常接近初始状态的显微定义状态。庞加莱回归时间是指回归前经过的时间长度。它极其漫长，可能比宇宙的寿命还要长，并且敏感地依赖于被热力学操作拆除的墙体的几何形状。递归定理可能被认为是明显与热力学第二定律相矛盾的。然而，更明显的是，它只不过是一个微观模型，热力学平衡在一个孤立的系统中，通过移除两个系统之间的一道墙而形成。对于一个典型的热力学系统，重现时间是如此之大(比宇宙的生命周期长许多倍) ，以至于在所有的实际目的中，人们都不能观察到重现。然而，人们可能希望想象一下，可以等待庞加莱复发，然后重新插入被热力学操作移除的壁。然后很明显，不可逆性的出现是由于庞加莱循环的完全不可预测性，只要初始状态是热力学平衡，就像宏观热力学的情况一样。即使可以等待，也没有实际可能性选择合适的时间重新插入墙壁。庞加莱始态复现定理为 Loschmidt 悖论提供了一个解决方案。如果一个孤立的热力学系统可以被监测到在越来越多的平均 poincar 递归时间的倍数上，系统的热力学行为将在时间反转下变得不变。

James Clerk Maxwell

詹姆斯·克拉克·麦克斯韦

Maxwell's demon

麦克斯韦的魔鬼

模板:Unreferenced

模板:Main article

James Clerk Maxwell imagined one container divided into two parts, A and B. Both parts are filled with the same gas at equal temperatures and placed next to each other, separated by a wall. Observing the molecules on both sides, an imaginary demon guards a microscopic trapdoor in the wall. When a faster-than-average molecule from A flies towards the trapdoor, the demon opens it, and the molecule will fly from A to B. The average speed of the molecules in B will have increased while in A they will have slowed down on average. Since average molecular speed corresponds to temperature, the temperature decreases in A and increases in B, contrary to the second law of thermodynamics.

詹姆斯·克拉克·麦克斯韦想象一个容器分成两部分，a 和 b。两个部分在相同的温度下充入相同的气体，并被一堵墙隔开，挨着放置。通过观察两边的分子，一个想象中的恶魔守卫着墙上的一个微型暗门。当一个来自 a 的比平均速度快的分子飞向活板门时，魔鬼打开了它，分子就会从 a 飞到 b。B 中分子的平均速度会增加，而 a 中分子的平均速度会减慢。由于平均分子速度与温度相对应，因此 a 中的温度降低，b 中的温度升高，这与热力学第二定律相反。

One response to this question was suggested in 1929 by Leó Szilárd and later by Léon Brillouin. Szilárd pointed out that a real-life Maxwell's demon would need to have some means of measuring molecular speed, and that the act of acquiring information would require an expenditure of energy.

1929年，Leó Szilárd 和后来的 l on brilouin 对这个问题提出了一个答案。Szil rd 指出，现实生活中的麦克斯韦恶魔需要一些测量分子速度的方法，而获取信息需要消耗大量能量。

Maxwell's 'demon' repeatedly alters the permeability of the wall between A and B. It is therefore performing thermodynamic operations on a microscopic scale, not just observing ordinary spontaneous or natural macroscopic thermodynamic processes.

麦克斯韦的“魔鬼”不断地改变 a 和 b 之间墙体的渗透性。因此，它是在微观尺度上执行热力学操作，而不仅仅是观察普通的自发或自然的宏观热力学过程。

Quotations

语录

模板:Wikiquote

/* Styling for Template:Quote */ .templatequote { overflow: hidden; margin: 1em 0; padding: 0 40px; } .templatequote .templatequotecite {

   line-height: 1.5em;
   /* @noflip */
   text-align: left;
   /* @noflip */
   padding-left: 1.6em;
   margin-top: 0;

}

/* Styling for Template:Quote */ .templatequote { overflow: hidden; margin: 1em 0; padding: 0 40px; } .templatequote .templatequotecite {

   line-height: 1.5em;
   /* @noflip */
   text-align: left;
   /* @noflip */
   padding-left: 1.6em;
   margin-top: 0;

}

/* Styling for Template:Quote */ .templatequote { overflow: hidden; margin: 1em 0; padding: 0 40px; } .templatequote .templatequotecite {

   line-height: 1.5em;
   /* @noflip */
   text-align: left;
   /* @noflip */
   padding-left: 1.6em;
   margin-top: 0;

}

References

参考资料

↑ http://web.mit.edu/16.unified/www/FALL/thermodynamics/notes/node38.html#SECTION05224000000000000000
↑ Atkins and de Paula, p.78
↑ Zohuri, Bahman (2016). Dimensional Analysis Beyond the Pi Theorem. Springer. p. 111. ISBN 978-3-319-45726-0. https://books.google.com/books?id=pRVuDQAAQBAJ.
↑ Jaffe, R.L., Taylor, W. (2018). The Physics of Energy, Cambridge University Press, Cambridge UK, pages 150, 151, 259, 772, 743.
↑ Planck, M. (1897/1903), pp. 40–41.
↑ Munster A. (1970), pp. 8–9, 50–51.
↑ Mandl 1988
↑ Planck, M. (1897/1903), pp. 79–107.
↑ Bailyn, M. (1994), Section 71, pp. 113–154.
↑ Bailyn, M. (1994), p. 120.
↑ ^11.0 ^11.1 ^11.2 Mortimer, R. G. Physical Chemistry. 3rd ed., p. 120, Academic Press, 2008.
↑ Fermi, E. Thermodynamics, footnote on p. 48, Dover Publications,1956 (still in print).
↑ Adkins, C.J. (1968/1983), p. 75.
↑ ^14.0 ^14.1 ^14.2 Münster, A. (1970), p. 45.
↑ ^15.0 ^15.1 ^15.2 Schmidt-Rohr, K. (2014). "Expansion Work without the External Pressure, and Thermodynamics in Terms of Quasistatic Irreversible Processes" J. Chem. Educ. 91: 402-409. https://dx.doi.org/10.1021/ed3008704

↑ ^16.0 ^16.1 Oxtoby, D. W; Gillis, H.P., Butler, L. J. (2015).Principles of Modern Chemistry, Brooks Cole. p. 617.

↑ Pokrovskii V.N. (2005) Extended thermodynamics in a discrete-system approach, Eur. J. Phys. vol. 26, 769–781.
↑ Pokrovskii, Vladimir N. (2013). "A Derivation of the Main Relations of Nonequilibrium Thermodynamics". ISRN Thermodynamics. 2013: 1–9. doi:10.1155/2013/906136.
↑ J. S. Dugdale (1996). Entropy and its Physical Meaning. Taylor & Francis. p. 13. ISBN 978-0-7484-0569-5. "This law is the basis of temperature."
↑ Zemansky, M.W. (1968), pp. 207–209.
↑ Quinn, T.J. (1983), p. 8.
↑ "Concept and Statements of the Second Law". web.mit.edu. Retrieved 2010-10-07.
↑ Carnot, S. (1824/1986).
↑ Carnot, S. (1824/1986), p. 51.
↑ Carnot, S. (1824/1986), p. 46.
↑ Carnot, S. (1824/1986), p. 68.
↑ Truesdell, C. (1980), Chapter 5.
↑ Adkins, C.J. (1968/1983), pp. 56–58.
↑ Münster, A. (1970), p. 11.
↑ Kondepudi, D., Prigogine, I. (1998), pp.67–75.
↑ Lebon, G., Jou, D., Casas-Vázquez, J. (2008), p. 10.
↑ Eu, B.C. (2002), pp. 32–35.
↑ Planck, M. (1897/1903), p. 86.
↑ Roberts, J.K., Miller, A.R. (1928/1960), p. 319.
↑ ter Haar, D., Wergeland, H. (1966), p. 17.
↑ Rao, Y. V. C. (1997). Chemical Engineering Thermodynamics. Universities Press. p. 158. ISBN 978-81-7371-048-3.
↑ Planck, M. (1897/1903), p. 100.
↑ Planck, M. (1926), p. 463, translation by Uffink, J. (2003), p. 131.
↑ Roberts, J.K., Miller, A.R. (1928/1960), p. 382. This source is partly verbatim from Planck's statement, but does not cite Planck. This source calls the statement the principle of the increase of entropy.
↑ Uhlenbeck, G.E., Ford, G.W. (1963), p. 16.
↑ Carathéodory, C. (1909).
↑ Buchdahl, H.A. (1966), p. 68.
↑ Sychev, V. V. (1991). The Differential Equations of Thermodynamics. Taylor & Francis. ISBN 978-1-56032-121-7.
↑ ^44.0 ^44.1 Planck, M. (1926).
↑ Buchdahl, H.A. (1966), p. 69.
↑ Uffink, J. (2003), pp. 129–132.

↑ Truesdell, C., Muncaster, R.G. (1980). Fundamentals of Maxwell's Kinetic Theory of a Simple Monatomic Gas, Treated as a Branch of Rational Mechanics, Academic Press, New York,

, p. 15.

↑ Planck, M. (1897/1903), p. 81.
↑ Planck, M. (1926), p. 457, Wikipedia editor's translation.
↑ Lieb, E.H., Yngvason, J. (2003), p. 149.
↑ Borgnakke, C., Sonntag., R.E. (2009), p. 304.
↑ van Gool, W.; Bruggink, J.J.C. (Eds) (1985). Energy and time in the economic and physical sciences. North-Holland. pp. 41–56. ISBN 978-0-444-87748-2.
↑ Grubbström, Robert W. (2007). "An Attempt to Introduce Dynamics Into Generalised Exergy Considerations". Applied Energy. 84 (7–8): 701–718. doi:10.1016/j.apenergy.2007.01.003.
↑ Clausius theorem at Wolfram Research

↑ Denbigh, K.G., Denbigh, J.S. (1985). Entropy in Relation to Incomplete Knowledge, Cambridge University Press, Cambridge UK,

, pp. 43–44.

↑ Grandy, W.T., Jr (2008). Entropy and the Time Evolution of Macroscopic Systems, Oxford University Press, Oxford,

, pp. 55–58.

↑ Entropy Sites — A Guide Content selected by Frank L. Lambert
↑ Gyenis, Balazs (2017). "Maxwell and the normal distribution: A colored story of probability, independence, and tendency towards equilibrium". Studies in History and Philosophy of Modern Physics. 57: 53–65. arXiv:1702.01411. Bibcode:2017SHPMP..57...53G. doi:10.1016/j.shpsb.2017.01.001.
↑ Hawking, SW (1985). "Arrow of time in cosmology". Phys. Rev. D. 32 (10): 2489–2495. Bibcode:1985PhRvD..32.2489H. doi:10.1103/PhysRevD.32.2489. PMID 9956019.
↑ Greene, Brian (2004). The Fabric of the Cosmos. Alfred A. Knopf. p. 171. ISBN 978-0-375-41288-2. https://archive.org/details/fabricofcosmossp00gree.
↑ Lebowitz, Joel L. (September 1993). "Boltzmann's Entropy and Time's Arrow" (PDF). Physics Today. 46 (9): 32–38. Bibcode:1993PhT....46i..32L. doi:10.1063/1.881363. Retrieved 2013-02-22.
↑ Léon Brillouin Science and Information Theory (Academic Press, 1962) (Dover, 2004)
↑ ^63.0 ^63.1 Grandy, W.T. (Jr) (2008), p. 151.
↑ Callen, H.B. (1960/1985), p. 15.
↑ Lieb, E.H., Yngvason, J. (2003), p. 190.
↑ Gyarmati, I. (1967/1970), pp. 4-14.
↑ Glansdorff, P., Prigogine, I. (1971).
↑ Müller, I. (1985).
↑ Müller, I. (2003).
↑ Callender, Craig (29 July 2011). "Thermodynamic Asymmetry in Time". {{cite web}}: Unknown parameter |encyclopedia= ignored (help)
↑ Halliwell, J.J. (1994). Physical Origins of Time Asymmetry. Cambridge. ISBN 978-0-521-56837-1. chapter 6
↑ Schrödinger, E. (1950), p. 192.

Sources

资料来源

Adkins, C.J. (1968/1983). Equilibrium Thermodynamics, (1st edition 1968), third edition 1983, Cambridge University Press, Cambridge UK,

.

Atkins, P.W., de Paula, J. (2006). Atkins' Physical Chemistry, eighth edition, W.H. Freeman, New York,

.

Attard, P. (2012). Non-equilibrium Thermodynamics and Statistical Mechanics: Foundations and Applications, Oxford University Press, Oxford UK,

.

Baierlein, R. (1999). Thermal Physics, Cambridge University Press, Cambridge UK,

.

Bailyn, M. (1994). A Survey of Thermodynamics, American Institute of Physics, New York,

.

Blundell, Stephen J.; Blundell, Katherine M. (2010). Concepts in thermal physics (2nd ed.). Oxford: Oxford University Press. doi:10.1093/acprof:oso/9780199562091.001.0001. ISBN 9780199562107. OCLC 607907330. http://cds.cern.ch/record/1235139.

Boltzmann, L. (1896/1964). Lectures on Gas Theory, translated by S.G. Brush, University of California Press, Berkeley.

Borgnakke, C., Sonntag., R.E. (2009). Fundamentals of Thermodynamics, seventh edition, Wiley,

.

Buchdahl, H.A. (1966). The Concepts of Classical Thermodynamics, Cambridge University Press, Cambridge UK.

Bridgman, P.W. (1943). The Nature of Thermodynamics, Harvard University Press, Cambridge MA.

Callen, H.B. (1960/1985). Thermodynamics and an Introduction to Thermostatistics, (1st edition 1960) 2nd edition 1985, Wiley, New York,

.

C. Carathéodory (1909). [http://gdz.sub.uni-goettingen.de/index.php?id=11&PPN=PPN235181684_0067&DMDID=DMDLOG_0033&L=1

2010年3月15日 "Untersuchungen über die Grundlagen der Thermodynamik"]. Mathematische Annalen. 67 (3): 355–386. doi:10.1007/bf01450409. Axiom II: In jeder beliebigen Umgebung eines willkürlich vorgeschriebenen Anfangszustandes gibt es Zustände, die durch adiabatische Zustandsänderungen nicht beliebig approximiert werden können. (p.363) {{cite journal}}: Check |url= value (help); Text "第355-386页" ignored (help); line feed character in |url= at position 93 (help). A translation may be found here. Also a mostly reliable translation is to be found at Kestin, J. (1976). The Second Law of Thermodynamics, Dowden, Hutchinson & Ross, Stroudsburg PA.

|quote=Axiom II: In jeder beliebigen Umgebung eines willkürlich vorgeschriebenen Anfangszustandes gibt es Zustände, die durch adiabatische Zustandsänderungen nicht beliebig approximiert werden können. (p.363)|doi=10.1007/bf01450409}}. A translation may be found here. Also a mostly reliable translation is to be found at Kestin, J. (1976). The Second Law of Thermodynamics, Dowden, Hutchinson & Ross, Stroudsburg PA.

|quote=Axiom II: In jeder beliebigen Umgebung eines willkürlich vorgeschriebenen Anfangszustandes gibt es Zustände, die durch adiabatische Zustandsänderungen nicht beliebig approximiert werden können.(p. 363) | doi 10.1007 / bf01450409}.译文可以在这里找到[ http://neo-classical-physics.info/uploads/3/0/6/5/3065888/caratheodory_-_thermodynamics.pdf ]。同时，在 Kestin，j。(1976).热力学第二定律，Dowden，Hutchinson & Ross，Stroudsburg PA. 。

Carnot, S. (1824/1986). Reflections on the motive power of fire, Manchester University Press, Manchester UK,

. Also here.

Chapman, S., Cowling, T.G. (1939/1970). The Mathematical Theory of Non-uniform gases. An Account of the Kinetic Theory of Viscosity, Thermal Conduction and Diffusion in Gases, third edition 1970, Cambridge University Press, London.

Clausius, R. (1850). "Ueber Die Bewegende Kraft Der Wärme Und Die Gesetze, Welche Sich Daraus Für Die Wärmelehre Selbst Ableiten Lassen". Annalen der Physik. 79 (4): 368–397, 500–524. Bibcode:1850AnP...155..500C. doi:10.1002/andp.18501550403. hdl:2027/uc1.$b242250. Retrieved 26 June 2012. {{cite journal}}: Invalid |ref=harv (help) Translated into English: Clausius, R. (July 1851). "On the Moving Force of Heat, and the Laws regarding the Nature of Heat itself which are deducible therefrom". London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 4th. 2 (VIII): 1–21, 102–119. doi:10.1080/14786445108646819. Retrieved 26 June 2012.

|doi=10.1080/14786445108646819}}

10.1080 / 14786445108646819}

Clausius, R. (1854). "Über eine veränderte Form des zweiten Hauptsatzes der mechanischen Wärmetheorie" (PDF). Annalen der Physik. xciii (12): 481–506. Bibcode:1854AnP...169..481C. doi:10.1002/andp.18541691202. Retrieved 24 March 2014. {{cite journal}}: Invalid |ref=harv (help) Translated into English: Clausius, R. (July 1856). "On a Modified Form of the Second Fundamental Theorem in the Mechanical Theory of Heat". London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 4th. 2: 86. Bibcode:1854AnP...169..481C. Retrieved 24 March 2014. Translated into English: Clausius, R. (July 1856). "On a Modified Form of the Second Fundamental Theorem in the Mechanical Theory of Heat". London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 4th. 2: 86. Retrieved 242014年3月. {{cite journal}}: Check date values in: |accessdate= (help); Text "bibcode 1854AnP... 169. 1856年7月" ignored (help); Text "https://www.biodiversitylibrary.org/item/20044#page/100/mode/1up" ignored (help); Text "第2卷" ignored (help); Text "第4页" ignored (help); Text "第86页" ignored (help) Reprinted in: Clausius, R. (1867). The Mechanical Theory of Heat – with its Applications to the Steam Engine and to Physical Properties of Bodies. London: John van Voorst. https://archive.org/details/mechanicaltheor04claugoog. Retrieved 19 June 2012. "editions:PwR_Sbkwa8IC." Reprinted in: Clausius, R. (1867). The Mechanical Theory of Heat – with its Applications to the Steam Engine and to Physical Properties of Bodies. London: John van Voorst. https://archive.org/details/mechanicaltheor04claugoog. Retrieved 19 June 2012

热力学理论及其在蒸汽机和物体物理性质中的应用. "editions:pwr_sbkwa8ic。 2012年6月19日"

}}

Denbigh, K. (1954/1981). The Principles of Chemical Equilibrium. With Applications in Chemistry and Chemical Engineering, fourth edition, Cambridge University Press, Cambridge UK,

.

Eu, B.C. (2002). Generalized Thermodynamics. The Thermodynamics of Irreversible Processes and Generalized Hydrodynamics, Kluwer Academic Publishers, Dordrecht,

.

Gibbs, J.W. (1876/1878). On the equilibrium of heterogeneous substances, Trans. Conn. Acad., 3: 108-248, 343-524, reprinted in The Collected Works of J. Willard Gibbs, Ph.D, LL. D., edited by W.R. Longley, R.G. Van Name, Longmans, Green & Co., New York, 1928, volume 1, pp. 55–353.

Griem, H.R. (2005). Principles of Plasma Spectroscopy (Cambridge Monographs on Plasma Physics), Cambridge University Press, New York

.

Glansdorff, P., Prigogine, I. (1971). Thermodynamic Theory of Structure, Stability, and Fluctuations, Wiley-Interscience, London, 1971,

.

Grandy, W.T., Jr (2008). Entropy and the Time Evolution of Macroscopic Systems. Oxford University Press.

.

Greven, A., Keller, G., Warnecke (editors) (2003). Entropy, Princeton University Press, Princeton NJ,

.

Guggenheim, E.A. (1949). 'Statistical basis of thermodynamics', Research, 2: 450–454.

Guggenheim, E.A. (1967). Thermodynamics. An Advanced Treatment for Chemists and Physicists, fifth revised edition, North Holland, Amsterdam.

Gyarmati, I. (1967/1970) Non-equilibrium Thermodynamics. Field Theory and Variational Principles, translated by E. Gyarmati and W.F. Heinz, Springer, New York.

Kittel, C., Kroemer, H. (1969/1980). Thermal Physics, second edition, Freeman, San Francisco CA,

.

Kondepudi, D., Prigogine, I. (1998). Modern Thermodynamics: From Heat Engines to Dissipative Structures, John Wiley & Sons, Chichester,

.

Lebon, G., Jou, D., Casas-Vázquez, J. (2008). Understanding Non-equilibrium Thermodynamics: Foundations, Applications, Frontiers, Springer-Verlag, Berlin,

.

Lieb, E. H.; Yngvason, J. (1999). "The Physics and Mathematics of the Second Law of Thermodynamics". Physics Reports. 310 (1): 1–96. arXiv:cond-mat/9708200. Bibcode:1999PhR...310....1L. doi:10.1016/S0370-1573(98)00082-9. {{cite journal}}: Invalid |ref=harv (help)

Lieb, E.H., Yngvason, J. (2003). The Entropy of Classical Thermodynamics, pp. 147–195, Chapter 8 of Entropy, Greven, A., Keller, G., Warnecke (editors) (2003).

Mandl, F. (1988). Statistical physics (second ed.). Wiley & Sons. ISBN 978-0-471-91533-1.

Maxwell, J.C. (1867). "On the dynamical theory of gases". Phil. Trans. R. Soc. Lond. 157: 49–88. doi:10.1098/rstl.1867.0004.

Müller, I. (1985). Thermodynamics, Pitman, London,

.

Müller, I. (2003). Entropy in Nonequilibrium, pp. 79–109, Chapter 5 of Entropy, Greven, A., Keller, G., Warnecke (editors) (2003).

Münster, A. (1970), Classical Thermodynamics, translated by E.S. Halberstadt, Wiley–Interscience, London,

.

Pippard, A.B. (1957/1966). Elements of Classical Thermodynamics for Advanced Students of Physics, original publication 1957, reprint 1966, Cambridge University Press, Cambridge UK.

Planck, M. (1897/1903). Treatise on Thermodynamics, translated by A. Ogg, Longmans Green, London, p. 100.

Planck. M. (1914). The Theory of Heat Radiation, a translation by Masius, M. of the second German edition, P. Blakiston's Son & Co., Philadelphia.

Planck, M. (1926). Über die Begründung des zweiten Hauptsatzes der Thermodynamik, Sitzungsberichte der Preussischen Akademie der Wissenschaften: Physikalisch-mathematische Klasse: 453–463.

Pokrovskii V.N. (2005) Extended thermodynamics in a discrete-system approach, Eur. J. Phys. vol. 26, 769-781.

Pokrovskii, Vladimir N. (2013). "A Derivation of the Main Relations of Nonequilibrium Thermodynamics". ISRN Thermodynamics. 2013: 1–9. doi:10.1155/2013/906136.

Quinn, T.J. (1983). Temperature, Academic Press, London,

.

Rao, Y.V.C. (2004). An Introduction to thermodynamics. Universities Press. p. 213. ISBN 978-81-7371-461-0. https://books.google.com/books?id=iYWiCXziWsEC&pg=PA213.

Roberts, J.K., Miller, A.R. (1928/1960). Heat and Thermodynamics, (first edition 1928), fifth edition, Blackie & Son Limited, Glasgow.

Schrödinger, E. (1950). Irreversibility, Proc. R. Ir. Acad., A53: 189–195.

ter Haar, D., Wergeland, H. (1966). Elements of Thermodynamics, Addison-Wesley Publishing, Reading MA.

Thomson, W. (1851). "On the Dynamical Theory of Heat, with numerical results deduced from Mr Joule's equivalent of a Thermal Unit, and M. Regnault's Observations on Steam". Transactions of the Royal Society of Edinburgh. XX (part II): 261–268, 289–298. {{cite journal}}: Invalid |ref=harv (help) Also published in Thomson, W. (December 1852). "On the Dynamical Theory of Heat, with numerical results deduced from Mr Joule's equivalent of a Thermal Unit, and M. Regnault's Observations on Steam". Philos. Mag. 4. IV (22): 13. Retrieved 25 June 2012.

Thomson, W. (1852). On the universal tendency in nature to the dissipation of mechanical energy Philosophical Magazine, Ser. 4, p. 304.

Tisza, L. (1966). Generalized Thermodynamics, M.I.T Press, Cambridge MA.

Truesdell, C. (1980). The Tragicomical History of Thermodynamics 1822–1854, Springer, New York,

.

Uffink, J. (2001). Bluff your way in the second law of thermodynamics, Stud. Hist. Phil. Mod. Phys., 32(3): 305–394.

Uffink, J. (2003). Irreversibility and the Second Law of Thermodynamics, Chapter 7 of Entropy, Greven, A., Keller, G., Warnecke (editors) (2003), Princeton University Press, Princeton NJ,

.

Uhlenbeck, G.E., Ford, G.W. (1963). Lectures in Statistical Mechanics, American Mathematical Society, Providence RI.

Zemansky, M.W. (1968). Heat and Thermodynamics. An Intermediate Textbook, fifth edition, McGraw-Hill Book Company, New York.

External links

外部链接

Stanford Encyclopedia of Philosophy: "Philosophy of Statistical Mechanics" – by Lawrence Sklar.

Second law of thermodynamics in the MIT Course Unified Thermodynamics and Propulsion from Prof. Z. S. Spakovszky

E.T. Jaynes, 1988, "The evolution of Carnot's principle," in G. J. Erickson and C. R. Smith (eds.)Maximum-Entropy and Bayesian Methods in Science and Engineering, Vol 1: p. 267.

Caratheodory, C., "Examination of the foundations of thermodynamics," trans. by D. H. Delphenich

The Second Law of Thermodynamics, BBC Radio 4 discussion with John Gribbin, Peter Atkins & Monica Grady (In Our Time, Dec. 16, 2004)

Entropy (journal), 2004

The Journal of the International Society for the History of Philosophy of Science, 2012

Category:Concepts in physics

分类: 物理概念

2

Category:Non-equilibrium thermodynamics

类别: 非平衡态热力学

Category:Philosophy of thermal and statistical physics

类别: 热力学和统计物理学哲学

This page was moved from wikipedia:en:Second law of thermodynamics. Its edit history can be viewed at 热力学第二定律/edithistory

[1] ttp://web.mit.edu/16.unified/www/FALL/thermodynamics/notes/node38.html#SECTION05224000000000000000

[2] Atkins and de Paula, p.78

[3] Zohuri, Bahman (2016). Dimensional Analysis Beyond the Pi Theorem. Springer. p. 111. ISBN 978-3-319-45726-0. https://books.google.com/books?id=pRVuDQAAQBAJ.

[4] Jaffe, R.L., Taylor, W. (2018). The Physics of Energy, Cambridge University Press, Cambridge UK, pages 150, 151, 259, 772, 743.

[5] Planck, M. (1897/1903), pp. 40–41.

[6] Munster A. (1970), pp. 8–9, 50–51.

[7] Mandl 1988

[8] Planck, M. (1897/1903), pp. 79–107.

[9] Bailyn, M. (1994), Section 71, pp. 113–154.

[10] Bailyn, M. (1994), p. 120.

[MortimerBook-11] 11.0 ^11.1 ^11.2 Mortimer, R. G. Physical Chemistry. 3rd ed., p. 120, Academic Press, 2008.

[FermiBook-12] Fermi, E. Thermodynamics, footnote on p. 48, Dover Publications,1956 (still in print).

[:0-13] Adkins, C.J. (1968/1983), p. 75.

[Munster_45-14] 14.0 ^14.1 ^14.2 Münster, A. (1970), p. 45.

[Schmidt-Rohr_14-15] 15.0 ^15.1 ^15.2 Schmidt-Rohr, K. (2014). "Expansion Work without the External Pressure, and Thermodynamics in Terms of Quasistatic Irreversible Processes" J. Chem. Educ. 91: 402-409. https://dx.doi.org/10.1021/ed3008704

[Oxtoby8th-16] 16.0 ^16.1 Oxtoby, D. W; Gillis, H.P., Butler, L. J. (2015).Principles of Modern Chemistry, Brooks Cole. p. 617.
v
t
e
Inline tags
Attribution

{{Attribution needed}}

{{By whom}}

{{Weasel-inline}}

{{Which?}}

{{Who}}

Citation

{{Better source}}

{{Citation needed}}
{{Citation needed span}}

{{Reference necessary}}

{{Citation needed (lead)}}

{{Failed verification}}

{{Full}}

{{Primary source-inline}}

{{Request quotation}}

{{Retracted}}

{{Third-party-inline}}

Incomplete

{{Author missing}}

{{Author incomplete}}

{{Date missing}}

{{ISBN missing}}

{{Page needed}}

{{Publisher missing}}

{{Title incomplete}}

{{Year missing}}

{{Dead link}}

Content

{{Contradict-inline}}

{{Contradiction-inline}}

{{Dubious|talk page section name}}

{{Examples}}

{{Inconsistent}}

{{List fact}}

{{Lopsided}}

{{POV-statement}}

Date and place

{{Clarify timeframe}}

{{Quantify}}

{{Update after}}

{{Update-small}}

{{When}}

{{Where}}

{{Year needed}}

Wikification

{{Disambiguation needed}}

{{Pronunciation needed}}

Wording

{{Ambiguous}}

{{Awkward}}

{{Buzz}}

{{Clarify}}

{{Clarify span}}

{{Definition}}

{{Elucidate}}

{{Expand acronym}}

{{Technical-statement}}

{{Vague|optional message to be displayed on mouseover}}

{{Why?}}

Category

[17] v

[18] t

[19] e

[20] {{Attribution needed}}

[21] {{By whom}}

[22] {{Weasel-inline}}

[23] {{Which?}}

[24] {{Who}}

[25] {{Better source}}

[26] {{Citation needed}}
{{Citation needed span}}

{{Reference necessary}}

[27] {{Citation needed span}}

[28] {{Reference necessary}}

[29] {{Citation needed (lead)}}

[30] {{Failed verification}}

[31] {{Full}}

[32] {{Primary source-inline}}

[33] {{Request quotation}}

[34] {{Retracted}}

[35] {{Third-party-inline}}

[36] {{Author missing}}

[37] {{Author incomplete}}

[38] {{Date missing}}

[39] {{ISBN missing}}

[40] {{Page needed}}

[41] {{Publisher missing}}

[42] {{Title incomplete}}

[43] {{Year missing}}

[44] {{Dead link}}

[45] {{Contradict-inline}}

[46] {{Contradiction-inline}}

[47] {{Dubious|talk page section name}}

[48] {{Examples}}

[49] {{Inconsistent}}

[50] {{List fact}}

[51] {{Lopsided}}

[52] {{POV-statement}}

[53] {{Clarify timeframe}}

[54] {{Quantify}}

[55] {{Update after}}

[56] {{Update-small}}

[57] {{When}}

[58] {{Where}}

[59] {{Year needed}}

[60] {{Disambiguation needed}}

[61] {{Pronunciation needed}}

[62] {{Ambiguous}}

[63] {{Awkward}}

[64] {{Buzz}}

[65] {{Clarify}}

[66] {{Clarify span}}

[67] {{Definition}}

[68] {{Elucidate}}

[69] {{Expand acronym}}

[70] {{Technical-statement}}

[71] {{Vague|optional message to be displayed on mouseover}}

[72] {{Why?}}

[17] Pokrovskii V.N. (2005) Extended thermodynamics in a discrete-system approach, Eur. J. Phys. vol. 26, 769–781.

[18] Pokrovskii, Vladimir N. (2013). "A Derivation of the Main Relations of Nonequilibrium Thermodynamics". ISRN Thermodynamics. 2013: 1–9. doi:10.1155/2013/906136.

[dugdale-19] J. S. Dugdale (1996). Entropy and its Physical Meaning. Taylor & Francis. p. 13. ISBN 978-0-7484-0569-5. "This law is the basis of temperature."

[20] Zemansky, M.W. (1968), pp. 207–209.

[21] Quinn, T.J. (1983), p. 8.

[MIT-22] "Concept and Statements of the Second Law". web.mit.edu. Retrieved 2010-10-07.

[23] Carnot, S. (1824/1986).

[24] Carnot, S. (1824/1986), p. 51.

[25] Carnot, S. (1824/1986), p. 46.

[26] Carnot, S. (1824/1986), p. 68.

[27] Truesdell, C. (1980), Chapter 5.

[28] Adkins, C.J. (1968/1983), pp. 56–58.

[29] Münster, A. (1970), p. 11.

[30] Kondepudi, D., Prigogine, I. (1998), pp.67–75.

[31] Lebon, G., Jou, D., Casas-Vázquez, J. (2008), p. 10.

[32] Eu, B.C. (2002), pp. 32–35.

[33] Planck, M. (1897/1903), p. 86.

[34] Roberts, J.K., Miller, A.R. (1928/1960), p. 319.

[35] ter Haar, D., Wergeland, H. (1966), p. 17.

[Rao-36] Rao, Y. V. C. (1997). Chemical Engineering Thermodynamics. Universities Press. p. 158. ISBN 978-81-7371-048-3.

[Planck_100-37] Planck, M. (1897/1903), p. 100.

[Planck_463-38] Planck, M. (1926), p. 463, translation by Uffink, J. (2003), p. 131.

[Roberts_.26_Miller_382-39] Roberts, J.K., Miller, A.R. (1928/1960), p. 382. This source is partly verbatim from Planck's statement, but does not cite Planck. This source calls the statement the principle of the increase of entropy.

[40] Uhlenbeck, G.E., Ford, G.W. (1963), p. 16.

[41] Carathéodory, C. (1909).

[42] Buchdahl, H.A. (1966), p. 68.

[Sychev1991-43] Sychev, V. V. (1991). The Differential Equations of Thermodynamics. Taylor & Francis. ISBN 978-1-56032-121-7.

[Planck_1926-44] 44.0 ^44.1 Planck, M. (1926).

[45] Buchdahl, H.A. (1966), p. 69.

[46] Uffink, J. (2003), pp. 129–132.

[47] Truesdell, C., Muncaster, R.G. (1980). Fundamentals of Maxwell's Kinetic Theory of a Simple Monatomic Gas, Treated as a Branch of Rational Mechanics, Academic Press, New York,
v
t
e
Inline tags
Attribution

{{Attribution needed}}

{{By whom}}

{{Weasel-inline}}

{{Which?}}

{{Who}}

Citation

{{Better source}}

{{Citation needed}}
{{Citation needed span}}

{{Reference necessary}}

{{Citation needed (lead)}}

{{Failed verification}}

{{Full}}

{{Primary source-inline}}

{{Request quotation}}

{{Retracted}}

{{Third-party-inline}}

Incomplete

{{Author missing}}

{{Author incomplete}}

{{Date missing}}

{{ISBN missing}}

{{Page needed}}

{{Publisher missing}}

{{Title incomplete}}

{{Year missing}}

{{Dead link}}

Content

{{Contradict-inline}}

{{Contradiction-inline}}

{{Dubious|talk page section name}}

{{Examples}}

{{Inconsistent}}

{{List fact}}

{{Lopsided}}

{{POV-statement}}

Date and place

{{Clarify timeframe}}

{{Quantify}}

{{Update after}}

{{Update-small}}

{{When}}

{{Where}}

{{Year needed}}

Wikification

{{Disambiguation needed}}

{{Pronunciation needed}}

Wording

{{Ambiguous}}

{{Awkward}}

{{Buzz}}

{{Clarify}}

{{Clarify span}}

{{Definition}}

{{Elucidate}}

{{Expand acronym}}

{{Technical-statement}}

{{Vague|optional message to be displayed on mouseover}}

{{Why?}}

Category
, p. 15.

[104] v

[105] t

[106] e

[107] {{Attribution needed}}

[108] {{By whom}}

[109] {{Weasel-inline}}

[110] {{Which?}}

[111] {{Who}}

[112] {{Better source}}

[113] {{Citation needed}}
{{Citation needed span}}

{{Reference necessary}}

[114] {{Citation needed span}}

[115] {{Reference necessary}}

[116] {{Citation needed (lead)}}

[117] {{Failed verification}}

[118] {{Full}}

[119] {{Primary source-inline}}

[120] {{Request quotation}}

[121] {{Retracted}}

[122] {{Third-party-inline}}

[123] {{Author missing}}

[124] {{Author incomplete}}

[125] {{Date missing}}

[126] {{ISBN missing}}

[127] {{Page needed}}

[128] {{Publisher missing}}

[129] {{Title incomplete}}

[130] {{Year missing}}

[131] {{Dead link}}

[132] {{Contradict-inline}}

[133] {{Contradiction-inline}}

[134] {{Dubious|talk page section name}}

[135] {{Examples}}

[136] {{Inconsistent}}

[137] {{List fact}}

[138] {{Lopsided}}

[139] {{POV-statement}}

[140] {{Clarify timeframe}}

[141] {{Quantify}}

[142] {{Update after}}

[143] {{Update-small}}

[144] {{When}}

[145] {{Where}}

[146] {{Year needed}}

[147] {{Disambiguation needed}}

[148] {{Pronunciation needed}}

[149] {{Ambiguous}}

[150] {{Awkward}}

[151] {{Buzz}}

[152] {{Clarify}}

[153] {{Clarify span}}

[154] {{Definition}}

[155] {{Elucidate}}

[156] {{Expand acronym}}

[157] {{Technical-statement}}

[158] {{Vague|optional message to be displayed on mouseover}}

[159] {{Why?}}

[48] Planck, M. (1897/1903), p. 81.

[49] Planck, M. (1926), p. 457, Wikipedia editor's translation.

[50] Lieb, E.H., Yngvason, J. (2003), p. 149.

[51] Borgnakke, C., Sonntag., R.E. (2009), p. 304.

[52] van Gool, W.; Bruggink, J.J.C. (Eds) (1985). Energy and time in the economic and physical sciences. North-Holland. pp. 41–56. ISBN 978-0-444-87748-2.

[53] Grubbström, Robert W. (2007). "An Attempt to Introduce Dynamics Into Generalised Exergy Considerations". Applied Energy. 84 (7–8): 701–718. doi:10.1016/j.apenergy.2007.01.003.

[54] Clausius theorem at Wolfram Research

[55] Denbigh, K.G., Denbigh, J.S. (1985). Entropy in Relation to Incomplete Knowledge, Cambridge University Press, Cambridge UK,
v
t
e
Inline tags
Attribution

{{Attribution needed}}

{{By whom}}

{{Weasel-inline}}

{{Which?}}

{{Who}}

Citation

{{Better source}}

{{Citation needed}}
{{Citation needed span}}

{{Reference necessary}}

{{Citation needed (lead)}}

{{Failed verification}}

{{Full}}

{{Primary source-inline}}

{{Request quotation}}

{{Retracted}}

{{Third-party-inline}}

Incomplete

{{Author missing}}

{{Author incomplete}}

{{Date missing}}

{{ISBN missing}}

{{Page needed}}

{{Publisher missing}}

{{Title incomplete}}

{{Year missing}}

{{Dead link}}

Content

{{Contradict-inline}}

{{Contradiction-inline}}

{{Dubious|talk page section name}}

{{Examples}}

{{Inconsistent}}

{{List fact}}

{{Lopsided}}

{{POV-statement}}

Date and place

{{Clarify timeframe}}

{{Quantify}}

{{Update after}}

{{Update-small}}

{{When}}

{{Where}}

{{Year needed}}

Wikification

{{Disambiguation needed}}

{{Pronunciation needed}}

Wording

{{Ambiguous}}

{{Awkward}}

{{Buzz}}

{{Clarify}}

{{Clarify span}}

{{Definition}}

{{Elucidate}}

{{Expand acronym}}

{{Technical-statement}}

{{Vague|optional message to be displayed on mouseover}}

{{Why?}}

Category
, pp. 43–44.

[168] v

[169] t

[170] e

[171] {{Attribution needed}}

[172] {{By whom}}

[173] {{Weasel-inline}}

[174] {{Which?}}

[175] {{Who}}

[176] {{Better source}}

[177] {{Citation needed}}
{{Citation needed span}}

{{Reference necessary}}

[178] {{Citation needed span}}

[179] {{Reference necessary}}

[180] {{Citation needed (lead)}}

[181] {{Failed verification}}

[182] {{Full}}

[183] {{Primary source-inline}}

[184] {{Request quotation}}

[185] {{Retracted}}

[186] {{Third-party-inline}}

[187] {{Author missing}}

[188] {{Author incomplete}}

[189] {{Date missing}}

[190] {{ISBN missing}}

[191] {{Page needed}}

[192] {{Publisher missing}}

[193] {{Title incomplete}}

[194] {{Year missing}}

[195] {{Dead link}}

[196] {{Contradict-inline}}

[197] {{Contradiction-inline}}

[198] {{Dubious|talk page section name}}

[199] {{Examples}}

[200] {{Inconsistent}}

[201] {{List fact}}

[202] {{Lopsided}}

[203] {{POV-statement}}

[204] {{Clarify timeframe}}

[205] {{Quantify}}

[206] {{Update after}}

[207] {{Update-small}}

[208] {{When}}

[209] {{Where}}

[210] {{Year needed}}

[211] {{Disambiguation needed}}

[212] {{Pronunciation needed}}

[213] {{Ambiguous}}

[214] {{Awkward}}

[215] {{Buzz}}

[216] {{Clarify}}

[217] {{Clarify span}}

[218] {{Definition}}

[219] {{Elucidate}}

[220] {{Expand acronym}}

[221] {{Technical-statement}}

[222] {{Vague|optional message to be displayed on mouseover}}

[223] {{Why?}}

[56] Grandy, W.T., Jr (2008). Entropy and the Time Evolution of Macroscopic Systems, Oxford University Press, Oxford,
v
t
e
Inline tags
Attribution

{{Attribution needed}}

{{By whom}}

{{Weasel-inline}}

{{Which?}}

{{Who}}

Citation

{{Better source}}

{{Citation needed}}
{{Citation needed span}}

{{Reference necessary}}

{{Citation needed (lead)}}

{{Failed verification}}

{{Full}}

{{Primary source-inline}}

{{Request quotation}}

{{Retracted}}

{{Third-party-inline}}

Incomplete

{{Author missing}}

{{Author incomplete}}

{{Date missing}}

{{ISBN missing}}

{{Page needed}}

{{Publisher missing}}

{{Title incomplete}}

{{Year missing}}

{{Dead link}}

Content

{{Contradict-inline}}

{{Contradiction-inline}}

{{Dubious|talk page section name}}

{{Examples}}

{{Inconsistent}}

{{List fact}}

{{Lopsided}}

{{POV-statement}}

Date and place

{{Clarify timeframe}}

{{Quantify}}

{{Update after}}

{{Update-small}}

{{When}}

{{Where}}

{{Year needed}}

Wikification

{{Disambiguation needed}}

{{Pronunciation needed}}

Wording

{{Ambiguous}}

{{Awkward}}

{{Buzz}}

{{Clarify}}

{{Clarify span}}

{{Definition}}

{{Elucidate}}

{{Expand acronym}}

{{Technical-statement}}

{{Vague|optional message to be displayed on mouseover}}

{{Why?}}

Category
, pp. 55–58.

[225] v

[226] t

[227] e

[228] {{Attribution needed}}

[229] {{By whom}}

[230] {{Weasel-inline}}

[231] {{Which?}}

[232] {{Who}}

[233] {{Better source}}

[234] {{Citation needed}}
{{Citation needed span}}

{{Reference necessary}}

[235] {{Citation needed span}}

[236] {{Reference necessary}}

[237] {{Citation needed (lead)}}

[238] {{Failed verification}}

[239] {{Full}}

[240] {{Primary source-inline}}

[241] {{Request quotation}}

[242] {{Retracted}}

[243] {{Third-party-inline}}

[244] {{Author missing}}

[245] {{Author incomplete}}

[246] {{Date missing}}

[247] {{ISBN missing}}

[248] {{Page needed}}

[249] {{Publisher missing}}

[250] {{Title incomplete}}

[251] {{Year missing}}

[252] {{Dead link}}

[253] {{Contradict-inline}}

[254] {{Contradiction-inline}}

[255] {{Dubious|talk page section name}}

[256] {{Examples}}

[257] {{Inconsistent}}

[258] {{List fact}}

[259] {{Lopsided}}

[260] {{POV-statement}}

[261] {{Clarify timeframe}}

[262] {{Quantify}}

[263] {{Update after}}

[264] {{Update-small}}

[265] {{When}}

[266] {{Where}}

[267] {{Year needed}}

[268] {{Disambiguation needed}}

[269] {{Pronunciation needed}}

[270] {{Ambiguous}}

[271] {{Awkward}}

[272] {{Buzz}}

[273] {{Clarify}}

[274] {{Clarify span}}

[275] {{Definition}}

[276] {{Elucidate}}

[277] {{Expand acronym}}

[278] {{Technical-statement}}

[279] {{Vague|optional message to be displayed on mouseover}}

[280] {{Why?}}

[Lambert-57] Entropy Sites — A Guide Content selected by Frank L. Lambert

[58] Gyenis, Balazs (2017). "Maxwell and the normal distribution: A colored story of probability, independence, and tendency towards equilibrium". Studies in History and Philosophy of Modern Physics. 57: 53–65. arXiv:1702.01411. Bibcode:2017SHPMP..57...53G. doi:10.1016/j.shpsb.2017.01.001.

[Hawking_AOT-59] Hawking, SW (1985). "Arrow of time in cosmology". Phys. Rev. D. 32 (10): 2489–2495. Bibcode:1985PhRvD..32.2489H. doi:10.1103/PhysRevD.32.2489. PMID 9956019.

[60] Greene, Brian (2004). The Fabric of the Cosmos. Alfred A. Knopf. p. 171. ISBN 978-0-375-41288-2. https://archive.org/details/fabricofcosmossp00gree.

[Lebowitz-61] Lebowitz, Joel L. (September 1993). "Boltzmann's Entropy and Time's Arrow" (PDF). Physics Today. 46 (9): 32–38. Bibcode:1993PhT....46i..32L. doi:10.1063/1.881363. Retrieved 2013-02-22.

[62] Léon Brillouin Science and Information Theory (Academic Press, 1962) (Dover, 2004)

[Grandy_151-63] 63.0 ^63.1 Grandy, W.T. (Jr) (2008), p. 151.

[64] Callen, H.B. (1960/1985), p. 15.

[65] Lieb, E.H., Yngvason, J. (2003), p. 190.

[66] Gyarmati, I. (1967/1970), pp. 4-14.

[67] Glansdorff, P., Prigogine, I. (1971).

[68] Müller, I. (1985).

[69] Müller, I. (2003).

[70] Callender, Craig (29 July 2011). "Thermodynamic Asymmetry in Time". {{cite web}}: Unknown parameter |encyclopedia= ignored (help)

[71] Halliwell, J.J. (1994). Physical Origins of Time Asymmetry. Cambridge. ISBN 978-0-521-56837-1. chapter 6

[72] Schrödinger, E. (1950), p. 192.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[35]

[36]

[37]

[38]

[39]

[40]

[41]

[42]

[43]

[44]

[45]

[46]

[47]

[48]

[49]

[50]

[51]

[52]

[53]

[54]

[55]

[56]

[57]

[58]

[59]

[60]

[61]

[62]

[63]

[64]

[65]

[66]

[67]

[68]

[69]

[70]

[71]

[72]

热力学第二定律

Introduction

Introduction

Various statements of the law

Various statements of the law

Carnot's principle

Carnot's principle

Clausius statement

Clausius statement

Kelvin statements

Kelvin statements

Equivalence of the Clausius and the Kelvin statements

Equivalence of the Clausius and the Kelvin statements

Planck's proposition

Planck's proposition

Relation between Kelvin's statement and Planck's proposition

Relation between Kelvin's statement and Planck's proposition

Planck's statement

Planck's statement

Principle of Carathéodory

Principle of Carathéodory

Planck's principle

Planck's principle

Statement for a system that has a known expression of its internal energy as a function of its extensive state variables

Statement for a system that has a known expression of its internal energy as a function of its extensive state variables

Corollaries

Corollaries

Perpetual motion of the second kind

Perpetual motion of the second kind

Carnot theorem

Carnot theorem

Clausius inequality

Clausius inequality

Thermodynamic temperature

Thermodynamic temperature

Entropy

Entropy

Energy, available useful work

Energy, available useful work

The second law in chemical thermodynamics

The second law in chemical thermodynamics

History

History

Account given by Clausius

Account given by Clausius

Statistical mechanics

Statistical mechanics

Derivation from statistical mechanics

Derivation from statistical mechanics

Derivation of the entropy change for reversible processes

Derivation of the entropy change for reversible processes

Derivation for systems described by the canonical ensemble

Derivation for systems described by the canonical ensemble

Living organisms

Living organisms

Gravitational systems

Gravitational systems

Non-equilibrium states

Non-equilibrium states

Non-equilibrium states

Arrow of time

Arrow of time

Irreversibility

Irreversibility

Loschmidt's paradox

Loschmidt's paradox

Poincaré recurrence theorem

Poincaré recurrence theorem

Maxwell's demon

Maxwell's demon

Quotations

Quotations

See also

See also

References

References

Sources

Sources

Further reading

Further reading