信息论

此词条暂由彩云小译翻译，未经人工整理和审校，带来阅读不便，请见谅。模板:Distinguish

Information theory studies the quantification, storage, and communication of information. It was originally proposed by Claude Shannon in 1948 to find fundamental limits on signal processing and communication operations such as data compression, in a landmark paper titled "A Mathematical Theory of Communication". Its impact has been crucial to the success of the Voyager missions to deep space, the invention of the compact disc, the feasibility of mobile phones, the development of the Internet, the study of linguistics and of human perception, the understanding of black holes, and numerous other fields.

Information theory studies the quantification, storage, and communication of information. It was originally proposed by Claude Shannon in 1948 to find fundamental limits on signal processing and communication operations such as data compression, in a landmark paper titled "A Mathematical Theory of Communication". Its impact has been crucial to the success of the Voyager missions to deep space, the invention of the compact disc, the feasibility of mobile phones, the development of the Internet, the study of linguistics and of human perception, the understanding of black holes, and numerous other fields.

信息论研究的是信息的量化、存储与传播。信息论最初是由Claude Shannon在1948年的一篇题为"A Mathematical Theory of Communication"的论文中提出的，其目的是找到信号处理和通信操作（如数据压缩）的基本限制。信息论对于旅行者号深空探测任务的成功、光盘的发明、移动电话的可行性、互联网的发展、语言学和人类感知的研究、对黑洞的理解以及许多其他领域的研究都是至关重要的。

The field is at the intersection of mathematics, statistics, computer science, physics, neurobiology, information engineering, and electrical engineering. The theory has also found applications in other areas, including statistical inference, natural language processing, cryptography, neurobiology, human vision, the evolution and function of molecular codes (bioinformatics), model selection in statistics, thermal physics, quantum computing, linguistics, plagiarism detection, pattern recognition, and anomaly detection. Important sub-fields of information theory include source coding, algorithmic complexity theory, algorithmic information theory, information-theoretic security, Grey system theory and measures of information.

</ref> Important sub-fields of information theory include source coding, algorithmic complexity theory, algorithmic information theory, information-theoretic security, Grey system theory and measures of information.

信息论的重要分支包括信源编码、算法复杂性理论、算法信息论、资讯理论安全性、灰色系统理论和信息度量。

Applications of fundamental topics of information theory include lossless data compression (e.g. ZIP files), lossy data compression (e.g. MP3s and JPEGs), and channel coding (e.g. for DSL). Information theory is used in information retrieval, intelligence gathering, gambling, and even in musical composition.

Applications of fundamental topics of information theory include lossless data compression (e.g. ZIP files), lossy data compression (e.g. MP3s and JPEGs), and channel coding (e.g. for DSL). Information theory is used in information retrieval, intelligence gathering, gambling, and even in musical composition.

信息论基本主题的应用包括无损数据压缩(例如:ZIP压缩文件)、有损数据压缩(例如:Mp3和jpeg格式) ，以及频道编码(例如:DSL)。信息论应用于信息检索、情报收集、赌博，甚至在音乐创作中也有应用。

A key measure in information theory is entropy. Entropy quantifies the amount of uncertainty involved in the value of a random variable or the outcome of a random process. For example, identifying the outcome of a fair coin flip (with two equally likely outcomes) provides less information (lower entropy) than specifying the outcome from a roll of a 模板:Dice (with six equally likely outcomes). Some other important measures in information theory are mutual information, channel capacity, error exponents, and relative entropy.

A key measure in information theory is entropy. Entropy quantifies the amount of uncertainty involved in the value of a random variable or the outcome of a random process. For example, identifying the outcome of a fair coin flip (with two equally likely outcomes) provides less information (lower entropy) than specifying the outcome from a roll of a (with six equally likely outcomes). Some other important measures in information theory are mutual information, channel capacity, error exponents, and relative entropy.

信息论中的一个关键度量是熵。熵量化了一个随机变量的值或者一个随机过程的结果所包含的不确定性。例如，识别一次公平抛硬币的结果(有两个同样可能的结果)所提供的信息(较低的熵)少于指定一卷 a 的结果(有六个同样可能的结果)。信息论中的其他一些重要指标有：互信息、信道容量、误差指数和相对熵。

Overview

概览

Information theory studies the transmission, processing, extraction, and utilization of information. Abstractly, information can be thought of as the resolution of uncertainty. In the case of communication of information over a noisy channel, this abstract concept was made concrete in 1948 by Claude Shannon in his paper "A Mathematical Theory of Communication", in which "information" is thought of as a set of possible messages, where the goal is to send these messages over a noisy channel, and then to have the receiver reconstruct the message with low probability of error, in spite of the channel noise. Shannon's main result, the noisy-channel coding theorem showed that, in the limit of many channel uses, the rate of information that is asymptotically achievable is equal to the channel capacity, a quantity dependent merely on the statistics of the channel over which the messages are sent.

Information theory studies the transmission, processing, extraction, and utilization of information. Abstractly, information can be thought of as the resolution of uncertainty. In the case of communication of information over a noisy channel, this abstract concept was made concrete in 1948 by Claude Shannon in his paper "A Mathematical Theory of Communication", in which "information" is thought of as a set of possible messages, where the goal is to send these messages over a noisy channel, and then to have the receiver reconstruct the message with low probability of error, in spite of the channel noise. Shannon's main result, the noisy-channel coding theorem showed that, in the limit of many channel uses, the rate of information that is asymptotically achievable is equal to the channel capacity, a quantity dependent merely on the statistics of the channel over which the messages are sent.

信息论主要研究信息的传递、处理、提取和利用。抽象地说，信息可以作为不确定性的解决方案。1948年，Claude Shannon在他的论文"A Mathematical Theory of Communication"中将这个抽象的概念具体化，在这篇论文中“信息”被认为是一组可能的信息，其目标是通过噪声信道发送这些信息，然后让接收器在信道噪声的影响下以较低的错误概率来重构信息。Shannon的主要结果为：噪信道编码定理表明，在许多信道（这个数量仅仅依赖于信息发送所经过的信道的统计信息）使用的限制下，信道容量为渐近可达到的信息传输速率，。

Information theory is closely associated with a collection of pure and applied disciplines that have been investigated and reduced to engineering practice under a variety of rubrics throughout the world over the past half century or more: adaptive systems, anticipatory systems, artificial intelligence, complex systems, complexity science, cybernetics, informatics, machine learning, along with systems sciences of many descriptions. Information theory is a broad and deep mathematical theory, with equally broad and deep applications, amongst which is the vital field of coding theory.

Information theory is closely associated with a collection of pure and applied disciplines that have been investigated and reduced to engineering practice under a variety of rubrics throughout the world over the past half century or more: adaptive systems, anticipatory systems, artificial intelligence, complex systems, complexity science, cybernetics, informatics, machine learning, along with systems sciences of many descriptions. Information theory is a broad and deep mathematical theory, with equally broad and deep applications, amongst which is the vital field of coding theory.

信息论与一系列纯粹的、应用的学科密切相关，在过去半个世纪甚至更久的时间里，在全球范围内已经有各种专栏下被研究和简化为工程实践，比如在自适应系统，预期系统，人工智能，复杂系统，复杂性科学，控制论，信息学，机器学习，以及许多描述的系统科学等学科中的研究与应用。信息论是一个广泛而深入的数学理论，同样也具有广泛而深入的应用，其中编码理论是至关重要的领域。

Coding theory is concerned with finding explicit methods, called codes, for increasing the efficiency and reducing the error rate of data communication over noisy channels to near the channel capacity. These codes can be roughly subdivided into data compression (source coding) and error-correction (channel coding) techniques. In the latter case, it took many years to find the methods Shannon's work proved were possible.

Coding theory is concerned with finding explicit methods, called codes, for increasing the efficiency and reducing the error rate of data communication over noisy channels to near the channel capacity. These codes can be roughly subdivided into data compression (source coding) and error-correction (channel coding) techniques. In the latter case, it took many years to find the methods Shannon's work proved were possible.

编码理论与寻找明确的方法（编码）有关，用于提高效率和将噪声信道上传输的数据错误率降低到接近信道容量。这些编码可大致分为数据压缩编码(信源编码)和纠错(信道编码)技术。在后一种技术中，花了很多年才证明Shannon的工作是可行的。

A third class of information theory codes are cryptographic algorithms (both codes and ciphers). Concepts, methods and results from coding theory and information theory are widely used in cryptography and cryptanalysis. See the article ban (unit) for a historical application.

A third class of information theory codes are cryptographic algorithms (both codes and ciphers). Concepts, methods and results from coding theory and information theory are widely used in cryptography and cryptanalysis. See the article ban (unit) for a historical application.

第三类信息论代码是密码算法(包括代码和密码)。编码理论和信息论的概念、方法和结果在密码学和密码分析中得到了广泛的应用。有关历史应用，请参阅文章禁令（单位）。

Historical background

历史背景

Main article: History of information theory

The landmark event that established the discipline of information theory and brought it to immediate worldwide attention was the publication of Claude E. Shannon's classic paper "A Mathematical Theory of Communication" in the Bell System Technical Journal in July and October 1948.

The landmark event that established the discipline of information theory and brought it to immediate worldwide attention was the publication of Claude E. Shannon's classic paper "A Mathematical Theory of Communication" in the Bell System Technical Journal in July and October 1948.

1948年7月和10月，Claude Shannon在Bell System Technical Journal上发表了经典论文："A Mathematical Theory of Communication"，这是建立信息论学科并立即引起全世界关注的里程碑事件。

Prior to this paper, limited information-theoretic ideas had been developed at Bell Labs, all implicitly assuming events of equal probability. Harry Nyquist's 1924 paper, Certain Factors Affecting Telegraph Speed, contains a theoretical section quantifying "intelligence" and the "line speed" at which it can be transmitted by a communication system, giving the relation W = K log m (recalling Boltzmann's constant), where W is the speed of transmission of intelligence, m is the number of different voltage levels to choose from at each time step, and K is a constant. Ralph Hartley's 1928 paper, Transmission of Information, uses the word information as a measurable quantity, reflecting the receiver's ability to distinguish one sequence of symbols from any other, thus quantifying information as H = log Sⁿ = n log S, where S was the number of possible symbols, and n the number of symbols in a transmission. The unit of information was therefore the decimal digit, which has since sometimes been called the hartley in his honor as a unit or scale or measure of information. Alan Turing in 1940 used similar ideas as part of the statistical analysis of the breaking of the German second world war Enigma ciphers.

Prior to this paper, limited information-theoretic ideas had been developed at Bell Labs, all implicitly assuming events of equal probability. Harry Nyquist's 1924 paper, Certain Factors Affecting Telegraph Speed, contains a theoretical section quantifying "intelligence" and the "line speed" at which it can be transmitted by a communication system, giving the relation (recalling Boltzmann's constant), where W is the speed of transmission of intelligence, m is the number of different voltage levels to choose from at each time step, and K is a constant. Ralph Hartley's 1928 paper, Transmission of Information, uses the word information as a measurable quantity, reflecting the receiver's ability to distinguish one sequence of symbols from any other, thus quantifying information as , where S was the number of possible symbols, and n the number of symbols in a transmission. The unit of information was therefore the decimal digit, which has since sometimes been called the hartley in his honor as a unit or scale or measure of information. Alan Turing in 1940 used similar ideas as part of the statistical analysis of the breaking of the German second world war Enigma ciphers.

在此之前，贝尔实验室已经提出了有限的信息论思想，所有这些理论都隐含地假设了概率均等的事件。Harry Nyquist 在1924年发表的论文”Certain Factors Affecting Telegraph Speed”中包含一个理论部分，量化了“智能”和通信系统可以传输的“线路速度”，并给出了关系式(检索Boltzmann常数) ，其中 w 是智能传输的速度，m 是每个时间步长可以选择的不同电压电平的数，k 是常数。Ralph Hartley在1928年发表的论文” Transmission of Information”中，将单词信息作为一个可测量的量，以此反映接收器区分一系列符号的能力，从而将信息量化，其中 s 是可能符号的数量，n 是传输中符号的数量。因此信息的单位就是十进制数字，为了表示对他的尊敬，这个单位有时被称为Hartley，作为信息的单位、尺度或度量。1940年，Alan Turing在对德国二战时期破解迷密码（Enigma ciphers）的统计分析中使用了类似的思想。

Much of the mathematics behind information theory with events of different probabilities were developed for the field of thermodynamics by Ludwig Boltzmann and J. Willard Gibbs. Connections between information-theoretic entropy and thermodynamic entropy, including the important contributions by Rolf Landauer in the 1960s, are explored in Entropy in thermodynamics and information theory.

Much of the mathematics behind information theory with events of different probabilities were developed for the field of thermodynamics by Ludwig Boltzmann and J. Willard Gibbs. Connections between information-theoretic entropy and thermodynamic entropy, including the important contributions by Rolf Landauer in the 1960s, are explored in Entropy in thermodynamics and information theory.

信息论背后的许多数学理论（包括不同概率的事件）都是由Ludwig Boltzmann和 j. Willard Gibbs 为热力学领域而发展起来的。信息论中的熵和热力学中的熵之间的联系，包括 Rolf Landauer 在20世纪60年代的重要贡献，在热力学和信息论的熵中进行了探讨。

In Shannon's revolutionary and groundbreaking paper, the work for which had been substantially completed at Bell Labs by the end of 1944, Shannon for the first time introduced the qualitative and quantitative model of communication as a statistical process underlying information theory, opening with the assertion that

In Shannon's revolutionary and groundbreaking paper, the work for which had been substantially completed at Bell Labs by the end of 1944, Shannon for the first time introduced the qualitative and quantitative model of communication as a statistical process underlying information theory, opening with the assertion that

1944年底之前，Shannon的工作在贝尔实验室已基本完成。在Shannon的开创性的论文中首次引入了定性和定量的通信模型，将其作为信息理论基础的统计过程。

"The fundamental problem of communication is that of reproducing at one point, either exactly or approximately, a message selected at another point."

"The fundamental problem of communication is that of reproducing at one point, either exactly or approximately, a message selected at another point."

通信的基本问题是在一点上精确地或近似地再现在另一点上选择的信息

With it came the ideas of

With it came the ideas of

相关观点

• the information entropy and redundancy of a source, and its relevance through the source coding theorem;

• the mutual information, and the channel capacity of a noisy channel, including the promise of perfect loss-free communication given by the noisy-channel coding theorem;

• the practical result of the Shannon–Hartley law for the channel capacity of a Gaussian channel; as well as

• the bit—a new way of seeing the most fundamental unit of information.

Quantities of information

资料数量

Main article: Quantities of information

Information theory is based on probability theory and statistics. Information theory often concerns itself with measures of information of the distributions associated with random variables. Important quantities of information are entropy, a measure of information in a single random variable, and mutual information, a measure of information in common between two random variables. The former quantity is a property of the probability distribution of a random variable and gives a limit on the rate at which data generated by independent samples with the given distribution can be reliably compressed. The latter is a property of the joint distribution of two random variables, and is the maximum rate of reliable communication across a noisy channel in the limit of long block lengths, when the channel statistics are determined by the joint distribution.

Information theory is based on probability theory and statistics. Information theory often concerns itself with measures of information of the distributions associated with random variables. Important quantities of information are entropy, a measure of information in a single random variable, and mutual information, a measure of information in common between two random variables. The former quantity is a property of the probability distribution of a random variable and gives a limit on the rate at which data generated by independent samples with the given distribution can be reliably compressed. The latter is a property of the joint distribution of two random variables, and is the maximum rate of reliable communication across a noisy channel in the limit of long block lengths, when the channel statistics are determined by the joint distribution.

信息理论是基于概率论和统计学的。信息论常常涉及到与随机变量相关的分布信息的度量。重要的信息量是熵和互信息，前者是单一随机变量中信息的度量，后者是两个随机变量之间信息的度量。前者是一个随机变量的概率分布的性质，并且给出了一个限制，在给定分布的独立样本生成的数据可以被可靠压缩的速率。后者是两个随机变量联合分布的一个性质，是当信道统计量由联合分布确定时，在长块长度的限制下通过噪声信道的可靠通信的最大速率。

The choice of logarithmic base in the following formulae determines the unit of information entropy that is used. A common unit of information is the bit, based on the binary logarithm. Other units include the nat, which is based on the natural logarithm, and the decimal digit, which is based on the common logarithm.

The choice of logarithmic base in the following formulae determines the unit of information entropy that is used. A common unit of information is the bit, based on the binary logarithm. Other units include the nat, which is based on the natural logarithm, and the decimal digit, which is based on the common logarithm.

以下公式中对数底的选择决定了使用的熵单位。一个常见的信息单位是位，基于以2爲底的对数。其他单位包括基于自然对数的 nat 和基于常用对数的十进制数字。

In what follows, an expression of the form p log p is considered by convention to be equal to zero whenever p = 0. This is justified because [math]\displaystyle{ \lim_{p \rightarrow 0+} p \log p = 0 }[/math] for any logarithmic base.

In what follows, an expression of the form is considered by convention to be equal to zero whenever . This is justified because [math]\displaystyle{ \lim_{p \rightarrow 0+} p \log p = 0 }[/math] for any logarithmic base.

在接下来的部分中，按照惯例，只要存在一个表达式，该表达式就被认为等于零。这是合理的，因为 math lim { p right tarrow 0 + } p log p0 / math 适用于任何对数底。

Entropy of an information source

信息源的熵

Based on the probability mass function of each source symbol to be communicated, the Shannon entropy H, in units of bits (per symbol), is given by

Based on the probability mass function of each source symbol to be communicated, the Shannon entropy , in units of bits (per symbol), is given by

基于要通信的每个源符号的概率质量函数，香农熵以比特为单位(每个符号)由

[math]\displaystyle{ H = - \sum_{i} p_i \log_2 (p_i) }[/math]

[math]\displaystyle{ H = - \sum_{i} p_i \log_2 (p_i) }[/math]

数学 h- sum { i } i log 2(pi) / math

where p_i is the probability of occurrence of the i-th possible value of the source symbol. This equation gives the entropy in the units of "bits" (per symbol) because it uses a logarithm of base 2, and this base-2 measure of entropy has sometimes been called the shannon in his honor. Entropy is also commonly computed using the natural logarithm (base e, where e is Euler's number), which produces a measurement of entropy in nats per symbol and sometimes simplifies the analysis by avoiding the need to include extra constants in the formulas. Other bases are also possible, but less commonly used. For example, a logarithm of base 2⁸ = 256 will produce a measurement in bytes per symbol, and a logarithm of base 10 will produce a measurement in decimal digits (or hartleys) per symbol.

where is the probability of occurrence of the -th possible value of the source symbol. This equation gives the entropy in the units of "bits" (per symbol) because it uses a logarithm of base 2, and this base-2 measure of entropy has sometimes been called the shannon in his honor. Entropy is also commonly computed using the natural logarithm (base E (mathematical constant)|, where is Euler's number), which produces a measurement of entropy in nats per symbol and sometimes simplifies the analysis by avoiding the need to include extra constants in the formulas. Other bases are also possible, but less commonly used. For example, a logarithm of base will produce a measurement in bytes per symbol, and a logarithm of base 10 will produce a measurement in decimal digits (or hartleys) per symbol.

其中是源符号的第-个可能值出现的概率。这个方程给出了以“比特”(每个符号)为单位的熵，因为它使用了以2为底的对数，而这个以2为底的熵度量有时被称为香农(shannon) ，以纪念他。熵的计算也通常使用自然对数(基数 e (数学常数) | ，其中是欧拉数) ，它产生以每个符号的 nats 为单位的熵的测量，有时通过避免在公式中包含额外常数来简化分析。其他基地也是可能的，但不常用。例如，以为底的对数将产生以每个符号的字节为单位的测量值，以10为底的对数将产生以每个符号的十进制数字(或哈特利)为单位的测量值。

Intuitively, the entropy H_X of a discrete random variable X is a measure of the amount of uncertainty associated with the value of X when only its distribution is known.

Intuitively, the entropy of a discrete random variable is a measure of the amount of uncertainty associated with the value of when only its distribution is known.

直观上，离散型随机变量的熵是一种度量，当只有它的分布是已知的时候，与它的值相关的不确定性的量度。

The entropy of a source that emits a sequence of N symbols that are independent and identically distributed (iid) is N ⋅ H bits (per message of N symbols). If the source data symbols are identically distributed but not independent, the entropy of a message of length N will be less than N ⋅ H.

The entropy of a source that emits a sequence of symbols that are independent and identically distributed (iid) is bits (per message of symbols). If the source data symbols are identically distributed but not independent, the entropy of a message of length will be less than .

发出独立且同分布的符号序列(iid)的源的熵是位(每个符号消息)。如果源数据符号是同分布的，但不是独立的，则消息长度的熵将小于。

The entropy of a Bernoulli trial as a function of success probability, often called the 模板:Em, H_b(p). The entropy is maximized at 1 bit per trial when the two possible outcomes are equally probable, as in an unbiased coin toss.

The entropy of a Bernoulli trial as a function of success probability, often called the , . The entropy is maximized at 1 bit per trial when the two possible outcomes are equally probable, as in an unbiased coin toss.

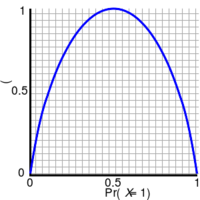
作为成功概率的函数，[ Bernoulli 试验的熵，通常称为，。当两种可能的结果的概率相等时，每次试验的熵最大化为1位，就像无偏的掷硬币一样。]

If one transmits 1000 bits (0s and 1s), and the value of each of these bits is known to the receiver (has a specific value with certainty) ahead of transmission, it is clear that no information is transmitted. If, however, each bit is independently equally likely to be 0 or 1, 1000 shannons of information (more often called bits) have been transmitted. Between these two extremes, information can be quantified as follows. If 𝕏 is the set of all messages 模板:Mset that X could be, and p(x) is the probability of some [math]\displaystyle{ x \in \mathbb X }[/math], then the entropy, H, of X is defined:

If one transmits 1000 bits (0s and 1s), and the value of each of these bits is known to the receiver (has a specific value with certainty) ahead of transmission, it is clear that no information is transmitted. If, however, each bit is independently equally likely to be 0 or 1, 1000 shannons of information (more often called bits) have been transmitted. Between these two extremes, information can be quantified as follows. If 𝕏 is the set of all messages }} that could be, and is the probability of some [math]\displaystyle{ x \in \mathbb X }[/math], then the entropy, , of is defined:

如果一个人在传输之前传输1000位(0和1) ，并且接收者知道每个位的值(有一个确定的特定值) ，那么很明显没有信息被传输。然而，如果每个比特都是独立的，那么它们传输的信息量可能是0或1,1000个信息子(通常被称为比特)。在这两个极端之间，信息可以被量化如下。如果 x 是所有消息}}的集合，并且是某个 mathbb x / math 中某个数学 x 的概率，那么熵，，的定义如下:

[math]\displaystyle{ H(X) = \mathbb{E}_{X} [I(x)] = -\sum_{x \in \mathbb{X}} p(x) \log p(x). }[/math]

[math]\displaystyle{ H(X) = \mathbb{E}_{X} [I(x)] = -\sum_{x \in \mathbb{X}} p(x) \log p(x). }[/math]

Math h (x) mathbb { x }[ i (x)]-sum { x in mathbb { x } p (x) log p (x) . / math

(Here, I(x) is the self-information, which is the entropy contribution of an individual message, and 𝔼_X is the expected value.) A property of entropy is that it is maximized when all the messages in the message space are equiprobable p(x) = 1/n; i.e., most unpredictable, in which case H(X) = log n.

(Here, is the self-information, which is the entropy contribution of an individual message, and is the expected value.) A property of entropy is that it is maximized when all the messages in the message space are equiprobable ; i.e., most unpredictable, in which case .

(这里是自信息，它是单个信息的熵贡献，也是期望值。)熵的一个特性是，当消息空间中的所有消息都是等概率时，熵就会最大化; 也就是说，在这种情况下，熵是最不可预测的。

The special case of information entropy for a random variable with two outcomes is the binary entropy function, usually taken to the logarithmic base 2, thus having the shannon (Sh) as unit:

The special case of information entropy for a random variable with two outcomes is the binary entropy function, usually taken to the logarithmic base 2, thus having the shannon (Sh) as unit:

对于具有两个结果的随机变量，熵的特殊情况是二元熵函数，通常以对数为底2，因此以 shannon (Sh)为单位:

[math]\displaystyle{ H_{\mathrm{b}}(p) = - p \log_2 p - (1-p)\log_2 (1-p). }[/math]

[math]\displaystyle{ H_{\mathrm{b}}(p) = - p \log_2 p - (1-p)\log_2 (1-p). }[/math]

(p)-p log 2 p-(1-p) log 2(1-p) . / math

Joint entropy

联合熵

The 模板:Em of two discrete random variables X and Y is merely the entropy of their pairing: (X, Y). This implies that if X and Y are independent, then their joint entropy is the sum of their individual entropies.

The of two discrete random variables and is merely the entropy of their pairing: . This implies that if and are independent, then their joint entropy is the sum of their individual entropies.

两个离散随机变量的熵，仅仅是它们配对的熵: 。这意味着如果和是独立的，那么它们的联合熵就是它们各自熵的总和。

For example, if (X, Y) represents the position of a chess piece — X the row and Y the column, then the joint entropy of the row of the piece and the column of the piece will be the entropy of the position of the piece.

For example, if represents the position of a chess piece — the row and the column, then the joint entropy of the row of the piece and the column of the piece will be the entropy of the position of the piece.

例如，如果代表棋子的位置ー行和列，那么棋子行和列的联合熵就是棋子位置的联合熵。

[math]\displaystyle{ H(X, Y) = \mathbb{E}_{X,Y} [-\log p(x,y)] = - \sum_{x, y} p(x, y) \log p(x, y) \, }[/math]

[math]\displaystyle{ H(X, Y) = \mathbb{E}_{X,Y} [-\log p(x,y)] = - \sum_{x, y} p(x, y) \log p(x, y) \, }[/math]

数学 h (x，y) mathbb { x，y }[- log p (x，y)]- sum { x，y } p (x，y) log p (x，y) ，/ math

Despite similar notation, joint entropy should not be confused with 模板:Em.

Despite similar notation, joint entropy should not be confused with .

尽管符号相似，联合熵不应与。

Conditional entropy (equivocation)

条件熵(含糊其辞)

The 模板:Em or conditional uncertainty of X given random variable Y (also called the equivocation of X about Y) is the average conditional entropy over Y:

The or conditional uncertainty of given random variable (also called the equivocation of about ) is the average conditional entropy over :

给定随机变量的或条件不确定性(也称为约的模糊性)是除以以下条件熵的平均值:

[math]\displaystyle{ H(X|Y) = \mathbb E_Y [H(X|y)] = -\sum_{y \in Y} p(y) \sum_{x \in X} p(x|y) \log p(x|y) = -\sum_{x,y} p(x,y) \log p(x|y). }[/math]

[math]\displaystyle{ H(X|Y) = \mathbb E_Y [H(X|y)] = -\sum_{y \in Y} p(y) \sum_{x \in X} p(x|y) \log p(x|y) = -\sum_{x,y} p(x,y) \log p(x|y). }[/math]

数学 h (x | y) mathbb e y [ h (x | y)]- sum { y } p (y) sum { x } p (x | y) log p (x | y)- sum { x，y } p (x，y) log p (x | y)。 数学

Because entropy can be conditioned on a random variable or on that random variable being a certain value, care should be taken not to confuse these two definitions of conditional entropy, the former of which is in more common use. A basic property of this form of conditional entropy is that:

Because entropy can be conditioned on a random variable or on that random variable being a certain value, care should be taken not to confuse these two definitions of conditional entropy, the former of which is in more common use. A basic property of this form of conditional entropy is that:

因为熵可以取决于一个随机变量或者一个确定的随机变量，所以应该注意不要混淆条件熵的这两个定义，前者更为常用。这种条件熵的一个基本属性是:

[math]\displaystyle{ H(X|Y) = H(X,Y) - H(Y) .\, }[/math]

[math]\displaystyle{  H(X|Y) = H(X,Y) - H(Y) .\, }[/math]

数学 h (x | y) h (x，y)-h (y)。 ，/ 数学

Mutual information (transinformation)

互信息(交换信息)

Mutual information measures the amount of information that can be obtained about one random variable by observing another. It is important in communication where it can be used to maximize the amount of information shared between sent and received signals. The mutual information of X relative to Y is given by:

Mutual information measures the amount of information that can be obtained about one random variable by observing another. It is important in communication where it can be used to maximize the amount of information shared between sent and received signals. The mutual information of relative to is given by:

互信息测量的是通过观察另一个随机变量可以获得的信息量。在通信中，它可以用来最大限度地在发送和接收信号之间共享信息量，这一点非常重要。相对于的相互信息是通过以下方式给出的:

[math]\displaystyle{ I(X;Y) = \mathbb{E}_{X,Y} [SI(x,y)] = \sum_{x,y} p(x,y) \log \frac{p(x,y)}{p(x)\, p(y)} }[/math]

[math]\displaystyle{ I(X;Y) = \mathbb{E}_{X,Y} [SI(x,y)] = \sum_{x,y} p(x,y) \log \frac{p(x,y)}{p(x)\, p(y)} }[/math]

数学 i (x; y) mathbb { x，y }[ SI (x，y)] sum { x，y } p (x，y) log frac { p (x，y)} ，p (y)} / math

where SI (Specific mutual Information) is the pointwise mutual information.

where (Specific mutual Information) is the pointwise mutual information.

其中(特定的相互信息)是点间互信息。

A basic property of the mutual information is that

A basic property of the mutual information is that

互信息的一个基本属性是

[math]\displaystyle{ I(X;Y) = H(X) - H(X|Y).\, }[/math]

[math]\displaystyle{ I(X;Y) = H(X) - H(X|Y).\, }[/math]

数学 i (x; y) h (x)-h (x | y)。 ，/ 数学

That is, knowing Y, we can save an average of I(X; Y) bits in encoding X compared to not knowing Y.

That is, knowing Y, we can save an average of bits in encoding X compared to not knowing Y.

也就是说，了解了 y，我们就可以在编码 x 时比不知道 y 平均节省位。

Mutual information is symmetric:

Mutual information is symmetric:

互信息是对称的:

[math]\displaystyle{ I(X;Y) = I(Y;X) = H(X) + H(Y) - H(X,Y).\, }[/math]

[math]\displaystyle{ I(X;Y) = I(Y;X) = H(X) + H(Y) - H(X,Y).\, }[/math]

数学 i (x; y) i (y; x) h (x) + h (y)-h (x，y)。 ，/ math

Mutual information can be expressed as the average Kullback–Leibler divergence (information gain) between the posterior probability distribution of X given the value of Y and the prior distribution on X:

Mutual information can be expressed as the average Kullback–Leibler divergence (information gain) between the posterior probability distribution of X given the value of Y and the prior distribution on X:

在给定 y 值和 x 的先验分布的情况下，互信息可以表示为 x 的后验概率之间的平均 Kullback-Leibler 散度(信息增益) :

[math]\displaystyle{ I(X;Y) = \mathbb E_{p(y)} [D_{\mathrm{KL}}( p(X|Y=y) \| p(X) )]. }[/math]

[math]\displaystyle{ I(X;Y) = \mathbb E_{p(y)} [D_{\mathrm{KL}}( p(X|Y=y) \| p(X) )]. }[/math]

Math i (x; y) mathbb e { p (y)}[ d { mathrm { KL }(p (x | y) | p (x))] . / math

In other words, this is a measure of how much, on the average, the probability distribution on X will change if we are given the value of Y. This is often recalculated as the divergence from the product of the marginal distributions to the actual joint distribution:

In other words, this is a measure of how much, on the average, the probability distribution on X will change if we are given the value of Y. This is often recalculated as the divergence from the product of the marginal distributions to the actual joint distribution:

换句话说，这是一种衡量方法，如果我们给出 y 的值，平均来说，x 上的概率分布将会改变多少。这经常被重新计算为从边际分布乘积到实际联合分布的背离:

[math]\displaystyle{ I(X; Y) = D_{\mathrm{KL}}(p(X,Y) \| p(X)p(Y)). }[/math]

[math]\displaystyle{ I(X; Y) = D_{\mathrm{KL}}(p(X,Y) \| p(X)p(Y)). }[/math]

Math i (x; y) d { mathrum { KL }(p (x，y) | p (x) p (y)) . / math

Mutual information is closely related to the log-likelihood ratio test in the context of contingency tables and the multinomial distribution and to Pearson's χ² test: mutual information can be considered a statistic for assessing independence between a pair of variables, and has a well-specified asymptotic distribution.

Mutual information is closely related to the log-likelihood ratio test in the context of contingency tables and the multinomial distribution and to Pearson's χ² test: mutual information can be considered a statistic for assessing independence between a pair of variables, and has a well-specified asymptotic distribution.

互信息与列联表和多项分布上的对数似然比检验以及 Pearson 的 sup 2 / sup 检验密切相关: 互信息可以被看作是一个评估一对变量之间独立性的统计量，并且具有良好的指定的渐近分布。

Kullback–Leibler divergence (information gain)

Kullback-Leibler 分歧(信息增益)

The Kullback–Leibler divergence (or information divergence, information gain, or relative entropy) is a way of comparing two distributions: a "true" probability distribution p(X), and an arbitrary probability distribution q(X). If we compress data in a manner that assumes q(X) is the distribution underlying some data, when, in reality, p(X) is the correct distribution, the Kullback–Leibler divergence is the number of average additional bits per datum necessary for compression. It is thus defined

The Kullback–Leibler divergence (or information divergence, information gain, or relative entropy) is a way of comparing two distributions: a "true" probability distribution p(X), and an arbitrary probability distribution q(X). If we compress data in a manner that assumes q(X) is the distribution underlying some data, when, in reality, p(X) is the correct distribution, the Kullback–Leibler divergence is the number of average additional bits per datum necessary for compression. It is thus defined

Kullback-Leibler 分歧(或相对熵，信息增益，或相对熵)是一种比较两种分布的方法: 一种是“真实的”概率分布 p (x) ，另一种是任意的概率分布 q (x)。如果我们假设 q (x)是某些数据的分布，而实际上 p (x)是正确的分布，那么 Kullback-Leibler 散度就是每个数据压缩所需的平均附加比特数。它就是这样定义的

[math]\displaystyle{ D_{\mathrm{KL}}(p(X) \| q(X)) = \sum_{x \in X} -p(x) \log {q(x)} \, - \, \sum_{x \in X} -p(x) \log {p(x)} = \sum_{x \in X} p(x) \log \frac{p(x)}{q(x)}. }[/math]

[math]\displaystyle{ D_{\mathrm{KL}}(p(X) \| q(X)) = \sum_{x \in X} -p(x) \log {q(x)} \, - \, \sum_{x \in X} -p(x) \log {p(x)} = \sum_{x \in X} p(x) \log \frac{p(x)}{q(x)}. }[/math]

数学 d { mathrm { KL }(p (x) | q (x)) sum { x }-p (x) log { q (x)} ,-，sum { x }-p (x) log { p (x) log { sum { p (x)}{ q (x)}。 数学

Although it is sometimes used as a 'distance metric', KL divergence is not a true metric since it is not symmetric and does not satisfy the triangle inequality (making it a semi-quasimetric).

Although it is sometimes used as a 'distance metric', KL divergence is not a true metric since it is not symmetric and does not satisfy the triangle inequality (making it a semi-quasimetric).

尽管有时它被用作一个距离度量，KL 散度不是一个真正的度量，因为它不是对称的，也不满足三角不等式(使它成为一个半准度量)。

Another interpretation of the KL divergence is the "unnecessary surprise" introduced by a prior from the truth: suppose a number X is about to be drawn randomly from a discrete set with probability distribution p(x). If Alice knows the true distribution p(x), while Bob believes (has a prior) that the distribution is q(x), then Bob will be more surprised than Alice, on average, upon seeing the value of X. The KL divergence is the (objective) expected value of Bob's (subjective) surprisal minus Alice's surprisal, measured in bits if the log is in base 2. In this way, the extent to which Bob's prior is "wrong" can be quantified in terms of how "unnecessarily surprised" it is expected to make him.

Another interpretation of the KL divergence is the "unnecessary surprise" introduced by a prior from the truth: suppose a number X is about to be drawn randomly from a discrete set with probability distribution p(x). If Alice knows the true distribution p(x), while Bob believes (has a prior) that the distribution is q(x), then Bob will be more surprised than Alice, on average, upon seeing the value of X. The KL divergence is the (objective) expected value of Bob's (subjective) surprisal minus Alice's surprisal, measured in bits if the log is in base 2. In this way, the extent to which Bob's prior is "wrong" can be quantified in terms of how "unnecessarily surprised" it is expected to make him.

对 KL 分歧的另一种解释是“不必要的惊讶” ，由真理之前引入: 假设一个数字 x 是从一个离散的集合随机抽取的概率分布 p (x)。如果爱丽丝知道真正的分布 p (x) ，而鲍勃认为(有先验)分布是 q (x) ，那么平均而言，鲍勃在看到 x 的值时会比爱丽丝更惊讶。Kl 发散度是 Bob (主观)惊喜的(客观)预期值减去 Alice 的惊喜值，如果日志位于以2为基数，则以位为单位进行测量。通过这种方式，鲍勃的先验“错误”的程度可以量化为预期会让他“不必要地惊讶”的程度。

Other quantities

其他数量

Other important information theoretic quantities include Rényi entropy (a generalization of entropy), differential entropy (a generalization of quantities of information to continuous distributions), and the conditional mutual information.

Other important information theoretic quantities include Rényi entropy (a generalization of entropy), differential entropy (a generalization of quantities of information to continuous distributions), and the conditional mutual information.

其他重要的信息理论量包括 r nyi 熵(熵的推广) ，微分熵(信息量的推广到连续分布) ，以及条件互信息。

Coding theory

编码理论

Main article: Coding theory

A picture showing scratches on the readable surface of a CD-R. Music and data CDs are coded using error correcting codes and thus can still be read even if they have minor scratches using error detection and correction.

A picture showing scratches on the readable surface of a CD-R. Music and data CDs are coded using error correcting codes and thus can still be read even if they have minor scratches using error detection and correction.

在可读光盘的表面上显示划痕的图片。 音乐和数据光盘使用纠错编码进行编码，因此即使它们有轻微的划痕，也可以通过[纠错]进行读取

Coding theory is one of the most important and direct applications of information theory. It can be subdivided into source coding theory and channel coding theory. Using a statistical description for data, information theory quantifies the number of bits needed to describe the data, which is the information entropy of the source.

Coding theory is one of the most important and direct applications of information theory. It can be subdivided into source coding theory and channel coding theory. Using a statistical description for data, information theory quantifies the number of bits needed to describe the data, which is the information entropy of the source.

编码理论是信息论最重要和最直接的应用之一。它可以细分为信源编码理论和信道编码理论。利用数据的统计描述，信息理论量化描述数据所需的位数，这是数据源的熵。

• Data compression (source coding): There are two formulations for the compression problem:

• lossless data compression: the data must be reconstructed exactly;

• lossy data compression: allocates bits needed to reconstruct the data, within a specified fidelity level measured by a distortion function. This subset of information theory is called rate–distortion theory.

• Error-correcting codes (channel coding): While data compression removes as much redundancy as possible, an error correcting code adds just the right kind of redundancy (i.e., error correction) needed to transmit the data efficiently and faithfully across a noisy channel.

This division of coding theory into compression and transmission is justified by the information transmission theorems, or source–channel separation theorems that justify the use of bits as the universal currency for information in many contexts. However, these theorems only hold in the situation where one transmitting user wishes to communicate to one receiving user. In scenarios with more than one transmitter (the multiple-access channel), more than one receiver (the broadcast channel) or intermediary "helpers" (the relay channel), or more general networks, compression followed by transmission may no longer be optimal. Network information theory refers to these multi-agent communication models.

This division of coding theory into compression and transmission is justified by the information transmission theorems, or source–channel separation theorems that justify the use of bits as the universal currency for information in many contexts. However, these theorems only hold in the situation where one transmitting user wishes to communicate to one receiving user. In scenarios with more than one transmitter (the multiple-access channel), more than one receiver (the broadcast channel) or intermediary "helpers" (the relay channel), or more general networks, compression followed by transmission may no longer be optimal. Network information theory refers to these multi-agent communication models.

这种将编码理论划分为压缩和传输的做法得到了信息传输定理或信源信道分离定理的证明，这些定理证明在许多情况下使用比特作为信息的通用货币是正确的。然而，这些定理只适用于一个发送用户希望与一个接收用户通信的情况。在多于一个发射器(多重接达频道)、多于一个接收器(广播频道)或中介”辅助器”(中继频道)或多个一般网络的情况下，先压缩后传输可能不再是最佳选择。网络信息理论就是指这些多 agent 通信模型。

Source theory

来源理论

Any process that generates successive messages can be considered a 模板:Em of information. A memoryless source is one in which each message is an independent identically distributed random variable, whereas the properties of ergodicity and stationarity impose less restrictive constraints. All such sources are stochastic. These terms are well studied in their own right outside information theory.

Any process that generates successive messages can be considered a of information. A memoryless source is one in which each message is an independent identically distributed random variable, whereas the properties of ergodicity and stationarity impose less restrictive constraints. All such sources are stochastic. These terms are well studied in their own right outside information theory.

任何生成连续消息的进程都可以被认为是一种信息。无记忆信源是指每个信息是一个独立的同分布随机变量，而遍历性和平稳性的性质对信源的限制较少。所有这些源都是随机的。这些术语本身在信息论之外已经得到了很好的研究。

Rate

速率! ——这部分与频道容量相关——

Information rate is the average entropy per symbol. For memoryless sources, this is merely the entropy of each symbol, while, in the case of a stationary stochastic process, it is

Information rate is the average entropy per symbol. For memoryless sources, this is merely the entropy of each symbol, while, in the case of a stationary stochastic process, it is

信息率是每个符号的平均熵。对于无记忆的源，这仅仅是每个符号的熵，而对于静止的随机过程来说，它是

[math]\displaystyle{ r = \lim_{n \to \infty} H(X_n|X_{n-1},X_{n-2},X_{n-3}, \ldots); }[/math]

[math]\displaystyle{ r = \lim_{n \to \infty} H(X_n|X_{n-1},X_{n-2},X_{n-3}, \ldots); }[/math]

(x n | x { n-1} ，x { n-2} ，x { n-3} ，ldots) ; / math

that is, the conditional entropy of a symbol given all the previous symbols generated. For the more general case of a process that is not necessarily stationary, the average rate is

that is, the conditional entropy of a symbol given all the previous symbols generated. For the more general case of a process that is not necessarily stationary, the average rate is

也就是说，一个符号的条件熵给出了所有之前产生的符号。对于一个不一定是平稳的过程的更一般的情况，平均速率是

[math]\displaystyle{ r = \lim_{n \to \infty} \frac{1}{n} H(X_1, X_2, \dots X_n); }[/math]

[math]\displaystyle{ r = \lim_{n \to \infty} \frac{1}{n} H(X_1, X_2, \dots X_n); }[/math]

(x1，x2， dots xn) ; / math

that is, the limit of the joint entropy per symbol. For stationary sources, these two expressions give the same result.

that is, the limit of the joint entropy per symbol. For stationary sources, these two expressions give the same result.

也就是说，每个符号的联合熵的极限。对于静止源，这两个表达式给出了相同的结果。

It is common in information theory to speak of the "rate" or "entropy" of a language. This is appropriate, for example, when the source of information is English prose. The rate of a source of information is related to its redundancy and how well it can be compressed, the subject of 模板:Em.

It is common in information theory to speak of the "rate" or "entropy" of a language. This is appropriate, for example, when the source of information is English prose. The rate of a source of information is related to its redundancy and how well it can be compressed, the subject of .

在信息论中，谈论一种语言的“速率”或“熵”是很常见的。这是适当的，例如，当信息来源是英语散文。信息来源的速度与它的冗余度以及它可以被压缩的程度有关。

Channel capacity

信道容量

Main article: Channel capacity

Communications over a channel—such as an ethernet cable—is the primary motivation of information theory. However, such channels often fail to produce exact reconstruction of a signal; noise, periods of silence, and other forms of signal corruption often degrade quality.

Communications over a channel—such as an ethernet cable—is the primary motivation of information theory. However, such channels often fail to produce exact reconstruction of a signal; noise, periods of silence, and other forms of signal corruption often degrade quality.

通过信道(如以太网电缆)进行通信是信息理论的主要动机。然而，这样的通道往往不能产生准确的重建信号; 噪声，静默时间，和其他形式的信号损坏往往降低质量。

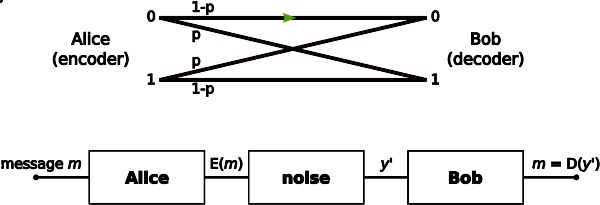
Consider the communications process over a discrete channel. A simple model of the process is shown below:

Consider the communications process over a discrete channel. A simple model of the process is shown below:

考虑一个离散通道上的通信过程。这个过程的一个简单模型如下:

Channel model

通道模型

Here X represents the space of messages transmitted, and Y the space of messages received during a unit time over our channel. Let p(y|x) be the conditional probability distribution function of Y given X. We will consider p(y|x) to be an inherent fixed property of our communications channel (representing the nature of the noise of our channel). Then the joint distribution of X and Y is completely determined by our channel and by our choice of f(x), the marginal distribution of messages we choose to send over the channel. Under these constraints, we would like to maximize the rate of information, or the signal, we can communicate over the channel. The appropriate measure for this is the mutual information, and this maximum mutual information is called the 模板:Em and is given by:

Here X represents the space of messages transmitted, and Y the space of messages received during a unit time over our channel. Let x)}} be the conditional probability distribution function of Y given X. We will consider x)}} to be an inherent fixed property of our communications channel (representing the nature of the noise of our channel). Then the joint distribution of X and Y is completely determined by our channel and by our choice of , the marginal distribution of messages we choose to send over the channel. Under these constraints, we would like to maximize the rate of information, or the signal, we can communicate over the channel. The appropriate measure for this is the mutual information, and this maximum mutual information is called the and is given by:

这里 x 表示传输的消息空间，y 表示单位时间内通过我们的信道接收的消息空间。设 x)}是给定 x 的 y 的条件概率分布函数。我们将考虑 x)}是我们通信信道的固有固定属性(表示我们信道噪声的性质)。那么，x 和 y 的联合分布完全取决于我们的渠道，以及我们选择通过渠道发送的信息边缘分布。在这些约束条件下，我们希望最大化信息速率，或者说信号速率，我们可以通过信道进行通信。对于这个问题的适当措施是互信息，这个最大的互信息被称为互信息，并由以下人员给出:

[math]\displaystyle{ C = \max_{f} I(X;Y).\! }[/math]

[math]\displaystyle{ C = \max_{f} I(X;Y).\! }[/math]

数学 c max { f } i (x; y) . ！数学

This capacity has the following property related to communicating at information rate R (where R is usually bits per symbol). For any information rate R < C and coding error ε > 0, for large enough N, there exists a code of length N and rate ≥ R and a decoding algorithm, such that the maximal probability of block error is ≤ ε; that is, it is always possible to transmit with arbitrarily small block error. In addition, for any rate R > C, it is impossible to transmit with arbitrarily small block error.

This capacity has the following property related to communicating at information rate R (where R is usually bits per symbol). For any information rate R < C and coding error ε > 0, for large enough N, there exists a code of length N and rate ≥ R and a decoding algorithm, such that the maximal probability of block error is ≤ ε; that is, it is always possible to transmit with arbitrarily small block error. In addition, for any rate R > C, it is impossible to transmit with arbitrarily small block error.

此容量具有以下与以信息速率 r (其中 r 通常为每个符号位)进行通信有关的属性。对于任意信息速率 rc 和编码错误0，对于足够大的 n，存在一个长度 n 和速率≥ r 的码和一个译码算法，使得块错误的最大概率≤ ，即总是可以在任意小的块错误下传输。此外，对于任何速率的 rc，它不可能传输任意小的块误差。

Channel coding is concerned with finding such nearly optimal codes that can be used to transmit data over a noisy channel with a small coding error at a rate near the channel capacity.

Channel coding is concerned with finding such nearly optimal codes that can be used to transmit data over a noisy channel with a small coding error at a rate near the channel capacity.

信道编码涉及到寻找这种接近最优的编码，它可以用于在噪声信道上以接近信道容量的速率传输数据，而且编码错误很小。

Capacity of particular channel models

特定渠道模型的容量

• A continuous-time analog communications channel subject to Gaussian noise — see Shannon–Hartley theorem.

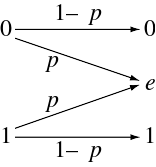
• A binary symmetric channel (BSC) with crossover probability p is a binary input, binary output channel that flips the input bit with probability p. The BSC has a capacity of 1 − H_b(p) bits per channel use, where H_b is the binary entropy function to the base-2 logarithm:

File:Binary symmetric channel.svg

文件: Binary symmetric channel.svg

• A binary erasure channel (BEC) with erasure probability p is a binary input, ternary output channel. The possible channel outputs are 0, 1, and a third symbol 'e' called an erasure. The erasure represents complete loss of information about an input bit. The capacity of the BEC is 1 − p bits per channel use.

File:Binary erasure channel.svg

文件: Binary erasure channel.svg

Applications to other fields

其他领域的应用

Intelligence uses and secrecy applications

情报使用和保密应用

Information theoretic concepts apply to cryptography and cryptanalysis. Turing's information unit, the ban, was used in the Ultra project, breaking the German Enigma machine code and hastening the end of World War II in Europe. Shannon himself defined an important concept now called the unicity distance. Based on the redundancy of the plaintext, it attempts to give a minimum amount of ciphertext necessary to ensure unique decipherability.

Information theoretic concepts apply to cryptography and cryptanalysis. Turing's information unit, the ban, was used in the Ultra project, breaking the German Enigma machine code and hastening the end of World War II in Europe. Shannon himself defined an important concept now called the unicity distance. Based on the redundancy of the plaintext, it attempts to give a minimum amount of ciphertext necessary to ensure unique decipherability.

信息论概念应用于密码学和密码分析。图灵的信息单元，即禁令，被用于 Ultra 项目，破解了德国的恩尼格玛密码，加速了二战在欧洲的结束。香农自己定义了一个重要的概念，现在称为单一性距离。基于明文的冗余性，它试图给出最小数量的密文，以确保独特的破译能力。

Information theory leads us to believe it is much more difficult to keep secrets than it might first appear. A brute force attack can break systems based on asymmetric key algorithms or on most commonly used methods of symmetric key algorithms (sometimes called secret key algorithms), such as block ciphers. The security of all such methods currently comes from the assumption that no known attack can break them in a practical amount of time.

Information theory leads us to believe it is much more difficult to keep secrets than it might first appear. A brute force attack can break systems based on asymmetric key algorithms or on most commonly used methods of symmetric key algorithms (sometimes called secret key algorithms), such as block ciphers. The security of all such methods currently comes from the assumption that no known attack can break them in a practical amount of time.

信息理论使我们相信，保守秘密比它最初可能出现时要困难得多。穷举法可以基于非对称密钥算法或最常用的对称密钥算法(有时称为秘密密钥算法) ，如分组密码破坏系统。目前所有这些方法的安全性都来自于这样一个假设，即任何已知的攻击都不能在实际的时间内破坏它们。

Information theoretic security refers to methods such as the one-time pad that are not vulnerable to such brute force attacks. In such cases, the positive conditional mutual information between the plaintext and ciphertext (conditioned on the key) can ensure proper transmission, while the unconditional mutual information between the plaintext and ciphertext remains zero, resulting in absolutely secure communications. In other words, an eavesdropper would not be able to improve his or her guess of the plaintext by gaining knowledge of the ciphertext but not of the key. However, as in any other cryptographic system, care must be used to correctly apply even information-theoretically secure methods; the Venona project was able to crack the one-time pads of the Soviet Union due to their improper reuse of key material.

Information theoretic security refers to methods such as the one-time pad that are not vulnerable to such brute force attacks. In such cases, the positive conditional mutual information between the plaintext and ciphertext (conditioned on the key) can ensure proper transmission, while the unconditional mutual information between the plaintext and ciphertext remains zero, resulting in absolutely secure communications. In other words, an eavesdropper would not be able to improve his or her guess of the plaintext by gaining knowledge of the ciphertext but not of the key. However, as in any other cryptographic system, care must be used to correctly apply even information-theoretically secure methods; the Venona project was able to crack the one-time pads of the Soviet Union due to their improper reuse of key material.

信息理论安全指的是诸如一次性垫子这样的方法，它不容易受到这种蛮力攻击。在这种情况下，明文和密文(以密钥为条件)之间的正向有条件的互信息可以确保适当的传输，而明文和密文之间的无条件互信息仍然为零，从而导致绝对安全的通信。换句话说，窃听者不能通过获得密文的知识而不是密钥来改进他或她对明文的猜测。但是，如同任何其他密码系统一样，必须小心谨慎，甚至正确应用信息——理论上安全的方法; Venona 项目能够破解苏联的一次性密封垫，因为它们不适当地重复使用关键材料。

Pseudorandom number generation

伪随机数生成

Pseudorandom number generators are widely available in computer language libraries and application programs. They are, almost universally, unsuited to cryptographic use as they do not evade the deterministic nature of modern computer equipment and software. A class of improved random number generators is termed cryptographically secure pseudorandom number generators, but even they require random seeds external to the software to work as intended. These can be obtained via extractors, if done carefully. The measure of sufficient randomness in extractors is min-entropy, a value related to Shannon entropy through Rényi entropy; Rényi entropy is also used in evaluating randomness in cryptographic systems. Although related, the distinctions among these measures mean that a random variable with high Shannon entropy is not necessarily satisfactory for use in an extractor and so for cryptography uses.

Pseudorandom number generators are widely available in computer language libraries and application programs. They are, almost universally, unsuited to cryptographic use as they do not evade the deterministic nature of modern computer equipment and software. A class of improved random number generators is termed cryptographically secure pseudorandom number generators, but even they require random seeds external to the software to work as intended. These can be obtained via extractors, if done carefully. The measure of sufficient randomness in extractors is min-entropy, a value related to Shannon entropy through Rényi entropy; Rényi entropy is also used in evaluating randomness in cryptographic systems. Although related, the distinctions among these measures mean that a random variable with high Shannon entropy is not necessarily satisfactory for use in an extractor and so for cryptography uses.

伪随机数发生器广泛应用于计算机语言库和应用程序中。它们几乎普遍不适合加密使用，因为它们不回避现代计算机设备和软件的确定性本质。一类改进的随机数生成器被称为密码安全的伪随机数生成器，但即使它们也需要软件外部的随机种子才能正常工作。这些可以通过提取器获得，如果仔细做。提取器中充分随机性的度量是最小熵，这是一个通过 r nyi 熵与 Shannon 熵相关的值，r nyi 熵也用于评估密码系统中的随机性。虽然相关，这些措施之间的区别意味着具有高香农熵的随机变量不一定令人满意的使用在提取器和密码学使用。

Seismic exploration

地震勘探

One early commercial application of information theory was in the field of seismic oil exploration. Work in this field made it possible to strip off and separate the unwanted noise from the desired seismic signal. Information theory and digital signal processing offer a major improvement of resolution and image clarity over previous analog methods.

One early commercial application of information theory was in the field of seismic oil exploration. Work in this field made it possible to strip off and separate the unwanted noise from the desired seismic signal. Information theory and digital signal processing offer a major improvement of resolution and image clarity over previous analog methods.

信息论的一个早期商业应用是在地震石油勘探领域。这一领域的工作使从所需的地震信号中剔除和分离不需要的噪声成为可能。信息理论和数字信号处理提供了一个重大改善的分辨率和图像清晰度比以前的模拟方法。

Semiotics

符号学

Semioticians Doede Nauta and Winfried Nöth both considered Charles Sanders Peirce as having created a theory of information in his works on semiotics. Nauta defined semiotic information theory as the study of "the internal processes of coding, filtering, and information processing."

Semioticians Doede Nauta and Winfried Nöth both considered Charles Sanders Peirce as having created a theory of information in his works on semiotics. Nauta defined semiotic information theory as the study of "the internal processes of coding, filtering, and information processing."

符号学家 Doede Nauta 和 Winfried n 都认为查尔斯·桑德斯·皮尔士在他的符号学著作中创造了信息理论。诺塔将符号信息理论定义为研究“编码、过滤和信息处理的内部过程”

Concepts from information theory such as redundancy and code control have been used by semioticians such as Umberto Eco and Ferruccio Rossi-Landi to explain ideology as a form of message transmission whereby a dominant social class emits its message by using signs that exhibit a high degree of redundancy such that only one message is decoded among a selection of competing ones.

Concepts from information theory such as redundancy and code control have been used by semioticians such as Umberto Eco and Ferruccio Rossi-Landi to explain ideology as a form of message transmission whereby a dominant social class emits its message by using signs that exhibit a high degree of redundancy such that only one message is decoded among a selection of competing ones.

来自信息论的概念，如冗余和代码控制，已经被符号学家如 Umberto Eco 和 Ferruccio Rossi-Landi 用来解释意识形态作为一种信息传递的形式，主导社会阶层通过使用高度冗余的标志来发出信息，这样在一系列相互竞争的标志中只有一个信息被解码。

Miscellaneous applications

杂项申请

Information theory also has applications in Gambling and information theory, black holes, and bioinformatics.

Information theory also has applications in Gambling and information theory, black holes, and bioinformatics.

信息理论在赌博和信息理论、黑洞和生物信息学中也有应用。

See also

参见

• Algorithmic probability

• Bayesian inference

• Communication theory

• Constructor theory - a generalization of information theory that includes quantum information

• Inductive probability

• Info-metrics

• Minimum message length

• Minimum description length

• List of important publications

• Philosophy of information

Applications

申请

• Active networking

• Cryptanalysis

• Cryptography

• Cybernetics

• Entropy in thermodynamics and information theory

• Gambling

• Intelligence (information gathering)

• Seismic exploration

History

历史

• Hartley, R.V.L.

• History of information theory

• Shannon, C.E.

• Timeline of information theory

• Yockey, H.P.

Theory

理论

• Coding theory

• Detection theory

• Estimation theory

• Fisher information

• Information algebra

• Information asymmetry

• Information field theory

• Information geometry

• Information theory and measure theory

• Kolmogorov complexity

• List of unsolved problems in information theory

• Logic of information

• Network coding

• Philosophy of information

• Quantum information science

• Source coding

Concepts

概念

• Ban (unit)

• Channel capacity

• Communication channel

• Communication source

• Conditional entropy

• Covert channel

• Data compression

• Decoder

• Differential entropy

• Fungible information

• Information fluctuation complexity

• Information entropy

• Joint entropy

• Kullback–Leibler divergence

• Mutual information

• Pointwise mutual information (PMI)

• Receiver (information theory)

• Redundancy

• Rényi entropy

• Self-information

• Unicity distance

• Variety

• Hamming distance

References

参考资料

The classic work

经典之作

Other journal articles

其他期刊文章

Textbooks on information theory

信息论教材

Other books

Other books

其他书籍

MOOC on information theory

MOOC on information theory

信息理论大型开放式课程

• Raymond W. Yeung, "Information Theory" (The Chinese University of Hong Kong)

External links

External links

外部链接

• 模板:SpringerEOM

• Lambert F. L. (1999), "Shuffled Cards, Messy Desks, and Disorderly Dorm Rooms - Examples of Entropy Increase? Nonsense!", Journal of Chemical Education

• IEEE Information Theory Society and ITSOC Monographs, Surveys, and Reviews

Category:Computer science

类别: 计算机科学

Category:Cybernetics

类别: 控制论

Category:Formal sciences

类别: 正规科学

Category:Information Age

类别: 信息时代

This page was moved from wikipedia:en:Information theory. Its edit history can be viewed at 信息论/edithistory