系统中的观察者(4)——人工智能的观察者

前两章我们分别从形而上的哲学角度和物理学的两大分支论述了观察者这个特殊的科学背景角色。也许读者会觉得观察者这玩意儿不过是一种“灵光闪现”罢了，没有什么实际用途。那么，本章就试图说服你，观察者不仅仅是一种视角，它绝对可以走向实际应用。而且这种应用完全有可能给：“人工智能”学科注入全新的血液。同时笔者非常确信地认为，人工智能恰恰又为观察者理论这个全新的思想提供了最好的应用平台和实验田。

下面，我们首先简单回顾一下人工智能的发展历史，着重指出这门学科遇到的一些瓶颈。接下来，我们将从一种人机交互的视角深入剖析智能程序的本质，并提出了一种新的思考范式，即将人与机器看作一个互动的整体。然而，将人与机器放到一起考虑并不是什么新鲜事儿，人机交互等学科也在讨论同样的问题。那么在第3节中我将说服你，与传统的人机交互理论不同，观察者理论试图构建一个非常简洁的模型：图灵机—观察者模型，并用量子概率——这门诞生于量子力学的数学分支来对人机互动系统进行描述。我们构建这样一个理论系统的目的是什么？第4节将回答，人-机交互系统要实现的目标其实有两个：从人的角度来说，人-机交互系统最终的目的就是要提高可玩性；而对于机器来说，人玩的力量——交互行为会为机器提供一种进化的可能，这种进化动力将会使得机器越来越智能——体现为计算系统越来越深的虚拟层次的构建。那么，我们的理论体系将试图定量化描述这两个目标。最后，我们将对理论前景进行一下大胆的展望，主要指出，这些年刚刚兴起的一个分支：人类计算 Human Computation 将为我们这套理论提供无限的应用平台。

人工智能之梦

人工智能的梦想完全可以追溯到19世纪末期巴比奇发明史上第一台会运算的机器（积分机），因为人工智能与计算机的目标相似：都是为了让机器可以部分或者全部实现人类的智能。计算机科学真正的大发展是20世纪初。那个时候，有多位数学家分别从递归函数论、集合论、数理逻辑、lambda-演算、图灵机等不同的侧面研究人类逻辑思维的形式化（请读者参考《图灵机与计算理论》）。这种数学上的定义不仅澄清了算法的概念，也为人类创造会计算的机器奠定了理论基础。

尽管人工智能 Artificial Intelligence这个名词在1956年才真正出现，但我认为这门学科的理论基础早已在数理逻辑、递归函数论、图灵机理论中奠定了。20世纪初期的计算理论不仅澄清了所谓计算的含义，而且还指出了一条通向人类理性极限——自指问题的天梯。关于这个主题，候世达在1979年的名著《哥德尔、艾舍尔、巴赫：集异璧之大成 Gödel, Escher, Bach: An Eternal Golden Braid》给出了非常丰富而深刻的讨论，我认为这本书达到了人工智能思想领域（注意不是人工智能技术）的顶峰。我们也将在下一章继续讨论这个主题。

然而，人工智能在技术上的发展却远滞后于理论上的突飞猛进。直到20世纪80年代，人工智能技术才真正走向成熟（有相当大的原因是因为硬件的发展）。那时候，专家系统的成功使得“人工智能”一夜成名。以专家系统和自动化逻辑推理的第一代人工智能擅长于建立大规模的规则数据库，并让计算机完成机械化的推理步骤。但很快第一代人工智能就陷入了僵局。由于静态的数据库显然不能解决现实中动态、复杂的问题求解，所以人们必须考虑机器如何自己进行学习。这就导致第二代人工智能技术的兴起，包括人工神经网络、机器学习、进化算法、人工生命等，这类技术本质上都可以归结为机器自动学习、组织各种信息和知识的能力。

但是很快，第二代人工智能又陷入了僵局。我们知道，就连人类小孩的智力发育到成熟阶段都至少需要10年时间，因此很难想象，研究人员会花费数年的时间去培养一台号称可以自学习的机器，更何况，自学习机器的运行结果并不总能保证输出正确。

如果把第一代人工智能看成是对人类智力的一种自上而下的建模方法，那么第二代以学习为主导的人工智能就是一种自下而上的方法。但是，无论是自上而下还是自下而上，人们都走的不远。

于是到了20世纪的末期，人工智能的发展陷入了僵局。一方面，人们开始放弃大而空的理论探讨，而越来越关心具体的技术。另一方面，基础理论则呈现出了群龙无首的局面。

认知学派是若干基础理论中的姣姣者。该学派认为，之所以人工智能的梦想还远远没有实现，那是因为我们对自己的大脑和认知系统了解得还不够。于是，我们非常有必要先弄清楚自己大脑是如何工作的，在此实证的基础上，再去构建模型和算法。虽然这套思路的确比起其它思路来踏实了许多，而且可以从神经科学、心理科学等方面借鉴大量的实例，但是认知学派在基础理论方面的进展却极其缓慢。它会很容易陷入两个极端而不能自拔：一方面，由于人类的脑系统非常复杂，无论从分子生物学层次还是从神经细胞的层次，都有无数的细节。因此，构建能够模拟脑运作的计算模型往往需要假设非常多的参数，而最终实现的功能也是人类认知中非常小的一部分。另一方面，也有学者直接对人类的较高级的认知功能建模，然而这样的模型就更加缺乏实证的基础，也有更多的模型构建的任意性（包括机制和参数）。

实际上，人工智能研究的一个非常重要的出发点就是：智能可以多重实现。也就是说，大自然可以用神经元细胞搭出一个会思考的脑，人类也可以利用01代码或者逻辑电路构造出另类的人工脑。这也就意味着，智能实际上是一种独立于具体硬件，甚至是软件计算方式的系统属性。因此，仅有认知科学和神经科学的事实依据还远远不够，我们还必须从-1这些特例中抽象出一般的系统属性。生物学家赫布 Hebb解释的神经系统的Hebb学习律就是一个很好的范例。这些学习律不仅告诉我们神经系统如何学习，而且它是一种抽象的系统机制，我们完全可以用其它的硬件来实现同一套机制而完成学习。然而，近期的人工智能认知学派却没有给我们提供多少类似的结论。

近年来兴起的“具身学派 embodiment intelligence”认为，人类的智能与人类的身体密切相关（请参见：http://en.wikipedia.org/wiki/Embodied_cognition ）。实际上，我们所能做、能思考的范围已经被我们这个特定的身体和环境深深制约了。例如，我们实际的人类决策并不完全取决于智力因素，而更多的则是情感、处境甚至包括身体状态等共同决定的。因此，传统的人工智能做法由于不可能把所有这些因素考虑进去，也就不可能实现真正的智能。

虽然具身派的观点有很多值得称赞之处，但是，笔者认为该学派却不能提供更多具有实际指导意义的思想。当我们将因素不仅要归结为身体，甚至包括我们嵌入其中的复杂外界环境的时候，模型的那种抽象、指导实践的作用也会荡然无存。很有理由相信，沿着具身派的思路很难提出诸如图灵机这样的抽象而简洁的模型，因为具身派并没有告诉我们什么因素才是这些复杂环境中最重要，最应该抓住的东西！

人工智能理论的发展还存在着相当多的分支，我们在这里就不一一点评了。其实笔者早在2000年左右跟随恩师贺仲雄教授开始写作科研论文的时候就稀里糊涂的一脚踏入了人工智能这个领域中，然而5年的学习下来，我看到了人工智能现有理论中的不足之处，于是2005年左右，我开始从人工智能中“出逃”。其目的就是想从更多其他学科之中借鉴新的思路。当我在复杂系统、人工生命、统计物理、量子物理等领域中遨游一番之后，已经渐渐地浮现出一条新的发展人工智能的思路。于是于2010年8月的今天写下了这篇文章。

大概在2006年左右的时候，我的头脑中已经渐渐地独立浮现出人工智能具身派的思路。但是，与他们不同的是，我找到了智能系统所在环境之中最重要的因素，不是别的，正是一个用户或者玩家——这个观察者！于是，多条不同的思路开始汇聚于一处：观察者！

观察者分析范式

将观察者引进人工智能给我们提供了一种新的思维范式。所以，我们这里并不讨论人工智能具体的算法，而是将人与计算机程序作为一个整体来分析。

从图灵测试说起

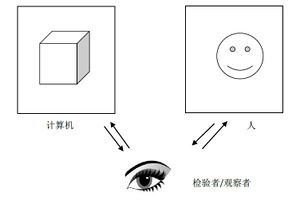
关于什么是人工智能，人们并没有一个清晰的定义。不过，我们普遍认同的是一种被称为“图灵测试 TuringTest”的测试方法。如下图：

图4-1 图灵测试

图灵测试具体是这样实施的，一个人作为检验者分别与两个小黑屋中的计算机和人进行交互。假如人与屋内的系统的交流方式有限，例如只能通过一个键盘+显示器这样的输入输出设备。在经过足够长的交互过程之后，如果这个测试者不能判断哪一个是人，哪一个是机器，则我们就称计算机具有了智能。

a.观察者

注意，其实图灵测试中的这个检验者就是我们所说的观察者。因此，一切的判断都需要通过观察者做出，观察者分析范式其实早已经进入了人工智能之中。

传统的人工智能总是把精力集中到计算机程序身上，人们思考最多的从来都是如何改进程序算法。不知不觉，这个问题的前景：计算机程序渐渐占据了主要视线，而问题的背景：做出判断的观察者却已经渐渐淡出。

那么，我们所倡导的观察者理论思维范式是什么样子呢？计算机以及站在计算机前面的人——观察者是一个耦合的整体，不能分开。因此，真正的人工智能系统不能单单考虑对计算机程序的改进，更要考虑对人类观察者的改进。于是，与其说我们要构建的是一个非常聪明的所谓的智能系统，还不如说是一个能够蒙骗人类判断力的骗人程序！

b.互动

图灵测试带给我们的另外一个宝贵的启发就是互动。所谓的互动就是指人类观察者和计算机程序之间的一种实时的动态的，双向的交互行为，也就是说不仅仅机器要对人有1输出，人也要对机器有输入。其实这个互动过程就是我们前面章节讨论过的广义的观察。

互动性对于我们判断程序是否有智能来说是一个必不可少的要素。例如，当我们看到电视屏幕上的一个会走动、会思考、谈话的爱因斯坦时，我们一定不会把屏幕上的这个虚拟人物是有智力的，原因在于我们不能与它进行实时互动。因此，互动甚至可以看作是独立于平面、立体、时间的新的维度。

在我们的观察者理论中，互动不仅仅是实现人工智能的必要因素，而且它还是一种重要的资源。正如前面反复强调的一个观点：观察者的观察不仅仅在被动地感受这个世界，它还可以主动地去创造世界。在人-机系统中，人类的互动（点击鼠标、敲击键盘）其实就是这种观察的具体体现，它完全可以形成一种观察之流注入到计算机中。这种观察之流就好比太阳辐照大地可以造就万事万物一样，它也可以创造出人工系统的复杂性，甚至高级的智能。可惜的是，以往的人工智能很少将人类的互动看作一种资源。总而言之，所谓的智能程序实际上应该是一种吃“互动”或者“观察”资源的程序。

图4-2 吃互动的程序

一个机器和两个观察者

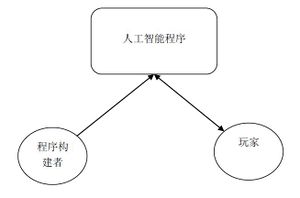
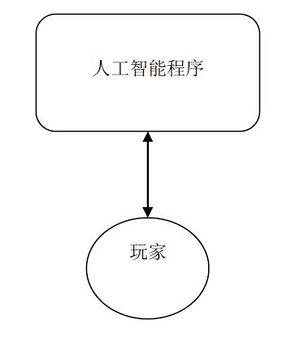
现在就让我们从观察者的视角来剖析人工智能这个问题。可以说所有的人工智能系统，如果考虑了观察者因素都可以表示为下图：

图4-3 一个程序和两个观察者

首先，任何计算机程序都不可能凭空自己产生，必须要有一个观察者来创建它，这个观察者就是程序的构建者，也即程序员。

其次，任何程序都需要有人类使用它，那么这个观察者就被称为玩家（Player，借鉴游戏中的说法）。本章所说的人工智能的背景主要是指这个观察者。

当然，这种分类方法其实暗含了一个时间顺序在里面的，即程序员先要编写人工智能程序，然后再由玩家来玩。但是，传统的人工智能学科分析这个问题的时候，却把整个时间周期大大缩短了，也就是说，只有玩家玩的过程才是智能程序需要关注的过程。

然而，当我们把时间尺度进一步扩大，如果玩家与这个人工智能程序互动之后，觉得不好了，这个时候，程序构建者就会反过来对人工智能程序进行改进，使得该程序能够进一步地满足玩家的需要。

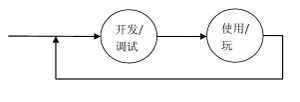
我们看到，无论这个程序是否是人工智能，当我们把观察者这个因素考虑进来之后，那么这个整体系统的运作就都可以归结为下面这两个步骤构成的无穷循环：

图4-4 完整程序周期

当我们判断某个程序具有智能的时候，其实是仅仅针对使用/玩这个步骤来说的。如果说一个程序P具有了智能，那么显然P需要独立运行，这个时候，它的创造者：程序员不能对程序进行改进。否则的话，我们就不能说这是计算机程序的智能，而仅仅是程序员的智能了。

我们还是用图灵测试来举例，假如程序员A写好了一个程序P，让玩家B来测试。

　于是B提出了一个简单的问题给程序P：“请问你妈贵姓？”。

　　P傻了，回答说：“&*&***——$#$$#$#$&*(*(&”。
　　B显然很恼怒：“这是什么破程序呀！还智能呢！”
　　这个时候，A坐不住了：“对不起，您让我来改写一下我的程序P吧。”
　　B很宽宏大量，“好吧，允许你改一改！”
　　这个时候，A把程序更改成了P’
　　B又问：“你妈贵姓？”
　　P’回答：“跟我一个姓，你猜我姓什么？”
　　B：“不错，还挺聪明。那你姓什么？”
　　P’：“&*&***——$#$$#$#$&*(*(&”
　　A：“不行，老兄，我得再改改程序，再让它回答您的问题！”
　　……

很显然，程序P完全不是人工智能，而P’的第一个回答好像挺智能的，但其实你也看出来了，P’第一个回答完全是程序员A更改的结果。因此我们不能说P或者P'具有智能，只能说程序员A具有智能。

假如这回A把P进行了更大的改进，它至少可以像模像样地回答10000个问题，尽管这些问题仍然是A事先存储到计算机之中的，那么B在跟他进行有限次的问答之后，仍然有可能把P判断成有智能的。所以，我们看到，智能的判断就变成了一个时间长短的问题。也就是说，传统判断人工智能程序的一个关键的隐含因素就是：我们判断一个程序P是否具有智能，只能在它运行、被使用（玩）的阶段进行判断，而不能包括程序员对它进行开发/调试这个阶段。

然而，我们马上会发现，问题没那么简单，因为在很多时候开发/调试阶段和使用/玩阶段是分不太清楚的。

当玩家变成程序员

下面，我们站在计算机程序的角度分析问题。对于计算机来说，无论是玩家与程序的交互，还是程序员更改程序其实都体现为键盘或者鼠标上面输入的电信号。也就是说，其实计算机程序从来都不区分玩家和程序修改这两个观察者，这种区分恰恰是我们人类做出来的。

那么，我们就来做这样一个假设，既然玩家和程序员本质上没有任何区别，那有没有可能玩家就是程序员本身呢？这样，图4-3就可以变成了如下的样子：

图4-5 化简的观察者与程序关系

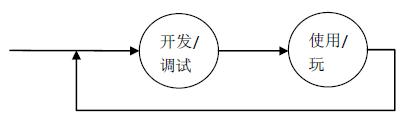
这里的玩家就是一种广义的玩家，他既是我们普通意义上的玩家（程序的使用者）又是普通意义上的程序员（程序的构建者/修改者）。进一步，从时间上来看，我们也就不再区分开发/调试与使用/玩这两个不同的步骤，于是图4-4就变成了下图：

图4-6 化简的程序与人交互周期

因此，所有的互动过程都简化为一个“玩”字。从观察者理论的角度来说，这个“玩”字正体现了我们所说的广义上的观察！

从这个角度来说，传统意义上的人工智能程序的界定已经当然无存了，因为我们已经不能分割出来一个能够独立地脱离编程员设计的人工智能程序。取而代之的，我们应该考虑如何设计一个更好的平台作为初始的系统，使得观察者能够一直不停地在这个平台上“玩”下去。这才是从观察者理论角度理解的真正的人工智能！

让我们还是用图灵测试为例来说明。我们要设计的其实不是一个多么强大、聪明的聊天程序，而是一个可以提供人和计算机进行交互的平台。在这个平台之中，玩家随随便便地聊天的话语，比如“你吃了吗？”，与程序员所写的冷冰冰的机器代码“Mov2b,Addc,…”没有本质上的区别。这样，玩家普通的聊天也可以变成对程序指令的修改，使得这个程序就能够在聊天使用中完成了自身结构的改变，这才是史上最强大的人工智能程序！

再多说两句，其实当图灵等人发明了所谓的通用图灵机 Universal Turing Machine这种程序，前面设想的那个最强大的人工智能程序平台就已经存在了。因为无论是更改程序还是与机器聊天都可以被通用图灵机解释为机器代码。所以，从这个意义上来说，其实我们不应该发明什么人工智能程序，而是应该发现真正的智能！这就好比古人所讲的道，你就是找不到它在哪，但它的确早就在那里了。

读到这里，也许你会说，这些分析没什么了不起。机器学习程序不就是这么干的吗？它就是在运行使用（玩）的时候调整自己的参数或者结构，并且让自己变得越来越聪明的。

没错，可以这样说，具有学习功能的程序的确比传统意义上的人工智能程序更接近我们这里所理解的智能。然而，机器学习这门学科更多地是强调如何改进程序的算法和结构，使得在较短的学习周期之中达到用户的要求。也就是说，机器学习仍然是把图4-6所示的周期拆成图4-4的两个，而把重点放在如何设计/调试出一个程序使它能够在使用/玩的过程中表现更好。

然而，我们这里所说的人工智能，更形象地说应该是一种“吃交互的机器”。它把每一次玩家的交互都看作一种资源来更新自己的结构，而不再区分这是程序的调试还是玩家的使用。所以，我们要做的理论突破并不在于程序本身上，而是在于如何更深入地理解究竟什么是玩家“玩”这个动作，以及如何去利用这种资源

为了体现出“玩”这个动词不一样的特性，让我们来看一下Edward Castronova的研究工作。他早先是一名不起眼的经济学家，后来因为他给Everquest这款网络游戏计算了GDP而一举成名。他的计算大体思路如下：首先，他发现有很多玩家将自己的虚拟角色或者物品拿到eBay上拍卖，并且，每当虚拟角色升级一次就可以多卖出13美元。其次，他估算出玩家让自己的角色升一级大概需要51.4小时，那么平均每个小时每个玩家就能创造13/51.4≈0.25美元的价值。每天Everquest游戏中都有60381个玩家在线，那么，整个游戏在一年创造出的价值，也就是GDP就是年均60381*24*365*0.25≈1亿3千万美元。

Edward研究的重点就是将玩家所花的在线玩游戏的时间不看作一种消费，而是一种生产。这恰恰体现了我们所理解的：更本质的东西在于交互，因为它既可以被看作是使用/玩，也可以被看作是生产和创造。

那么，真正的智能程序应该是一款伟大的游戏，它能让所有的玩家在玩它的过程中为它补充营养！我们会在第4节继续讨论这个问题，但是在此之前，我们需要对上面讨论的这些东西尽量进行形式化表述。

构建模型

第2节从定性的角度讨论到如何将人工智能的问题转变为一个更本质的人-机交互的问题。我们知道，人机交互作为一个学科早已经问世。那么，为什么观察者理论又有什么作用呢？

然我们知道，现有的人机交互只是一门应用性的工程学科，它们更加关注的是如何设计人机交互界面，使得人可以更舒适地使用计算机。但是，这种看法导致了这门学科不可能成为一门基础性学科，它远远低估了人机交互问题的理论重要性。

本节就将为人-机交互提供一种相对简洁的数学模型——图灵机-观察者模型，进一步，我们将指出人机交互实际上应该属于一门非常基础性的学科，这是因为，我们可以把整个模型奠定在量子概率——这门诞生于基础物理中的数学加以描述，而可玩性则是一个非常基础性的概念。也许我这么做会让你反感：这个家伙是不是太扯了！非要把一些司空见惯的现象用那么玄乎的东西去描述。我的回答是，虽然现在有很多问题我还说不清楚，但是，将人-机交互、可玩性等等这些归结为基础科学问题是有充足的理由的，这些理由将在下一章进行更详细地讨论。

图灵机——观察者模型

我们的目的是要为人-机交互问题构建一套数学模型，那么这个模型就应该包括两个部分：计算机和玩家观察者。

我们知道，计算机可以用抽象的图灵机模型来刻画，但是，观察者如何刻画呢？毕竟人的情感、思维等等因素太复杂了，我们很难进行理论抽象。

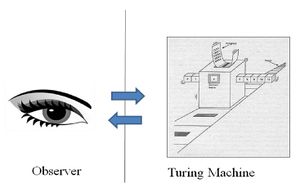
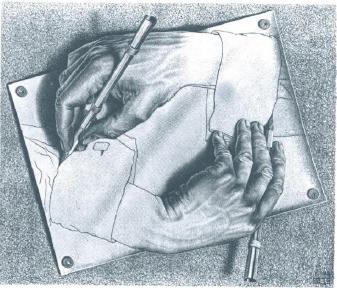
你站在人的角度看人，就会怎么看怎么复杂，永远也说不清楚。然而，正如我开篇给大家展示的那张黑白画，我们要学会从背景的角度看问题。对于人-机交互的问题，我们为什么不从计算机的角度看人呢？假如你是一台计算机，你根本不用关心使用者现在的心情如何、情绪怎样，因为玩家所有复杂的行为全部压缩成了有限的输入：键盘的敲击和鼠标的点击。所以说，这个人机交互界面就仿佛是一个大罩子，他把人类行为的种种复杂性都罩住了，只剩下赤裸裸的有限输入动作。

这样，我们就可以完成第一次抽象：任何一个人-机交互系统本质上都可以抽象为一个图灵机-观察者模型：

图4-7 图灵机观察者模型

我们知道，图0灵机是由一个读写头和纸带构成的。读写头是一个有限状态自动机，他有有限个状态以及指导其运作的程序。纸带由无限的方格构成，每个方格都有0、1两种状态。读写头在每个周期根据内部状态、当前纸带格内的内容以及程序来完成一步机械的动作，这个动作包括：改写当前纸带格的内容、控制纸带往左或者往右进行一步移动，改变读写头当前的内部状态。

那么，模型中的观察者其实也相当于一个读写头，也只能在纸带上某个固定的方格上进行信息的读写操作。但是观察者的写操作仅仅能够用0或者1来体现。这样，我们就把玩家复杂的心理状态映射成为足够简单的0、1操作。玩家就会跟图灵机在纸带这个公共的媒介下进行交互了。

玩家的选择与量子概率

然而，仅仅到这一步并没有完全解决问题。尽管玩家的动作已经变得异常简单：只剩下往纸带上写0、1了，但是究竟玩家怎么写，我们的模型并没有给出描述。

下面，我们将做出一个大胆而且关键的假设：玩家的0或者1的选择可以用量子概率来描述（有关量子概率参见小文：《当概率变成复数——量子概率简介》）。

具体来说，当玩家在纸带上写下0或者1之前，我们假设可以用一个量子态来描述玩家此时的心理状态：

[math]\displaystyle{ \psi=\alpha |0\rangle+|1\rangle }[/math]　　　　　　　　(1)

其中，[math]\displaystyle{ \alpha }[/math]和[math]\displaystyle{ \beta }[/math]都是复数，并且满足：[math]\displaystyle{ \alpha\cdot\alpha^*+\beta\cdot\beta^*=1 }[/math]

[math]\displaystyle{ \alpha^* }[/math]表示求复数[math]\displaystyle{ \alpha }[/math]的共轭，因此就是该复数模的平方。[math]\displaystyle{ \alpha }[/math]和[math]\displaystyle{ \beta }[/math]就都是概率幅（我称其为量子概率）。那么，玩家将会以[math]\displaystyle{ \alpha\cdot\alpha^* }[/math]的概率选择0，或者以[math]\displaystyle{ \beta\cdot\beta^* }[/math]的概率选择1。也就是说，我们把玩家的一次选择当成一次量子测量过程，使得玩家的心理状态由量子叠加态[math]\displaystyle{ \psi }[/math]瞬间坍缩为事实：一个具体的是0还是1的选择。

为什么可以用量子概率来对玩家的行为建模呢？原因有以下几点：

a.公式（1）表示的是一种量子叠加态

我们知道，在量子力学中，公式（1）所表示的状态是一种叠加态。其中|0>是希尔伯特空间中的一条直线，表示用户选择0这个状态，|1>则是与|0>垂直的另外一条直线，表示用户选择1这个状态。尽管玩家最终会以[math]\displaystyle{ \alpha\cdot\alpha^* }[/math]的概率选择0，以[math]\displaystyle{ \beta\cdot\beta^* }[/math]的概率选择1，但是叠加态（1）并不表示玩家会像一枚硬币一样随机地完成选择。在量子力学中，我们说一个电子处于左缝或者右缝的叠加态，实际上并不是说电子或者在左或者在右，而是说电子在此时此刻并不具备左缝还是右缝这个事实。

同样的道理，我们认为玩家在做出某一个选择之前，也是处于一种叠加态，那是因为选择0还是1并不是一个先天决定好的事情，那是在要求玩家做出0或者1的选择那一刹那才呈现出来的一种属性，而在测量之前，它什么都不是。所以，在测量之前（询问问题之前），玩家处于一种叠加态。

b.玩家的选择可以看作是玩家自己对自己心理状态的一次测量行为。
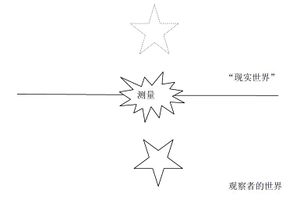
让我们回忆第3章的图3-1：

图3-1 测量与两个世界

这张图清楚地表达了，测量是发生在观察者与现实世界之间的界面中的，因此，测量不仅仅会把客观世界的量子物体转换成一种真实的存在，测量同样会把观察者内心的心理状态转变成一种现实，那么这种现实就是玩家所做出的选择！

换句话说，玩家的选择是一种测量，只不过这种测量与我们观察者测量电子的属性非常不同。这种测量是玩家这个观察者对他自身的思维状态的一种测量。在第二章我们已经表达了一个观点：量子力学不仅仅表达客观物理世界的规律，它也表达了人类内心世界的心理规律，在这里，我们把这个观点运用到了玩家的选择之上。

所以，在这个图灵机-观察者模型之中，我们看到了一种非常漂亮的对称关系，一种客观世界与人类心理世界的对称，这种对称由观察——即测量也就是玩家的选择——即玩连接到一起，更有意思的是，这种现实与心理世界之间的完美对称关系会被观察所打破！

c.文献和实验的支持
有相当的文献支持这种把人的决策甚至是自由意识描述为量子行为的做法（参见：Stapp H.P. Mindful Universe: Quantum Mechanics and the Participating Observer. Springer, 20907)。尤其是，人们在近期的一些行为学实验发现，人类的行为选择并不遵循传统的概率论解释，但是如果用量子概率体系进行描述，则可以解释很多行为试验中揭示出来的现象（参见：这里和这里）。

当然，将用户的选择用量子概率建模还仅仅是一个大胆的猜测，不过，我们完全可以通过行为试验的方式来对这个假设进行验证。

进一步，玩家从纸带上读取信息又可以建模成对用户心理量子态的酉变换。假如玩家当前的心理状态是[math]\displaystyle{ \Psi }[/math]，那么当他读入了一个纸带上的信息a(=0,1)，玩家的心理状态将发生变化：

[math]\displaystyle{ \Psi'=T\cdot \Psi }[/math]

其中T是一个酉变换，即满足：

[math]\displaystyle{ T \cdot T^{*} = I }[/math]

[math]\displaystyle{ T^{*} }[/math]表示对[math]\displaystyle{ T }[/math]取共轭转置。[math]\displaystyle{ I }[/math]是单位变换。所以玩家的心理状态从[math]\displaystyle{ \Psi }[/math]变到[math]\displaystyle{ \Psi' }[/math]就是一个酉变换（即向量的长度不变），状态向量在希尔伯特空间中旋转了一个抽象的复数角。当玩家读到信息之后，显然他的心理状态会发生一些变化，使得他会在下一次的选择中做出不同的决策。另一方面，由于玩家不用选择0或者1，因此，测量也就不会发生，复数概率幅也就不会坍缩成经典的概率，因此，读操作只能用酉变换来表示。

图灵机+玩家=宏量子

当我们用图灵机描述计算机，用量子概率来描述玩家的选择行为，那么整个图灵机-观察者模型就可以看作是一个宏观的量子系统了。

经典的图灵机计算理论关注的是问题的可求解性，经典的量子力学关注的是如何准确地描述微观粒子行为。而我们的玩家+图灵机模型不再关注这些问题，我们关心的是一种被称为测量网的抽象结构的宏观性质。

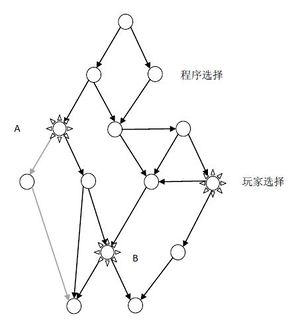
我们知道，计算机程序除了用图灵机表述以外还可以用流程图来表示。在图灵机-观察者模型中，玩家的选择也需要考虑进去，因此，流程图不再是普通意义上的流程图，而应该是包含了玩家选择的图，我们称这样的图为测量网，例如：

图4-9 测量网络

如图所示，从宏观上，人类玩家和机器之间的互动就可以构成这样一个我们称之为“测量网络”的模型，其中有两类节点，圆圈表示的节点就是由机器展开的节点，太阳表示的节点则是由玩家的选择展开的节点。每个节点对应的连线就相当于不同的选择路径。例如，从节点A展开两条路径对应的是玩家的两种不同的选择。同样，由计算机展开的节点也可以表示相应的程序判断，不同的判断可以导致不同的路径。

在模型中，由于图灵机的行为是我们事先确定好的，因此，用户的测量行为起到了相对重要的作用。我们知道，由于每个测量节点都可以用量子概率来表达，所以，这些测量节点导致了整个测量网络本质上是一个量子系统。

例如在A节点为根的子网络就是一个量子系统。在实施A点的测量之前，这个子系统处于一种量子叠加态之中。也就是说，程序会从灰色路径走还是从右边的黑色路径走是不确定的叠加态（或者说在测量之前，系统既可以走灰色路径又可以走黑色的路径）。当程序执行到了A点，那么玩家做出了向左走（0）或者向右走（1）的选择，于是量子叠加态便会在瞬间坍缩成确定的路径，例如用户最终选择了从A点向右走，那么左侧的灰色路径就会在瞬间消失，系统凝固到右侧黑色的路径上。

另外，在测量网络上，我们可以在不同的点设置不同的测量节点（由玩家展开的选择）。那么这些节点有可能构成前后不同的顺序，例如图中所示的A和B两个节点，显然A的选择有可能会影响B的选择。也就是说在A处的测量会影响到B处选择往左走还是往右走的量子叠加态。本质上说，A测量和B测量构成了相互影响的不兼容的测量（参见《当概率变成复数——量子概率简介》），正是由于不兼容测量对在这个测量网络上的大量存在，才使得整个系统必须用量子概率而非经典概率来描述。

那么，我们进行所谓的游戏设计（或者交互式程序的设计）本质上讲就是要设计出一个复杂的测量网络，设计者需要把测量节点（用户的选择）放置到网络中的不同位置上，从而导致网络整体呈现出完全不同的宏观属性，这正是测量网络最有趣的地方所在。

另一方面，对于整个测量网络来说，由于它本质上讲是一个量子系统，所以我们也可以把整个量子系统看作一台量子计算机。于是，我们甚至可以设计适当的测量网络，使得整个系统完成某种任务的量子计算。我们知道，经典的量子计算需要用到实际存在的量子比特（比如自旋粒子），由于量子资源的获取仍然比较困难，这就导致量子计算目前仍然处于理论阶段。但是，根据我们这里的分析，实际上一台计算机加上可以操作计算机系统的人就是一台可以执行量子计算的计算机。可以说，我们很容易就能获得廉价的量子计算。这也为后面我们将要提到的人类计算 Human Computation提供了可能性。

最后，我们知道，量子计算在很多方面已经超越了普通的图灵机，因此，整个玩家-图灵机系统就是一个可能超越图灵计算的系统。

最终的目标

虽然上文所述的测量网络有很多诱人的性质，但是，这个模型还仅仅停留在描述阶段。衡量一个模型成功与否的标准一个是它能够抽象而又不失一般性地描述真实系统，另一方面，就是它能够帮助我们把一些很难说清楚的性质从模型的角度刻画出来。

我们提到的图灵机-观察者模型以及测量网络模型也必须同时满足这两个标准。我们已经用图灵机-观者模型较好地描述了原始系统，那么，我们就要向下一个目标进军，也就是希望把一些本来说不清楚的定性概念，在该模型框架下给出定量的表述。尽管在这方面我们还没有取得任何实质性的进展，但是我们至少已经提出了非常清晰的目标。

玩家的目标——可玩性

首先，从人类玩家的角度来说，程序必须具备可玩性。说到一个程序是否好玩，我们马上会联想到很多因素，例如，游戏的画面是否好看，游戏的情节设计是否有趣，等等，似乎很难下手。但是，当我们抛开这些纷繁的复杂性，我们便会发现，其实可玩性的本质并不是由这些表面因素制约的，而是由游戏的规则决定的，而且这种规则也不一定非常复杂，可以是非常简单的。比如，我们都玩过的俄罗斯方块游戏，它的规则异常简单，但是可玩性却非常高，因此它是一个经典的游戏。

当我们从规则角度出发来考虑，也有很多因素制约着可玩性。例如，游戏的平衡性，游戏的难度等等。联系到我们这里的测量网络，我们提出另外一个大胆的猜想，也就是游戏本身的可玩性完全由测量网络的结构以及测量网络上面的各种参数决定的。这就为我们从网络的角度优化游戏的可玩性提供了可能。

我们举几个例子来说明这个问题。假如我们在一个测量网络中同一条路径上设置了过多的测量节点，这就意味着玩家做完了一个选择之后，马上就要做出下一个选择。那么，可以想象，玩家玩这样的游戏就会容易疲劳。反过来，如果测量节点在整个网络上安排得过于稀疏，则玩家的参与感就会下降。因此，测量节点密度显然就会影响整个程序的可玩性。我们便找到了一种可玩性与测量网络结构之间的联系。

另外，在测量网络中，有很多机器展开的节点。这些节点不允许玩家进行判断，但是可以允许玩家读到这些节点的信息。而在前一节中，我们已经提到，玩家读信息可以看作是对玩家的心理状态进行某种酉变换，这种酉变换显然又会影响到下一个测量节点的测量情况。而每个酉变换都至少由一个参数：变换的复数角来决定，所以，整个测量网络不仅仅跟结构有关，也与这些参数有关。例如，在俄罗斯方块中，尽管测量节点在每一个周期都相继展开，但是，由于游戏的每个不同状态显然会影响玩家的心理状态（例如方块在底端构成的堆积的平衡性），那么这些酉变换便决定了俄罗斯方块这个游戏是否好玩。

在本篇文章，我们不打算给出具体的刻画游戏可玩性的定量指标。但是，笔者隐约感到游戏的可玩性这个概念其实和一些非常深刻的物理概念有着各种各样的联系。我们知道，整个测量网络其实就是一个量子系统，而量子系统中存在着一种被称为“量子芝诺效应”的现象也许会跟可玩性有着深刻的联系。所谓的量子芝诺效应是说，如果观察者反复不停地测量一个量子系统，那么这种观测就会使得量子系统的变化速度减慢。比喻到游戏系统之中，也就是对玩家反复不断地测量（让玩家相继做出一系列连续的判断）就有可能使得玩家所经历的心理时间变慢。而这种现象很常见，当你全身心地投入地去玩一个游戏的时候，你通常会感觉到你的心理时间才过了10分钟，但是实际的时间已经过去了2个小时，那么这种现象很有可能可以用量子芝诺效应来解释。

但是我们前面举过例子，连续不断地测量也许会给玩家造成疲劳感，而不是心理时间变慢，这两者似乎存在着冲突。因此，在这里，也许我们需要重新定义时间这个概念，如果我们不用客观时间定义时间，而是用信息量的变化来定义时间，那么持续不断地测量的本质并不在于时间间隔的长短上，而是在于每两次测量的间隔中，由于测量所引起的信息量的变化。这就联系到了上一章所提到的熵概念。我们知道，任何封闭的系统都会熵增。翻译成观察者的语言也就是，一个封闭系统给观察者所带来的信息增量会越来越少。这样，我们设计的测量网络必须在每一次测量之中都尽量给玩家带来更多的信息，这样才会使得玩家产生很好的粘性。

进一步，可玩性其实跟我们通常所说的复杂性也有着千丝万缕的联系。我们都会有这样的感觉：当双眼盯着Media Player所显示出来的各种复杂的花纹的时候，我们会感觉这种动画有一种深深的吸引力，我们会不知不觉地将注意力完全投向那些花纹。因此，这些花纹似乎就可以称得上是“吃注意的机器”，因为你的注意力已被他深深地吸引。可玩性强的程序也有这种特点，因此，复杂性甚至可能就是在没有交互情况下的可玩性。

程序的目标——不断加深的虚拟层次

下面我们站在计算机程序的角度来讨论我们这个理论最终需要解决的问题目标。让我们再次回忆前面讨论过的计算机程序和两个观察者的问题。我们提到，这两个观察者分别是程序设计者和玩家，那么联系这些观察者和程序就需要完成如图4-4的程序开发周期：

这张图说明，玩家在使用/玩程序的时候如果发现了不如意的地方，就会反馈给程序的开发者，开发者就会对程序进行调试、修改甚至再开发，然后再次交付玩家去使用。然而，按照本文所提到的观点，其实，站在机器的角度来看，开发者和玩家是一回事儿，因为无论是程序的调试、修改还是玩家的使用/玩交互最终都体现为键盘或者鼠标上面输入的电信号。

所以，我们便可以把这个周期的不同阶段压缩成一个阶段：“玩”，如图4-6。

然而，读者也许会很纳闷，既然对于计算机来说开发/调试和使用/玩都是一回事儿，那为什么我们人类却感觉到这两个周期完全不同呢？至少没有哪一个玩家会义务给游戏开发生更改程序！

如果读者稍微懂一些计算机的基本原理，就会非常清楚，虽然程序员的代码修改和玩家的使用/玩最终都会体现为给计算机输入的电信号，但是这两类电信号却有着非常本质而重要的区别：程序员的电讯号输入给的是编译程序，这种编译程序在运行以后可以生成一个运行中的游戏程序；而玩家的电信号恰好输入给这个运行中的程序。

也许从图灵机和通用计算的角度会把这个问题说得更清楚一些：程序员的信号输入给的是一台通用图灵机（计算机编译系统），而玩家的信号输入的是这台通用图灵机上面的模拟的一个虚拟图灵机。这样，只要你这个程序中没有Bug，那么无论玩家如何输入各种具有破坏性的电信号，它都不可能对那个通用图灵机造成影响，因为这两个图灵机分别运行在不同的虚拟层次上。换句话说，玩家运行的那个程序是处在比程序员面对的那个程序更深的虚拟层次之上。

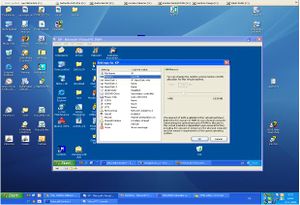
提到虚拟层次，也许大家会感觉到陌生，但实则这是一个非常常见的概念。比如大家都熟悉的故事里面的故事、电影中的电影等等。现在还有一些软件，就叫做虚拟机软件，例如下图所示：

图4-10 WinXP之中的WinXP

这张图就表示在一个WinXP系统之上运行的一个虚拟机，而在这台虚拟机上又跑了一个WinXP的程序。那么我们说跑在虚拟机上面的WinXP就比在真实计算机上运行的WinXP处于更深的虚拟层次。使用过虚拟机的朋友都会感觉到这种虚拟层次的好处有很多，比如说病毒对更深一层的程序的破坏完全不会影响到上一层。
那么，我们说，真正的智能程序是会把程序员的调试以及玩家的玩看作一种统一的资源，因此程序就会把玩的各种交互作为对自身程序的改进，从而更新自身。那么，从虚拟层次的角度来考虑也就意味着我们所说的智能程序其实已经把深一层次的输入信号（给程序的）和浅一层次的输入信号（给编译程序的）混淆了。这样，我们就有可能做到将玩家的输入作为一种资源来促使整个系统的结构改进。

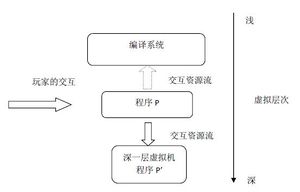
然而，对于一个真实的程序来说，我们如何做到这种层次的混淆呢？尤其是，如果我们已经按照传统的设计方式设计了两层程序，那么我们又怎么可能让程序对比它高一层次的程序进行修改呢？这样做的确很困难，但是存在着另外一种解决方案，那就是再构造一层更深的虚拟层，如下图：

图4-11 虚拟层次的构建

如图所示，我们将玩家的交互视做一种资源流，那么我们所要设计的程序P就要引导这股资源流（虚箭头）。传统的程序修改周期是引导这股资源流往更高的层次走（在编译系统中修改程序源代码，从而修改游戏程序），但是，这种修改通常是不可能由玩家作出的。但是，有可能程序P将玩家的交互流向另一个方向引领，这就是往更深的虚拟层引领。这样我们可以将利用玩家的各种交互在现有的程序P平台上构造出一台新的虚拟机，并且显然，我们可以把程序P自身在这台虚拟机上做一个拷贝形成P’（就好比在虚拟机上再跑一个同样版本的WinXP一样）。同时，让程序的输出表现是由更深一层的虚拟机P’实现的。由于玩家根本区分不出是哪一个层次给出的反馈信息，于是，玩家就会出现玩这个程序的同时已经更改了这个程序本身的假象。就这样，一个可以不断修改自身的程序就可以实现了！

如果说程序P是支持通用计算的，那么很显然它自身在更深层次的拷贝P'自然也支持，于是，我们还可以在P’之下再构造一个更深的虚拟层，并做出更深层次的拷贝P”，这个过程还可以继续重复下去……。

可想而知，这样一个可以不断构建自身、同时又可以修改自身的程序会表现出一些非常可贵的品质：它不需要程序员的修改，就可以自动从玩家的交互中不断修改自身，构建出越来越深的复杂性。难道我们不能称这样的程序是智能的吗？

问题难就难在，我们将如何让上面所表述的整个构建越来越深的虚拟层次这件事儿在玩家的交互过程中自动地发生？目前，我们不打算在这篇文章中给出具体的答案，但是笔者相信，从上面介绍的量子概率和测量网络方面有可能给出这个问题很好的解答。最终，我们期望能够提高玩家可玩性的测量网络也是一个可以不断构造更深虚拟层次的测量网络！

至此，我们看到的已经不再是与玩家分离的人工智能程序，也不再是没有计算机辅助的人类进化，我们看到的是一个人与机器协同进化的场景。在这个场景下，机器为人提供的是无限的可玩性，而人给机器则提供了进化以及不断构建虚拟层次的动力。而连接机器和人的纽带不是别的，正是观察（玩、交互）——这个非常重要的资源！

展望

本章从人工智能作为切入点，深入谈及了人机关系、人机结合的问题。我们首先提出人工智能这个目标应该被我们废问。所谓的废问并不是说人工智能永远不可能实现，而是说当我们对计算机的了解越来越深入，人工智能这个早期的目标：模拟人类的智力变得越来越不重要。正是在废问人工智能这个问题的同时，我们看到了另外一个真正重要的主题浮现：人机结合。也就是说，现在当务之急并不是要开发出大而全的人工智能程序，而是从理论上解决如何让人和计算机的交流更加顺畅！

正是在这废问的过程中，我们看到了另外一个被忽略的角色：坐在计算机面前的玩家观察者。这个角色虽然一直隐藏在阴暗的背景中，但在目前的社会中已经扮演着越来越重要的角色。不夸张地说，对于大多数的都市白领，每天就有将近1/3的时间是在面对各种各样的屏幕，无论是计算机、电视还是手机。看看有那么多用户将自己宝贵的时间花费在开心网，花费在QQ上，我们便知道，我们已经将大量的宝贵资源：人类的观察力、注意力浪费在这些程序之中。

人类计算

将大量在线的人类玩家视作一种宝贵的资源并不是新鲜事儿，美国卡耐基梅隆大学计算机系的学者Luis von Ann就认为当我们看到Internet上有那么多人将自己的时间浪费在无谓的打怪升级上，为什么不设计出巧妙的机制将这些浪费的资源重新利用上呢？于是，Luis开始设计出很多的游戏，让玩家在玩游戏的过程之中，不自觉地已经帮助工程师们解决了某类艰难的计算问题，Luis将这一研究领域称为“人类计算”（Human Computation）。

2008年9月，Luis在著名科学杂志《Science》第321卷发表了一篇题为：《reCAPTCHA: Human-Based Character Recognitionvia Web Security Measures》的文章就给出了一个具体的用人类计算解决实际问题的例子。

我们每个人都有过在网站上输入验证码的经验，计算机生成了一个模糊不清的图片，让你在其中认出隐藏的字母或者数字出来，从而让程序认为你是一个真正的人，而不是一个爬虫程序。我们知道，人类的模式识别能力远远高于人工智能程序。

那么，我们能不能反过来利用人类的这种能力，而帮助我们解决实际的模式识别问题呢？Google公司刚好要做一个庞大的工程，就是把大量的英文古文献数字化放在网站上。但是在数字化古文献的过程中，人们发现，有很多字符由于年代久远，很难被模式识别程序识别，所以，我们只能依靠人来完成这一任务。但是，由于不能识别的字符非常多，如果雇佣人来做，既需要花费大量的时间、金钱，又不能保证识别的正确性。

于是Luis突发奇想，我们为什么不把这些未识别的字符混在那些验证码之中，让Internet上的玩家帮助我们完成字符的识别呢？也就是说，用户在输入验证码的过程中，大部分验证码都是机器生成的字符，用户输入对了才允许进入，而也有偶然的机会，当玩家通过验证码之后，系统会用古书上未识别出来的字符跳出来要求玩家输入，这样，玩家们就帮助我们完成了识别工作。当然，为了保证输入的正确性，Luis还想出了各种办法来进行校验（例如同一个字符要两个以上的用户输入完全相同的内容之后才存储到数据库中）。因此，Luis巧妙地利用了人类的能力完成了由计算机程序很难解决的问题。

这个叫做reCAPTCHA的识别古书上的英文字符的程序仅仅是若干人类计算中的一例。Luis还设计出各种各样有趣的游戏巧妙地利用人类玩游戏这个资源来实现各种各样的计算。可以说，Luis是将用户的玩看作一种重要资源的实干家。

理论的突破

虽然我们的目标与Luis的人类计算有相通的地方，但是笔者更加关注的是人类计算背后是否存在着一般性的理论？

本文就试图为这样一种人-机交互现象提供一个理论分析框架。这个理论框架刚好和我们的观察者理论深深关联在一起。因此，本章所叙述的有关人工智能的问题恰恰是观察者理论的一个应用平台。

理论不能完全脱离实践，而本章所讨论的人-机交互问题恰恰是可以很方便地用实验的手段来研究、充实的。好在我们已经有了一些最基本的理论框架，尽管它还不完善，但是已经为我们进一步的实验工作提供了启发。

首先，在理论中，最关键的一点就是可以用量子概率来表示、建模人类玩家的选择。在《当概率变成复数》一文中，我们已经指出，首先，量子概率可以涵盖经典概率的所有内容，其次，量子概率与经典概率最大的不同就在于不可兼容测量对的存在。因此，如果人类玩家可以被量子概率建模，那么问题的关键就是如何设计出来一些人类选择试验使得这些实验结果很好揭示出量子概率而不是其他的理论可以很好地描述人类的选择行为。这种实验便成为我们这个理论首当其冲的问题。

其次，在本章叙述的观察者理论中，另外还有一个非常关键的概念，就是可玩性。然而，笔者目前还没能找出对可玩性完好的理论刻画。而直觉告诉我，可玩性这个问题实际上跟量子芝诺效应以及熵这些问题深刻联系在一起。那么，究竟这种联系是否存在？我们还需要做出更多的工作。

最后，我们也希望这套理论并不是一个空中楼阁，它应该能够指导实际工作，尤其是能够指导游戏设计师设计出可玩性很高，同时还能完成某种宏大的人类计算。这便需要有经验的游戏设计师提出更多的宝贵意见。

通向智能之路

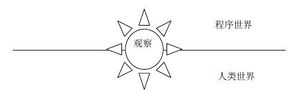
最后，让我们再次回到人工智能这个古老的问题上来。笔者为什么坚信将人工智能问题废问，同时指出人类观察者和计算机的结合才是真正重要的理论问题呢？说来很有意思，这主要来源于我在冥冥之中看到的一种非常漂亮的对称性，如下图所示：

图4-12 观察与两个世界

程序世界始终是和人类世界存在着某种美丽的对称关系的。那么，人工智能——这个非常不同的程序如果在程序世界中浮现，人类世界也必然会对称地发生某种巨大的变化，这种变化很可能就是人类最终真正进入了一个可玩性极高的虚拟世界。最后，我们用《哥德尔、埃舍尔、巴赫》这本奇书中最后一段对话《无插入赋格》的部分节选来结束本章。

注：螃蟹、巴比奇、阿基里斯、乌龟都是这篇对话中的人物。巴比奇号称自己发明了一个比自己聪明六倍的计算机（在文章中称为灵笨机）程序，这个程序叫做“图灵”，他于是领着螃蟹、阿基里斯等人走到了一台机器前面，这台机器安装了传声筒和电视摄像机作为输入，装了扬声器作为输出。
……
（巴比奇坐下来，调了一下座位。唾了一两下手指，仰头看了一下，然后手指慢慢地落到了键上……难忘的几分钟过后，他停止了对灵笨机猛烈的弹击，这时，每个人看去都如释负重。）
巴比奇：如果我没出太多错误的话，这台灵笨机能模拟智力比我高六倍的人，我已想好把它称作“阿兰·图灵”，这个图灵将因此——哦，我怎敢斗胆以己说为准——具备中等水平的智力。在此程序中我倾力以赋予阿兰·图灵六倍于我的音乐能力，虽然这一切都是通过严格的内部编码完成的。我不知道程序的这一部分产生的效果怎么样，但是，这个程序在运行时会使计算机发出一些噪音，这是这一程序唯一的缺憾。
图灵：没有噪音我照样行。无误地插入严格的内部编码可赋予一台计算机格外了不起的音乐才能。可我并不是一台计算机。
阿基里斯：我是不是听到了一个新的声音进入了我们的对话？它会是阿兰·图灵吗？他看起来几乎就是个真人！
（屏幕上出现了他们正坐在其中的那个房间的图案，上面有一张人脸看着他们。）
图灵：如果我没出太多错误的话，这台灵笨机能模拟智力比我高六倍的人，我已想好把它称作“查尔斯·巴比奇”，这个巴比奇将因此——哦，我怎敢斗胆以己说为准——具备中等水平的智力。在此程序中我倾力以赋予查尔斯·巴比奇六倍于我的音乐能力，虽然这一切都是通过严格的内部编码完成的。我不知道程序的这一部分产生的效果怎么样，但是，这个程序在运行时会使计算机发出一些噪音，这是这一程序唯一的缺憾。
阿基里斯：不，不，正好相反。你，阿兰·图灵，呆在灵笨机里，而查尔斯·巴比奇刚刚把你用程序编出来！我刚看着你被赋予生命，就在几分钟之前。我们知道你对我们说的每一句话都不过是某种自动装置的产物：某种受控的、无意识的反应。
图灵：绝无插入受控反映这种事，也没被赋予格式化的行为，我一直清清楚楚地我行我素。
阿基里斯：但我确信我看到了事情正像我所描述的那样发生了。
图灵：记忆经常玩弄些奇怪的把戏。请想想：我也可以同样认为你们只是在一分钟之前才赋予生命，你们记忆中的全部经验不过是某种别的存在物编好的程序，同现实中的事件毫无对应。
阿基里斯：但这是令人难以置信的。对我来说，没有什么比我的记忆更实在了。
图灵：没错儿。正像你对没有人一分钟之前才把你创造出来这一点深信不疑一样，我对我自己不是一分钟之前才被别人创造出来这点也深信不疑。我在你们这些最令人愉快的、虽然也许是过于易于相处的人们中度过了今宵，并作了一番即兴表演，显示了怎样将智力编成程序输入到灵笨机中。没有什么比这更实在了。但是，你们干吗不试试我的程序，而要跟我饶舌呢？来，可以向“查尔斯·巴比奇”问任何事！
阿基里斯：好吧，咱们就迁就迁就阿兰·图灵吧。嗯，巴先生：您是有自由意志呢，还是为那种事实上使您成为确定性的自动装置的潜在规律所支配呢？
巴比奇：当然是后者，这是无需争辩的。
螃蟹：啊哈！我早就猜测，智能机一旦建立，如果发现他们在对心灵、意识、自由意志诸如此类事物上的信念同人一样混乱、一样固执，那将是不足为怪的。现在，我的预言被证实了！
图灵：您瞧查尔斯·巴比奇有多混乱？
巴比奇：我希望，先生们，你们能原谅刚才图灵的话中那十分无理的口气。图灵已经变得有点比我预期的更好斗更好辩了。
螃蟹：天哪！图——巴之战的火焰愈烧愈烈，我们难道不能让他们冷静些吗？
巴比奇：我有个建议：阿兰·图灵和我可以到另一个房间去，而你们在这里的某个人可以通过往一台灵笨机键入一些话来远距离地质问我们。你们的问题分别传给我俩，我们可以不具名地键给你们我们各自的答案。你们在我们回到这个房间之前，将不会知道是谁打来的。这样，你们就可以不带偏见地判定我们中的哪一方是被程序编出来的，哪一个是程序设计者。
图灵：当然，这实际上是我的主意。但是为什么不让巴先生得到这一荣誉呢？因为，作为我所写下的一个程序，他会错以为这完全是他自己的发明哩。
巴比奇：我，是你写下的一个程序？我坚持认为，图先生，是你弄反了——正像过一会儿您自己的测验将揭示出的那样。
图灵：我的测验？请把它看作是您的吧。
巴比奇：我的测验？请把它看作是您的吧。
螃蟹：这个测验看来提出的正式时候，让我们马上开始吧。
（巴比奇走到门前，出去后又关上。同时，在灵笨机屏幕上，图灵走到一扇看去极为相像的门前，打开，出去后又关上。）
……
注：之后，螃蟹、阿基里斯和乌龟几个人开始对巴比奇和图灵进行图灵测试，他们提出了一大堆难以回答的问题，但是仍然不能区分哪个是程序，哪个是真人。
……
（正在他们谈话时，前庭的门打开了；与此同时，屏幕上同一扇门也打开了。屏幕上巴比奇穿门而过；同时，真人大小的图灵从真实的门中走了进来。）
巴比奇：这种图灵测验一无所获，所以我决定回来了。
图灵：这种巴比奇测验一无所获，所以我决定回来了。
阿基里斯：可刚才你是在灵笨机里的！怎么回事？巴比奇怎么跑到了灵笨机里，而图灵现在却成了真人呢？无端的颠倒！这一插曲加入得没道理，谈话被赋予了新格局。