路径 path

此词条暂由彩云小译翻译，未经人工整理和审校，带来阅读不便，请见谅。

For the family of graphs known as paths, see Path graph.

A three-dimensional hypercube graph showing a Hamiltonian path in red, and a longest induced path in bold black.

A three-dimensional hypercube graph showing a Hamiltonian path in red, and a longest induced path in bold black.

一个三维的[超立方体图表显示一个红色的哈密顿图，和一个黑色的最长诱导路径]

In graph theory, a path in a graph is a finite or infinite sequence of edges which joins a sequence of vertices which, by most definitions, are all distinct (and since the vertices are distinct, so are the edges). A directed path (sometimes called dipath) in a directed graph is a finite or infinite sequence of edges which joins a sequence of distinct vertices, but with the added restriction that the edges be all directed in the same direction.

In graph theory, a path in a graph is a finite or infinite sequence of edges which joins a sequence of vertices which, by most definitions, are all distinct (and since the vertices are distinct, so are the edges). A directed path (sometimes called dipath) in a directed graph is a finite or infinite sequence of edges which joins a sequence of distinct vertices, but with the added restriction that the edges be all directed in the same direction.

在图论中，图中的路是一个有限或无限的边序列，这些边连接着一系列顶点，这些顶点在大多数定义中都是不同的(因为顶点是不同的，所以边也是不同的)。有向图中的有向路(有时称为 dipath)是一个有限或无限的边序列，它连接一系列不同的顶点，但有附加的限制，即所有的边都朝向同一个方向。

Paths are fundamental concepts of graph theory, described in the introductory sections of most graph theory texts. See e.g. Bondy and Murty (1976), Gibbons (1985), or Diestel (2005). Korte et al. (1990) cover more advanced algorithmic topics concerning paths in graphs.

Paths are fundamental concepts of graph theory, described in the introductory sections of most graph theory texts. See e.g. Bondy and Murty (1976), Gibbons (1985), or Diestel (2005). Korte et al. (1990) cover more advanced algorithmic topics concerning paths in graphs.

路径是图论的基本概念，在大多数图论文本的导论部分都有描述。参见。邦迪和默蒂(1976) ，吉本斯(1985) ，或迪斯特尔(2005)。等人。(1990)涵盖了更多关于图中路径的高级算法主题。

Definitions

Walk, trail, path

right

对

• A walk is a finite or infinite sequence of edges which joins a sequence of vertices.模板:Sfn

Let G = (V, E, ϕ) be a graph. A finite walk is a sequence of edges (e₁, e₂, …, e_{n − 1}) for which there is a sequence of vertices (v₁, v₂, …, v_n) such that 模板:Nowrap beginϕ(e_i) = {v_i, v_{i + 1}}模板:Nowrap end for i = 1, 2, …, n − 1. (v₁, v₂, …, v_n) is the vertex sequence of the walk. This walk is closed if 模板:Nowrap beginv₁ = v_n模板:Nowrap end, and open else. An infinite walk is a sequence of edges of the same type described here, but with no first or last vertex, and a semi-infinite walk (or ray) has a first vertex but no last vertex.

Let  be a graph. A finite walk is a sequence of edges  for which there is a sequence of vertices  such that ϕ(ei) = {vi, vi + 1} for .  is the vertex sequence of the walk. This walk is  closed if v1 = vn, and open else. An infinite walk is a sequence of edges of the same type described here, but with no first or last vertex, and a semi-infinite walk (or ray) has a first vertex but no last vertex.

让我们做一个图。有限行走是一系列的边，其顶点序列(e < sub > i ) = { v < sub > i ，v < sub > i + 1 }。是行走的顶点序列。如果 v < sub > 1 = v < sub > n ，则此步行关闭，并打开 else。一个无限漫游是一系列的边，它们的类型与这里描述的相同，但是没有第一个顶点或最后一个顶点，而一个半无限漫游(或光线)有第一个顶点，但是没有最后一个顶点。

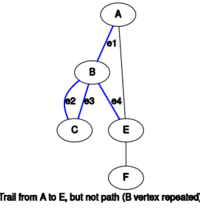
• A trail is a walk in which all edges are distinct.模板:Sfn

• A path is a trail in which all vertices (and therefore also all edges) are distinct.模板:Sfn

If w = (e₁, e₂, …, e_{n − 1}) is a finite walk with vertex sequence (v₁, v₂, …, v_n) then w is said to be a walk from v₁ to v_n. Similarly for a trail or a path. If there is a finite walk between two distinct vertices then there is also a finite trail and a finite path between them.

If is a finite walk with vertex sequence then w is said to be a walk from v₁ to v_n. Similarly for a trail or a path. If there is a finite walk between two distinct vertices then there is also a finite trail and a finite path between them.

如果是有顶点序列的有限步行，那么 w 就是从 v < sub > 1 到 v < sub > n 的步行。同样，对于一条小路或者一条小径也是如此。如果在两个不同的顶点之间有一个有限的行走，那么在它们之间也有一个有限的轨迹和一个有限的路径。

Some authors do not require that all vertices of a path be distinct and instead use the term simple path to refer to such a path.

Some authors do not require that all vertices of a path be distinct and instead use the term simple path to refer to such a path.

有些作者并不要求路径的所有顶点都是不同的，而是使用术语简单路径来指代这样的路径。

A weighted graph associates a value (weight) with every edge in the graph. The weight of a walk (or trail or path) in a weighted graph is the sum of the weights of the traversed edges. Sometimes the words cost or length are used instead of weight.

A weighted graph associates a value (weight) with every edge in the graph. The weight of a walk (or trail or path) in a weighted graph is the sum of the weights of the traversed edges. Sometimes the words cost or length are used instead of weight.

一个加权图将一个值(权)与图中的每条边相关联。一个加权图中的行走(或轨迹或路径)的权是所有行走边的权之和。有时，“成本”或“长度”这两个词用来代替“重量”。

Directed walk, trail, path

• A directed walk is a finite or infinite sequence of edges directed in the same direction which joins a sequence of vertices.模板:Sfn

Let G = (V, E, ϕ) be a directed graph. A finite directed walk is a sequence of edges (e₁, e₂, …, e_{n − 1}) for which there is a sequence of vertices (v₁, v₂, …, v_n) such that ϕ(e_i) = (v_i, v_{i + 1}) for i = 1, 2, …, n − 1. (v₁, v₂, …, v_n) is the vertex sequence of the directed walk. An infinite directed walk is a sequence of edges of the same type described here, but with no first or last vertex, and a semi-infinite directed walk (or ray) has a first vertex but no last vertex.

Let  be a directed graph. A finite directed walk is a sequence of edges  for which there is a sequence of vertices  such that  for .  is the vertex sequence of the directed walk. An infinite directed walk is a sequence of edges of the same type described here, but with no first or last vertex, and a semi-infinite directed walk (or ray) has a first vertex but no last vertex.

设是一个有向图。有限有向行走是一系列的边，对于这些边，存在一系列的顶点。是有向行走的顶点序列。无限有向行走是一个边序列，其类型与本文描述的相同，但没有第一个顶点或最后一个顶点，而半无限有向行走(或射线)有第一个顶点，但没有最后一个顶点。

• A directed trail is a directed walk in which all edges are distinct.模板:Sfn

• A directed path is a directed trail in which all vertices are distinct.模板:Sfn

If w = (e₁, e₂, …, e_{n − 1}) is a finite directed walk with vertex sequence (v₁, v₂, …, v_n) then w is said to be a walk from v₁ to v_n. Similarly for a directed trail or a path. If there is a finite directed walk between two distinct vertices then there is also a finite directed trail and a finite directed path between them.

If is a finite directed walk with vertex sequence then w is said to be a walk from v₁ to v_n. Similarly for a directed trail or a path. If there is a finite directed walk between two distinct vertices then there is also a finite directed trail and a finite directed path between them.

如果是一个顶点序列有限的有向步行，那么 w 就是从 v < sub > 1 到 v < sub > n 的步行。同样，对于有向轨迹或路径也是如此。如果在两个不同的顶点之间存在有限有向游动，那么在它们之间也存在有限有向轨迹和有限有向路。

Some authors do not require that all vertices of a directed path be distinct and instead use the term simple directed path to refer to such a directed path.

Some authors do not require that all vertices of a directed path be distinct and instead use the term simple directed path to refer to such a directed path.

有些作者并不要求有向路的所有顶点都是不同的，而是用简单有向路这个术语来表示这样一个有向路。

A weighted directed graph associates a value (weight) with every edge in the directed graph. The weight of a directed walk (or trail or path) in a weighted directed graph is the sum of the weights of the traversed edges. Sometimes the words cost or length are used instead of weight.

A weighted directed graph associates a value (weight) with every edge in the directed graph. The weight of a directed walk (or trail or path) in a weighted directed graph is the sum of the weights of the traversed edges. Sometimes the words cost or length are used instead of weight.

一个加权有向图将一个值(权)与有向图中的每条边相关联。加权有向图中有向行走(或路径)的权是有向行走边权的和。有时，“成本”或“长度”这两个词用来代替“重量”。

Examples

• A graph is connected if there are paths containing each pair of vertices.

• A directed graph is strongly connected if there are oppositely oriented directed paths containing each pair of vertices.

• A path such that no graph edges connect two nonconsecutive path vertices is called an induced path.

• A path that includes every vertex of the graph is known as a Hamiltonian path.

• Two paths are vertex-independent (alternatively, internally vertex-disjoint) if they do not have any internal vertex in common. Similarly, two paths are edge-independent (or edge-disjoint) if they do not have any internal edge in common. Two internally vertex-disjoint paths are edge-disjoint, but the converse is not necessarily true.

• The distance between two vertices in a graph is the length of a shortest path between them, if one exists, and otherwise the distance is infinity.

• The diameter of a connected graph is the largest distance (defined above) between pairs of vertices of the graph.

Finding paths

Several algorithms exist to find shortest and longest paths in graphs, with the important distinction that the former problem is computationally much easier than the latter.

Several algorithms exist to find shortest and longest paths in graphs, with the important distinction that the former problem is computationally much easier than the latter.

图的最短路径和最长路径的求解有几种算法，但前者的计算比后者简单得多，这是一个重要区别。

Dijkstra's algorithm produces a list of shortest paths from a source vertex to every other vertex in directed and undirected graphs with non-negative edge weights (or no edge weights), whilst the Bellman–Ford algorithm can be applied to directed graphs with negative edge weights. The Floyd–Warshall algorithm can be used to find the shortest paths between all pairs of vertices in weighted directed graphs.

Dijkstra's algorithm produces a list of shortest paths from a source vertex to every other vertex in directed and undirected graphs with non-negative edge weights (or no edge weights), whilst the Bellman–Ford algorithm can be applied to directed graphs with negative edge weights. The Floyd–Warshall algorithm can be used to find the shortest paths between all pairs of vertices in weighted directed graphs.

Dijkstra 算法产生了一个从源顶点到无向有向图中每个顶点的最短路径列表，而 Bellman-Ford 算法可以应用于具有负边权的有向图。利用 Floyd-Warshall 算法可以求出加权有向图中所有顶点对之间的最短路径。

See also

• Glossary of graph theory

• Path graph

• Polygonal chain

• Shortest path problem

• Longest path problem

• Dijkstra's algorithm

• Bellman–Ford algorithm

• Floyd–Warshall algorithm

• Self-avoiding walk

• Shortest-path graph

References

• Bender, Edward A.; Williamson, S. Gill (2010). Lists, Decisions and Graphs. With an Introduction to Probability. https://books.google.fr/books?id=vaXv_yhefG8C. 

• Bondy, J. A.; Murty, U. S. R. (1976). Graph Theory with Applications. North Holland. p. 12-21. ISBN 0-444-19451-7. https://archive.org/details/graphtheorywitha0000bond/page/12. 

• Diestel, Reinhard (2005). Graph Theory. Springer-Verlag. p. 6-9. ISBN 3-540-26182-6. http://www.math.uni-hamburg.de/home/diestel/books/graph.theory/. 

• Gibbons, A. (1985). Algorithmic Graph Theory. Cambridge University Press. p. 5-6. ISBN 0-521-28881-9. 

• Korte, Bernhard; Lovász, László; Prömel, Hans Jürgen; Schrijver, Alexander (1990). Paths, Flows, and VLSI-Layout. Springer-Verlag. ISBN 0-387-52685-4. https://archive.org/details/pathsflowsvlsila0000unse. 

Category:Graph theory objects

范畴: 图论对象

Category:Graph connectivity

类别: 图形连接性

This page was moved from wikipedia:en:Path (graph theory). Its edit history can be viewed at 路径/edithistory