枢纽
此词条暂由彩云小译翻译,未经人工整理和审校,带来阅读不便,请见谅。
In network science, a hub is a node with a number of links that greatly exceeds the average. Emergence of hubs is a consequence of a scale-free property of networks.[1] While hubs cannot be observed in a random network, they are expected to emerge in scale-free networks. The uprise of hubs in scale-free networks is associated with power-law distribution. Hubs have a significant impact on the network topology. Hubs can be found in many real networks, such as Brain Network or Internet.
In network science, a hub is a node with a number of links that greatly exceeds the average. Emergence of hubs is a consequence of a scale-free property of networks. While hubs cannot be observed in a random network, they are expected to emerge in scale-free networks. The uprise of hubs in scale-free networks is associated with power-law distribution. Hubs have a significant impact on the network topology. Hubs can be found in many real networks, such as Brain Network or Internet.
在网络科学中,集线器是一个节点,它的链接数量大大超过了平均值。集线器的出现是网络无标度特性的结果。虽然在随机网络中不能观察到集线器,但是它们可能出现在无标度网络中。无标度网络中节点的起伏与幂律分布有关。中心对网络拓扑有着重要的影响。集线器可以在很多真实的网络中找到,比如大脑网络或者互联网。
right
对
A hub is a component of a network with a high-degree node. Hubs have a significantly larger number of links in comparison with other nodes in the network. The number of links (degrees) for a hub in a scale-free network is much higher than for the biggest node in a random network, keeping the size N of the network and average degree <k> constant. The existence of hubs is the biggest difference between random networks and scale-free networks. In random networks, the degree k is comparable for every node; it is therefore not possible for hubs to emerge. In scale-free networks, a few nodes (hubs) have a high degree k while the other nodes have a small number of links.
rightA hub is a component of a network with a high-degree node. Hubs have a significantly larger number of links in comparison with other nodes in the network. The number of links (degrees) for a hub in a scale-free network is much higher than for the biggest node in a random network, keeping the size N of the network and average degree <k> constant. The existence of hubs is the biggest difference between random networks and scale-free networks. In random networks, the degree k is comparable for every node; it is therefore not possible for hubs to emerge. In scale-free networks, a few nodes (hubs) have a high degree k while the other nodes have a small number of links.
rightA hub 是具有高度节点的网络的一个组件。与网络中的其他节点相比,集线器的链路数量要大得多。无尺度网络中枢纽的链路数(度)远远高于随机网络中最大的节点,保持网络的大小 n 和平均度 < k > 不变。枢纽的存在是随机网络和无标度网络的最大区别。在随机网络中,每个节点的度 k 是可比的,因此不可能出现集线器。在无标度网络中,少数节点(集线器)具有高度 k,而其他节点只有少量链路。
Emergence
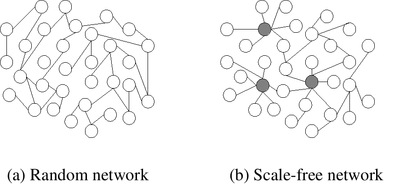
Random network (a) and scale-free network (b). In the scale-free network, the larger hubs are highlighted.
随机网络(a)和无尺度网络(b)。在无尺度网络中,较大的枢纽被突出显示。
Emergence of hubs can be explained by the difference between scale-free networks and random networks. Scale-free networks (Barabási–Albert model) are different from random networks (Erdős–Rényi model) in two aspects: (a) growth, (b) preferential attachment.引用错误:没有找到与</ref>对应的<ref>标签
|arxiv = cond-mat/0106096 }}</ref>
|arxiv = cond-mat/0106096 }}</ref>
- (a) Scale-free networks assume a continuous growth of the number of nodes N, compared to random networks which assume a fixed number of nodes. In scale-free networks the degree of the largest hub rises polynomially with the size of the network. Therefore, the degree of a hub can be high in a scale-free network. In random networks the degree of the largest node rises logaritmically (or slower) with N, thus the hub number will be small even in a very large network.
- (b) A new node in a scale-free network has a tendency to link to a node with a higher degree, compared to a new node in a random network which links itself to a random node. This process is called preferential attachment. The tendency of a new node to link to a node with a high degree k is characterized by power-law distribution (also known as rich-gets-richer process). This idea was introduced by Vilfredo Pareto and it explained why a small percentage of the population earns most of the money. This process is present in networks as well, for example 80 percent of web links point to 15 percent of webpages. The emergence of scale-free networks is not typical only of networks created by human action, but also of such networks as metabolic networks or illness networks.[2] This phenomenon may be explained by the example of hubs on the World Wide Web such as Facebook or Google. These webpages are very well known and therefore the tendency of other webpages pointing to them is much higher than linking to random small webpages.
The mathematical explanation for Barabási–Albert model:
The mathematical explanation for Barabási–Albert model:
Barabási-Albert 模型的数学解释:
The steps of the growth of the network according to the Barabasi–Albert model ([math]\displaystyle{ m_0=m=2 }[/math])
根据 Barabasi-Albert 模型(< math > m _ 0 = m = 2 </math >)分析了网络生长的步骤
The network begins with an initial connected network of [math]\displaystyle{ m_0 }[/math] nodes.
The network begins with an initial connected network of [math]\displaystyle{ m_0 }[/math] nodes.
这个网络从一个初始的连接网络开始,这个网络由 < math > m _ 0 </math > 节点组成。
New nodes are added to the network one at a time. Each new node is connected to [math]\displaystyle{ m \le m_0 }[/math] existing nodes with a probability that is proportional to the number of links that the existing nodes already have. Formally, the probability [math]\displaystyle{ p_i }[/math] that the new node is connected to node [math]\displaystyle{ i }[/math] is[3]
New nodes are added to the network one at a time. Each new node is connected to [math]\displaystyle{ m \le m_0 }[/math] existing nodes with a probability that is proportional to the number of links that the existing nodes already have. Formally, the probability [math]\displaystyle{ p_i }[/math] that the new node is connected to node [math]\displaystyle{ i }[/math] is
每次向网络添加一个新节点。每个新的节点都被连接到 < math > m le m _ 0 </math > 现有的节点,其概率与现有节点已经拥有的链接数量成正比。形式上,新节点与节点 < math > i </math > 相连的概率是
- [math]\displaystyle{ p_i = \frac{k_i}{\sum_j k_j}, }[/math]
[math]\displaystyle{ p_i = \frac{k_i}{\sum_j k_j}, }[/math]
[数学][数学]
where [math]\displaystyle{ k_i }[/math] is the degree of the node [math]\displaystyle{ i }[/math] and the sum is taken over all pre-existing nodes [math]\displaystyle{ j }[/math] (i.e. the denominator results in twice the current number of edges in the network).
where [math]\displaystyle{ k_i }[/math] is the degree of the node [math]\displaystyle{ i }[/math] and the sum is taken over all pre-existing nodes [math]\displaystyle{ j }[/math] (i.e. the denominator results in twice the current number of edges in the network).
其中 < math > k _ i </math > 是节点的度数 < math > i </math > ,这个和取自所有预先存在的节点 < math > j </math > 。分母的结果是当前网络中边的两倍)。
Emergence of hubs in networks is also related to time. In scale-free networks, nodes which emerged earlier have a higher chance of becoming a hub than latecomers. This phenomenon is called first-mover advantage and it explains why some nodes become hubs and some do not. However, in a real network, the time of emergence is not the only factor that influences the size of the hub. For example, Facebook emerged 8 years later after Google became the largest hub on the World Wide Web and yet in 2011 Facebook became the largest hub of WWW. Therefore, in real networks the growth and the size of a hub depends also on various attributes such as popularity, quality or the aging of a node.
Emergence of hubs in networks is also related to time. In scale-free networks, nodes which emerged earlier have a higher chance of becoming a hub than latecomers. This phenomenon is called first-mover advantage and it explains why some nodes become hubs and some do not. However, in a real network, the time of emergence is not the only factor that influences the size of the hub. For example, Facebook emerged 8 years later after Google became the largest hub on the World Wide Web and yet in 2011 Facebook became the largest hub of WWW. Therefore, in real networks the growth and the size of a hub depends also on various attributes such as popularity, quality or the aging of a node.
网络中集线器的出现也与时间有关。在无标度网络中,较早出现的节点比后来者更有可能成为枢纽。这种现象被称为先发优势,它解释了为什么一些节点成为枢纽,而一些没有。然而,在一个真实的网络中,出现的时间并不是影响枢纽规模的唯一因素。例如,在谷歌成为全球最大的互联网中心8年后,Facebook 出现了,然而在2011年,Facebook 成为了全球最大的互联网中心。因此,在实际网络中,枢纽的增长和规模也取决于各种属性,如节点的流行程度、质量或老化程度。
Attributes
There are several attributes of Hubs in a Scale-Free Network
There are several attributes of Hubs in a Scale-Free Network
无尺度网络中心有几个属性
Shortening the path lengths in a network
The more observable hubs are in a network, the more they shrink distances between nodes. In a scale-free network, hubs serve as bridges between the small degree nodes.[4] Since the distance of two random nodes in a scale-free network is small, we refer to scale-free networks as "small" or "ultra small". While the difference between path distance in a very small network may not be noticeable, the difference in the path distance between a large random network and a scale-free network is remarkable.
The more observable hubs are in a network, the more they shrink distances between nodes. In a scale-free network, hubs serve as bridges between the small degree nodes. Since the distance of two random nodes in a scale-free network is small, we refer to scale-free networks as "small" or "ultra small". While the difference between path distance in a very small network may not be noticeable, the difference in the path distance between a large random network and a scale-free network is remarkable.
网络中可观察到的集线器越多,节点之间的距离就越小。在无尺度网络中,枢纽是连接度小节点的桥梁。由于无尺度网络中随机节点间的距离很小,我们称无标度网络为“小”或“超小”网络。虽然在一个非常小的网络中,路径距离的差异可能并不明显,但是在大型随机网络和无尺度网络网络中,路径距离的差异是显著的。
Average path length in scale-free networks:
Average path length in scale-free networks:
无标度网络中的平均路径长度:
[math]\displaystyle{ \ell\sim\frac{\ln N}{\ln \ln N}. }[/math]
[math]\displaystyle{ \ell\sim\frac{\ln N}{\ln \ln N}. }[/math]
[数学] . [数学]
Aging of hubs (nodes)
The phenomenon present in real networks, when older hubs are shadowed in a network. This phenomenon is responsible for changes in evolution and topology of networks.[5] The example of aging phenomenon may be the case of Facebook overtaking the position of the largest hub on the Web, Google(which was the largest node since 2000).[citation needed]
The phenomenon present in real networks, when older hubs are shadowed in a network. This phenomenon is responsible for changes in evolution and topology of networks. The example of aging phenomenon may be the case of Facebook overtaking the position of the largest hub on the Web, Google(which was the largest node since 2000).
在真实网络中出现的现象,当旧的集线器被隐藏在网络中时。这种现象导致了网络演化和拓扑结构的变化。老龄化现象的例子可能是 Facebook 超越了网络中最大的中心 Google (自2000年以来最大的节点)的位置。
Robustness and Attack Tolerance
During the random failure of nodes or targeted attack hubs are key components of the network. During the random failure of nodes in network hubs are responsible for exceptional robustness of network.引用错误:没有找到与</ref>对应的<ref>标签 The chance that a random failure would delete the hub is very small, because hubs coexists with a large number of small degree nodes. The removal of small degree nodes does not have a large effect on integrity of network. Even though the random removal would hit the hub, the chance of fragmantation of network is very small because the remaining hubs would hold the network together. In this case, hubs are the strength of a scale-free networks.
</ref> The chance that a random failure would delete the hub is very small, because hubs coexists with a large number of small degree nodes. The removal of small degree nodes does not have a large effect on integrity of network. Even though the random removal would hit the hub, the chance of fragmantation of network is very small because the remaining hubs would hold the network together. In this case, hubs are the strength of a scale-free networks.
</ref > 随机故障删除 hub 的可能性非常小,因为 hub 与大量小度节点共存。去除小节点对网络的完整性影响不大。即使随机删除会到达枢纽,网络碎片化的可能性非常小,因为剩余的枢纽将把网络连接在一起。在这种情况下,集线器就是无标度网络的力量。
During a targeted attack on hubs, the integrity of a network will fall apart relatively fast. Since small nodes are predominantly linked to hubs, the targeted attack on the largest hubs results in destroys the network in a short period of time. The financial market meltdown in 2008 is an example of such a network failure, when bankruptcy of the largest players (hubs) led to a continuous breakdown of the whole system.[6] On the other hand, it may have a positive effect when removing hubs in a terrorist network; targeted node deletion may destroy the whole terrorist group. The attack tolerance of a network may be increased by connecting its peripheral nodes, however it requires to double the number of links.
During a targeted attack on hubs, the integrity of a network will fall apart relatively fast. Since small nodes are predominantly linked to hubs, the targeted attack on the largest hubs results in destroys the network in a short period of time. The financial market meltdown in 2008 is an example of such a network failure, when bankruptcy of the largest players (hubs) led to a continuous breakdown of the whole system. On the other hand, it may have a positive effect when removing hubs in a terrorist network; targeted node deletion may destroy the whole terrorist group. The attack tolerance of a network may be increased by connecting its peripheral nodes, however it requires to double the number of links.
在针对集线器的攻击中,网络的完整性会相对较快地崩溃。由于小节点主要与集线器相连,对最大集线器的有针对性攻击会在短时间内摧毁网络。2008年的金融市场崩溃就是这种网络失灵的一个例子,当时最大的参与者(枢纽)的破产导致了整个系统的持续崩溃。另一方面,删除恐怖主义网络中的枢纽可能会产生积极的影响,删除目标节点可能会摧毁整个恐怖组织。一个网络的攻击容忍度可以通过连接它的外围节点来增加,但是它需要将链路的数量增加一倍。
Degree correlation
The perfect degree correlation means that each degree-k node is connected only to the same degree-k nodes. Such connectivity of nodes decide the topology of networks, which has an effect on robustness of network, the attribute discussed above. If the number of links between the hubs is the same as would be expected by chance, we refer to this network as Neutral Network. If hubs tend to connected to each other while avoiding linking to small-degree nodes we refer to this network as Assortative Network. This network is relatively resistant against attacks, because hubs form a core group, which is more reduntant against hub removal. If hubs avoid connecting to each other while linking to small-degree nodes, we refer to this network as Disassortative Network. This network has a hub-and-spoke character. Therefore, if we remove the hub in this type of network, it may damage or destroy the whole network.
The perfect degree correlation means that each degree-k node is connected only to the same degree-k nodes. Such connectivity of nodes decide the topology of networks, which has an effect on robustness of network, the attribute discussed above. If the number of links between the hubs is the same as would be expected by chance, we refer to this network as Neutral Network. If hubs tend to connected to each other while avoiding linking to small-degree nodes we refer to this network as Assortative Network. This network is relatively resistant against attacks, because hubs form a core group, which is more reduntant against hub removal. If hubs avoid connecting to each other while linking to small-degree nodes, we refer to this network as Disassortative Network. This network has a hub-and-spoke character. Therefore, if we remove the hub in this type of network, it may damage or destroy the whole network.
完全度相关意味着每个度 k 节点只连接到相同的度 k 节点。节点之间的这种连通性决定了网络的拓扑结构,从而影响了网络的鲁棒性。如果集线器之间的链接数量与偶然预期的相同,我们将这个网络称为中立网络。如果集线器倾向于相互连接,同时避免链接到小度的节点,我们将这个网络称为选型网络。这个网络对攻击的抵抗力相对较强,因为集线器形成了一个核心组,这个核心组对于集线器的移除更有抵抗力。如果集线器避免相互连接,同时连接到小度的节点,我们将这个网络称为反相称网络。这个网络具有中心辐射特征。因此,如果我们删除这种类型的网络中的集线器,它可能会破坏或摧毁整个网络。
Spreading phenomenon
The hubs are also responsible for effective spreading of material on network. In an analysis of disease spreading or information flow, hubs are referred to as super-spreaders. Super-spreaders may have a positive impact, such as effective information flow, but also devastating in a case of epidemic spreading such as H1N1 or AIDS. The mathematical models such as model of H1H1 Epidemic prediction [7] may allow us to predict the spread of diseases based on human mobility networks, infectiousness, or social interactions among humans. Hubs are also important in the eradication of disease. In a scale-free network hubs are most likely to be infected, because of the large number of connections they have. After the hub is infected, it broadcasts the disease to the nodes it is linked to. Therefore, the selective immunization of hubs may be the cost-effective strategy in eradication of spreading disease.
The hubs are also responsible for effective spreading of material on network. In an analysis of disease spreading or information flow, hubs are referred to as super-spreaders. Super-spreaders may have a positive impact, such as effective information flow, but also devastating in a case of epidemic spreading such as H1N1 or AIDS. The mathematical models such as model of H1H1 Epidemic prediction may allow us to predict the spread of diseases based on human mobility networks, infectiousness, or social interactions among humans. Hubs are also important in the eradication of disease. In a scale-free network hubs are most likely to be infected, because of the large number of connections they have. After the hub is infected, it broadcasts the disease to the nodes it is linked to. Therefore, the selective immunization of hubs may be the cost-effective strategy in eradication of spreading disease.
这些中心还负责有效地在网络上传播材料。在疾病传播或信息流的分析中,枢纽被称为超级传播者。超级传播者可能会产生积极的影响,如有效的信息流动,但在 H1N1或艾滋病等流行病传播的情况下也会产生毁灭性的影响。数学模型,如 H1H1流行病预测模型,可以让我们预测疾病的传播,基于人类流动网络,传染性,或人与人之间的社会互动。在根除疾病方面,中心也很重要。在无尺度网络集线器是最有可能被感染的,因为他们有大量的连接。在集线器被感染后,它将疾病广播到它所链接的节点。因此,选择性免疫中枢可能是消灭传播性疾病的成本效益策略。
References
- ↑ Barabási, Albert-László. Network Science: Graph Theory., p. 27
- ↑ Barabási, Albert-László. Network Science: The Scale-Free Property., p. 8.[1]
- ↑ 引用错误:无效
<ref>标签;未给name属性为RMP的引用提供文字 - ↑ Barabási, Albert-László. Network Science: The Scale-Free Property., p. 23.[2]
- ↑ Barabási, Albert-László. Network Science: Evolving Networks., p. 3
- ↑ S. V. Buldyrev; R. Parshani; G. Paul; H. E. Stanley; S. Havlin (2010). "Catastrophic cascade of failures in interdependent networks". Nature. 464 (7291): 1025–28. arXiv:1012.0206. Bibcode:2010Natur.464.1025B. doi:10.1038/nature08932. PMID 20393559.
- ↑ Balcan, Duygu; Hu, Hao; Goncalves, Bruno; Bajardi, Paolo; Poletto, Chiara; Ramasco, Jose J.; Paolotti, Daniela; Perra, Nicola; Tizzoni, Michele; Van den Broeck, Wouter; Colizza, Vittoria; Vespignani, Alessandro (14 September 2009). "Seasonal transmission potential and activity peaks of the new influenza A(H1N1): a Monte Carlo likelihood analysis based on human mobility". BMC Medicine. 7 (45): 29. arXiv:0909.2417. doi:10.1186/1741-7015-7-45. PMC 2755471. PMID 19744314.
Category:Network theory
范畴: 网络理论
This page was moved from wikipedia:en:Hub (network science). Its edit history can be viewed at 枢纽节点/edithistory