层次聚类
此词条暂由彩云小译翻译,未经人工整理和审校,带来阅读不便,请见谅。
In data mining and statistics, hierarchical clustering (also called hierarchical cluster analysis or HCA) is a method of cluster analysis which seeks to build a hierarchy of clusters. Strategies for hierarchical clustering generally fall into two types:[1]
In data mining and statistics, hierarchical clustering (also called hierarchical cluster analysis or HCA) is a method of cluster analysis which seeks to build a hierarchy of clusters. Strategies for hierarchical clustering generally fall into two types:
在数据挖掘和统计学中,层次聚类(也称为层次数据聚类聚类或 HCA)是一种数据聚类聚类的方法,它寻求建立一个集群层次结构。层次聚类的策略通常分为两类:
- Agglomerative: This is a "bottom-up" approach: each observation starts in its own cluster, and pairs of clusters are merged as one moves up the hierarchy.
- Divisive: This is a "top-down" approach: all observations start in one cluster, and splits are performed recursively as one moves down the hierarchy.
In general, the merges and splits are determined in a greedy manner. The results of hierarchical clustering引用错误:没有找到与</ref>对应的<ref>标签 are usually presented in a dendrogram.
chapter=Chapter 8: Hierarchical Clustering | url=https://www.springer.com/gp/book/9783319219028 |chapter-url=https://www.researchgate.net/publication/314700681 }}</ref> are usually presented in a dendrogram.
第八章: 层次聚类 | url = https://www.springer.com/gp/book/9783319219028 | Chapter-url = https://www.researchgate.net/publication/314700681} </ref > 通常在树状图中呈现。
The standard algorithm for hierarchical agglomerative clustering (HAC) has a time complexity of [math]\displaystyle{ \mathcal{O}(n^3) }[/math] and requires [math]\displaystyle{ \mathcal{O}(n^2) }[/math] memory, which makes it too slow for even medium data sets. However, for some special cases, optimal efficient agglomerative methods (of complexity [math]\displaystyle{ \mathcal{O}(n^2) }[/math]) are known: SLINK[2] for single-linkage and CLINK[3] for complete-linkage clustering. With a heap the runtime of the general case can be reduced to [math]\displaystyle{ \mathcal{O}(n^2 \log n) }[/math] at the cost of further increasing the memory requirements. In many cases, the memory overheads of this approach are too large to make it practically usable.
The standard algorithm for hierarchical agglomerative clustering (HAC) has a time complexity of [math]\displaystyle{ \mathcal{O}(n^3) }[/math] and requires [math]\displaystyle{ \mathcal{O}(n^2) }[/math] memory, which makes it too slow for even medium data sets. However, for some special cases, optimal efficient agglomerative methods (of complexity [math]\displaystyle{ \mathcal{O}(n^2) }[/math]) are known: SLINK for single-linkage and CLINK for complete-linkage clustering. With a heap the runtime of the general case can be reduced to [math]\displaystyle{ \mathcal{O}(n^2 \log n) }[/math] at the cost of further increasing the memory requirements. In many cases, the memory overheads of this approach are too large to make it practically usable.
层次凝聚聚类(HAC)的标准算法的时间复杂度为 < math > mathical { o }(n ^ 3) </math > ,并且需要 < math > mathcal { o }(n ^ 2) </math > 内存,这使得它对于中等数据集来说太慢了。然而,对于某些特殊情况,已知的最佳有效凝聚方法(复杂度 < math > mathcal { o }(n ^ 2) </math >)是: 单连锁的 SLINK < ! ——粗体 wp: r # pla-- > 和完全连锁的 CLINK。对于堆,一般情况下的运行时可以缩减为 < math > mathcal { o }(n ^ 2 log n) </math > ,代价是进一步增加内存需求。在许多情况下,这种方法的内存开销太大,无法实际使用。
Except for the special case of single-linkage, none of the algorithms (except exhaustive search in [math]\displaystyle{ \mathcal{O}(2^n) }[/math]) can be guaranteed to find the optimum solution.
Except for the special case of single-linkage, none of the algorithms (except exhaustive search in [math]\displaystyle{ \mathcal{O}(2^n) }[/math]) can be guaranteed to find the optimum solution.
除了单链路的特殊情况外,所有算法(除了 < math > mathcal { o }(2 ^ n) </math > 中的穷举搜索)都不能保证找到最优解。
Divisive clustering with an exhaustive search is [math]\displaystyle{ \mathcal{O}(2^n) }[/math], but it is common to use faster heuristics to choose splits, such as k-means.
Divisive clustering with an exhaustive search is [math]\displaystyle{ \mathcal{O}(2^n) }[/math], but it is common to use faster heuristics to choose splits, such as k-means.
穷举搜索的分裂聚类是 < math > mathcal { o }(2 ^ n) </math > ,但是通常使用更快的启发式来选择分裂,比如 k-means。
Cluster dissimilarity
In order to decide which clusters should be combined (for agglomerative), or where a cluster should be split (for divisive), a measure of dissimilarity between sets of observations is required. In most methods of hierarchical clustering, this is achieved by use of an appropriate metric (a measure of distance between pairs of observations), and a linkage criterion which specifies the dissimilarity of sets as a function of the pairwise distances of observations in the sets.
In order to decide which clusters should be combined (for agglomerative), or where a cluster should be split (for divisive), a measure of dissimilarity between sets of observations is required. In most methods of hierarchical clustering, this is achieved by use of an appropriate metric (a measure of distance between pairs of observations), and a linkage criterion which specifies the dissimilarity of sets as a function of the pairwise distances of observations in the sets.
为了决定哪些集群应该被组合起来(用于聚合) ,或者哪些集群应该被分割(用于分裂) ,需要在观察组之间进行不同程度的度量。在大多数层次聚类方法中,这是通过使用适当的度量(对观测值之间的距离度量)和联系准则来实现的,联系准则将集合的不同指定为观测值在集合中的成对距离的函数。
Metric
The choice of an appropriate metric will influence the shape of the clusters, as some elements may be close to one another according to one distance and farther away according to another. For example, in a 2-dimensional space, the distance between the point (1,0) and the origin (0,0) is always 1 according to the usual norms, but the distance between the point (1,1) and the origin (0,0) can be 2 under Manhattan distance, [math]\displaystyle{ \scriptstyle\sqrt{2} }[/math] under Euclidean distance, or 1 under maximum distance.
The choice of an appropriate metric will influence the shape of the clusters, as some elements may be close to one another according to one distance and farther away according to another. For example, in a 2-dimensional space, the distance between the point (1,0) and the origin (0,0) is always 1 according to the usual norms, but the distance between the point (1,1) and the origin (0,0) can be 2 under Manhattan distance, [math]\displaystyle{ \scriptstyle\sqrt{2} }[/math] under Euclidean distance, or 1 under maximum distance.
选择合适的度量将影响星系团的形状,因为某些元素可能根据一个距离彼此接近,而根据另一个距离彼此更远。例如,在一个二维空间中,点(1,0)和原点(0,0)之间的距离通常是1,但是点(1,1)和原点(0,0)之间的距离在曼哈顿距离下可以是2,在欧几里得度量下可以是1,在最大距离下可以是1。
Some commonly used metrics for hierarchical clustering are:[4]
Some commonly used metrics for hierarchical clustering are:
一些常用的层次聚类指标如下:
| Names | Names | 名字 | Formula | Formula | 方程式 |
|---|---|---|---|---|---|
| Euclidean distance | Euclidean distance | Euclidean distance | [math]\displaystyle{ \|a-b \|_2 = \sqrt{\sum_i (a_i-b_i)^2} }[/math] | [math]\displaystyle{ \|a-b \|_2 = \sqrt{\sum_i (a_i-b_i)^2} }[/math] | a-b | _ 2 = sqrt { sum _ i (a _ i-b _ i) ^ 2} </math > |
| Squared Euclidean distance | Squared Euclidean distance | Squared Euclidean distance | [math]\displaystyle{ \|a-b \|_2^2 = \sum_i (a_i-b_i)^2 }[/math] | [math]\displaystyle{ \|a-b \|_2^2 = \sum_i (a_i-b_i)^2 }[/math] | a-b | 2 ^ 2 = sum _ i (a _ i-b _ i) ^ 2 |
| Manhattan distance | Manhattan distance | 曼哈顿距离 | [math]\displaystyle{ \|a-b \|_1 = \sum_i |a_i-b_i| }[/math] | [math]\displaystyle{ \|a-b \|_1 = \sum_i |a_i-b_i| }[/math]
[数学][数学][数学] | |
| Maximum distance | Maximum distance | 最大距离 | [math]\displaystyle{ \|a-b \|_\infty = \max_i |a_i-b_i| }[/math] | [math]\displaystyle{ \|a-b \|_\infty = \max_i |a_i-b_i| }[/math]
[数学][数学][数学] | |
| Mahalanobis distance | Mahalanobis distance
马氏距离 |
[math]\displaystyle{ \sqrt{(a-b)^{\top}S^{-1}(a-b)} }[/math] where S is the Covariance matrix | [math]\displaystyle{ \sqrt{(a-b)^{\top}S^{-1}(a-b)} }[/math] where S is the Covariance matrix | < math > sqrt {(a-b) ^ { top } s ^ {-1}(a-b)} </math > 其中 s 是协方差矩阵 |
|}
For text or other non-numeric data, metrics such as the Hamming distance or Levenshtein distance are often used.
For text or other non-numeric data, metrics such as the Hamming distance or Levenshtein distance are often used.
对于文本或其他非数字数据,常常使用汉明距离或莱文斯坦距离等度量标准。
A review of cluster analysis in health psychology research found that the most common distance measure in published studies in that research area is the Euclidean distance or the squared Euclidean distance.[citation needed]
A review of cluster analysis in health psychology research found that the most common distance measure in published studies in that research area is the Euclidean distance or the squared Euclidean distance.
一项对数据聚类健康心理学研究的回顾发现,在该研究领域已发表的研究中,最常见的距离测量方法是欧几里得度量距离或欧几里得度量距离的平方。
Linkage criteria
The linkage criterion determines the distance between sets of observations as a function of the pairwise distances between observations.
The linkage criterion determines the distance between sets of observations as a function of the pairwise distances between observations.
链接准则决定了观测值之间的距离,它是观测值之间成对距离的函数。
Some commonly used linkage criteria between two sets of observations A and B are:[5][6]
Some commonly used linkage criteria between two sets of observations A and B are:
两组观测值 a 和 b 之间一些常用的联系标准如下:
| Names | Names | 名字 | Formula | Formula | 方程式 |
|---|---|---|---|---|---|
| Maximum or complete-linkage clustering | Maximum or complete-linkage clustering | 最大或完全链接群集 | [math]\displaystyle{ \max \, \{\, d(a,b) : a \in A,\, b \in B \,\}. }[/math] | [math]\displaystyle{ \max \, \{\, d(a,b) : a \in A,\, b \in B \,\}. }[/math] | < math > max,{ ,d (a,b) : a 在 a,b 在 b,}。数学 |
| Minimum or single-linkage clustering | Minimum or single-linkage clustering | 最小或单链接群集 | [math]\displaystyle{ \min \, \{\, d(a,b) : a \in A,\, b \in B \,\}. }[/math] | [math]\displaystyle{ \min \, \{\, d(a,b) : a \in A,\, b \in B \,\}. }[/math] | < math > min,{ ,d (a,b) : a in a,,b in b,}.数学 |
| Unweighted average linkage clustering (or UPGMA) | Unweighted average linkage clustering (or UPGMA) | Unweighted average linkage clustering (或 UPGMA) | [math]\displaystyle{ \frac{1}{|A|\cdot|B|} \sum_{a \in A }\sum_{ b \in B} d(a,b). }[/math] | [math]\displaystyle{ \frac{1}{|A|\cdot|B|} \sum_{a \in A }\sum_{ b \in B} d(a,b). }[/math] | a | cdot | b | } sum _ { a } sum _ { b } d (a,b).数学 |
| Weighted average linkage clustering (or WPGMA) | Weighted average linkage clustering (or WPGMA) | 加权平均数链接聚类(或 WPGMA) | [math]\displaystyle{ d(i \cup j, k) = \frac{d(i, k) + d(j, k)}{2}. }[/math] | [math]\displaystyle{ d(i \cup j, k) = \frac{d(i, k) + d(j, k)}{2}. }[/math] | < math > d (i cup j,k) = frac { d (i,k) + d (j,k)}{2}.数学 |
| Centroid linkage clustering, or UPGMC | Centroid linkage clustering, or UPGMC | 质心链接集群,或 UPGMC | [math]\displaystyle{ \|c_s - c_t \| }[/math] where [math]\displaystyle{ c_s }[/math] and [math]\displaystyle{ c_t }[/math] are the centroids of clusters s and t, respectively. | [math]\displaystyle{ \|c_s - c_t \| }[/math] where [math]\displaystyle{ c_s }[/math] and [math]\displaystyle{ c_t }[/math] are the centroids of clusters s and t, respectively. | c _ s-c _ t | </math > 其中 < math > c _ s </math > 和 < math > c _ t </math > 分别是集群 s 和 t 的中心。 |
| Minimum energy clustering | Minimum energy clustering | 最小能量聚类 | [math]\displaystyle{ \frac {2}{nm}\sum_{i,j=1}^{n,m} \|a_i- b_j\|_2 - \frac {1}{n^2}\sum_{i,j=1}^{n} \|a_i-a_j\|_2 - \frac{1}{m^2}\sum_{i,j=1}^{m} \|b_i-b_j\|_2 }[/math] | [math]\displaystyle{ \frac {2}{nm}\sum_{i,j=1}^{n,m} \|a_i- b_j\|_2 - \frac {1}{n^2}\sum_{i,j=1}^{n} \|a_i-a_j\|_2 - \frac{1}{m^2}\sum_{i,j=1}^{m} \|b_i-b_j\|_2 }[/math] | a _ i-b _ j | 2-frac {1}{ n ^ 2} sum { i,j = 1}{ n } | a _ i-a _ j | 2-frac {1}{ m ^ 2} sum { i,j = 1 ^ { m } | b _ i-b _ j | 2 </math > |
|}
where d is the chosen metric. Other linkage criteria include:
where d is the chosen metric. Other linkage criteria include:
其中 d 是选定的度量单位。其他联系准则包括:
- The sum of all intra-cluster variance.
- The increase in variance for the cluster being merged (Ward's criterion).[7]
}}</ref>
} </ref >
- The probability that candidate clusters spawn from the same distribution function (V-linkage).
- The product of in-degree and out-degree on a k-nearest-neighbour graph (graph degree linkage).[8]
- The increment of some cluster descriptor (i.e., a quantity defined for measuring the quality of a cluster) after merging two clusters.[9][10][11]
Discussion
Hierarchical clustering has the distinct advantage that any valid measure of distance can be used. In fact, the observations themselves are not required: all that is used is a matrix of distances.
Hierarchical clustering has the distinct advantage that any valid measure of distance can be used. In fact, the observations themselves are not required: all that is used is a matrix of distances.
层次聚类具有明显的优势,可以使用任何有效的距离度量。事实上,观测本身并不是必需的: 所用的只是一个距离矩阵。
Agglomerative clustering example
Raw data
原始数据
For example, suppose this data is to be clustered, and the Euclidean distance is the distance metric.
For example, suppose this data is to be clustered, and the Euclidean distance is the distance metric.
例如,假设要对这些数据进行聚类,距离欧几里得度量就是距离度量。
The hierarchical clustering dendrogram would be as such:
The hierarchical clustering dendrogram would be as such:
系统聚类树状图如下:
Traditional representation
传统表现
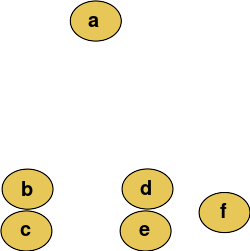
Cutting the tree at a given height will give a partitioning clustering at a selected precision. In this example, cutting after the second row (from the top) of the dendrogram will yield clusters {a} {b c} {d e} {f}. Cutting after the third row will yield clusters {a} {b c} {d e f}, which is a coarser clustering, with a smaller number but larger clusters.
Cutting the tree at a given height will give a partitioning clustering at a selected precision. In this example, cutting after the second row (from the top) of the dendrogram will yield clusters {a} {b c} {d e} {f}. Cutting after the third row will yield clusters {a} {b c} {d e f}, which is a coarser clustering, with a smaller number but larger clusters.
在给定的高度切割树将以选定的精度提供分区聚类。在这个示例中,在树状图的第二行(从顶部开始)之后切割将产生集群{ a }{ b }{ d }{ f }。在第三行之后进行切割将产生集群{ a }{ b }{ d e f } ,这是一个粗糙的集群,具有较小的数量但较大的集群。
This method builds the hierarchy from the individual elements by progressively merging clusters. In our example, we have six elements {a} {b} {c} {d} {e} and {f}. The first step is to determine which elements to merge in a cluster. Usually, we want to take the two closest elements, according to the chosen distance.
This method builds the hierarchy from the individual elements by progressively merging clusters. In our example, we have six elements {a} {b} {c} {d} {e} and {f}. The first step is to determine which elements to merge in a cluster. Usually, we want to take the two closest elements, according to the chosen distance.
此方法通过逐步合并集群,从单个元素构建层次结构。在我们的示例中,有六个元素{ a }{ b }{ c }{ d }{ e }和{ f }。第一步是确定在集群中合并哪些元素。通常,我们希望根据选定的距离获取两个最接近的元素。
Optionally, one can also construct a distance matrix at this stage, where the number in the i-th row j-th column is the distance between the i-th and j-th elements. Then, as clustering progresses, rows and columns are merged as the clusters are merged and the distances updated. This is a common way to implement this type of clustering, and has the benefit of caching distances between clusters. A simple agglomerative clustering algorithm is described in the single-linkage clustering page; it can easily be adapted to different types of linkage (see below).
Optionally, one can also construct a distance matrix at this stage, where the number in the i-th row j-th column is the distance between the i-th and j-th elements. Then, as clustering progresses, rows and columns are merged as the clusters are merged and the distances updated. This is a common way to implement this type of clustering, and has the benefit of caching distances between clusters. A simple agglomerative clustering algorithm is described in the single-linkage clustering page; it can easily be adapted to different types of linkage (see below).
还可以选择在这个阶段构造一个距离矩阵,其中第 i 行 j-th 列中的数字是 i-th 和 j-th 元素之间的距离。然后,随着集群的进展,在合并集群和更新距离时合并行和列。这是实现此类集群的常用方法,并且具有缓存集群之间的距离的优点。在单链接聚类页面中描述了一个简单的凝聚聚类算法; 它可以很容易地适应不同类型的链接(见下文)。
Suppose we have merged the two closest elements b and c, we now have the following clusters {a}, {b, c}, {d}, {e} and {f}, and want to merge them further. To do that, we need to take the distance between {a} and {b c}, and therefore define the distance between two clusters.
Suppose we have merged the two closest elements b and c, we now have the following clusters {a}, {b, c}, {d}, {e} and {f}, and want to merge them further. To do that, we need to take the distance between {a} and {b c}, and therefore define the distance between two clusters.
假设我们已经合并了两个最接近的元素 b 和 c,现在我们有以下集群{ a }、{ b、 c }、{ d }、{ e }和{ f } ,并希望进一步合并它们。为此,我们需要计算{ a }和{ b c }之间的距离,从而定义两个集群之间的距离。
Usually the distance between two clusters [math]\displaystyle{ \mathcal{A} }[/math] and [math]\displaystyle{ \mathcal{B} }[/math] is one of the following:
Usually the distance between two clusters [math]\displaystyle{ \mathcal{A} }[/math] and [math]\displaystyle{ \mathcal{B} }[/math] is one of the following:
通常情况下,两组数字之间的距离是下列数字之一:
- The maximum distance between elements of each cluster (also called complete-linkage clustering):
- [math]\displaystyle{ \max \{\, d(x,y) : x \in \mathcal{A},\, y \in \mathcal{B}\,\}. }[/math]
[math]\displaystyle{ \max \{\, d(x,y) : x \in \mathcal{A},\, y \in \mathcal{B}\,\}. }[/math]
< math > max { ,d (x,y) : x in mathcal { a } ,,y in mathcal { b } ,}.数学
- The minimum distance between elements of each cluster (also called single-linkage clustering):
- [math]\displaystyle{ \min \{\, d(x,y) : x \in \mathcal{A},\, y \in \mathcal{B} \,\}. }[/math]
[math]\displaystyle{ \min \{\, d(x,y) : x \in \mathcal{A},\, y \in \mathcal{B} \,\}. }[/math]
< math > min { ,d (x,y) : x in mathcal { a } ,,y in mathcal { b } ,}.数学
- The mean distance between elements of each cluster (also called average linkage clustering, used e.g. in UPGMA):
- [math]\displaystyle{ {1 \over {|\mathcal{A}|\cdot|\mathcal{B}|}}\sum_{x \in \mathcal{A}}\sum_{ y \in \mathcal{B}} d(x,y). }[/math]
[math]\displaystyle{ {1 \over {|\mathcal{A}|\cdot|\mathcal{B}|}}\sum_{x \in \mathcal{A}}\sum_{ y \in \mathcal{B}} d(x,y). }[/math]
{1 over { | mathcal { a } | cdot | mathcal { b } | } sum { x in mathcal { a } sum { y in mathcal { b } d (x,y)).数学
- The sum of all intra-cluster variance.
- The increase in variance for the cluster being merged (Ward's method[7])
- The probability that candidate clusters spawn from the same distribution function (V-linkage).
In case of tied minimum distances, a pair is randomly chosen, thus being able to generate several structurally different dendrograms. Alternatively, all tied pairs may be joined at the same time, generating a unique dendrogram.[12]
In case of tied minimum distances, a pair is randomly chosen, thus being able to generate several structurally different dendrograms. Alternatively, all tied pairs may be joined at the same time, generating a unique dendrogram.
在系结最小距离的情况下,一对是随机选择的,因此能够产生几个结构不同的树状图。或者,所有的绑定对可以在同一时间结合,产生一个唯一的树状图。
One can always decide to stop clustering when there is a sufficiently small number of clusters (number criterion). Some linkages may also guarantee that agglomeration occurs at a greater distance between clusters than the previous agglomeration, and then one can stop clustering when the clusters are too far apart to be merged (distance criterion). However, this is not the case of, e.g., the centroid linkage where the so-called reversals[13] (inversions, departures from ultrametricity) may occur.
One can always decide to stop clustering when there is a sufficiently small number of clusters (number criterion). Some linkages may also guarantee that agglomeration occurs at a greater distance between clusters than the previous agglomeration, and then one can stop clustering when the clusters are too far apart to be merged (distance criterion). However, this is not the case of, e.g., the centroid linkage where the so-called reversals (inversions, departures from ultrametricity) may occur.
人们总是可以决定停止群集时,有一个足够少的群集(数目标准)。有些联系还可能保证集群之间的距离大于以前的集群,然后当集群之间的距离太远而无法合并时就可以停止集群(距离标准)。然而,这不是例如,质心链接的情况下,所谓的逆转(反转,偏离超节拍)可能发生的情况。
Divisive clustering
The basic principle of divisive clustering was published as the DIANA (DIvisive ANAlysis Clustering) algorithm.[14] Initially, all data is in the same cluster, and the largest cluster is split until every object is separate.
The basic principle of divisive clustering was published as the DIANA (DIvisive ANAlysis Clustering) algorithm. Initially, all data is in the same cluster, and the largest cluster is split until every object is separate.
分裂聚类的基本原理被公布为 DIANA (分裂分析聚类)算法。最初,所有数据都位于同一个集群中,最大的集群被拆分,直到每个对象都是独立的。
Because there exist [math]\displaystyle{ O(2^n) }[/math] ways of splitting each cluster, heuristics are needed. DIANA chooses the object with the maximum average dissimilarity and then moves all objects to this cluster that are more similar to the new cluster than to the remainder.
Because there exist [math]\displaystyle{ O(2^n) }[/math] ways of splitting each cluster, heuristics are needed. DIANA chooses the object with the maximum average dissimilarity and then moves all objects to this cluster that are more similar to the new cluster than to the remainder.
因为存在拆分每个集群的方法,所以需要启发式算法。DIANA 选择平均差异最大的对象,然后将所有与新集群相似的对象移动到这个集群中,而不是移动到其余的对象。
Software
Open source implementations
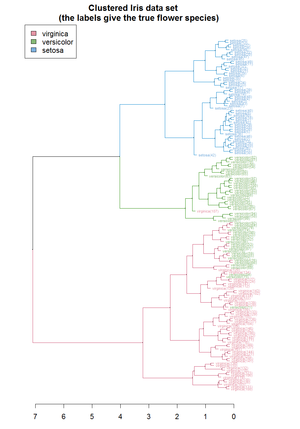
Hierarchical clustering [[dendrogram of the Iris dataset (using R). Source ]]
层次聚类[[虹膜数据集的树状图(使用 r)]。[ https://cran.r-project.org/web/packages/dendextend/vignettes/cluster_analysis.html 来源]

Orange data mining suite.]]
橙色数据挖掘套件]
- ALGLIB implements several hierarchical clustering algorithms (single-link, complete-link, Ward) in C++ and C# with O(n²) memory and O(n³) run time.
- ELKI includes multiple hierarchical clustering algorithms, various linkage strategies and also includes the efficient SLINK,[2] CLINK[3] and Anderberg algorithms, flexible cluster extraction from dendrograms and various other cluster analysis algorithms.
- Orange, a data mining software suite, includes hierarchical clustering with interactive dendrogram visualisation.
- R has many packages that provide functions for hierarchical clustering.
- SciPy implements hierarchical clustering in Python, including the efficient SLINK algorithm.
- scikit-learn also implements hierarchical clustering in Python.
- Weka includes hierarchical cluster analysis.
Commercial implementations
- MATLAB includes hierarchical cluster analysis.
- SAS includes hierarchical cluster analysis in PROC CLUSTER.
- Mathematica includes a Hierarchical Clustering Package.
- NCSS includes hierarchical cluster analysis.
- SPSS includes hierarchical cluster analysis.
- Qlucore Omics Explorer includes hierarchical cluster analysis.
- Stata includes hierarchical cluster analysis.
- CrimeStat includes a nearest neighbor hierarchical cluster algorithm with a graphical output for a Geographic Information System.
See also
References
- ↑ Rokach, Lior, and Oded Maimon. "Clustering methods." Data mining and knowledge discovery handbook. Springer US, 2005. 321-352.
- ↑ 2.0 2.1 R. Sibson (1973). "SLINK: an optimally efficient algorithm for the single-link cluster method" (PDF). The Computer Journal. British Computer Society. 16 (1): 30–34. doi:10.1093/comjnl/16.1.30.
- ↑ 3.0 3.1 D. Defays (1977). "An efficient algorithm for a complete-link method". The Computer Journal. British Computer Society. 20 (4): 364–366. doi:10.1093/comjnl/20.4.364.
- ↑ "The DISTANCE Procedure: Proximity Measures". SAS/STAT 9.2 Users Guide. SAS Institute. Retrieved 2009-04-26.
- ↑ "The CLUSTER Procedure: Clustering Methods". SAS/STAT 9.2 Users Guide. SAS Institute. Retrieved 2009-04-26.
- ↑ Székely, G. J.; Rizzo, M. L. (2005). "Hierarchical clustering via Joint Between-Within Distances: Extending Ward's Minimum Variance Method". Journal of Classification. 22 (2): 151–183. doi:10.1007/s00357-005-0012-9.
- ↑ 7.0 7.1 Ward, Joe h. (1963). "用于优化目标函数的层次分组". Journal of the American Statistical Association 美国统计协会杂志. 58 (301): 236–244. doi:[//doi.org/10.2307%2F2282967%0A%0A10.2307%2F2282967 10.2307/2282967
10.2307/2282967]. JSTOR [//www.jstor.org/stable/2282967
2282967 2282967
2282967]. MR [//www.ams.org/mathscinet-getitem?mr=0148188%0A%0A0148188%E5%85%88%E7%94%9F 0148188
0148188先生].
{{cite journal}}: Check|doi=value (help); Check|jstor=value (help); Check|mr=value (help); line feed character in|doi=at position 16 (help); line feed character in|journal=at position 48 (help); line feed character in|jstor=at position 8 (help); line feed character in|mr=at position 8 (help) - ↑ Zhang, Wei; Wang, Xiaogang; Zhao, Deli; Tang, Xiaoou (2012). Fitzgibbon, Andrew; Lazebnik, Svetlana; Perona, Pietro; Sato, Yoichi; Schmid, Cordelia (eds.). "Graph Degree Linkage: Agglomerative Clustering on a Directed Graph". Computer Vision – ECCV 2012. Lecture Notes in Computer Science (in English). Springer Berlin Heidelberg. 7572: 428–441. arXiv:1208.5092. Bibcode:2012arXiv1208.5092Z. doi:10.1007/978-3-642-33718-5_31. ISBN 9783642337185. See also: https://github.com/waynezhanghk/gacluster
- ↑ Zhang, et al. "Agglomerative clustering via maximum incremental path integral." Pattern Recognition (2013).
- ↑ Zhao, and Tang. "Cyclizing clusters via zeta function of a graph."Advances in Neural Information Processing Systems. 2008.
- ↑ Ma, et al. "Segmentation of multivariate mixed data via lossy data coding and compression." IEEE Transactions on Pattern Analysis and Machine Intelligence, 29(9) (2007): 1546-1562.
- ↑ Fernández, Alberto; Gómez, Sergio (2008). "Solving Non-uniqueness in Agglomerative Hierarchical Clustering Using Multidendrograms". Journal of Classification. 25 (1): 43–65. arXiv:cs/0608049. doi:10.1007/s00357-008-9004-x.
- ↑ Legendre, P.; Legendre, L. (2003). Numerical Ecology. Elsevier Science BV.
- ↑ Kaufman, L., & Roussew, P. J. (1990). Finding Groups in Data - An Introduction to Cluster Analysis. A Wiley-Science Publication John Wiley & Sons.
Further reading
- Kaufman, L.; Rousseeuw, P.J. (1990). Finding Groups in Data: An Introduction to Cluster Analysis (1 ed.). New York: John Wiley. ISBN 0-471-87876-6. https://archive.org/details/findinggroupsind00kauf.
- Hastie, Trevor; Tibshirani, Robert; Friedman, Jerome (2009). "14.3.12 Hierarchical clustering". The Elements of Statistical Learning (2nd ed.). New York: Springer. pp. 520–528. ISBN 978-0-387-84857-0. Archived from the original on 2009-11-10. http://www-stat.stanford.edu/~tibs/ElemStatLearn/. Retrieved 2009-10-20.
Category:Network analysis
分类: 网络分析
Category:Cluster analysis algorithms
类别: 数据聚类算法
This page was moved from wikipedia:en:Hierarchical clustering. Its edit history can be viewed at 层次聚类/edithistory
- 有参考文献错误的页面
- 调用重复模板参数的页面
- CS1 errors: invisible characters
- CS1 errors: MR
- CS1 errors: JSTOR
- CS1 errors: DOI
- CS1 English-language sources (en)
- Articles with hatnote templates targeting a nonexistent page
- Missing redirects
- Articles with short description
- All articles with unsourced statements
- Articles with unsourced statements from April 2009
- Articles with invalid date parameter in template
- Network analysis
- Cluster analysis algorithms
- 待整理页面