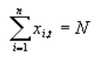程序名称：人工模拟股市
作者：Santa Fe Instutive(Swarm版)，jake(java版)
源代码：ASM_swarm.zip asm_java.zip

人工模拟股市

程序简介

人工股市（Artificial Stock Market，简称ASM）是模拟股市运作的一个程序。在这个电脑中的虚拟市场中，若干被称为交易者的人工智能程序(Agent)通过观察它们所在的数字世界中股价和股息的不断变换而做出预测，并且根据这些预测做出购买股票与否以及购买股票数量的决策。反过来，所有的交易者的决策又决定了股票的价格，这样，整个的股票交易市场就构成了一个自我封闭的计算系统。同时，这些交易者都具有学习的能力，可以根据以前预测的成功或者失败对自己的决策进行调整，并且通过一种被称为遗传算法的方法产生创新能力。总之，ASM是一个电脑中不断进化的虚拟股票市场！通过研究ASM，我们可以更好的理解现实世界的行为，并且它提供了一个很好的现实股市的隐喻。

程序运行说明

点击下排的开始按钮，则股市开始运作。首先，程序需要对每个Agent和整个世界进行初始化，然后才进入ASM的实际运行阶段，这个时候，你可以点击曲线图、柱状图等按钮察看世界运行的情况，得到价格、股息等信息的直观显示。当点击结束的时候，股市停止运行，这个时候你可以设置一些参数，再次点击开始可以在新的参数下运行程序。察看规则部分可以让你看到每个Agent的内部规则，并且可以看到它们与真实世界价格、股息、编码的对比情况。点击暂停按钮后，你还可以单步运行股市。

详细说明

1.参数说明:

遗传算法概率：每隔多长周期执行一次遗传算法。
变异率：执行遗传算法的时候，变异操作的概率。
交叉率：执行遗传算法的时候交叉操作的概率。
Agent的数量：进行股票交易的交易者数量。
规则的数量：每个Agent所拥有的预测规则的数量。

2.图形说明:

世界的状态显示的是有关整个股市的状况，包括股价、股息等等，风险中性价格即股息/利息的值。Agent的状况则显示了每个Agent的变量的变化趋势。曲线图画出了单一变量与时间的关系，柱状图主要显示了各个变量的Agent之间的对比情况。

3.关于图形操作:

曲线图，可以在一个坐标系下察看两种变量的情况。蓝色表示一个变量，红色表示另一个，可以从下面的选择框选择不同的变量。关于柱状图，可以变换不同的变量察看情况。

4.关于规则察看的操作:

在上面列表中显示了当前的Agent拥有的所有的规则，选择最下方的Agent编号，可以察看不同的Agent的规则，选择中间的察看方式：全部规则还是激活规则则可以分别察看当前Agent的所有规则和被激活的规则。点击列表框中的一个规则，则在下面的文本框中显示了该规则的具体对应的条件部分的编码，和代表的预测意义。世界状态则表示了当前世界股票价格、股息等变量的二进制编码。下面显示的价格和股息都是当前股市的股价和股息。

关于本程序

该程序是作者对SFI的ASM2.2版本运用java进行重写和改造。其中有不少对源程序的改动，可能会造成一些运行结果与源程序的不同，也可能存在着一些bug，所以我们提供了该java版本程序的下载以及Swarm源程序的下载

关于人工股市的具体原理请看下面的文章：

人工股市(ASM)介绍

张江

经济系统、股票交易系统中的复杂性

新古典主义经济学告诉我们，我们赖以生存的经济系统是由若干被称作“经济人”的个体组成的，这些“经济人”具有完全的理性、并且对整个市场的具有完全信息，因此经济学家证明了，市场最终将处于一种均衡的状态，在这种状态下需求量刚好等于供给量，并且在没有外部的干扰条件下，系统将静止不再演变。

然而看看我们身处的经济系统，它并不是理论家们预言的那个样子。首先经济中的个体并不是全知全能且具有完全理性的，当然这些个体也不是完全随机相互作用的一群无规则运动的分子，他们更像是处于完全理性与随机性之间的一种状态。关键是，这些个体是具有学习功能的，他们并不是像一台计算的机器一样总是做出理性的判断和决策，而是通过经济活动的实践逐渐积累经验，通过与其周围有限环境内的其它经济个体的交互中，慢慢的适应，从而进行有限理性的行为。当环境发生变化的时候，他们往往可以调整自己的策略，从而使得自己能够尽量的谋得经济利益。由这样的适应性个体组织成的经济系统是一个复杂的系统，而且这个系统会因为每个个体的不断调整从而永不停息的变化着，似乎现实的经济系统从来不会平衡下来，而是象一个有机的生命体一样始终处于复杂的运动变化当中。

复杂系统的方法[1]致力于用一种全新的观点理解经济系统中的复杂性。在微观上，首先，按照前面的叙述，人们扬弃了完全理性、全知全能的“经济人”的假设取而代之的是能够学习和适应环境的运用归纳法决策的有限理性人。其次，在微观上，人们用“规则”代替计算来给每一个个体进行建模；在宏观上，人们扬弃了简单的还原论思想—即认为研究清楚系统组分的行为就相当于认识了系统的行为思想，把经济系统就看成是由若干相互作用的个体进行复杂交互的复杂系统；在方法论上，人们扬弃了纯粹的数学推理的方法，取而代之的是计算机模拟技术。

股市无非是若干复杂经济系统中的一个特例。传统的股市模型假设股票交易者根据全局的行情进行完全理性的判断，并利用理性的预期进行决策。在这种模型的假设前提下，股市更像一个“死”的物理系统。而现实的股市远不是如此，人们常常用诸如“股市持续低迷”、“狂涨”等等类似描述人类心理现象的语言描述股市，而且还常常出现类似“黑色星期五”这种有关股市心理的现象。由此可见，我们需要用复杂系统的理论来对其进行重新的理解，看看能够得到什么结果。“人工股市”[2](Artificial Stock Market简称ASM)是由圣塔菲研究所（Santa Fe Institute）的W.Brian Arthur和John Holland于1987年提出来的一个模拟股市运作的计算机系统，它用具有学习能力的AI（人工智能）程序代替全知全能的股票交易者，在电脑中重建一个模拟的股票交易环境，看看在这样的计算机世界中能不能得到与现实股市相近的数码股市的拷贝。

在下面的讨论中，第2节概述了人工股市系统的运作机理，第3节详细介绍模型的内部结构，其中包括股市环境、相互作用的作用者模型、学习算法等等细节问题。第4节介绍系统的运行情况与仿真结果，看看这样一种有归纳的作用这形成的股市系统到底有什么神奇之处。

ASM系统模型概述

系统结构

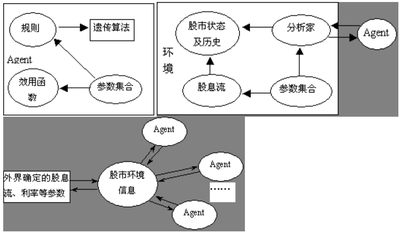
ASM系统主要分成两个大部分，一部分是股票交易者（我们称其为Agent，意为智能代理），另一部分是每个Agent所面临的环境。它主要模拟了单一股票的交易情况（也就是说市场上仅仅有一种股票发行）。

其中Agent模型又是由预测规则、效用函数、财富状态以及参数集合四个部分组成的。预测规则是形如if [condition] then [result]这样的规则，其中[condition]部分都是经过编码后的01序列抽象信息，[result]是当agent采用当前规则所采取的动作。为了模拟现实中的交易者的多样性，每个Agent都有一组不同的规则，而且学习效应是在规则层次体现的。具体说来，就是Agent通过不断的运用规则对股票的价格进行预测从而进行买入或者卖出或者持有的决策，然后根据预测的后果来对他们运用的规则进行评价，从而确定每个规则作用的排序，然后运用一种称为“遗传算法”的方法模拟大自然的优胜劣汰，淘汰掉评价不好的规则，同时产生新的更好的规则。Agent的效用函数表达了每个Agent对股票价格以及股票持有量之间的偏好，给定当前的股票价格、该Agent对未来股价的预期就可以得到Agent对股票持有的需求量。为了设计简便，系统给每个Agent设计了同一类型的效用函数。Agent的财富状态主要包括当前该Agent的股票持有量和现金量。Agent的参数集合定义了Agent在运行过程中的不同行为参数，包括效用函数的具体参数、遗传算法的参数、最大（小）持有股票量等等。

ASM的环境主要包括下列几个部分：股市的状态以及状态的历史信息、一个分析专家、一个随机股息流（可以认为单一股票的股息是由外部不确定信息确定的）、股市的参数集合。具体说来，股市的状态包括了股票当前的价格、股息、利率、风险中性价格（也就是利率与股息的比值）、股票交易量。状态历史就是股市状态在最近几期内的历史纪录，其中历史的记录长度是事先由用户给定的，系统还会根据当前的股市状态以及状态的历史信息进行编码从而得到一串01编码传递给Agent，Agent根据这些编码可以查找哪条规则的condition部分与其匹配从而激活这条规则进行预测。分析专家的作用是根据市场供求关系确定股票的交易价格等作用。随机股息流就是一个满足正态的独立同分布的随机过程。参数集合定义了股市运作过程中的一些参数，包括历史纪录的长度、正态分布的具体参数等等。

综合起来，我们可以得到下面的三个图分别来说明Agent的结构、股市环境的结构，以及Agent与股市的相互作用结构。

系统运行

系统的运行是在离散的时间基础上周期性的不断演化的。在每个周期内，Agent要完成决策、学习的运作，环境完成交易并保证股票市场的出清。Agent在进行决策时需要根据股市上的信息不断利用自己的规则对股票的价格进行预测，然后根据这个预测的结果与自己的偏好进行是应该抛出股票还是买进股票或者是持有当前的股票坐吃股息的决策。如果Agent抛出股票，这能够为他在短期内赚取一定量的现金，并且持有现金可以让他在每个周期内赚取现金的利息，但是同时他的股票减少了，因此它损失了股票的股息；如果Agent买进了股票，那么它的现金少了并损失了现金的利息，但同时它能够争取更多的股息；如果Agent不采取任何动作，虽然它能够坐吃股息和利息但是它同时要被征税，征税是根据Agent的总资产即股票价值与现金价值的总和决定的。因此从整体上，每个Agent必须对自己是否买进或者卖出股票做出决策，同时征税保证了每个Agent不能永远停止不动（否则它的财富会被征税征收光）。而因为股息是一个随机过程上下波动，所以每个Agent对股票的需求量和供给量就会随时间变化，通过需求与供给的相互竞争的结果决定了股票的当前价格，而股票的价格又反过来决定了每个Agent的财富拥有量。因此我们看到，我们得到了一个封闭的系统，在这个系统中Agent的决策决定了系统的环境状况，环境的状况同时又影响了每个生存在这个环境中的Agent拥有的财富。

当系统多次循环以后，每个Agent便有机会对自己所采用过的规则进行评价。因为在每一种环境中，Agent都有机会选择很多与当前情况匹配的规则做出决策，而显然这些规则有些能够很好的预测了股票的价格，有些不能够预测，因此这就造成了规则按照评价结果的排序。利用遗传算法对这些规则进行优胜劣汰并创造新的规则就能完成Agent的学习过程。Agent在学习变得越来越聪明的同时也会影响整体股市环境，而上文已经说了股市翻过来会再次影响Agent的行为，这样我们可以看到，人工股市是一个多个Agent共同进化的生态环境。

在系统运行的初始时刻，我们先给每个Agent分配了等量的现金和股票持有量，让他们有一个平等竞争的开始，但随着系统的运行，有些Agent能够对环境的变化做出积极的反应，有些不行，因此贫富差距开始加大，总之整个系统的动态只有在运作系统后才能看出来，运用ASM我们可以观察到很多真实股市中的有趣现象。

ASM的系统结构和算法

上一节，我们简单的介绍了ASM的结构和运行机理，对人工股市有了一个感性的认识，下面我们要详细的介绍人工股市的内部结构和具体的运行算法。详细介绍主要分环境和个体两部分进行。

股市环境

在上一节我们已经大概介绍了股市的环境由股市的状态以及状态的历史信息、分析专家、随机股息流、股市的参数集合这五个部分组成，下面分别进行介绍：

1.股市状态及状态历史编码

在ASM模型中，股市的状态包括下面这些量：当前的仿真周期（用t表示）、t周期内的股票价格（用pt表示）、当前股票的股息（用dt表示）、当前的现金利息率（用r表示，在我们的模型中假设r不随时间变化）。这些状态信息中，只有pt和dt是常常随时间变化的，他们都可以用实数来表示，这样状态的历史就记载了从t-h期到t期的pt和dt的历史信息。所以，状态历史可以用下面的集合表示：

   （1）

其中参数h为历史记忆的深度，t-h期以外的状态将被“遗忘”，每进行一个新的周期则历史信息更新一次。

为了能够让Agent使用的规则识别出当前环境的整个运行状态及信息，我们需要对状态历史信息进行编码。在这里我们用一个60位长的二进制串对股市的状态历史编码，其中这个二进制串的一个位就代表股市历史Ht符合一个描述判断。具体说来，我们可以采用一组诸如“股息上升”、“股息在5个周期内的平均值持续上升”、“当前股息大于最近100个周期内的股息平均值”以及“价格在4个周期内一直上升”、“价格*利率与股息的比大于1/2”等等这样的语句来描述股市状态以及历史信息，这样每一个语句就构成了对股市的一个判断，所以我们把一个二进制位对应一个语句。这样，就得到了一个环境编码和与其对应的语句集合：

环境编码：其中[File:3.png|100px]]

语句集合：其中是一个语句，

两个向量有对应关系，如果表示si语句被满足，反之为si不满足。系统的环境状态模块部分负责根据当前的股市状态以及状态的历史翻译成不同的语句判断，并形成二进制编码。在实验中，语句一共可以分成10个组分别记录了股息走势、股息均值的走势、当前股息与其均值的大小关系、股息短期均值与长期均值的关系、股息与股息总体均值之间的比例()、股票价格*利率/股息（50px）、股价的走势、股价均值的走势、股价与不同时期均值的关系、股票价格短期均值与长期均值的关系等信息。

2.分析专家

股市分析专家的作用为：在每个仿真周期内，收集所有Agent的股票需求量并按照一定的规则设定股票的价格，使得在这个价格下，股票市场能够得到出清（也就是说让需求量与供给量达到均衡）。

我们假设系统中一共有n个交易者（即Agent），并且发行的单一股票数量为N保持不变，假设交易者Agenti在t时刻对股票的持有量需求用Xi,t表示（包括Agent i手中原来就持有的股票数）。这样，因为股票发行的总量不变为N，

则显然有：（2）

但是在仿真的任意一个周期里，每个Agent的股票需求量和供给量不会一下子达到平衡，因此分析专家的职能就是负责规定当前股票的交易价格Pt并传递给每个交易者，交易者再根据新的交易价格Pt修改对这个股票价格和股息的预期，从而根据效用函数重新计算需求量。这样如果交易量没达到平衡则在按照上述步骤重新计算，直到平衡为止。如果我们设Agenti对价格的预期为E_i(p_t+1|I_t)，这表示在t时刻，Agenti根据当前的信息I_t（包括股票价格、股息）对t+1期的股价及股息做出预测为E_i(p_t+1+d_t+1|I_t)，Agenti的效用函数决定了在给定股价、股价的预期的情况下该Agent对股票的需求量X_i,t，简单的表示成：

X_i,t=U_i(pt, E_i(P_t+1+D_t+1|I_t)) （3）

那么分析家解决市场出清的算法可以表示如下：

(1)将当前的P_t传递给每个Agent，并让他们根据X_i,t=U_i(p_t, E_i(p_t+1|I_t))计算股票持有的需求量；

(2)如果市场出清，即，（为事先给定的一个小量），则算法结束返回均衡价格P_t，以及每个Agent的真实股票持有量即x_i,t+1；

(3)否则判断是否大于或小于0，根据所有Agent的总和边际效用（）调整股票价格即根据重新计算P_t，返回第1步。

3.随机股息流

   在ASM模型中，股息被认为是一个由外部确定的随机过程，具体的，我们用下面式子计算股息：

       （4）

   其中表示当期t的股息；表示股息波动的基准线由用户事先确定；可以理解为一种惯性系数，也就是说当期的股息与上期的股息相关的程度，也是由用户事先给定；是一个满足分布即标准正态分布的随机过程。

   根据上面的式子，系统不断计算t时刻的股息流注入系统中。
  另外，关于参数集合部分就是对各部分参数的付值过程，在此处不进行详细讨论。

Agent内部结构与算法

   Agent是股票交易者的模型，是真实世界中的股票交易者的模拟，它们是一些具有学习和创新能力的人工智能程序，每个Agent都由一组规则、效用函数和参数集合构成，这其中若干规则是完成Agent的决策、学习、创新的主要部分，在下面的部分中我们首先简单介绍效用函数，然后详细介绍规则的构成以及学习算法和运作机理等。

3.2.1、效用函数

   文章[2]指出，在ASM模型里面，假设所有的Agent都是风险厌恶的决策者，并且它们具有(CARA)型效用函数，即。如果在t时刻Agenti对股市运行状态在t+1时刻的预期为Ei(pt+1+dt+1)，方差为：，并且假设它是当前股价和股息的线性函数，也就是说：

       （5）

   其中a和b为两个参数，不同的Agent在不同的时刻使用不同的规则的时候，a与b的值都不一样，因此得到的对股价和股息的预期也会不一样。如果该预期满足正态分布，则根据CARA效用函数，我们能计算出Agenti对股票的持有量需求为：

       （6）

   因此，边际需求量为：

           （7）

   有了效用函数，在确定了股价、股息以及对股价与股息的预期情况下就能精确的确定出Agenti对股票的持有量了。

3.2.2、规则

   我们已经反复强调了，Agenti进行决策、学习的核心部分就是它的一组规则。具体来讲，如果Agenti具有m个规则，那么，对任意一条规则rulej来讲，它是形如下面这样的判断语句：

     （8）

   其中conditionj是条件部分，它是一个长度为60（与环境的编码长度一样）的位串：

         其中，#为通配符表示0或者1都可以，(aj,bj)为预期中的系数。因此不同的规则就会给出不同的预测。

   下面举例来进行具体的说明。假设Agenti有3条规则分别是（简化对环境的编码采用7位）：

1：if 01001## then (0.5,0.2)

2：if 0100110 then (0.4,0.8)

3：if 10###110 then (4.3,2)

   那么在运行中，如果在环境的编码为10010110，它刚好与第三条规则的条件部分匹配（注意#代表的是0或者1都可以匹配），那么Agenti就会采用规则3来对股票价格和股息进行预测，也就是利用4.3*(pt+dt)+2来得到t+1时刻的pt+1+dt+1。

   又例如当前环境的编码为0100110的话，可以看出规则1和2都与环境的编码匹配，那么我们就称规则1和规则2处于被激活状态。究竟用1或者2的哪一条规则呢？这需要Agenti对这些激活的规则进行排序，确定出在一个具体的条件下采用哪个规则。我们可以通过给每一条规则赋予一个实数值表示的强度来给激活的规则排序，也就是强度越大规则就会排在前面，反之排在后面。假设规则rulej的强度为，那么强度的计算公式就是：

     （9）

   其中，M是一个预先设定的常数，也是预先设定的系数，s是规则rulej的条件部分中为#的位数，例如上例中的规则1的s=2，规则2的s=0，是规则rulej的预测精度，一般随着系统的运行，通过比较预测与实际的差值来确定该项，具体使用下面的公式跌代：

     （10）

  其中为权重参数，，因此不同的规则得到不同的预测，从而根据实际运行的结果得到真实的来确定每一条规则预测的准确性。

   这样看来，如果在某种情况下有多条规则同时被激活的时候，那些预测准确的、能够得到具体条件的（也就是说s值偏小）的规则能够优先被使用。通过按照强度把激活规则进行排序，Agenti选出一个强度最高的规则来进行预测。当有两个以上的规则强度值相同的时候，则只能在这些规则中随机的选择一个了。这样，在我们上面的例子中，一般情况下规则2的强度大于规则1，所以Agenti选择用规则2来进行预测，从而用公式0.4*(pt+dt)+0.8得出对股价和股息的预测值。

3.3.3、===Agent的学习与创新功能===

   当在时刻t每个Agent的预测都结束了以后，根据第2节的叙述，环境部分中的分析专家就会根据每个Agent的股票需求量定出真实的t+1时刻的股票价格，并且随机过程会确定t+1时刻的股息。这个时候Agenti会根据这些真实的情况进行学习。所谓的学习就是要对m条规则的强度进行更新并且重新确定这m条规则的强度排序。强度更新主要是对规则的预测精度进行的，即按照（10）式进行更新。

   每个Agent还可以通过遗传算法进行创新，也就是通过变异和交叉来产生新的规则并利用选择的机制淘汰旧的规则。下面具体介绍遗传算法的运行机理。
  首先，根据强度我们可以把m条规则进行排序，从而得到一个序列：

     （11）

   其中排在前面的强度小，排在后面的强度大。然后挑出排在前面的k个规则淘汰掉，并且用k个新规则代替这些规则，这k个新的规则在剩下的m-k个规则基础上运用交叉与变异的操作得到。

   下面以例子说明变异和交叉是如何进行的，假如规则库中有两条规则是rule1: if 01001##011 then (3.5,6.8)和 rule2: if 01#0111#10 then (2,6.5)。

   首先说明变异操作，系统在m-k条不被淘汰的规则中任意选中一条规则进行变异，比如选中的规则就是rule1。针对条件部分，任意选择一位把这位上的编码转换成其它的，比如选择了第3位，那么把0变为#就得到了新规则的条件部分。针对结果部分可以让新规则的(a,b)在允许范围内随机的任意选值。比如a,b都在[-10,10]内取值，那么新的(a,b)就可以是(-5,2.8)，这样从规则1变异出的新规则为if 01#01##011 then (-5,2.8)。上述的变异过程如下示：

if 01001##011 then (3.5,6.8) -> if 01#01##011 then (-5,2.8)

   交叉操作首先需要在不被淘汰的规则选择两个规则作为父母，比如选择到rule1,rule2为父母进行交叉操作。针对条件部分，首先随机的选取一个位作为交叉位置，然后把两个串进行首尾的交换得到新的串，比如我们选择交叉位置为第5位，那么交叉操作如下图所示：

   针对结果部分，我们可以采取加权平均的办法得到新规则的结果。比如新规则的(a,b)可以通过,得到，其中w是权重系数，可以随机的确定。

   无论是交叉还是变异，得到的新规则的精确度都可以根据父母继承得到。Agent通过遗传算法可以得到新的规则并且淘汰旧的规则，这就既保证了创新性（由交叉和变异操作保证），又保证了优胜略汰的机制（由初始的规则排序并淘汰一部分规则保证）。另外，为了保证系统不会因为经常运用遗传算法而变得混乱不堪，所以我们制定了一个参数v表示运行遗传算法的概率，例如如果v=0.001则表示系统每运行1000次仿真周期才进行一次遗传算法的操作。

   至此，我们已经介绍了ASM模型的全部部分，下面看看，从这样的归纳学习系统中，我们到底能得到什么样的涌现结果。

本中文词条由许许编辑，欢迎在讨论页面留言。

本词条内容源自公开资料，遵守 CC3.0协议。