相变

来自集智百科 - 复杂系统|人工智能|复杂科学|复杂网络|自组织
Jie（讨论 | 贡献）2020年9月7日 (一) 01:17的版本
跳到导航 跳到搜索

此词条由Jie翻译


此图显示了不同相变的命名法

The term phase transition (or phase change) is most commonly used to describe transitions between solid, liquid, and gaseous states of matter, as well as plasma in rare cases. A phase of a thermodynamic system and the states of matter have uniform physical properties. During a phase transition of a given medium, certain properties of the medium change, often discontinuously, as a result of the change of external conditions, such as temperature, pressure, or others. For example, a liquid may become gas upon heating to the boiling point, resulting in an abrupt change in volume. The measurement of the external conditions at which the transformation occurs is termed the phase transition. Phase transitions commonly occur in nature and are used today in many technologies.

The term phase transition (or phase change) is most commonly used to describe transitions between solid, liquid, and gaseous states of matter, as well as plasma in rare cases. A phase of a thermodynamic system and the states of matter have uniform physical properties. During a phase transition of a given medium, certain properties of the medium change, often discontinuously, as a result of the change of external conditions, such as temperature, pressure, or others. For example, a liquid may become gas upon heating to the boiling point, resulting in an abrupt change in volume. The measurement of the external conditions at which the transformation occurs is termed the phase transition. Phase transitions commonly occur in nature and are used today in many technologies.

相变Phase transition (or phase change)一词常用于描述物质固态，液态和气态之间的转变，在极少数情况下还涉及到等离子体。热力学系统的相和物质的状态一样，均具有统一的物理特性。由于外部条件（例如温度，压力或其他）的变化，在给定介质的相变过程中，它的某些属性通常发生不连续地变化。例如，液体在加热到沸点的时候可能会变成气体，导致体积大小突然改变。当这种转变发生时，外部条件的度量称为相变。相变通常发生在自然界，不过如今越来越多地被用于科技行业。


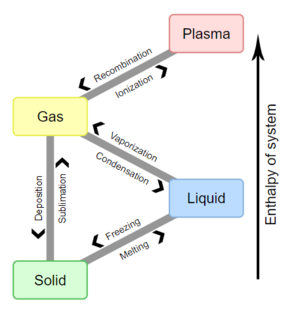
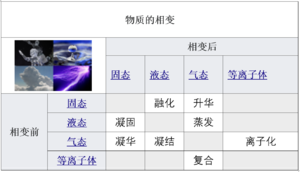
Types of phase transition 相变的种类

该图为典型的相图。其中虚线部分表示了水的反常行为

Examples of phase transitions include: Examples of phase transitions include: 关于相变的例子包括：


  • The transitions between the solid, liquid, and gaseous phases of a single component, due to the effects of temperature and/or pressure:

由于温度和/或压力的影响，单个成分物质的固态，液态和气态之间会产生相互变化：

参见蒸汽压和相图


文件:Argon ice 1.jpg
A small piece of rapidly melting solid argon simultaneously shows the transitions from solid to liquid and liquid to gas.

A small piece of rapidly melting solid argon simultaneously shows the transitions from solid to liquid and liquid to gas.

一小块快速熔化的固体氩同时显示固体到液体和液体到气体的转变

文件:Comparison carbon dioxide water phase diagrams.svg
Comparison of phase diagrams of carbon dioxide (red) and water (blue) explaining their different phase transitions at 1 atmosphere

Comparison of phase diagrams of carbon dioxide (red) and water (blue) explaining their different phase transitions at 1 atmosphere

二氧化碳(红色)和水(蓝色)相图解释它们在1个大气中不同相变的比较

Condensed matter physics
文件:QuantumPhaseTransition.svg
Phases模板:· Phase transition模板:· QCP
States of matter
Solid模板:· Liquid模板:· Gas模板:· Plasma模板:· Bose–Einstein condensate模板:· Bose gas模板:· Fermionic condensate模板:· Fermi gas模板:· Fermi liquid模板:· Supersolid模板:· Superfluidity模板:· Luttinger liquid 模板:· Time crystal




  • A eutectic transformation, in which a two-component single-phase liquid is cooled and transforms into two solid phases. The same process, but beginning with a solid instead of a liquid is called a eutectoid transformation.


  • A metastable to equilibrium phase transformation. A metastable polymorph which forms rapidly due to lower surface energy will transform to an equilibrium phase given sufficient thermal input to overcome an energetic barrier.


  • A peritectic transformation, in which a two-component single-phase solid is heated and transforms into a solid phase and a liquid phase.


  • A spinodal decomposition, in which a single phase is cooled and separates into two different compositions of that same phase.








  • The dependence of the adsorption geometry on coverage and temperature, such as for hydrogen on iron (110).


  • The emergence of superconductivity in certain metals and ceramics when cooled below a critical temperature.


  • The transition between different molecular structures (polymorphs, allotropes or [[polyamorphism|polyamorphs模板:Not a typo]]), especially of solids, such as between an amorphous structure and a crystal structure, between two different crystal structures, or between two amorphous structures.



  • The breaking of symmetries in the laws of physics during the early history of the universe as its temperature cooled.


  • Isotope fractionation occurs during a phase transition, the ratio of light to heavy isotopes in the involved molecules changes. When water vapor condenses (an equilibrium fractionation), the heavier water isotopes (18O and 2H) become enriched in the liquid phase while the lighter isotopes (16O and 1H) tend toward the vapor phase.[1]

}}</ref>

{} / ref



Phase transitions occur when the thermodynamic free energy of a system is non-analytic for some choice of thermodynamic variables (cf. phases). This condition generally stems from the interactions of a large number of particles in a system, and does not appear in systems that are too small. It is important to note that phase transitions can occur and are defined for non-thermodynamic systems, where temperature is not a parameter. Examples include: quantum phase transitions, dynamic phase transitions, and topological (structural) phase transitions. In these types of systems other parameters take the place of temperature. For instance, connection probability replaces temperature for percolating networks.

Phase transitions occur when the thermodynamic free energy of a system is non-analytic for some choice of thermodynamic variables (cf. phases). This condition generally stems from the interactions of a large number of particles in a system, and does not appear in systems that are too small. It is important to note that phase transitions can occur and are defined for non-thermodynamic systems, where temperature is not a parameter. Examples include: quantum phase transitions, dynamic phase transitions, and topological (structural) phase transitions. In these types of systems other parameters take the place of temperature. For instance, connection probability replaces temperature for percolating networks.

当系统的热力学自由能对于某些热力学变量的选择是非解析的时候，相变就发生了。阶段)。这种情况通常源于系统中大量粒子的相互作用，而不会出现在太小的系统中。重要的是要注意，相变可以发生，并定义了非热力学系统，其中温度不是一个参数。例子包括: 量子相变，动态相变，拓扑(结构)相变。在这些类型的系统中，其他参数取代了温度。例如，渗流网络的连接概率代替了温度。



At the phase transition point (for instance, boiling point) the two phases of a substance, liquid and vapor, have identical free energies and therefore are equally likely to exist. Below the boiling point, the liquid is the more stable state of the two, whereas above the gaseous form is preferred.

At the phase transition point (for instance, boiling point) the two phases of a substance, liquid and vapor, have identical free energies and therefore are equally likely to exist. Below the boiling point, the liquid is the more stable state of the two, whereas above the gaseous form is preferred.

在相变点(例如沸点) ，物质的两个相，液体和蒸汽，具有相同的自由能，因此存在的可能性相等。在沸点以下，液体是两者中较为稳定的状态，而在沸点以上的液体是首选的。



It is sometimes possible to change the state of a system diabatically (as opposed to adiabatically) in such a way that it can be brought past a phase transition point without undergoing a phase transition. The resulting state is metastable, i.e., less stable than the phase to which the transition would have occurred, but not unstable either. This occurs in superheating, supercooling, and supersaturation, for example.

It is sometimes possible to change the state of a system diabatically (as opposed to adiabatically) in such a way that it can be brought past a phase transition point without undergoing a phase transition. The resulting state is metastable, i.e., less stable than the phase to which the transition would have occurred, but not unstable either. This occurs in superheating, supercooling, and supersaturation, for example.

有时候可以通过不经历相变的方式来改变一个系统的状态(与绝热相反) ，使它能够通过一个相变点而不经历相变。结果状态是亚稳态的，也就是说，不如发生转变的相稳定，但也不是不稳定的。这发生在过热、过冷和过饱和，例如。


Classifications

分类



Ehrenfest classification

埃伦菲斯特分类法



Paul Ehrenfest classified phase transitions based on the behavior of the thermodynamic free energy as a function of other thermodynamic variables.[2] Under this scheme, phase transitions were labeled by the lowest derivative of the free energy that is discontinuous at the transition. First-order phase transitions exhibit a discontinuity in the first derivative of the free energy with respect to some thermodynamic variable.[3] The various solid/liquid/gas transitions are classified as first-order transitions because they involve a discontinuous change in density, which is the (inverse of the) first derivative of the free energy with respect to pressure. Second-order phase transitions are continuous in the first derivative (the order parameter, which is the first derivative of the free energy with respect to the external field, is continuous across the transition) but exhibit discontinuity in a second derivative of the free energy.[3] These include the ferromagnetic phase transition in materials such as iron, where the magnetization, which is the first derivative of the free energy with respect to the applied magnetic field strength, increases continuously from zero as the temperature is lowered below the Curie temperature. The magnetic susceptibility, the second derivative of the free energy with the field, changes discontinuously. Under the Ehrenfest classification scheme, there could in principle be third, fourth, and higher-order phase transitions.

Paul Ehrenfest classified phase transitions based on the behavior of the thermodynamic free energy as a function of other thermodynamic variables. Under this scheme, phase transitions were labeled by the lowest derivative of the free energy that is discontinuous at the transition. First-order phase transitions exhibit a discontinuity in the first derivative of the free energy with respect to some thermodynamic variable. The various solid/liquid/gas transitions are classified as first-order transitions because they involve a discontinuous change in density, which is the (inverse of the) first derivative of the free energy with respect to pressure. Second-order phase transitions are continuous in the first derivative (the order parameter, which is the first derivative of the free energy with respect to the external field, is continuous across the transition) but exhibit discontinuity in a second derivative of the free energy. These include the ferromagnetic phase transition in materials such as iron, where the magnetization, which is the first derivative of the free energy with respect to the applied magnetic field strength, increases continuously from zero as the temperature is lowered below the Curie temperature. The magnetic susceptibility, the second derivative of the free energy with the field, changes discontinuously. Under the Ehrenfest classification scheme, there could in principle be third, fourth, and higher-order phase transitions.

根据热力学自由能的行为，Paul Ehrenfest 将相变分类为其他热力学变量的函数。在这种方案下，相变被标记为自由能的最低导数，在相变处是不连续的。自由能对一些热力学变量的一阶导数表现出不连续性。不同的固体 / 液体 / 气体跃迁被归类为一级跃迁，因为它们涉及到密度的不连续变化，而密度变化是自由能对压强的一阶导数的倒数。二阶相变在一阶导数中是连续的(阶参数是自由能对外场的一阶导数，在二阶导数中是连续的) ，但在自由能的二阶导数中表现出不连续性。这些现象包括铁等材料中的铁磁相变，其中的磁化强度是自由能相对于外加磁场强度的一阶导数，当温度降到居里点以下时，磁化强度从零开始不断增加。磁化率，自由能与场的二阶导数，不连续地变化。在 Ehrenfest 分类方案下，原则上可能存在第三、第四和更高阶的相变。



The Ehrenfest classification implicitly allows for continuous phase transformations, where the bonding character of a material changes, but there is no discontinuity in any free energy derivative. An example of this occurs at the supercritical liquid–gas boundaries.

The Ehrenfest classification implicitly allows for continuous phase transformations, where the bonding character of a material changes, but there is no discontinuity in any free energy derivative. An example of this occurs at the supercritical liquid–gas boundaries.

Ehrenfest 的分类隐含地允许连续的相变，即物质的成键特性发生变化，但是在任何自由能导数中没有不连续性。这方面的一个例子发生在超临界液体-气体边界。



Modern classifications

现代分类

In the modern classification scheme, phase transitions are divided into two broad categories, named similarly to the Ehrenfest classes:[2]

In the modern classification scheme, phase transitions are divided into two broad categories, named similarly to the Ehrenfest classes:

在现代分类方案中，相变分为两大类，与 Ehrenfest 类似:



First-order phase transitions are those that involve a latent heat. During such a transition, a system either absorbs or releases a fixed (and typically large) amount of energy per volume. During this process, the temperature of the system will stay constant as heat is added: the system is in a "mixed-phase regime" in which some parts of the system have completed the transition and others have not.[4][5] Familiar examples are the melting of ice or the boiling of water (the water does not instantly turn into vapor, but forms a turbulent mixture of liquid water and vapor bubbles). Imry and Wortis showed that quenched disorder can broaden a first-order transition. That is, the transformation is completed over a finite range of temperatures, but phenomena like supercooling and superheating survive and hysteresis is observed on thermal cycling.[6][7][8]

First-order phase transitions are those that involve a latent heat. During such a transition, a system either absorbs or releases a fixed (and typically large) amount of energy per volume. During this process, the temperature of the system will stay constant as heat is added: the system is in a "mixed-phase regime" in which some parts of the system have completed the transition and others have not. Familiar examples are the melting of ice or the boiling of water (the water does not instantly turn into vapor, but forms a turbulent mixture of liquid water and vapor bubbles). Imry and Wortis showed that quenched disorder can broaden a first-order transition. That is, the transformation is completed over a finite range of temperatures, but phenomena like supercooling and superheating survive and hysteresis is observed on thermal cycling.

一级相变是指涉及潜热的相变。在这样的转变过程中，一个系统或者吸收或者释放一个固定的(通常是大量的)每卷能量。在这个过程中，随着加热，系统的温度将保持不变: 系统处于“混合相状态” ，其中系统的某些部分已经完成了过渡，而其他部分没有。我们熟悉的例子是冰的融化或水的沸腾(水不会立即变成水蒸气，而是形成液态水和水蒸气泡的混合物)。Imry 和 Wortis 的研究表明，淬灭无序扩展了一级转变。也就是说，相变是在一个有限的温度范围内完成的，但是在热循环过程中观察到过冷和过热保存以及滞后现象。



Second-order phase transitions are also called "continuous phase transitions". They are characterized by a divergent susceptibility, an infinite correlation length, and a power law decay of correlations near criticality. Examples of second-order phase transitions are the ferromagnetic transition, superconducting transition (for a Type-I superconductor the phase transition is second-order at zero external field and for a Type-II superconductor the phase transition is second-order for both normal-state—mixed-state and mixed-state—superconducting-state transitions) and the superfluid transition. In contrast to viscosity, thermal expansion and heat capacity of amorphous materials show a relatively sudden change at the glass transition temperature[9] which enables accurate detection using differential scanning calorimetry measurements. Lev Landau gave a phenomenological theory of second-order phase transitions.

Second-order phase transitions are also called "continuous phase transitions". They are characterized by a divergent susceptibility, an infinite correlation length, and a power law decay of correlations near criticality. Examples of second-order phase transitions are the ferromagnetic transition, superconducting transition (for a Type-I superconductor the phase transition is second-order at zero external field and for a Type-II superconductor the phase transition is second-order for both normal-state—mixed-state and mixed-state—superconducting-state transitions) and the superfluid transition. In contrast to viscosity, thermal expansion and heat capacity of amorphous materials show a relatively sudden change at the glass transition temperature which enables accurate detection using differential scanning calorimetry measurements. Lev Landau gave a phenomenological theory of second-order phase transitions.

二阶相变也称为“连续相变”。它们分别是发散极化率、无限相关长度和临界拥有属性附近关联衰减的幂次定律。二阶相变的例子有铁磁相变、超导相变和超流相变(一个第一类超导体的相变在零外场下为二阶，ii 型超导体的相变在正常态ー混合态和混合态ー超导态转变中均为二阶)。与粘度不同的是，非晶材料的热膨胀和热容在玻璃化转变温度处表现出相对突然的变化，这使得使用差示扫描量热法测量能够准确地检测出来。列夫 · 朗道提出了二阶相变的唯象理论。



Apart from isolated, simple phase transitions, there exist transition lines as well as multicritical points, when varying external parameters like the magnetic field or composition.

Apart from isolated, simple phase transitions, there exist transition lines as well as multicritical points, when varying external parameters like the magnetic field or composition.

除了孤立的、简单的相变外，当外部参数(如磁场或成分)变化时，还存在转变线和多临界点。



Several transitions are known as infinite-order phase transitions.

Several transitions are known as infinite-order phase transitions.

一些跃迁被称为无限级相变。

They are continuous but break no symmetries. The most famous example is the Kosterlitz–Thouless transition in the two-dimensional XY model. Many quantum phase transitions, e.g., in two-dimensional electron gases, belong to this class.

They are continuous but break no symmetries. The most famous example is the Kosterlitz–Thouless transition in the two-dimensional XY model. Many quantum phase transitions, e.g., in two-dimensional electron gases, belong to this class.

它们是连续的，但没有破坏对称性。最著名的例子是二维 XY 模型中的 Kosterlitz-千变万化。许多量子相变，例如在二维电子气体中，就属于这一类。



The liquid–glass transition is observed in many polymers and other liquids that can be supercooled far below the melting point of the crystalline phase. This is atypical in several respects. It is not a transition between thermodynamic ground states: it is widely believed that the true ground state is always crystalline. Glass is a quenched disorder state, and its entropy, density, and so on, depend on the thermal history. Therefore, the glass transition is primarily a dynamic phenomenon: on cooling a liquid, internal degrees of freedom successively fall out of equilibrium. Some theoretical methods predict an underlying phase transition in the hypothetical limit of infinitely long relaxation times.[10][11] No direct experimental evidence supports the existence of these transitions.

The liquid–glass transition is observed in many polymers and other liquids that can be supercooled far below the melting point of the crystalline phase. This is atypical in several respects. It is not a transition between thermodynamic ground states: it is widely believed that the true ground state is always crystalline. Glass is a quenched disorder state, and its entropy, density, and so on, depend on the thermal history. Therefore, the glass transition is primarily a dynamic phenomenon: on cooling a liquid, internal degrees of freedom successively fall out of equilibrium. Some theoretical methods predict an underlying phase transition in the hypothetical limit of infinitely long relaxation times. No direct experimental evidence supports the existence of these transitions.

在许多聚合物和其他液体中可以观察到液-玻转变，这些聚合物和液体可以被过冷到远低于结晶相的熔点。这在几个方面是非典型的。它不是热力学基态之间的过渡: 人们普遍认为真正的基态总是晶态的。玻璃是一种淬火无序态，其熵、密度等都依赖于热历史。因此，玻璃化转变主要是一种动态现象: 在冷却液体时，内部自由度相继失去平衡。一些理论方法预测了在无限长弛豫时间的假设极限下的潜在相变。没有直接的实验证据支持这些跃迁的存在。



Characteristic properties

特征属性



Phase coexistence

相共存

A disorder-broadened first-order transition occurs over a finite range of temperatures where the fraction of the low-temperature equilibrium phase grows from zero to one (100%) as the temperature is lowered. This continuous variation of the coexisting fractions with temperature raised interesting possibilities. On cooling, some liquids vitrify into a glass rather than transform to the equilibrium crystal phase. This happens if the cooling rate is faster than a critical cooling rate, and is attributed to the molecular motions becoming so slow that the molecules cannot rearrange into the crystal positions.[12] This slowing down happens below a glass-formation temperature Tg, which may depend on the applied pressure.[9][13] If the first-order freezing transition occurs over a range of temperatures, and Tg falls within this range, then there is an interesting possibility that the transition is arrested when it is partial and incomplete. Extending these ideas to first-order magnetic transitions being arrested at low temperatures, resulted in the observation of incomplete magnetic transitions, with two magnetic phases coexisting, down to the lowest temperature. First reported in the case of a ferromagnetic to anti-ferromagnetic transition,[14] such persistent phase coexistence has now been reported across a variety of first-order magnetic transitions. These include colossal-magnetoresistance manganite materials,[15][16] magnetocaloric materials,[17] magnetic shape memory materials,[18] and other materials.[19]

A disorder-broadened first-order transition occurs over a finite range of temperatures where the fraction of the low-temperature equilibrium phase grows from zero to one (100%) as the temperature is lowered. This continuous variation of the coexisting fractions with temperature raised interesting possibilities. On cooling, some liquids vitrify into a glass rather than transform to the equilibrium crystal phase. This happens if the cooling rate is faster than a critical cooling rate, and is attributed to the molecular motions becoming so slow that the molecules cannot rearrange into the crystal positions. This slowing down happens below a glass-formation temperature Tg, which may depend on the applied pressure. If the first-order freezing transition occurs over a range of temperatures, and Tg falls within this range, then there is an interesting possibility that the transition is arrested when it is partial and incomplete. Extending these ideas to first-order magnetic transitions being arrested at low temperatures, resulted in the observation of incomplete magnetic transitions, with two magnetic phases coexisting, down to the lowest temperature. First reported in the case of a ferromagnetic to anti-ferromagnetic transition, such persistent phase coexistence has now been reported across a variety of first-order magnetic transitions. These include colossal-magnetoresistance manganite materials, magnetocaloric materials, magnetic shape memory materials, and other materials.

在有限的温度范围内，随着温度的降低，低温平衡相的比例从零增长到一(100%) ，发生了无序扩展的一级转变。这种共存组分随温度的连续变化提供了有趣的可能性。在冷却时，一些液体玻璃化成玻璃而不是转变成平衡的晶体相。如果冷却速度比临界冷却速度快，就会发生这种情况，这是由于分子运动变得如此缓慢，以至于分子不能重新排列到晶体位置。这种减速发生在玻璃形成温度 Tg 以下，Tg 的高低可能取决于外加压力。如果一级冰冻转变发生在一定温度范围内，Tg 也在这个范围内，那么有一种有趣的可能性，即当转变是部分的和不完全的时候，转变就被阻止了。将这些想法扩展到低温下阻止的一级磁跃迁，导致观察到不完全的磁跃迁，两个磁相共存，直到最低温度。首先报道了在铁磁到反铁磁相变的情况下，这种持久的相共存现象现在已经在各种一级磁相变中被报道。这些材料包括庞磁电阻锰氧化物材料、磁热材料、磁形状记忆材料和其他材料。

The interesting feature of these observations of Tg falling within the temperature range over which the transition occurs is that the first-order magnetic transition is influenced by magnetic field, just like the structural transition is influenced by pressure. The relative ease with which magnetic fields can be controlled, in contrast to pressure, raises the possibility that one can study the interplay between Tg and Tc in an exhaustive way. Phase coexistence across first-order magnetic transitions will then enable the resolution of outstanding issues in understanding glasses.

The interesting feature of these observations of Tg falling within the temperature range over which the transition occurs is that the first-order magnetic transition is influenced by magnetic field, just like the structural transition is influenced by pressure. The relative ease with which magnetic fields can be controlled, in contrast to pressure, raises the possibility that one can study the interplay between Tg and Tc in an exhaustive way. Phase coexistence across first-order magnetic transitions will then enable the resolution of outstanding issues in understanding glasses.

观测到的玻璃化转变温度范围内的玻璃化转变的有趣特征是，一级磁转变受到磁场的影响，就像结构转变受到压力的影响一样。与压力相比，控制磁场的相对容易，使人们有可能详尽地研究 Tg 和 Tc 之间的相互作用。一阶磁跃迁中的相共存将使理解玻璃中突出问题的解决成为可能。


Critical points

关键点

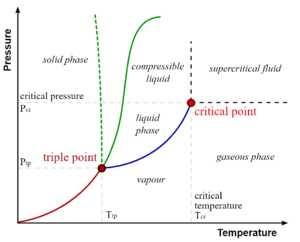
In any system containing liquid and gaseous phases, there exists a special combination of pressure and temperature, known as the critical point, at which the transition between liquid and gas becomes a second-order transition. Near the critical point, the fluid is sufficiently hot and compressed that the distinction between the liquid and gaseous phases is almost non-existent. This is associated with the phenomenon of critical opalescence, a milky appearance of the liquid due to density fluctuations at all possible wavelengths (including those of visible light).

In any system containing liquid and gaseous phases, there exists a special combination of pressure and temperature, known as the critical point, at which the transition between liquid and gas becomes a second-order transition. Near the critical point, the fluid is sufficiently hot and compressed that the distinction between the liquid and gaseous phases is almost non-existent. This is associated with the phenomenon of critical opalescence, a milky appearance of the liquid due to density fluctuations at all possible wavelengths (including those of visible light).

在任何含有液相和气相的体系中，都存在一种特殊的压力和温度组合，称为临界点，在这个临界点上液相和气相之间的转变成为二级转变。在临界点附近，流体温度足够高，受到压缩，几乎不存在液相和气相之间的区别。这与临界乳光现象有关，这种液体由于在所有可能的波长(包括可见光波长)上的密度波动而呈现出乳白色的外观。




Symmetry

对称性

Phase transitions often involve a symmetry breaking process. For instance, the cooling of a fluid into a crystalline solid breaks continuous translation symmetry: each point in the fluid has the same properties, but each point in a crystal does not have the same properties (unless the points are chosen from the lattice points of the crystal lattice). Typically, the high-temperature phase contains more symmetries than the low-temperature phase due to spontaneous symmetry breaking, with the exception of certain accidental symmetries (e.g. the formation of heavy virtual particles, which only occurs at low temperatures).[20]

Phase transitions often involve a symmetry breaking process. For instance, the cooling of a fluid into a crystalline solid breaks continuous translation symmetry: each point in the fluid has the same properties, but each point in a crystal does not have the same properties (unless the points are chosen from the lattice points of the crystal lattice). Typically, the high-temperature phase contains more symmetries than the low-temperature phase due to spontaneous symmetry breaking, with the exception of certain accidental symmetries (e.g. the formation of heavy virtual particles, which only occurs at low temperatures).

相变通常涉及一个对称性破缺过程。例如，将一种流体冷却到晶体中，就破坏了连续的平移对称性: 流体中的每个点都具有相同的属性，但是晶体中的每个点却不具有相同的属性(除非这些点是从晶格的点阵中选择的)。一般来说，由于自发对称性破缺的存在，高温相比低温相包含更多的对称性，除了某些偶然的对称性(例如:。重的虚粒子的形成，这只发生在低温下)。


Order parameters

订购参数! ——“订购参数”和“订购参数”重定向为 --

An order parameter is a measure of the degree of order across the boundaries in a phase transition system; it normally ranges between zero in one phase (usually above the critical point) and nonzero in the other.[21] At the critical point, the order parameter susceptibility will usually diverge.

An order parameter is a measure of the degree of order across the boundaries in a phase transition system; it normally ranges between zero in one phase (usually above the critical point) and nonzero in the other. At the critical point, the order parameter susceptibility will usually diverge.

一个序参数! ——每 wp: r # pla- 黑体字是一个相变系统中跨越边界的有序程度的度量; 它通常在一个相中的零(通常高于临界点)和另一个相中的非零之间。在临界点，有序参数极化率通常会发生偏离。



An example of an order parameter is the net magnetization in a ferromagnetic system undergoing a phase transition. For liquid/gas transitions, the order parameter is the difference of the densities.

An example of an order parameter is the net magnetization in a ferromagnetic system undergoing a phase transition. For liquid/gas transitions, the order parameter is the difference of the densities.

序参数的一个例子是正在发生相变的铁磁系统的净磁化。对于液体 / 气体跃迁，序参数是密度之差。



From a theoretical perspective, order parameters arise from symmetry breaking. When this happens, one needs to introduce one or more extra variables to describe the state of the system. For example, in the ferromagnetic phase, one must provide the net magnetization, whose direction was spontaneously chosen when the system cooled below the Curie point. However, note that order parameters can also be defined for non-symmetry-breaking transitions.

From a theoretical perspective, order parameters arise from symmetry breaking. When this happens, one needs to introduce one or more extra variables to describe the state of the system. For example, in the ferromagnetic phase, one must provide the net magnetization, whose direction was spontaneously chosen when the system cooled below the Curie point. However, note that order parameters can also be defined for non-symmetry-breaking transitions.

从理论的角度来看，顺序参数来源于对称性破缺。当这种情况发生时，需要引入一个或多个额外的变量来描述系统的状态。例如，在铁磁相中，必须提供净磁化强度，当系统冷却到居里点以下时，净磁化强度的方向是自发选择的。然而，请注意，序参数也可以定义为非对称破缺跃迁。



Some phase transitions, such as superconducting and ferromagnetic, can have order parameters for more than one degree of freedom. In such phases, the order parameter may take the form of a complex number, a vector, or even a tensor, the magnitude of which goes to zero at the phase transition.

Some phase transitions, such as superconducting and ferromagnetic, can have order parameters for more than one degree of freedom. In such phases, the order parameter may take the form of a complex number, a vector, or even a tensor, the magnitude of which goes to zero at the phase transition.

某些相变，如超导和铁磁，可以有一个以上自由度的有序参数。在这些阶段中，序参数可以采用复数、矢量甚至张量的形式，其大小在相变时为零。



There also exist dual descriptions of phase transitions in terms of disorder parameters. These indicate the presence of line-like excitations such as vortex- or defect lines.

There also exist dual descriptions of phase transitions in terms of disorder parameters. These indicate the presence of line-like excitations such as vortex- or defect lines.

此外，还存在用无序参数描述相变的双重描述。这些表明存在线状激发，如涡旋线或缺陷线。



Relevance in cosmology

宇宙学的相关性

Symmetry-breaking phase transitions play an important role in cosmology. As the universe expanded and cooled, the vacuum underwent a series of symmetry-breaking phase transitions. For example, the electroweak transition broke the SU(2)×U(1) symmetry of the electroweak field into the U(1) symmetry of the present-day electromagnetic field. This transition is important to understanding the asymmetry between the amount of matter and antimatter in the present-day universe (see electroweak baryogenesis).

Symmetry-breaking phase transitions play an important role in cosmology. As the universe expanded and cooled, the vacuum underwent a series of symmetry-breaking phase transitions. For example, the electroweak transition broke the SU(2)×U(1) symmetry of the electroweak field into the U(1) symmetry of the present-day electromagnetic field. This transition is important to understanding the asymmetry between the amount of matter and antimatter in the present-day universe (see electroweak baryogenesis).

对称破缺相变在宇宙学中占有重要地位。随着宇宙的膨胀和冷却，真空经历了一系列对称性破缺的相变。例如，电弱跃迁破坏了电弱场的 SU (2) u (1)对称性，进而破坏了现今电磁场的 u (1)对称性。这种转变对于理解当今宇宙中物质和反物质数量的不对称性很重要(见弱电子重子发生)。



Progressive phase transitions in an expanding universe are implicated in the development of order in the universe, as is illustrated by the work of Eric Chaisson[22] and David Layzer.[23]

Progressive phase transitions in an expanding universe are implicated in the development of order in the universe, as is illustrated by the work of Eric Chaisson and David Layzer.

正如 Eric Chaisson 和 David Layzer 的工作所说明的那样，在膨胀的宇宙中，渐进的相变牵涉到宇宙秩序的发展。



See also relational order theories and order and disorder.

See also relational order theories and order and disorder.

参见关系秩序理论和秩序与混乱。



Critical exponents and universality classes

临界指数和通用类

Main article: critical exponent


Continuous phase transitions are easier to study than first-order transitions due to the absence of latent heat, and they have been discovered to have many interesting properties. The phenomena associated with continuous phase transitions are called critical phenomena, due to their association with critical points.

Continuous phase transitions are easier to study than first-order transitions due to the absence of latent heat, and they have been discovered to have many interesting properties. The phenomena associated with continuous phase transitions are called critical phenomena, due to their association with critical points.

由于没有潜热，连续相变比一级相变更容易研究，并且已经发现它们具有许多有趣的性质。与连续相变有关的现象称为临界现象，因为它们与临界点有关。



It turns out that continuous phase transitions can be characterized by parameters known as critical exponents. The most important one is perhaps the exponent describing the divergence of the thermal correlation length by approaching the transition. For instance, let us examine the behavior of the heat capacity near such a transition. We vary the temperature T of the system while keeping all the other thermodynamic variables fixed, and find that the transition occurs at some critical temperature Tc . When T is near Tc , the heat capacity C typically has a power law behavior,

It turns out that continuous phase transitions can be characterized by parameters known as critical exponents. The most important one is perhaps the exponent describing the divergence of the thermal correlation length by approaching the transition. For instance, let us examine the behavior of the heat capacity near such a transition. We vary the temperature of the system while keeping all the other thermodynamic variables fixed, and find that the transition occurs at some critical temperature Tc . When is near Tc , the heat capacity typically has a power law behavior,

结果表明，连续的相变可以被称为临界指数的拥有属性参数。最重要的可能是描述热相关长度接近跃迁发散的指数。例如，让我们研究在这样一个转变附近的热容的行为。在保持其它热力学变量不变的情况下，改变体系的温度，发现转变发生在临界温度 t 子 c / sub。当接近 t 子 c / sub 时，热容通常具有幂律特性,

[math]\displaystyle{ C \propto |T_c - T|^{-\alpha}. }[/math]

[math]\displaystyle{ C \propto |T_c - T|^{-\alpha}. }[/math]

数学 c propto | tc-t | ^ {- alpha } . / math



The heat capacity of amorphous materials has such a behaviour near the glass transition temperature where the universal critical exponent α = 0.59[24] A similar behavior, but with the exponent ν instead of α, applies for the correlation length.

The heat capacity of amorphous materials has such a behaviour near the glass transition temperature where the universal critical exponent α = 0.59 A similar behavior, but with the exponent instead of , applies for the correlation length.

非晶态材料的热容在玻璃化转变温度附近具有这样的行为，在这个温度附近，通用临界指数0.59 a 具有类似的行为，但相关长度是指数而不是。



The exponent ν is positive. This is different with α. Its actual value depends on the type of phase transition we are considering.

The exponent is positive. This is different with . Its actual value depends on the type of phase transition we are considering.

指数是正的。这是不同的。它的实际价值取决于我们正在考虑的相变类型。



It is widely believed that the critical exponents are the same above and below the critical temperature. It has now been shown that this is not necessarily true: When a continuous symmetry is explicitly broken down to a discrete symmetry by irrelevant (in the renormalization group sense) anisotropies, then some exponents (such as [math]\displaystyle{ \gamma }[/math], the exponent of the susceptibility) are not identical.[25]

It is widely believed that the critical exponents are the same above and below the critical temperature. It has now been shown that this is not necessarily true: When a continuous symmetry is explicitly broken down to a discrete symmetry by irrelevant (in the renormalization group sense) anisotropies, then some exponents (such as [math]\displaystyle{ \gamma }[/math], the exponent of the susceptibility) are not identical.

人们普遍认为，临界指数在临界温度上下是相同的。现在已经证明，这并不一定是正确的: 当一个连续对称被显式地分解为离散对称由无关的(在重整化群意义上)各向异性，然后一些指数(如数学伽马 / 数学，易感性指数)是不相同的。



For −1 < α < 0, the heat capacity has a "kink" at the transition temperature. This is the behavior of liquid helium at the lambda transition from a normal state to the superfluid state, for which experiments have found α = -0.013±0.003.

For −1 < α < 0, the heat capacity has a "kink" at the transition temperature. This is the behavior of liquid helium at the lambda transition from a normal state to the superfluid state, for which experiments have found = -0.013±0.003.

对于 -10，热容在转变温度处有一个“扭结”。这是 Lambda相变中液氦从正常状态到超流体状态的行为，实验发现-0.0130.003。

At least one experiment was performed in the zero-gravity conditions of an orbiting satellite to minimize pressure differences in the sample.[26] This experimental value of α agrees with theoretical predictions based on variational perturbation theory.[27]

At least one experiment was performed in the zero-gravity conditions of an orbiting satellite to minimize pressure differences in the sample. This experimental value of α agrees with theoretical predictions based on variational perturbation theory.

在轨道卫星的零重力条件下至少进行了一次实验，以尽量减小样品中的压力差。这个实验值与基于变分摄动理论的理论预测一致。



For 0 < α < 1, the heat capacity diverges at the transition temperature (though, since α < 1, the enthalpy stays finite). An example of such behavior is the 3D ferromagnetic phase transition. In the three-dimensional Ising model for uniaxial magnets, detailed theoretical studies have yielded the exponent α ∼ +0.110.

For 0 < < 1, the heat capacity diverges at the transition temperature (though, since < 1, the enthalpy stays finite). An example of such behavior is the 3D ferromagnetic phase transition. In the three-dimensional Ising model for uniaxial magnets, detailed theoretical studies have yielded the exponent ∼ +0.110.

对于01，热容在转变温度处发生分化(尽管自1以来，焓保持有限)。这种行为的一个例子是三维铁磁相变。在单轴磁体的三维伊辛模型中，详细的理论研究得到了指数∼0.110。



Some model systems do not obey a power-law behavior. For example, mean field theory predicts a finite discontinuity of the heat capacity at the transition temperature, and the two-dimensional Ising model has a logarithmic divergence. However, these systems are limiting cases and an exception to the rule. Real phase transitions exhibit power-law behavior.

Some model systems do not obey a power-law behavior. For example, mean field theory predicts a finite discontinuity of the heat capacity at the transition temperature, and the two-dimensional Ising model has a logarithmic divergence. However, these systems are limiting cases and an exception to the rule. Real phase transitions exhibit power-law behavior.

有些模型系统不遵守幂律行为。例如，平均场理论预测在转变温度下热容有限的不连续性，而二维伊辛模型具有对数发散性。然而，这些系统是有限的情况和规则的例外。实际相变呈现幂律行为。



Several other critical exponents, β, γ, δ, ν, and η, are defined, examining the power law behavior of a measurable physical quantity near the phase transition. Exponents are related by scaling relations, such as

Several other critical exponents, , and , are defined, examining the power law behavior of a measurable physical quantity near the phase transition. Exponents are related by scaling relations, such as

定义了其他几个临界指数，，和，检验了在相变附近可测量的物理量的幂律行为。指数通过缩放关系相关，例如

[math]\displaystyle{ \beta=\gamma/(\delta-1) , \qquad \nu=\gamma/(2-\eta) }[/math].

[math]\displaystyle{ \beta=\gamma/(\delta-1) , \qquad \nu=\gamma/(2-\eta) }[/math].

数学 beta gamma / ( delta-1) qquad nu gamma / (2- eta) / math。

It can be shown that there are only two independent exponents, e.g. ν and η.

It can be shown that there are only two independent exponents, e.g. and .

可以证明只有两个独立的指数，例如。及。



It is a remarkable fact that phase transitions arising in different systems often possess the same set of critical exponents. This phenomenon is known as universality. For example, the critical exponents at the liquid–gas critical point have been found to be independent of the chemical composition of the fluid.

It is a remarkable fact that phase transitions arising in different systems often possess the same set of critical exponents. This phenomenon is known as universality. For example, the critical exponents at the liquid–gas critical point have been found to be independent of the chemical composition of the fluid.

在不同系统中出现的相变通常具有相同的临界指数，这是一个值得注意的事实。这种现象被称为普遍性。例如，已经发现液气临界点的临界指数与流体的化学成份无关。



More impressively, but understandably from above, they are an exact match for the critical exponents of the ferromagnetic phase transition in uniaxial magnets. Such systems are said to be in the same universality class. Universality is a prediction of the renormalization group theory of phase transitions, which states that the thermodynamic properties of a system near a phase transition depend only on a small number of features, such as dimensionality and symmetry, and are insensitive to the underlying microscopic properties of the system. Again, the divergence of the correlation length is the essential point.

More impressively, but understandably from above, they are an exact match for the critical exponents of the ferromagnetic phase transition in uniaxial magnets. Such systems are said to be in the same universality class. Universality is a prediction of the renormalization group theory of phase transitions, which states that the thermodynamic properties of a system near a phase transition depend only on a small number of features, such as dimensionality and symmetry, and are insensitive to the underlying microscopic properties of the system. Again, the divergence of the correlation length is the essential point.

更令人印象深刻的是，从上面可以理解，它们与单轴磁体中铁磁相变的临界指数完全匹配。这样的系统据说属于同一个普遍性类别。普适性是重整化群相变理论的一种预测，该理论认为相变附近系统的热力学性质只依赖于少量的特征，如维数和对称性，并且对系统的潜在微观性质不敏感。同样，相关长度的散度是本质点。



Critical slowing down and other phenomena

临界减速和其他现象

There are also other critical phenomena; e.g., besides static functions there is also critical dynamics. As a consequence, at a phase transition one may observe critical slowing down or speeding up. The large static universality classes of a continuous phase transition split into smaller dynamic universality classes. In addition to the critical exponents, there are also universal relations for certain static or dynamic functions of the magnetic fields and temperature differences from the critical value.

There are also other critical phenomena; e.g., besides static functions there is also critical dynamics. As a consequence, at a phase transition one may observe critical slowing down or speeding up. The large static universality classes of a continuous phase transition split into smaller dynamic universality classes. In addition to the critical exponents, there are also universal relations for certain static or dynamic functions of the magnetic fields and temperature differences from the critical value.

还有其他关键现象，例如，除了静态函数之外，还有关键动力学。因此，在相变过程中，我们可以观察到关键的减速或加速。连续相变的大静态普适性类分裂为较小的动态普适性类。除了临界指数外，磁场的某些静态或动态函数与临界值之间的温度差也存在普遍关系。



Percolation theory

逾渗理论

Another phenomenon which shows phase transitions and critical exponents is percolation. The simplest example is perhaps percolation in a two dimensional square lattice. Sites are randomly occupied with probability p. For small values of p the occupied sites form only small clusters. At a certain threshold pc a giant cluster is formed and we have a second-order phase transition.[28] The behavior of P∞ near pc is, P∞~(p-pc)β, where β is a critical exponent.

Another phenomenon which shows phase transitions and critical exponents is percolation. The simplest example is perhaps percolation in a two dimensional square lattice. Sites are randomly occupied with probability p. For small values of p the occupied sites form only small clusters. At a certain threshold pc a giant cluster is formed and we have a second-order phase transition. The behavior of P∞ near pc is, P∞~(p-pc)β, where β is a critical exponent.

另一个显示相变和临界指数的现象是逾渗。最简单的例子也许是二维正方形格子中的渗流。位点以概率 p 随机占据。对于 p 的小值，占据的位点只形成小的集群。在一定的阈值条件下，形成了一个巨大的团簇，并且发生了二阶相变。P 子∞ / 子在 p 子 c / 子附近的行为是，p 子∞ / 子 ~ (p-p 子 c / 子) sup / sup，这里是临界指数。


! -- 相变的平均场理论 --


! -- 波动 --


! -- 相变的重整化群理论 --


! -- om sairam--




Phase transitions in biological systems

生物系统中的相变

Phase transitions play many important roles in biological systems. Examples include the lipid bilayer formation, the coil-globule transition in the process of protein folding and DNA melting, liquid crystal-like transitions in the process of DNA condensation, and cooperative ligand binding to DNA and proteins with the character of phase transition.[29]

Phase transitions play many important roles in biological systems. Examples include the lipid bilayer formation, the coil-globule transition in the process of protein folding and DNA melting, liquid crystal-like transitions in the process of DNA condensation, and cooperative ligand binding to DNA and proteins with the character of phase transition.

相变在生物体系中起着重要的作用。其中包括脂质双分子层的形成，蛋白质折叠和 DNA 熔融过程中的线圈-球状转变，DNA 凝聚过程中的液晶转变，以及具有相变特征的配体与 DNA 和蛋白质的合作结合。



In biological membranes, gel to liquid crystalline phase transitions play a critical role in physiological functioning of biomembranes. In gel phase, due to low fluidity of membrane lipid fatty-acyl chains, membrane proteins have restricted movement and thus are restrained in exercise of their physiological role. Plants depend critically on photosynthesis by chloroplast thylakoid membranes which are exposed cold environmental temperatures. Thylakoid membranes retain innate fluidity even at relatively low temperatures because of high degree of fatty-acyl disorder allowed by their high content of linolenic acid, 18-carbon chain with 3-double bonds.[30] Gel-to-liquid crystalline phase transition temperature of biological membranes can be determined by many techniques including calorimetry, fluorescence, spin label electron paramagnetic resonance and NMR by recording measurements of the concerned parameter by at series of sample temperatures. A simple method for its determination from 13-C NMR line intensities has also been proposed.[31]

In biological membranes, gel to liquid crystalline phase transitions play a critical role in physiological functioning of biomembranes. In gel phase, due to low fluidity of membrane lipid fatty-acyl chains, membrane proteins have restricted movement and thus are restrained in exercise of their physiological role. Plants depend critically on photosynthesis by chloroplast thylakoid membranes which are exposed cold environmental temperatures. Thylakoid membranes retain innate fluidity even at relatively low temperatures because of high degree of fatty-acyl disorder allowed by their high content of linolenic acid, 18-carbon chain with 3-double bonds. Gel-to-liquid crystalline phase transition temperature of biological membranes can be determined by many techniques including calorimetry, fluorescence, spin label electron paramagnetic resonance and NMR by recording measurements of the concerned parameter by at series of sample temperatures. A simple method for its determination from 13-C NMR line intensities has also been proposed.

在生物膜中，凝胶到液晶的相变对生物膜的生理功能起着至关重要的作用。在凝胶期，由于膜脂脂肪酰基链的低流动性，膜蛋白的运动受到限制，从而限制了其生理作用的发挥。植物主要依靠暴露在低温环境下的叶绿体类囊体膜的光合作用。类囊体膜即使在相对较低的温度下也能保持固有的流动性，这是由于其高含量的亚麻酸、18碳链和3- 双键所致的高度脂肪酰基无序所致。生物膜的凝胶-液晶相变温度可以通过量热法、荧光法、自旋标记电子自旋共振法和核磁共振(NMR)等多种方法测定。本文还提出了一种从13-C NMR 谱线强度测定其含量的简便方法。



It has been proposed that some biological systems might lie near critical points. Examples include neural networks in the salamander retina,[32] bird flocks[33]

It has been proposed that some biological systems might lie near critical points. Examples include neural networks in the salamander retina, bird flocks

有人提出，一些生物系统可能处于临界点附近。例如蝾螈视网膜中的神经网络，鸟群

gene expression networks in Drosophila,[34] and protein folding.[35] However, it is not clear whether or not alternative reasons could explain some of the phenomena supporting arguments for criticality.[36] It has also been suggested that biological organisms share two key properties of phase transitions: the change of macroscopic behavior and the coherence of a system at a critical point.[37]

gene expression networks in Drosophila, and protein folding. However, it is not clear whether or not alternative reasons could explain some of the phenomena supporting arguments for criticality. It has also been suggested that biological organisms share two key properties of phase transitions: the change of macroscopic behavior and the coherence of a system at a critical point.

果蝇的基因表达网络和蛋白质折叠。然而，尚不清楚替代原因是否可以解释支持临界性论点的一些现象。还有人提出，生物有机体具有相变的两个关键属性: 宏观行为的变化和系统在临界点的一致性。



In groups of organisms in stress (when approaching critical transitions), correlations tend to increase, while at the same time, fluctuations also increase. This effect is supported by many experiments and observations of groups of people, mice, trees, and grassy plants.[38]

In groups of organisms in stress (when approaching critical transitions), correlations tend to increase, while at the same time, fluctuations also increase. This effect is supported by many experiments and observations of groups of people, mice, trees, and grassy plants.

在受到压力的生物群体中(当接近临界转变时) ，相关性倾向于增加，同时波动也增加。这种效应得到了许多实验和观察的支持，这些实验和观察对象包括人群、老鼠、树木和草本植物。




Experimental

实验性的

A variety of methods are applied for studying the various effects. Selected examples are:

A variety of methods are applied for studying the various effects. Selected examples are:

各种方法被用来研究各种效应。选定的例子如下:





  • SQUID (measurement of magnetic transitions)



  • Mössbauer spectroscopy (simultaneous measurement of magnetic and non-magnetic transitions. Limited up to about 800-1000 °C)





See also

参见























References

参考资料

  1. ↑ Carol Kendall 作者: Carol Kendall (2004 2004年). [http://wwwrcamnl.wr.usgs.gov/isoig/res/funda.html Http://wwwrcamnl.wr.usgs.gov/isoig/res/funda.html "Fundamentals of Stable Isotope Geochemistry 稳定同位素地质学的基本原理"]. USGS 美国地质勘探局. Retrieved 10 April 2014 2014年4月10日. {{cite web}}: Check |url= value (help); Check date values in: |accessdate= and |year= (help); line feed character in |accessdate= at position 14 (help); line feed character in |author= at position 14 (help); line feed character in |publisher= at position 5 (help); line feed character in |title= at position 44 (help); line feed character in |url= at position 50 (help); line feed character in |year= at position 5 (help)
  2. ↑ 2.0 2.1 Jaeger, Gregg (1 May 1998). "The Ehrenfest Classification of Phase Transitions: Introduction and Evolution". Archive for History of Exact Sciences. 53 (1): 51–81. doi:10.1007/s004070050021.
  3. ↑ 3.0 3.1 Blundell, Stephen J.; Katherine M. Blundell (2008). Concepts in Thermal Physics. Oxford University Press. ISBN 978-0-19-856770-7. 
  4. ↑ Faghri, A., and Zhang, Y., Transport Phenomena in Multiphase Systems, Elsevier, Burlington, MA, 2006,
  5. ↑ Faghri, A., and Zhang, Y., Fundamentals of Multiphase Heat Transfer and Flow, Springer, New York, NY, 2020
  6. ↑ Imry, Y.; Wortis, M. (1979). "Influence of quenched impurities on first-order phase transitions". Phys. Rev. B. 19 (7): 3580–3585. Bibcode:1979PhRvB..19.3580I. doi:10.1103/physrevb.19.3580.
  7. ↑ Kumar, Kranti; Pramanik, A. K.; Banerjee, A.; Chaddah, P.; Roy, S. B.; Park, S.; Zhang, C. L.; Cheong, S.-W. (2006). "Relating supercooling and glass-like arrest of kinetics for phase separated systems: DopedCeFe2and(La,Pr,Ca)MnO3". Physical Review B. 73 (18): 184435. arXiv:cond-mat/0602627. Bibcode:2006PhRvB..73r4435K. doi:10.1103/PhysRevB.73.184435. ISSN 1098-0121.
  8. ↑ Pasquini, G.; Daroca, D. Pérez; Chiliotte, C.; Lozano, G. S.; Bekeris, V. (2008). "Ordered, Disordered, and Coexistent Stable Vortex Lattices inNbSe2Single Crystals". Physical Review Letters. 100 (24): 247003. arXiv:0803.0307. Bibcode:2008PhRvL.100x7003P. doi:10.1103/PhysRevLett.100.247003. ISSN 0031-9007. PMID 18643617.
  9. ↑ 9.0 9.1 Ojovan, M.I. (2013). "Ordering and structural changes at the glass-liquid transition". J. Non-Cryst. Solids. 382: 79–86. Bibcode:2013JNCS..382...79O. doi:10.1016/j.jnoncrysol.2013.10.016.
  10. ↑ Gotze, Wolfgang. "Complex Dynamics of Glass-Forming Liquids: A Mode-Coupling Theory."
  11. ↑ Lubchenko, V. Wolynes; Wolynes, Peter G. (2007). "Theory of Structural Glasses and Supercooled Liquids". Annual Review of Physical Chemistry. 58: 235–266. arXiv:cond-mat/0607349. Bibcode:2007ARPC...58..235L. doi:10.1146/annurev.physchem.58.032806.104653. PMID 17067282.
  12. ↑ Greer, A. L. (1995). "Metallic Glasses". Science. 267 (5206): 1947–1953. Bibcode:1995Sci...267.1947G. doi:10.1126/science.267.5206.1947. PMID 17770105.
  13. ↑ Tarjus, G. (2007). "Materials science: Metal turned to glass". Nature. 448 (7155): 758–759. Bibcode:2007Natur.448..758T. doi:10.1038/448758a. PMID 17700684.
  14. ↑ Manekar, M. A.; Chaudhary, S.; Chattopadhyay, M. K.; Singh, K. J.; Roy, S. B.; Chaddah, P. (2001). "First-order transition from antiferromagnetism to ferromagnetism inCe(Fe0.96Al0.04)2". Physical Review B. 64 (10): 104416. arXiv:cond-mat/0012472. Bibcode:2001PhRvB..64j4416M. doi:10.1103/PhysRevB.64.104416. ISSN 0163-1829.
  15. ↑ Banerjee, A; Pramanik, A K; Kumar, Kranti; Chaddah, P (2006). "Coexisting tunable fractions of glassy and equilibrium long-range-order phases in manganites". Journal of Physics: Condensed Matter. 18 (49): L605. arXiv:cond-mat/0611152. Bibcode:2006JPCM...18L.605B. doi:10.1088/0953-8984/18/49/L02.
  16. ↑ Wu W, Israel C, Hur N, Park S, Cheong SW, de Lozanne A (2006). "Magnetic imaging of a supercooling glass transition in a weakly disordered ferromagnet". Nature Materials. 5 (11): 881–886. Bibcode:2006NatMa...5..881W. doi:10.1038/nmat1743. PMID 17028576.
  17. ↑ Roy, S. B.; Chattopadhyay, M. K.; Chaddah, P.; Moore, J. D.; Perkins, G. K.; Cohen, L. F.; Gschneidner, K. A.; Pecharsky, V. K. (2006). "Evidence of a magnetic glass state in the magnetocaloric materialGd5Ge4". Physical Review B. 74 (1): 012403. Bibcode:2006PhRvB..74a2403R. doi:10.1103/PhysRevB.74.012403. ISSN 1098-0121.
  18. ↑ Lakhani, Archana; Banerjee, A; Chaddah, P; Chen, X; Ramanujan, R V (2012). "Magnetic glass in shape memory alloy: Ni45Co5Mn38Sn12". Journal of Physics: Condensed Matter. 24 (38): 386004. arXiv:1206.2024. Bibcode:2012JPCM...24L6004L. doi:10.1088/0953-8984/24/38/386004. ISSN 0953-8984. PMID 22927562.
  19. ↑ Kushwaha, Pallavi; Lakhani, Archana; Rawat, R.; Chaddah, P. (2009). "Low-temperature study of field-induced antiferromagnetic-ferromagnetic transition in Pd-doped Fe-Rh". Physical Review B. 80 (17): 174413. arXiv:0911.4552. Bibcode:2009PhRvB..80q4413K. doi:10.1103/PhysRevB.80.174413. ISSN 1098-0121.
  20. ↑ Ivancevic, Vladimir G.; Ivancevic, Tijiana, T. (2008). Complex Nonlinearity. Berlin: Springer. pp. 176–177. ISBN 978-3-540-79357-1. https://books.google.com/?id=wpsPgHgtxEYC&pg=PA177. Retrieved 12 October 2014. 
  21. ↑ A. D. McNaught and A. Wilkinson, ed. (1997). Compendium of Chemical Terminology. IUPAC. ISBN 978-0-86542-684-9. http://goldbook.iupac.org/goldbook/O04323.html. Retrieved 2007-10-23. https://en.wikipedia.org/wiki/Defekte_Weblinks?dwl={{{url}}} Seite nicht mehr abrufbar], Suche in Webarchiven: Kategorie:Wikipedia:Weblink offline (andere Namensräume)[http://timetravel.mementoweb.org/list/2010/Kategorie:Wikipedia:Vorlagenfehler/Vorlage:Toter Link/URL_fehlt
  22. ↑ Chaisson, Eric J. (2001). Cosmic Evolution. Harvard University Press. ISBN 9780674003422. https://archive.org/details/cosmicevolutionr00chai. 
  23. ↑ David Layzer, Cosmogenesis, The Development of Order in the Universe, Oxford Univ. Press, 1991
  24. ↑ Ojovan, Michael I; Lee, William E (2006). "Topologically disordered systems at the glass transition" (PDF). Journal of Physics: Condensed Matter. 18 (50): 11507–11520. Bibcode:2006JPCM...1811507O. doi:10.1088/0953-8984/18/50/007.
  25. ↑ Leonard, F.; Delamotte, B. (2015). "Critical exponents can be different on the two sides of a transition". Phys. Rev. Lett. 115 (20): 200601. arXiv:1508.07852. Bibcode:2015PhRvL.115t0601L. doi:10.1103/PhysRevLett.115.200601. PMID 26613426.
  26. ↑ Lipa, J.; Nissen, J.; Stricker, D.; Swanson, D.; Chui, T. (2003). "Specific heat of liquid helium in zero gravity very near the lambda point". Physical Review B. 68 (17): 174518. arXiv:cond-mat/0310163. Bibcode:2003PhRvB..68q4518L. doi:10.1103/PhysRevB.68.174518.
  27. ↑ Kleinert, Hagen (1999). "Critical exponents from seven-loop strong-coupling φ4 theory in three dimensions". Physical Review D. 60 (8): 085001. arXiv:hep-th/9812197. Bibcode:1999PhRvD..60h5001K. doi:10.1103/PhysRevD.60.085001.
  28. ↑ Armin Bunde and Shlomo Havlin (1996). Fractals and Disordered Systems. Springer. http://havlin.biu.ac.il/Shlomo%20Havlin%20books_fds.php. 
  29. ↑ D.Y. Lando and V.B. Teif (2000). "Long-range interactions between ligands bound to a DNA molecule give rise to adsorption with the character of phase transition of the first kind". J. Biomol. Struct. Dynam. 17 (5): 903–911. doi:10.1080/07391102.2000.10506578. PMID 10798534.
  30. ↑ YashRoy, R.C. (1987). "13-C NMR studies of lipid fatty acyl chains of chloroplast membranes". Indian Journal of Biochemistry and Biophysics. 24 (6): 177–178.
  31. ↑ YashRoy, R C (1990). "Determination of membrane lipid phase transition temperature from 13-C NMR intensities". Journal of Biochemical and Biophysical Methods. 20 (4): 353–356. doi:10.1016/0165-022X(90)90097-V. PMID 2365951.
  32. ↑ Tkacik, Gasper; Mora, Thierry; Marre, Olivier; Amodei, Dario; Berry II, Michael J.; Bialek, William (2014). "Thermodynamics for a network of neurons: Signatures of criticality". arXiv:1407.5946 [q-bio.NC].
  33. ↑ Bialek, W; Cavagna, A; Giardina, I (2014). "Social interactions dominate speed control in poising natural flocks near criticality". PNAS. 111 (20): 7212–7217. arXiv:1307.5563. Bibcode:2014PNAS..111.7212B. doi:10.1073/pnas.1324045111. PMC 4034227. PMID 24785504.
  34. ↑ Krotov, D; Dubuis, J O; Gregor, T; Bialek, W (2014). "Morphogenesis at criticality". PNAS. 111 (10): 3683–3688. arXiv:1309.2614. Bibcode:2014PNAS..111.3683K. doi:10.1073/pnas.1324186111. PMC 3956198. PMID 24516161.
  35. ↑ Mora, Thierry; Bialek, William (2011). "Are biological systems poised at criticality?". Journal of Statistical Physics. 144 (2): 268–302. arXiv:1012.2242. Bibcode:2011JSP...144..268M. doi:10.1007/s10955-011-0229-4.
  36. ↑ Schwab, David J; Nemenman, Ilya; Mehta, Pankaj (2014). "Zipf's law and criticality in multivariate data without fine-tuning". Physical Review Letters. 113 (6): 068102. arXiv:1310.0448. Bibcode:2014PhRvL.113f8102S. doi:10.1103/PhysRevLett.113.068102. PMC 5142845. PMID 25148352.
  37. ↑ Longo, G.; Montévil, M. (2011-08-01). "From physics to biology by extending criticality and symmetry breakings". Progress in Biophysics and Molecular Biology. Systems Biology and Cancer. 106 (2): 340–347. arXiv:1103.1833. doi:10.1016/j.pbiomolbio.2011.03.005. PMID 21419157.
  38. ↑ Gorban, A.N.; Smirnova, E.V.; Tyukina, T.A. (August 2010). "Correlations, risk and crisis: From physiology to finance". Physica A: Statistical Mechanics and Its Applications. 389 (16): 3193–3217. arXiv:0905.0129. Bibcode:2010PhyA..389.3193G. doi:10.1016/j.physa.2010.03.035.




Further reading

进一步阅读




  • Goldenfeld, N., Lectures on Phase Transitions and the Renormalization Group, Perseus Publishing (1992).



  • M.R.Khoshbin-e-Khoshnazar, Ice Phase Transition as a sample of finite system phase transition, (Physics Education(India)Volume 32. No. 2, Apr - Jun 2016)[1]


取自“https://wiki.swarma.org/index.php?title=相变&oldid=13749”