匹配生长模型

来自集智百科 - 复杂系统|人工智能|复杂科学|复杂网络|自组织
Moonscar（讨论 | 贡献）2020年9月8日 (二) 22:08的版本 （Moved page from wikipedia:en:Complex network (history)）
(差异) ←上一版本 | 最后版本 (差异) | 下一版本→ (差异)
跳到导航 跳到搜索

此词条暂由彩云小译翻译，未经人工整理和审校，带来阅读不便，请见谅。

"Complex networks" redirects here. For the company, see Complex Networks.
Network science
模板:CSS image crop
模板:Hlist
Network types
Graphs
Features
Types
模板:Hlist
Models
Topology
Dynamics
模板:Hlist

In the context of network theory, a complex network is a graph (network) with non-trivial topological features—features that do not occur in simple networks such as lattices or random graphs but often occur in graphs modelling of real systems. The study of complex networks is a young and active area of scientific research[1][2][3] (since 2000) inspired largely by the empirical study of real-world networks such as computer networks, biological networks, technological networks, brain networks, climate networks and social networks.

In the context of network theory, a complex network is a graph (network) with non-trivial topological features—features that do not occur in simple networks such as lattices or random graphs but often occur in graphs modelling of real systems. The study of complex networks is a young and active area of scientific research (since 2000) inspired largely by the empirical study of real-world networks such as computer networks, biological networks, technological networks, brain networks, climate networks and social networks.

在网络理论的背景下，复杂网络是一个具有非平凡拓扑特征的图形(网络)——这些特征不会出现在简单的网络中，如格子或随机图，而是经常出现在真实系统的图形建模中。复杂网络研究是一个年轻而活跃的科学研究领域(自2000年以来) ，其灵感主要来自对现实世界网络的实证研究，如计算机网络、生物网络、技术网络、大脑网络、气候网络和社会网络。


Definition

Most social, biological, and technological networks display substantial non-trivial topological features, with patterns of connection between their elements that are neither purely regular nor purely random. Such features include a heavy tail in the degree distribution, a high clustering coefficient, assortativity or disassortativity among vertices, community structure, and hierarchical structure. In the case of directed networks these features also include reciprocity, triad significance profile and other features. In contrast, many of the mathematical models of networks that have been studied in the past, such as lattices and random graphs, do not show these features. The most complex structures can be realized by networks with a medium number of interactions.[4] This corresponds to the fact that the maximum information content (entropy) is obtained for medium probabilities.

Most social, biological, and technological networks display substantial non-trivial topological features, with patterns of connection between their elements that are neither purely regular nor purely random. Such features include a heavy tail in the degree distribution, a high clustering coefficient, assortativity or disassortativity among vertices, community structure, and hierarchical structure. In the case of directed networks these features also include reciprocity, triad significance profile and other features. In contrast, many of the mathematical models of networks that have been studied in the past, such as lattices and random graphs, do not show these features. The most complex structures can be realized by networks with a medium number of interactions. This corresponds to the fact that the maximum information content (entropy) is obtained for medium probabilities.

大多数社会、生物和技术网络表现出大量非平凡的拓扑特征，它们的元素之间的连接模式既不是纯正规则的也不是纯粹随机的。这些特征包括程度分布的重尾，高集聚系数，顶点之间的协调性或不协调性，社区结构和等级结构。在有向网络的情况下，这些特征还包括互惠性、三元显著性特征和其他特征。相比之下，许多过去研究过的网络数学模型，如格和随机图，并没有表现出这些特征。最复杂的结构可以通过具有中等数量相互作用的网络来实现。这相当于这样一个事实，即对于中等概率而言，最大信息量(熵)是获得的。


Two well-known and much studied classes of complex networks are scale-free networks[5] and small-world networks,[6][7] whose discovery and definition are canonical case-studies in the field. Both are characterized by specific structural features—power-law degree distributions for the former and short path lengths and high clustering for the latter. However, as the study of complex networks has continued to grow in importance and popularity, many other aspects of network structure have attracted attention as well.

Two well-known and much studied classes of complex networks are scale-free networks and small-world networks, whose discovery and definition are canonical case-studies in the field. Both are characterized by specific structural features—power-law degree distributions for the former and short path lengths and high clustering for the latter. However, as the study of complex networks has continued to grow in importance and popularity, many other aspects of network structure have attracted attention as well.

无标度网络和小世界网络是复杂网络研究的热点，它们的发现和定义是该领域的典型案例。两者都是拥有属性特有的结构特征---- 前者的幂律度分布和后者的短路径长度和高聚集性。然而，随着复杂网络研究的重要性和普及性不断提高，网络结构的许多其他方面也引起了人们的关注。


Recently, the study of complex networks has been expanded to networks of networks.[8] If those networks are interdependent, they become significantly more vulnerable to random failures and targeted attacks and exhibit cascading failures and first-order percolation transitions.[9]

Recently, the study of complex networks has been expanded to networks of networks. If those networks are interdependent, they become significantly more vulnerable to random failures and targeted attacks and exhibit cascading failures and first-order percolation transitions.

近年来，复杂网络的研究已经扩展到网络的网络。如果这些网络是相互依存的，它们极易受到随机故障和有针对性的攻击，并出现级联故障和一级渗透过渡。


Furthermore, the collective behavior of a network in the presence of nodes failure and recovery has been studied.[10] It was found that such a network can have spontaneous failures and spontaneous recoveries.

Furthermore, the collective behavior of a network in the presence of nodes failure and recovery has been studied. It was found that such a network can have spontaneous failures and spontaneous recoveries.

此外，还研究了节点失效和恢复情况下网络的集体行为。研究发现，这样的网络可能会自发失败和自发恢复。


The field continues to develop at a brisk pace, and has brought together researchers from many areas including mathematics, physics, electric power systems,[11] biology[12], climate[13], computer science, sociology, epidemiology[14], and others.[15] Ideas from network science and engineering have been applied to the analysis of metabolic and genetic regulatory networks; the study of ecosystem stability and robustness;[16] clinical science;[17] the modeling and design of scalable communication networks such as the generation and visualization of complex wireless networks;[18] the development of vaccination strategies for the control of disease; and a broad range of other practical issues. Research on networks are regularly published in the most visible scientific journals and obtain vigorous funding in many countries. Network theory has been found recently useful to identify bottlenecks in city traffic.[19] Network science is the topic of many conferences in a variety of different fields, and has been the subject of numerous books both for the lay person and for the expert.

The field continues to develop at a brisk pace, and has brought together researchers from many areas including mathematics, physics, electric power systems, biology, climate, computer science, sociology, epidemiology, and others. Ideas from network science and engineering have been applied to the analysis of metabolic and genetic regulatory networks; the study of ecosystem stability and robustness; clinical science; the modeling and design of scalable communication networks such as the generation and visualization of complex wireless networks; the development of vaccination strategies for the control of disease; and a broad range of other practical issues. Research on networks are regularly published in the most visible scientific journals and obtain vigorous funding in many countries. Network theory has been found recently useful to identify bottlenecks in city traffic. Network science is the topic of many conferences in a variety of different fields, and has been the subject of numerous books both for the lay person and for the expert.

这个领域继续以快速的步伐发展，汇集了来自数学、物理学、电力系统、生物学、气候学、计算机科学、社会学、流行病学等许多领域的研究人员。来自网络科学和工程学的思想已经应用于代谢和基因调控网络的分析; 生态系统稳定性和健壮性的研究; 临床科学; 可扩展通信网络的建模和设计，例如复杂无线网络的生成和可视化; 疫苗接种战略的发展以控制疾病; 以及广泛的其他实际问题。关于网络的研究定期在最引人注目的科学期刊上发表，并在许多国家获得大量资金。近年来，人们发现网络理论有助于识别城市交通中的瓶颈。网络科学是各个领域许多会议的主题，也是众多外行人和专家著作的主题。


Scale-free networks

Main article: Scale-free networks
An example of complex scale-free network.

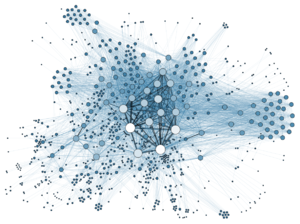
A network is said to be scale-free[5][20]  if its degree distribution, i.e., the probability that a node selected uniformly at random has a certain number of links (degree), follows a mathematical function called a power law. The power law implies that the degree distribution of these networks has no characteristic scale. In contrast, networks with a single well-defined scale are somewhat similar to a lattice in that every node has (roughly) the same degree. Examples of networks with a single scale include the Erdős–Rényi (ER) random graph, random regular graphs, regular lattices, and hypercubes. Some models of growing networks that produce scale-invariant degree distributions are the Barabási–Albert model and the fitness model. In a network with a scale-free degree distribution, some vertices have a degree that is orders of magnitude larger than the average - these vertices are often called "hubs", although this language is misleading as, by definition, there is no inherent threshold above which a node can be viewed as a hub. If there were such a threshold, the network would not be scale-free.

An example of complex scale-free network.A network is said to be scale-free  if its degree distribution, i.e., the probability that a node selected uniformly at random has a certain number of links (degree), follows a mathematical function called a power law. The power law implies that the degree distribution of these networks has no characteristic scale. In contrast, networks with a single well-defined scale are somewhat similar to a lattice in that every node has (roughly) the same degree. Examples of networks with a single scale include the Erdős–Rényi (ER) random graph, random regular graphs, regular lattices, and hypercubes. Some models of growing networks that produce scale-invariant degree distributions are the Barabási–Albert model and the fitness model. In a network with a scale-free degree distribution, some vertices have a degree that is orders of magnitude larger than the average - these vertices are often called "hubs", although this language is misleading as, by definition, there is no inherent threshold above which a node can be viewed as a hub. If there were such a threshold, the network would not be scale-free.

复杂无标度网络的一个例子。如果一个网络的度分布(即随机选择的节点均匀地具有一定数量的链路(度)的概率)遵循一个称为幂律的数学函数，那么这个网络就是无标度的。指数定律表明，这些网络的度分布没有特征尺度。相比之下，具有单一定义良好的尺度的网络在某种程度上类似于格子，因为每个节点具有(大致)相同的度数。单尺度网络的例子包括 erd s-Rényi (ER)随机图、随机正则图、正则格和超立方体。Barabási-Albert 模型和适应度模型是产生尺度不变度分布的一些成长网络模型。在一个无标度分布的网络中，一些顶点的度大于平均数量级——这些顶点通常被称为“集线器” ，尽管这种语言具有误导性，因为根据定义，没有固有的阈值可以将一个节点视为一个集线器。如果存在这样一个阈值，网络就不会是无标度的。


Interest in scale-free networks began in the late 1990s with the reporting of discoveries of power-law degree distributions in real world networks such as the World Wide Web, the network of Autonomous systems (ASs), some networks of Internet routers, protein interaction networks, email networks, etc. Most of these reported "power laws" fail when challenged with rigorous statistical testing, but the more general idea of heavy-tailed degree distributions -- which many of these networks do genuinely exhibit (before finite-size effects occur) -- are very different from what one would expect if edges existed independently and at random (i.e., if they followed a Poisson distribution). There are many different ways to build a network with a power-law degree distribution. The Yule process is a canonical generative process for power laws, and has been known since 1925. However, it is known by many other names due to its frequent reinvention, e.g., The Gibrat principle by Herbert A. Simon, the Matthew effect, cumulative advantage and, preferential attachment by Barabási and Albert for power-law degree distributions. Recently, Hyperbolic Geometric Graphs have been suggested as yet another way of constructing scale-free networks.

Interest in scale-free networks began in the late 1990s with the reporting of discoveries of power-law degree distributions in real world networks such as the World Wide Web, the network of Autonomous systems (ASs), some networks of Internet routers, protein interaction networks, email networks, etc. Most of these reported "power laws" fail when challenged with rigorous statistical testing, but the more general idea of heavy-tailed degree distributions -- which many of these networks do genuinely exhibit (before finite-size effects occur) -- are very different from what one would expect if edges existed independently and at random (i.e., if they followed a Poisson distribution). There are many different ways to build a network with a power-law degree distribution. The Yule process is a canonical generative process for power laws, and has been known since 1925. However, it is known by many other names due to its frequent reinvention, e.g., The Gibrat principle by Herbert A. Simon, the Matthew effect, cumulative advantage and, preferential attachment by Barabási and Albert for power-law degree distributions. Recently, Hyperbolic Geometric Graphs have been suggested as yet another way of constructing scale-free networks.

对无标度网络的兴趣始于1990年代后期，当时报告了在现实世界网络中幂律度分布的发现，如万维网、自治系统网络、一些互联网路由器网络、蛋白质互动网络、电子邮件网络等。大多数报道的“幂定律”在面对严格的统计测试时都会失败，但是重尾度分布这一更为普遍的概念——其中许多网络确实表现出(在有限大小效应发生之前)——与人们所期望的如果边独立和随机存在(例如，如果它们遵循泊松分佈分布)的概念大相径庭。建立具有幂律度分布的网络有许多不同的方法。圣诞过程是幂定律的典型生成过程，自1925年就为人所知。然而，由于其频繁的重新发明，它被许多其他的名字所熟知，例如，赫伯特·西蒙的吉布拉特原则，马太效应，累积优势，巴拉巴西和阿尔伯特的幂律度分布的优先依恋。近年来，双曲几何图被认为是构造无标度网络的又一种方法。


Some networks with a power-law degree distribution (and specific other types of structure) can be highly resistant to the random deletion of vertices—i.e., the vast majority of vertices remain connected together in a giant component.[21] Such networks can also be quite sensitive to targeted attacks aimed at fracturing the network quickly. When the graph is uniformly random except for the degree distribution, these critical vertices are the ones with the highest degree, and have thus been implicated in the spread of disease (natural and artificial) in social and communication networks, and in the spread of fads (both of which are modeled by a percolation or branching process). While random graphs (ER) have an average distance of order log N[6] between nodes, where N is the number of nodes, scale free graph can have a distance of log log N. Such graphs are called ultra small world networks.[22]

Some networks with a power-law degree distribution (and specific other types of structure) can be highly resistant to the random deletion of vertices—i.e., the vast majority of vertices remain connected together in a giant component. Such networks can also be quite sensitive to targeted attacks aimed at fracturing the network quickly. When the graph is uniformly random except for the degree distribution, these critical vertices are the ones with the highest degree, and have thus been implicated in the spread of disease (natural and artificial) in social and communication networks, and in the spread of fads (both of which are modeled by a percolation or branching process). While random graphs (ER) have an average distance of order log N

一些具有幂律度分布的网络(以及其他特定类型的网络结构)可以很好地抵抗顶点的随机删除ーー即，绝大多数顶点保持连接在一个巨大的组件中。这种网络对于旨在快速破坏网络的有针对性的攻击也非常敏感。当图是均匀随机的，除了度分布，这些临界顶点是最高度的，因此牵涉到疾病的传播(自然和人为的)在社会和通信网络，并在时尚的传播(两者都是模型渗流或分支过程)。而随机图(ER)的平均有序距离 log n


Small-world networks

Main article: Small-world network

A network is called a small-world network[6] by analogy with the small-world phenomenon (popularly known as six degrees of separation). The small world hypothesis, which was first described by the Hungarian writer Frigyes Karinthy in 1929, and tested experimentally by Stanley Milgram (1967), is the idea that two arbitrary people are connected by only six degrees of separation, i.e. the diameter of the corresponding graph of social connections is not much larger than six. In 1998, Duncan J. Watts and Steven Strogatz published the first small-world network model, which through a single parameter smoothly interpolates between a random graph and a lattice.[6] Their model demonstrated that with the addition of only a small number of long-range links, a regular graph, in which the diameter is proportional to the size of the network, can be transformed into a "small world" in which the average number of edges between any two vertices is very small (mathematically, it should grow as the logarithm of the size of the network), while the clustering coefficient stays large. It is known that a wide variety of abstract graphs exhibit the small-world property, e.g., random graphs and scale-free networks. Further, real world networks such as the World Wide Web and the metabolic network also exhibit this property.

A network is called a small-world network by analogy with the small-world phenomenon (popularly known as six degrees of separation). The small world hypothesis, which was first described by the Hungarian writer Frigyes Karinthy in 1929, and tested experimentally by Stanley Milgram (1967), is the idea that two arbitrary people are connected by only six degrees of separation, i.e. the diameter of the corresponding graph of social connections is not much larger than six. In 1998, Duncan J. Watts and Steven Strogatz published the first small-world network model, which through a single parameter smoothly interpolates between a random graph and a lattice. Their model demonstrated that with the addition of only a small number of long-range links, a regular graph, in which the diameter is proportional to the size of the network, can be transformed into a "small world" in which the average number of edges between any two vertices is very small (mathematically, it should grow as the logarithm of the size of the network), while the clustering coefficient stays large. It is known that a wide variety of abstract graphs exhibit the small-world property, e.g., random graphs and scale-free networks. Further, real world networks such as the World Wide Web and the metabolic network also exhibit this property.

类比于小世界现象(通常被称为小世界网络六度分隔理论) ，网络被称为网络。1929年匈牙利作家 Frigyes Karinthy 首次提出了小世界假说，并由 Stanley Milgram (1967)进行了实验验证。该假说认为，两个任意的人之间只有一个六度分隔理论，即。相应的社会关系图的直径不会大于6。1998年，Duncan j. Watts 和 Steven Strogatz 发表了第一个小世界网络模型，该模型通过一个单参数平滑地插值在一个随机图形和一个格子之间。他们的模型证明，只要增加少量的长程链接，一个正则图，其直径与网络大小成正比，就可以转换成一个“小世界” ，其中任意两个顶点之间的平均边数都非常小(从数学上讲，它应该增长为网络大小的对数) ，而集聚系数则保持大。众所周知，各种各样的抽象图都具有小世界特性，例如，随机图和无标度网络。此外，真实世界的网络，如万维网和代谢网络也展示了这一特性。


In the scientific literature on networks, there is some ambiguity associated with the term "small world". In addition to referring to the size of the diameter of the network, it can also refer to the co-occurrence of a small diameter and a high clustering coefficient. The clustering coefficient is a metric that represents the density of triangles in the network. For instance, sparse random graphs have a vanishingly small clustering coefficient while real world networks often have a coefficient significantly larger. Scientists point to this difference as suggesting that edges are correlated in real world networks.

In the scientific literature on networks, there is some ambiguity associated with the term "small world". In addition to referring to the size of the diameter of the network, it can also refer to the co-occurrence of a small diameter and a high clustering coefficient. The clustering coefficient is a metric that represents the density of triangles in the network. For instance, sparse random graphs have a vanishingly small clustering coefficient while real world networks often have a coefficient significantly larger. Scientists point to this difference as suggesting that edges are correlated in real world networks.

在关于网络的科学文献中，”小世界”一词有一些含糊之处。除了指网络的直径大小之外，它还可以指小直径和高集聚系数的同现现象。集聚系数是一个表示网络中三角形密度的度量单位。例如，稀疏随机图的集聚系数极小，而现实世界网络的系数通常大得多。科学家指出，这种差异表明，在现实世界的网络中，边缘是相关的。


See also


Books

取自“https://wiki.swarma.org/index.php?title=匹配生长模型&oldid=13811”