贝叶斯网络

此词条暂由水流心不竞初译，未经审校，带来阅读不便，请见谅。

文件:SimpleBayesNetNodes.svg

A simple Bayesian network. Rain influences whether the sprinkler is activated, and both rain and the sprinkler influence whether the grass is wet.

A simple Bayesian network. Rain influences whether the sprinkler is activated, and both rain and the sprinkler influence whether the grass is wet.

一个简单的贝氏网路。雨水会影响喷头是否被激活，雨水和喷头都会影响草地是否湿润。

! -- 注意: 为了保持引用格式的一致性，请使用“引用”系列模板。-->

A Bayesian network, Bayes network, belief network, decision network, Bayes(ian) model or probabilistic directed acyclic graphical model is a probabilistic graphical model (a type of statistical model) that represents a set of variables and their conditional dependencies via a directed acyclic graph (DAG). Bayesian networks are ideal for taking an event that occurred and predicting the likelihood that any one of several possible known causes was the contributing factor. For example, a Bayesian network could represent the probabilistic relationships between diseases and symptoms. Given symptoms, the network can be used to compute the probabilities of the presence of various diseases.

A Bayesian network, Bayes network, belief network, decision network, Bayes(ian) model or probabilistic directed acyclic graphical model is a probabilistic graphical model (a type of statistical model) that represents a set of variables and their conditional dependencies via a directed acyclic graph (DAG). Bayesian networks are ideal for taking an event that occurred and predicting the likelihood that any one of several possible known causes was the contributing factor. For example, a Bayesian network could represent the probabilistic relationships between diseases and symptoms. Given symptoms, the network can be used to compute the probabilities of the presence of various diseases.

贝氏网路Bayesian network、贝叶斯网络 Bayes network、信念网络、决策网络、贝叶斯模型或概率有向无环图模型是一种概率图模型(一种统计模型) ，它通过有向无环图无环图(DAG)表示一组变量及其条件依赖关系。贝叶斯网络是理想的事件发生和预测的可能性，任何一个几个可能的已知原因是影响因素。例如， 贝氏网路Bayesian network可以表示疾病和症状之间的概率关系。在给定症状的情况下，该网络可用于计算各种疾病出现的概率。

Efficient algorithms can perform inference and learning in Bayesian networks. Bayesian networks that model sequences of variables (e.g. speech signals or protein sequences) are called dynamic Bayesian networks. Generalizations of Bayesian networks that can represent and solve decision problems under uncertainty are called influence diagrams.

Efficient algorithms can perform inference and learning in Bayesian networks. Bayesian networks that model sequences of variables (e.g. speech signals or protein sequences) are called dynamic Bayesian networks. Generalizations of Bayesian networks that can represent and solve decision problems under uncertainty are called influence diagrams.

有效的算法可以在 贝叶斯网络 Bayes network中进行推理和学习。 贝叶斯网络 Bayes network模型序列的变量(例如。语音信号或蛋白质序列)被称为动态贝叶斯网络。能够表示和解决不确定性决策问题的贝叶斯网络的推广称为影响图。

Graphical model图模型

Formally, Bayesian networks are directed acyclic graphs (DAGs) whose nodes represent variables in the Bayesian sense: they may be observable quantities, latent variables, unknown parameters or hypotheses. Edges represent conditional dependencies; nodes that are not connected (no path connects one node to another) represent variables that are conditionally independent of each other. Each node is associated with a probability function that takes, as input, a particular set of values for the node's parent variables, and gives (as output) the probability (or probability distribution, if applicable) of the variable represented by the node. For example, if [math]\displaystyle{ m }[/math] parent nodes represent [math]\displaystyle{ m }[/math] Boolean variables, then the probability function could be represented by a table of [math]\displaystyle{ 2^m }[/math] entries, one entry for each of the [math]\displaystyle{ 2^m }[/math] possible parent combinations. Similar ideas may be applied to undirected, and possibly cyclic, graphs such as Markov networks.

Formally, Bayesian networks are directed acyclic graphs (DAGs) whose nodes represent variables in the Bayesian sense: they may be observable quantities, latent variables, unknown parameters or hypotheses. Edges represent conditional dependencies; nodes that are not connected (no path connects one node to another) represent variables that are conditionally independent of each other. Each node is associated with a probability function that takes, as input, a particular set of values for the node's parent variables, and gives (as output) the probability (or probability distribution, if applicable) of the variable represented by the node. For example, if [math]\displaystyle{ m }[/math] parent nodes represent [math]\displaystyle{ m }[/math] Boolean variables, then the probability function could be represented by a table of [math]\displaystyle{ 2^m }[/math] entries, one entry for each of the [math]\displaystyle{ 2^m }[/math] possible parent combinations. Similar ideas may be applied to undirected, and possibly cyclic, graphs such as Markov networks.

在形式上， 贝叶斯网络 Bayes network是有向无环图(DAGs) ，其节点表示贝叶斯意义上的变量: 它们可以是可观测量、潜在变量、未知参数或假设。边表示条件依赖; 未连接(没有路径连接一个节点到另一个节点)的节点表示彼此有条件独立的变量。每个节点都与一个 概率密度函数Probability function 节点相关联，该节点接受一组特定的父变量值作为输入，并给出(作为输出)该节点表示的变量的概率(或概率分布，如果适用的话)。例如，如果 math m / math 父节点表示 math m / math 布尔变量，那么概率密度函数可以用一个小 math 2 ^ m / math / small 条目表示，每个小 math 2 ^ m / math / small 可能的父节点都有一个条目。类似的想法可以应用于无向图，也可能是循环图，如马尔可夫网络。

Example举例

A simple Bayesian network with conditional probability tables

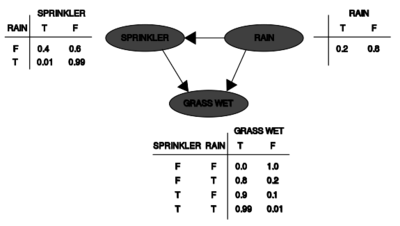
A simple Bayesian network with conditional probability tables

一个简单的贝氏网路 / 条件概率表

Two events can cause grass to be wet: an active sprinkler or rain. Rain has a direct effect on the use of the sprinkler (namely that when it rains, the sprinkler usually is not active). This situation can be modeled with a Bayesian network (shown to the right). Each variable has two possible values, T (for true) and F (for false).

Two events can cause grass to be wet: an active sprinkler or rain. Rain has a direct effect on the use of the sprinkler (namely that when it rains, the sprinkler usually is not active). This situation can be modeled with a Bayesian network (shown to the right). Each variable has two possible values, T (for true) and F (for false).

有两种情况会导致草地湿润: 主动洒水或者下雨。雨对洒水车的使用有直接的影响(也就是说，当下雨时，洒水车通常是不活跃的)。这种情况可以用贝氏网路来模拟(如右图所示)。每个变量有两个可能的值，t (表示真)和 f (表示假)。

The joint probability function is:

The joint probability function is:

联合概率密度函数Joint probability function是:

[math]\displaystyle{ \Pr(G,S,R)=\Pr(G\mid S,R) \Pr(S\mid R)\Pr(R) }[/math]

[math]\displaystyle{ \Pr(G,S,R)=\Pr(G\mid S,R) \Pr(S\mid R)\Pr(R) }[/math]

Math Pr (g，s，r) Pr (g mid s，r) Pr (s mid r) Pr (r) / math

where G = "Grass wet (true/false)", S = "Sprinkler turned on (true/false)", and R = "Raining (true/false)".

where G = "Grass wet (true/false)", S = "Sprinkler turned on (true/false)", and R = "Raining (true/false)".

G“ Grass wet (true / false)” ，s“ Sprinkler turned on (true / false)” ，r“ Raining (true / false)”。

The model can answer questions about the presence of a cause given the presence of an effect (so-called inverse probability) like "What is the probability that it is raining, given the grass is wet?" by using the conditional probability formula and summing over all nuisance variables:

The model can answer questions about the presence of a cause given the presence of an effect (so-called inverse probability) like "What is the probability that it is raining, given the grass is wet?" by using the conditional probability formula and summing over all nuisance variables:

这个模型可以在给定一个效应(所谓的逆概率)的情况下回答关于一个原因是否存在的问题，比如“给定草是湿的，下雨的概率是多少? ”通过使用条件概率公式和对所有滋扰变量的求和:

[math]\displaystyle{ \Pr(R=T\mid G=T) =\frac{\Pr(G=T,R=T)}{\Pr(G=T)} = \frac{\sum_{S \in \{T, F\}}\Pr(G=T, S,R=T)}{\sum_{S, R \in \{T, F\}} \Pr(G=T,S,R)} }[/math]

[math]\displaystyle{ \Pr(R=T\mid G=T) =\frac{\Pr(G=T,R=T)}{\Pr(G=T)} = \frac{\sum_{S \in \{T, F\}}\Pr(G=T, S,R=T)}{\sum_{S, R \in \{T, F\}} \Pr(G=T,S,R)} }[/math]

数学[ Pr (r t 中 g t) frac (g t，r t)}{ Pr (g t)}} frac { t，f } Pr (g t，s，r t)} sum { s，r in，t，f Pr (g t，s，r)} / math

Using the expansion for the joint probability function [math]\displaystyle{ \Pr(G,S,R) }[/math] and the conditional probabilities from the conditional probability tables (CPTs) stated in the diagram, one can evaluate each term in the sums in the numerator and denominator. For example,

Using the expansion for the joint probability function [math]\displaystyle{ \Pr(G,S,R) }[/math] and the conditional probabilities from the conditional probability tables (CPTs) stated in the diagram, one can evaluate each term in the sums in the numerator and denominator. For example,

使用联合的概率密度函数数学 Pr (g，s，r) / 数学的展开式和图中列出的条件概率表的条件概率，我们可以用分子和分母的和来计算每个项。比如说,

[math]\displaystyle{ \begin{align} \lt math\gt \begin{align} 数学 begin { align } \Pr(G=T, S=T,R=T) & = \Pr(G=T\mid S=T,R=T)\Pr(S=T\mid R=T)\Pr(R=T) \\ \Pr(G=T, S=T,R=T) & = \Pr(G=T\mid S=T,R=T)\Pr(S=T\mid R=T)\Pr(R=T) \\ Pr (g t，s t，r t) & Pr (g t mid s t，r t) Pr (s t mid r t) Pr (r t) & = 0.99 \times 0.01 \times 0.2 \\ & = 0.99 \times 0.01 \times 0.2 \\ 0.99 * 0.01 * 0.2 * & = 0.00198. & = 0.00198. & = 0.00198. \end{align} \end{align} End { align } }[/math]

</math>

数学

Then the numerical results (subscripted by the associated variable values) are

Then the numerical results (subscripted by the associated variable values) are

然后数值结果(由相关的变量值下标)是

[math]\displaystyle{ \Pr(R=T\mid G=T) = \frac{ 0.00198_{TTT} + 0.1584_{TFT} }{ 0.00198_{TTT} + 0.288_{TTF} + 0.1584_{TFT} + 0.0_{TFF} } = \frac{891}{2491}\approx 35.77 \%. }[/math]

[math]\displaystyle{ \Pr(R=T\mid G=T) = \frac{ 0.00198_{TTT} + 0.1584_{TFT} }{ 0.00198_{TTT} + 0.288_{TTF} + 0.1584_{TFT} + 0.0_{TFF} } = \frac{891}{2491}\approx 35.77 \%. }[/math]

0.00198{ TTT } + 0.288{ TTF } + 0.1584{ TFT } + 0.1584{ TFT } + 0.891}{2491}{35.77} / math

To answer an interventional question, such as "What is the probability that it would rain, given that we wet the grass?" the answer is governed by the post-intervention joint distribution function

To answer an interventional question, such as "What is the probability that it would rain, given that we wet the grass?" the answer is governed by the post-intervention joint distribution function

回答一个介入性的问题，比如“既然我们把草弄湿了，那么下雨的可能性有多大? ”答案取决于干预后的联合分配函数

[math]\displaystyle{ \Pr(S,R\mid\text{do}(G=T)) = \Pr(S\mid R) \Pr(R) }[/math]

[math]\displaystyle{ \Pr(S,R\mid\text{do}(G=T)) = \Pr(S\mid R) \Pr(R) }[/math]

[math]\displaystyle{ \Pr(S,R\mid\text{do}(G=T)) = \Pr(S\mid R) \Pr(R) }[/math]

obtained by removing the factor [math]\displaystyle{ \Pr(G\mid S,R) }[/math] from the pre-intervention distribution. The do operator forces the value of G to be true. The probability of rain is unaffected by the action:

obtained by removing the factor [math]\displaystyle{ \Pr(G\mid S,R) }[/math] from the pre-intervention distribution. The do operator forces the value of G to be true. The probability of rain is unaffected by the action:

通过从干预前的分布中去除因子 math Pr (g mid s，r) / math，得到干预前的分布。Do 运算符强制 g 的值为真。下雨的可能性不受行动的影响:

[math]\displaystyle{ \Pr(R\mid\text{do}(G=T)) = \Pr(R). }[/math]

[math]\displaystyle{ \Pr(R\mid\text{do}(G=T)) = \Pr(R). }[/math]

[math]\displaystyle{ \Pr(R\mid\text{do}(G=T)) = \Pr(R). }[/math]

To predict the impact of turning the sprinkler on:

To predict the impact of turning the sprinkler on:

预测开启洒水装置的影响:

[math]\displaystyle{ \Pr(R,G\mid\text{do}(S=T)) = \Pr(R)\Pr(G\mid R,S=T) }[/math]

[math]\displaystyle{ \Pr(R,G\mid\text{do}(S=T)) = \Pr(R)\Pr(G\mid R,S=T) }[/math]

[math]\displaystyle{ \Pr(R,G\mid\text{do}(S=T)) = \Pr(R)\Pr(G\mid R,S=T) }[/math]

with the term [math]\displaystyle{ \Pr(S=T\mid R) }[/math] removed, showing that the action affects the grass but not the rain.

with the term [math]\displaystyle{ \Pr(S=T\mid R) }[/math] removed, showing that the action affects the grass but not the rain.

移除了 math Pr (s t mid r) / math 这个术语，表明这种行为影响的是草，而不是雨。

These predictions may not be feasible given unobserved variables, as in most policy evaluation problems. The effect of the action [math]\displaystyle{ \text{do}(x) }[/math] can still be predicted, however, whenever the back-door criterion is satisfied. It states that, if a set Z of nodes can be observed that d-separates (or blocks) all back-door paths from X to Y then

These predictions may not be feasible given unobserved variables, as in most policy evaluation problems. The effect of the action [math]\displaystyle{ \text{do}(x) }[/math] can still be predicted, however, whenever the back-door criterion is satisfied. It states that, if a set Z of nodes can be observed that d-separates (or blocks) all back-door paths from X to Y then

这些预测可能不可行的给予未观测的变量，因为在大多数政策评估问题。但是，只要满足后门准则，仍然可以预测操作 math text { do }(x) / math 的效果。它指出，如果一组 z 节点可以观察到 d-分隔(或阻塞)从 x 到 y 的所有后门路径

[math]\displaystyle{ \Pr(Y,Z\mid\text{do}(x)) = \frac{\Pr(Y,Z,X=x)}{\Pr(X=x\mid Z)}. }[/math]

[math]\displaystyle{ \Pr(Y,Z\mid\text{do}(x)) = \frac{\Pr(Y,Z,X=x)}{\Pr(X=x\mid Z)}. }[/math]

[math]\displaystyle{ \Pr(Y,Z\mid\text{do}(x)) = \frac{\Pr(Y,Z,X=x)}{\Pr(X=x\mid Z)}. }[/math]

A back-door path is one that ends with an arrow into X. Sets that satisfy the back-door criterion are called "sufficient" or "admissible." For example, the set Z = R is admissible for predicting the effect of S = T on G, because R d-separates the (only) back-door path S ← R → G. However, if S is not observed, no other set d-separates this path and the effect of turning the sprinkler on (S = T) on the grass (G) cannot be predicted from passive observations. In that case P(G | do(S = T)) is not "identified". This reflects the fact that, lacking interventional data, the observed dependence between S and G is due to a causal connection or is spurious

A back-door path is one that ends with an arrow into X. Sets that satisfy the back-door criterion are called "sufficient" or "admissible." For example, the set Z = R is admissible for predicting the effect of S = T on G, because R d-separates the (only) back-door path S ← R → G. However, if S is not observed, no other set d-separates this path and the effect of turning the sprinkler on (S = T) on the grass (G) cannot be predicted from passive observations. In that case P(G | do(S = T)) is not "identified". This reflects the fact that, lacking interventional data, the observed dependence between S and G is due to a causal connection or is spurious

后门路径是以 x 的箭头结束的路径。满足后门标准的集合称为“充分”或“可接受”例如，集合 z r 可以用来预测 s t 对 g 的影响，因为 rd- 分离了(仅)后门路径 s ← r → g。但是，如果 s 没有被观测到，没有其他集合 d-分离这条路径，并且不能从被动观测预测草(g)上喷头打开的影响。在这种情况下，p (g | do (s t))不被“识别”。这反映了这样一个事实，即缺乏干预性数据，所观察到的 s 和 g 之间的依赖性是由于一个因果关系或是伪造的

(apparent dependence arising from a common cause, R). (see Simpson's paradox)

(apparent dependence arising from a common cause, R). (see Simpson's paradox)

(由共同原因引起的明显依赖关系，r)。(见辛普森悖论)

To determine whether a causal relation is identified from an arbitrary Bayesian network with unobserved variables, one can use the three rules of "do-calculus" and test whether all do terms can be removed from the expression of that relation, thus confirming that the desired quantity is estimable from frequency data.

To determine whether a causal relation is identified from an arbitrary Bayesian network with unobserved variables, one can use the three rules of "do-calculus" and test whether all do terms can be removed from the expression of that relation, thus confirming that the desired quantity is estimable from frequency data.

为了确定一个因果关系是否可以从一个任意的含有未观测变量的贝氏网路中识别出来，我们可以使用“ do-calculus”的三个规则来检验是否所有的 do 项都可以从这个关系的表达式中去掉，从而确认所需的量是可以从频率数据中估计出来的。

Using a Bayesian network can save considerable amounts of memory over exhaustive probability tables, if the dependencies in the joint distribution are sparse. For example, a naive way of storing the conditional probabilities of 10 two-valued variables as a table requires storage space for [math]\displaystyle{ 2^{10} = 1024 }[/math] values. If no variable's local distribution depends on more than three parent variables, the Bayesian network representation stores at most [math]\displaystyle{ 10\cdot2^3 = 80 }[/math] values.

Using a Bayesian network can save considerable amounts of memory over exhaustive probability tables, if the dependencies in the joint distribution are sparse. For example, a naive way of storing the conditional probabilities of 10 two-valued variables as a table requires storage space for [math]\displaystyle{ 2^{10} = 1024 }[/math] values. If no variable's local distribution depends on more than three parent variables, the Bayesian network representation stores at most [math]\displaystyle{ 10\cdot2^3 = 80 }[/math] values.

如果依赖关系在联合分布中是稀疏的，那么在详尽的概率表上使用贝氏网路分布可以节省相当大的内存。例如，将10个二值变量的条件概率存储为一个表的简单方法需要存储 math 2 ^ {10}1024 / math 值。如果没有变量的局部分布依赖于3个以上的父变量，那么贝氏网路表示最多只存储 math 10 cdot2 ^ 380 / math 值。

One advantage of Bayesian networks is that it is intuitively easier for a human to understand (a sparse set of) direct dependencies and local distributions than complete joint distributions.

One advantage of Bayesian networks is that it is intuitively easier for a human to understand (a sparse set of) direct dependencies and local distributions than complete joint distributions.

贝叶斯网络的一个优点是它比完全联合分布更易于人类直观地理解(一组稀疏的)直接依赖关系和局部分布。

Inference and learning推论与学习

Bayesian networks perform three main inference tasks:

Bayesian networks perform three main inference tasks:

贝叶斯网络执行三个主要推理任务:

Inferring unobserved variables预测隐含变量

Because a Bayesian network is a complete model for its variables and their relationships, it can be used to answer probabilistic queries about them. For example, the network can be used to update knowledge of the state of a subset of variables when other variables (the evidence variables) are observed. This process of computing the posterior distribution of variables given evidence is called probabilistic inference. The posterior gives a universal sufficient statistic for detection applications, when choosing values for the variable subset that minimize some expected loss function, for instance the probability of decision error. A Bayesian network can thus be considered a mechanism for automatically applying Bayes' theorem to complex problems.

Because a Bayesian network is a complete model for its variables and their relationships, it can be used to answer probabilistic queries about them. For example, the network can be used to update knowledge of the state of a subset of variables when other variables (the evidence variables) are observed. This process of computing the posterior distribution of variables given evidence is called probabilistic inference. The posterior gives a universal sufficient statistic for detection applications, when choosing values for the variable subset that minimize some expected loss function, for instance the probability of decision error. A Bayesian network can thus be considered a mechanism for automatically applying Bayes' theorem to complex problems.

因为贝氏网路是变量及其关系的完整模型，所以它可以用来回答关于变量的概率查询。例如，当观察到其他变量(证据变量)时，网络可用于更新变量子集的状态知识。这个计算给定证据的变量后验概率的过程被称为概率推理。后验方法为检测应用提供了一个通用的充分的统计量，当为变量子集选择值时，可以最小化一些期望损失函数，例如决策错误的概率。因此，贝氏网路可以被看作是一种自动应用贝叶斯定理解决复杂问题的机制。

The most common exact inference methods are: variable elimination, which eliminates (by integration or summation) the non-observed non-query variables one by one by distributing the sum over the product; clique tree propagation, which caches the computation so that many variables can be queried at one time and new evidence can be propagated quickly; and recursive conditioning and AND/OR search, which allow for a space–time tradeoff and match the efficiency of variable elimination when enough space is used. All of these methods have complexity that is exponential in the network's treewidth. The most common approximate inference algorithms are importance sampling, stochastic MCMC simulation, mini-bucket elimination, loopy belief propagation, generalized belief propagation and variational methods.

The most common exact inference methods are: variable elimination, which eliminates (by integration or summation) the non-observed non-query variables one by one by distributing the sum over the product; clique tree propagation, which caches the computation so that many variables can be queried at one time and new evidence can be propagated quickly; and recursive conditioning and AND/OR search, which allow for a space–time tradeoff and match the efficiency of variable elimination when enough space is used. All of these methods have complexity that is exponential in the network's treewidth. The most common approximate inference algorithms are importance sampling, stochastic MCMC simulation, mini-bucket elimination, loopy belief propagation, generalized belief propagation and variational methods.

最常用的精确推理方法有: 变量消除法，通过积分或求和的方式将未观察到的非查询变量逐一消除; 分支树传播法，它将计算过程缓存，使得可以同时查询多个变量，并快速传播新的证据; 递归条件化和 / 或搜索法，它考虑了时空折衷，并且在使用足够空间时与变量消除法的效率相匹配。所有这些方法的复杂度都是网络树宽的指数级。最常见的近似推理算法有重要性抽样法、随机 MCMC 模拟法、小桶消去法、循环置信传播法、广义置信传播法和变分法。

Parameter learning参数预测

In order to fully specify the Bayesian network and thus fully represent the joint probability distribution, it is necessary to specify for each node X the probability distribution for X conditional upon X's parents. The distribution of X conditional upon its parents may have any form. It is common to work with discrete or Gaussian distributions since that simplifies calculations. Sometimes only constraints on a distribution are known; one can then use the principle of maximum entropy to determine a single distribution, the one with the greatest entropy given the constraints. (Analogously, in the specific context of a dynamic Bayesian network, the conditional distribution for the hidden state's temporal evolution is commonly specified to maximize the entropy rate of the implied stochastic process.)

In order to fully specify the Bayesian network and thus fully represent the joint probability distribution, it is necessary to specify for each node X the probability distribution for X conditional upon Xs parents. The distribution of X conditional upon its parents may have any form. It is common to work with discrete or Gaussian distributions since that simplifies calculations. Sometimes only constraints on a distribution are known; one can then use the principle of maximum entropy to determine a single distribution, the one with the greatest entropy given the constraints. (Analogously, in the specific context of a dynamic Bayesian network, the conditional distribution for the hidden state's temporal evolution is commonly specified to maximize the entropy rate of the implied stochastic process.)

为了完全指定贝氏网路节点，从而完全代表联合分布节点，有必要为每个节点 x 指定基于 x s 父节点的概率分布节点 x。以其父母为条件的 x 的分布可以有任何形式。它是共同的工作与离散或高斯分布，因为这简化了计算。有时只有分布上的约束是已知的; 然后可以使用最大熵原理分布来确定一个单一的分布，即给定约束条件下熵最大的分布。类似地，在动态贝氏网路的特定上下文中，隐状态时间演化的条件分布通常被指定为最大化隐含随机过程的熵率

Often these conditional distributions include parameters that are unknown and must be estimated from data, e.g., via the maximum likelihood approach. Direct maximization of the likelihood (or of the posterior probability) is often complex given unobserved variables. A classical approach to this problem is the expectation-maximization algorithm, which alternates computing expected values of the unobserved variables conditional on observed data, with maximizing the complete likelihood (or posterior) assuming that previously computed expected values are correct. Under mild regularity conditions this process converges on maximum likelihood (or maximum posterior) values for parameters.

Often these conditional distributions include parameters that are unknown and must be estimated from data, e.g., via the maximum likelihood approach. Direct maximization of the likelihood (or of the posterior probability) is often complex given unobserved variables. A classical approach to this problem is the expectation-maximization algorithm, which alternates computing expected values of the unobserved variables conditional on observed data, with maximizing the complete likelihood (or posterior) assuming that previously computed expected values are correct. Under mild regularity conditions this process converges on maximum likelihood (or maximum posterior) values for parameters.

通常这些条件分布包括未知的参数，必须从数据中估计，例如，通过最大似然法。直接最大化的可能性(或后验概率)往往是复杂的给定未观测的变量。这个问题的一个经典方法是期望最大化算法，它以观测数据为条件，交替计算未观测变量的期望值，并假设先前计算的期望值是正确的，最大化完全似然(或后验)。在温和的正则性条件下，这个过程收敛于参数的最大似然值(或最大后验值)。

A more fully Bayesian approach to parameters is to treat them as additional unobserved variables and to compute a full posterior distribution over all nodes conditional upon observed data, then to integrate out the parameters. This approach can be expensive and lead to large dimension models, making classical parameter-setting approaches more tractable.

A more fully Bayesian approach to parameters is to treat them as additional unobserved variables and to compute a full posterior distribution over all nodes conditional upon observed data, then to integrate out the parameters. This approach can be expensive and lead to large dimension models, making classical parameter-setting approaches more tractable.

一个更完整的贝叶斯参数方法是将它们视为附加的未观测变量，并根据观测数据计算所有节点的完整后验概率，然后整合出参数。这种方法可能代价高昂，并导致大规模模型，使经典的参数设置方法更易于处理。

Structure learning结构预测

In the simplest case, a Bayesian network is specified by an expert and is then used to perform inference. In other applications the task of defining the network is too complex for humans. In this case the network structure and the parameters of the local distributions must be learned from data.

In the simplest case, a Bayesian network is specified by an expert and is then used to perform inference. In other applications the task of defining the network is too complex for humans. In this case the network structure and the parameters of the local distributions must be learned from data.

在最简单的情况下，专家指定一个贝氏网路，然后用它来执行推理。在其他应用程序中，定义网络的任务对于人类来说过于复杂。在这种情况下，必须从数据中学习网络结构和局部分布的参数。

Automatically learning the graph structure of a Bayesian network (BN) is a challenge pursued within machine learning. The basic idea goes back to a recovery algorithm developed by Rebane and Pearl and rests on the distinction between the three possible patterns allowed in a 3-node DAG:

Automatically learning the graph structure of a Bayesian network (BN) is a challenge pursued within machine learning. The basic idea goes back to a recovery algorithm developed by Rebane and Pearl and rests on the distinction between the three possible patterns allowed in a 3-node DAG:

自动学习贝氏网路的图形结构是机器学习的一个挑战。其基本思想可以追溯到由 Rebane 和 Pearl 开发的恢复算法，该算法基于三节点有向无环图中允许的三种可能模式的区别:

{ | class“ wikitable”

Junction patterns

Junction patterns

+ 连接模式	Pattern	Pattern	模式	Model	Model	模特
Chain	Chain 链接	[math]\displaystyle{ X \rightarrow Y \rightarrow Z }[/math]	[math]\displaystyle{ X \rightarrow Y \rightarrow Z }[/math]	math x right tarrow y right tarrow z / math
Fork	Fork 叉子	[math]\displaystyle{ X \leftarrow Y \rightarrow Z }[/math]	[math]\displaystyle{ X \leftarrow Y \rightarrow Z }[/math]	math x left tarrow y right tarrow z / math
Collider	Collider 碰撞器	[math]\displaystyle{ X \rightarrow Y \leftarrow Z }[/math]	[math]\displaystyle{ X \rightarrow Y \leftarrow Z }[/math]	math x right tarrow y leftarrow z / math

|}

The first 2 represent the same dependencies ([math]\displaystyle{ X }[/math] and [math]\displaystyle{ Z }[/math] are independent given [math]\displaystyle{ Y }[/math]) and are, therefore, indistinguishable. The collider, however, can be uniquely identified, since [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Z }[/math] are marginally independent and all other pairs are dependent. Thus, while the skeletons (the graphs stripped of arrows) of these three triplets are identical, the directionality of the arrows is partially identifiable. The same distinction applies when [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Z }[/math] have common parents, except that one must first condition on those parents. Algorithms have been developed to systematically determine the skeleton of the underlying graph and, then, orient all arrows whose directionality is dictated by the conditional independences observed.

The first 2 represent the same dependencies ([math]\displaystyle{ X }[/math] and [math]\displaystyle{ Z }[/math] are independent given [math]\displaystyle{ Y }[/math]) and are, therefore, indistinguishable. The collider, however, can be uniquely identified, since [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Z }[/math] are marginally independent and all other pairs are dependent. Thus, while the skeletons (the graphs stripped of arrows) of these three triplets are identical, the directionality of the arrows is partially identifiable. The same distinction applies when [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Z }[/math] have common parents, except that one must first condition on those parents. Algorithms have been developed to systematically determine the skeleton of the underlying graph and, then, orient all arrows whose directionality is dictated by the conditional independences observed.

前2个表示相同的依赖关系(数学 x / math 和数学 z / math 在给定数学 y / math 时是独立的) ，因此无法区分。然而，碰撞器可以被唯一地标识，因为数学 x / math 和数学 z / math 是边际独立的，而其他所有对都是依赖的。因此，虽然这三个三元组的框架(去掉箭头的图)是相同的，箭头的方向是部分可识别的。当数学 x / math 和数学 z / math 有着共同的父母时，同样的区别也适用，除了父母必须有第一个条件。算法已经发展到系统地确定骨架的基础图，然后定向所有箭头的方向性是由条件独立观察。

An alternative method of structural learning uses optimization-based search. It requires a scoring function and a search strategy. A common scoring function is posterior probability of the structure given the training data, like the BIC or the BDeu. The time requirement of an exhaustive search returning a structure that maximizes the score is superexponential in the number of variables. A local search strategy makes incremental changes aimed at improving the score of the structure. A global search algorithm like Markov chain Monte Carlo can avoid getting trapped in local minima. Friedman et al. discuss using mutual information between variables and finding a structure that maximizes this. They do this by restricting the parent candidate set to k nodes and exhaustively searching therein.

An alternative method of structural learning uses optimization-based search. It requires a scoring function and a search strategy. A common scoring function is posterior probability of the structure given the training data, like the BIC or the BDeu. The time requirement of an exhaustive search returning a structure that maximizes the score is superexponential in the number of variables. A local search strategy makes incremental changes aimed at improving the score of the structure. A global search algorithm like Markov chain Monte Carlo can avoid getting trapped in local minima. Friedman et al. discuss using mutual information between variables and finding a structure that maximizes this. They do this by restricting the parent candidate set to k nodes and exhaustively searching therein.

另一种结构学习方法使用基于优化的搜索。它需要一个评分函数和一个搜索策略。一个常见的评分函数是给定训练数据的结构' '后验概率Posterior probability，比如 BIC 或 BDeu。穷举搜索返回最大化得分结构的时间要求在变量数上是超指数的。局部搜索策略进行增量改变，目的是改进结构的得分。像马尔科夫蒙特卡洛这样的全局搜索算法可以避免陷入局部极小。弗里德曼等人。讨论使用变量之间的互信息，并找到一个结构，最大化这一点。他们通过将父候选节点集限制为 k 节点并在其中进行穷尽式搜索来实现这一点。

A particularly fast method for exact BN learning is to cast the problem as an optimization problem, and solve it using integer programming. Acyclicity constraints are added to the integer program (IP) during solving in the form of cutting planes. Such method can handle problems with up to 100 variables.

A particularly fast method for exact BN learning is to cast the problem as an optimization problem, and solve it using integer programming. Acyclicity constraints are added to the integer program (IP) during solving in the form of cutting planes. Such method can handle problems with up to 100 variables.

一个特别快速的方法为精确的 BN 学习是铸造的问题作为一个最佳化问题，并解决它使用整数规划。以切割面的形式求解整数规划问题时，在整数规划中加入了不规则性约束。这种方法可以处理多达100个变量的问题。

In order to deal with problems with thousands of variables, a different approach is necessary. One is to first sample one ordering, and then find the optimal BN structure with respect to that ordering. This implies working on the search space of the possible orderings, which is convenient as it is smaller than the space of network structures. Multiple orderings are then sampled and evaluated. This method has been proven to be the best available in literature when the number of variables is huge.

In order to deal with problems with thousands of variables, a different approach is necessary. One is to first sample one ordering, and then find the optimal BN structure with respect to that ordering. This implies working on the search space of the possible orderings, which is convenient as it is smaller than the space of network structures. Multiple orderings are then sampled and evaluated. This method has been proven to be the best available in literature when the number of variables is huge.

为了处理成千上万个变量的问题，一种不同的方法是必要的。一种是先对一种有序化进行取样，然后根据这种有序化找到最优的氮化硼结构。这意味着可能排序的搜索空间比网络结构的搜索空间小，因而方便。然后对多重排序进行采样和评估。这种方法已被证明是最好的可用的文献时，变量的数量是巨大的。

Another method consists of focusing on the sub-class of decomposable models, for which the MLE have a closed form. It is then possible to discover a consistent structure for hundreds of variables.

Another method consists of focusing on the sub-class of decomposable models, for which the MLE have a closed form. It is then possible to discover a consistent structure for hundreds of variables.

另一种方法是将重点放在可分解模型的子类上，其最大似然估计具有封闭形式。这样就有可能为数百个变量发现一致的结构。

Learning Bayesian networks with bounded treewidth is necessary to allow exact, tractable inference, since the worst-case inference complexity is exponential in the treewidth k (under the exponential time hypothesis). Yet, as a global property of the graph, it considerably increases the difficulty of the learning process. In this context it is possible to use K-tree for effective learning.

Learning Bayesian networks with bounded treewidth is necessary to allow exact, tractable inference, since the worst-case inference complexity is exponential in the treewidth k (under the exponential time hypothesis). Yet, as a global property of the graph, it considerably increases the difficulty of the learning process. In this context it is possible to use K-tree for effective learning.

学习树宽有限的贝叶斯网络是必要的，以允许精确的，易于处理的推理，因为最坏情况下的推理复杂度是指数在树宽 k (在指数时间假说下)。然而，作为图表的全局属性，它大大增加了学习过程的难度。在这种情况下，可以使用 k 树进行有效的学习。

Statistical introduction统计简介

Main article: Bayesian statistics

Given data [math]\displaystyle{ x\,\! }[/math] and parameter [math]\displaystyle{ \theta }[/math], a simple Bayesian analysis starts with a prior probability (prior) [math]\displaystyle{ p(\theta) }[/math] and likelihood [math]\displaystyle{ p(x\mid\theta) }[/math] to compute a posterior probability [math]\displaystyle{ p(\theta\mid x) \propto p(x\mid\theta)p(\theta) }[/math].

Given data [math]\displaystyle{ x\,\! }[/math] and parameter [math]\displaystyle{ \theta }[/math], a simple Bayesian analysis starts with a prior probability (prior) [math]\displaystyle{ p(\theta) }[/math] and likelihood [math]\displaystyle{ p(x\mid\theta) }[/math] to compute a posterior probability [math]\displaystyle{ p(\theta\mid x) \propto p(x\mid\theta)p(\theta) }[/math].

给定数据数学 x ！ / math and parameter math theta / math，一个简单的贝叶斯分析从先验概率数学 p ( theta) / 数学和似然数学 p (x mid theta) / 数学计算后验概率数学 p ( theta mid x) propto p (x mid theta) p ( theta) / 数学开始。

Often the prior on [math]\displaystyle{ \theta }[/math] depends in turn on other parameters [math]\displaystyle{ \varphi }[/math] that are not mentioned in the likelihood. So, the prior [math]\displaystyle{ p(\theta) }[/math] must be replaced by a likelihood [math]\displaystyle{ p(\theta\mid \varphi) }[/math], and a prior [math]\displaystyle{ p(\varphi) }[/math] on the newly introduced parameters [math]\displaystyle{ \varphi }[/math] is required, resulting in a posterior probability

Often the prior on [math]\displaystyle{ \theta }[/math] depends in turn on other parameters [math]\displaystyle{ \varphi }[/math] that are not mentioned in the likelihood. So, the prior [math]\displaystyle{ p(\theta) }[/math] must be replaced by a likelihood [math]\displaystyle{ p(\theta\mid \varphi) }[/math], and a prior [math]\displaystyle{ p(\varphi) }[/math] on the newly introduced parameters [math]\displaystyle{ \varphi }[/math] is required, resulting in a posterior probability

通常，math theta / math 的优先级依次取决于其他参数的数学 varphi / math，这些参数在可能性中没有被提到。因此，必须用似然数学 p ( theta mid varphi) / 数学代替先前的数学 p ( theta mid varphi) / 数学，并且必须用先前的数学 p ( varphi) / 数学代替新引入的参数数学 varphi / 数学，从而产生后验概率

[math]\displaystyle{ p(\theta,\varphi\mid x) \propto p(x\mid\theta)p(\theta\mid\varphi)p(\varphi). }[/math]

[math]\displaystyle{ p(\theta,\varphi\mid x) \propto p(x\mid\theta)p(\theta\mid\varphi)p(\varphi). }[/math]

数学 p ( theta， varphi mid) propto p (x mid theta) p ( theta mid varphi) p ( varphi) / math

This is the simplest example of a hierarchical Bayes model.模板:Clarify

This is the simplest example of a hierarchical Bayes model.

这是层次贝叶斯模型最简单的例子。

The process may be repeated; for example, the parameters [math]\displaystyle{ \varphi }[/math] may depend in turn on additional parameters [math]\displaystyle{ \psi\,\! }[/math], which require their own prior. Eventually the process must terminate, with priors that do not depend on unmentioned parameters.

The process may be repeated; for example, the parameters [math]\displaystyle{ \varphi }[/math] may depend in turn on additional parameters [math]\displaystyle{ \psi\,\! }[/math], which require their own prior. Eventually the process must terminate, with priors that do not depend on unmentioned parameters.

这个过程可能会重复; 例如，参数 math varphi / math 可能依次依赖于其他参数 math psi， ！ 数学，这需要他们自己的优先权。最终，这个过程必须终止，其优先级不依赖于未提到的参数。

Introductory examples工业实例

Given the measured quantities [math]\displaystyle{ x_1,\dots,x_n\,\! }[/math]each with normally distributed errors of known standard deviation [math]\displaystyle{ \sigma\,\! }[/math],

Given the measured quantities [math]\displaystyle{ x_1,\dots,x_n\,\! }[/math]each with normally distributed errors of known standard deviation [math]\displaystyle{ \sigma\,\! }[/math],

给定测量量数学 x1， dots，xn ， ! / 每个数学与已知标准差数学的正态分布误差,

[math]\displaystyle{ \lt math\gt 数学 x_i \sim N(\theta_i, \sigma^2) x_i \sim N(\theta_i, \sigma^2) x_i \sim N(\theta_i, \sigma^2) }[/math]

</math>

数学

Suppose we are interested in estimating the [math]\displaystyle{ \theta_i }[/math]. An approach would be to estimate the [math]\displaystyle{ \theta_i }[/math] using a maximum likelihood approach; since the observations are independent, the likelihood factorizes and the maximum likelihood estimate is simply

Suppose we are interested in estimating the [math]\displaystyle{ \theta_i }[/math]. An approach would be to estimate the [math]\displaystyle{ \theta_i }[/math] using a maximum likelihood approach; since the observations are independent, the likelihood factorizes and the maximum likelihood estimate is simply

假设我们有兴趣估计数学 theta i / math。一种方法是使用最大似然法来估计 math theta i / math; 由于观测值是独立的，似然分解和最大似然估计是简单的

[math]\displaystyle{ \lt math\gt 数学 \theta_i = x_i. \theta_i = x_i. Theta i x i. }[/math]

</math>

数学

However, if the quantities are related, so that for example the individual [math]\displaystyle{ \theta_i }[/math]have themselves been drawn from an underlying distribution, then this relationship destroys the independence and suggests a more complex model, e.g.,

However, if the quantities are related, so that for example the individual [math]\displaystyle{ \theta_i }[/math]have themselves been drawn from an underlying distribution, then this relationship destroys the independence and suggests a more complex model, e.g.,

然而，如果数量是相关的，例如个别的 math theta i / math 本身就是从一个潜在的分布中抽取出来的，那么这种关系破坏了独立性，并建议使用一个更复杂的模型，例如:

[math]\displaystyle{ \lt math\gt 数学 x_i \sim N(\theta_i,\sigma^2), x_i \sim N(\theta_i,\sigma^2), x_i \sim N(\theta_i,\sigma^2), }[/math]

</math>

数学

[math]\displaystyle{ \lt math\gt 数学 \theta_i\sim N(\varphi, \tau^2), \theta_i\sim N(\varphi, \tau^2), Theta i sim n ( varphi tau ^ 2) , }[/math]

</math>

数学

with improper priors [math]\displaystyle{ \varphi\sim\text{flat} }[/math], [math]\displaystyle{ \tau\sim\text{flat} \in (0,\infty) }[/math]. When [math]\displaystyle{ n\ge 3 }[/math], this is an identified model (i.e. there exists a unique solution for the model's parameters), and the posterior distributions of the individual [math]\displaystyle{ \theta_i }[/math] will tend to move, or shrink away from the maximum likelihood estimates towards their common mean. This shrinkage is a typical behavior in hierarchical Bayes models.

with improper priors [math]\displaystyle{ \varphi\sim\text{flat} }[/math], [math]\displaystyle{ \tau\sim\text{flat} \in (0,\infty) }[/math]. When [math]\displaystyle{ n\ge 3 }[/math], this is an identified model (i.e. there exists a unique solution for the model's parameters), and the posterior distributions of the individual [math]\displaystyle{ \theta_i }[/math] will tend to move, or shrink away from the maximum likelihood estimates towards their common mean. This shrinkage is a typical behavior in hierarchical Bayes models.

数学，数学，数学，数学，数学，数学，数学，数学。当 math n ge 3 / math 时，这是一个确定的模型(即。模型参数存在唯一解) ，并且个体 math theta i / math 的后验分布趋向于移动，或者从最大似然估计收缩到共同均值。这种收缩是分层贝叶斯模型中的典型行为。

Restrictions on priors优先权限

Some care is needed when choosing priors in a hierarchical model, particularly on scale variables at higher levels of the hierarchy such as the variable [math]\displaystyle{ \tau\,\! }[/math] in the example. The usual priors such as the Jeffreys prior often do not work, because the posterior distribution will not be normalizable and estimates made by minimizing the expected loss will be inadmissible.

Some care is needed when choosing priors in a hierarchical model, particularly on scale variables at higher levels of the hierarchy such as the variable [math]\displaystyle{ \tau\,\! }[/math] in the example. The usual priors such as the Jeffreys prior often do not work, because the posterior distribution will not be normalizable and estimates made by minimizing the expected loss will be inadmissible.

在层次结构模型中选择优先级时需要特别注意，尤其是在层次结构的更高级别的尺度变量上，比如变量 math tau ， ！ 例子中的数学。通常的先验，例如 Jeffreys 的先验常常不起作用，因为后验概率不会是正常化的，通过最小化预期损失得出的估计也不会被采纳。

Definitions and concepts定义与概念

See also: Glossary of graph theory § Directed acyclic graphs

Several equivalent definitions of a Bayesian network have been offered. For the following, let G = (V,E) be a directed acyclic graph (DAG) and let X = (X_v), v ∈ V be a set of random variables indexed by V.

Several equivalent definitions of a Bayesian network have been offered. For the following, let G = (V,E) be a directed acyclic graph (DAG) and let X = (X_v), v ∈ V be a set of random variables indexed by V.

贝氏网路的几个等价定义已经被提出。设 g (v，e)是有向无环图(DAG) ，x (x 子 v / sub) ，v ∈ v 是 v 指示的一组随机变量。

Factorization definition因子分解定义

X is a Bayesian network with respect to G if its joint probability density function (with respect to a product measure) can be written as a product of the individual density functions, conditional on their parent variables:模板:Sfn

X is a Bayesian network with respect to G if its joint probability density function (with respect to a product measure) can be written as a product of the individual density functions, conditional on their parent variables:

X 是 g 的贝氏网路，如果它的联合概率密度函数(关于乘积测度)可以写成单个密度函数的乘积，条件是它们的父变量:

[math]\displaystyle{ p (x) = \prod_{v \in V} p \left(x_v \,\big|\, x_{\operatorname{pa}(v)} \right) }[/math]

[math]\displaystyle{  p (x) = \prod_{v \in V} p \left(x_v \,\big|\,  x_{\operatorname{pa}(v)} \right)  }[/math]

数学 p (x) prod { in v } p 左(x v ，big | ，x { operatorname { pa (v)}右) / math

where pa(v) is the set of parents of v (i.e. those vertices pointing directly to v via a single edge).

where pa(v) is the set of parents of v (i.e. those vertices pointing directly to v via a single edge).

其中 pa (v)是 v 的父母的集合(即。这些顶点通过一条边直接指向 v)。

For any set of random variables, the probability of any member of a joint distribution can be calculated from conditional probabilities using the chain rule (given a topological ordering of X) as follows:模板:Sfn

For any set of random variables, the probability of any member of a joint distribution can be calculated from conditional probabilities using the chain rule (given a topological ordering of X) as follows:

对于任何一组随机变量，联合分布的任何成员的概率可以通过使用链式规则(给定一个 x 的拓扑排序)从条件概率计算出来，如下所示:

[math]\displaystyle{ \operatorname P(X_1=x_1, \ldots, X_n=x_n) = \prod_{v=1}^n \operatorname P \left(X_v=x_v \mid X_{v+1}=x_{v+1}, \ldots, X_n=x_n \right) }[/math]

[math]\displaystyle{ \operatorname P(X_1=x_1, \ldots, X_n=x_n) = \prod_{v=1}^n \operatorname P \left(X_v=x_v \mid X_{v+1}=x_{v+1}, \ldots, X_n=x_n \right) }[/math]

数学名称 p (x1x1， ldots，xn) prod { v 1} n operatorname p left (xvx + 1} x { v + 1} x { v + 1} ， ldots，xn 右) / math

Using the definition above, this can be written as:

Using the definition above, this can be written as:

使用上面的定义，可以这样写:

[math]\displaystyle{ \operatorname P(X_1=x_1, \ldots, X_n=x_n) = \prod_{v=1}^n \operatorname P (X_v=x_v \mid X_j=x_j \text{ for each } X_j\, \text{ that is a parent of } X_v\, ) }[/math]

[math]\displaystyle{ \operatorname P(X_1=x_1, \ldots, X_n=x_n) = \prod_{v=1}^n \operatorname P (X_v=x_v \mid X_j=x_j \text{ for each } X_j\, \text{ that is a parent of } X_v\, ) }[/math]

数学运算符名称 p (x1x1， ldots，xn xn) prod { v 1} ^ n 运算符名称 p (x v 中 x j text { for each } x j，text { that is a parent of } x v,) / math

The difference between the two expressions is the conditional independence of the variables from any of their non-descendants, given the values of their parent variables.

The difference between the two expressions is the conditional independence of the variables from any of their non-descendants, given the values of their parent variables.

这两个表达式之间的区别是给定其父变量值的任何非子变量的条件独立。

Local Markov property局部马尔可夫性质

X is a Bayesian network with respect to G if it satisfies the local Markov property: each variable is conditionally independent of its non-descendants given its parent variables:模板:Sfn

X is a Bayesian network with respect to G if it satisfies the local Markov property: each variable is conditionally independent of its non-descendants given its parent variables:

如果满足局部马尔可夫性，则 x 关于 g 是一个贝氏网路: 给定父变量，每个变量有条件地独立于其非后代变量:

[math]\displaystyle{ X_v \perp\!\!\!\perp X_{V \,\smallsetminus\, \operatorname{de}(v)} \mid X_{\operatorname{pa}(v)} \quad\text{for all }v \in V }[/math]

[math]\displaystyle{ X_v \perp\!\!\!\perp X_{V \,\smallsetminus\, \operatorname{de}(v)} \mid X_{\operatorname{pa}(v)} \quad\text{for all }v \in V }[/math]

数学 x perp! ! ! perp x v，smallsetminus，operatorname { de }(v)} mid x operatorname { pa (v)} quad text { for all } v / math

where de(v) is the set of descendants and V \ de(v) is the set of non-descendants of v.

where de(v) is the set of descendants and V \ de(v) is the set of non-descendants of v.

其中 de (v)是后裔集合，v de (v)是 v 的非后裔集合。

This can be expressed in terms similar to the first definition, as

This can be expressed in terms similar to the first definition, as

这可以用类似于第一个定义的术语来表示，如

[math]\displaystyle{ \lt math\gt 数学 \begin{align} \begin{align} Begin { align } & \operatorname P(X_v=x_v \mid X_i=x_i \text{ for each } X_i \text{ that is not a descendant of } X_v\, ) \\[6pt] & \operatorname P(X_v=x_v \mid X_i=x_i \text{ for each } X_i \text{ that is not a descendant of } X_v\, ) \\[6pt] & 运算符名称 p (x v v 中 x i i i text {非} x v ,)[6 pt ] = {} & P(X_v=x_v \mid X_j=x_j \text{ for each } X_j \text{ that is a parent of } X_v\, ) = {} & P(X_v=x_v \mid X_j=x_j \text{ for each } X_j \text{ that is a parent of } X_v\, ) {} & p (x v mid x j j { for each } x j text { that is a parent of } x v ,) \end{align} \end{align} End { align } }[/math]

</math>

数学

The set of parents is a subset of the set of non-descendants because the graph is acyclic.

The set of parents is a subset of the set of non-descendants because the graph is acyclic.

父节点集是非子节点集的一个子集，因为该图是非循环的。

Developing Bayesian networks发展贝叶斯网络

Developing a Bayesian network often begins with creating a DAG G such that X satisfies the local Markov property with respect to G. Sometimes this is a causal DAG. The conditional probability distributions of each variable given its parents in G are assessed. In many cases, in particular in the case where the variables are discrete, if the joint distribution of X is the product of these conditional distributions, then X is a Bayesian network with respect to G.

Developing a Bayesian network often begins with creating a DAG G such that X satisfies the local Markov property with respect to G. Sometimes this is a causal DAG. The conditional probability distributions of each variable given its parents in G are assessed. In many cases, in particular in the case where the variables are discrete, if the joint distribution of X is the product of these conditional distributions, then X is a Bayesian network with respect to G.

开发一个贝氏网路通常从创建一个 DAG g 开始，这样 x 就满足了 g 的局部马尔可夫性，有时这就是一个因果 DAG。评估了 g 中每个变量给定其父变量的条件概率分布。在许多情况下，特别是在变量是离散的情况下，如果 x 的联合分布是这些条件分布的乘积，那么 x 就是 g 的贝氏网路。

Markov blanket马尔科夫毯

The Markov blanket of a node is the set of nodes consisting of its parents, its children, and any other parents of its children. The Markov blanket renders the node independent of the rest of the network; the joint distribution of the variables in the Markov blanket of a node is sufficient knowledge for calculating the distribution of the node. X is a Bayesian network with respect to G if every node is conditionally independent of all other nodes in the network, given its Markov blanket.模板:Sfn

The Markov blanket of a node is the set of nodes consisting of its parents, its children, and any other parents of its children. The Markov blanket renders the node independent of the rest of the network; the joint distribution of the variables in the Markov blanket of a node is sufficient knowledge for calculating the distribution of the node. X is a Bayesian network with respect to G if every node is conditionally independent of all other nodes in the network, given its Markov blanket.

一个节点的马尔可夫覆盖层是由其父节点、其子节点和其子节点的任何其他父节点组成的节点集。马尔可夫包络使节点独立于网络的其余部分，节点的马尔可夫包络中变量的联合分布是计算节点分布的充分知识。如果网络中的每个节点都有条件地独立于网络中的所有其他节点，那么 x 就是 g 的贝氏网路。

模板:Anchord-separation{{|d-分离}“d”-分离

This definition can be made more general by defining the "d"-separation of two nodes, where d stands for directional. We first define the "d"-separation of a trail and then we will define the "d"-separation of two nodes in terms of that.

This definition can be made more general by defining the "d"-separation of two nodes, where d stands for directional. We first define the "d"-separation of a trail and then we will define the "d"-separation of two nodes in terms of that.

通过定义两个节点的“ d”分离，这个定义可以变得更加通用，其中 d 代表方向。我们首先定义“ d”-分离的线索，然后我们将定义“ d”-分离的两个节点的条件。

Let P be a trail from node u to v. A trail is a loop-free, undirected (i.e. all edge directions are ignored) path between two nodes. Then P is said to be d-separated by a set of nodes Z if any of the following conditions holds:

Let P be a trail from node u to v. A trail is a loop-free, undirected (i.e. all edge directions are ignored) path between two nodes. Then P is said to be d-separated by a set of nodes Z if any of the following conditions holds:

设 p 是从节点 u 到节点 v 的路径，路径是无循环的、无向的(例如:。所有边方向被忽略)路径之间的两个节点。如果下列任何一个条件成立，则 p 被一组节点 z 分开:

• P contains (but does not need to be entirely) a directed chain, [math]\displaystyle{ u \cdots \leftarrow m \leftarrow \cdots v }[/math] or [math]\displaystyle{ u \cdots \rightarrow m \rightarrow \cdots v }[/math], such that the middle node m is in Z,

• P contains a fork, [math]\displaystyle{ u \cdots \leftarrow m \rightarrow \cdots v }[/math], such that the middle node m is in Z, or

• P contains an inverted fork (or collider), [math]\displaystyle{ u \cdots \rightarrow m \leftarrow \cdots v }[/math], such that the middle node m is not in Z and no descendant of m is in Z.

The nodes u and v are d-separated by Z if all trails between them are d-separated. If u and v are not d-separated, they are d-connected.

The nodes u and v are d-separated by Z if all trails between them are d-separated. If u and v are not d-separated, they are d-connected.

如果节点 u 和 v 之间的所有轨迹都是 d 分开的，则节点 u 和 v 被 z 分开。如果 u 和 v 不是 d- 分离的，则它们是 d- 连通的。

X is a Bayesian network with respect to G if, for any two nodes u, v:

X is a Bayesian network with respect to G if, for any two nodes u, v:

对于任意两个节点 u，v: ，x 是 g 的贝氏网路:

[math]\displaystyle{ X_u \perp\!\!\!\perp X_v \mid X_Z }[/math]

[math]\displaystyle{ X_u \perp\!\!\!\perp X_v \mid X_Z }[/math]

数学 x u perp ! ! perp x v mid x z / math

where Z is a set which d-separates u and v. (The Markov blanket is the minimal set of nodes which d-separates node v from all other nodes.)

where Z is a set which d-separates u and v. (The Markov blanket is the minimal set of nodes which d-separates node v from all other nodes.)

其中 z 是一个将 u 和 v 分离的集合(马尔可夫覆盖层是将节点 v 与其他所有节点分离的最小节点集合)

Causal networks因果网络

Although Bayesian networks are often used to represent causal relationships, this need not be the case: a directed edge from u to v does not require that X_v be causally dependent on X_u. This is demonstrated by the fact that Bayesian networks on the graphs:

Although Bayesian networks are often used to represent causal relationships, this need not be the case: a directed edge from u to v does not require that X_v be causally dependent on X_u. This is demonstrated by the fact that Bayesian networks on the graphs:

虽然贝叶斯网络经常被用来表示因果关系，但这并不需要: 从 u 到 v 的有向边并不要求 x 子 v / 子因果地依赖于 x 子 u / 子。图表上的贝叶斯网络证明了这一点:

[math]\displaystyle{ a \rightarrow b \rightarrow c \qquad \text{and} \qquad a \leftarrow b \leftarrow c }[/math]

[math]\displaystyle{ a \rightarrow b \rightarrow c \qquad \text{and} \qquad a \leftarrow b \leftarrow c }[/math]

数学 a right tarrow b right tarrow c qquad text { and } a leftarrow b leftarrow c / math

are equivalent: that is they impose exactly the same conditional independence requirements.

are equivalent: that is they impose exactly the same conditional independence requirements.

也就是说，它们施加的条件独立要求完全相同。

A causal network is a Bayesian network with the requirement that the relationships be causal. The additional semantics of causal networks specify that if a node X is actively caused to be in a given state x (an action written as do(X = x)), then the probability density function changes to that of the network obtained by cutting the links from the parents of X to X, and setting X to the caused value x. Using these semantics, the impact of external interventions from data obtained prior to intervention can be predicted.

A causal network is a Bayesian network with the requirement that the relationships be causal. The additional semantics of causal networks specify that if a node X is actively caused to be in a given state x (an action written as do(X = x)), then the probability density function changes to that of the network obtained by cutting the links from the parents of X to X, and setting X to the caused value x. Using these semantics, the impact of external interventions from data obtained prior to intervention can be predicted.

一个因果网络是一个因果关系必须是因果关系的贝氏网路。因果网络的附加语义规定，如果一个节点 x 主动地处于给定的状态 x (一个动作写成 do (x x)) ，那么这个概率密度函数就会改变为通过从 x 的父节点切断到 x 的链接，并将 x 设置为引起的值 x 而获得的网络的状态。利用这些语义，可以预测干预前获得的数据的外部干预的影响。

Inference complexity and approximation algorithms推理复杂度与近似算法

In 1990, while working at Stanford University on large bioinformatic applications, Cooper proved that exact inference in Bayesian networks is NP-hard. This result prompted research on approximation algorithms with the aim of developing a tractable approximation to probabilistic inference. In 1993, Dagum and Luby proved two surprising results on the complexity of approximation of probabilistic inference in Bayesian networks. This result prompted research on approximation algorithms with the aim of developing a tractable approximation to probabilistic inference. In 1993, Dagum and Luby proved two surprising results on the complexity of approximation of probabilistic inference in Bayesian networks. First, they proved that no tractable deterministic algorithm can approximate probabilistic inference to within an absolute error ɛ < 1/2. Second, they proved that no tractable randomized algorithm can approximate probabilistic inference to within an absolute error ɛ < 1/2 with confidence probability greater than 1/2.

</ref> First, they proved that no tractable deterministic algorithm can approximate probabilistic inference to within an absolute error ɛ < 1/2. Second, they proved that no tractable randomized algorithm can approximate probabilistic inference to within an absolute error ɛ < 1/2 with confidence probability greater than 1/2.

/ ref 首先，他们证明了任何易于处理的确定性算法都无法在绝对误差1 / 2以内近似进行概率推断。其次，他们证明了没有任何易于处理的随机化算法可以在置信概率大于1 / 2的情况下，在绝对误差1 / 2的范围内近似进行概率推断。

At about the same time, Roth proved that exact inference in Bayesian networks is in fact #P-complete (and thus as hard as counting the number of satisfying assignments of a conjunctive normal form formula (CNF) and that approximate inference within a factor 2^n1−ɛ for every ɛ > 0, even for Bayesian networks with restricted architecture, is NP-hard.

At about the same time, Roth proved that exact inference in Bayesian networks is in fact #P-complete (and thus as hard as counting the number of satisfying assignments of a conjunctive normal form formula (CNF) and that approximate inference within a factor 2^n1−ɛ for every ɛ > 0, even for Bayesian networks with restricted architecture, is NP-hard.

与此同时，Roth 证明了贝叶斯网络中的精确推理实际上是 # p 完全的(因此就像计算一个合取范式公式(CNF)的满意分配数一样困难) ，而且对于每个0，即使对于有限结构的贝叶斯网络来说，在因子2 sup n sup 1 / sup / sup 中的近似推理也是 np 困难的。

In practical terms, these complexity results suggested that while Bayesian networks were rich representations for AI and machine learning applications, their use in large real-world applications would need to be tempered by either topological structural constraints, such as naïve Bayes networks, or by restrictions on the conditional probabilities. The bounded variance algorithm was the first provable fast approximation algorithm to efficiently approximate probabilistic inference in Bayesian networks with guarantees on the error approximation. This powerful algorithm required the minor restriction on the conditional probabilities of the Bayesian network to be bounded away from zero and one by 1/p(n) where p(n) was any polynomial on the number of nodes in the network n.

In practical terms, these complexity results suggested that while Bayesian networks were rich representations for AI and machine learning applications, their use in large real-world applications would need to be tempered by either topological structural constraints, such as naïve Bayes networks, or by restrictions on the conditional probabilities. The bounded variance algorithm was the first provable fast approximation algorithm to efficiently approximate probabilistic inference in Bayesian networks with guarantees on the error approximation. This powerful algorithm required the minor restriction on the conditional probabilities of the Bayesian network to be bounded away from zero and one by 1/p(n) where p(n) was any polynomial on the number of nodes in the network n.

实际上，这些复杂性结果表明，虽然贝叶斯网络是人工智能和机器学习应用的丰富表现形式，但它们在大型实际应用中的使用需要通过拓扑结构约束(如天真的贝叶斯网络)或条件概率约束加以调整。有界方差算法是贝叶斯网络中第一个在误差近似下有效近似概率推理的可证明的快速近似演算法算法。这个强大的算法需要对贝氏网路的条件概率进行小的限制，使其远离0和1 / p (n) ，其中 p (n)是网络 n 中节点数的任意多项式。

Software软件

! ——这个列表中的条目与来源于维基百科的文章同样“值得注意”。参见 WP: GNG 和 WP: WTAF。-->

Notable software for Bayesian networks include:

Notable software for Bayesian networks include:

著名的贝叶斯网络软件包括:

• Just another Gibbs sampler (JAGS) – Open-source alternative to WinBUGS. Uses Gibbs sampling.

• OpenBUGS – Open-source development of WinBUGS.

• SPSS Modeler – Commercial software that includes an implementation for Bayesian networks.

• Stan (software) – Stan is an open-source package for obtaining Bayesian inference using the No-U-Turn sampler (NUTS), a variant of Hamiltonian Monte Carlo.

• PyMC3 – A Python library implementing an embedded domain specific language to represent bayesian networks, and a variety of samplers (including NUTS)

• WinBUGS – One of the first computational implementations of MCMC samplers. No longer maintained.

History历史

The term Bayesian network was coined by Judea Pearl in 1985 to emphasize:

|pages=329–334 |url=http://ftp.cs.ucla.edu/tech-report/198_-reports/850017.pdf%7Caccess-date=2009-05-01 |format=UCLA Technical Report CSD-850017}}</ref>

| 第329-334页 | 网址 / http://ftp.cs.UCLA.edu/tech-Report/198_-reports/850017.pdf%7Caccess-date=2009-05-01 / 格式 / UCLA 技术报告 / CSD-850017} / ref

• the often subjective nature of the input information

• the reliance on Bayes' conditioning as the basis for updating information

• the distinction between causal and evidential modes of reasoning

In the late 1980s Pearl's Probabilistic Reasoning in Intelligent Systems and Neapolitan's Probabilistic Reasoning in Expert Systems summarized their properties and established them as a field of study.

In the late 1980s Pearl's Probabilistic Reasoning in Intelligent Systems and Neapolitan's Probabilistic Reasoning in Expert Systems summarized their properties and established them as a field of study.

20世纪80年代后期，皮尔的《智能系统中的概率推理》和那不勒斯的《专家系统中的概率推理》总结了它们的性质，并将它们确立为一个研究领域。

See also又及

{ columns-list

The unnamed parameter 2= is no longer supported. Please see the documentation for {{columns-list}}.

colwidth 30em

}}

Further reading 延伸阅读

• Conrady, Stefan; Jouffe, Lionel (2015-07-01). [[[:模板:Google books]] Bayesian Networks and BayesiaLab – A practical introduction for researchers]. Franklin, Tennessee: Bayesian USA. ISBN 978-0-9965333-0-0. 模板:Google books. 

• Charniak, Eugene (Winter 1991). "Bayesian networks without tears" (PDF). AI Magazine. {{cite web}}: Unknown parameter |name-list-format= ignored (help)

• Kruse, Rudolf; Borgelt, Christian; Klawonn, Frank; Moewes, Christian; Steinbrecher, Matthias; Held, Pascal (2013). [[[:模板:Google books]] Computational Intelligence A Methodological Introduction]. London: Springer-Verlag. ISBN 978-1-4471-5012-1. 模板:Google books. 

• Borgelt, Christian; Steinbrecher, Matthias; Kruse, Rudolf (2009). [[[:模板:Google books]] Graphical Models – Representations for Learning, Reasoning and Data Mining] (Second ed.). Chichester: Wiley. ISBN 978-0-470-74956-2. 模板:Google books. 

External links 外部链接

• An Introduction to Bayesian Networks and their Contemporary Applications

• On-line Tutorial on Bayesian nets and probability

• Web-App to create Bayesian nets and run it with a Monte Carlo method

• Continuous Time Bayesian Networks

• Bayesian Networks: Explanation and Analogy

• A live tutorial on learning Bayesian networks

• A hierarchical Bayes Model for handling sample heterogeneity in classification problems, provides a classification model taking into consideration the uncertainty associated with measuring replicate samples.

• Hierarchical Naive Bayes Model for handling sample uncertainty, shows how to perform classification and learning with continuous and discrete variables with replicated measurements.

Category:Graphical models

类别: 图形模型

Category:Causality

分类: 因果关系

Category:Causal inference

类别: 因果推理

This page was moved from wikipedia:en:Bayesian network. Its edit history can be viewed at 贝叶斯网络/edithistory