KS检验

来自集智百科 - 复杂系统|人工智能|复杂科学|复杂网络|自组织
跳到导航 跳到搜索

此词条由Jie翻译。

文件:KS Example
Kolmogorov–Smirnov统计数据的图示。 红线是累积分布函数，蓝线是经验分布函数，黑色箭头是K–S统计量。

In statistics, the Kolmogorov–Smirnov test (K–S test or KS test) is a nonparametric test of the equality of continuous (or discontinuous, see Section 2.2), one-dimensional probability distributions that can be used to compare a sample with a reference probability distribution (one-sample K–S test), or to compare two samples (two-sample K–S test). It is named after Andrey Kolmogorov and Nikolai Smirnov.

In statistics, the Kolmogorov–Smirnov test (K–S test or KS test) is a nonparametric test of the equality of continuous (or discontinuous, see Section 2.2), one-dimensional probability distributions that can be used to compare a sample with a reference probability distribution (one-sample K–S test), or to compare two samples (two-sample K–S test). It is named after Andrey Kolmogorov and Nikolai Smirnov.

在统计学中，Kolmogorov–Smirnov检验（K-S检验或KS检验）属于非参数检验，具有一维概率分布的连续（或不连续，请参见第2.2节）均等性，可用于比较一个样本分布与参考概率分布（单一样本K-S检验），或比较两个样本分布（两个样本的K-S检验）。它以Andrey Kolmogorov和Nikolai Smirnov的名字命名。


The Kolmogorov–Smirnov statistic quantifies a distance between the empirical distribution function of the sample and the cumulative distribution function of the reference distribution, or between the empirical distribution functions of two samples. The null distribution of this statistic is calculated under the null hypothesis that the sample is drawn from the reference distribution (in the one-sample case) or that the samples are drawn from the same distribution (in the two-sample case). In the one-sample case, the distribution considered under the null hypothesis may be continuous (see Section 2), purely discrete or mixed (see Section 2.2). In the two-sample case (see Section 3), the distribution considered under the null hypothesis is a continuous distribution but is otherwise unrestricted.

The Kolmogorov–Smirnov statistic quantifies a distance between the empirical distribution function of the sample and the cumulative distribution function of the reference distribution, or between the empirical distribution functions of two samples. The null distribution of this statistic is calculated under the null hypothesis that the sample is drawn from the reference distribution (in the one-sample case) or that the samples are drawn from the same distribution (in the two-sample case). In the one-sample case, the distribution considered under the null hypothesis may be continuous (see Section 2), purely discrete or mixed (see Section 2.2). In the two-sample case (see Section 3), the distribution considered under the null hypothesis is a continuous distribution but is otherwise unrestricted.

Kolmogorov-Smirnov统计量化了样本分布的经验分布函数Empirical distribution function与参考分布的累积分布函数Cumulative distribution function之间的距离，或者是两个样本分布的经验分布函数之间的距离。该统计量的零分布Null distribution是基于零假设Null hypothesis（或称原始假设）下计算的，可以从参考分布中抽取样本（在单个样本的情况下），或者从相同分布中抽取样本组（在两个样本的情况下）。属于单样本情况的时候，零假设（原假设）考虑的分布可能是连续的（请参阅第2节），纯离散的或混合的（请参阅第2.2节）。然而在考虑两个样本情况下（请参阅第3节），原假设下的分布仅能确定为连续分布，在其他方面并不受限制。


The two-sample K–S test is one of the most useful and general nonparametric methods for comparing two samples, as it is sensitive to differences in both location and shape of the empirical cumulative distribution functions of the two samples.

The two-sample K–S test is one of the most useful and general nonparametric methods for comparing two samples, as it is sensitive to differences in both location and shape of the empirical cumulative distribution functions of the two samples.

K–S双样本检验是比较两个样本分布最有用，也是最通用的非参数方法之一，因为在对比两个样本时，K-S检验对其经验累积分布函数的位置和形状差异具有一定的敏感性。


The Kolmogorov–Smirnov test can be modified to serve as a goodness of fit test. In the special case of testing for normality of the distribution, samples are standardized and compared with a standard normal distribution. This is equivalent to setting the mean and variance of the reference distribution equal to the sample estimates, and it is known that using these to define the specific reference distribution changes the null distribution of the test statistic (see Test with estimated parameters). Various studies have found that, even in this corrected form, the test is less powerful for testing normality than the Shapiro–Wilk test or Anderson–Darling test.

The Kolmogorov–Smirnov test can be modified to serve as a goodness of fit test. In the special case of testing for normality of the distribution, samples are standardized and compared with a standard normal distribution. This is equivalent to setting the mean and variance of the reference distribution equal to the sample estimates, and it is known that using these to define the specific reference distribution changes the null distribution of the test statistic (see Test with estimated parameters). Various studies have found that, even in this corrected form, the test is less powerful for testing normality than the Shapiro–Wilk test or Anderson–Darling test. However, these other tests have their own disadvantages. For instance the Shapiro–Wilk test is known not to work well in samples with many identical values.

Kolmogorov–Smirnov检验经过修改以后可以作为拟合优度检验goodness of fit test。在测试分布正态性的特殊情况下，将样本先标准化再与标准正态分布进行比较。这相当于将参考分布的均值和方差设置为与样本估计值相等。显然，使用这些值和方差来定义特定参考分布会更改检验统计量的零分布（请参阅使用估算参数进行检验）。各种研究发现，即使采用这种校正形式，该测试也不能像Shapiro-Wilk检验或Anderson-Darling检验那样有效地检验正态性。当然，这些其他测试也有其自身的缺点。例如，Shapiro–Wilk检验在具有许多相同值的样本中效果并不好。


Kolmogorov–Smirnov statistic Kolmogorov-Smirnov统计

The empirical distribution function Fn for n independent and identically distributed (i.i.d.) ordered observations Xi is defined as

where I_{[-\infty,x]}(X_i) is the indicator function, equal to 1 if X_i \le x and equal to 0 otherwise.

The Kolmogorov–Smirnov statistic for a given cumulative distribution function F(x) is

[math]\displaystyle{ F_n(x)={1 \over n}\sum_{i=1}^n I_{[-\infty,x]}(X_i) }[/math]

D_n= \sup_x |F_n(x)-F(x)|

D _ n = sup _ x | f _ n (x)-f (x) |

where [math]\displaystyle{ I_{[-\infty,x]}(X_i) }[/math] is the indicator function, equal to 1 if [math]\displaystyle{ X_i \le x }[/math] and equal to 0 otherwise.

where supx is the supremum of the set of distances. By the Glivenko–Cantelli theorem, if the sample comes from distribution F(x), then Dn converges to 0 almost surely in the limit when n goes to infinity. Kolmogorov strengthened this result, by effectively providing the rate of this convergence (see Kolmogorov distribution). Donsker's theorem provides a yet stronger result.

In practice, the statistic requires a relatively large number of data points (in comparison to other goodness of fit criteria such as the Anderson–Darling test statistic) to properly reject the null hypothesis.


n个独立且均匀分布（i.i.d.）的有序观测值Xi的经验分布函数Fn定义为：

F_{n}(x)={1 \over n}\sum _{i=1}^{n}I_{[-\infty ,x]}(X_{i})

其中 {\displaystyle I_{[-\infty ,x]}(X_{i})}I_{[-\infty ,x]}(X_{i})是指标函数，如果 {\displaystyle X_{i}\leq x}X_{i}\leq x等于1，否则等于0。

给定累积分布函数F（x）的Kolmogorov–Smirnov统计量为：

D_{n}=\sup _{x}|F_{n}(x)-F(x)|

其中supx是距离集的最大值。根据Glivenko-Cantelli定理，如果样本来自分布F（x），则当n变为无穷大时，Dn几乎肯定会收敛于0。Kolmogorov通过有效加入收敛速率来增强此结果（请参阅Kolmogorov分布）。另外Donsker定理提供了更强的结果。

在实践中，该统计需要相对大量的数据点（与其他拟合优度标准相比，例如Anderson-Darling检验统计）才能正确地拒绝原假设。

Kolmogorov distribution Kolmogorov 分布

The Kolmogorov distribution is the distribution of the random variable

where B(t) is the Brownian bridge. The cumulative distribution function of K is given by

\operatorname{Pr}(K\leq x)=1-2\sum_{k=1}^\infty (-1)^{k-1} e^{-2k^2 x^2}=\frac{\sqrt{2\pi}}{x}\sum_{k=1}^\infty e^{-(2k-1)^2\pi^2/(8x^2)},

[math]\displaystyle{ K=\sup_{t\in[0,1]}|B(t)| }[/math]

Kolmogorov分布是随机变量的分布

[math]\displaystyle{ K=\sup_{t\in[0,1]}|B(t)| }[/math]

其中B（t）是布朗桥。K的累积分布函数为 \operatorname{Pr}(K\leq x)=1-2\sum_{k=1}^\infty (-1)^{k-1} e^{-2k^2 x^2}=\frac{\sqrt{2\pi}}{x}\sum_{k=1}^\infty e^{-(2k-1)^2\pi^2/(8x^2)},


which can also be expressed by the Jacobi theta function \vartheta_{01}(z=0;\tau=2ix^2/\pi). Both the form of the Kolmogorov–Smirnov test statistic and its asymptotic distribution under the null hypothesis were published by Andrey Kolmogorov, while a table of the distribution was published by Nikolai Smirnov. Recurrence relations for the distribution of the test statistic in finite samples are available.

Under null hypothesis that the sample comes from the hypothesized distribution F(x),

\operatorname{Pr}(K\leq K_\alpha)=1-\alpha.\,

[math]\displaystyle{ \sqrt{n}D_n\xrightarrow{n\to\infty}\sup_t |B(F(t))| }[/math]

in distribution, where B(t) is the Brownian bridge.

If F is continuous then under the null hypothesis [math]\displaystyle{ \sqrt{n}D_n }[/math] converges to the Kolmogorov distribution, which does not depend on F. This result may also be known as the Kolmogorov theorem. The accuracy of this limit as an approximation to the exact cdf of [math]\displaystyle{ K }[/math] when [math]\displaystyle{ n }[/math] is finite is not very impressive: even when [math]\displaystyle{ n=1000 }[/math], the corresponding maximum error is about [math]\displaystyle{ 0.9\% }[/math]; this error increases to [math]\displaystyle{ 2.6\% }[/math] when [math]\displaystyle{ n=100 }[/math] and to a totally unacceptable [math]\displaystyle{ 7\% }[/math] when [math]\displaystyle{ n=10 }[/math]. However, a very simple expedient of replacing [math]\displaystyle{ x }[/math] by

[math]\displaystyle{ x+\frac{1}{6\sqrt{n}}+ \frac{x-1}{4n} }[/math]


Using estimated parameters, the questions arises which estimation method should be used. Usually this would be the maximum likelihood method, but e.g. for the normal distribution MLE has a large bias error on sigma. Using a moment fit or KS minimization instead has a large impact on the critical values, and also some impact on test power. If we need to decide for Student-T data with df = 2 via KS test whether the data could be normal or not, then a ML estimate based on H0 (data is normal, so using the standard deviation for scale) would give much larger KS distance, than a fit with minimum KS. In this case we should reject H0, which is often the case with MLE, because the sample standard deviation might be very large for T-2 data, but with KS minimization we may get still a too low KS to reject H0. In the Student-T case, a modified KS test with KS estimate instead of MLE, makes the KS test indeed slightly worse. However, in other cases, such a modified KS test leads to slightly better test power.

in the argument of the Jacobi theta function reduces these errors to

[math]\displaystyle{ 0.003\% }[/math], [math]\displaystyle{ 0.027\% }[/math], and [math]\displaystyle{ 0.27\% }[/math] respectively; such accuracy would be usually considered more than adequate for all practical applications.

The goodness-of-fit test or the Kolmogorov–Smirnov test can be constructed by using the critical values of the Kolmogorov distribution. This test is asymptotically valid when [math]\displaystyle{ n \to\infty }[/math]. It rejects the null hypothesis at level [math]\displaystyle{ \alpha }[/math] if

where Kα is found from

From the right-continuity of F(x), it follows that F(F^{-1}(t)) \geq t and F^{-1}(F(x)) \leq x and hence, the distribution of D_{n} depends on the null distribution F(x), i.e., is no longer distribution-free as in the continuous case. Therefore, a fast and accurate method has been developed to compute the exact and asymptotic distribution of D_{n} when F(x) is purely discrete or mixed as part of the dgof package of the R language. Major statistical packages among which SAS PROC NPAR1WAY , Stata ksmirnov implement the KS test under the assumption that F(x) is continuous, which is more conservative if the null distribution is actually not continuous (see

The asymptotic power of this test is 1.

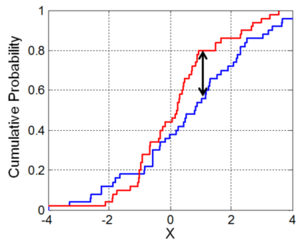
Illustration of the two-sample Kolmogorov–Smirnov statistic. Red and blue lines each correspond to an empirical distribution function, and the black arrow is the two-sample KS statistic.

Fast and accurate algorithms to compute the cdf [math]\displaystyle{ \operatorname{Pr}(D_n \leq x) }[/math] or its complement for arbitrary [math]\displaystyle{ n }[/math] and [math]\displaystyle{ x }[/math], are available from:

The Kolmogorov–Smirnov test may also be used to test whether two underlying one-dimensional probability distributions differ. In this case, the Kolmogorov–Smirnov statistic is

[6] and [7] for continuous null distributions with code in C and Java to be found in [6]. [8] for purely discrete, mixed or continuous null distribution implemented in the KSgeneral package [9] of the R project for statistical computing, which for a given sample also computes the KS test statistic and its p-value. Alternative C++ implementation is available from [8].

Test with estimated parameters

For large samples, the null hypothesis is rejected at level \alpha if

对于大样本，如果

If either the form or the parameters of F(x) are determined from the data Xi the critical values determined in this way are invalid. In such cases, Monte Carlo or other methods may be required, but tables have been prepared for some cases. Details for the required modifications to the test statistic and for the critical values for the normal distribution and the exponential distribution have been published,[1] and later publications also include the Gumbel distribution.[2] The Lilliefors test represents a special case of this for the normal distribution. The logarithm transformation may help to overcome cases where the Kolmogorov test data does not seem to fit the assumption that it came from the normal distribution.


D_{n,m}>c(\alpha)\sqrt{\frac{n + m}{n\cdot m}}.

D _ { n，m } > c (alpha) sqrt { frac { n + m }{ n cdot m }.

Using estimated parameters, the questions arises which estimation method should be used. Usually this would be the maximum likelihood method, but e.g. for the normal distribution MLE has a large bias error on sigma. Using a moment fit or KS minimization instead has a large impact on the critical values, and also some impact on test power. If we need to decide for Student-T data with df = 2 via KS test whether the data could be normal or not, then a ML estimate based on H0 (data is normal, so using the standard deviation for scale) would give much larger KS distance, than a fit with minimum KS. In this case we should reject H0, which is often the case with MLE, because the sample standard deviation might be very large for T-2 data, but with KS minimization we may get still a too low KS to reject H0. In the Student-T case, a modified KS test with KS estimate instead of MLE, makes the KS test indeed slightly worse. However, in other cases, such a modified KS test leads to slightly better test power.


Where n and m are the sizes of first and second sample respectively. The value of c({\alpha}) is given in the table below for the most common levels of \alpha

其中 n 和 m 分别是第一和第二个样本的尺寸。下表给出了最常见的 alpha 级别的 c ({ alpha })值

Discrete and mixed null distribution

{ | class = “ wikitable” Under the assumption that [math]\displaystyle{ F(x) }[/math] is non-decreasing and right-continuous, with countable (possibly infinite) number of jumps, the KS test statistic can be expressed as:
\alpha 0.20 0.15 0.10 0.05 0.025 0.01 0.005 0.001

0.15 | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 | 0.001

[math]\displaystyle{ D_n= \sup_x |F_n(x)-F(x)| = \sup_{0 \leq t \leq 1} |F_n(F^{-1}(t)) - F(F^{-1}(t))|. }[/math]
c({\alpha}) 1.073 1.138 1.224 1.358 1.48 1.628 1.731 1.949

1.073 | 1.138 | 1.224 | 1.358 | 1.48 | 1.628 | 1.731 | 1.949

From the right-continuity of [math]\displaystyle{ F(x) }[/math], it follows that [math]\displaystyle{ F(F^{-1}(t)) \geq t }[/math] and [math]\displaystyle{ F^{-1}(F(x)) \leq x }[/math] and hence, the distribution of [math]\displaystyle{ D_{n} }[/math] depends on the null distribution [math]\displaystyle{ F(x) }[/math], i.e., is no longer distribution-free as in the continuous case. Therefore, a fast and accurate method has been developed to compute the exact and asymptotic distribution of [math]\displaystyle{ D_{n} }[/math] when [math]\displaystyle{ F(x) }[/math] is purely discrete or mixed [3], implemented in C++ and in the KSgeneral package [4] of the R language. The functions disc_ks_test(), mixed_ks_test() and cont_ks_test() compute also the KS test statistic and p-values for purely discrete, mixed or continuous null distributions and arbitrary sample sizes. The KS test and its p-values for discrete null distributions and small sample sizes are also computed in [5] as part of the dgof package of the R language. Major statistical packages among which SAS PROC NPAR1WAY [6], Stata ksmirnov [7] implement the KS test under the assumption that [math]\displaystyle{ F(x) }[/math] is continuous, which is more conservative if the null distribution is actually not continuous (see [8]

|}

[9]

[10]).

and in general by

一般来说

Two-sample Kolmogorov–Smirnov test

c\left(\alpha\right)=\sqrt{-\ln\left(\tfrac{\alpha}{2}\right)\cdot \tfrac{1}{2}},

C left (alpha right) = sqrt {-ln left (tfrac { alpha }{2} right) cdot tfrac {1}{2} ,

Illustration of the two-sample Kolmogorov–Smirnov statistic. Red and blue lines each correspond to an empirical distribution function, and the black arrow is the two-sample KS statistic.


so that the condition reads

这样条件就是

The Kolmogorov–Smirnov test may also be used to test whether two underlying one-dimensional probability distributions differ. In this case, the Kolmogorov–Smirnov statistic is


D_{n,m}>\frac{1}{\sqrt{n}}\cdot\sqrt{-\ln\left(\tfrac{\alpha}{2}\right)\cdot \tfrac{1 + \tfrac{n}{m}}{2}}.

1}{ sqrt { n }} cdot sqrt {-ln left (tfrac { alpha }{2} right) cdot tfrac {1 + tfrac { n }{ m }{2}}.

[math]\displaystyle{ D_{n,m}=\sup_x |F_{1,n}(x)-F_{2,m}(x)|, }[/math]


Here, again, the larger the sample sizes, the more sensitive the minimal bound: For a given ratio of sample sizes (e.g. m=n), the minimal bound scales in the size of either of the samples according to its inverse square root.

在这里，样本容量越大，最小界限越敏感: 对于给定的样本容量比例(例如:。M = n) ，根据样本的逆平方根得到样本大小的最小界限尺度。

where [math]\displaystyle{ F_{1,n} }[/math] and [math]\displaystyle{ F_{2,m} }[/math] are the empirical distribution functions of the first and the second sample respectively, and [math]\displaystyle{ \sup }[/math] is the supremum function.


Note that the two-sample test checks whether the two data samples come from the same distribution. This does not specify what that common distribution is (e.g. whether it's normal or not normal). Again, tables of critical values have been published. A shortcoming of the Kolmogorov–Smirnov test is that it is not very powerful because it is devised to be sensitive against all possible types of differences between two distribution functions. and showed evidence that the Cucconi test, originally proposed for simultaneously comparing location and scale, is much more powerful than the Kolmogorov–Smirnov test when comparing two distribution functions.

注意，两个样本测试检查两个数据样本是否来自同一分布。这并没有指定公共分布是什么(例如,。是否正常)。同样，已经发布了临界值表。Kolmogorov-Smirnov 检验的一个缺点是它不是很强大，因为它被设计成对两个分布函数之间所有可能的差异类型都很敏感。证据表明，当比较两个分布函数时，最初为同时比较位置和规模而提出的 Cucconi 检验要比 Kolmogorov-Smirnov 检验强大得多。

For large samples, the null hypothesis is rejected at level [math]\displaystyle{ \alpha }[/math] if


[math]\displaystyle{ D_{n,m}\gt c(\alpha)\sqrt{\frac{n + m}{n\cdot m}}. }[/math]


Where [math]\displaystyle{ n }[/math] and [math]\displaystyle{ m }[/math] are the sizes of first and second sample respectively. The value of [math]\displaystyle{ c({\alpha}) }[/math] is given in the table below for the most common levels of [math]\displaystyle{ \alpha }[/math]

While the Kolmogorov–Smirnov test is usually used to test whether a given F(x) is the underlying probability distribution of Fn(x), the procedure may be inverted to give confidence limits on F(x) itself. If one chooses a critical value of the test statistic Dα such that P(Dn > Dα) = α, then a band of width ±Dα around Fn(x) will entirely contain F(x) with probability 1 − α.

虽然 Kolmogorov-Smirnov 检验通常用来检验给定的 f (x)是否是 Fn (x)的基本概率分布，但是这个过程可以被反转来给出 f (x)本身的置信限。如果选择检验统计量 dα 的一个临界值使 p (Dn > dα) = α，则 Fn (x)周围的一条宽度 ± dα 带将完全包含 f (x) ，概率为1-α。


A distribution-free multivariate Kolmogorov–Smirnov goodness of fit test has been proposed by Justel, Peña and Zamar (1997). The test uses a statistic which is built using Rosenblatt's transformation, and an algorithm is developed to compute it in the bivariate case. An approximate test that can be easily computed in any dimension is also presented. Justel、 Peña 和 Zamar (1997)提出了一种无分布多元 Kolmogorov-Smirnov 拟合优度检验方法。该检验使用了一个基于 Rosenblatt 变换的统计量，并开发了一个二元情况下的统计量计算算法。本文还给出了一个可以方便地计算任意维数的近似试验。 The Kolmogorov–Smirnov test statistic needs to be modified if a similar test is to be applied to multivariate data. This is not straightforward because the maximum difference between two joint cumulative distribution functions is not generally the same as the maximum difference of any of the complementary distribution functions. Thus the maximum difference will differ depending on which of \Pr(x < X \land y < Y) or \Pr(X < x \land Y > y) or any of the other two possible arrangements is used. One might require that the result of the test used should not depend on which choice is made. 如果要对多变量数据应用类似的检验，则需要修改 Kolmogorov-Smirnov 检验统计量。这并不简单，因为两个联合累积分布函数的最大差值通常不等于任何一个互补分布函数的最大差值。因此，最大的差异将取决于 Pr (x < x 土地 y < y)或 Pr (x < x 土地 y > y)或其他两种可能的安排中的任何一种。有人可能会要求所使用的测试的结果不应该取决于作出的选择。
[math]\displaystyle{ \alpha }[/math] 0.20 0.15 0.10 0.05 0.025 0.01 0.005 0.001
[math]\displaystyle{ c({\alpha}) }[/math] 1.073 1.138 1.224 1.358 1.48 1.628 1.731 1.949

One approach to generalizing the Kolmogorov–Smirnov statistic to higher dimensions which meets the above concern is to compare the cdfs of the two samples with all possible orderings, and take the largest of the set of resulting K–S statistics. In d dimensions, there are 2d−1 such orderings. One such variation is due to Peacock

将 Kolmogorov-Smirnov 统计量推广到更高维度的一种方法是将两个样本的 cdfs 与所有可能的排序进行比较，并取得最大的 k-s 统计量集合。在 d 维中，有2d-1这样的排列。一个这样的变化是由于孔雀


(see also Gosset

(参见戈塞特

and in general[11] by

for a 3D version)

3 d 版本)


and another to Fasano and Franceschini (see Lopes et al. for a comparison and computational details). Critical values for the test statistic can be obtained by simulations, but depend on the dependence structure in the joint distribution.

另一个是 Fasano 和 Franceschini (见 Lopes 等人。以便进行比较和计算细节)。通过仿真可以得到检验统计量的临界值，但这个临界值取决于联合分布中的相关结构。

[math]\displaystyle{ c\left(\alpha\right)=\sqrt{-\ln\left(\tfrac{\alpha}{2}\right)\cdot \tfrac{1}{2}}, }[/math]


In one dimension, the Kolmogorov–Smirnov statistic is identical to the so-called star discrepancy D, so another native KS extension to higher dimensions would be simply to use D also for higher dimensions. Unfortunately, the star discrepancy is hard to calculate in high dimensions.

在一个维度上，Kolmogorov-Smirnov 统计量与所谓的恒星差异 d 是一致的，所以另一个本地的 KS 对更高维度的扩展将是简单地对更高维度也使用 d。不幸的是，在高维空间中，恒星的差异很难计算。

so that the condition reads


[math]\displaystyle{ D_{n,m}\gt \frac{1}{\sqrt{n}}\cdot\sqrt{-\ln\left(\tfrac{\alpha}{2}\right)\cdot \tfrac{1 + \tfrac{n}{m}}{2}}. }[/math]

The Kolmogorov-Smirnov test (one or two sampled test verifies the equality of distributions) is implemented in many software programs:

Kolmogorov-Smirnov 检验(一个或两个抽样检验验证分布是否相等)在许多软件程序中实现:


Here, again, the larger the sample sizes, the more sensitive the minimal bound: For a given ratio of sample sizes (e.g. [math]\displaystyle{ m=n }[/math]), the minimal bound scales in the size of either of the samples according to its inverse square root.


Note that the two-sample test checks whether the two data samples come from the same distribution. This does not specify what that common distribution is (e.g. whether it's normal or not normal). Again, tables of critical values have been published. A shortcoming of the Kolmogorov–Smirnov test is that it is not very powerful because it is devised to be sensitive against all possible types of differences between two distribution functions. [12] and [13] showed evidence that the Cucconi test, originally proposed for simultaneously comparing location and scale, is much more powerful than the Kolmogorov–Smirnov test when comparing two distribution functions.


Setting confidence limits for the shape of a distribution function

模板:Main article


While the Kolmogorov–Smirnov test is usually used to test whether a given F(x) is the underlying probability distribution of Fn(x), the procedure may be inverted to give confidence limits on F(x) itself. If one chooses a critical value of the test statistic Dα such that P(Dn > Dα) = α, then a band of width ±Dα around Fn(x) will entirely contain F(x) with probability 1 − α.


The Kolmogorov–Smirnov statistic in more than one dimension

A distribution-free multivariate Kolmogorov–Smirnov goodness of fit test has been proposed by Justel, Peña and Zamar (1997).[14] The test uses a statistic which is built using Rosenblatt's transformation, and an algorithm is developed to compute it in the bivariate case. An approximate test that can be easily computed in any dimension is also presented.


The Kolmogorov–Smirnov test statistic needs to be modified if a similar test is to be applied to multivariate data. This is not straightforward because the maximum difference between two joint cumulative distribution functions is not generally the same as the maximum difference of any of the complementary distribution functions. Thus the maximum difference will differ depending on which of [math]\displaystyle{ \Pr(x \lt X \land y \lt Y) }[/math] or [math]\displaystyle{ \Pr(X \lt x \land Y \gt y) }[/math] or any of the other two possible arrangements is used. One might require that the result of the test used should not depend on which choice is made.


One approach to generalizing the Kolmogorov–Smirnov statistic to higher dimensions which meets the above concern is to compare the cdfs of the two samples with all possible orderings, and take the largest of the set of resulting K–S statistics. In d dimensions, there are 2d−1 such orderings. One such variation is due to Peacock[15]

(see also Gosset[16]

for a 3D version) 

 | last = Eadie

| last = Eadie

and another to Fasano and Franceschini[17] (see Lopes et al. for a comparison and computational details).[18] Critical values for the test statistic can be obtained by simulations, but depend on the dependence structure in the joint distribution. 

 | first = W.T. |author2=D. Drijard |author3=F.E. James |author4=M. Roos |author5=B. Sadoulet

第一个 = w.t。2 = d.3 = f.e.4 = m.5 = b.女名女子名 


 | title = Statistical Methods in Experimental Physics

实验物理中的统计方法

In one dimension, the Kolmogorov–Smirnov statistic is identical to the so-called star discrepancy D, so another native KS extension to higher dimensions would be simply to use D also for higher dimensions. Unfortunately, the star discrepancy is hard to calculate in high dimensions. 

 | publisher = North-Holland

| publisher = North-Holland 


 | year = 1971

1971年

Implementations

 | location = Amsterdam

地点: 阿姆斯特丹

The Kolmogorov-Smirnov test (one or two sampled test verifies the equality of distributions) is implemented in many software programs: 

 | pages = 269–271

| 页数 = 269-271 


 | isbn = 978-0-444-10117-4 }}

| isbn = 978-0-444-10117-4} 

 | last1 = Stuart

1 = Stuart

  • The R package "KSgeneral"[4] computes the KS test statistics and its p-values under arbitrary, possibly discrete, mixed or continuous null distribution.
 | first1 = Alan

1 = Alan

  • R's statistics base-package implements the test as ks.test {stats} in its "stats" package.
 | first2 = Keith

2 = Keith

  • SAS implements the test in its PROC NPAR1WAY procedure.
 | last2 = Ord

2 = Ord

  • Python has an implementation of this test provided by SciPy[19] by Statistical functions (scipy.stats)
 | first3=Steven [F.]

| first3 = Steven [ f. ]

  • SYSTAT (SPSS Inc., Chicago, IL)
 | last3=Arnold

3 = Arnold 

 | title=Classical Inference and the Linear Model

经典推理和线性模型

  • KNIME has a node implementing this test based on the above Java implementation[21]
 | edition=Sixth

第六版 

 | series = Kendall's Advanced Theory of Statistics

系列 = Kendall 的高级统计理论

  • Stata (Stata Corporation, College Station, TX) implements the test in ksmirnov (Kolmogorov–Smirnov equality-of-distributions test) command. [22]
 | volume = 2A

2A 

 | year = 1999

1999年

  • Excel runs the test as KSCRIT and KSPROB [23]
 | publisher = Arnold

阿诺德 


 | location = London

| 地点: 伦敦

See also

 | isbn=978-0-340-66230-4

| isbn = 978-0-340-66230-4 

 | mr=1687411

1687411先生 

 | pages = 25.37–25.43 }}

| pages = 25.37-25.43}


References

  1. ↑ Pearson, E. S., ed. (1972). Biometrika Tables for Statisticians. 2. Cambridge University Press. pp. 117–123, Tables 54, 55. ISBN 978-0-521-06937-3. 
  2. ↑ Shorack, Galen R.; Wellner, Jon A. (1986). Empirical Processes with Applications to Statistics. Wiley. p. 239. ISBN 978-0471867258. 
  3. ↑ 引用错误：无效<ref>标签；未给name属性为DKT2019的引用提供文字
  4. ↑ 4.0 4.1 引用错误：无效<ref>标签；未给name属性为KSgeneral的引用提供文字
  5. ↑ Arnold, Taylor B.; Emerson, John W. (2011). "Nonparametric Goodness-of-Fit Tests for Discrete Null Distributions" (PDF). The R Journal. 3 (2): 34\[Dash]39. doi:10.32614/rj-2011-016.
  6. ↑ "SAS/STAT(R) 14.1 User's Guide". support.sas.com. Retrieved 14 April 2018.
  7. ↑ "ksmirnov — Kolmogorov–Smirnov equality-of-distributions test" (PDF). stata.com. Retrieved 14 April 2018.
  8. ↑ Noether GE (1963). "Note on the Kolmogorov Statistic in the Discrete Case". Metrika. 7 (1): 115–116. doi:10.1007/bf02613966.
  9. ↑ Slakter MJ (1965). "A Comparison of the Pearson Chi-Square and Kolmogorov Goodness-of-Fit Tests with Respect to Validity". Journal of the American Statistical Association. 60 (311): 854–858. doi:10.2307/2283251. JSTOR 2283251.
  10. ↑ Walsh JE (1963). "Bounded Probability Properties of Kolmogorov–Smirnov and Similar Statistics for Discrete Data". Annals of the Institute of Statistical Mathematics. 15 (1): 153–158. doi:10.1007/bf02865912.
  11. ↑ Eq. (15) in Section 3.3.1 of Knuth, D.E., The Art of Computer Programming, Volume 2 (Seminumerical Algorithms), 3rd Edition, Addison Wesley, Reading Mass, 1998.
  12. ↑ Marozzi, Marco (2009). "Some Notes on the Location-Scale Cucconi Test". Journal of Nonparametric Statistics. 21 (5): 629–647. doi:10.1080/10485250902952435.
  13. ↑ Marozzi, Marco (2013). "Nonparametric Simultaneous Tests for Location and Scale Testing: a Comparison of Several Methods". Communications in Statistics – Simulation and Computation. 42 (6): 1298–1317. doi:10.1080/03610918.2012.665546.
  14. ↑ Justel, A.; Peña, D.; Zamar, R. (1997). "A multivariate Kolmogorov–Smirnov test of goodness of fit". Statistics & Probability Letters. 35 (3): 251–259. CiteSeerX 10.1.1.498.7631. doi:10.1016/S0167-7152(97)00020-5.
  15. ↑ Peacock J.A. (1983). "Two-dimensional goodness-of-fit testing in astronomy". Monthly Notices of the Royal Astronomical Society. 202 (3): 615–627. Bibcode:1983MNRAS.202..615P. doi:10.1093/mnras/202.3.615.
  16. ↑ Gosset E. (1987). "A three-dimensional extended Kolmogorov-Smirnov test as a useful tool in astronomy}". Astronomy and Astrophysics. 188 (1): 258–264. Bibcode:1987A&A...188..258G.
  17. ↑ Fasano, G., Franceschini, A. (1987). "A multidimensional version of the Kolmogorov–Smirnov test". Monthly Notices of the Royal Astronomical Society. 225: 155–170. Bibcode:1987MNRAS.225..155F. doi:10.1093/mnras/225.1.155. ISSN 0035-8711.{{cite journal}}: CS1 maint: uses authors parameter (link)
  18. ↑ Lopes, R.H.C., Reid, I., Hobson, P.R. (23–27 April 2007). The two-dimensional Kolmogorov–Smirnov test (PDF). XI International Workshop on Advanced Computing and Analysis Techniques in Physics Research. Amsterdam, the Netherlands.{{cite conference}}: CS1 maint: uses authors parameter (link)
  19. ↑ "scipy.stats.kstest". SciPy SciPy v0.14.0 Reference Guide. The Scipy community. Retrieved 18 June 2019.
  20. ↑ "KolmogorovSmirnovTes". Retrieved 18 June 2019.
  21. ↑ "New statistics nodes". Retrieved 25 June 2020.
  22. ↑ "ksmirnov — Kolmogorov –Smirnov equality-of-distributions test" (PDF). Retrieved 18 June 2019.
  23. ↑ "Kolmogorov-Smirnov Test for Normality Hypothesis Testing". Retrieved 18 June 2019.


Further reading

  • Eadie, W.T.; D. Drijard; F.E. James; M. Roos; B. Sadoulet (1971). Statistical Methods in Experimental Physics. Amsterdam: North-Holland. pp. 269–271

Category:Statistical tests

类别: 统计测试. ISBN 978-0-444-10117-4. 

Category:Statistical distance

类别: 统计距离

  • {{cite book

Category:Nonparametric statistics

类别: 无母数统计 

 | last1 = Stuart

Category:Normality tests

分类: 正常性测试


This page was moved from wikipedia:en:Kolmogorov–Smirnov test. Its edit history can be viewed at KS检验/edithistory

取自“https://wiki.swarma.org/index.php?title=KS检验&oldid=14357”