仓室模型

本词条由Agnes初步翻译

此词条暂由彩云小译翻译，未经人工整理和审校，带来阅读不便，请见谅。

Compartmental models simplify the mathematical modelling of infectious diseases. The population is assigned to compartments with labels - for example, S, I, or R, (Susceptible, Infectious, or Recovered). People may progress between compartments. The order of the labels usually shows the flow patterns between the compartments; for example SEIS means susceptible, exposed, infectious, then susceptible again.

Compartmental models simplify the mathematical modelling of infectious diseases. The population is assigned to compartments with labels - for example, S, I, or R, (Susceptible, Infectious, or Recovered). People may progress between compartments. The order of the labels usually shows the flow patterns between the compartments; for example SEIS means susceptible, exposed, infectious, then susceptible again.

传染病模型简化了传染病的数学模型。人口被划分到带有标签的类别，例如，S，I，或 R，(易感者，感病者，或康复者)。不同类别中的人数会发生变化。标签的顺序通常显示类别之间的流动模式，例如 SEIS模型意味着易感染成为暴露者、然后成为感病者，然后再次回到易感者。

==Agnes（讨论）[翻译]译者知识水平限制，通过多方查询资料对传染病模型有了基本了解之后，在“SEIS means susceptible, exposed, infectious, then susceptible again”的翻译中，选择增添了一些成分，但此部分的翻译仍然存疑

The origin of such models is the early 20th century, with an important work being that of Kermack and McKendrick in 1927.^[1]

The origin of such models is the early 20th century, with an important work being that of Kermack and McKendrick in 1927.

这些模型的起源于20世纪早期，其中克马克和麦克德里克1927年的著作意义重大。

The models are most often run with ordinary differential equations (which are deterministic), but can also be used with a stochastic (random) framework, which is more realistic but much more complicated to analyze.

这些模型通常使用常微分方程(确定的) ，但也可以使用随机框架（任意的），这种框架更加现实，但分析起来要复杂得多。

Models try to predict things such as how a disease spreads, or the total number infected, or the duration of an epidemic, and to estimate various epidemiological parameters such as the reproductive number. Such models can show how different public health interventions may affect the outcome of the epidemic, e.g., what the most efficient technique is for issuing a limited number of vaccines in a given population.

模型试图预测疾病的传播方式、感染总人数、流行病持续时间等，并估计各种流行病学参数，如生殖数量。这些模型可以显示不同的公共卫生干预措施对疫情结果的影响，例如，在指定人群中发放数量有限的疫苗时，最有效的技术是什么。

The SIR model

SIR模型

The SIR model^[2]^[3] is one of the simplest compartmental models, and many models are derivatives of this basic form. The model consists of three compartments:

The SIR model is one of the simplest compartmental models, and many models are derivatives of this basic form. The model consists of three compartments:

SIR 模型是最简单的传染病模型之一，许多模型都是这种基本形式的衍生物。该模式由三个部分组成:

S: The number of susceptible individuals. When a susceptible and an infectious individual come into "infectious contact", the susceptible individual contracts the disease and transitions to the infectious compartment.

S：易感者。当一个易感者和一个感病者产生“传染性接触”时，易感者就会感染这种疾病，并被归入感病者。

I: The number of infectious individuals. These are individuals who have been infected and are capable of infecting susceptible individuals.

I：感病者。这些人已经感染，并且有能力感染易感者。

R for the number of removed (and immune) or deceased individuals. These are individuals who have been infected and have either recovered from the disease and entered the removed compartment, or died. It is assumed that the number of deaths is negligible with respect to the total population. This compartment may also be called "recovered" or "resistant".

R: for the number of removed (and immune) or deceased individuals. These are individuals who have been infected and have either recovered from the disease and entered the removed compartment, or died. It is assumed that the number of deaths is negligible with respect to the total population. This compartment may also be called "recovered" or "resistant".

R：康复者或病死者。这些人已经感染，或者已经从疾病中康复并被归入康复者，或者已经死亡。假定死亡人数与总人口相比微不足道。这种类别也可称为“康复者”或“抵抗者”。

This model is reasonably predictive^[4] for infectious diseases that are transmitted from human to human, and where recovery confers lasting resistance, such as measles, mumps and rubella.

This model is reasonably predictive for infectious diseases that are transmitted from human to human, and where recovery confers lasting resistance, such as measles, mumps and rubella.

这个模型可以合理地预测传染病在人与人之间传播的情况，以及康复带来持久抵抗力的情况，如麻疹、腮腺炎和风疹等疾病。

Spatial SIR model simulation. Each cell can infect its eight immediate neighbors.

【图1：Spatial SIR model simulation. Each cell can infect its eight immediate neighbors.空间 SIR 模型仿真。每个细胞都能感染它的八个近邻。】

These variables (S, I, and R) represent the number of people in each compartment at a particular time. To represent that the number of susceptible, infectious and removed individuals may vary over time (even if the total population size remains constant), we make the precise numbers a function of t (time): S(t), I(t) and R(t). For a specific disease in a specific population, these functions may be worked out in order to predict possible outbreaks and bring them under control.^[4]

These variables (S, I, and R) represent the number of people in each compartment at a particular time. To represent that the number of susceptible, infectious and removed individuals may vary over time (even if the total population size remains constant), we make the precise numbers a function of t (time): S(t), I(t) and R(t). For a specific disease in a specific population, these functions may be worked out in order to predict possible outbreaks and bring them under control.

这些变量（S、I和R）表示特定时间每个类别内的人数。为了表示易感者、感病者和康复者数量可能随时间变化(总种群规模保持不变) ，我们将精确数字设为时间t的函数: S(t)、 I(t)和 R(t)。对于特定人群中的特定疾病，这些函数可以用于预测潜在的传染病暴发并控制它们。

As implied by the variable function of t, the model is dynamic in that the numbers in each compartment may fluctuate over time. The importance of this dynamic aspect is most obvious in an endemic disease with a short infectious period, such as measles in the UK prior to the introduction of a vaccine in 1968. Such diseases tend to occur in cycles of outbreaks due to the variation in number of susceptibles (S(t)) over time. During an epidemic, the number of susceptible individuals falls rapidly as more of them are infected and thus enter the infectious and removed compartments. The disease cannot break out again until the number of susceptibles has built back up, e.g. as a result of offspring being born into the susceptible compartment.

从t的变量函数中可以看出，该模型是动态的，因为每个分类中的数量可能随时间而波动。这一动态方面的重要性尤其体现在传染时间较短的地方性疾病中，如1968年引进疫苗之前英国的麻疹。由于易感者(S (t))随着时间发生变化，这类疾病往往会周期性爆发。在流行病爆发期间，易感者人数迅速下降，因为更多的人受到感染，从而进入感病者和康复者的类别。这种疾病只有易感者数量增加时才能再次爆发，例如：当后代出生在易感者区域中时。

Yellow=Susceptible, Maroon=Infectious, Teal=Recovered

【图2：Yellow=Susceptible, Maroon=Infectious, Teal=Recovered黄色=易感者，栗色=感病者，青色 =康复者】

Each member of the population typically progresses from susceptible to infectious to removed. This can be shown as a flow diagram in which the boxes represent the different compartments and the arrows the transition between compartments, i.e.

人群中的每个成员通常由易感者变到感染者，再回归康复者。这可以显示为一个流程图，在这个流程图中，盒子代表不同的类别，箭头代表类别之间的过渡，即：

SIR compartment model

【图3：SIR compartment modelSIR传染病模型】

Transition rates

传染率

For the full specification of the model, the arrows should be labeled with the transition rates between compartments. Between S and I, the transition rate is assumed to be d(S/N)/dt = -βSI/N², where N is the total population, β is the average number of contacts per person per time, multiplied by the probability of disease transmission in a contact between a susceptible and an infectious subject, and SI/N² is the fraction of those contacts between an infectious and susceptible individual which result in the susceptible person becoming infected. (This is mathematically similar to the law of mass action in chemistry in which random collisions between molecules result in a chemical reaction and the fractional rate is proportional to the concentration of the two reactants).

For the full specification of the model, the arrows should be labeled with the transition rates between compartments. Between S and I, the transition rate is assumed to be d(S/N)/dt = -βSI/N², where N is the total population, β is the average number of contacts per person per time, multiplied by the probability of disease transmission in a contact between a susceptible and an infectious subject, and SI/N² is the fraction of those contacts between an infectious and susceptible individual which result in the susceptible person becoming infected. (This is mathematically similar to the law of mass action in chemistry in which random collisions between molecules result in a chemical reaction and the fractional rate is proportional to the concentration of the two reactants).

为了完整说明这个模型，箭头应该标明类别之间的传染率。在S和I之间，传染率假定为d (S/N)/dt =-SI/N < sup > 2 ，其中 N 是总人口，β是平均每人每次接触的人数，乘以易感者和感病者之间接触传播疾病的概率，SI/N < sup > 2 是易感个体和感病个体之间接触之后导致易感个体感染的百分比。(这与化学中的质量作用定律在数学计算上类似，即分子之间的随机碰撞导致化学反应，反应速率与两种反应物的浓度成正比)。

Between I and R, the transition rate is assumed to be proportional to the number of infectious individuals which is γI. This is equivalent to assuming that the probability of an infectious individual recovering in any time interval dt is simply γdt. If an individual is infectious for an average time period D, then γ = 1/D. This is also equivalent to the assumption that the length of time spent by an individual in the infectious state is a random variable with an exponential distribution. The "classical" SIR model may be modified by using more complex and realistic distributions for the I-R transition rate (e.g the Erlang distribution^[5]).

Between I and R, the transition rate is assumed to be proportional to the number of infectious individuals which is γI. This is equivalent to assuming that the probability of an infectious individual recovering in any time interval dt is simply γdt. If an individual is infectious for an average time period D, then γ = 1/D. This is also equivalent to the assumption that the length of time spent by an individual in the infectious state is a random variable with an exponential distribution. The "classical" SIR model may be modified by using more complex and realistic distributions for the I-R transition rate (e.g the Erlang distribution).

在 I 和 R 之间，假设传染率与感病者的数目成正比，即γI。这相当于假设一个感病者在任何时间间隔内恢复的概率仅为γdt。如果平均每个人在时间段D内具有传染性，那么γ= 1/D。这也相当于假设一个人在感染状态下的时间长度是一个服从指数分布的随机变量。“经典的” SIR 模型可以通过更加复杂和现实的分布来修正I-R 传染率(例如爱尔朗分布)。

For the special case in which there is no removal from the infectious compartment (γ=0), the SIR model reduces to a very simple SI model, which has a logistic solution, in which every individual eventually becomes infected.

对于感病者全都没有康复的特殊情况（γ=0），SIR 模型就简化为一个非常简单的 SI 模型，该模型具有一个逻辑解，即其中每个人最终都会被感染。

The SIR model without vital dynamics

缺少生命动力学的SIR模型

The dynamics of an epidemic, for example, the flu, are often much faster than the dynamics of birth and death, therefore, birth and death are often omitted in simple compartmental models. The SIR system without so-called vital dynamics (birth and death, sometimes called demography) described above can be expressed by the following set of ordinary differential equations:^[6]^[3]

The dynamics of an epidemic, for example, the flu, are often much faster than the dynamics of birth and death, therefore, birth and death are often omitted in simple compartmental models. The SIR system without so-called vital dynamics (birth and death, sometimes called demography) described above can be expressed by the following set of ordinary differential equations:

流行病动力学，例如流感，往往比出生和死亡的动力学变化更快，因此，出生和死亡往往被简单的传染病模型所忽略。没有上述所谓的生命动力学(出生和死亡，有时称为人口统计学)的 SIR 系统可以用下列一组常微分方程表示:

[math]\displaystyle{ \lt math\gt \lt 数学\gt \begin{align} \begin{align} 开始{ align } & \frac{dS}{dt} = - \frac{\beta I S}{N}, \\[6pt] & \frac{dS}{dt} = - \frac{\beta I S}{N}, \\[6pt] & frac { dS }{ dt } =-frac { beta i s }{ n } ，[6 pt ] & \frac{dI}{dt} = \frac{\beta I S}{N}- \gamma I, \\[6pt] & \frac{dI}{dt} = \frac{\beta I S}{N}- \gamma I, \\[6pt] & frac { dI }{ dt } = frac { beta i s }{ n }-gamma i，[6 pt ] & \frac{dR}{dt} = \gamma I, & \frac{dR}{dt} = \gamma I, & \frac{dR}{dt} = \gamma I, \end{align} \end{align} 结束{ align } }[/math]

</math>

</数学>

where [math]\displaystyle{ S }[/math] is the stock of susceptible population, [math]\displaystyle{ I }[/math] is the stock of infected, [math]\displaystyle{ R }[/math] is the stock of removed population (either by death or recovery), and [math]\displaystyle{ N }[/math] is the sum of these three.

其中，S</math> 是易感人群的存量，[math]\displaystyle{ I }[/math] 是感染人群的存量，[math]\displaystyle{ R }[/math] 是康复人群的存量(死亡或康复) ，[math]\displaystyle{ N }[/math] 是这三者的总和。

This model was for the first time proposed by William Ogilvy Kermack and Anderson Gray McKendrick as a special case of what we now call Kermack–McKendrick theory, and followed work McKendrick had done with Ronald Ross.

这个模型是一个特例，是在继承了麦克德里克对罗纳德·罗斯所做研究的基础上，由威廉·奥格威·科尔马克和安德森·格雷·麦克德里克首次提出，现在称作科尔马克-麦克德里克理论。

This system is non-linear, however it is possible to derive its analytic solution in implicit form.^[2] Firstly note that from:

This system is non-linear, however it is possible to derive its analytic solution in implicit form. Firstly note that from:

这个系统是非线性的，但是可以用隐式形式得到它的解析解。首先，请注意:

[math]\displaystyle{ \frac{dS}{dt} + \frac{dI}{dt} + \frac{dR}{dt} = 0, }[/math]

0，</math > frac { dS }

it follows that:

接下来是:

[math]\displaystyle{ S(t) + I(t) + R(t) = \text{constant} = N, }[/math]

S (t) + i (t) + r (t) = text { constant } = n，</math >

expressing in mathematical terms the constancy of population [math]\displaystyle{ N }[/math]. Note that the above relationship implies that one need only study the equation for two of the three variables.

用数学术语来表达人口 [math]\displaystyle{ N }[/math]的稳定性。注意，上述关系意味着人们只需要研究三个变量中的两个的方程。

Secondly, we note that the dynamics of the infectious class depends on the following ratio:

其次，我们注意到传染种类的动态取决于以下比例:

[math]\displaystyle{ R_0 = \frac{\beta}{\gamma}, }[/math]

< math > r _ 0 = frac { beta }{ gamma } ，</math >

the so-called basic reproduction number (also called basic reproduction ratio). This ratio is derived as the expected number of new infections (these new infections are sometimes called secondary infections) from a single infection in a population where all subjects are susceptible.^[7]^[8] This idea can probably be more readily seen if we say that the typical time between contacts is [math]\displaystyle{ T_{c} = \beta^{-1} }[/math], and the typical time until removal is [math]\displaystyle{ T_{r} = \gamma^{-1} }[/math]. From here it follows that, on average, the number of contacts by an infectious individual with others before the infectious has been removed is: [math]\displaystyle{ T_{r}/T_{c}. }[/math]

the so-called basic reproduction number (also called basic reproduction ratio). This ratio is derived as the expected number of new infections (these new infections are sometimes called secondary infections) from a single infection in a population where all subjects are susceptible. This idea can probably be more readily seen if we say that the typical time between contacts is [math]\displaystyle{ T_{c} = \beta^{-1} }[/math], and the typical time until removal is [math]\displaystyle{ T_{r} = \gamma^{-1} }[/math]. From here it follows that, on average, the number of contacts by an infectious individual with others before the infectious has been removed is: [math]\displaystyle{ T_{r}/T_{c}. }[/math]

所谓的基本再生数(亦称基本再生率)。这个比率是根据一群易感者中单次感染后的预期的新感染人数(这些新感染有时称为二次感染)计算出来的。如果我们说两次感染之间的典型时间是 [math]\displaystyle{ T_{c}=\beta^{-1} }[/math]，而康复之前的典型时间是 [math]\displaystyle{ T_{r}=|\gamma^{-1} }[/math] ，那么这个想法可能更容易被看出来。由此可以得出，平均而言，在感染者康复之前，感染者与其他人的接触次数为: [math]\displaystyle{ T_{r}/T_{c}。\lt /数学\gt By dividing the first differential equation by the third, [[Separation of variables|separating the variables]] and integrating we get By dividing the first differential equation by the third, separating the variables and integrating we get 通过将第一个微分方程除以第三个，分离变量并进行积分，我们得到了 :\lt math\gt S(t) = S(0) e^{-R_0(R(t) - R(0))/N}, }[/math]

[math]\displaystyle{ S(t) = S(0) e^{-R_0(R(t) - R(0))/N}, }[/math]

< math > s (t) = s (0) e ^ {-r _ 0(r (t)-r (0))/n } ，</math >

where [math]\displaystyle{ S(0) }[/math] and [math]\displaystyle{ R(0) }[/math] are the initial numbers of, respectively, susceptible and removed subjects.

其中，[math]\displaystyle{ S(0) }[/math]和[math]\displaystyle{ R(0) }[/math]分别是易感者和康复者的初始人数。

Writing [math]\displaystyle{ s_0 = S(0) / N }[/math] for the initial proportion of susceptible individuals, and

为易感人群的初始比例编写[math]\displaystyle{ S_0=S(0)/N }[/math]，以及

[math]\displaystyle{ s_\infty = S(\infty) / N }[/math] and

[math] s infty = S(\infty)/N</math>并且

[math]\displaystyle{ r_\infty = R(\infty) / N }[/math] for the proportion of susceptible and removed individuals respectively

敏感个体和被感染个体的比例分别为R(\infty)/N</math>

in the limit [math]\displaystyle{ t \to \infty, }[/math] one has

在这个极限里，[math]\displaystyle{ t \to \infty, }[/math] 一个人又

[math]\displaystyle{ s_\infty = 1 - r_\infty = s_0 e^{-R_0(r_\infty - r_0)} }[/math]

< math > s_\infty = 1-r _\infty = s_0 e ^{-R_0(r _\infty -r _0)}</math >

(note that the infectious compartment empties in this limit).

(请注意，在这个限度内，没有感病者)。

This transcendental equation has a solution in terms of the Lambert $W$ function,^[9] namely

This transcendental equation has a solution in terms of the Lambert function, namely

这个超越方程有一个关于Lambert函数的解决方案，即

[math]\displaystyle{ s_\infty = 1-r_\infty = - R_0^{-1}\, W(-s_0 R_0 e^{-R_0(1-r_0)}). }[/math]

< math > s _ infty = 1-r _ infty =-r _ 0 ^ {-1} ，w (- s _ 0 r _ 0 e ^ {-r _ 0(1-r _ 0)}) </math >

This shows that at the end of an epidemic, unless [math]\displaystyle{ s_0=0 }[/math], not all individuals of the population have been removed, so some must remain susceptible. This means that the end of an epidemic is caused by the decline in the number of infectious individuals rather than an absolute lack of susceptible subjects.

这表明，在流行病结束时，除非[math]\displaystyle{ s_0=0 }[/math]，否则只要有人没有康复，一些人仍然易受感染。这意味着传染病的结束是由于感病者的减少，而不是由于完全没有易感者。

The role of both the basic reproduction number and the initial susceptibility are extremely important. In fact, upon rewriting the equation for infectious individuals as follows:

基本再生数的作用和最初的易感性都极其重要。事实上，将传染性个体的等式重写如下:

[math]\displaystyle{ \frac{dI}{dt} = \left(R_0 \frac{S}{N} - 1\right) \gamma I, }[/math]

[math]\displaystyle{ \frac{dI}{dt} = \left(R_0 \frac{S}{N} -1 \right) \gamma I, }[/math]

it yields that if:

它产生的条件是:

[math]\displaystyle{ R_{0} \cdot S(0) \gt N, }[/math]

then:

然后:

[math]\displaystyle{ \frac{dI}{dt}(0) \gt 0 , }[/math]

</math> \frac{dI}{dt}(0) > ,</math>

i.e., there will be a proper epidemic outbreak with an increase of the number of the infectious (which can reach a considerable fraction of the population). On the contrary, if

也就是说，随着感病者数量的增加(达到人口相当大的一个比例) ，将会有一场适当的流行病爆发。相反，如果

[math]\displaystyle{ R_{0} \cdot S(0) \lt N, }[/math]

then

那么

[math]\displaystyle{ \frac{dI}{dt}(0) \lt 0 , }[/math]

i.e., independently from the initial size of the susceptible population the disease can never cause a proper epidemic outbreak. As a consequence, it is clear that both the basic reproduction number and the initial susceptibility are extremely important.

也就是说，如果与易感者的初始规模无关，这种疾病将永远不会引起适当的流行病爆发。因此，很明显，基本生数和最初的易感性都极其重要。

The force of infection

感染力

Note that in the above model the function:

注意，在上面的模型中，函数是:

[math]\displaystyle{ F = \beta I, }[/math]

models the transition rate from the compartment of susceptible individuals to the compartment of infectious individuals, so that it is called the force of infection. However, for large classes of communicable diseases it is more realistic to consider a force of infection that does not depend on the absolute number of infectious subjects, but on their fraction (with respect to the total constant population [math]\displaystyle{ N }[/math]):

建立了从易感者到感病者的传染率模型，因此称之为感染力。然而，对于大类传染病来说，更现实的做法是考虑一种感染力，这种传染力并不取决于感染对象的绝对数量，而是取决于感染对象的比例(就总人口而言[math]\displaystyle{ N }[/math]) :

[math]\displaystyle{ F = \beta \frac{I}{N} . }[/math]

Capasso^[10] and, afterwards, other authors have proposed nonlinear forces of infection to model more realistically the contagion process.

Capasso and, afterwards, other authors have proposed nonlinear forces of infection to model more realistically the contagion process.

卡帕索和后来的其他作者提出了非线性的感染力以建立更现实的传染过程。

Exact analytical solutions to the SIR model

SIR 模型的精确解析解

In 2014, Harko and coauthors derived an exact analytical solution to the SIR model.^[2] In the case without vital dynamics setup, for [math]\displaystyle{ \mathcal{S}(u)=S(t) }[/math], etc., it corresponds to the following time parametrization

In 2014, Harko and coauthors derived an exact analytical solution to the SIR model. In the case without vital dynamics setup, for [math]\displaystyle{ \mathcal{S}(u)=S(t) }[/math], etc., it corresponds to the following time parametrization

2014年，Harko 和合作者推导出了 SIR 模型的精确解析解。在没有重要动力学设置的情况下，对于 [math]\displaystyle{ \mathcal{S}(u) =S(t) }[/math] 等，它对应以下参数化时间

[math]\displaystyle{ \mathcal{S}(u)= S(0)u }[/math]

[math]\displaystyle{ \mathcal{I}(u)= N -\mathcal{R}(u)-\mathcal{S}(u) }[/math]

[math]\displaystyle{ \mathcal{R}(u)=R(0) -\rho \ln(u) }[/math]

for

为了

[math]\displaystyle{ t= \frac{N}{\beta}\int_u^1 \frac{du^*}{u^*\mathcal{I}(u^*)} , \quad \rho=\frac{\gamma N}{\beta}, }[/math]

with initial conditions

和初始条件

[math]\displaystyle{ (\mathcal{S}(1),\mathcal{I}(1),\mathcal{R}(1))=(S(0),N -R(0)-S(0),R(0)), \quad u_T\lt u\lt 1, }[/math]

where [math]\displaystyle{ u_T }[/math] satisfies [math]\displaystyle{ \mathcal{I}(u_T)=0 }[/math]. By the transcendental equation for [math]\displaystyle{ R_{\infty} }[/math] above, it follows that [math]\displaystyle{ u_T=e^{-(R_{\infty}-R(0))/\rho}(=S_{\infty}/S(0) }[/math], if [math]\displaystyle{ S(0) \neq 0) }[/math] and [math]\displaystyle{ I_{\infty}=0 }[/math].

其中[math]\displaystyle{ u_T }[/math]满足[math]\displaystyle{ \mathcal{I}(u_T)=0 }[/math]。根据上面的超越方程 [math]\displaystyle{ R_{\infty} }[/math] ，如果[math]\displaystyle{ S(0) \neq 0) }[/math] and [math]\displaystyle{ I_{\infty}=0 }[/math]，那么遵守[math]\displaystyle{ u_T=e^{-(R_{\infty}-R(0))/\rho}(=S_{\infty}/S(0) }[/math]。

An equivalent analytical solution found by Miller^[11]^[12] yields

An equivalent analytical solution found by Miller yields

等价的解析解由米勒发现

[math]\displaystyle{ \lt math\gt \lt math\gt \begin{align} \begin{align} \开始{ align } S(t) & = S(0) e^{-\xi(t)} \\[8pt] S(t) & = S(0) e^{-\xi(t)} \\[8pt] S (t) & = s (0) e ^ {-xi (t)}[8 pt ] I(t) & = N-S(t)-R(t) \\[8pt] I(t) & = N-S(t)-R(t) \\[8pt] I (t) & = N-S (t)-r (t)[8 pt ] R(t) & = R(0) + \rho \xi(t) \\[8pt] R(t) & = R(0) + \rho \xi(t) \\[8pt] R (t) & = r (0) + rho xi (t)[8 pt ] \xi(t) & = \frac{\beta}{N}\int_0^t I(t^*) \, dt^* \xi(t) & = \frac{\beta}{N}\int_0^t I(t^*) \, dt^* Xi (t) & = frac { beta }{ n } int _ 0 ^ t i (t ^ *) ，dt ^ * \end{align} \end{align} 结束{ align } }[/math]

</math>

Here [math]\displaystyle{ \xi(t) }[/math] can be interpreted as the expected number of transmissions an individual has received by time [math]\displaystyle{ t }[/math]. The two solutions are related by [math]\displaystyle{ e^{-\xi(t)} = u }[/math].

在这里，[math]\displaystyle{ \xi(t) }[/math]可以解释为随着时间[math]\displaystyle{ t }[/math]变化一个人预期收到的传染数量。这两个解是通过[math]\displaystyle{ e^{-\xi(t)} = u }[/math]关联的。

Effectively the same result can be found in the original work by Kermack and McKendrick.^[1]

Effectively the same result can be found in the original work by Kermack and McKendrick.

实际上，同样的结果可以在科马克和麦克德里克的原著中找到。

These solutions may be easily understood by noting that all of the terms on the right-hand sides of the original differential equations are proportional to [math]\displaystyle{ I }[/math]. The equations may thus be divided through by [math]\displaystyle{ I }[/math], and the time rescaled so that the differential operator on the left-hand side becomes simply [math]\displaystyle{ d/d\tau }[/math], where [math]\displaystyle{ d\tau=I dt }[/math], i.e. [math]\displaystyle{ \tau=\int I dt }[/math]. The differential equations are now all linear, and the third equation, of the form [math]\displaystyle{ dR/d\tau = }[/math] const., shows that [math]\displaystyle{ \tau }[/math] and [math]\displaystyle{ R }[/math] (and [math]\displaystyle{ \xi }[/math] above) are simply linearly related.

注意到原微分方程右边的所有项都与“数学”成正比，这些解就很容易理解了。这样，方程组就可以通过[math]\displaystyle{ I }[/math]来分解，时间重新调整，使得左边的微分算子变成[math]\displaystyle{ d/d\tau }[/math]，其中[math]\displaystyle{ d\tau=I dt }[/math]，即 [math]\displaystyle{ \tau=\int I dt }[/math]。这些微分方程现在都是线性的，而第三个方程，即形式为[math]\displaystyle{ dR/d\tau = }[/math] 的常量，表明 [math]\displaystyle{ \tau }[/math]和[math]\displaystyle{ R }[/math](和上方的[math]\displaystyle{ \xi }[/math])仅仅是线性关系。

The SIR model with vital dynamics and constant population

具有生命动力学和稳定人口的SIR模型

Consider a population characterized by a death rate [math]\displaystyle{ \mu }[/math] and birth rate [math]\displaystyle{ \Lambda }[/math], and where a communicable disease is spreading^[3]. The model with mass-action transmission is:

Consider a population characterized by a death rate [math]\displaystyle{ \mu }[/math] and birth rate [math]\displaystyle{ \Lambda }[/math], and where a communicable disease is spreading. The model with mass-action transmission is:

考虑人口有死亡率[math]\displaystyle{ \mu }[/math]和出生率[math]\displaystyle{ \Lambda }[/math]的特点，以及正在传播的传染病。具有质量作用传递的模型是:

[math]\displaystyle{ \lt math\gt \lt math\gt \begin{align} \begin{align} \开始{ align } \frac{dS}{dt} & = \Lambda - \mu S - \frac{\beta I S}{N} \\[8pt] \frac{dS}{dt} & = \Lambda - \mu S - \frac{\beta I S}{N} \\[8pt] \frac{dS}{dt} & = \Lambda - \mu S - \frac{\beta I S}{N} \\[8pt] \frac{dI}{dt} & = \frac{\beta I S}{N} - \gamma I -\mu I \\[8pt] \frac{dI}{dt} & = \frac{\beta I S}{N} - \gamma I -\mu I \\[8pt] \frac{dI}{dt} & = \frac{\beta I S}{N} - \gamma I -\mu I \\[8pt] \frac{dR}{dt} & = \gamma I - \mu R \frac{dR}{dt} & = \gamma I - \mu R \frac{dR}{dt} & = \gamma I - \mu R \end{align} \end{align} 结束{ align } }[/math]

</math>

for which the disease-free equilibrium (DFE) is:

其无病平衡点为:

[math]\displaystyle{ \left(S(t),I(t),R(t)\right) =\left(\frac{\Lambda}{\mu},0,0\right). }[/math]

In this case, we can derive a basic reproduction number:

在这种情况下，我们可以得出一个基本再生数:

[math]\displaystyle{ R_0 = \frac{ \beta\Lambda }{\mu(\mu+\gamma)}, }[/math]

which has threshold properties. In fact, independently from biologically meaningful initial values, one can show that:

这种基本在生数具有临界性质。事实上，我们可以独立于具有生物学意义的初始值证明:

[math]\displaystyle{ R_0 \le 1 \Rightarrow \lim_{t \to \infty} (S(t),I(t),R(t)) = \textrm{DFE} = \left(\frac{\Lambda}{\mu},0,0\right) }[/math]

[math]\displaystyle{ R_0 \gt 1 , I(0)\gt 0 \Rightarrow \lim_{t \to \infty} (S(t),I(t),R(t)) = \textrm{EE} = \left(\frac{\gamma+\mu}{\beta},\frac{\mu}{\beta}\left(R_0-1\right), \frac{\gamma}{\beta} \left(R_0-1\right)\right). }[/math]

The point EE is called the Endemic Equilibrium (the disease is not totally eradicated and remains in the population). With heuristic arguments, one may show that [math]\displaystyle{ R_{0} }[/math] may be read as the average number of infections caused by a single infectious subject in a wholly susceptible population, the above relationship biologically means that if this number is less than or equal to one the disease goes extinct, whereas if this number is greater than one the disease will remain permanently endemic in the population.

EE点被称为地方病平衡点(这种疾病还没有完全根除，仍然存在于人群中)。通过启发式的论证，人们可以表明[math]\displaystyle{ R_{0} }[/math]可以理解为在一个完全易感人群中，由一个感染对象引起的平均感染人数，上述关系在生物学上意味着，如果这个数字小于或等于1，这种疾病就会灭绝，而如果这个数字大于1，这种疾病就会在人群中永久地流行下去。

Variations on the basic SIR model

基础SIR模型的变化

The SIS model

SIS模型

文件:SIS System Graph.svg

Yellow=Susceptible, Maroon=Infected

【图4：Yellow=Susceptible, Maroon=Infected黄色=易感，栗色=感染】

Some infections, for example, those from the common cold and influenza, do not confer any long-lasting immunity. Such infections do not give immunity upon recovery from infection, and individuals become susceptible again.

有些传染病，例如普通感冒和流感，并不能提供任何持久的免疫力。这种感染在感染康复后不会产生免疫力，个体易再次感染。

SIS compartmental model

【图5：SIS compartmental modelSIS传染病模型】

We have the model:

我们有一个模型:

[math]\displaystyle{ \lt math\gt \lt math\gt \begin{align} \begin{align} \开始{ align } \frac{dS}{dt} & = - \frac{\beta S I}{N} + \gamma I \\[6pt] \frac{dS}{dt} & = - \frac{\beta S I}{N} + \gamma I \\[6pt] \frac{dS}{dt} & = - \frac{\beta S I}{N} + \gamma I \\[6pt] \frac{dI}{dt} & = \frac{\beta S I}{N} - \gamma I \frac{dI}{dt} & = \frac{\beta S I}{N} - \gamma I \frac{dI}{dt} & = \frac{\beta S I}{N} - \gamma I \end{align} \end{align} \结束{ align } }[/math]

</math>

Note that denoting with N the total population it holds that:

注意，用N表示它所拥有的总人口:

[math]\displaystyle{ \frac{dS}{dt} + \frac{dI}{dt} = 0 \Rightarrow S(t)+I(t) = N }[/math].

It follows that:

由此可见:

[math]\displaystyle{ \frac{dI}{dt} = (\beta - \gamma) I - \frac{\beta}{N} I^2 }[/math],

i.e. the dynamics of infectious is ruled by a logistic function, so that [math]\displaystyle{ \forall I(0) \gt 0 }[/math]:

也就是。传染病的动态性是由Logistic函数控制的，所以对于所有的[math]\displaystyle{ \forall I(0) \gt 0 }[/math]:

[math]\displaystyle{ \lt math\gt \lt math\gt \begin{align} \begin{align} \开始{ align } & \frac{\beta}{\gamma} \le 1 \Rightarrow \lim_{t \to +\infty}I(t)=0, \\[6pt] & \frac{\beta}{\gamma} \le 1 \Rightarrow \lim_{t \to +\infty}I(t)=0, \\[6pt] & \frac{\beta}{\gamma} \le 1 \Rightarrow \lim_{t \to +\infty}I(t)=0, \\[6pt] & \frac{\beta}{\gamma} \gt 1 \Rightarrow \lim_{t \to +\infty}I(t) = \left(1 - \frac{\gamma}{\beta} \right) N. & \frac{\beta}{\gamma} \gt 1 \Rightarrow \lim_{t \to +\infty}I(t) = \left(1 - \frac{\gamma}{\beta} \right) N. & \frac{\beta}{\gamma} \gt 1 \Rightarrow \lim_{t \to +\infty}I(t) = \left(1 - \frac{\gamma}{\beta} \right) N. \end{align} \end{align} \结束{ align } }[/math]

</math>

It is possible to find an analytical solution to this model (by making a transformation of variables: [math]\displaystyle{ I = y^{-1} }[/math] and substituting this into the mean-field equations),^[13] such that the basic reproduction rate is greater than unity. The solution is given as

It is possible to find an analytical solution to this model (by making a transformation of variables: [math]\displaystyle{ I = y^{-1} }[/math] and substituting this into the mean-field equations), such that the basic reproduction rate is greater than unity. The solution is given as

这个模型可以找到一个解析解(通过对变量进行变换：[math]\displaystyle{ I = y^{-1} }[/math] 并将其代入平均场方程) ，使基本再生率大于单位数。给出了解决方案如下:

[math]\displaystyle{ I(t) = \frac{I_\infty}{1+V e^{-\chi t}} }[/math].

where [math]\displaystyle{ I_\infty = (1 -\gamma/\beta)N }[/math] is the endemic infectious population, [math]\displaystyle{ \chi = \beta-\gamma }[/math], and [math]\displaystyle{ V = I_\infty/I_0 - 1 }[/math]. As the system is assumed to be closed, the susceptible population is then [math]\displaystyle{ S(t) = N - I(t) }[/math].

其中 [math]\displaystyle{ I_\infty = (1 -\gamma/\beta)N }[/math]是地方性传染病人口，[math]\displaystyle{ \chi = \beta-\gamma }[/math]，和 [math]\displaystyle{ V = I_\infty/I_0 - 1 }[/math]。假设系统是封闭的，那么易感者是[math]\displaystyle{ S(t) = N - I(t) }[/math]。

As a special case, one obtains the usual logistic function by assuming [math]\displaystyle{ \gamma=0 }[/math]. This can be also considered in the SIR model with [math]\displaystyle{ R=0 }[/math], i.e. no removal will take place. That is the SI model.^[14] The differential equation system using [math]\displaystyle{ S=N-I }[/math] thus reduces to:

As a special case, one obtains the usual logistic function by assuming [math]\displaystyle{ \gamma=0 }[/math]. This can be also considered in the SIR model with [math]\displaystyle{ R=0 }[/math], i.e. no removal will take place. That is the SI model. The differential equation system using [math]\displaystyle{ S=N-I }[/math] thus reduces to:

作为一个特例，人们通过假设[math]\displaystyle{ R=0 }[/math]得到通常的 Logistic函数。这也可以在 SIR 模型中考虑，该模型具有[math]\displaystyle{ R=0 }[/math]，即没有康复者。这就是SI模型。微分方程系统使用[math]\displaystyle{ S=N-I }[/math]因此可以简化为:

[math]\displaystyle{ \lt math\gt \lt math\gt \frac{dI}{dt} \propto I\cdot (N-I). \frac{dI}{dt} \propto I\cdot (N-I). \frac{dI}{dt} \propto I\cdot (N-I). }[/math]

</math>

In the long run, in this model, all individuals will become infected.

从长远来看，在这种模式下，所有的个体都会被感染。

The SIRD model

SIRD模型

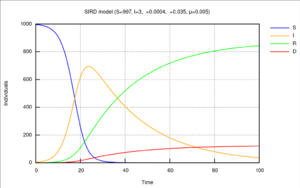
Diagram of the SIRD model with initial values [math]\displaystyle{ S(0)=997, I(0)=3, R(0)=0 }[/math] and the rates for infection [math]\displaystyle{ \beta=0.4 }[/math], recovery [math]\displaystyle{ \gamma=0.035 }[/math] and mortality [math]\displaystyle{ \mu=0.005 }[/math]

【图6：Diagram of the SIRD model with initial values [math]\displaystyle{ S(0)=997, I(0)=3, R(0)=0 }[/math] and the rates for infection [math]\displaystyle{ \beta=0.4 }[/math], recovery [math]\displaystyle{ \gamma=0.035 }[/math] and mortality [math]\displaystyle{ \mu=0.005 }[/math]SIRD模型示意图，初始值[math]\displaystyle{ S(0)=997，I(0)=3, R(0)=0 }[/math]，感染率[math]\displaystyle{ \beta=0.4 }[/math]，康复率[math]\displaystyle{ \gamma=0.035 }[/math]，死亡率 [math]\displaystyle{ \mu=0.005 }[/math]】

Animation of the SIRD model with initial values [math]\displaystyle{ S(0)=997, I(0)=3, R(0)=0 }[/math], initial rate for infection [math]\displaystyle{ \beta=0.5 }[/math] and constant rates for recovery [math]\displaystyle{ \gamma=0.035 }[/math] and mortality [math]\displaystyle{ \mu=0.005 }[/math]. If there is neither medicine nor vaccination available, it is only possible to reduce the infection rate (often referred to as „flattening the curve“) by appropriate measures (e. g. „social distancing“). This animation shows the impact of reducing the infection rate by 76 % (from [math]\displaystyle{ \beta=0.5 }[/math] down to [math]\displaystyle{ \beta=0.12 }[/math]).

【图7：Animation of the SIRD model with initial values [math]\displaystyle{ S(0)=997, I(0)=3, R(0)=0 }[/math], initial rate for infection [math]\displaystyle{ \beta=0.5 }[/math] and constant rates for recovery [math]\displaystyle{ \gamma=0.035 }[/math] and mortality [math]\displaystyle{ \mu=0.005 }[/math]. If there is neither medicine nor vaccination available, it is only possible to reduce the infection rate (often referred to as „flattening the curve“) by appropriate measures (e. g. „social distancing“). This animation shows the impact of reducing the infection rate by 76 % (from [math]\displaystyle{ \beta=0.5 }[/math] down to [math]\displaystyle{ \beta=0.12 }[/math])SIRD模型动画，初始值[math]\displaystyle{ S(0)=997I(0)=3, R(0)=0 }[/math]，初始感染率 [math]\displaystyle{ \beta=0.5 }[/math]和恒定康复率 [math]\displaystyle{ \gamma=0.035 }[/math] 和死亡率[math]\displaystyle{ \mu=0.005 }[/math]。如果既没有药物也没有疫苗可用，只有通过适当的措施(例如“社会距离”)才有可能降低感染率(通常称为“平缓曲线”)。这个动画展示了降低感染率76% 的效果(从 [math]\displaystyle{ \beta=0.5 }[/math]下降到[math]\displaystyle{ \beta=0.12 }[/math])。】

The Susceptible-Infectious-Recovered-Deceased-Model differentiates between Recovered (meaning specifically individuals having survived the disease and now immune) and Deceased.模板:Cn This model uses the following system of differential equations:

The Susceptible-Infectious-Recovered-Deceased-Model differentiates between Recovered (meaning specifically individuals having survived the disease and now immune) and Deceased. This model uses the following system of differential equations:

易感-感病-康复-死亡-模型区分恢复(特别是指从疾病中存活下来并且现在免疫)和死亡。该模型使用了下列微分方程组:

[math]\displaystyle{ \lt math\gt \lt math\gt \begin{align} \begin{align} \开始{ align } & \frac{dS}{dt} = - \frac{\beta I S}{N}, \\[6pt] & \frac{dS}{dt} = - \frac{\beta I S}{N}, \\[6pt] & \frac{dS}{dt} = - \frac{\beta I S}{N}, \\[6pt] & \frac{dI}{dt} = \frac{\beta I S}{N} - \gamma I - \mu I, \\[6pt] & \frac{dI}{dt} = \frac{\beta I S}{N} - \gamma I - \mu I, \\[6pt] & frac { dI }{ dt } = frac { beta i s }{ n }-gamma i-mu i，[6 pt ] & \frac{dR}{dt} = \gamma I, \\[6pt] & \frac{dR}{dt} = \gamma I, \\[6pt] & \frac{dR}{dt} = \gamma I, \\[6pt] & \frac{dD}{dt} = \mu I, & \frac{dD}{dt} = \mu I, 1 = mu i, \end{align} \end{align} \结束{ align } }[/math]

</math>

where [math]\displaystyle{ \beta, \gamma, \mu }[/math] are the rates of infection, recovery, and mortality, respectively.^[15]

where [math]\displaystyle{ \beta, \gamma, \mu }[/math] are the rates of infection, recovery, and mortality, respectively.

这里[math]\displaystyle{ \beta, \gamma, \mu }[/math]分别是感染率，康复率和死亡率。

The MSIR model

MSIR模型

For many infections, including measles, babies are not born into the susceptible compartment but are immune to the disease for the first few months of life due to protection from maternal antibodies (passed across the placenta and additionally through colostrum). This is called passive immunity. This added detail can be shown by including an M class (for maternally derived immunity) at the beginning of the model.

对于包括麻疹在内的许多传染病，婴儿出生时并不易感染，但由于母体抗体的保护(通过胎盘和初乳传播) ，婴儿在出生后的头几个月对该疾病免疫。这叫做被动免疫。这个额外的细节可以通过在模型的开头加入一个M类(用于母系免疫)来显示。

To indicate this mathematically, an additional compartment is added, M(t). This results in the following differential equations:

MSIR compartmental modelTo indicate this mathematically, an additional compartment is added, M(t). This results in the following differential equations:

【图8：MSIR compartmental modelTo indicate this mathematically, an additional compartment is added, M(t). This results in the following differential equations:MSIR 分隔模型为了从数学上表示这一点，增加了一个额外的分隔，M(t)。这导致了下列微分方程:】

[math]\displaystyle{ \lt math\gt \lt math\gt \begin{align} \begin{align} \开始{ align } \frac{dM}{dT} & = \Lambda - \delta M - \mu M\\[8pt] \frac{dM}{dT} & = \Lambda - \delta M - \mu M\\[8pt] { dM }{ dT } & = Lambda-delta m-mu m [8 pt ] \frac{dS}{dT} & = \delta M - \frac{\beta SI}{N} - \mu S\\[8pt] \frac{dS}{dT} & = \delta M - \frac{\beta SI}{N} - \mu S\\[8pt] Frac { dS }{ dT } & = delta m-frac { beta SI }{ n }-mu s [8 pt ] \frac{dI}{dT} & = \frac{\beta SI}{N} - \gamma I - \mu I\\[8pt] \frac{dI}{dT} & = \frac{\beta SI}{N} - \gamma I - \mu I\\[8pt] Frac { dI }{ dT } & = frac { beta SI }{ n }-gamma i-mu i [8 pt ] \frac{dR}{dT} & = \gamma I - \mu R \frac{dR}{dT} & = \gamma I - \mu R \frac{dR}{dT} & = \gamma I - \mu R \end{align} \end{align} \结束{ align } }[/math]

</math>

Carrier state

载体状态

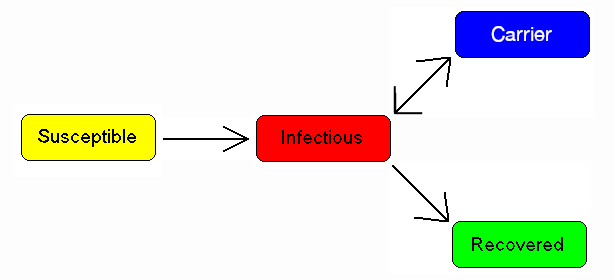
Some people who have had an infectious disease such as tuberculosis never completely recover and continue to carry the infection, whilst not suffering the disease themselves. They may then move back into the infectious compartment and suffer symptoms (as in tuberculosis) or they may continue to infect others in their carrier state, while not suffering symptoms. The most famous example of this is probably Mary Mallon, who infected 22 people with typhoid fever. The carrier compartment is labelled C.

一些患有肺结核等传染病的人永远不会完全康复，而是继续携带这种传染病，同时他们自己也不会患上这种疾病。然后他们可能回归到感病者并出现症状（如肺结核），或者他们可能继续以携带者的状态传染给其他人，而不出现症状。最著名的例子可能是玛丽·马伦，她将伤寒传染给了22个人。携带者被标记为C。

A simple modification of previous image by Viki Male to make the word "Carrier" plainly visible.

【图9：A simple modification of previous image by Viki Male to make the word "Carrier" plainly visible.对维基马累之前形象的一个简单修改使单词“携带者”清晰可见。】

The SEIR model

SEIR模型

For many important infections, there is a significant incubation period during which individuals have been infected but are not yet infectious themselves. During this period the individual is in compartment E (for exposed).

对于许多重要的感染，有一个重要的疾病潜伏期，在这期间个人已经被感染，但他们自己还没有感病。在此期间，这个人是属于类别E(为暴露)。

SEIR compartmental model

【图10：SEIR compartmental modelSEIR传染病模型】

Assuming that the incubation period is a random variable with exponential distribution with parameter [math]\displaystyle{ a }[/math] (i.e. the average incubation period is [math]\displaystyle{ a^{-1} }[/math]), and also assuming the presence of vital dynamics with birth rate [math]\displaystyle{ \Lambda }[/math] equal to death rate [math]\displaystyle{ \mu }[/math], we have the model:

假设疾病潜伏期是一个带有参数[math]\displaystyle{ ''a'' }[/math]，那么它就是一个服从指数分布的随机变量。平均疾病潜伏期是[math]\displaystyle{ a^{-1} }[/math])，并且假设存在出生率[math]\displaystyle{ \Lambda }[/math]等于死亡率[math]\displaystyle{ \mu }[/math]的生命动力学，我们有这样的模型:

[math]\displaystyle{ \lt math\gt \lt math\gt \begin{align} \begin{align} \开始{ align } \frac{dS}{dt} & = \Lambda - \mu S - \frac{\beta I S}{N} \\[8pt] \frac{dS}{dt} & = \Lambda - \mu S - \frac{\beta I S}{N} \\[8pt] { dS }{ dt } & = Lambda-mu s-frac { beta i s }{ n }[8 pt ] \frac{dE}{dt} & = \frac{\beta I S}{N} - (\mu +a ) E \\[8pt] \frac{dE}{dt} & = \frac{\beta I S}{N} - (\mu +a ) E \\[8pt] Frac { dE }{ dt } & = frac { beta i s }{ n }-(mu + a) e [8 pt ] \frac{dI}{dt} & = a E - (\gamma +\mu ) I \\[8pt] \frac{dI}{dt} & = a E - (\gamma +\mu ) I \\[8pt] Frac { dI }{ dt } & = a e-(gamma + mu) i [8 pt ] \frac{dR}{dt} & = \gamma I - \mu R. \frac{dR}{dt} & = \gamma I - \mu R. \frac{dR}{dt} & = \gamma I - \mu R. \end{align} \end{align} 结束{ align } }[/math]

</math>

We have [math]\displaystyle{ S+E+I+R=N, }[/math] but this is only constant because of the (degenerate) assumption that birth and death rates are equal; in general [math]\displaystyle{ N }[/math] is a variable.

我们有[math]\displaystyle{ S+E+I+R=N, }[/math]但是这只是常数，因为(退化的)假设出生率和死亡率是相等的; 一般来说[math]\displaystyle{ N }[/math]是一个变量。

For this model, the basic reproduction number is:

对于这种模式，基本再生数是:

[math]\displaystyle{ R_0 = \frac{a}{\mu+a}\frac{\beta}{\mu+\gamma}. }[/math]

Similarly to the SIR model, also, in this case, we have a Disease-Free-Equilibrium (N,0,0,0) and an Endemic Equilibrium EE, and one can show that, independently from biologically meaningful initial conditions

类似于 SIR 模型，在这种情况下，我们有一个无病平衡(N,0,0,0)和一个地方病平衡 EE，我们可以证明，独立于生物学上有意义的初始条件

[math]\displaystyle{ \left(S(0),E(0),I(0),R(0)\right) \in \left\{(S,E,I,R)\in [0,N]^4 : S \ge 0, E \ge 0, I\ge 0, R\ge 0, S+E+I+R = N \right\} }[/math]

[math]\displaystyle{ \左(S(0),E(0),I(0),R(0)\right) \in \left\{(S,E,I,R)\in [0,N]^4 : S \ge 0, E \ge 0, I\ge 0, R\ge 0, S+E+I+R = N \右\} }[/math]

it holds that:

它认为:

[math]\displaystyle{ R_0 \le 1 \Rightarrow \lim_{t \to +\infty} \left(S(t),E(t),I(t),R(t)\right) = DFE = (N,0,0,0), }[/math]

左(s (t) ，e (t) ，i (t) ，r (t)右) = DFE = (n，0,0,0,0) ，</math >

[math]\displaystyle{ R_0 \gt 1 , I(0)\gt 0 \Rightarrow \lim_{t \to +\infty} \left(S(t),E(t),I(t),R(t)\right) = EE. }[/math]

In case of periodically varying contact rate [math]\displaystyle{ \beta(t) }[/math] the condition for the global attractiveness of DFE is that the following linear system with periodic coefficients:

当周期性变化的接触率 < math > beta (t) </math > DFE 全局吸引性的条件是下列具有周期系数的线性系统:

[math]\displaystyle{ \lt math\gt \lt math\gt \begin{align} \begin{align} 开始{ align } \frac{dE_1}{dt} & = \beta(t) I_1 - (\gamma +a ) E_1 \\[8pt] \frac{dE_1}{dt} & = \beta(t) I_1 - (\gamma +a ) E_1 \\[8pt] Frac { dE _ 1}{ dt } & = beta (t) i _ 1-(gamma + a) e _ 1[8 pt ] \frac{dI_1}{dt} & = a E_1 - (\gamma +\mu ) I_1 \frac{dI_1}{dt} & = a E_1 - (\gamma +\mu ) I_1 压裂{ dI _ 1}{ dt } & = a e _ 1-(gamma + mu) i _ 1 \end{align} \end{align} 结束{ align } }[/math]

</math>

is stable (i.e. it has its Floquet's eigenvalues inside the unit circle in the complex plane).

是稳定的(它在复平面的单位圆内有它的 Floquet 特征值)。

The SEIS model

SEIS模型

The SEIS model is like the SEIR model (above) except that no immunity is acquired at the end.

SEIS 模型类似于 SEIR 模型(上图) ，只是最终没有获得免疫性。

[math]\displaystyle{ {\color{blue}{\mathcal{S} \to \mathcal{E} \to \mathcal{I} \to \mathcal{S}}} }[/math]

In this model an infection does not leave any immunity thus individuals that have recovered return to being susceptible, moving back into the S(t) compartment. The following differential equations describe this model:

在这个模型中，感染不会留下任何免疫性，因此个体已经恢复到易感状态，移回 s (t)隔间。下列微分方程描述了这一模型:

[math]\displaystyle{ \lt math\gt \lt math\gt \begin{align} \begin{align} 开始{ align } \frac{dS}{dT} & = \Lambda - \frac{\beta SI}{N} - \mu S + \gamma I \\[6pt] \frac{dS}{dT} & = \Lambda - \frac{\beta SI}{N} - \mu S + \gamma I \\[6pt] Frac { dS }{ dT } & = Lambda-frac { beta SI }{ n }-mu s + gamma i [6 pt ] \frac{dE}{dT} & = \frac{\beta SI}{N} - (\epsilon + \mu)E \\[6pt] \frac{dE}{dT} & = \frac{\beta SI}{N} - (\epsilon + \mu)E \\[6pt] Frac { dE }{ dT } & = frac { beta SI }{ n }-(epsilon + mu) e [6 pt ] \frac{dI}{dT} & = \varepsilon E - (\gamma + \mu)I \frac{dI}{dT} & = \varepsilon E - (\gamma + \mu)I (γ + mu) i \end{align} \end{align} 结束{ align } }[/math]

</math>

The MSEIR model

MSEIR模型

For the case of a disease, with the factors of passive immunity, and a latency period there is the MSEIR model.

以疾病为例，考虑被动免疫因素和潜伏期，建立了 MSEIR 模型。

[math]\displaystyle{ \color{blue}{\mathcal{M} \to \mathcal{S} \to \mathcal{E} \to \mathcal{I} \to \mathcal{R}} }[/math]

[math]\displaystyle{ \lt math\gt \lt math\gt \begin{align} \begin{align} 开始{ align } \frac{dM}{dT} & = \Lambda - \delta M - \mu M \\[6pt] \frac{dM}{dT} & = \Lambda - \delta M - \mu M \\[6pt] { dM }{ dT } & = Lambda-delta m-mu m [6 pt ] \frac{dS}{dT} & = \delta M - \frac{\beta SI}{N} - \mu S \\[6pt] \frac{dS}{dT} & = \delta M - \frac{\beta SI}{N} - \mu S \\[6pt] 压裂{ dS }{ dT } & = delta m-frac { beta SI }{ n }-mu s [6 pt ] \frac{dE}{dT} & = \frac{\beta SI}{N} - (\varepsilon + \mu)E \\[6pt] \frac{dE}{dT} & = \frac{\beta SI}{N} - (\varepsilon + \mu)E \\[6pt] Frac { dE }{ dT } & = frac { beta SI }{ n }-(varepsilon + mu) e [6 pt ] \frac{dI}{dT} & = \varepsilon E - (\gamma + \mu)I \\[6pt] \frac{dI}{dT} & = \varepsilon E - (\gamma + \mu)I \\[6pt] (γ + mu) i [6 pt ] \frac{dR}{dT} & = \gamma I - \mu R \frac{dR}{dT} & = \gamma I - \mu R \frac{dR}{dT} & = \gamma I - \mu R \end{align} \end{align} \结束{ align } }[/math]

</math>

The MSEIRS model

MSEIRS模型

An MSEIRS model is similar to the MSEIR, but the immunity in the R class would be temporary, so that individuals would regain their susceptibility when the temporary immunity ended.

MSEIRS 模型与 MSEIR 模型相似，但 r 类的免疫是暂时的，因此当暂时免疫结束时，个体将恢复其易感性。

[math]\displaystyle{ {\color{blue}{\mathcal{M} \to \mathcal{S} \to \mathcal{E} \to \mathcal{I} \to \mathcal{R} \to \mathcal{S}}} }[/math]

Variable contact rates

多样化接触率

It is well known that the probability of getting a disease is not constant in time. As a pandemic progresses, reactions to the pandemic may change the contact rates which are assumed constant in the simpler models. Counter-measures such as masks, social distancing and lockdown will alter the contact rate in a way to reduce the speed of the pandemic.

众所周知，患病的概率在时间上并不是一成不变的。随着大流行的发展，相关应对措施可能会改变接触率，而较简单模型中将接触率假定为恒定。口罩、社交距离和封锁等应对措施将改变接触率，从而降低大流行的速度。

In addition, Some diseases are seasonal, such as the common cold viruses, which are more prevalent during winter. With childhood diseases, such as measles, mumps, and rubella, there is a strong correlation with the school calendar, so that during the school holidays the probability of getting such a disease dramatically decreases. As a consequence, for many classes of diseases, one should consider a force of infection with periodically ('seasonal') varying contact rate

此外，有些疾病是季节性的，例如普通感冒病毒，这些病毒在冬季更为普遍。儿童疾病，如麻疹、腮腺炎和风疹，与上学日期有很强的相关性，因此在学校假期内患这种疾病的可能性大大降低。因此，对于许多种类的疾病，人们应该考虑周期性/“季节性”)变化接触率的感染力

[math]\displaystyle{ F = \beta(t) \frac{I}{N} , \quad \beta(t+T)=\beta(t) }[/math]

with period T equal to one year.

周期T等于一年。

Thus, our model becomes

因此，我们的模型变成了

[math]\displaystyle{ \lt math\gt \lt math\gt \begin{align} \begin{align} \开始{ align } \frac{dS}{dt} & = \mu N - \mu S - \beta(t) \frac{I}{N} S \\[8pt] \frac{dS}{dt} & = \mu N - \mu S - \beta(t) \frac{I}{N} S \\[8pt] Frac { dS }{ dt } & = mu n-mu s-beta (t) frac { i }{ n } s [8 pt ] \frac{dI}{dt} & = \beta(t) \frac{I}{N} S - (\gamma +\mu ) I \frac{dI}{dt} & = \beta(t) \frac{I}{N} S - (\gamma +\mu ) I { i }{ n } s-(gamma + mu) i \end{align} \end{align} \结束{ align } }[/math]

</math>

(the dynamics of recovered easily follows from [math]\displaystyle{ R=N-S-I }[/math]), i.e. a nonlinear set of differential equations with periodically varying parameters. It is well known that this class of dynamical systems may undergo very interesting and complex phenomena of nonlinear parametric resonance. It is easy to see that if:

(康的动力学很容易遵循[math]\displaystyle{ R=N-S-I }[/math])，也就是具有周期变化参数的非线性微分方程组。众所周知，这类动力系统可能会经历非常有趣和复杂的非线性参数共振现象。显然，如果:

[math]\displaystyle{ \frac 1 T \int_0^T \frac{\beta(t)}{\mu+\gamma} \, dt \lt 1 \Rightarrow \lim_{t \to +\infty} (S(t),I(t)) = DFE = (N,0), }[/math]

< math > frac 1t int _ 0 ^ t frac { beta (t)}{ mu + gamma } ，dt < 1 right tarrow lim _ { t to + infty }(s (t) ，i (t)) = DFE = (n，0) ，</math >

whereas if the integral is greater than one the disease will not die out and there may be such resonances. For example, considering the periodically varying contact rate as the 'input' of the system one has that the output is a periodic function whose period is a multiple of the period of the input.

反之，如果积分大于1，疾病就不会消失，可能会有这样的共振。例如，将周期性变化的接触率作为系统的输入，则输出是一个周期是输入周期的倍数的周期函数。

This allowed to give a contribution to explain the poly-annual (typically biennial) epidemic outbreaks of some infectious diseases as interplay between the period of the contact rate oscillations and the pseudo-period of the damped oscillations near the endemic equilibrium. Remarkably, in some cases, the behavior may also be quasi-periodic or even chaotic.

这就可以解释某些传染病的多年(常见为两年)流行病爆发，即接触率振荡周期和地方病平衡点附近阻尼振荡的伪周期之间的相互作用。值得注意的是，在某些情况下，这种行为也可能是准周期的，甚至是混沌的。

Modelling vaccination

疫苗接种模型

The SIR model can be modified to model vaccination引用错误：没有找到与</ref>对应的<ref>标签. Typically these introduce an additional compartment to the SIR model, [math]\displaystyle{ V }[/math], for vaccinated individuals. Below are some examples.

</ref>. Typically these introduce an additional compartment to the SIR model, [math]\displaystyle{ V }[/math], for vaccinated individuals. Below are some examples.

</ref >.典型地，这些引入了一个额外的类别，SIR 模型， [math]\displaystyle{ V }[/math] ，为免疫个体。下面是一些例子。

Vaccinating newborns

新生儿疫苗接种

In presence of a communicable diseases, one of main tasks is that of eradicating it via prevention measures and, if possible, via the establishment of a mass vaccination program. Consider a disease for which the newborn are vaccinated (with a vaccine giving lifelong immunity) at a rate [math]\displaystyle{ P \in (0,1) }[/math]:

面对传染病，主要任务之一是通过预防措施消除传染病，如果可能的话，通过建立大规模疫苗接种计划。假设一种新生儿接种疫苗(通过疫苗给予终身免疫力)的疾病，其发病率为 [math]\displaystyle{ P \in (0,1) }[/math]:

[math]\displaystyle{ \lt math\gt \lt math\gt \begin{align} \begin{align} 开始{ align } \frac{dS}{dt} & = \nu N (1-P) - \mu S - \beta \frac{I}{N} S \\[8pt] \frac{dS}{dt} & = \nu N (1-P) - \mu S - \beta \frac{I}{N} S \\[8pt] \frac{dS}{dt} & = \nu N (1-P) - \mu S - \beta \frac{I}{N} S \\[8pt] \frac{dI}{dt} & = \beta \frac{I}{N} S - (\mu+\gamma) I \\[8pt] \frac{dI}{dt} & = \beta \frac{I}{N} S - (\mu+\gamma) I \\[8pt] Frac { dI }{ dt } & = beta frac { i }{ n } s-(mu + gamma) i [8 pt ] \frac{dV}{dt} & = \nu N P - \mu V \frac{dV}{dt} & = \nu N P - \mu V \frac{dV}{dt} & = \nu N P - \mu V \end{align} \end{align} \结束{ align } }[/math]

</math>

where [math]\displaystyle{ V }[/math] is the class of vaccinated subjects. It is immediate to show that:

其中[math]\displaystyle{ V }[/math] 是指接种疫苗的人群。很快就可以看出:

[math]\displaystyle{ \lim_{t \to +\infty} V(t)= N P, }[/math]

< math > lim _ { t to + infty } v (t) = np，</math >

thus we shall deal with the long term behavior of [math]\displaystyle{ S }[/math] and [math]\displaystyle{ I }[/math], for which it holds that:

因此，我们将处理[math]\displaystyle{ S }[/math]和[math]\displaystyle{ I }[/math]的长期行为，它认为:

[math]\displaystyle{ R_0 (1-P) \le 1 \Rightarrow \lim_{t \to +\infty} \left(S(t),I(t)\right) = DFE = \left(N \left(1-P\right),0\right) }[/math]

[math]\displaystyle{ R_0 (1-P) \gt 1 , \quad I(0)\gt 0 \Rightarrow \lim_{t \to +\infty} \left(S(t),I(t)\right) = EE = \left(\frac{N}{R_0(1-P)},N \left(R_0 (1-P)-1\right)\right). }[/math]

< math > r0(1-P) > 1，quad i (0) > 0 right tarrow lim _ t to + infty }左(s (t) ，i (t)右) = EE = 左(frac { n }{ r0(1-P)} ，n 左(r0(1-P)-1右)。数学

In other words, if

也就是说，如果

[math]\displaystyle{ P \lt P^{*}= 1-\frac{1}{R_0} }[/math]

1-frac {1}{ r _ 0} </math >

the vaccination program is not successful in eradicating the disease, on the contrary, it will remain endemic, although at lower levels than the case of absence of vaccinations. This means that the mathematical model suggests that for a disease whose basic reproduction number may be as high as 18 one should vaccinate at least 94.4% of newborns in order to eradicate the disease.

疫苗接种计划在根除这种疾病方面并不成功，相反，它将继续流行下去，尽管它的水平低于缺乏疫苗接种的情况。这意味着数学模型表明，对于基本传染数可能高达18的疾病，应该至少为94.4% 的新生儿接种疫苗，以根除这种疾病。

Vaccination and information

疫苗接种与信息

Modern societies are facing the challenge of "rational" exemption, i.e. the family's decision to not vaccinate children as a consequence of a "rational" comparison between the perceived risk from infection and that from getting damages from the vaccine. In order to assess whether this behavior is really rational, i.e. if it can equally lead to the eradication of the disease, one may simply assume that the vaccination rate is an increasing function of the number of infectious subjects:

现代社会正面临着“理性”豁免的挑战，这个家庭决定不给孩子接种疫苗，是因为对感染的可感知风险和接种疫苗造成的损害进行了“合理”的比较。为了评估这种行为是否真的是理性的，即：如果它同样可以导致根除该疾病，人们可以简单地假定疫苗接种率是传染病人数的增加函数:

[math]\displaystyle{ P=P(I), \quad P'(I)\gt 0. }[/math]

P = p (i) ，p’(i) > 0

In such a case the eradication condition becomes:

在这种情况下，根除条件是:

[math]\displaystyle{ P(0) \ge P^{*}, }[/math]

i.e. the baseline vaccination rate should be greater than the "mandatory vaccination" threshold, which, in case of exemption, cannot hold. Thus, "rational" exemption might be myopic since it is based only on the current low incidence due to high vaccine coverage, instead taking into account future resurgence of infection due to coverage decline.

也就是说基线疫苗接种率应高于“强制接种”的门槛，而在豁免情况下，“强制接种”不能持续。因此，“合理的”豁免可能是短视的，因为它只是基于目前由于疫苗覆盖率高而发病率低的情况，而不是考虑到由于覆盖率下降而导致的未来感染死灰复燃的情况。

Vaccination of non-newborns

非新生儿疫苗接种

In case there also are vaccinations of non newborns at a rate ρ the equation for the susceptible and vaccinated subject has to be modified as follows:

如果还有非新生儿的疫苗接种率，易感者和接种者的等式必须修改如下:

[math]\displaystyle{ \lt math\gt \lt math\gt \begin{align} \begin{align} 开始{ align } \frac{dS}{dt} & = \mu N (1-P) - \mu S - \rho S - \beta \frac{I}{N} S \\[8pt] \frac{dS}{dt} & = \mu N (1-P) - \mu S - \rho S - \beta \frac{I}{N} S \\[8pt] Frc { dS }{ dt } & = mu n (1-P)-mu s-rho s-beta frc { i }{ n } s [8 pt ] \frac{dV}{dt} & = \mu N P + \rho S - \mu V \frac{dV}{dt} & = \mu N P + \rho S - \mu V \frac{dV}{dt} & = \mu N P + \rho S - \mu V \end{align} \end{align} 结束{ align } }[/math]

</math>

leading to the following eradication condition:

导致以下的根除条件:

[math]\displaystyle{ P \ge 1- \left(1+\frac{\rho}{\mu}\right)\frac{1}{R_0} }[/math]

Pulse vaccination strategy

脉冲接种疫苗策略

This strategy repeatedly vaccinates a defined age-cohort (such as young children or the elderly) in a susceptible population over time. Using this strategy, the block of susceptible individuals is then immediately removed, making it possible to eliminate an infectious disease, (such as measles), from the entire population. Every T time units a constant fraction p of susceptible subjects is vaccinated in a relatively short (with respect to the dynamics of the disease) time. This leads to the following impulsive differential equations for the susceptible and vaccinated subjects:

随着时间的推移，这种策略反复对特定年龄组群(如幼儿或老年人)的易感人群进行疫苗接种。使用这种策略，易感者类别立即康复，从而有可能从整个人群中消灭传染病病毒(如麻疹)。每T时间单位一个常数分数p的易感受试者接种疫苗在一个相对较短的时间内(相对于疾病的动态)。这就导致了以下易受感染和接种疫苗的受试者的脉冲微分方程:

[math]\displaystyle{ \lt math\gt \lt math\gt \begin{align} \begin{align} 开始{ align } \frac{dS}{dt} & = \mu N - \mu S - \beta \frac{I}{N} S, \quad S(n T^+) = (1-p) S(n T^-), & & n=0,1,2,\ldots \\[8pt] \frac{dS}{dt} & = \mu N - \mu S - \beta \frac{I}{N} S, \quad S(n T^+) = (1-p) S(n T^-), & & n=0,1,2,\ldots \\[8pt] Frc { dS }{ dt } & = mu n-mu s-beta frc { i }{ n } s，方 s (n t ^ +) = (1-p) s (n t ^ -) ，& n = 0,1,2，ldots [8 pt ] \frac{dV}{dt} & = - \mu V, \quad V(n T^+) = V(n T^-) + p S(n T^-), & & n=0,1,2,\ldots \frac{dV}{dt} & = - \mu V, \quad V(n T^+) = V(n T^-) + p S(n T^-), & & n=0,1,2,\ldots Frc { dV }{ dt } & =-mu v，quad v (n t ^ +) = v (n t ^ -) + p s (n t ^ -) ，& n = 0,1,2，ldots \end{align} \end{align} 结束{ align } }[/math]

</math>

It is easy to see that by setting $I = 0$ one obtains that the dynamics of the susceptible subjects is given by:

It is easy to see that by setting one obtains that the dynamics of the susceptible subjects is given by:

很容易看出，通过设置，人们得到的易感体动力学是由以下因素决定的:

[math]\displaystyle{ S^*(t) = 1- \frac{p}{1-(1-p)E^{-\mu T}} E^{-\mu MOD(t,T)} }[/math]

< math > s ^ * (t) = 1-frac { p }{1-(1-p) e ^ {-mu t } e ^ {-mu MOD (t，t)} </math >

and that the eradication condition is:

而根除条件是:

[math]\displaystyle{ R_0 \int_0^T S^*(t) \, dt \lt 1 }[/math]

< math > r0 int _ 0 ^ t s ^ * (t) ，dt < 1 </math >

The influence of age: age-structured models

Age has a deep influence on the disease spread rate in a population, especially the contact rate. This rate summarizes the effectiveness of contacts between susceptible and infectious subjects. Taking into account the ages of the epidemic classes [math]\displaystyle{ s(t,a),i(t,a),r(t,a) }[/math] (to limit ourselves to the susceptible-infectious-removed scheme) such that:

年龄对疾病在人群中的传播速度有很大的影响，尤其是接触率。这个比率概括了易感人群和感染人群之间接触的有效性。考虑到流行病的年龄[math]\displaystyle{ s(t,a),i(t,a),r(t,a) }[/math](将我们限制在易感者-感病者-康复的计划) ，这样:

[math]\displaystyle{ S(t)=\int_0^{a_M} s(t,a)\,da }[/math]

[math]\displaystyle{ I(t)=\int_0^{a_M} i(t,a)\,da }[/math]

[math]\displaystyle{ R(t)=\int_0^{a_M} r(t,a)\,da }[/math]

< math > r (t) = int _ 0 ^ { a _ m } r (t，a) ，da </math >

(where [math]\displaystyle{ a_M \le +\infty }[/math] is the maximum admissible age) and their dynamics is not described, as one might think, by "simple" partial differential equations, but by integro-differential equations:

(其中[math]\displaystyle{ a_M \le +\infty }[/math] 是最大可接受的年龄) ，它们的动力学并不像人们想象的那样用“简单的”偏微分方程描述，而是用积分-微分方程描述:

[math]\displaystyle{ \partial_t s(t,a) + \partial_a s(t,a) = -\mu(a) s(a,t) - s(a,t)\int_0^{a_M} k(a,a_1;t)i(a_1,t)\,da_1 }[/math]

< math > partial _ ts (t，a) + partial _ a s (t，a) =-mu (a，t) s (a，t)-s (a，t) int _ 0 ^ { a _ m } k (a，a _ 1; t) i (a _ 1，t) ，da _ 1 </math >

[math]\displaystyle{ \partial_t i(t,a) + \partial_a i(t,a) = s(a,t)\int_{0}^{a_M}{k(a,a_1;t)i(a_1,t)da_1} -\mu(a) i(a,t) - \gamma(a)i(a,t) }[/math]

< math > partial _ ti (t，a) + partial _ a i (t，a) = s (a，t) int _ {0} ^ { a _ m }{ k (a，a _ 1; t) i (a _ 1，t) da _ 1}-mu (a) i (a，t)-gamma (a) i (a，t) </math >

[math]\displaystyle{ \partial_t r(t,a) + \partial_a r(t,a) = -\mu(a) r(a,t) + \gamma(a)i(a,t) }[/math]

< math > partial _ tr (t，a) + partial _ a r (t，a) =-mu (a) r (a，t) + gamma (a) i (a，t) </math >

where:

其中:

[math]\displaystyle{ F(a,t,i(\cdot,\cdot))=\int_0^{a_M} k(a,a_1;t)i(a_1,t) \, da_1 }[/math]

(a，t，i (cdot，cdot)) = int _ 0 ^ { a _ m } k (a，a _ 1; t) i (a _ 1，t) ，da _ 1 </math >

is the force of infection, which, of course, will depend, though the contact kernel [math]\displaystyle{ k(a,a_1;t) }[/math] on the interactions between the ages.

当然，虽然联系核心[math]\displaystyle{ k(a,a_1;t) }[/math]在于年龄之间的相互作用，但这将取决于感染力。

Complexity is added by the initial conditions for newborns (i.e. for a=0), that are straightforward for infectious and removed:

新生婴儿的初始条件(即对于 a = 0) ，可以直接用于传染和康复:

[math]\displaystyle{ i(t,0)=r(t,0)=0 }[/math]

but that are nonlocal for the density of susceptible newborns:

但对于易感新生儿的密度来说，这是非本地的:

[math]\displaystyle{ s(t,0)= \int_0^{a_M} \left(\varphi_s(a) s(a,t)+\varphi_i(a) i(a,t)+\varphi_r(a) r(a,t)\right) \, da }[/math]

< math > s (t，0) = int _ 0 ^ { a _ m } left (varphi _ s (a，t) + varphi _ i (a) i (a，t) + varphi _ r (a) r (a，t) right) ，da </math >

where [math]\displaystyle{ \varphi_j(a), j=s,i,r }[/math] are the fertilities of the adults.

其中，[math]\displaystyle{ \varphi_j(a), j=s,i,r }[/math]是成人的受精能力。

Moreover, defining now the density of the total population [math]\displaystyle{ n(t,a)=s(t,a)+i(t,a)+r(t,a) }[/math] one obtains:

此外，现在定义总人口的密度[math]\displaystyle{ n(t,a)=s(t,a)+i(t,a)+r(t,a) }[/math] 1得到:

[math]\displaystyle{ \partial_t n(t,a) + \partial_a n(t,a) = -\mu(a) n(a,t) }[/math]

< math > partial _ tc (t，a) + partial _ a n (t，a) =-mu (a) n (a，t) </math >

In the simplest case of equal fertilities in the three epidemic classes, we have that in order to have demographic equilibrium the following necessary and sufficient condition linking the fertility [math]\displaystyle{ \varphi(.) }[/math] with the mortality [math]\displaystyle{ \mu(a) }[/math] must hold:

在三个流行等级生育率相等的最简单情况下，我们得到了人口平衡与生育率相关的下列充要条件出生率[math]\displaystyle{ \varphi(.)和死亡率 }[/math][math]\displaystyle{ \mu(a) }[/math]灵活性间的联系，必须坚持:

[math]\displaystyle{ 1 = \int_0^{a_M} \varphi(a) \exp\left(- \int_0^a{\mu(q)dq} \right) \, da }[/math]

1 = int _ 0 ^ { a _ m } varphi (a) exp left (- int _ 0 ^ a { mu (q) dq } right) ，da </math >

and the demographic equilibrium is

人口平衡是

[math]\displaystyle{ n^*(a)=C \exp\left(- \int_0^a \mu(q) \, dq \right), }[/math]

= c exp left (- int _ 0 ^ a mu (q) ，dq right) ，</math >

automatically ensuring the existence of the disease-free solution:

自动确保无疾病解决方案的存在:

[math]\displaystyle{ DFS(a)= (n^*(a),0,0). }[/math]

A basic reproduction number can be calculated as the spectral radius of an appropriate functional operator.

基本再生数可以用一个适当的函数算符的谱半径来计算。

Other considerations within compartmental epidemic models

其他传染病模型的考虑因素

Vertical transmission

垂直传染

In the case of some diseases such as AIDS and Hepatitis B, it is possible for the offspring of infected parents to be born infected. This transmission of the disease down from the mother is called Vertical Transmission. The influx of additional members into the infected category can be considered within the model by including a fraction of the newborn members in the infected compartment.^[16]

In the case of some diseases such as AIDS and Hepatitis B, it is possible for the offspring of infected parents to be born infected. This transmission of the disease down from the mother is called Vertical Transmission. The influx of additional members into the infected category can be considered within the model by including a fraction of the newborn members in the infected compartment.

在艾滋病和乙型肝炎等一些疾病的情况下，受感染父母的后代有可能在出生时就受到感染。这种从母体向下传染的疾病叫做垂直传染。在模型中，可以通过将一部分新生儿成员包括在受感染的隔间中来考虑额外成员流入受感染类别的情况。

Vector transmission

水平传染

Diseases transmitted from human to human indirectly, i.e. malaria spread by way of mosquitoes, are transmitted through a vector. In these cases, the infection transfers from human to insect and an epidemic model must include both species, generally requiring many more compartments than a model for direct transmission.^[16]^[17]

Diseases transmitted from human to human indirectly, i.e. malaria spread by way of mosquitoes, are transmitted through a vector. In these cases, the infection transfers from human to insect and an epidemic model must include both species, generally requiring many more compartments than a model for direct transmission.

由人间接传播的疾病，即。疟疾通过蚊子传播，通过媒介传播。在这种情况下，从人到昆虫的感染转移和一个流行病模型必须包括这两个物种，通常需要更多的区域比模型直接传染。

Others

其他

Other occurrences which may need to be considered when modeling an epidemic include things such as the following:^[16]

Other occurrences which may need to be considered when modeling an epidemic include things such as the following:

在建立流行病模型时可能需要考虑的其他事件包括以下事项:

Non-homogeneous mixing

Variable infectivity

Distributions that are spatially non-uniform

Diseases caused by macroparasites

Deterministic versus stochastic epidemic models

It is important to stress that the deterministic models presented here are valid only in case of sufficiently large populations, and as such should be used cautiously.^[18]

It is important to stress that the deterministic models presented here are valid only in case of sufficiently large populations, and as such should be used cautiously.

重要的是要强调，这里提出的确定性模型只有在足够大人口的情况下才有效，因此应谨慎使用。

To be more precise, these models are only valid in the thermodynamic limit, where the population is effectively infinite. In stochastic models, the long-time endemic equilibrium derived above, does not hold, as there is a finite probability that the number of infected individuals drops below one in a system. In a true system then, the pathogen may not propagate, as no host will be infected. But, in deterministic mean-field models, the number of infected can take on real, namely, non-integer values of infected hosts, and the number of hosts in the model can be less than one, but more than zero, thereby allowing the pathogen in the model to propagate. The reliability of compartmental models is limited to compartmental applications.

更准确地说，这些模型只适用于中东热力学极限，那里的人口实际上是无限的。在随机模型中，由上述推导出的长期地方病平衡并不成立，因为在一个系统中，感染个体的数量下降到1以下的概率是有限的。在一个真正的系统中，病原体可能不会繁殖，因为没有宿主会被感染。但是，在确定性平均场模型中，被感染的病原体数量可以呈现实数值，即被感染宿主的非整数值，模型中的宿主数量可以小于1，但大于零，从而使模型中的病原体得以繁殖。传染病模型的可靠性仅限应用于传染病。

One of the possible extensions of mean-field models considers the spreading of epidemics on a network based on percolation theory concepts.^[19]

One of the possible extensions of mean-field models considers the spreading of epidemics on a network based on percolation theory concepts.

平均场模型的一个可能的扩展是基于渗流理论的概念来考虑流行病在网络上的传播。

References

参考文献

↑ ^1.0 ^1.1 Kermack, W. O.; McKendrick, A. G. (1927). "A Contribution to the Mathematical Theory of Epidemics". Proceedings of the Royal Society A. 115 (772): 700–721. Bibcode:1927RSPSA.115..700K. doi:10.1098/rspa.1927.0118.
↑ ^2.0 ^2.1 ^2.2 Harko, Tiberiu; Lobo, Francisco S. N.; Mak, M. K. (2014). "Exact analytical solutions of the Susceptible-Infected-Recovered (SIR) epidemic model and of the SIR model with equal death and birth rates". Applied Mathematics and Computation (in English). 236: 184–194. arXiv:1403.2160. Bibcode:2014arXiv1403.2160H. doi:10.1016/j.amc.2014.03.030.
↑ ^3.0 ^3.1 ^3.2 Beckley, Ross; Weatherspoon, Cametria; Alexander, Michael; Chandler, Marissa; Johnson, Anthony; Batt, Ghan S. (2013). "Modeling epidemics with differential equations" (PDF). Tenessee State University internal report. Retrieved July 19, 2020.
↑ ^4.0 ^4.1 Yang, Wuyue; Zhang, Dongyan; Peng, Liangrong; Zhuge, Changjing; Liu, Liu (2020). "Rational evaluation of various epidemic models based on the COVID-19 data of China" (PDF). arXiv:2003.05666v1 (q-bio.PE). Retrieved July 19, 2020.
↑ Krylova, O.; Earn, DJ (May 15, 2013). "Effects of the infectious period distribution on predicted transitions in childhood disease dynamics". J R Soc Interface. 10 (84). doi:10.1098/rsif.2013.0098. Retrieved June 13, 2020.
↑ Hethcote H (2000). "The Mathematics of Infectious Diseases". SIAM Review. 42 (4): 599–653. Bibcode:2000SIAMR..42..599H. doi:10.1137/s0036144500371907.
↑ Bailey, Norman T. J. (1975). The mathematical theory of infectious diseases and its applications (2nd ed.). London: Griffin. ISBN 0-85264-231-8.
↑ Sonia Altizer; Nunn, Charles (2006). Infectious diseases in primates: behavior, ecology and evolution. Oxford Series in Ecology and Evolution. Oxford [Oxfordshire]: Oxford University Press. ISBN 0-19-856585-2.
↑ Wolfram Research, Inc. "Mathematica, Version 12.1". Champaign IL, 2020.
↑ Capasso, V. (1993). Mathematical Structure of Epidemic Systems. Berlin: Springer. ISBN 3-540-56526-4.
↑ Miller, J.C. (2012). "A note on the derivation of epidemic final sizes". Bulletin of Mathematical Biology. 74 (9). section 4.1. doi:10.1007/s11538-012-9749-6. PMC 3506030. PMID 22829179.
↑ Miller, J.C. (2017). "Mathematical models of SIR disease spread with combined non-sexual and sexual transmission routes". Infectious Disease Modelling. 2 (1). section 2.1.3. doi:10.1016/j.idm.2016.12.003. PMC 5963332. PMID 29928728.
↑ Hethcote, Herbert W. (1989). "Three Basic Epidemiological Models". In Levin, Simon A.; Hallam, Thomas G.; Gross, Louis J.. Applied Mathematical Ecology. Biomathematics. 18. Berlin: Springer. pp. 119–144. doi:10.1007/978-3-642-61317-3_5. ISBN 3-540-19465-7.
↑ (p. 19) The SI Model
↑ The first and second differential equations are transformed and brought to the same form as for the SIR model above.
↑ ^16.0 ^16.1 ^16.2 Brauer, F.; Castillo-Chávez, C. (2001). Mathematical Models in Population Biology and Epidemiology. NY: Springer. ISBN 0-387-98902-1.
↑ For more information on this type of model see Anderson, R. M., ed. (1982). Population Dynamics of Infectious Diseases: Theory and Applications. London-New York: Chapman and Hall. ISBN 0-412-21610-8.
↑ Bartlett MS (1957). "Measles periodicity and community size". Journal of the Royal Statistical Society, Series A. 120 (1): 48–70. doi:10.2307/2342553. JSTOR 2342553. S2CID 91114210.
↑ Croccolo F. and Roman H.E. (2020). "Spreading of infections on random graphs: A percolation-type model for COVID-19". Chaos, Solitons & Fractals. 139: 110077. doi:10.1016/j.chaos.2020.110077.

External links

外部链接

SIR model: Online experiments with JSXGraph

"Simulating an epidemic". 3Blue1Brown. March 27, 2020 – via YouTube.

编辑推荐

[1]

美国新冠病毒肺炎流行病如何引发种族仇恨 | 网络科学论文速度36篇

[2]

用Links建模网络动力学

模板:Computer modeling

Category:Epidemiology

类别: 流行病学

Category:Scientific modeling

类别: 科学建模

This page was moved from wikipedia:en:Compartmental models in epidemiology. Its edit history can be viewed at 复杂传染病/edithistory

[Kermack.E2.80.93McKendrick-1] 1.0 ^1.1 Kermack, W. O.; McKendrick, A. G. (1927). "A Contribution to the Mathematical Theory of Epidemics". Proceedings of the Royal Society A. 115 (772): 700–721. Bibcode:1927RSPSA.115..700K. doi:10.1098/rspa.1927.0118.

[Harko-2] 2.0 ^2.1 ^2.2 Harko, Tiberiu; Lobo, Francisco S. N.; Mak, M. K. (2014). "Exact analytical solutions of the Susceptible-Infected-Recovered (SIR) epidemic model and of the SIR model with equal death and birth rates". Applied Mathematics and Computation (in English). 236: 184–194. arXiv:1403.2160. Bibcode:2014arXiv1403.2160H. doi:10.1016/j.amc.2014.03.030.

[Beckley-3] 3.0 ^3.1 ^3.2 Beckley, Ross; Weatherspoon, Cametria; Alexander, Michael; Chandler, Marissa; Johnson, Anthony; Batt, Ghan S. (2013). "Modeling epidemics with differential equations" (PDF). Tenessee State University internal report. Retrieved July 19, 2020.

[Yang2020-4] 4.0 ^4.1 Yang, Wuyue; Zhang, Dongyan; Peng, Liangrong; Zhuge, Changjing; Liu, Liu (2020). "Rational evaluation of various epidemic models based on the COVID-19 data of China" (PDF). arXiv:2003.05666v1 (q-bio.PE). Retrieved July 19, 2020.

[Krylova2013-5] Krylova, O.; Earn, DJ (May 15, 2013). "Effects of the infectious period distribution on predicted transitions in childhood disease dynamics". J R Soc Interface. 10 (84). doi:10.1098/rsif.2013.0098. Retrieved June 13, 2020.

[Hethcote2000-6] Hethcote H (2000). "The Mathematics of Infectious Diseases". SIAM Review. 42 (4): 599–653. Bibcode:2000SIAMR..42..599H. doi:10.1137/s0036144500371907.

[Bailey1975-7] Bailey, Norman T. J. (1975). The mathematical theory of infectious diseases and its applications (2nd ed.). London: Griffin. ISBN 0-85264-231-8.

[nunn2006-8] Sonia Altizer; Nunn, Charles (2006). Infectious diseases in primates: behavior, ecology and evolution. Oxford Series in Ecology and Evolution. Oxford [Oxfordshire]: Oxford University Press. ISBN 0-19-856585-2.

[9] Wolfram Research, Inc. "Mathematica, Version 12.1". Champaign IL, 2020.

[Capasso-10] Capasso, V. (1993). Mathematical Structure of Epidemic Systems. Berlin: Springer. ISBN 3-540-56526-4.

[11] Miller, J.C. (2012). "A note on the derivation of epidemic final sizes". Bulletin of Mathematical Biology. 74 (9). section 4.1. doi:10.1007/s11538-012-9749-6. PMC 3506030. PMID 22829179.

[12] Miller, J.C. (2017). "Mathematical models of SIR disease spread with combined non-sexual and sexual transmission routes". Infectious Disease Modelling. 2 (1). section 2.1.3. doi:10.1016/j.idm.2016.12.003. PMC 5963332. PMID 29928728.

[Hethcote1989-13] Hethcote, Herbert W. (1989). "Three Basic Epidemiological Models". In Levin, Simon A.; Hallam, Thomas G.; Gross, Louis J.. Applied Mathematical Ecology. Biomathematics. 18. Berlin: Springer. pp. 119–144. doi:10.1007/978-3-642-61317-3_5. ISBN 3-540-19465-7.

[14] (p. 19) The SI Model

[15] The first and second differential equations are transformed and brought to the same form as for the SIR model above.

[:2-16] 16.0 ^16.1 ^16.2 Brauer, F.; Castillo-Chávez, C. (2001). Mathematical Models in Population Biology and Epidemiology. NY: Springer. ISBN 0-387-98902-1.

[17] For more information on this type of model see Anderson, R. M., ed. (1982). Population Dynamics of Infectious Diseases: Theory and Applications. London-New York: Chapman and Hall. ISBN 0-412-21610-8.

[18] Bartlett MS (1957). "Measles periodicity and community size". Journal of the Royal Statistical Society, Series A. 120 (1): 48–70. doi:10.2307/2342553. JSTOR 2342553. S2CID 91114210.

[19] Croccolo F. and Roman H.E. (2020). "Spreading of infections on random graphs: A percolation-type model for COVID-19". Chaos, Solitons & Fractals. 139: 110077. doi:10.1016/j.chaos.2020.110077.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

仓室模型

目录

The SIR model

Transition rates

The SIR model without vital dynamics

The force of infection

Exact analytical solutions to the SIR model

The SIR model with vital dynamics and constant population

Variations on the basic SIR model

The SIS model

The SIRD model

The MSIR model

Carrier state

The SEIR model

The SEIS model

The MSEIR model

The MSEIRS model

Variable contact rates

Modelling vaccination

Vaccinating newborns

Vaccination and information

Vaccination of non-newborns

Pulse vaccination strategy

The influence of age: age-structured models

Other considerations within compartmental epidemic models

Vertical transmission

Vector transmission

Others

Deterministic versus stochastic epidemic models

See also

References

Further reading

External links

编辑推荐

导航菜单

搜索