K近邻聚类

“近朱者赤，近墨者黑。”

简介

K近邻聚类算法（K-Nearest Neighbor Algorithm）的一个基本假设在于，一个观测点最可能所属于的类别，取决于它周围的小伙伴们。

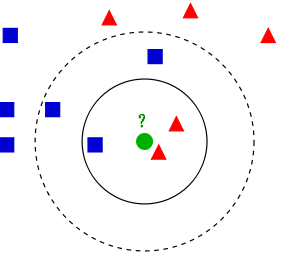
如图所示，为了判断一个新来的观测点（绿色）到底属于红色类还是蓝色类，我们可以考察它周围离它最近的一定数目的观测点，看属于哪一类的最多。如果这个数目一开始被设置为3，绿色观测点就会被归在红色类里面；如果这个数目被设置为5，那么这个节点就会被归在蓝色类里面了。

这个算法可以解决半监督与无监督分类学习问题。

算法

• 首先将待分类的点随机的标记为某些已知的类——当然，已经有分好类的点就不用这样标记了；
• 同时对每一个待分类的点进行一次重新标记，标记规则就是通过其周围K个最近邻判断它会最新属于哪类，而所谓“近”的含义通过点之间的距离函数给出；
• 循环直到收敛：考虑到重标注过程有可能不能达到收敛，甚至会导致陷入某些状态的循环，我们可以设置调整参数（如距离函数或近邻数）或者设置停止准则使其停止。

定义距离函数

• 欧式距离

[math]\displaystyle{ d(x,y)= {||x-y||}_2 = \sqrt{\sum_i{(x_i-y_i)^2}} }[/math]

• 曼哈顿距离

[math]\displaystyle{ d(x,y)= {||x-y||}_1 = \sum_i{|x_i-y_i|} }[/math]

• 汉明距离

[math]\displaystyle{ d(x,y)= \sum_i{(x_i-y_i)^0}=\sum_i{(x_i \neq y_i)} }[/math]

• [math]\displaystyle{ L_p }[/math]空间距离

[math]\displaystyle{ d(x,y)= {||x-y||}_p = (\sum_i{(x_i-y_i)^p})^{1/p} }[/math]

相关wiki

• K-means聚类
• Affinity propagation 聚类
• K近邻聚类