用Levy Flight模型模拟在线社区中的用户交互行为
背景
模型
- 实证中观察到的超线性增长
- 人类在线行为的基本模型
- 实证和模型中得到的注意力流网络
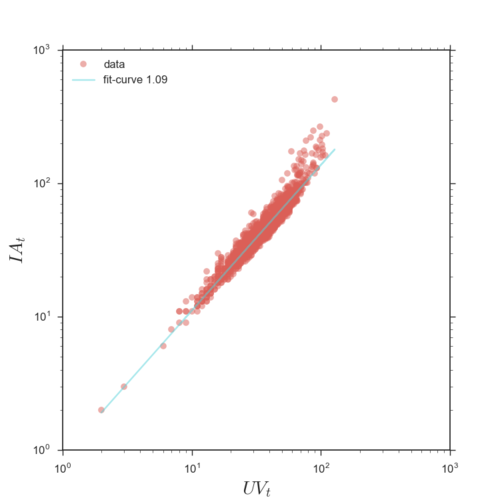
通过实证分析,我们发现在不同的在线社区的用户数 [math]\displaystyle{ UV_t }[/math] 与用户产生的活动数 [math]\displaystyle{ IA_t }[/math] 存在超线性的幂律关系 [math]\displaystyle{ IA_t=UV_t^{\theta} }[/math],这就意味着当 [math]\displaystyle{ UV_t }[/math] 增长一定的量时,[math]\displaystyle{ IA_t }[/math] 增长的越多。我们以百度贴吧和Stack Overflow为例,计算了他们的 [math]\displaystyle{ {\theta} }[/math] 值。
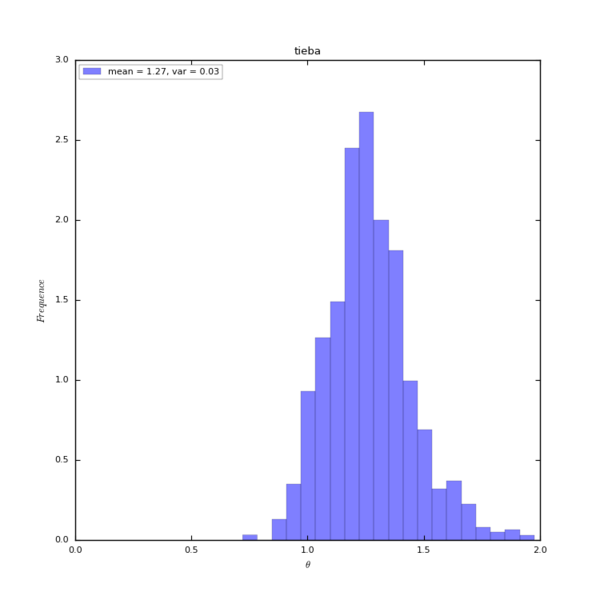
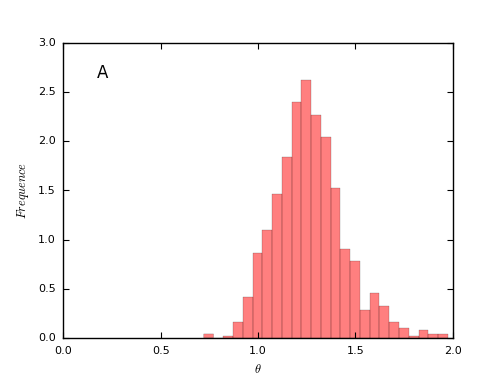
1000个百度贴吧的 [math]\displaystyle{ {\theta} }[/math] 值分布情况:
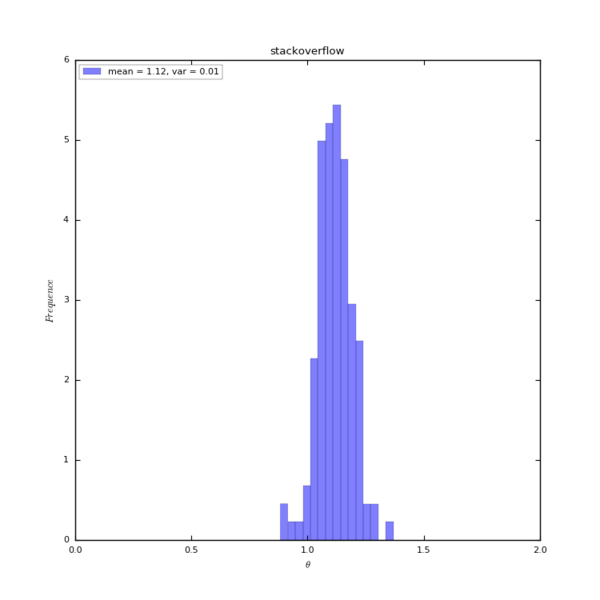
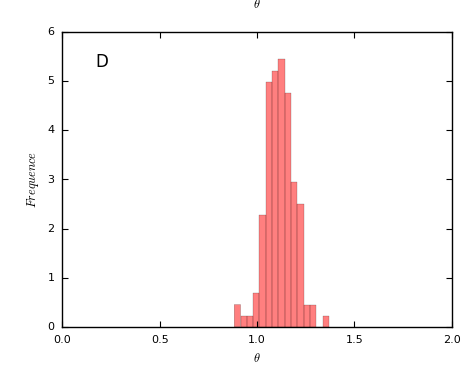
136个Stack Exchange子站的 [math]\displaystyle{ {\theta} }[/math] 值分布情况:
下表是我们计算得到的部分在线社区的 [math]\displaystyle{ {\theta} }[/math] 数值表,可以看到不同类型的社区的值并不相同,这个值能够反映出不同类型社区的内在“性格”。
| Site | [math]\displaystyle{ {\theta} }[/math] |
|---|---|
| Tieba | 1.27 |
| Stack Overflow | 1.12 |
| githubArchive | 0.91 |
| Delicious | 1.07 |
| Flickr | 1.04 |
| Yelp tip | 1.11 |
| Digg | 1.16 |
| Taobao news | 0.99 |
模型构建:
假设存在一个L*L的二维网格空间([math]\displaystyle{ L\rightarrow \infty }[/math])表示用户可能的兴趣空间S。我们用空间上的随机游走粒子建模用户。每个用户在每一时刻都会发生兴趣转移,即完成一步在S上的随机跳跃。我们假设用户的跳转按照列维飞行的方式进行,即用户跳转到长度l满足:
[math]\displaystyle{ P(l)\sim l^{-\alpha} }[/math]
这里的 [math]\displaystyle{ {\alpha} }[/math] 为列维飞行的指数,可以刻画用户随机游走的离散程度。
每当用户访问到某一个格点的时候,就会在此格点做上一个标记,表示它在这个兴趣空间中发表了一个帖子或者博客。
接下来,我们将考虑多个用户在兴趣空间之间的交互,以及用户的兴趣保持特征。假设有N个用户同时在这个空间中游走,当某个用户踩到了一个做了标记的格点之后就能以概率p继续随机游走,以1-p的概率死掉。其中,p为一个自由参数,模拟了用户在读到其它用户产生的内容之后继续游走的概率。如果粒子所在的当前格点为空,则粒子即可死掉。
这个过程建模了用户之间的交互,每一步跳转对应用户当前注意力在兴趣空间中的转移,当它的兴趣点在物理学的时候,如果刚好有一个别的用户发表的博客是在讲物理学,那么用户的兴趣需求得到了满足,它就会继续在这个社区里跳转看帖子,这个保留的程度就用p来刻画了。反过来,加入当前时刻用户的兴趣点在物理,但是其它用户留下的帖子都是有关明星、健身等的内容(这些标记位于远离物理这个格点的位置),那么用户就会对这个社区失去了兴趣,从而离开。
具体的步骤是:
- 1.初始时刻,随机地在二维平面上撒上N个粒子,这些粒子落在M个不同的单元格上面,意味着它们生产了M个帖子(M小于等于N)。即相当于某在线社区初始时有N个用户在线,这些用户生产了M个内容;
- 2.随后,N个粒子按照列维飞行的模式开始游走,每个粒子走了1个步长后,又到了一个单元格,意味着又可以产生了一个新的内容(产生得新内容包括发布新的帖子、点击别人的帖子、回复别人的帖子等交互行为)。此时,需要判断这个单元格上的粒子是否能继续进行下一次的游走。判断的依据是,粒子现在所在的单元格在之前或者当前是否有别的粒子来过,如有,则这个粒子会以一定的概率PP继续游走,否则它就会在这一轮死掉。与人们在网络社区上的行为进行类比,就是说当一个用户发表了一个新帖子后,如果没有其他人来浏览互动,同时,互动的条件是其他前来浏览帖子的用户以一定的概率q点击或者回复这一帖子,用户对帖子话题内容的兴趣是决定概率q的因素,否则,如果仅仅是浏览而没有交互,这个帖子就会沉没,发表帖子的用户也会积极性受挫,失去继续在网络社区浏览互动的兴趣。这样,这种交互式的列维飞行模型就能较好地与现实生活中人们的上网行为对应起来。
- 3.剩下存活的粒子重复进行2中的游走,直至所有粒子死掉。统计出N个粒子全部生产的内容数量IA(Interactive Activities)。
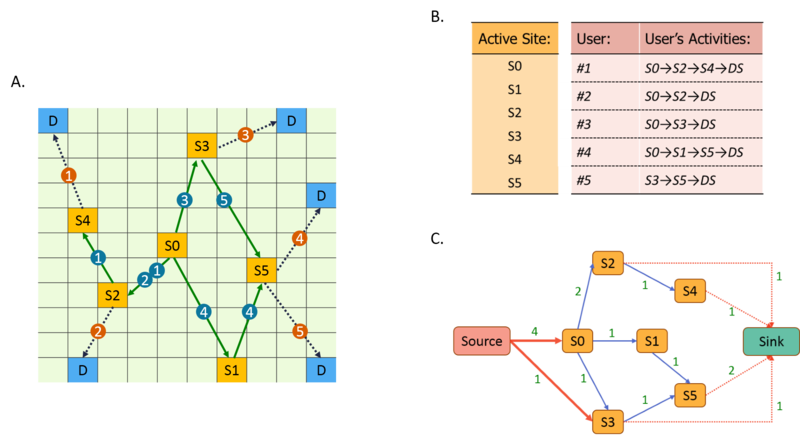
在此模型中,每个用户在游走的过程中都会留下自己的游走轨迹。例如在下图中,#1用户的游走轨迹是:source->s0->s2->s4->sink,这样对于大量的用户,我们可以得到一组它的访问行为轨迹。之后,我们可以用一种称之为注意力流网络的工具来建模这N个粒子在虚拟空间中游走的集体行为。
在上图中,图A表示的是用户在兴趣空间中进行跳转的模拟图,黄色方块表示的是用户产生的活动,蓝色的方块D表示的是用户最后离开的行为。根据图A可以得到图B中的用户点击记录数据集,对图B的数据集进行整理就可以得到图C中的流网络。
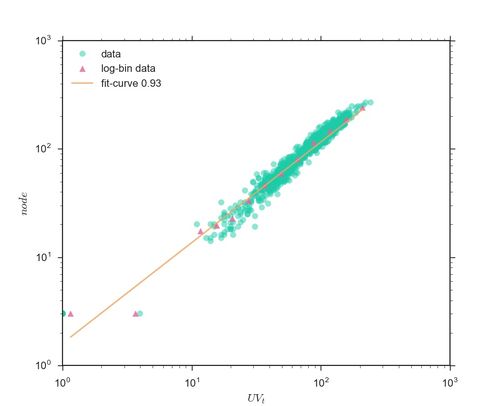
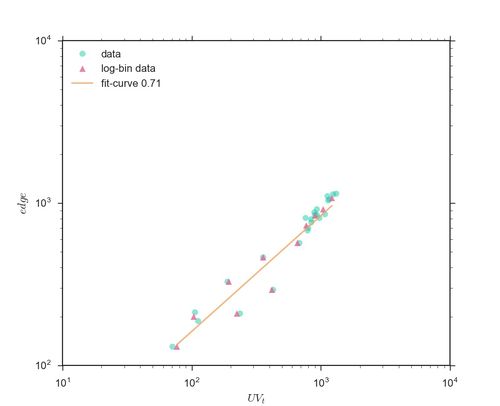
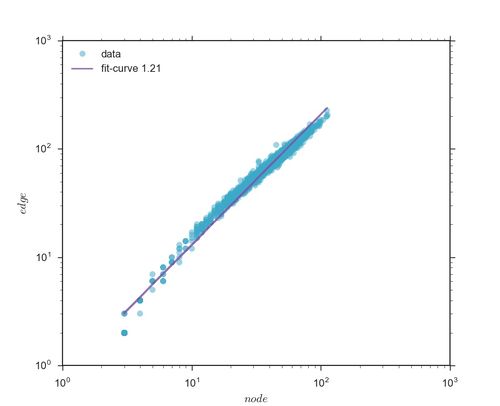
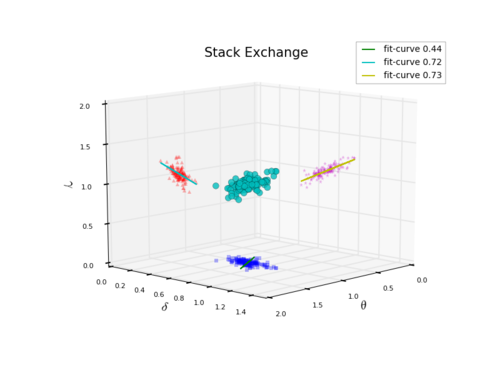
从图C中的流网络,我们可以提取出几个关键性统计指标,从而将模型与实证数据进行对照。这些统计指标包括到网络的节点数 [math]\displaystyle{ N_t }[/math] 以及连边数 [math]\displaystyle{ E_t }[/math],节点数可以看做用户发布的内容即帖子数,连边数可以看做在不同的帖子之间进行跳转的用户人数。这些数量之间也存在着幂律关系:[math]\displaystyle{ N_t=UV_t^{\delta} }[/math],[math]\displaystyle{ E_t=UV_t^{\gamma} }[/math],[math]\displaystyle{ E_t=N_t^{\lambda} }[/math],它们中有些是超线性有些是亚线性。
结果
模型模拟结果
交互粘性及其加速生长
在实证研究中发现,在线社区的用户数 [math]\displaystyle{ UV_t }[/math] 与用户产生的活动数 [math]\displaystyle{ IA_t }[/math] 存在超线性的幂律关系[math]\displaystyle{ IA_t=UV_t^{\theta} }[/math],这就意味着当 [math]\displaystyle{ UV_t }[/math] 增长一定的量时,[math]\displaystyle{ IA_t }[/math] 增长的越多。同时我们还发现,不同的在线社区的[math]\displaystyle{ \theta }[/math] 值不一样,越“火”的社区值越大。下图分别是某个贴吧和某个Stack Exchange子站的[math]\displaystyle{ IA_t=UV_t^{\theta} }[/math]关系图,实证中发现贴吧的[math]\displaystyle{ \theta }[/math] 普遍大于Stack Exchange。[math]\displaystyle{ \theta }[/math] 反映的是一个社区的活跃度,或者更通俗的说是粘性值,[math]\displaystyle{ \theta }[/math] 值越大的在线社区,用户越活跃,用户之间的交互也越多。
某个贴吧的关系图:
1000个贴吧theta值的概率密度图:
某个Stack Exchange子站的关系图:
136个Stack Exchange子站theta值的概率密度图:
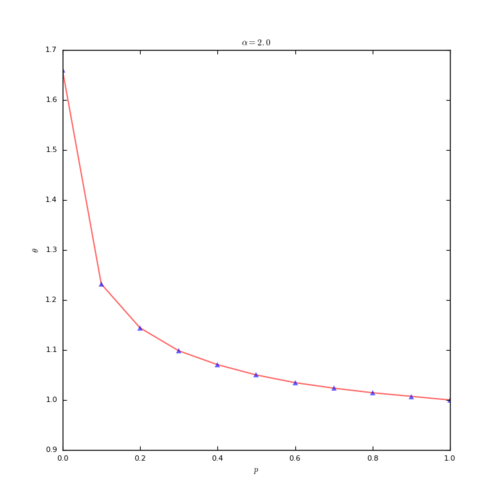
同时,通过列维飞行模型的模拟,也得到了这一性质:
上图显示的是设定列维飞行的指数[math]\displaystyle{ \alpha = 2 }[/math] 时,[math]\displaystyle{ \theta }[/math] 随用户交互概率P (P =1 - PP)变化的关系图。
其它各类scaling law
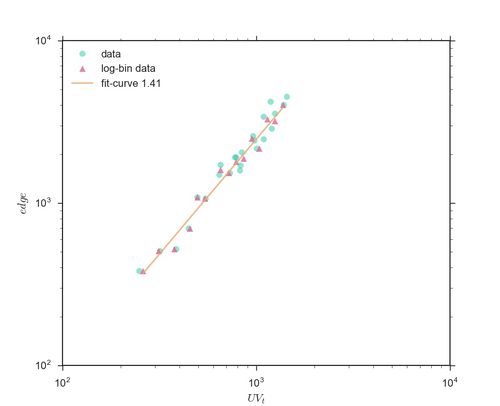
此外,通过构建的流网络,还可以得到网络的节点数 [math]\displaystyle{ N_t }[/math] 以及连边数 [math]\displaystyle{ E_t }[/math],节点数可以看做用户发布的内容即帖子数,连边数可以看做在不同的帖子之间进行跳转的用户人数。这些数量之间也存在着幂律关系:[math]\displaystyle{ N_t=UV_t^{\delta} }[/math],[math]\displaystyle{ E_t=UV_t^{\gamma} }[/math],[math]\displaystyle{ E_t=N_t^{\lambda} }[/math],它们中有些是超线性有些是亚线性。
下图显示的是某个Stack子站的 [math]\displaystyle{ N_t=UV_t^{\delta} }[/math] 关系图:
下图显示的是某个贴吧的 [math]\displaystyle{ E_t=UV_t^{\gamma} }[/math] 关系图:
下图显示的是某个Stack子站的 [math]\displaystyle{ E_t=N_t^{\lambda} }[/math] 关系图:
[math]\displaystyle{ \delta }[/math] 反映的是在线社区的内容多样性,即用户在社区上发布的内容(帖子)的多样性。因为在根据用户的点击行为所构建的流网络中,网络的节点表示的是不同的帖子或者网页,节点之间的链接表示的是用户在不同帖子或者网页之间的跳转。此时,用户数与用户发布的内容数之间是亚线性的幂律关系,表明了在线社区的用户群体兴趣空间的有界性,用户们都在一个有限的兴趣中游走。虽然社区里的用户在不断增多,但他们产生的兴趣的规模不是线性或超线性增长的。
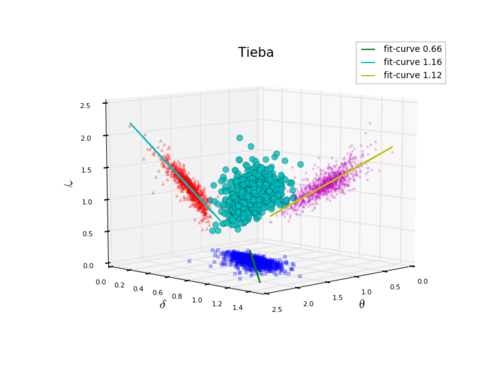
指数之间的关系
贴吧的指数之间的关系:
Stack Exchange的指数之间的关系:
有限尺度效应
结论
本工作研究了人类注意力和兴趣的演变模式,明确了在线社区上的群体中的交互行为对于兴趣空间中的移动的影响。并且,本模型还揭示出了人类行为中的复杂性的机制。
参考文献
[1] Gonza´lez, M. C., Hidalgo, C. A. & Baraba´si, A.-L. Understanding individual human mobility patterns. Nature 453, 779–782 (2008).
[2] Cheng, Z., Caverlee, J., Lee, K. & Sui, D. Z. Exploring millions of footprints in location sharing services. ICWSM 2011, 81–88 (2011).
[3] Jansen, V. A. A., Mashanova, A. & Petrovskii, S. Comment on Le´vy walks evolve through interaction between movement and environmental complexity. Science 335, 918 (2012).
[4] Petrovskii, S., Mashanova, A. & Jansen, V. A. A. Variation in individual walking behaviour creates the impression of a Le´vy flight. Proc. Natl Acad. Sci. USA 108,8704–8707 (2011).
[5] Edwards, A. M. Overturning conclusions of Le´vy flight movement patterns by fishing boats and foraging animals. Ecology 92, 1247–1257 (2011).
[6] Edwards, A. M. et al. Revisiting Le´vy flight search patterns of wandering albatrosses, bumblebees and deer. Nature 449, 1044–1048 (2007). category:旧词条迁移