流网络的引力定律

所谓流网络的引力定律是指任意边上的流量与该连边两个顶点上的流量的乘积具有幂律关系。假设一条i,j连边上的流量是f_ij，i上的流量是T_i，j上的流量是T_j，那么万有引力定律可以写为：

[math]\displaystyle{ f_{ij}\propto (T_i T_j)^{\alpha} }[/math]

有时，为了能够更好地拟合真实数据，我们也采用双参数拟合，也就是写成下式：

[math]\displaystyle{ f_{ij}\propto T_i^{\alpha}T_j^{\beta} }[/math]

式中有两个幂律指数αβ分别拟合ij连边的起始点i的流量和终点j的流量对ij连边流量的预测贡献。

引力定律

我们都熟悉，牛顿著名的万有引力公式可以表达为：

[math]\displaystyle{ f_{ij}=\frac{Gm_im_j}{r_{ij}^2} }[/math]

其中f_ij为两个物体i和j之间的万有引力，m_i和m_j分别表示两个物体的质量，r_ij表示两个物体之间的距离。

有意思的是，在复杂系统中，这个公式也普遍成立。例如，在城市系统中，任意两个城市之间的交通流、物资流遵循类似的万有引力公式：

[math]\displaystyle{ f_{ij}=k\frac{(P_iP_j)^{\alpha}}{r_{ij}^{\beta}} }[/math]

这里的f_ij为两个城市之间的流量（交通流、通讯流等等）。P_i和P_j分别表示各个城市的人口，r_ij表示两个城市之间的距离。k是一个类似万有引力常数一样的常数。α和β是两个需要拟合的指数。与牛顿的万有引力不同，两城市之间的流量可能不与城市人口乘积刚好呈正比。同样的道理，对于距离也不一定呈二次方反比，而有可能是任意的指数α和β（可能依不同国家的城市系统而不同）。

人们也曾尝试用万有引力来拟合任意两个国家之间的贸易流动，但是发现，标准的万有引力形式可能并不能很好地拟合，而如果对该公式进行扩展则有可能拟合得很好。更多讨论请参看复杂系统中的引力定律。

在通常的流网络中，节点之间是不存在空间距离的，但是，类似的万有引力公式仍然成立。所谓流网络的万有引力定律是指任意边上的流量与该连边两个顶点上的流量的乘积具有幂律关系。假设一条i,j连边上的流量是f_ij，i上的流量是T_i，j上的流量是T_j，那么万有引力定律可以写为：

[math]\displaystyle{ f_{ij}=c (T_i T_j)^{\alpha} }[/math]

(eq1)

其中c为常数，α为引力指数。有时，为了能够更好地拟合真实数据，我们也采用双参数拟合，也就是写成下式：

[math]\displaystyle{ f_{ij}=c T_i^{\alpha}T_j^{\beta} }[/math]

(eq2)

其中，有两个幂律指数αβ分别拟合ij连边的起始点i的流量和终点j的流量对ij连边流量的预测贡献。采用不同的指数α和β表明流动中起点和终点的非对称性。

各种实证网络的引力定律

生态流网络

在生态流网络中，每条边上的流量对应的是物种之间由于捕食关系而发生的能量转移。对于实证网络来说，我们发现eq1普遍成立。例如，下图展示的就是Mondego Estuary - Zostrea site(简称Mondego网)的用eq1式表达的引力定律。

500px

其中，拟合的指数为0.5868，R²达到了0.85。而下图则展示的是由eq2表达的引力定律。

500px

我们看到，这张图的效果会稍好一些，R²达到了0.86，这说明生态流网络的引力定律具有一定的不对称性。但是这种不对称性并不明显，这体现在两个指数的差异上并不大。

我们进一步考察了可获得的19个生态流网络的引力定律的拟合数据，见下表

网络名称	单变量引力指数	单变量R2	双变量引力指数α	双变量引力指数β	双变量R2
CrystalD	0.63	0.70	0.57	0.75	0.74
CrystalC	0.53	0.65	0.50	0.57	0.65
Chesapeake	0.68	0.84	0.62	0.77	0.85
ChesLower	0.70	0.75	0.61	0.84	0.76
ChesMiddle	0.67	0.77	0.60	0.78	0.78
ChesUpper	0.64	0.64	0.62	0.67	0.64
Narragan	0.54	0.81	0.49	0.60	0.81
Michigan	0.62	0.86	0.57	0.72	0.87
StMarks	0.68	0.74	0.76	0.56	0.75
Mondego	0.79	0.85	0.83	0.70	0.86
Cypwet	0.70	0.84	0.85	0.55	0.87
Cypdry	0.68	0.81	0.81	0.57	0.83
Gramdry	0.66	0.76	0.61	0.73	0.77
Gramwet	0.71	0.81	0.66	0.79	0.81
Mangdry	0.58	0.77	0.60	0.56	0.77
Mangwet	0.59	0.77	0.60	0.57	0.77
Baywet	0.62	0.79	0.67	0.54	0.80
Baydry	0.61	0.78	0.68	0.52	0.78
Florida	0.62	0.79	0.67	0.54	0.80

首先，我们观察到，该表中所有生物流网络的R²都显著大于0.5，说明，引力定律都存在。其次，双变量指数αβ的差别不大。这说明引力定律基本是对称的。

国际贸易网

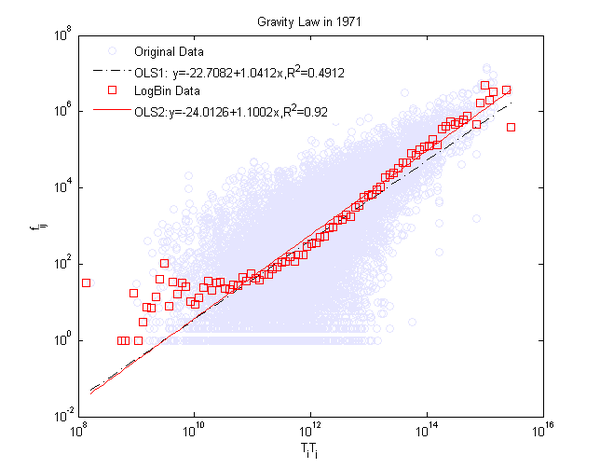
我们研究了国际贸易网的引力定律。例如，用1971的数据来看，引力定律大体成立：

在图中，浅蓝色的点为原始数据点，红色的方框为对原始数据进行Log Bin处理以后的数据。这种处理就是将整个数据划分成log轴上均等的小区间，然后用每个小区间中的数据点的平均值作为y值，这样可以把原始数据的噪声消除掉，以使得趋势更加明显。对原始数据进行OLS估计以及对Log Bin处理后的数据做OLS回归，就得到两条直线（黑色的点划线和红色的直线）。注意，对于国际贸易网来说，引力指数基本都大于1.

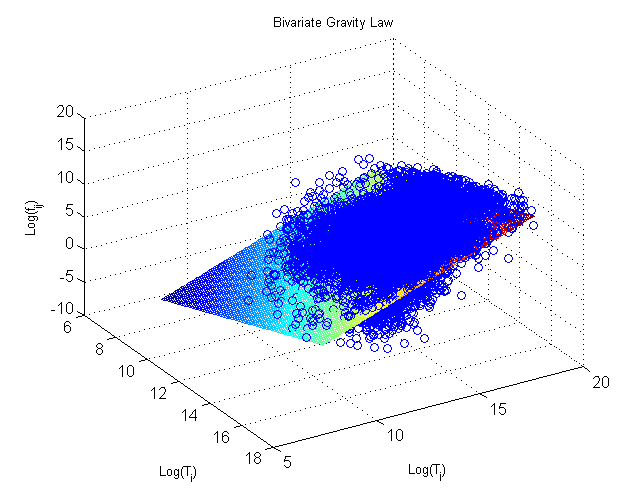
如果采用方程eq2，则我们可以得到下图：

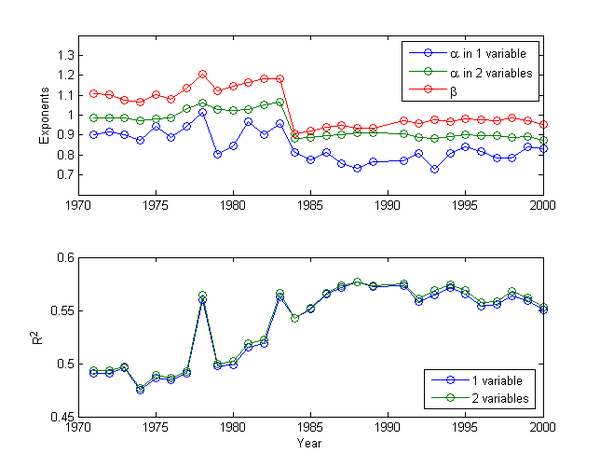
图中平面的方程是：[math]\displaystyle{ f_{ij}=\exp(-22.8513)T_i^{0.9874}T_j^{1.1043} }[/math]，R方为0.4938，指数β比α稍大，表示两国之间的贸易流f_ij更敏感地依赖于入口国的总贸易流量。我们计算了从1971年到2000年（不包括1990年）的所有的拟合指数以及R方，如下图：

我们看到随着时间的增长，引力定律的拟合优度越来越强，这说明国际贸易网络的整体演化越来越趋近于引力定律所描述的自组织规律，而所有的指数都大体上趋近于1。

相关WIKI

流网络

复杂系统的引力定律