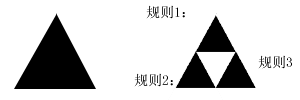随机函数迭代系统
- 名 称:随机函数跌代系统
- 作 者:Keats
- 源代码:ifs.zip
程序运行说明
首先要保证你的浏览器支持java applet,然后能够正确加载这个程序。在此前提下,按开始按钮,你会看到一片叶子慢慢的呈现在你的眼前。选择右面的选择框,你可以变换不同的图形,总之,开始是一些奇妙的点乱七八糟的点到屏幕上,但是慢慢的,点多了,规规矩矩的图形就会慢慢的呈现出来了。就好像一朵花隐藏在水中,慢慢的,水落下去了,花就展现在你的面前!因此给这个程序命名为出水芙蓉(当然,这里用的是出水芙蓉的本意而非引申意)。
点击设置按钮,你可以设定一些参数。“出水芙蓉”的画图原理是函数跌代系统,也就是根据几个变换规则生成图形。因此,你可以改变每个规则的参数。点击制定规则按钮可以编辑单个的规则,并且在图形中直观的看出图形变换是怎样完成的。
在底下有关于图形的操作,你可以拖放平移整个图形,也可以就整个图形进行缩放,从而达到最佳的观察效果。
原理
这是一种绘制分形图的方法,即所谓的随机函数跌代系统。具体说明在程序里有。简单的讲,图形的生成受几条简单规则的制约,每种规则都是一个仿射变换。什么是仿射变换?不严格的讲,就是一种照哈哈镜的变换。我们知道,对一个平面图形可以施加旋转、平移、缩放的变换,一般来讲,这种变换都可以用坐标变换的方式写出来:
[math]\displaystyle{ x^'=ax+by+c }[/math] [math]\displaystyle{ y^'=dx+ey+f }[/math]
这其中,a,b,c,d,e,f都是系数,x,y为图形原来的坐标,x',y'为经过变换得到的新坐标。不同的系数会对图形进行不同的变换,包括平移、旋转、缩放,如果x方向和y方向的缩放比例不一样,那么就会对图形产生某种扭曲,因此,总体上来讲,这种对图形的变换就象是照哈哈镜一样。
对一个图形进行一组(即多个)这样的变换,并且,让计算机以一定的概率选择这些规则。那么就能产生我们看到的分形图。这似乎有些神奇。为什么变换就能产生分形图呢?让我们以“金字塔”为例进行说明。
考虑上面的三角形,从左边的大三角形变成右边的三个小三角形,显然,这是受三条规则同时制约的,考虑规则1。它是先把大三角形缩小一半(假设以大三角形的左下角为原点坐标),然后再往上平移一半,往右平移sqrt(3)/4,sqrt(3)表示根号3。因此,规则1就可以写为:
另外的两条规则也可以写成这样的形式。接下来,我们就要接着对三个小三角进行变形。考虑最上面的小三角,我们应用规则1变换,即先缩小一半,然后再平移,这跟在上一步中把大三角形运用规则1的效果是一样的,对其它两个小三角形运用规则1我们就能得到下面的图:
运用规则2、3我们能得到类似的结论。因此,当考虑跌代几百步甚至上千步的时候,程序中的金字塔就会出现了。
当然,我们上面讲的是对开始的大三角形运用三条规则。如果对任意一个平面上的点会怎样呢?实际上,经过足够多跌代以后,最终的图形仍然是“金字塔”,这是因为金字塔是图形变换的极限。至于程序中为什么金字塔是逐渐浮现出来的,这要源于我们在跌代的过程中随机的选择规则了。程序是对平面上的任意一点比如(0,0)随机的选择一条规则进行运算变换得到点x1,y1画出来,然后再随机选择一条规则对x1,y1进行变换得到x2,y2画出来,……。最后所有这些点组成的图形,也就是最后呈现出来的你看到的金字塔。当然,由于程序中的坐标系原点是在左上角,因此系数跟我们刚才讲的不一样,而且并且我们为了能充满屏幕,金字塔略胖了一些。
其它的诸如树叶、山等图形也是用同样的道理画出来的,只不过它们的变换规则中的系数不一样。