度
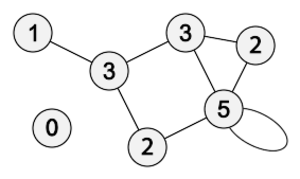
在图论 Graph theory中,图中顶点的度 Degree(或价)是入射到该顶点的边的数量。在多重图 Multigraph中,自环 Loops会被计算两次。顶点的度数可表示为[math]\displaystyle{ \deg(v) }[/math]或[math]\displaystyle{ \deg v }[/math]。一个图[math]\displaystyle{ G }[/math]的最大度值可表示为[math]\displaystyle{ \Delta(G) }[/math],最小度值可表示为 [math]\displaystyle{ \delta(G) }[/math]。在右侧的多重图中,最大度值为5,最小度值为0。
在正则图 Regular Graph中,每个顶点都具有相同的度数,因此我们可以将其称之为该图的度数。一个完全图 Complete Graph(表示为[math]\displaystyle{ K_n }[/math],其中[math]\displaystyle{ n }[/math]是图中顶点的数目)是一种特殊的正则图,它所有顶点都有最大度值,[math]\displaystyle{ n-1 }[/math]。
握手引理
度和公式 Degree Sum Formula表明,任意给定一个图[math]\displaystyle{ G=(V, E) }[/math],都有
[math]\displaystyle{ \sum_{v \in V} \deg(v) = 2|E|\, . }[/math]
此公式表明,在任何无向图中,拥有奇数度值的顶点的个数是偶数。这一阐释(以及度和公式)被称为握手引理 Handshaking Lemma。该名称来自一个有趣的数学问题,即求证无论该群体内有多少人,与奇数个人握过手的人数总是偶数。
度序列
无向图的度序列是指将其各顶点度值按非递增方式排序,对于上述图是(5,3,3,2,2,1,0)。度序列是图不变量 Graph Invariant,因此同构图 Non-isomorphic Graphs(两个图中顶点的度值都相同,但形状不同)具有相同的度序列。然而,度序列通常不能唯一地标识一个图,在某些情况下,非同构图也会具有相同的度序列。
度序列问题 Degree Sequence Problem,是指寻找给定以非增方式排列的正整数的度序列的局部或全部图的问题。(序列尾部的零可能会被忽略,因为通过向图中添加适当数量的孤立顶点就可以轻松实现序列尾部不断加零。)一个序列是某个图的度序列,即一个度序列问题有解时,该序列称为图形序列。由于度和公式的存在,任何具有奇数和的序列,如(3,3,1) ,都不会是图的度序列。反之亦然: 如果一个序列和是偶数,它就是重图的度序列。我们可以轻易地构造一个图: 匹配奇数度值的顶点并成对连接起来,然后剩余的偶数度值顶点都连出一条边指向图形/起点本身。
“一个给定的度序列是否可以用一个简单的图进行表示”是一个具有挑战性的问题。这个问题也称为图实现 Graph Realization Problem问题,但它可以用Erdős–Gallai定理 Erdős–Gallai Theoreme解决,也可以用Havel-Hakimi算法 Havel–Hakimi Algorithm解决。
基于给定度序列寻找或估计可能的图的个数,是图枚举 Graph Enumeration领域中的一个问题。
一般来说,超图 Hypergraph的度序列是其顶点度的非递增序列。如果一个序列是[math]\displaystyle{ k-uniform }[/math]超图的度序列,那么它即是[math]\displaystyle{ k-graphic }[/math]。特别地,[math]\displaystyle{ 2 }[/math]-graphic序列是图形。决定一个给定的序列是否是[math]\displaystyle{ k }[/math]-graphic可以在 [math]\displaystyle{ k=2 }[/math]的多项式时间内通过Erdős–Gallai定理实现,但是当[math]\displaystyle{ k\ge 3 }[/math]时该问题可转化为NP完全问题 NP-complete[1]。
特殊值
- 度数为0的顶点成为孤立顶点 Isolated Vertex
- 度数为1的顶点称为叶顶点或尾顶点,该顶点的入射边称为悬挂边 Pendant Edge。在右侧的图中,{3,5}就是一个悬挂边。在图论中,该术语主要在研究树 Tree时使用,特别是具有树形结构的数据。
- 在有n个顶点的图中,度数为n-1的顶点叫作主导顶点 Dominating Vertex
全局属性
- 如果一个图中的所有顶点的度值都为k,那么该图被称为k-正则图 k-regular graph,该图的度数也为k。同样的,同侧每两个顶点都具有相同度数的二分图叫作二分正则图 Biregular Graph。
- 当且仅当一个图具有0或2个奇数度的顶点时,无向连通图才具有欧拉路径 Eulerian Path。 如果它具有0个奇数度的顶点,则欧拉路径为欧拉回路 Eulerian Circuit。
- 当且仅当每个顶点的度数最大值为1时称该图为有向图伪森林 Pseudoforest。功能图 Functional Graph是伪森林的特例,其中每个顶点的度数都恰好为1。
- 根据布鲁克斯定理,除团簇或奇数循环外,任何图的色度数最大为Δ,而根据维辛定理,任何图的色度指数最大为Δ+ 1。
- k简并图 K-Degenerate Graph 是其中每个子图最多具有度数为k的顶点的图。
参阅
- 有向图的入度和出度 Indegree,Outdegree For Digraph
- 度分布 Degree Distribution
- 二分图的度序列 Degree Sequence For Bipartite Graphs
笔记
- ↑ Deza, Antoine; Levin, Asaf; Meesum, Syed M.; Onn, Shmuel (January 2018). "Optimization over Degree Sequences". SIAM Journal on Discrete Mathematics (in English). 32 (3): 2067–2079. arXiv:1706.03951. doi:10.1137/17M1134482. ISSN 0895-4801.
参考
- Diestel, Reinhard, Graph Theory (3rd ed.), Berlin, New York: Springer-Verlag.
- "Gráfok előírt fokszámú pontokkal" (PDF), Matematikai Lapok (in magyar), 11: 264–274, 1960.
- "A remark on the existence of finite graphs", Časopis pro pěstování matematiky (in čeština), 80: 477–480, 1955, retrieved 2019-04-23
- "On realizability of a set of integers as degrees of the vertices of a linear graph. I", Journal of the Society for Industrial and Applied Mathematics, 10: 496–506, 1962.
- Sierksma, Gerard; Hoogeveen, Han (1991), "Seven criteria for integer sequences being graphic", Journal of Graph Theory, 15 (2): 223–231, doi:10.1002/jgt.3190150209.
本中文词条由Ryan 参与编译, CecileLi 审校,不是海绵宝宝编辑,欢迎在讨论页面留言。
本词条内容源自wikipedia及公开资料,遵守 CC3.0协议。