量子计算

来自集智百科 - 复杂系统|人工智能|复杂科学|复杂网络|自组织
Moonscar（讨论 | 贡献）2020年10月25日 (日) 17:44的版本 （Moved page from wikipedia:en:Quantum computing (history)）
跳到导航 跳到搜索

此词条暂由彩云小译翻译，翻译字数共279，未经人工整理和审校，带来阅读不便，请见谅。


模板:Tone

Quantum computing is the use of quantum phenomena such as superposition and entanglement to perform computation. Computers that perform quantum computations are known as quantum computers.[1]:I-5 Quantum computers are believed to be able to solve certain computational problems, such as integer factorization (which underlies RSA encryption), substantially faster than classical computers. The study of quantum computing is a subfield of quantum information science.

Quantum computing is the use of quantum phenomena such as superposition and entanglement to perform computation. Computers that perform quantum computations are known as quantum computers. There are currently a number of significant obstacles in the way of constructing useful quantum computers. In particular, it is difficult to maintain the quantum states of qubits as they are prone to quantum decoherence, and quantum computers require significant error correction as they are far more prone to errors than classical computers. which is a subclass of PSPACE.

量子计算是利用量子现象，如叠加和纠缠来执行计算。执行量子计算的计算机被称为量子计算机。目前在建造有用的量子计算机的道路上有许多重大的障碍。特别是，量子比特的量子状态很难维持，因为它们容易发生量子退相干错误，而量子计算机需要显著的错误纠正，因为它们比传统计算机更容易发生错误。它是 PSPACE 的一个子类。



< ! ——对更先进类型量子计算机的推测—— >

Quantum computing began in the early 1980s, when physicist Paul Benioff proposed a quantum mechanical model of the Turing machine.[2] Richard Feynman and Yuri Manin later suggested that a quantum computer had the potential to simulate things that a classical computer could not.[3][4] In 1994, Peter Shor developed a quantum algorithm for factoring integers that had the potential to decrypt RSA-encrypted communications.[5] Despite ongoing experimental progress since the late 1990s, most researchers believe that "fault-tolerant quantum computing [is] still a rather distant dream."[6] In recent years, investment into quantum computing research has increased in both the public and private sector.[7][8] On 23 October 2019, Google AI, in partnership with the U.S. National Aeronautics and Space Administration (NASA), claimed to have performed a quantum computation that is infeasible on any classical computer.[9]

It has been speculated that further advances in physics could lead to even faster computers. For instance, it has been shown that a non-local hidden variable quantum computer based on Bohmian Mechanics could implement a search of an [math]\displaystyle{ N }[/math]-item database in at most [math]\displaystyle{ O(\sqrt[3]{N}) }[/math] steps, a slight speedup over Grover's algorithm, which runs in [math]\displaystyle{ O(\sqrt{N}) }[/math] steps. Note, however, that neither search method would allow quantum computers to solve NP-complete problems in polynomial time. Theories of quantum gravity, such as M-theory and loop quantum gravity, may allow even faster computers to be built. However, defining computation in these theories is an open problem due to the problem of time; that is, within these physical theories there is currently no obvious way to describe what it means for an observer to submit input to a computer at one point in time and then receive output at a later point in time.

据推测，物理学的进一步发展可能会导致计算机的速度更快。例如，已经证明，基于 Bohmian Mechanics 的非局部隐变量量子计算机可以在最多 < math > o (sqrt [3]{ n }) </math > 步骤中实现对一个 < math > n </math > 项数据库的搜索，这比 Grover 的算法稍微快了一点，该算法运行在 < math > o (sqrt { n }) </math > 步骤中。然而，请注意，这两种搜索方法都不允许量子计算机在多项式时间内解决 np 完全问题。量子引力理论，比如 m 理论和回圈量子重力理论，可能允许建造更快的计算机。然而，由于时间问题，在这些理论中定义计算是一个开放的问题; 也就是说，在这些物理理论中，目前没有明显的方法来描述观察者在一个时间点向计算机提交输入，然后在稍后的时间点接收输出意味着什么。



There are several models of quantum computing, including the quantum circuit model, quantum Turing machine, adiabatic quantum computer, one-way quantum computer, and various quantum cellular automata. The most widely used model is the quantum circuit. Quantum circuits are based on the quantum bit, or "qubit", which is somewhat analogous to the bit in classical computation. Qubits can be in a 1 or 0 quantum state, or they can be in a superposition of the 1 and 0 states. However, when qubits are measured the result of the measurement is always either a 0 or a 1; the probabilities of these two outcomes depend on the quantum state that the qubits were in immediately prior to the measurement. Computation is performed by manipulating qubits with quantum logic gates, which are somewhat analogous to classical logic gates.


< ! -- 新链接请按字母顺序排列 -- >


{ columns-list
The unnamed parameter 2= is no longer supported. Please see the documentation for {{columns-list}}.


There are currently two main approaches to physically implementing a quantum computer: analog and digital. Analog approaches are further divided into quantum simulation, quantum annealing, and adiabatic quantum computation. Digital quantum computers use quantum logic gates to do computation. Both approaches use qubits.[1]:2–13 There are currently a number of significant obstacles in the way of constructing useful quantum computers. In particular, it is difficult to maintain the quantum states of qubits as they are prone to quantum decoherence, and quantum computers require significant error correction as they are far more prone to errors than classical computers.[10][11]



Any computational problem that can be solved by a classical computer can also, in principle, be solved by a quantum computer. Conversely, quantum computers obey the Church–Turing thesis; that is, any computational problem that can be solved by a quantum computer can also be solved by a classical computer. While this means that quantum computers provide no additional advantages over classical computers in terms of computability, they do in theory enable the design of algorithms for certain problems that have significantly lower time complexities than known classical algorithms. Notably, quantum computers are believed to be able to quickly solve certain problems that no classical computer could solve in any feasible amount of time—a feat known as "quantum supremacy." The study of the computational complexity of problems with respect to quantum computers is known as quantum complexity theory.


Quantum operations

The Bloch sphere is a representation of a qubit, the fundamental building block of quantum computers.


The prevailing model of quantum computation describes the computation in terms of a network of quantum logic gates.[12]


A memory consisting of [math]\displaystyle{ n }[/math] bits of information has [math]\displaystyle{ 2^n }[/math] possible states. A vector representing all memory states thus has [math]\displaystyle{ 2^n }[/math] entries (one for each state). This vector is viewed as a probability vector and represents the fact that the memory is to be found in a particular state.


In the classical view, one entry would have a value of 1 (i.e. a 100% probability of being in this state) and all other entries would be zero.

In quantum mechanics, probability vectors are generalized to density operators. This is the technically rigorous mathematical foundation for quantum logic gates, but the intermediate quantum state vector formalism is usually introduced first because it is conceptually simpler. This article focuses on the quantum state vector formalism for simplicity.


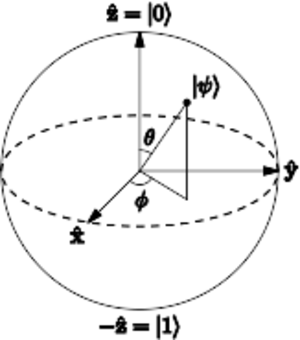
We begin by considering a simple memory consisting of only one bit. This memory may be found in one of two states: the zero state or the one state. We may represent the state of this memory using Dirac notation so that

[math]\displaystyle{ |0\rangle := \begin{pmatrix} 1 \\ 0 \end{pmatrix};\quad |1\rangle := \begin{pmatrix} 0 \\ 1 \end{pmatrix} }[/math]

A quantum memory may then be found in any quantum superposition [math]\displaystyle{ |\psi\rangle }[/math] of the two classical states [math]\displaystyle{ |0\rangle }[/math] and [math]\displaystyle{ |1\rangle }[/math]:

[math]\displaystyle{ |\psi\rangle := \alpha\,|0\rangle + \beta\,|1\rangle = \begin{pmatrix} \alpha \\ \beta \end{pmatrix};\quad |\alpha|^2 + |\beta|^2 = 1. }[/math]

In general, the coefficients [math]\displaystyle{ \alpha }[/math] and [math]\displaystyle{ \beta }[/math] are complex numbers. In this scenario, one qubit of information is said to be encoded into the quantum memory. The state [math]\displaystyle{ |\psi\rangle }[/math] is not itself a probability vector but can be connected with a probability vector via a measurement operation. If the quantum memory is measured to determine if the state is [math]\displaystyle{ |0\rangle }[/math] or [math]\displaystyle{ |1\rangle }[/math] (this is known as a computational basis measurement), the zero state would be observed with probability [math]\displaystyle{ |\alpha|^2 }[/math] and the one state with probability [math]\displaystyle{ |\beta|^2 }[/math]. The numbers [math]\displaystyle{ \alpha }[/math] and [math]\displaystyle{ \beta }[/math] are called quantum amplitudes.


The state of this one-qubit quantum memory can be manipulated by applying quantum logic gates, analogous to how classical memory can be manipulated with classical logic gates. One important gate for both classical and quantum computation is the NOT gate, which can be represented by a matrix

}}

[math]\displaystyle{ X := \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}. }[/math]

Mathematically, the application of such a logic gate to a quantum state vector is modelled with matrix multiplication. Thus [math]\displaystyle{ X|0\rangle = |1\rangle }[/math] and [math]\displaystyle{ X|1\rangle = |0\rangle }[/math].


The mathematics of single qubit gates can be extended to operate on multiqubit quantum memories in two important ways. One way is simply to select a qubit and apply that gate to the target qubit whilst leaving the remainder of the memory unaffected. Another way is to apply the gate to its target only if another part of the memory is in a desired state. These two choices can be illustrated using another example. The possible states of a two-qubit quantum memory are

[math]\displaystyle{ |00\rangle := \begin{pmatrix} 1 \\ 0 \\ 0 \\ 0 \end{pmatrix};\quad |01\rangle := \begin{pmatrix} 0 \\ 1 \\ 0 \\ 0 \end{pmatrix};\quad |10\rangle := \begin{pmatrix} 0 \\ 0 \\ 1 \\ 0 \end{pmatrix};\quad |11\rangle := \begin{pmatrix} 0 \\ 0 \\ 0 \\ 1 \end{pmatrix}. }[/math]

The CNOT gate can then be represented using the following matrix:

[math]\displaystyle{ CNOT := \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{pmatrix}. }[/math]

As a mathematical consequence of this definition, [math]\displaystyle{ CNOT|00\rangle = |00\rangle }[/math], [math]\displaystyle{ CNOT|01\rangle = |01\rangle }[/math], [math]\displaystyle{ CNOT|10\rangle = |11\rangle }[/math], and [math]\displaystyle{ CNOT|11\rangle = |10\rangle }[/math]. In other words, the CNOT applies a NOT gate ([math]\displaystyle{ X }[/math] from before) to the second qubit if and only if the first qubit is in the state [math]\displaystyle{ |1\rangle }[/math]. If the first qubit is [math]\displaystyle{ |0\rangle }[/math], nothing is done to either qubit.


In summary, a quantum computation can be described as a network of quantum logic gates and measurements. Any measurement can be deferred to the end of a quantum computation, though this deferment may come at a computational cost. Because of this possibility of deferring a measurement, most quantum circuits depict a network consisting only of quantum logic gates and no measurements. More information can be found in the following articles: universal quantum computer, Shor's algorithm, Grover's algorithm, Deutsch–Jozsa algorithm, amplitude amplification, quantum Fourier transform, quantum gate, quantum adiabatic algorithm and quantum error correction.


Any quantum computation can be represented as a network of quantum logic gates from a fairly small family of gates. A choice of gate family that enables this construction is known as a universal gate set. One common such set includes all single-qubit gates as well as the CNOT gate from above. This means any quantum computation can be performed by executing a sequence of single-qubit gates together with CNOT gates. Though this gate set is infinite, it can be replaced with a finite gate set by appealing to the Solovay-Kitaev theorem. The representation of multiple qubits can be shown as Qsphere.


Potential applications

Cryptography

Main article: Quantum cryptography

Integer factorization, which underpins the security of public key cryptographic systems, is believed to be computationally infeasible with an ordinary computer for large integers if they are the product of few prime numbers (e.g., products of two 300-digit primes).[13] By comparison, a quantum computer could efficiently solve this problem using Shor's algorithm to find its factors. This ability would allow a quantum computer to break many of the cryptographic systems in use today, in the sense that there would be a polynomial time (in the number of digits of the integer) algorithm for solving the problem. In particular, most of the popular public key ciphers are based on the difficulty of factoring integers or the discrete logarithm problem, both of which can be solved by Shor's algorithm. In particular, the RSA, Diffie–Hellman, and elliptic curve Diffie–Hellman algorithms could be broken. These are used to protect secure Web pages, encrypted email, and many other types of data. Breaking these would have significant ramifications for electronic privacy and security.


Lectures

讲座

However, other cryptographic algorithms do not appear to be broken by those algorithms.[14][15] Some public-key algorithms are based on problems other than the integer factorization and discrete logarithm problems to which Shor's algorithm applies, like the McEliece cryptosystem based on a problem in coding theory.[14][16] Lattice-based cryptosystems are also not known to be broken by quantum computers, and finding a polynomial time algorithm for solving the dihedral hidden subgroup problem, which would break many lattice based cryptosystems, is a well-studied open problem.[17] It has been proven that applying Grover's algorithm to break a symmetric (secret key) algorithm by brute force requires time equal to roughly 2n/2 invocations of the underlying cryptographic algorithm, compared with roughly 2n in the classical case,[18] meaning that symmetric key lengths are effectively halved: AES-256 would have the same security against an attack using Grover's algorithm that AES-128 has against classical brute-force search (see Key size).


Quantum cryptography could potentially fulfill some of the functions of public key cryptography. Quantum-based cryptographic systems could, therefore, be more secure than traditional systems against quantum hacking.[19]


Quantum search

Besides factorization and discrete logarithms, quantum algorithms offering a more than polynomial speedup over the best known classical algorithm have been found for several problems,[20] including the simulation of quantum physical processes from chemistry and solid state physics, the approximation of Jones polynomials, and solving Pell's equation. No mathematical proof has been found that shows that an equally fast classical algorithm cannot be discovered, although this is considered unlikely.[21] However, quantum computers offer polynomial speedup for some problems. The most well-known example of this is quantum database search, which can be solved by Grover's algorithm using quadratically fewer queries to the database than that are required by classical algorithms. In this case, the advantage is not only provable but also optimal, it has been shown that Grover's algorithm gives the maximal possible probability of finding the desired element for any number of oracle lookups. Several other examples of provable quantum speedups for query problems have subsequently been discovered, such as for finding collisions in two-to-one functions and evaluating NAND trees.[citation needed]


Problems that can be addressed with Grover's algorithm have the following properties:[citation needed]

  1. There is no searchable structure in the collection of possible answers,
  1. The number of possible answers to check is the same as the number of inputs to the algorithm, and
  1. There exists a boolean function which evaluates each input and determines whether it is the correct answer


Category:Models of computation

类别: 计算模型

For problems with all these properties, the running time of Grover's algorithm on a quantum computer will scale as the square root of the number of inputs (or elements in the database), as opposed to the linear scaling of classical algorithms. A general class of problems to which Grover's algorithm can be applied[22] is Boolean satisfiability problem. In this instance, the database through which the algorithm is iterating is that of all possible answers. An example (and possible) application of this is a password cracker that attempts to guess the password or secret key for an encrypted file or system. Symmetric ciphers such as Triple DES and AES are particularly vulnerable to this kind of attack.[citation needed] This application of quantum computing is a major interest of government agencies.[23]

Category:Quantum cryptography

类别: 量子密码学


Category:Information theory

范畴: 信息论

Quantum simulation

Category:Computational complexity theory

类别: 计算复杂性理论

Main article: Quantum simulator

Category:Classes of computers

类别: 电脑类别

Since chemistry and nanotechnology rely on understanding quantum systems, and such systems are impossible to simulate in an efficient manner classically, many believe quantum simulation will be one of the most important applications of quantum computing.[24] Quantum simulation could also be used to simulate the behavior of atoms and particles at unusual conditions such as the reactions inside a collider.[25]

Category:Theoretical computer science

类别: 理论计算机科学


Category:Open problems

类别: 开放性问题

Quantum annealing and adiabatic optimization

Category:Computer-related introductions in 1980

类别: 1980年与计算机有关的介绍

Quantum annealing or Adiabatic quantum computation relies on the adiabatic theorem to undertake calculations. A system is placed in the ground state for a simple Hamiltonian, which is slowly evolved to a more complicated Hamiltonian whose ground state represents the solution to the problem in question. The adiabatic theorem states that if the evolution is slow enough the system will stay in its ground state at all times through the process.

Category:Emerging technologies

类别: 新兴技术


This page was moved from wikipedia:en:Quantum computing. Its edit history can be viewed at 量子计算/edithistory

  1. ↑ 1.0 1.1 The National Academies of Sciences, Engineering, and Medicine (2019). Quantum Computing : Progress and Prospects (2018). Washington, DC: National Academies Press. p. I-5. doi:10.17226/25196. ISBN 978-0-309-47969-1. OCLC 1081001288. 
  2. ↑ Benioff, Paul (1980). "The computer as a physical system: A microscopic quantum mechanical Hamiltonian model of computers as represented by Turing machines". Journal of Statistical Physics. 22 (5): 563–591. Bibcode:1980JSP....22..563B. doi:10.1007/bf01011339. S2CID 122949592.
  3. ↑ Feynman, Richard (June 1982). "Simulating Physics with Computers" (PDF). International Journal of Theoretical Physics. 21 (6/7): 467–488. Bibcode:1982IJTP...21..467F. doi:10.1007/BF02650179. S2CID 124545445. Archived from the original (PDF) on 8 January 2019. Retrieved 28 February 2019.
  4. ↑ Manin, Yu. I. (1980) (in Russian). Vychislimoe i nevychislimoe. Sov.Radio. pp. 13–15. Archived from the original on 2013-05-10. https://web.archive.org/web/20130510173823/http://publ.lib.ru/ARCHIVES/M/MANIN_Yuriy_Ivanovich/Manin_Yu.I._Vychislimoe_i_nevychislimoe.(1980).%5Bdjv%5D.zip. Retrieved 2013-03-04. 
  5. ↑ 模板:Cite document
  6. ↑ John Preskill (2018). "Quantum Computing in the NISQ era and beyond". Quantum. 2: 79. arXiv:1801.00862. doi:10.22331/q-2018-08-06-79. S2CID 44098998.
  7. ↑ Gibney, Elizabeth (2 October 2019). "Quantum gold rush: the private funding pouring into quantum start-ups". Nature. 574 (7776): 22–24. Bibcode:2019Natur.574...22G. doi:10.1038/d41586-019-02935-4. PMID 31578480.
  8. ↑ Rodrigo, Chris Mills (12 February 2020). "Trump budget proposal boosts funding for artificial intelligence, quantum computing". The Hill.{{cite news}}: CS1 maint: url-status (link)
  9. ↑ "On "Quantum Supremacy"". IBM Research Blog (in English). 2019-10-22. Retrieved 2020-01-21.
  10. ↑ Franklin, Diana; Chong, Frederic T. (2004). "Challenges in Reliable Quantum Computing". Nano, Quantum and Molecular Computing. pp. 247–266. doi:10.1007/1-4020-8068-9_8. ISBN 1-4020-8067-0. 
  11. ↑ Pakkin, Scott; Coles, Patrick (10 June 2019). "The Problem with Quantum Computers". Scientific American.
  12. ↑ Nielsen, Michael A.; Chuang, Isaac L. (2010). Quantum Computation and Quantum Information: 10th Anniversary Edition. Cambridge: Cambridge University Press. doi:10.1017/cbo9780511976667. ISBN 9780511976667. http://cds.cern.ch/record/465953. 
  13. ↑ Lenstra, Arjen K. (2000). "Integer Factoring" (PDF). Designs, Codes and Cryptography. 19 (2/3): 101–128. doi:10.1023/A:1008397921377. S2CID 9816153. Archived from the original (PDF) on 2015-04-10.
  14. ↑ 14.0 14.1 Bernstein, Daniel J. (2009). "Introduction to post-quantum cryptography". Post-Quantum Cryptography. 549. pp. 1–14. doi:10.1007/978-3-540-88702-7_1. ISBN 978-3-540-88701-0. PMID 28905891. 
  15. ↑ See also pqcrypto.org, a bibliography maintained by Daniel J. Bernstein and Tanja Lange on cryptography not known to be broken by quantum computing.
  16. ↑ McEliece, R. J. (January 1978). "A Public-Key Cryptosystem Based On Algebraic Coding Theory" (PDF). DSNPR. 44: 114–116. Bibcode:1978DSNPR..44..114M.
  17. ↑ Kobayashi, H.; Gall, F.L. (2006). "Dihedral Hidden Subgroup Problem: A Survey". Information and Media Technologies. 1 (1): 178–185. doi:10.2197/ipsjdc.1.470.
  18. ↑ Bennett, Charles H.; Bernstein, Ethan; Brassard, Gilles; Vazirani, Umesh (October 1997). "Strengths and Weaknesses of Quantum Computing". SIAM Journal on Computing. 26 (5): 1510–1523. arXiv:quant-ph/9701001. Bibcode:1997quant.ph..1001B. doi:10.1137/s0097539796300933. S2CID 13403194.
  19. ↑ Katwala, Amit (5 March 2020). "Quantum computers will change the world (if they work)". Wired UK.
  20. ↑ Quantum Algorithm Zoo -{zh-cn:互联网档案馆; zh-tw:網際網路檔案館; zh-hk:互聯網檔案館;}-的存檔，存档日期2018-04-29. – Stephen Jordan's Homepage
  21. ↑ Schiller, Jon (2009-06-19). Quantum Computers. ISBN 9781439243497. https://books.google.com/books?id=l217ma2sWkoC&pg=PA11. 模板:Self-published inline
  22. ↑ Ambainis, Ambainis (June 2004). "Quantum search algorithms". ACM SIGACT News. 35 (2): 22–35. arXiv:quant-ph/0504012. Bibcode:2005quant.ph..4012A. doi:10.1145/992287.992296. S2CID 11326499.
  23. ↑ Rich, Steven; Gellman, Barton (2014-02-01). "NSA seeks to build quantum computer that could crack most types of encryption". Washington Post.
  24. ↑ Norton, Quinn (2007-02-15). "The Father of Quantum Computing". Wired.
  25. ↑ Ambainis, Andris (Spring 2014). "What Can We Do with a Quantum Computer?". Institute for Advanced Study.
取自“https://wiki.swarma.org/index.php?title=量子计算&oldid=16886”