自由度

此词条暂由彩云小译翻译，翻译字数共930，未经人工整理和审校，带来阅读不便，请见谅。

In physics and chemistry, a degree of freedom is an independent physical parameter in the formal description of the state of a physical system. The set of all states of a system is known as the system's phase space, and the degrees of freedom of the system are the dimensions of the phase space.

In physics and chemistry, a degree of freedom is an independent physical parameter in the formal description of the state of a physical system. The set of all states of a system is known as the system's phase space, and the degrees of freedom of the system are the dimensions of the phase space.

在物理学和化学中，自由度是物理系统状态形式描述中一个独立的物理参数。系统所有状态的集合称为系统的相空间，系统的自由度称为系统的相空间的维数。

The location of a particle in three-dimensional space requires three position coordinates. Similarly, the direction and speed at which a particle moves can be described in terms of three velocity components, each in reference to the three dimensions of space. If the time evolution of the system is deterministic, where the state at one instant uniquely determines its past and future position and velocity as a function of time, such a system has six degrees of freedom.^{[citation needed]} If the motion of the particle is constrained to a lower number of dimensions – for example, the particle must move along a wire or on a fixed surface – then the system has fewer than six degrees of freedom. On the other hand, a system with an extended object that can rotate or vibrate can have more than six degrees of freedom.

The location of a particle in three-dimensional space requires three position coordinates. Similarly, the direction and speed at which a particle moves can be described in terms of three velocity components, each in reference to the three dimensions of space. If the time evolution of the system is deterministic, where the state at one instant uniquely determines its past and future position and velocity as a function of time, such a system has six degrees of freedom. If the motion of the particle is constrained to a lower number of dimensions – for example, the particle must move along a wire or on a fixed surface – then the system has fewer than six degrees of freedom. On the other hand, a system with an extended object that can rotate or vibrate can have more than six degrees of freedom.

粒子在三维空间中的位置需要3个位置坐标。同样，粒子运动的方向和速度可以用三个速度分量来描述，每个分量都参照空间的三个维度。如果系统的时间演化是确定的，状态在某一时刻唯一地决定了它的过去和未来的位置和速度作为时间的函数，这样的系统有六个自由度。如果粒子的运动被限制在较低的维数上——例如，粒子必须沿着导线或在固定的表面上运动——那么系统的自由度就少于6度。另一方面，一个系统与一个扩展的对象，可以旋转或振动可以有六个以上的自由度。

In classical mechanics, the state of a point particle at any given time is often described with position and velocity coordinates in the Lagrangian formalism, or with position and momentum coordinates in the Hamiltonian formalism.

在经典力学中，一个点粒子在任意给定时间的状态通常用拉格朗日公式中的位置和速度坐标来描述，或者用哈密顿公式中的位置和动量坐标来描述。

In statistical mechanics, a degree of freedom is a single scalar number describing the microstate of a system.^[1] The specification of all microstates of a system is a point in the system's phase space.

In statistical mechanics, a degree of freedom is a single scalar number describing the microstate of a system.

在统计力学中，一个自由度是描述系统微观状态的单个标量数。

In the 3D ideal chain model in chemistry, two angles are necessary to describe the orientation of each monomer.

{ | class = “ wikitable” It is often useful to specify quadratic degrees of freedom. These are degrees of freedom that contribute in a quadratic function to the energy of the system. In three-dimensional space, three degrees of freedom are associated with the movement of a particle. A diatomic gas molecule has 6 degrees of freedom模板:Dubious. This set may be decomposed in terms of translations, rotations, and vibrations of the molecule. The center of mass motion of the entire molecule accounts for 3 degrees of freedom. In addition, the molecule has two rotational degrees of motion and one模板:Dubious vibrational mode. The rotations occur around the two axes perpendicular to the line between the two atoms. The rotation around the atom–atom bond is not a physical rotation模板:Dubious. This yields, for a diatomic molecule, a decomposition of:

For a body consisting of 2 particles (ex. a diatomic molecule) in a 3-D space with constant distance between them (let's say d) we can show (below) its degrees of freedom to be 5.

Vibrational temperatures are between 10³ K and 10⁴ K.^[1]

Monatomic

单原子的

Gas molecules

Linear molecules

线性分子

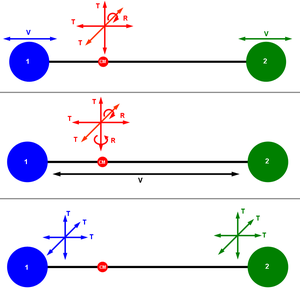Different ways of visualizing the 6 degrees of freedom of a diatomic molecule. (CM: center of mass of the system, T: translational motion, R: rotational motion, V: vibrational motion.)

Non-linear molecules

非线性分子

Translation (, , and )

翻译(，，和)

[math]\displaystyle{ N = 6 = 3 + 2 + 1. }[/math]

3

For a general, non-linear molecule, all 3 rotational degrees of freedom are considered, resulting in the decomposition:

3

[math]\displaystyle{ 3N = 3 + 3 + (3N - 6) }[/math]

Rotation (, , and )

旋转(、和)

which means that an $N$ -atom molecule has $3 N - 6$ vibrational degrees of freedom for $N > 2$ . In special cases, such as adsorbed large molecules, the rotational degrees of freedom can be limited to only one.^[2]

0

2

As defined above one can also count degrees of freedom using the minimum number of coordinates required to specify a position. This is done as follows:

3

For a single particle we need 2 coordinates in a 2-D plane to specify its position and 3 coordinates in 3-D space. Thus its degree of freedom in a 3-D space is 3.

Total (disregarding Vibration at room temperatures)

总计(不包括室温下的振动)

Let's say one particle in this body has coordinate $(x 1, y 1, z 1)$ and the other has coordinate $(x 2, y 2, z 2)$ with $z 2$ unknown. Application of the formula for distance between two coordinates

3

[math]\displaystyle{ d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2+(z_2-z_1)^2} }[/math]

5

results in one equation with one unknown, in which we can solve for $z 2$ .

6

One of $x 1$ , $x 2$ , $y 1$ , $y 2$ , $z 1$ , or $z 2$ can be unknown.

Vibration

震动

Contrary to the classical equipartition theorem, at room temperature, the vibrational motion of molecules typically makes negligible contributions to the heat capacity. This is because these degrees of freedom are frozen because the spacing between the energy eigenvalues exceeds the energy corresponding to ambient temperatures ( $k B T$ ). In the following table such degrees of freedom are disregarded because of their low effect on total energy. Then only the translational and rotational degrees of freedom contribute, in equal amounts, to the heat capacity ratio. This is why $γ$ = $模板:Sfrac$ for monatomic gases and $γ$ = $模板:Sfrac$ for diatomic gases at room temperature.

0

However, at very high temperatures, on the order of the vibrational temperature (Θ_vib), vibrational motion cannot be neglected.

Total (including Vibration)

总数(包括振动)

3

3N	3N
3N	3N

! Monatomic

! Linear molecules

! Non-linear molecules

The set of degrees of freedom of a system is independent if the energy associated with the set can be written in the following form:

系统的自由度集合是独立的，如果与该自由度集合相关的能量可以写成下列形式:

|-

[math]\displaystyle{ E = \sum_{i=1}^N E_i(X_i), }[/math]

[数学] ，[数学]

| Translation ( $x$ , $y$ , and $z$ )

| align="center" | 3

where is a function of the sole variable .

这里是唯一变量的函数。

| align="center" | 3

example: if and are two degrees of freedom, and is the associated energy:

例如: 如果和是两个自由度，关联的能量是:

|-

If [math]\displaystyle{ E = X_1^4 + X_2^4 }[/math], then the two degrees of freedom are independent.

如果 < math > e = x _ 1 ^ 4 + x _ 2 ^ 4 </math > ，那么这两个自由度是独立的。

| Rotation ( $x$ , $y$ , and $z$ )

If [math]\displaystyle{ E = X_1^4 + X_1 X_2 + X_2^4 }[/math], then the two degrees of freedom are not independent. The term involving the product of and is a coupling term that describes an interaction between the two degrees of freedom.

如果 < math > e = x 1 ^ 4 + x 1 x 2 + x 2 ^ 4 </math > ，那么这两个自由度不是独立的。包含和乘积的术语是描述两个自由度之间相互作用的耦合术语。

| align="center" | 0

| align="center" | 2

For from 1 to , the value of the th degree of freedom is distributed according to the Boltzmann distribution. Its probability density function is the following:

对于从1到1，第四自由度的值是按照美国波兹曼分布协会的标准分配的。它的概率密度函数如下:

| align="center" | 3

[math]\displaystyle{ p_i(X_i) = \frac{e^{-\frac{E_i}{k_B T}}}{\int dX_i \, e^{-\frac{E_i}{k_B T}}} }[/math],

[数学][数学]

|-

| Total (disregarding Vibration at room temperatures)

In this section, and throughout the article the brackets [math]\displaystyle{ \langle \rangle }[/math] denote the mean of the quantity they enclose.

在本节中，整篇文章中括号 < math > langle rangle </math > 表示它们所包含的量的平均值。

| align="center" | 3

| align="center" | 5

The internal energy of the system is the sum of the average energies associated with each of the degrees of freedom:

系统的内能是与每个自由度有关的平均能量之和:

| align="center" | 6

[math]\displaystyle{ \langle E \rangle = \sum_{i=1}^N \langle E_i \rangle. }[/math]

数学，数学，数学

|-

| Vibration

| align="center" | 0

A degree of freedom is quadratic if the energy terms associated with this degree of freedom can be written as

如果与这个自由度相关的能量项可以写成二次方程，则该自由度为二次方程

| align="center" | $3 N - 5$

[math]\displaystyle{ E = \alpha_i\,\,X_i^2 + \beta_i \,\, X_i Y }[/math],

数学 e = alpha _ i，，x _ i ^ 2 + beta _ i，，x _ i y,

| align="center" | $3 N - 6$

|-

where is a linear combination of other quadratic degrees of freedom.

其他二次自由度的线性组合。

| Total (including Vibration)

| align="center" | 3

example: if and are two degrees of freedom, and is the associated energy:

例如: 如果和是两个自由度，关联的能量是:

| align="center" | 3N

If [math]\displaystyle{ E = X_1^4 + X_1^3 X_2 + X_2^4 }[/math], then the two degrees of freedom are not independent and non-quadratic.

如果 < math > e = x _ 1 ^ 4 + x _ 1 ^ 3 x _ 2 + x _ 2 ^ 4 </math > ，那么这两个自由度不是独立的和非二次的。

| align="center" | 3N

If [math]\displaystyle{ E = X_1^4 + X_2^4 }[/math], then the two degrees of freedom are independent and non-quadratic.

如果 < math > e = x _ 1 ^ 4 + x _ 2 ^ 4 </math > ，那么这两个自由度是独立的和非二次的。

|}

If [math]\displaystyle{ E = X_1^2 + X_1 X_2 + 2X_2^2 }[/math], then the two degrees of freedom are not independent but are quadratic.

如果 < math > e = x 1 ^ 2 + x 1 x 2 + 2 x 2 ^ 2 </math > ，那么这两个自由度不是独立的，而是二次的。

If [math]\displaystyle{ E = X_1^2 + 2X_2^2 }[/math], then the two degrees of freedom are independent and quadratic.

如果 < math > e = x _ 1 ^ 2 + 2 x _ 2 ^ 2 </math > ，那么这两个自由度是独立的和二次的。

Independent degrees of freedom

The set of degrees of freedom $X 1, ... , X N$ of a system is independent if the energy associated with the set can be written in the following form:

For example, in Newtonian mechanics, the dynamics of a system of quadratic degrees of freedom are controlled by a set of homogeneous linear differential equations with constant coefficients.

例如，在牛顿运动定律，二次自由度系统的动力学是由一组常系数齐次线性微分方程组控制的。

[math]\displaystyle{ E = \sum_{i=1}^N E_i(X_i), }[/math]

where $E i$ is a function of the sole variable $X i$ .

are quadratic and independent degrees of freedom if the energy associated with a microstate of the system they represent can be written as:

是二次自由度和独立自由度，如果与它们所代表的系统的微观状态相关的能量可以写成:

[math]\displaystyle{ E = \sum_{i=1}^N \alpha_i X_i^2 }[/math]

< math > e = sum { i = 1} ^ n alpha _ i x _ i ^ 2

example: if $X 1$ and $X 2$ are two degrees of freedom, and $E$ is the associated energy:

If [math]\displaystyle{ E = X_1^4 + X_2^4 }[/math], then the two degrees of freedom are independent.

If [math]\displaystyle{ E = X_1^4 + X_1 X_2 + X_2^4 }[/math], then the two degrees of freedom are not independent. The term involving the product of $X 1$ and $X 2$ is a coupling term that describes an interaction between the two degrees of freedom.

In the classical limit of statistical mechanics, at thermodynamic equilibrium, the internal energy of a system of quadratic and independent degrees of freedom is:

在统计力学的经典极限下，在热力学平衡，一个二次独立自由度系统的内能是:

[math]\displaystyle{ U = \langle E \rangle = N\,\frac{k_B T}{2} }[/math]

[数学] u = langle e rangle = n，frac { k _ b t }{2}[数学]

For $i$ from 1 to $N$ , the value of the $i$ th degree of freedom $X i$ is distributed according to the Boltzmann distribution. Its probability density function is the following:

[math]\displaystyle{ p_i(X_i) = \frac{e^{-\frac{E_i}{k_B T}}}{\int dX_i \, e^{-\frac{E_i}{k_B T}}} }[/math],

Here, the mean energy associated with a degree of freedom is:

在这里，与一定自由度相关的平均能是:

[math]\displaystyle{ \langle E_i \rangle = \int dX_i\,\,\alpha_i X_i^2\,\, p_i(X_i) = \frac{\int dX_i\,\,\alpha_i X_i^2\,\, e^{-\frac{\alpha_i X_i^2}{k_B T}}}{\int dX_i\,\, e^{-\frac{\alpha_i X_i^2}{k_B T}}} }[/math]

2，，p _ i (xi) = frac { int dX _ i，，alpha _ i x _ i ^ 2，，e ^ {-frac { alpha _ i x _ i ^ 2，，e ^ {-frac { i x _ i ^ 2}}{ k _ b t }}{ int dX _ i，e ^ {-frac { alpha _ i x _ i ^ 2}}{ k _ b _ i，e ^ {-frac { i x _ i ^ 2}{ k _ b _ t }} </math >

In this section, and throughout the article the brackets [math]\displaystyle{ \langle \rangle }[/math] denote the mean of the quantity they enclose.

[math]\displaystyle{ \langle E_i \rangle = \frac{k_B T}{2}\frac{\int dx\,\,x^2\,\, e^{-\frac{x^2}{2}}}{\int dx\,\, e^{-\frac{x^2}{2}}} = \frac{k_B T}{2} }[/math]

2} frac { k _ b }{ int dx，，x ^ 2，，e ^ {-frac { x ^ 2}{2}}}{ int dx，，e ^ {-frac { x ^ 2}{2}}}{ e ^ {-frac { x ^ 2}{2}}}}} = frac { k _ b }{2}{2} </math >

The internal energy of the system is the sum of the average energies associated with each of the degrees of freedom:

Since the degrees of freedom are independent, the internal energy of the system is equal to the sum of the mean energy associated with each degree of freedom, which demonstrates the result.

由于自由度是独立的，系统的内能等于与每个自由度相关的平均能量之和，从而证明了这一结果。

[math]\displaystyle{ \langle E \rangle = \sum_{i=1}^N \langle E_i \rangle. }[/math]

Quadratic degrees of freedom

The description of a system's state as a point in its phase space, although mathematically convenient, is thought to be fundamentally inaccurate. In quantum mechanics, the motion degrees of freedom are superseded with the concept of wave function, and operators which correspond to other degrees of freedom have discrete spectra. For example, intrinsic angular momentum operator (which corresponds to the rotational freedom) for an electron or photon has only two eigenvalues. This discreteness becomes apparent when action has an order of magnitude of the Planck constant, and individual degrees of freedom can be distinguished.

将一个系统的状态描述为其相空间中的一个点，虽然在数学上很方便，但被认为是根本不准确的。在量子力学中，运动自由度被波函数的概念所取代，相应于其他自由度的运算符具有离散谱。例如，一个电子或光子的内禀角动量算符(相当于转动自由度)只有两个本征值。当作用力的数量级为普朗克常数时，这种离散性就变得明显，个体自由度也可以区分开来。

A degree of freedom $X i$ is quadratic if the energy terms associated with this degree of freedom can be written as

[math]\displaystyle{ E = \alpha_i\,\,X_i^2 + \beta_i \,\, X_i Y }[/math],

where $Y$ is a linear combination of other quadratic degrees of freedom.

example: if $X 1$ and $X 2$ are two degrees of freedom, and $E$ is the associated energy:

If [math]\displaystyle{ E = X_1^4 + X_1^3 X_2 + X_2^4 }[/math], then the two degrees of freedom are not independent and non-quadratic.

If [math]\displaystyle{ E = X_1^4 + X_2^4 }[/math], then the two degrees of freedom are independent and non-quadratic.

If [math]\displaystyle{ E = X_1^2 + X_1 X_2 + 2X_2^2 }[/math], then the two degrees of freedom are not independent but are quadratic.

If [math]\displaystyle{ E = X_1^2 + 2X_2^2 }[/math], then the two degrees of freedom are independent and quadratic.

For example, in Newtonian mechanics, the dynamics of a system of quadratic degrees of freedom are controlled by a set of homogeneous linear differential equations with constant coefficients.

Quadratic and independent degree of freedom

Category:Concepts in physics

分类: 物理概念

$X 1, ... , X N$ are quadratic and independent degrees of freedom if the energy associated with a microstate of the system they represent can be written as:

Category:Dimension

类别: 维度

This page was moved from wikipedia:en:Degrees of freedom (physics and chemistry). Its edit history can be viewed at 自由度/edithistory

↑ ^1.0 ^1.1 Reif, F. (2009). Fundamentals of Statistical and Thermal Physics. Long Grove, IL: Waveland Press, Inc.. p. 51. ISBN 1-57766-612-7.
↑ Waldmann, Thomas; Klein, Jens; Hoster, Harry E.; Behm, R. Jürgen (2013). "Stabilization of Large Adsorbates by Rotational Entropy: A Time-Resolved Variable-Temperature STM Study". ChemPhysChem. 14 (1): 162–9. doi:10.1002/cphc.201200531. PMID 23047526.

[:0-1] 1.0 ^1.1 Reif, F. (2009). Fundamentals of Statistical and Thermal Physics. Long Grove, IL: Waveland Press, Inc.. p. 51. ISBN 1-57766-612-7.

[2] Waldmann, Thomas; Klein, Jens; Hoster, Harry E.; Behm, R. Jürgen (2013). "Stabilization of Large Adsorbates by Rotational Entropy: A Time-Resolved Variable-Temperature STM Study". ChemPhysChem. 14 (1): 162–9. doi:10.1002/cphc.201200531. PMID 23047526.

[1]

[2]