自由能原理

来自集智百科 - 复杂系统|人工智能|复杂科学|复杂网络|自组织
Moonscar（讨论 | 贡献）2020年10月25日 (日) 17:53的版本 （Moved page from wikipedia:en:Free energy principle (history)）
跳到导航 跳到搜索

此词条暂由彩云小译翻译，翻译字数共282，未经人工整理和审校，带来阅读不便，请见谅。

The free energy principle is a formal statement that explains how living and non-living systems remain in non-equilibrium steady-states by restricting themselves to a limited number of states.[1] It establishes that systems minimise a free energy function of their internal states, which entail beliefs about hidden states in their environment. The implicit minimisation of free energy is formally related to variational Bayesian methods and was originally introduced by Karl Friston as an explanation for embodied perception in neuroscience,[2] where it is also known as active inference.

The free energy principle is a formal statement that explains how living and non-living systems remain in non-equilibrium steady-states by restricting themselves to a limited number of states.

自由能原理是一个正式的陈述，它解释了生物系统和非生物系统如何通过将自己限制在有限的几个状态而保持在非平衡稳态。


The free energy principle explains the existence of a given system by modeling it through a Markov blanket that tries to minimize the difference between their model of the world and their sense and associated perception. This difference can be described as "surprise" and is minimized by continuous correction of the world model of the system. As such, the principle is based on the Bayesian idea of the brain as an “inference engine”. Friston added a second route to minimization: action. By actively changing the world into the expected state, systems can also minimize the free energy of the system. Friston assumes this to be the principle of all biological reaction.[3] Friston also believes his principle applies to mental disorders as well as to artificial intelligence. AI implementations based on the active inference principle have shown advantages over other methods.[3]

The free energy principle has been criticized for being very difficult to understand, even for experts. However, this means that internal states must also minimise free energy, because free energy is a function of sensory and internal states:

自由能原理被批评为很难理解，即使是专家也难以理解。然而，这意味着内部状态也必须最小化自由能，因为自由能是感官和内部状态的函数:


The free energy principle has been criticized for being very difficult to understand, even for experts.[4] Discussions of the principle have also been criticized as invoking metaphysical assumptions far removed from a testable scientific prediction, making the principle unfalsifiable.[5] In a 2018 interview, Friston acknowledged that the free energy principle is not properly falsifiable: "the free energy principle is what it is — a principle. Like Hamilton’s Principle of Stationary Action, it cannot be falsified. It cannot be disproven. In fact, there’s not much you can do with it, unless you ask whether measurable systems conform to the principle."[6] 

[math]\displaystyle{   a(t) = \underset{a}{\operatorname{arg\,min}}   \{ F(s(t),\mu(t)) \} }[/math]

[ math > a (t) = underset { a }{ operatorname { arg，min }{ f (s (t) ，mu (t))}} </math > 


[math]\displaystyle{ \mu(t) = \underset{\mu}{\operatorname{arg\,min}} \{ F(s(t),\mu)) \}   }[/math]

[ math > mu (t) = underset { mu }{ operatorname { arg，min }{ f (s (t) ，mu)}} </math >

Background

[math]\displaystyle{ \underset{\mathrm{free-energy}} {\underbrace{F(s,\mu)}} = \underset{\mathrm{energy}} {\underbrace{ E_q[-\log p(s,\psi \mid m)]}} - \underset{\mathrm{entropy}} {\underbrace{ H[q(\psi \mid \mu)]}}

{ underbrace { f (s，mu)} = underset { mathrm { energy }{ underbrace { e _ q [-log p (s，psi mid m)]}}-underset { mathrm { entropy }{ underbrace { h (psi mid mu)]}}}

The notion that [[self-organisation|self-organising]] biological systems – like a cell or brain – can be understood as minimising variational free energy is based upon [[Hermann von Helmholtz|Helmholtz]]’s work on [[unconscious inference]]\lt ref name="Helmholtz"\gt Helmholtz, H. (1866/1962). Concerning the perceptions in general. In Treatise on physiological optics (J. Southall, Trans., 3rd ed., Vol. III). New York: Dover.\lt /ref\gt   and subsequent treatments in psychology\lt ref\gt {{cite journal | title=Perceptions as hypotheses | journal=Philosophical Transactions of the Royal Society of London. B, Biological Sciences | publisher=The Royal Society | volume=290 | issue=1038 | date=1980-07-08 | issn=0080-4622 | doi=10.1098/rstb.1980.0090 | pmid=6106237 | bibcode=1980RSPTB.290..181G | pages=181–197|jstor=2395424| last1=Gregory | first1=R. L. | doi-access=free }}\lt /ref\gt  and machine learning.\lt ref name="Dayan"\gt {{cite journal | last1=Dayan | first1=Peter | last2=Hinton | first2=Geoffrey E. | last3=Neal | first3=Radford M. | last4=Zemel | first4=Richard S. | title=The Helmholtz Machine | journal=Neural Computation | publisher=MIT Press - Journals | volume=7 | issue=5 | year=1995 | issn=0899-7667 | doi=10.1162/neco.1995.7.5.889 | pmid=7584891 | pages=889–904| s2cid=1890561 |url=http://www.gatsby.ucl.ac.uk/~dayan/papers/hm95.pdf}}\lt /ref\gt  Variational free energy is a function of observations and a probability density over their hidden causes. This [[Calculus of variations|variational]] density is defined in relation to a probabilistic model that generates predicted observations from hypothesized causes. In this setting, free energy provides an approximation to [[Marginal likelihood|Bayesian model evidence]].\lt ref\gt Beal, M. J. (2003). [http://www.cse.buffalo.edu/faculty/mbeal/papers/beal03.pdf Variational Algorithms for Approximate Bayesian Inference]. Ph.D. Thesis, University College London.\lt /ref\gt  Therefore, its minimisation can be seen as a Bayesian inference process. When a system actively makes observations to minimise free energy, it implicitly performs active inference and maximises the evidence for its model of the world.

= \underset{\mathrm{surprise}} {\underbrace{ -\log p(s \mid m)}} + \underset{\mathrm{divergence}} {\underbrace{ D_{\mathrm{KL}}[q(\psi \mid \mu) \parallel p(\psi \mid s,m)]}} 

= underset { mathrm { surprise }{ underbrace {-log p (mid m)} + underset { mathrm {散度}{ underbrace { d _ { mathrm { KL }}[ q (psi mid mu) parallel p (psi mid s，m)]}}



  \geq \underset{\mathrm{surprise}} {\underbrace{ -\log p(s \mid m)}}  }[/math]

下集{ mathrm { surprise }{ underbrace {-log p (s mid m)}}} </math >

However, free energy is also an upper bound on the self-information of outcomes, where the long-term average of surprise is entropy. This means that if a system acts to minimise free energy, it will implicitly place an upper bound on the entropy of the outcomes – or sensory states – it samples.[7][8]模板:Better source


This induces a dual minimisation with respect to action and internal states that correspond to action and perception respectively.

这导致了对行为和内在状态的双重最小化，这两种状态分别对应于行为和感知。

Relationship to other theories

Active inference is closely related to the good regulator theorem[9] and related accounts of self-organisation,[10][11] such as self-assembly, pattern formation, autopoiesis[12] and practopoiesis[13]. It addresses the themes considered in cybernetics, synergetics[14] and embodied cognition. Because free energy can be expressed as the expected energy of observations under the variational density minus its entropy, it is also related to the maximum entropy principle.[15] Finally, because the time average of energy is action, the principle of minimum variational free energy is a principle of least action.


Definition

Free energy minimisation has been proposed as a hallmark of self-organising systems when cast as random dynamical systems. This relates free energy minimization to the principle of minimum redundancy and provides a normative (Bayesian) theory of neuronal processing. The associated process theory of neuronal dynamics is based on minimising free energy through gradient descent. This corresponds to generalised Bayesian filtering (where ~ denotes a variable in generalised coordinates of motion and [math]\displaystyle{ D }[/math] is a derivative matrix operator): this corresponds to optimizing the excitability of superficial pyramidal cells and has been interpreted in terms of attentional gain. action selection, consciousness, hysteria and psychosis. Explanations of action in active inference often depend on the idea that the brain has 'stubborn predictions' which it cannot update, leading to actions that cause these predictions to come true.

自由能最小化已被提出作为自组织系统的标志时，铸造为随机动态系统。这将自由能最小化原则与最小冗余原则联系起来，为神经元处理提供了一个规范的(贝叶斯)理论。神经动力学的相关过程理论是基于通过梯度下降法最小化自由能。这相当于一般化的贝叶斯滤波(其中 ~ 表示一个变量在一般化的运动坐标和 < math > d </math > 是一个导数矩阵运算符) : 这相当于优化表面锥体细胞的兴奋性，并被解释为注意增益。行为选择，意识，歇斯底里和精神病。对主动推理中行为的解释往往依赖于这样一种观点，即大脑具有无法更新的“顽固预测” ，导致这些预测成为现实的行为。


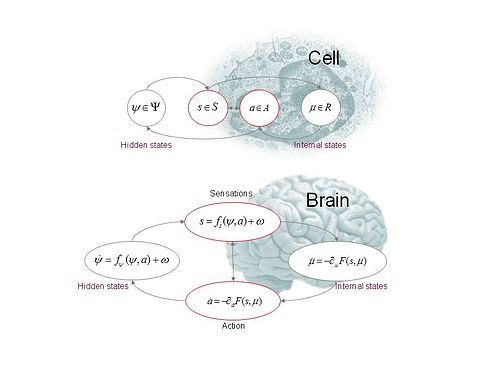
These schematics illustrate the partition of states into internal and hidden or external states that are separated by a Markov blanket – comprising sensory and active states. The lower panel shows this partition as it would be applied to action and perception in the brain; where active and internal states minimise a free energy functional of sensory states. The ensuing self-organisation of internal states then correspond perception, while action couples brain states back to external states. The upper panel shows exactly the same dependencies but rearranged so that the internal states are associated with the intracellular states of a cell, while the sensory states become the surface states of the cell membrane overlying active states (e.g., the actin filaments of the cytoskeleton).


Definition (continuous formulation): Active inference rests on the tuple [math]\displaystyle{ (\Omega,\Psi,S,A,R,q,p) }[/math],

  • A sample space [math]\displaystyle{ \Omega }[/math] – from which random fluctuations [math]\displaystyle{ \omega \in \Omega }[/math] are drawn
  • Hidden or external states [math]\displaystyle{ \Psi:\Psi\times A \times \Omega \to \mathbb{R} }[/math] – that cause sensory states and depend on action
  • Sensory states [math]\displaystyle{ S:\Psi \times A \times \Omega \to \mathbb{R} }[/math] – a probabilistic mapping from action and hidden states
  • Action [math]\displaystyle{ A:S\times R \to \mathbb{R} }[/math] – that depends on sensory and internal states
  • Internal states [math]\displaystyle{ R:R\times S \to \mathbb{R} }[/math] – that cause action and depend on sensory states
  • Generative density [math]\displaystyle{ p(s, \psi \mid m) }[/math] – over sensory and hidden states under a generative model [math]\displaystyle{ m }[/math]
  • Variational density [math]\displaystyle{ q(\psi \mid \mu) }[/math] – over hidden states [math]\displaystyle{ \psi \in \Psi }[/math] that is parameterised by internal states [math]\displaystyle{ \mu \in R }[/math]


Action and perception

The objective is to maximise model evidence [math]\displaystyle{ p(s\mid m) }[/math] or minimise surprise [math]\displaystyle{ -\log p(s\mid m) }[/math]. This generally involves an intractable marginalisation over hidden states, so surprise is replaced with an upper variational free energy bound.[16] However, this means that internal states must also minimise free energy, because free energy is a function of sensory and internal states:


[math]\displaystyle{ a(t) = \underset{a}{\operatorname{arg\,min}} \{ F(s(t),\mu(t)) \} }[/math]
[math]\displaystyle{ \mu(t) = \underset{\mu}{\operatorname{arg\,min}} \{ F(s(t),\mu)) \} }[/math]


[math]\displaystyle{ \underset{\mathrm{free-energy}} {\underbrace{F(s,\mu)}} = \underset{\mathrm{energy}} {\underbrace{ E_q[-\log p(s,\psi \mid m)]}} - \underset{\mathrm{entropy}} {\underbrace{ H[q(\psi \mid \mu)]}} = \underset{\mathrm{surprise}} {\underbrace{ -\log p(s \mid m)}} + \underset{\mathrm{divergence}} {\underbrace{ D_{\mathrm{KL}}[q(\psi \mid \mu) \parallel p(\psi \mid s,m)]}} \geq \underset{\mathrm{surprise}} {\underbrace{ -\log p(s \mid m)}} }[/math]


This induces a dual minimisation with respect to action and internal states that correspond to action and perception respectively.


Free energy minimisation

Category:Biological systems

类别: 生物系统


Category:Systems theory

范畴: 系统论

Free energy minimisation and self-organisation

Category:Computational neuroscience

类别: 计算神经科学


Category:Mathematical and theoretical biology

类别: 数学和理论生物学


This page was moved from wikipedia:en:Free energy principle. Its edit history can be viewed at 自由能原理/edithistory

  1. ↑ Ashby, W. R. (1962). Principles of the self-organizing system.in Principles of Self-Organization: Transactions of the University of Illinois Symposium, H. Von Foerster and G. W. Zopf, Jr. (eds.), Pergamon Press: London, UK, pp. 255–278.
  2. ↑ Friston, Karl; Kilner, James; Harrison, Lee (2006). "A free energy principle for the brain" (PDF). Journal of Physiology-Paris. Elsevier BV. 100 (1–3): 70–87. doi:10.1016/j.jphysparis.2006.10.001. ISSN 0928-4257. PMID 17097864. S2CID 637885.
  3. ↑ 3.0 3.1 Shaun Raviv: The Genius Neuroscientist Who Might Hold the Key to True AI. In: Wired, 13. November 2018
  4. ↑ Freed, Peter (2010). "Research Digest". Neuropsychoanalysis. Informa UK Limited. 12 (1): 103–106. doi:10.1080/15294145.2010.10773634. ISSN 1529-4145. S2CID 220306712.
  5. ↑ Colombo, Matteo; Wright, Cory (2018-09-10). "First principles in the life sciences: the free-energy principle, organicism, and mechanism". Synthese. Springer Science and Business Media LLC. doi:10.1007/s11229-018-01932-w. ISSN 0039-7857.
  6. ↑ Friston, Karl (2018). "Of woodlice and men: A Bayesian account of cognition, life and consciousness. An interview with Karl Friston (by Martin Fortier & Daniel Friedman)". ALIUS Bulletin. 2: 17–43.
  7. ↑ Karl, Friston (2012-10-31). "A Free Energy Principle for Biological Systems" (PDF). Entropy. MDPI AG. 14 (11): 2100–2121. Bibcode:2012Entrp..14.2100K. doi:10.3390/e14112100. ISSN 1099-4300. PMC 3510653. PMID 23204829.
  8. ↑ Colombo, Matteo; Wright, Cory (2018-09-10). "First principles in the life sciences: the free-energy principle, organicism, and mechanism". Synthese. Springer Science and Business Media LLC. doi:10.1007/s11229-018-01932-w. ISSN 0039-7857.
  9. ↑ Conant, R. C., & Ashby, R. W. (1970). Every Good Regulator of a system must be a model of that system. Int. J. Systems Sci. , 1 (2), 89–97.
  10. ↑ Kauffman, S. (1993). The Origins of Order: Self-Organization and Selection in Evolution. Oxford: Oxford University Press.
  11. ↑ Nicolis, G., & Prigogine, I. (1977). Self-organization in non-equilibrium systems. New York: John Wiley.
  12. ↑ Maturana, H. R., & Varela, F. (1980). Autopoiesis: the organization of the living. In V. F. Maturana HR (Ed.), Autopoiesis and Cognition. Dordrecht, Netherlands: Reidel.
  13. ↑ Nikolić, D. (2015). Practopoiesis: Or how life fosters a mind. Journal of theoretical biology, 373, 40-61.
  14. ↑ Haken, H. (1983). Synergetics: An introduction. Non-equilibrium phase transition and self-organisation in physics, chemistry and biology (3rd ed.). Berlin: Springer Verlag.
  15. ↑ Jaynes, E. T. (1957). Information Theory and Statistical Mechanics. Physical Review Series II, 106 (4), 620–30.
  16. ↑ 引用错误：无效<ref>标签；未给name属性为Dayan的引用提供文字
取自“https://wiki.swarma.org/index.php?title=自由能原理&oldid=16913”