玻尔兹曼方程
此词条暂由彩云小译翻译,翻译字数共1657,未经人工整理和审校,带来阅读不便,请见谅。
The equation is a nonlinear integro-differential equation, and the unknown function in the equation is a probability density function in six-dimensional space of a particle position and momentum. The problem of existence and uniqueness of solutions is still not fully resolved, but some recent results are quite promising.
这个方程是一个非线性积分微分方程,方程中的未知函数是粒子位置和动量的概率密度函数六维。解的存在唯一性问题还没有完全解决,但最近的一些研究结果很有希望。
The Boltzmann equation or Boltzmann transport equation (BTE) describes the statistical behaviour of a thermodynamic system not in a state of equilibrium, devised by Ludwig Boltzmann in 1872.[2]
The classic example of such a system is a fluid with temperature gradients in space causing heat to flow from hotter regions to colder ones, by the random but biased transport of the particles making up that fluid. In the modern literature the term Boltzmann equation is often used in a more general sense, referring to any kinetic equation that describes the change of a macroscopic quantity in a thermodynamic system, such as energy, charge or particle number.
Note that some authors use the particle velocity v instead of momentum p; they are related in the definition of momentum by p = mv.
请注意,有些作者使用粒子速度 v 代替动量 p; 它们在动量的定义中与 p = mv 有关。
The equation arises not by analyzing the individual positions and momenta of each particle in the fluid but rather by considering a probability distribution for the position and momentum of a typical particle—that is, the probability that the particle occupies a given very small region of space (mathematically the volume element [math]\displaystyle{ \mathrm{d}^3 \bf{r} }[/math]) centered at the position [math]\displaystyle{ \bf{r} }[/math], and has momentum nearly equal to a given momentum vector [math]\displaystyle{ \bf{p} }[/math] (thus occupying a very small region of momentum space [math]\displaystyle{ \mathrm{d}^3 \bf{p} }[/math]), at an instant of time.
The Boltzmann equation can be used to determine how physical quantities change, such as heat energy and momentum, when a fluid is in transport. One may also derive other properties characteristic to fluids such as viscosity, thermal conductivity, and electrical conductivity (by treating the charge carriers in a material as a gas).[2] See also convection–diffusion equation.
Consider particles described by f, each experiencing an external force F not due to other particles (see the collision term for the latter treatment).
考虑由 f 描述的粒子,每个粒子都受到一个外力 f,而不是由于其他粒子(后一种处理方法见碰撞术语)。
The equation is a nonlinear integro-differential equation, and the unknown function in the equation is a probability density function in six-dimensional space of a particle position and momentum. The problem of existence and uniqueness of solutions is still not fully resolved, but some recent results are quite promising.[3][4]
[math]\displaystyle{ 《数学》 ==Overview== f \left (\mathbf{r}+\frac{\mathbf{p}}{m} \, \Delta t,\mathbf{p}+\mathbf{F} \, \Delta t, t+\Delta t \right )\,d^3\mathbf{r}\,d^3\mathbf{p} = f(\mathbf{r}, \mathbf{p},t) \, d^3\mathbf{r} \, d^3\mathbf{p} F left (mathbf { r } + frac { p }{ m } ,Delta t,mathbf { p } + mathbf { f } ,Delta t,t + Delta t 右) ,d ^ 3 mathbf { r } ,d ^ 3 mathbf { p } = f (math{ r } ,mathbf { p } ,t) ,d ^ 3 mathbf { r } ,d ^ 3 mathbf { p } }[/math]
数学
The phase space and density function
The set of all possible positions r and momenta p is called the phase space of the system; in other words a set of three coordinates for each position coordinate x, y, z, and three more for each momentum component px, py, pz. The entire space is 6-dimensional: a point in this space is (r, p) = (x, y, z, px, py, pz), and each coordinate is parameterized by time t. The small volume ("differential volume element") is written
Note that we have used the fact that the phase space volume element [math]\displaystyle{ d^3\bf{r} }[/math] [math]\displaystyle{ d^3\bf{p} }[/math] is constant, which can be shown using Hamilton's equations (see the discussion under Liouville's theorem). However, since collisions do occur, the particle density in the phase-space volume [math]\displaystyle{ d^3\bf{r} }[/math] '[math]\displaystyle{ d^3\bf{p} }[/math] changes, so
注意,我们已经使用了相空间体积元 < math > d ^ 3 bf { r } </math > < math > d ^ 3 bf { p } </math > 是常数的事实,这可以用哈密尔顿方程表示(见刘维尔定理下的讨论)。然而,由于碰撞确实发生了,相空间体积中的粒子密度 < 数学 > d ^ 3 bf { r } </math > ’ < 数学 > d ^ 3 bf { p } </math > 改变了,所以呢
- [math]\displaystyle{ \text{d}^3\mathbf{r}\,\text{d}^3\mathbf{p} = \text{d}x\,\text{d}y\,\text{d}z\,\text{d}p_x\,\text{d}p_y\,\text{d}p_z. }[/math]
-
({{{3}}})
|}}
- [math]\displaystyle{ \begin{align} where Δf is the total change in f. Dividing () by \lt math\gt d^3\bf{r} }[/math] [math]\displaystyle{ d^3\bf{p} }[/math] Δt and taking the limits Δt → 0 and Δf → 0, we have
其中 δf 是 f 的总变化除以()除以 < math > d ^ 3 bf { r } </math > < math > d ^ 3 bf { p } </math > δt 并取极限 δt →0和 δf →0,我们得到了
N & = \int\limits_\mathrm{momenta} \text{d}^3\mathbf{p} \int\limits_\mathrm{positions} \text{d}^3\mathbf{r}\,f (\mathbf{r},\mathbf{p},t) \\[5pt]
& = \iiint\limits_\mathrm{momenta} \quad \iiint\limits_\mathrm{positions} f(x,y,z,p_x,p_y,p_z,t) \, \text{d}x \, \text{d}y \, \text{d}z \, \text{d}p_x \, \text{d}p_y \, \text{d}p_z
-
-
\end{align}
[math]\displaystyle{ \frac{d f}{d t} = \left(\frac{\partial f}{\partial t} \right)_\mathrm{coll} }[/math]
左(frac { partial f }{ partial t } right) _ mathrum { coll } </math >
</math>
()
()
-
which is a 6-fold integral. While f is associated with a number of particles, the phase space is for one-particle (not all of them, which is usually the case with deterministic many-body systems), since only one r and p is in question. It is not part of the analysis to use r1, p1 for particle 1, r2, p2 for particle 2, etc. up to rN, pN for particle N.
The total differential of f is:
F 的全微分是:
It is assumed the particles in the system are identical (so each has an identical mass m). For a mixture of more than one chemical species, one distribution is needed for each, see below.
-
{{{2}}}
({{{3}}})
{m}dt + \frac{\partial f}{\partial \mathbf{p}}\cdot \mathbf{F} \, dt
1.1.2.2.2.2.2.2.2.2.2.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.3.2.3.3.3.3.3.3.3.3.3.3
where the "force" term corresponds to the forces exerted on the particles by an external influence (not by the particles themselves), the "diff" term represents the diffusion of particles, and "coll" is the collision term – accounting for the forces acting between particles in collisions. Expressions for each term on the right side are provided below.[5]
\end{align}</math>
结束{ align } </math >
|}}
|}}
Note that some authors use the particle velocity v instead of momentum p; they are related in the definition of momentum by p = mv.
where ∇ is the gradient operator, · is the dot product,
其中 something 是梯度算符,是点积,
The force and diffusion terms
[math]\displaystyle{ 《数学》 Consider particles described by ''f'', each experiencing an ''external'' force '''F''' not due to other particles (see the collision term for the latter treatment). \frac{\partial f}{\partial \mathbf{p}} = \mathbf{\hat{e}}_x\frac{\partial f}{\partial p_x} + \mathbf{\hat{e}}_y\frac{\partial f}{\partial p_y} + \mathbf{\hat{e}}_z \frac{\partial f}{\partial p_z}= \nabla_\mathbf{p}f Fasc { partial mathbf { p }}} = mathbf { hat { e } x frac { partial f } + mathbf { hat { e } y frac { partial f } + mathbf { hat { e } z fasc }{ partial f } = nabla { p } f } f }[/math]
数学
Suppose at time t some number of particles all have position r within element [math]\displaystyle{ d^3\bf{r} }[/math] and momentum p within [math]\displaystyle{ d^3\bf{p} }[/math]. If a force F instantly acts on each particle, then at time t + Δt their position will be r + Δr = r + pΔt/m and momentum p + Δp = p + FΔt. Then, in the absence of collisions, f must satisfy
is a shorthand for the momentum analogue of ∇, and êx, êy, êz are Cartesian unit vectors.
是 something 的动量模拟的简写,并且使得 < sub > x ,< sub > y ,< sub > z 是笛卡尔单位向量。
- [math]\displaystyle{ f \left (\mathbf{r}+\frac{\mathbf{p}}{m} \, \Delta t,\mathbf{p}+\mathbf{F} \, \Delta t, t+\Delta t \right )\,d^3\mathbf{r}\,d^3\mathbf{p} = f(\mathbf{r}, \mathbf{p},t) \, d^3\mathbf{r} \, d^3\mathbf{p} }[/math]
Dividing () by dt and substituting into () gives:
用 dt 除以()并代入()得出:
Note that we have used the fact that the phase space volume element [math]\displaystyle{ d^3\bf{r} }[/math] [math]\displaystyle{ d^3\bf{p} }[/math] is constant, which can be shown using Hamilton's equations (see the discussion under Liouville's theorem). However, since collisions do occur, the particle density in the phase-space volume [math]\displaystyle{ d^3\bf{r} }[/math] '[math]\displaystyle{ d^3\bf{p} }[/math] changes, so
[math]\displaystyle{ \frac{\partial f}{\partial t} + \frac{\mathbf{p}}{m}\cdot\nabla f + \mathbf{F} \cdot \frac{\partial f}{\partial \mathbf{p}} = \left(\frac{\partial f}{\partial t} \right)_\mathrm{coll} }[/math]
[数学][部分数学][部分数学][部分数学][部分数学][部分数学][部分数学][部分数学][部分数学][部分数学][部分数学][部分数学][部分数学][部分数学][部分数学][部分数学][部分数学][部分数学][部分数学][部分数学][部分数学][部分数学][部分数
-
[math]\displaystyle{ \begin{align} In this context, F(r, t) is the force field acting on the particles in the fluid, and m is the mass of the particles. The term on the right hand side is added to describe the effect of collisions between particles; if it is zero then the particles do not collide. The collisionless Boltzmann equation, where individual collisions are replaced with long-range aggregated interactions, e.g. Coulomb interactions, is often called the Vlasov equation. 在这种情况下,f (r,t)是作用于流体中粒子的力场,m 是粒子的质量。右边的术语是用来描述粒子间碰撞的效果; 如果为零,那么粒子就不会碰撞。无碰撞玻尔兹曼方程,其中个体碰撞被长程聚合的相互作用所取代,例如:。库仑相互作用,通常被称为弗拉索夫方程。 dN_\mathrm{coll} & = \left(\frac{\partial f}{\partial t} \right)_\mathrm{coll}\Delta td^3\mathbf{r} d^3\mathbf{p} \\[5pt] & = f \left (\mathbf{r}+\frac{\mathbf{p}}{m}\Delta t,\mathbf{p} + \mathbf{F}\Delta t, t+\Delta t \right)d^3\mathbf{r}d^3\mathbf{p} - f(\mathbf{r}, \mathbf{p}, t) \, d^3\mathbf{r} \, d^3\mathbf{p} \\[5pt] This equation is more useful than the principal one above, yet still incomplete, since f cannot be solved unless the collision term in f is known. This term cannot be found as easily or generally as the others – it is a statistical term representing the particle collisions, and requires knowledge of the statistics the particles obey, like the Maxwell–Boltzmann, Fermi–Dirac or Bose–Einstein distributions. 这个方程比上面的主方程更有用,但仍然不完整,因为除非知道 f 中的碰撞项,否则 f 就不能求解。这个术语不能像其他术语那样容易或普遍地找到——它是一个统计术语,代表粒子碰撞,并且需要粒子服从的统计知识,如麦克斯韦-玻尔兹曼、费米-狄拉克或玻色-爱因斯坦分布。 & = \Delta f \, d^3\mathbf{r} \, d^3\mathbf{p} \end{align} }[/math]
(1)
where Δf is the total change in f. Dividing (1) by [math]\displaystyle{ d^3\bf{r} }[/math] [math]\displaystyle{ d^3\bf{p} }[/math] Δt and taking the limits Δt → 0 and Δf → 0, we have
A key insight applied by Boltzmann was to determine the collision term resulting solely from two-body collisions between particles that are assumed to be uncorrelated prior to the collision. This assumption was referred to by Boltzmann as the "" and is also known as the "molecular chaos assumption". Under this assumption the collision term can be written as a momentum-space integral over the product of one-particle distribution functions:
Boltzmann 应用的一个关键洞察力是确定仅仅由粒子之间的两体碰撞产生的碰撞项,而这种碰撞被假定为在碰撞之前是不相关的。这个假设被玻尔兹曼称为“” ,也被称为“分子混沌假设”。在这种假设下,碰撞项可以写成单粒子分布函数乘积上的动量空间积分:
[math]\displaystyle{ 《数学》 {{NumBlk|:| \left(\frac{\partial f}{\partial t}\right)_\text{coll} = 左(frac { partial f }{ partial t } right) _ text { coll } = \lt math\gt \frac{d f}{d t} = \left(\frac{\partial f}{\partial t} \right)_\mathrm{coll} }[/math]
\iint gI(g, \Omega)[f(\mathbf{r},\mathbf{p'}_A, t) f(\mathbf{r},\mathbf{p'}_B,t) - f(\mathbf{r},\mathbf{p}_A,t) f(\mathbf{r},\mathbf{p}_B,t)] \,d\Omega \,d^3\mathbf{p}_A \,d^3\mathbf{p}_B,
I int gI (g,Omega)[ f (mathbf { r } ,mathbf { p’} _ a,t) f (mathbf { r } ,mathbf { p’} _ b,t)-f (mathbf { r } ,mathbf { p } _ a,t) f (mathbf { r } ,mathbf { p } _ b,t)] ,d,Omega,d ^ 3 mathbf { p } _ a,d ^ 3 bf { p } _ b,
|2}}
</math>
数学
where pA and pB are the momenta of any two particles (labeled as A and B for convenience) before a collision, p′A and p′B are the momenta after the collision,
其中 p < sub > a 和 p < sub > b 是碰撞前任意两个粒子(为方便起见,分别标为 a 和 b)的动量,p & prime; < sub > a 和 p & prime; < sub > b 是碰撞后的动量,
The total differential of f is:
[math]\displaystyle{ 《数学》 g = |\mathbf{p}_B - \mathbf{p}_A| = |\mathbf{p'}_B - \mathbf{p'}_A| G = | mathbf { p } _ b-mathbf { p } _ a | = | mathbf { p’} _ b-mathbf { p’} _ a | {{NumBlk|:| }[/math]
数学
[math]\displaystyle{ \begin{align} is the magnitude of the relative momenta (see relative velocity for more on this concept), and I(g, Ω) is the differential cross section of the collision, in which the relative momenta of the colliding particles turns through an angle θ into the element of the solid angle dΩ, due to the collision. 是相对动量的大小(详见相对速度) ,i (g,ω)是碰撞的微分截面,碰撞中粒子的相对动量通过一个角度 θ 转入固体角度 dω 的元素,由于碰撞。 d f & = \frac{\partial f}{\partial t} \, dt +\left(\frac{\partial f}{\partial x} \, dx +\frac{\partial f}{\partial y} \, dy Since much of the challenge in solving the Boltzmann equation originates with the complex collision term, attempts have been made to "model" and simplify the collision term. The best known model equation is due to Bhatnagar, Gross and Krook. 由于解决玻尔兹曼方程冲突的大部分挑战来自于复杂的冲突术语,因此人们尝试对冲突术语进行“模型化”和简化。最著名的模型方程是由于 Bhatnagar,Gross 和 Krook。 +\frac{\partial f}{\partial z} \, dz \right) \lt math\gt \frac{\partial f_i}{\partial t} + \frac{\mathbf{p}_i}{m_i} \cdot \nabla f_i + \mathbf{F} \cdot \frac{\partial f_i}{\partial \mathbf{p}_i} = \left(\frac{\partial f_i}{\partial t} \right)_\text{coll}, }[/math]
[数学][数学][部分数学][部分数学][部分数学][部分数学][部分数学][部分数学][部分数学][部分数学][部分数学][部分数学][部分数学][部分数学][部分数学][部分数学][部分数学][部分数学][部分数学][部分数学][部分数学][部分数学][部分数学][部分数学][部分数学][部分数学][
+\left(\frac{\partial f}{\partial p_x} \, dp_x
+\frac{\partial f}{\partial p_y} \, dp_y
where fi = fi(r, pi, t), and the collision term is
其中 f < sub > i = f i (r,p < sub > i ,t) ,碰撞项是
+\frac{\partial f}{\partial p_z} \, dp_z
\right)\\[5pt]
[math]\displaystyle{ 《数学》 & = \frac{\partial f}{\partial t}dt +\nabla f \cdot d\mathbf{r} + \frac{\partial f}{\partial \mathbf{p}}\cdot d\mathbf{p} \\[5pt] \left(\frac{\partial f_i}{\partial t} \right)_{\mathrm{coll}} = \sum_{j=1}^n \iint g_{ij} I_{ij}(g_{ij}, \Omega)[f'_i f'_j - f_if_j] \,d\Omega\,d^3\mathbf{p'}, 左(frac { partial f i }{ partial t } right){ mathrm { coll } = sum { j = 1} ^ n iint g { ij }(g { ij } ,Omega)[ f’ i f’ j-f if _ j ] ,d ω,d ^ 3 mathbf { p’} , & = \frac{\partial f}{\partial t}dt +\nabla f \cdot \frac{\mathbf{p}}{m}dt + \frac{\partial f}{\partial \mathbf{p}}\cdot \mathbf{F} \, dt }[/math]
数学
\end{align}</math>
|3}}
where f′ = f′(p′i, t), the magnitude of the relative momenta is
其中 f & prime = f & prime; (p & prime; < sub > i ,t) ,相对动量的大小是
where ∇ is the gradient operator, · is the dot product,
[math]\displaystyle{ g_{ij} = |\mathbf{p}_i - \mathbf{p}_j| = |\mathbf{p'}_i - \mathbf{p'}_j|, }[/math]
如果你想知道更多,请点击这里查看更多
- [math]\displaystyle{ and I\lt sub\gt ij\lt /sub\gt is the differential cross-section, as before, between particles i and j. The integration is over the momentum components in the integrand (which are labelled i and j). The sum of integrals describes the entry and exit of particles of species i in or out of the phase-space element. I \lt sub \gt ij \lt /sub \gt 是粒子 i 和 j 之间的微分截面。积分是在被积函数中的动量分量之上(被标记为 i 和 j)。积分之和描述了粒子 i 进入或退出相空间元的过程。 \frac{\partial f}{\partial \mathbf{p}} = \mathbf{\hat{e}}_x\frac{\partial f}{\partial p_x} + \mathbf{\hat{e}}_y\frac{\partial f}{\partial p_y} + \mathbf{\hat{e}}_z \frac{\partial f}{\partial p_z}= \nabla_\mathbf{p}f }[/math]
is a shorthand for the momentum analogue of ∇, and êx, êy, êz are Cartesian unit vectors.
Final statement
The Boltzmann equation can be used to derive the fluid dynamic conservation laws for mass, charge, momentum, and energy.
玻尔兹曼方程可以用来推导质量、电荷、动量和能量的流体动力学守恒定律。
Dividing (3) by dt and substituting into (2) gives:
[math]\displaystyle{ \frac{\partial}{\partial t}\rho + \frac{\partial}{\partial x_j}(\rho V_j) = 0, }[/math]
(数学) = 0,</math >
- [math]\displaystyle{ \frac{\partial f}{\partial t} + \frac{\mathbf{p}}{m}\cdot\nabla f + \mathbf{F} \cdot \frac{\partial f}{\partial \mathbf{p}} = \left(\frac{\partial f}{\partial t} \right)_\mathrm{coll} }[/math]
where [math]\displaystyle{ \rho = mn }[/math] is the mass density, and [math]\displaystyle{ V_i = \langle w_i\rangle }[/math] is the average fluid velocity.
其中质量密度为 rho = mn,质量密度为 v i = langle w i rangle,流体平均速度为 max。
In this context, F(r, t) is the force field acting on the particles in the fluid, and m is the mass of the particles. The term on the right hand side is added to describe the effect of collisions between particles; if it is zero then the particles do not collide. The collisionless Boltzmann equation, where individual collisions are replaced with long-range aggregated interactions, e.g. Coulomb interactions, is often called the Vlasov equation.
Letting [math]\displaystyle{ A = p_i }[/math], the momentum of the particle, the integrated Boltzmann equation becomes the conservation of momentum equation:
让 a = p/math,粒子的动量,积分后的玻尔兹曼方程成为动量守恒方程:
This equation is more useful than the principal one above, yet still incomplete, since f cannot be solved unless the collision term in f is known. This term cannot be found as easily or generally as the others – it is a statistical term representing the particle collisions, and requires knowledge of the statistics the particles obey, like the Maxwell–Boltzmann, Fermi–Dirac or Bose–Einstein distributions.
[math]\displaystyle{ \frac{\partial}{\partial t}(\rho V_i) + \frac{\partial}{\partial x_j}(\rho V_i V_j+P_{ij}) - nF_i = 0, }[/math]
(rho v i) + frac { partial x j }(rho v i v j + p { ij })-nF i = 0,</math >
The collision term (Stosszahlansatz) and molecular chaos
where [math]\displaystyle{ P_{ij} = \rho \langle (w_i-V_i) (w_j-V_j) \rangle }[/math] is the pressure tensor (the viscous stress tensor plus the hydrostatic pressure).
其中,压力张量(粘性应力张量加静水压力) = rho langle (w _ i-v _ i)(w _ j-v _ j) =/math。
Two-body collision term
Letting [math]\displaystyle{ A =\frac{p_i p_i}{2m} }[/math], the kinetic energy of the particle, the integrated Boltzmann equation becomes the conservation of energy equation:
让 a = frac { p i p i }{2m } </math > ,粒子的动能,积分玻尔兹曼方程成为能量守恒方程:
A key insight applied by Boltzmann was to determine the collision term resulting solely from two-body collisions between particles that are assumed to be uncorrelated prior to the collision. This assumption was referred to by Boltzmann as the "脚本错误:没有“lang”这个模块。" and is also known as the "molecular chaos assumption". Under this assumption the collision term can be written as a momentum-space integral over the product of one-particle distribution functions:[2]
- [math]\displaystyle{ \lt math\gt \frac{\partial}{\partial t}(u + \tfrac{1}{2}\rho V_i V_i) + \frac{\partial}{\partial x_j} (uV_j + \tfrac{1}{2}\rho V_i V_i V_j + J_{qj} + P_{ij}V_i) - nF_iV_i = 0, }[/math]
1}(u + tfrac {1}{2} rho v i v i) + frac { partial x j }(uV j + tfrac {1}{2} rho v i v j + j { j } v i)-iv i = 0,</math >
\left(\frac{\partial f}{\partial t}\right)_\text{coll} =
\iint gI(g, \Omega)[f(\mathbf{r},\mathbf{p'}_A, t) f(\mathbf{r},\mathbf{p'}_B,t) - f(\mathbf{r},\mathbf{p}_A,t) f(\mathbf{r},\mathbf{p}_B,t)] \,d\Omega \,d^3\mathbf{p}_A \,d^3\mathbf{p}_B,
where [math]\displaystyle{ u = \tfrac{1}{2} \rho \langle (w_i-V_i) (w_i-V_i) \rangle }[/math] is the kinetic thermal energy density, and [math]\displaystyle{ J_{qi} = \tfrac{1}{2} \rho \langle(w_i - V_i)(w_k - V_k)(w_k - V_k)\rangle }[/math] is the heat flux vector.
其中动能密度为 u = tfrac {1}{2} rho 角(w _ i-v _ i)(w _ i-v _ i) ,动能密度为 j _ { qi } = tfrac {1}{2} rho 角(w _ i-v _ i)(w _ k-v _ k)(w _ k-v _ k) </math > 为热流矢量。
</math>
where pA and pB are the momenta of any two particles (labeled as A and B for convenience) before a collision, p′A and p′B are the momenta after the collision,
- [math]\displaystyle{ g = |\mathbf{p}_B - \mathbf{p}_A| = |\mathbf{p'}_B - \mathbf{p'}_A| In Hamiltonian mechanics, the Boltzmann equation is often written more generally as 在20世纪90年代哈密顿力学,玻尔兹曼方程通常被写成 }[/math]
[math]\displaystyle{ \hat{\mathbf{L}}[f]=\mathbf{C}[f], \, }[/math]
[数学] ,,[数学]
is the magnitude of the relative momenta (see relative velocity for more on this concept), and I(g, Ω) is the differential cross section of the collision, in which the relative momenta of the colliding particles turns through an angle θ into the element of the solid angle dΩ, due to the collision.
where L is the Liouville operator (there is an inconsistent definition between the Liouville operator as defined here and the one in the article linked) describing the evolution of a phase space volume and C is the collision operator. The non-relativistic form of L is
其中 l 是 Liouville 运算符(在这里定义的 Liouville 运算符和本文链接的那个运算符之间有不一致的定义) ,描述了相空间体的演化,c 是碰撞运算符。L 的非相对论形式是
Simplifications to the collision term
[math]\displaystyle{ \hat{\mathbf{L}}_\mathrm{NR} = \frac{\partial}{\partial t} + \frac{\mathbf{p}}{m} \cdot \nabla + \mathbf{F}\cdot\frac{\partial}{\partial \mathbf{p}}\,. }[/math]
[数学][数学][数学][数学][数学]
Since much of the challenge in solving the Boltzmann equation originates with the complex collision term, attempts have been made to "model" and simplify the collision term. The best known model equation is due to Bhatnagar, Gross and Krook.[6] The assumption in the BGK approximation is that the effect of molecular collisions is to force a non-equilibrium distribution function at a point in physical space back to a Maxwellian equilibrium distribution function and that the rate at which this occurs is proportional to the molecular collision frequency. The Boltzmann equation is therefore modified to the BGK form:
- [math]\displaystyle{ \frac{\partial f}{\partial t} + \frac{\mathbf{p}}{m}\cdot\nabla f + \mathbf{F} \cdot \frac{\partial f}{\partial \mathbf{p}} = \nu (f_0 - f), }[/math]
It is possible to write down relativistic quantum Boltzmann equations for relativistic quantum systems in which the number of particles is not conserved in collisions. This has several applications in physical cosmology, In the very dense medium formed by the primordial plasma after the Big Bang, particles are continuously created and annihilated. In such an environment quantum coherence and the spatial extension of the wavefunction can affect the dynamics, making it questionable whether the classical phase space distribution f that appears in the Boltzmann equation is suitable to describe the system. In many cases it is, however, possible to derive an effective Boltzmann equation for a generalized distribution function from first principles of quantum field theory. This includes the formation of the light elements in Big Bang nucleosynthesis, the production of dark matter and baryogenesis.
在碰撞中粒子数不守恒的相对论量子系统中,可以写出相对论量子玻耳兹曼方程。这在21物理宇宙学有几个应用---- 在宇宙大爆炸后原始等离子体形成的非常致密的介质中,粒子被不断地创造和湮灭。在这样的环境中,量子相干性和波函数的空间扩展会影响系统的动力学行为,使得玻尔兹曼方程中出现的经典相空间分布 f 是否适合描述系统成为疑问。然而,在许多情况下,从量子场论的第一原理导出广义分布函数的有效玻尔兹曼方程是可能的。这包括太初核合成中轻元素的形成,暗物质的产生和重子形成。
where [math]\displaystyle{ \nu }[/math] is the molecular collision frequency, and [math]\displaystyle{ f_0 }[/math] is the local Maxwellian distribution function given the gas temperature at this point in space.
General equation (for a mixture)
Exact solutions to the Boltzmann equations have been proven to exist in some cases; this analytical approach provides insight, but is not generally usable in practical problems.
波尔兹曼方程的精确解在某些情况下已被证明存在; 这种分析方法提供了洞察力,但在实际问题中通常不能使用。
For a mixture of chemical species labelled by indices i = 1, 2, 3, ..., n the equation for species i is[2]
Instead, numerical methods (including finite elements) are generally used to find approximate solutions to the various forms of the Boltzmann equation. Example applications range from hypersonic aerodynamics in rarefied gas flows to plasma flows.
相反,数值方法(包括有限元)通常被用来寻找各种形式的玻尔兹曼方程的近似解。示例应用范围从稀薄气流中的高超音速空气动力学到等离子体流。
- [math]\displaystyle{ \frac{\partial f_i}{\partial t} + \frac{\mathbf{p}_i}{m_i} \cdot \nabla f_i + \mathbf{F} \cdot \frac{\partial f_i}{\partial \mathbf{p}_i} = \left(\frac{\partial f_i}{\partial t} \right)_\text{coll}, }[/math]
Close to local equilibrium, solution of the Boltzmann equation can be represented by an asymptotic expansion in powers of Knudsen number (the Chapman-Enskog expansion). The first two terms of this expansion give the Euler equations and the Navier-Stokes equations. The higher terms have singularities. The problem of developing mathematically the limiting processes, which lead from the atomistic view (represented by Boltzmann's equation) to the laws of motion of continua, is an important part of Hilbert's sixth problem.
在接近局部均衡的情况下,玻尔兹曼方程的解可以用一个克努森数的渐近展开表示(Chapman-Enskog 展开式)。这个展开式的前两项给出了欧拉方程和纳维-斯托克斯方程。较高的项有奇点。从原子观点(以玻尔兹曼方程为代表)到连续统运动定律的极限过程的数学发展问题,是希尔伯特第六个问题的重要组成部分。
where fi = fi(r, pi, t), and the collision term is
- [math]\displaystyle{ \left(\frac{\partial f_i}{\partial t} \right)_{\mathrm{coll}} = \sum_{j=1}^n \iint g_{ij} I_{ij}(g_{ij}, \Omega)[f'_i f'_j - f_if_j] \,d\Omega\,d^3\mathbf{p'}, \lt !--*BGK equation \lt ! -- * BGK 方程 }[/math]
where f′ = f′(p′i, t), the magnitude of the relative momenta is
- [math]\displaystyle{ g_{ij} = |\mathbf{p}_i - \mathbf{p}_j| = |\mathbf{p'}_i - \mathbf{p'}_j|, }[/math]
and Iij is the differential cross-section, as before, between particles i and j. The integration is over the momentum components in the integrand (which are labelled i and j). The sum of integrals describes the entry and exit of particles of species i in or out of the phase-space element.
Applications and extensions
Conservation equations
The Boltzmann equation can be used to derive the fluid dynamic conservation laws for mass, charge, momentum, and energy.[7]:p 163 For a fluid consisting of only one kind of particle, the number density n is given by
- [math]\displaystyle{ n = \int f \,d^3p. }[/math]
The average value of any function A is
- [math]\displaystyle{ \langle A \rangle = \frac 1 n \int A f \,d^3p. }[/math]
| last1= Harris
1 = Harris
| first1= Stewart
1 = Stewart
Since the conservation equations involve tensors, the Einstein summation convention will be used where repeated indices in a product indicate summation over those indices. Thus [math]\displaystyle{ \mathbf{x} \mapsto x_i }[/math] and [math]\displaystyle{ \mathbf{p} \mapsto p_i = m w_i }[/math], where [math]\displaystyle{ w_i }[/math] is the particle velocity vector. Define [math]\displaystyle{ A(p_i) }[/math] as some function of momentum [math]\displaystyle{ p_i }[/math] only, which is conserved in a collision. Assume also that the force [math]\displaystyle{ F_i }[/math] is a function of position only, and that f is zero for [math]\displaystyle{ p_i \to \pm\infty }[/math]. Multiplying the Boltzmann equation by A and integrating over momentum yields four terms, which, using integration by parts, can be expressed as
|author1-link=
1-link =
| title= An introduction to the theory of the Boltzmann equation | publisher=Dover Books|pages=221 | year= 1971 | isbn=978-0-486-43831-3|url=https://books.google.com/books?id=KfYK1lyq3VYC}}. Very inexpensive introduction to the modern framework (starting from a formal deduction from Liouville and the Bogoliubov–Born–Green–Kirkwood–Yvon hierarchy (BBGKY) in which the Boltzmann equation is placed). Most statistical mechanics textbooks like Huang still treat the topic using Boltzmann's original arguments. To derive the equation, these books use a heuristic explanation that does not bring out the range of validity and the characteristic assumptions that distinguish Boltzmann's from other transport equations like Fokker–Planck or Landau equations.
| title = 玻尔兹曼方程理论导论 | 出版商 = Dover Books | pages = 221 | year = 1971 | isbn = 978-0-486-43831-3 | url = https://Books.google.com/Books?id=kfyk1lyq3vyc }。非常便宜的现代框架介绍(从一个正式的推论从 Liouville 和 Bogoliubov-Born-Green-Kirkwood-伊冯等级(BBGKY)的玻尔兹曼方程是放置)。大多数统计力学的教科书,比如 Huang,仍然使用 Boltzmann 的原始论点来处理这个话题。为了推导这个方程,这些书使用了一种启发式的解释,这种解释没有提出波尔兹曼方程与其他传输方程(如福克-普朗克方程或兰道方程)区别开来的有效性范围和特征性假设。
- [math]\displaystyle{ \int A \frac{\partial f}{\partial t} \,d^3p = \frac{\partial }{\partial t} (n \langle A \rangle), }[/math]
- [math]\displaystyle{ \int \frac{p_j A}{m}\frac{\partial f}{\partial x_j} \,d^3p = \frac{1}{m}\frac{\partial}{\partial x_j}(n\langle A p_j \rangle), }[/math]
| last1= Arkeryd
| last1= Arkeryd
- [math]\displaystyle{ \int A F_j \frac{\partial f}{\partial p_j} \,d^3p = -nF_j\left\langle \frac{\partial A}{\partial p_j}\right\rangle, }[/math]
| first1= Leif
1 = Leif
|author1-link= Leif Arkeryd
1-link = Leif Arkeryd
- [math]\displaystyle{ \int A \left(\frac{\partial f}{\partial t}\right)_\text{coll} \,d^3p = 0, }[/math]
| title= On the Boltzmann equation part II: The full initial value problem | journal= Arch. Rational Mech. Anal. | volume= 45 | issue= 1
第二部分: 完整的初始值问题 | 日志 = 玻尔兹曼方程。Rational Mech.肛交。45 | issue = 1
| pages= 17–34 | year= 1972 | doi = 10.1007/BF00253393 | bibcode = 1972ArRMA..45...17A | s2cid= 119481100
17-34 | year = 1972 | doi = 10.1007/BF00253393 | bibcode = 1972ArRMA. 45... 17A | s2cid = 119481100
where the last term is zero, since A is conserved in a collision. Letting [math]\displaystyle{ A = m }[/math], the mass of the particle, the integrated Boltzmann equation becomes the conservation of mass equation:[7]:pp 12,168
}}
}}
- [math]\displaystyle{ \frac{\partial}{\partial t}\rho + \frac{\partial}{\partial x_j}(\rho V_j) = 0, }[/math]
where [math]\displaystyle{ \rho = mn }[/math] is the mass density, and [math]\displaystyle{ V_i = \langle w_i\rangle }[/math] is the average fluid velocity.
Letting [math]\displaystyle{ A = p_i }[/math], the momentum of the particle, the integrated Boltzmann equation becomes the conservation of momentum equation:[7]:pp 15,169
- [math]\displaystyle{ \frac{\partial}{\partial t}(\rho V_i) + \frac{\partial}{\partial x_j}(\rho V_i V_j+P_{ij}) - nF_i = 0, }[/math]
Category:Partial differential equations
类别: 偏微分方程
Category:Statistical mechanics
类别: 统计力学
where [math]\displaystyle{ P_{ij} = \rho \langle (w_i-V_i) (w_j-V_j) \rangle }[/math] is the pressure tensor (the viscous stress tensor plus the hydrostatic pressure).
Category:Transport phenomena
类别: 运输现象
Category:Equations of physics
类别: 物理方程
Letting [math]\displaystyle{ A =\frac{p_i p_i}{2m} }[/math], the kinetic energy of the particle, the integrated Boltzmann equation becomes the conservation of energy equation:[7]:pp 19,169
Equation
方程式
Category:1872 in science
类别: 1872年的科学
- [math]\displaystyle{ \frac{\partial}{\partial t}(u + \tfrac{1}{2}\rho V_i V_i) + \frac{\partial}{\partial x_j} (uV_j + \tfrac{1}{2}\rho V_i V_i V_j + J_{qj} + P_{ij}V_i) - nF_iV_i = 0, }[/math]
Category:1872 in Germany
类别: 1872年在德国
This page was moved from wikipedia:en:Boltzmann equation. Its edit history can be viewed at 玻尔兹曼方程/edithistory
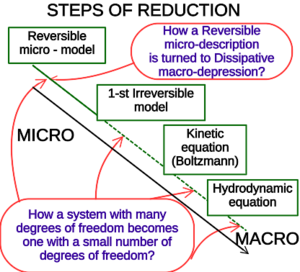
- ↑ The place of the Boltzmann kinetic equation on the stairs of model reduction from microscopic dynamics to macroscopic continuum dynamics (illustration to the content of the book See also [[convection–diffusion equation. 从微观动力学到宏观连续介质动力学,Boltzmann 动力学方程在模型简化阶梯上的位置(对本书内容的说明也参见[对流-扩散方程。 {Gorban, Alexander N.; Karlin, Ilya V. (2005). Invariant Manifolds for Physical and Chemical Kinetics. Lecture Notes in Physics (LNP, vol. 660). Berlin, Heidelberg: Springer. doi:10.1007/b98103. ISBN 978-3-540-22684-0. https://www.academia.edu/17378865. Alt URL
- ↑ 2.0 2.1 2.2 2.3 Encyclopaedia of Physics (2nd Edition), R. G. Lerner, G. L. Trigg, VHC publishers, 1991, ISBN (Verlagsgesellschaft) 3-527-26954-1, ISBN (VHC Inc.) 0-89573-752-3.
- ↑ DiPerna, R. J.; Lions, P.-L. (1989). "On the Cauchy problem for Boltzmann equations: global existence and weak stability". Ann. of Math. 2. 130 (2): 321–366. doi:10.2307/1971423. JSTOR 1971423. Suppose at time t some number of particles all have position r within element [math]\displaystyle{ d^3\bf{r} }[/math] and momentum p within [math]\displaystyle{ d^3\bf{p} }[/math]. If a force F instantly acts on each particle, then at time t + Δt their position will be r + Δr = r + pΔt/m and momentum p + Δp = p + FΔt. Then, in the absence of collisions, f must satisfy 假设在 t 时刻,某些粒子在元素 < math > d ^ 3 bf { r } </math > 和动量 p < math > d ^ 3 bf { p } </math > 中的位置都是 r。如果一个力 f 立即作用在每个粒子上,那么在时间 t + δt 时,它们的位置将是 r + δr = r + pδt/m 和动量 p + δp = p + FΔt。那么,在没有碰撞的情况下,f 必须满足
- ↑ Philip T. Gressman & Robert M. Strain (2010). "Global classical solutions of the Boltzmann equation with long-range interactions". Proceedings of the National Academy of Sciences. 107 (13): 5744–5749. arXiv:1002.3639. Bibcode:2010PNAS..107.5744G. doi:10.1073/pnas.1001185107. PMC 2851887. PMID 20231489.
- ↑ 引用错误:无效
<ref>标签;未给name属性为McGrawHill的引用提供文字 - ↑ Bhatnagar, P. L.; Gross, E. P.; Krook, M. (1954-05-01). "A Model for Collision Processes in Gases. I. Small Amplitude Processes in Charged and Neutral One-Component Systems". Physical Review. 94 (3): 511–525. Bibcode:1954PhRv...94..511B. doi:10.1103/PhysRev.94.511.
- ↑ 7.0 7.1 7.2 7.3 de Groot, S. R.; Mazur, P. (1984). Non-Equilibrium Thermodynamics. New York: Dover Publications Inc.. ISBN 978-0-486-64741-8.