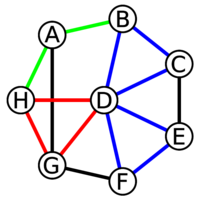
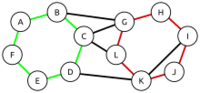
环
在图论 graph theory中,一个图中的环Cycle是一个非空轨迹,其中唯一重复的点是起点和终点。一个有向图中的 有向环Directed cycle同样是非空有向迹线,其中唯一重复的点也是起点和终点。
没有环的图称为无环图 acyclic graph。一个有向图,但是没有有向环,称为有向无环图Directed acyclic graph。没有环的连接图称为 树 Tree。
定义
回路,环
- 回路Circuit如图所示,以一个具有顶点序列的非空轨迹环为例,其中第一个和最后一个顶点重合。设图G =(V,E,ϕ),那么回路是具有顶点序列(v1,v2,...,vn,v1)的非空路径(e1,e2,…,en)。
- 在一个环或简单回路中,唯一重复的顶点是起点和终点。
- 一个回路(或环)的长度指的是相关连边的数量。
有向回路,环
- 有向回路是一个非空有向路径,其中第一个和最后一个顶点重合出现。设有向图G =(V,E,ϕ),其有向回路是具有顶点序列(v1,v2,...,vn,v1)的非空有向路径(e1,e2,……,en)。
- 在一个有向环或简单有向回路中,唯一重合的顶点是起点和终点。
无弦环
一个图中的 无弦环Chordless cycles(也可以称为 孔Hole或 导出环Induced cycle),指的是该环中没有两个顶点通过不属于该环的边相连。其反孔部分为此图孔的补图。无弦环i可用于表征 完美图Perfect graphs:通过强完美图定理 strong perfect graph theorem,当且仅当它的孔或反孔部分中无奇数(且大于3)个顶点时,图才是完美的。弦图是完美图的特殊形式,即没有任何长度大于三的孔。
图的 围长Girth是其最小环的长度;并且这个环必须是无弦的。 笼Cages定义为具有给定度和围长组合的最小正则图。
一个图中的 边环Peripheral cycle具有以下性质:不在此边环上的两条连边可以通过一条特殊路径连接;该路径内部顶点均不在此边环上。如果一个图中的某条环不是通过添加一条边形成的,那么其边环肯定是导出环。
环空间
The term cycle may also refer to an element of the cycle space of a graph. There are many cycle spaces, one for each coefficient field or ring. The most common is the binary cycle space (usually called simply the cycle space), which consists of the edge sets that have even degree at every vertex; it forms a vector space over the two-element field. By Veblen's theorem, every element of the cycle space may be formed as an edge-disjoint union of simple cycles. A cycle basis of the graph is a set of simple cycles that forms a basis of the cycle space.
The term cycle may also refer to an element of the cycle space of a graph. There are many cycle spaces, one for each coefficient field or ring. The most common is the binary cycle space (usually called simply the cycle space), which consists of the edge sets that have even degree at every vertex; it forms a vector space over the two-element field. By Veblen's theorem, every element of the cycle space may be formed as an edge-disjoint union of simple cycles. A cycle basis of the graph is a set of simple cycles that forms a basis of the cycle space.
“ 环Cycle”还可以指代一个图中 环空间Cycle space内的一个元素。在、一个图中存在很多环空间,且每个都有对应的 系数域Coefficient field或 环Ring(代数)。最常见的是 二元环空间Binary cycle space(通常简称为环空间),它是由在该图中每个顶点上具有偶数度的边集组成。二元环空间在二元域上形成了一个 向量空间Vector space。根据 维布伦定理Veblen's theorem,该环空间的每个元素都可以形成为简单环的不相交边的并集。该图的 环基Cycle basis相当于一组简单环,它们构成了环空间的基。
Using ideas from algebraic topology, the binary cycle space generalizes to vector spaces or modules over other rings such as the integers, rational or real numbers, etc.[1]
Using ideas from algebraic topology, the binary cycle space generalizes to vector spaces or modules over other rings such as the integers, rational or real numbers, etc.
根据 代数拓扑Algebraic topology的思想, 二元环空间Binary cycle space可以推广为其它 环Ring中的 向量空间Vector spaces或 模Module,例如整数,有理数或实数等。
环检测
The existence of a cycle in directed and undirected graphs can be determined by whether depth-first search (DFS) finds an edge that points to an ancestor of the current vertex (it contains a back edge). In an undirected graph, the edge to the parent of a node should not be counted as a back edge, but finding any other already visited vertex will indicate a back edge. In the case of undirected graphs, only O(n) time is required to find a cycle in an n-vertex graph, since at most n − 1 edges can be tree edges.
The existence of a cycle in directed and undirected graphs can be determined by whether depth-first search (DFS) finds an edge that points to an ancestor of the current vertex (it contains a back edge).All the back edges which DFS skips over are part of cycles. In an undirected graph, the edge to the parent of a node should not be counted as a back edge, but finding any other already visited vertex will indicate a back edge. In the case of undirected graphs, only O(n) time is required to find a cycle in an n-vertex graph, since at most n − 1 edges can be tree edges.
关于环在有向或无向图中的存在,可以通过 深度优先搜索(DFS)来确定。具体方法是查找是否存在一条连边指向当前顶点的原始点(包括回边)。DFS跳过的所有回边都是环的一部分。在无向图中,指向一个节点上级的连边不应算作后边,但是如果找到任何其他已访问的顶点可以视为后边。在无向图的情况下,只需要O(n)时间即可在n个顶点图中找到一个循环,因为最多n-1个边可以是树边。
Many topological sorting algorithms will detect cycles too, since those are obstacles for topological order to exist. Also, if a directed graph has been divided into strongly connected components, cycles only exist within the components and not between them, since cycles are strongly connected.
Many topological sorting algorithms will detect cycles too, since those are obstacles for topological order to exist. Also, if a directed graph has been divided into strongly connected components, cycles only exist within the components and not between them, since cycles are strongly connected.
很多 拓扑排序Topological sorting算法也可以用于检测环,因为这些环阻碍了拓扑排序。另外,因为环本身性质是强连接的,所以如果一个有向图被划分为具有强连接的不同组成部分,则环仅存在于这些组成部分内,也并非它们之间。
For directed graphs, distributed message based algorithms can be used. These algorithms rely on the idea that a message sent by a vertex in a cycle will come back to itself. Distributed cycle detection algorithms are useful for processing large-scale graphs using a distributed graph processing system on a computer cluster (or supercomputer).
For directed graphs, distributed message based algorithms can be used. These algorithms rely on the idea that a message sent by a vertex in a cycle will come back to itself. Distributed cycle detection algorithms are useful for processing large-scale graphs using a distributed graph processing system on a computer cluster (or supercomputer).
对于有向图的环检测,可以使用基于分布式消息的算法。其概念是环中的某一个顶点发出了一条消息并最终返回,因此被称为 分布式环检测算法Distributed cycle detection algorithms。通过在计算机集群(或超级计算机)上使用分布式图形处理系统,该方法非常适合大规模图的运算。
Applications of cycle detection include the use of wait-for graphs to detect deadlocks in concurrent systems.
Applications of cycle detection include the use of wait-for graphs to detect deadlocks in concurrent systems.
环检测的应用还包括使用 等待图Wait-for graphs来检测并发系统中的 死锁Deadlocks。
环覆盖图
In his 1736 paper on the Seven Bridges of Königsberg, widely considered to be the birth of graph theory, Leonhard Euler proved that, for a finite undirected graph to have a closed walk that visits each edge exactly once, it is necessary and sufficient that it be connected except for isolated vertices (that is, all edges are contained in one component) and have even degree at each vertex. The corresponding characterization for the existence of a closed walk visiting each edge exactly once in a directed graph is that the graph be strongly connected and have equal numbers of incoming and outgoing edges at each vertex. In either case, the resulting walk is known as an Euler cycle or Euler tour. If a finite undirected graph has even degree at each of its vertices, regardless of whether it is connected, then it is possible to find a set of simple cycles that together cover each edge exactly once: this is Veblen's theorem When a connected graph does not meet the conditions of Euler's theorem, a closed walk of minimum length covering each edge at least once can nevertheless be found in polynomial time by solving the route inspection problem.
In his 1736 paper on the Seven Bridges of Königsberg, widely considered to be the birth of graph theory, Leonhard Euler proved that, for a finite undirected graph to have a closed walk that visits each edge exactly once, it is necessary and sufficient that it be connected except for isolated vertices (that is, all edges are contained in one component) and have even degree at each vertex. The corresponding characterization for the existence of a closed walk visiting each edge exactly once in a directed graph is that the graph be strongly connected and have equal numbers of incoming and outgoing edges at each vertex. In either case, the resulting walk is known as an Euler cycle or Euler tour. If a finite undirected graph has even degree at each of its vertices, regardless of whether it is connected, then it is possible to find a set of simple cycles that together cover each edge exactly once: this is Veblen's theorem. When a connected graph does not meet the conditions of Euler's theorem, a closed walk of minimum length covering each edge at least once can nevertheless be found in polynomial time by solving the route inspection problem.
莱昂哈德·欧拉Leonhard Euler在1736年发表的关于 柯尼斯堡七桥Seven Bridges of Königsberg的论文后来被广泛认为是图论的起源。论文中,欧拉做出了以下证明:对于一个具有封闭行走路线的有限无向图,要求访问者恰好经过每条边一次。其充要条件是除了孤立的顶点(即,所有边都被两两顶点相连)之外,其他每个顶点都是偶数度。一旦该有向图满足能一次性访问所有边不重复的特征,那么它就具有强连接性,并且每个顶点的进入次数和离开次数必定相等。无论哪种情况,其访问轨迹均被称为欧拉环或欧拉环游。如果一个有限的无向图在其每个顶点上都具有偶数度,那么不管其是否相连,均有可能找到一组简单的环,使满足恰好覆盖该图的每个边一次:这即是 维勃伦定理Veblen's theorem。当一个连通图不满足欧拉定理的条件时,通过解决 邮路问题Route inspection problem,可以在多项式时间中找到覆盖每个边的最短闭合路径。
The problem of finding a single simple cycle that covers each vertex exactly once, rather than covering the edges, is much harder. Such a cycle is known as a Hamiltonian cycle, and determining whether it exists is NP-complete.
The problem of finding a single simple cycle that covers each vertex exactly once, rather than covering the edges, is much harder. Such a cycle is known as a Hamiltonian cycle, and determining whether it exists is NP-complete.
相较之下,寻找覆盖每个顶点仅一次而不是覆盖连边的简单环问题要困难得多。这种环被称为 哈密顿环Hamiltonian cycle,确定其存在性的过程属于NP-完全问题。目前诸多包含哈密顿环的相关图类研究被发表。其中一个例子是 奥尔定理Ore's theorem,如果一个图中每个不相邻的顶点对的度数之和最少等于该图中顶点总数,那么该图中必然有哈密顿环。
The cycle double cover conjecture states that, for every bridgeless graph, there exists a multiset of simple cycles that covers each edge of the graph exactly twice. Proving that this is true (or finding a counterexample) remains an open problem.<ref>{{citation
The cycle double cover conjecture states that, for every bridgeless graph, there exists a multiset of simple cycles that covers each edge of the graph exactly twice. Proving that this is true (or finding a counterexample) remains an open problem.<ref>{{citation
双圈覆盖猜想Cycle double cover conjecture指出,对于每个无桥图,都存在一组简单环可以将图的每个边缘恰好覆盖两次。然而目前其是否成立(或找到反例)仍然是一个悬而未决的问题。
Graph classes defined by cycles 根据环定义的图类
Several important classes of graphs can be defined by or characterized by their cycles. These include:
Several important classes of graphs can be defined by or characterized by their cycles. These include:
图的几个重要类别可以由其环定义或表征。其中包括:
- Bipartite graph, a graph without odd cycles (cycles with an odd number of vertices).
- Cactus graph, a graph in which every nontrivial biconnected component is a cycle
- Cycle graph, a graph that consists of a single cycle.
- Chordal graph, a graph in which every induced cycle is a triangle
- Directed acyclic graph, a directed graph with no cycles
- Line perfect graph, a graph in which every odd cycle is a triangle
- Perfect graph, a graph with no induced cycles or their complements of odd length greater than three
- Pseudoforest, a graph in which each connected component has at most one cycle
- Strangulated graph, a graph in which every peripheral cycle is a triangle
- Strongly connected graph, a directed graph in which every edge is part of a cycle
- Triangle-free graph, a graph without three-vertex cycles
- 二分图Bipartite graph,其中无奇数环(具有奇数个顶点的环)。
- 仙人掌图Cactus graph,其中每个非平凡的双向连通分量都是一个环。
- 环图Cycle graph,由一个环组成的图。
- 弦图Chordal graph,其中每个导出环都是三角形。
- 有向无环图Directed acyclic graph,无环的有向图。
- 线完美图Line perfect graph,其中每个奇环都是三角形。
- 完美图Perfect graph,无导出环或大于3的奇数路径长度的环。
- 伪森林Pseudoforest,其中每个连通分量最多只有一个环。
- 绞窄图Strangulated graph,其中每个边环都是三角形。
- 强连通图Strongly connected graph,一种有向图,其中每个边都是环的一部分。
- 无三角形图Triangle-free graph,无三个顶点环的图
See also 其他参考资料
- Cycle detection in a sequence of iterated function values 通过迭代函数值序列进行环检测
== References 参考文献
==
- ↑ Diestel, Reinhard (2012), "1.9 Some linear algebra", Graph Theory, Graduate Texts in Mathematics, vol. 173, Springer, pp. 23–28.
- Balakrishnan, V. K. (2005). Schaum's outline of theory and problems of graph theory ([Nachdr.] ed.). McGraw–Hill. ISBN 978-0070054899.
- Bender, Edward A.; Williamson, S. Gill (2010). Lists, Decisions and Graphs. With an Introduction to Probability. https://books.google.fr/books?id=vaXv_yhefG8C.
Category:Graph theory objects
范畴: 图论对象
This page was moved from wikipedia:en:Cycle (graph theory). Its edit history can be viewed at 环/edithistory
此词条由Jie翻译。 由CecileLi初步审校。