图动力系统

此词条暂由水流心不竞初译，未经审校，带来阅读不便，请见谅。

In mathematics, the concept of graph dynamical systems can be used to capture a wide range of processes taking place on graphs or networks. A major theme in the mathematical and computational analysis of GDSs is to relate their structural properties (e.g. the network connectivity) and the global dynamics that result.

In mathematics, the concept of graph dynamical systems can be used to capture a wide range of processes taking place on graphs or networks. A major theme in the mathematical and computational analysis of GDSs is to relate their structural properties (e.g. the network connectivity) and the global dynamics that result.

在数学领域中， 图动态系统'Graph dynamical systems的概念可以用来捕捉发生在图或网络上的广泛的过程。Gds 数学和计算分析的一个主题是将它们的结构特性联系起来(如网络连接)和全球动力学的结果。

The work on GDSs considers finite graphs and finite state spaces. As such, the research typically involves techniques from, e.g., graph theory, combinatorics, algebra, and dynamical systems rather than differential geometry. In principle, one could define and study GDSs over an infinite graph (e.g. cellular automata or probabilistic cellular automata over [math]\displaystyle{ \mathbb{Z}^k }[/math] or interacting particle systems when some randomness is included), as well as GDSs with infinite state space (e.g. [math]\displaystyle{ \mathbb{R} }[/math] as in coupled map lattices); see, for example, Wu.^[1] In the following, everything is implicitly assumed to be finite unless stated otherwise.

The work on GDSs considers finite graphs and finite state spaces. As such, the research typically involves techniques from, e.g., graph theory, combinatorics, algebra, and dynamical systems rather than differential geometry. In principle, one could define and study GDSs over an infinite graph (e.g. cellular automata or probabilistic cellular automata over [math]\displaystyle{ \mathbb{Z}^k }[/math] or interacting particle systems when some randomness is included), as well as GDSs with infinite state space (e.g. [math]\displaystyle{ \mathbb{R} }[/math] as in coupled map lattices); see, for example, Wu. In the following, everything is implicitly assumed to be finite unless stated otherwise.

Gdss 的工作是研究有限图和有限状态空间。因此，研究通常涉及到的技术是图论，组合学，代数和动力系统，而不是微分几何。原则上，我们可以在一个无限图上定义和研究 gds (例如:。元胞自动机或概率元胞自动机在 math mathbb { z } ^ k / math 或相互作用的粒子系统(包括一些随机性)上，以及具有无限状态空间的 gds (例如:在耦合映象格子中的 math mathbb { r } / math) ; 例如，见 Wu。在下文中，除非另有说明，否则一切图和空间都默认为有限。

Formal definition 正式定义

A graph dynamical system is constructed from the following components:

图动力系统'Graph dynamical systems是由以下部分构成的:

块引号

A finite graph Y with vertex set v[Y] = {1,2, ... , n}. Depending on the context the graph can be directed or undirected.

具有变量集v[Y] = {1,2, ... , n}的有限图 Y。根据上下文，可以为有向图或无向图。

A state x_v for each vertex v of Y taken from a finite set K. The system state is the n-tuple x = (x₁, x₂, ... , x_n), and x[v] is the tuple consisting of the states associated to the vertices in the 1-neighborhood of v in Y (in some fixed order).

Y的取自有限集合“K”的每个顶点v的状态，“系统状态”是“n”元组“x”= (x₁, x₂, ... , x_n)，“x”[“v”]是由与垂直相关的状态组成的元组。

A vertex function f_v for each vertex v. The vertex function maps the state of vertex v at time t to the vertex state at time t + 1 based on the states associated to the 1-neighborhood of v in Y.

每个顶点v的顶点函数f_v 。顶点函数将时间“t”的顶点“v”的状态映射到时间t + 1 ，1基于与“Y”中“v”的1邻域相关的状态。

An update scheme specifying the mechanism by which the mapping of individual vertex states is carried out so as to induce a discrete dynamical system with map F: Kⁿ → Kⁿ.

一个“更新方案”，通过它可以实现对单个顶点状态的映射，从而得到一个映射为“F”的离散动力系统：“Kⁿ”。

/ blockquote

The phase space associated to a dynamical system with map F: Kⁿ → Kⁿ is the finite directed graph with vertex set Kⁿ and directed edges (x, F(x)). The structure of the phase space is governed by the properties of the graph Y, the vertex functions (f_i)_i, and the update scheme. The research in this area seeks to infer phase space properties based on the structure of the system constituents. The analysis has a local-to-global character.

The phase space associated to a dynamical system with map F: Kⁿ → Kⁿ is the finite directed graph with vertex set Kⁿ and directed edges (x, F(x)). The structure of the phase space is governed by the properties of the graph Y, the vertex functions (f_i)_i, and the update scheme. The research in this area seeks to infer phase space properties based on the structure of the system constituents. The analysis has a local-to-global character.

动力系统的相空间是有限有向图，其顶点集为 ksup n / sup，有向边(x，f (x))。相空间的结构由图 y 的性质、顶点函数(f 子 i / sub)子 i / sub 和更新方案决定。该领域的研究试图推断相空间特性的基础上的结构的系统组成。这种分析具有局部到全局的特点。

Generalized cellular automata (GCA) 广义细胞自动机

If, for example, the update scheme consists of applying the vertex functions synchronously one obtains the class of generalized cellular automata (CA). In this case, the global map F: Kⁿ → Kⁿ is given by

If, for example, the update scheme consists of applying the vertex functions synchronously one obtains the class of generalized cellular automata (CA). In this case, the global map F: Kⁿ → Kⁿ is given by

例如，如果新方案由同时应用顶点函数组成，那么我们获得Generalized cellular automata (GCA) 广义细胞自动机(CA)类。在这种情况下，整体映射 f: k sup n / sup → k sup n / sup 是由

[math]\displaystyle{ F(x)_v = f_v(x[v]) \;. }[/math]

数学 f (x) v v (x [ v ]) ; . / math

This class is referred to as generalized cellular automata since the classical or standard cellular automata are typically defined and studied over regular graphs or grids, and the vertex functions are typically assumed to be identical.

这个类别被称为Generalized cellular automata (GCA) 广义细胞自动机，因为经典的或标准的细胞自动机通常定义和研究在正则图或网格上，并且我们通常假定顶点函数是相同的。

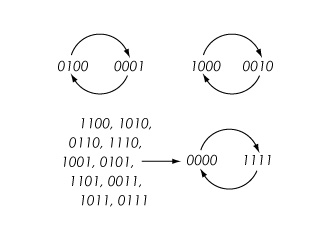
Example: Let Y be the circle graph on vertices {1,2,3,4} with edges {1,2}, {2,3}, {3,4} and {1,4}, denoted Circ₄. Let K = {0,1} be the state space for each vertex and use the function nor₃ : K³ → K defined by nor₃(x,y,z) = (1 + x)(1 + y)(1 + z) with arithmetic modulo 2 for all vertex functions. Then for example the system state (0,1,0,0) is mapped to (0, 0, 0, 1) using a synchronous update. All the transitions are shown in the phase space below.

Example: Let Y be the circle graph on vertices {1,2,3,4} with edges {1,2}, {2,3}, {3,4} and {1,4}, denoted Circ₄. Let K = {0,1} be the state space for each vertex and use the function nor₃ : K³ → K defined by nor₃(x,y,z) = (1 + x)(1 + y)(1 + z) with arithmetic modulo 2 for all vertex functions. Then for example the system state (0,1,0,0) is mapped to (0, 0, 0, 1) using a synchronous update. All the transitions are shown in the phase space below.

再例如: 设 y 是顶点{1,2,3,4}上的圆图，边{1,2} ，{2,3} ，{3,4}和{1,4} ，表示 Circ 子4 / 子。设 k {0,1}为每个顶点的状态空间，对所有顶点函数使用 nor 子3 / sub: k sup 3 / sup → k，该函数由 nor 子3 / sub (x，y，z)(1 + x)(1 + y)(1 + z)定义，算术模为2。然后，例如，使用同步更新将系统状态(0,1,0,0)映射到(0,0,0,1)。所有的相变都显示在下面的相空间中。

326

Sequential dynamical systems (SDS) 序列动力系统

If the vertex functions are applied asynchronously in the sequence specified by a word w = (w₁, w₂, ... , w_m) or permutation [math]\displaystyle{ \pi }[/math] = ( [math]\displaystyle{ \pi_1 }[/math], [math]\displaystyle{ \pi_2,\dots,\pi_n }[/math]) of v[Y] one obtains the class of Sequential dynamical systems (SDS).^[2] In this case it is convenient to introduce the Y-local maps F_i constructed from the vertex functions by

If the vertex functions are applied asynchronously in the sequence specified by a word w = (w₁, w₂, ... , w_m) or permutation [math]\displaystyle{ \pi }[/math] = ( [math]\displaystyle{ \pi_1 }[/math], [math]\displaystyle{ \pi_2,\dots,\pi_n }[/math]) of v[Y] one obtains the class of Sequential dynamical systems (SDS). In this case it is convenient to introduce the Y-local maps F_i constructed from the vertex functions by

如果顶点函数按照 v [ y ]中 w (w 子1 / sub，w 子2 / sub，... ，w 子 m / sub)或置换数学 pi / math (math pi 1 / math，math pi 2， dots， pi n / math)指定的序列异步应用，那么我们可以得到' Sequential dynamical systems (SDS) 序列动力系统的类。在这种情况下，可以方便地引入由顶点函数构造的 y 局部映射 f 子 i / 子

[math]\displaystyle{ F_i (x) = (x_1, x_2,\ldots, x_{i-1}, f_i(x[i]), x_{i+1}, \ldots , x_n) \;. }[/math]

[math]\displaystyle{ F_i (x) = (x_1, x_2,\ldots, x_{i-1}, f_i(x[i]), x_{i+1}, \ldots , x_n) \;.  }[/math]

数学 f i (x)(x1，x2， ldots，x { i-1} ，f i (x [ i ]) ，x { i + 1} ， ldots，xn) ;。数学

The SDS map F = [F_Y , w] : Kⁿ → Kⁿ is the function composition

The SDS map F = [F_Y map F = [F_Y , w] : Kⁿ → Kⁿ is the function composition

Sds 映射 f [ f sub y / sub，w ] : k sup n / sup → k sup n / sup 是复合函数

[math]\displaystyle{ [F_Y ,w] = F_{w(m)} \circ F_{w(m-1)} \circ \cdots \circ F_{w(2)} \circ F_{w(1)} \;. }[/math]

[math]\displaystyle{ [F_Y ,w] = F_{w(m)} \circ F_{w(m-1)} \circ \cdots \circ F_{w(2)} \circ F_{w(1)} \;.  }[/math]

数学[ f y，w ] f { w (m)} circ { w (m-1)} cdots circ { w (2)} circ { w (1)} ;。数学

If the update sequence is a permutation one frequently speaks of a permutation SDS to emphasize this point.

If the update sequence is a permutation one frequently speaks of a permutation SDS to emphasize this point.

如果更新序列是置换序列，则经常提到置换 SDS map F = [F_Y 以强调这一点。

Example: Let Y be the circle graph on vertices {1,2,3,4} with edges {1,2}, {2,3}, {3,4} and {1,4}, denoted Circ₄. Let K={0,1} be the state space for each vertex and use the function nor₃ : K³ → K defined by nor₃(x, y, z) = (1 + x)(1 + y)(1 + z) with arithmetic modulo 2 for all vertex functions. Using the update sequence (1,2,3,4) then the system state (0, 1, 0, 0) is mapped to (0, 0, 1, 0). All the system state transitions for this sequential dynamical system are shown in the phase space below.

Example: Let Y be the circle graph on vertices {1,2,3,4} with edges {1,2}, {2,3}, {3,4} and {1,4}, denoted Circ₄. Let K={0,1} be the state space for each vertex and use the function nor₃ : K³ → K defined by nor₃(x, y, z) = (1 + x)(1 + y)(1 + z) with arithmetic modulo 2 for all vertex functions. Using the update sequence (1,2,3,4) then the system state (0, 1, 0, 0) is mapped to (0, 0, 1, 0). All the system state transitions for this sequential dynamical system are shown in the phase space below.

例如: 设 y 是顶点{1,2,3,4}上的圆图，边{1,2} ，{2,3} ，{3,4}和{1,4} ，表示 Circ 子4 / 子。设 k {0,1}为每个顶点的状态空间，对所有顶点函数使用 nor 子3 / sub: k sup 3 / sup → k，该函数由 nor 子3 / sub (x，y，z)(1 + x)(1 + y)(1 + z)定义，算术模为2。使用更新序列(1,2,3,4) ，然后将系统状态(0,1,0,0)映射到(0,0,1,0)。所有的系统状态，转换下这个动力系统依次显示在下面的相空间。

326

Stochastic graph dynamical systems随机图动力系统

From, e.g., the point of view of applications it is interesting to consider the case where one or more of the components of a GDS contains stochastic elements. Motivating applications could include processes that are not fully understood (e.g. dynamics within a cell) and where certain aspects for all practical purposes seem to behave according to some probability distribution. There are also applications governed by deterministic principles whose description is so complex or unwieldy that it makes sense to consider probabilistic approximations.

例如，从应用程序的角度来看，考虑 GDS的一个或多个组件包含随机元素的情况是有趣的。激励应用程序可以包括不完全理解的过程(例如:。细胞内部的动力学) ，以及所有实际用途的某些方面似乎都符合某些概率分布。还有一些由确定性原理控制的应用程序，它们的描述是如此复杂或笨拙，以至于考虑概率近似是有意义的。

Every element of a graph dynamical system can be made stochastic in several ways. For example, in a sequential dynamical system the update sequence can be made stochastic. At each iteration step one may choose the update sequence w at random from a given distribution of update sequences with corresponding probabilities. The matching probability space of update sequences induces a probability space of SDS maps. A natural object to study in this regard is the Markov chain on state space induced by this collection of SDS maps. This case is referred to as update sequence stochastic GDS and is motivated by, e.g., processes where "events" occur at random according to certain rates (e.g. chemical reactions), synchronization in parallel computation/discrete event simulations, and in computational paradigms described later.

Every element of a graph dynamical system can be made stochastic in several ways. For example, in a sequential dynamical system the update sequence can be made stochastic. At each iteration step one may choose the update sequence w at random from a given distribution of update sequences with corresponding probabilities. The matching probability space of update sequences induces a probability space of SDS maps. A natural object to study in this regard is the Markov chain on state space induced by this collection of SDS maps. This case is referred to as update sequence stochastic GDS and is motivated by, e.g., processes where "events" occur at random according to certain rates (e.g. chemical reactions), synchronization in parallel computation/discrete event simulations, and in computational paradigms described later.

图动力系统graph dynamical system的每个元素都可以通过几种方式随机化。例如，在顺序动力系统中，更新序列可以是随机的。在每个迭代步骤中，可以从给定的更新序列分布中随机选择具有相应概率的更新序列 w。更新序列的匹配概率空间引出 SDS 地图的概率空间。在这方面需要研究的一个自然对象是 SDS 映射集合在状态空间上产生的 马尔可夫链Markov chain 。这种情况被称为更新序列随机 GDS，其动机是，例如，“事件”按照一定的速率随机发生的过程(例如:。化学反应) ，在并行计算 / 离散事件模拟中的同步，以及在后面描述的计算范例中的同步! ——确保这个交叉引用保持 / 工作。-->.

This specific example with stochastic update sequence illustrates two general facts for such systems: when passing to a stochastic graph dynamical system one is generally led to (1) a study of Markov chains (with specific structure governed by the constituents of the GDS), and (2) the resulting Markov chains tend to be large having an exponential number of states. A central goal in the study of stochastic GDS is to be able to derive reduced models.

这个带有随机更新序列的具体例子说明了这类系统的两个一般事实: 当传递到一个 随机图动力系统Stochastic graph dynamical system时，一般会导致: (1)对 马尔可夫链Markov chain 的研究(其具体结构由 GDS 的组成部分控制) ，和(2)由此产生的 马尔可夫链Markov chain 趋向于具有指数数量的状态。随机 GDS 研究的一个中心目标是能够推导出简化模型。

One may also consider the case where the vertex functions are stochastic, i.e., function stochastic GDS. For example, Random Boolean networks are examples of function stochastic GDS using a synchronous update scheme and where the state space is K = {0, 1}. Finite probabilistic cellular automata (PCA) is another example of function stochastic GDS. In principle the class of Interacting particle systems (IPS) covers finite and infinite PCA, but in practice the work on IPS is largely concerned with the infinite case since this allows one to introduce more interesting topologies on state space.

One may also consider the case where the vertex functions are stochastic, i.e., function stochastic GDS. For example, Random Boolean networks are examples of function stochastic GDS using a synchronous update scheme and where the state space is K = {0, 1}. Finite probabilistic cellular automata (PCA) is another example of function stochastic GDS. In principle the class of Interacting particle systems (IPS) covers finite and infinite PCA, but in practice the work on IPS is largely concerned with the infinite case since this allows one to introduce more interesting topologies on state space.

我们也可以考虑顶点函数是随机的情况，即函数是随机的 GDS。例如，随机布尔网络是函数随机 GDS 使用同步更新方案的例子，其中状态空间为 k {0,1}。有限概率 细胞自动机（PCA)是功能随机 GDS 的另一个例子。原则上，相互作用粒子系统(IPS)包括有限和无限的 PCA，但实际上，IPS 的工作主要是关注无限的情况，因为这允许在状态空间中引入更多有趣的拓扑Topologies 。

Applications应用

Graph dynamical systems constitute a natural framework for capturing distributed systems such as biological networks and epidemics over social networks, many of which are frequently referred to as complex systems.

图形动力系统Graph dynamical systems是捕获分布式系统(如生物网络和社会网络上的传染病)的自然框架，其中许多常常被称为 复杂系统Complex systems。

References参考文献

↑ Wu, Chai Wah (2005). "Synchronization in networks of nonlinear dynamical systems coupled via a directed graph". Nonlinearity. 18 (3): 1057–1064. Bibcode:2005Nonli..18.1057W. doi:10.1088/0951-7715/18/3/007.
↑ Mortveit, Henning S.; Reidys, Christian M. (2008). An introduction to sequential dynamical systems. Universitext. New York: Springer Verlag. ISBN 978-0-387-30654-4.

External links外部链接

Graph Dynamical Systems – A Mathematical Framework for Interaction-Based Systems, Their Analysis and Simulations by Henning Mortveit

Category:Dynamical systems

类别: 动力系统

Category:Algebra

类别: 代数

Category:Graph theory

范畴: 图论

Category:Combinatorics

分类: 组合数学

This page was moved from wikipedia:en:Graph dynamical system. Its edit history can be viewed at 图动力系统/edithistory

[wu-05-1] Wu, Chai Wah (2005). "Synchronization in networks of nonlinear dynamical systems coupled via a directed graph". Nonlinearity. 18 (3): 1057–1064. Bibcode:2005Nonli..18.1057W. doi:10.1088/0951-7715/18/3/007.

[Mortveit-08-2] Mortveit, Henning S.; Reidys, Christian M. (2008). An introduction to sequential dynamical systems. Universitext. New York: Springer Verlag. ISBN 978-0-387-30654-4.

[1]

[2]