层次聚类
在数据挖掘和统计学中,层次聚类 Hierarchical clustering(也被称为“层次聚类算法 hierarchical cluster analysis(HCA)”)是一种通过建立一个集群层次结构来聚类分析的方法。实现层次聚类的方法通常有两种:[1]
- 凝聚聚类 Agglomerative:这是一种“自上而下又自下而上/纵向”的方法:每个被观察数据从自己的簇类中开始,当一个观察组数据向上层移动时,成对的簇类集群被合并。
- 分裂聚类 Divisive: 这是一种“自上而下”的方法:所有的被观察数据都从一个簇类集群中开始,当一个簇类向下移动时,整个观察组数据群会递归地执行分割。
一般来说,合并和分裂是基于贪心算法 greedy algorithm决定的。层次聚类的结果 [2] 通常在树状图中呈现。
层次凝聚聚类 Hierarchical agglomerative clustering(HAC)标准算法的时间复杂度为[math]\displaystyle{ \mathcal{O}(n^3) }[/math] ,并且需要 [math]\displaystyle{ \mathcal{O}(n^2) }[/math] 占用内存,这使得它对于中等数据集来说效率太低了。然而,对于某些特殊情况,已知的最有效凝聚方法(复杂度 [math]\displaystyle{ \mathcal{O}(n^2) }[/math])是: SLINK 用于单连接聚类 Single-linkage clustering[3], CLINK用于完全连接聚类 complete-linkage clustering[4]。一般情况下的运行时可以缩减为[math]\displaystyle{ \mathcal{O}(n^2 \log n) }[/math] ,代价是进一步增加内存需求。在多数情况下,这种方法的内存消耗太大,并不实用。
除了单连接的特殊情况外,所有算法(除了时间复杂度为[math]\displaystyle{ \mathcal{O}(2^n) }[/math]的全局搜索 exhaustive search)都不能保证找到最优解。
分裂聚类全局搜索的时间复杂度为[math]\displaystyle{ \mathcal{O}(2^n) }[/math],但通常使用更快的启发式 heuristics来选择分裂,比如k-means。
簇异性 Cluster dissimilarity
为了决定哪些簇应该被组合起来(用于聚合),或者哪些簇应该被分离(用于分裂) ,测量簇之间的相异度 dissimilarity。在大多数层次聚类方法中,这是通过使用适当的度量 metric(两个簇之间的距离度量)和连接准则来实现的。连接标准决定了两个簇之间的距离函数。
度量标准 Metric
更多信息请查看度量标准 Metric
度量方式的选择将影响数据簇类的形状,因为某些元素依据一个距离可能彼此接近,而依据另一个距离可能彼此远离。例如,在一个二维空间中,点(1,0)和原点(0,0)之间的距离通常是1,但是点(1,1)和原点(0,0)之间的距离在曼哈顿距离下可以是2,在欧几里得度量下可以是 [math]\displaystyle{ \scriptstyle\sqrt{2} }[/math],在最大距离下可以是1。
一些常用的指标如下:[5]
| 名字 | 公式 |
|---|---|
| 欧氏距离 Euclidean distance | [math]\displaystyle{ \|a-b \|_2 = \sqrt{\sum_i (a_i-b_i)^2} }[/math] |
| 平方欧氏距离 Squared Euclidean distance | [math]\displaystyle{ \|a-b \|_2^2 = \sum_i (a_i-b_i)^2 }[/math] |
| 曼哈顿距离 Manhattan distance | [math]\displaystyle{ \|a-b \|_1 = \sum_i |a_i-b_i| }[/math] |
| 最大距离 Maximum distance | [math]\displaystyle{ \|a-b \|_\infty = \max_i |a_i-b_i| }[/math] |
| 马氏距离 Mahalanobis distance | [math]\displaystyle{ \sqrt{(a-b)^{\top}S^{-1}(a-b)} }[/math] 其中S是协方差矩阵 |
对于文本文字或其他非数字数据,常常使用汉明距离 Hamming distance或编辑距离 Levenshtein distance等度量标准。
通过对数据聚类健康心理学研究的回顾发现,在该研究领域已发表的研究中,最常见的距离测量方法是欧氏距离或平方欧氏距离。
连接准则 Linkage criteria
连接标准决定了集合内簇之间的距离作为两个簇之间距离的函数。簇A和簇B之间一些常用的连接标准如下:[6][7]
| 名字 | 公式 |
|---|---|
| 最大或完全连接聚类 | [math]\displaystyle{ \max \, \{\, d(a,b) : a \in A,\, b \in B \,\} }[/math] |
| 最小或单连接聚类 | [math]\displaystyle{ \min \, \{\, d(a,b) : a \in A,\, b \in B \,\} }[/math] |
| 未加权平均连接聚类 Unweighted average linkage clustering (或UPGMA) | [math]\displaystyle{ \frac{1}{|A|\cdot|B|} \sum_{a \in A }\sum_{ b \in B} d(a,b) }[/math] |
| 加权平均数连接聚类 Weighted average linkage clustering (或WPGMA) | [math]\displaystyle{ d(i \cup j, k) = \frac{d(i, k) + d(j, k)}{2} }[/math] |
| 质心连接集群 Centroid linkage clustering (或UPGMC) | [math]\displaystyle{ \|c_s - c_t \| }[/math]分别是 s类和 t类的中心. |
| 最小能量聚类Minimum energy clustering | [math]\displaystyle{ \frac {2}{nm}\sum_{i,j=1}^{n,m} \|a_i- b_j\|_2 - \frac {1}{n^2}\sum_{i,j=1}^{n} \|a_i-a_j\|_2 - \frac{1}{m^2}\sum_{i,j=1}^{m} \|b_i-b_j\|_2 }[/math] |
其中 d 是选定的度量单位。其他连接准则包括:
- 簇内方差之和。
- 候选簇从同一分布函数(V-连接 V-linkage)衍生的概率。
- k-最近邻 k-nearest-neighbour图 (KNN,图度连接)上的入度与出度的乘积[9]
讨论
层次聚类具有明显的优势,它可以使用任何有效的距离度量。事实上,观测本身也并不是必需的,层次聚类所需要用的只是一个距离矩阵。
凝聚聚类实例
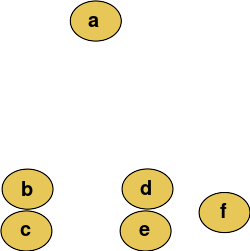
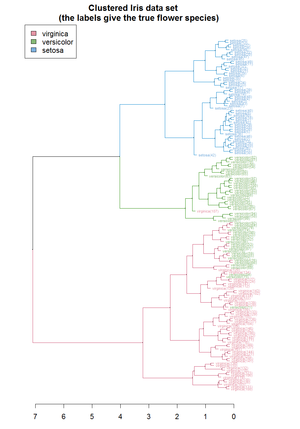
例如,假设要对这些数据进行聚类,将欧式距离作为度量。系统聚类树状图如下:
在给定的高度切割树状图中,将以选定的精度提供分区聚类。在这个示例中,在树状图的第二行(从顶部开始)之后切割将产生类别{a} {b c} {d e} {f}。在第三行之后进行切割将产生类别{a} {b c} {d e f},这是一个较为粗略的聚类,其数量少但簇群较大。
此方法通过逐步合并簇,从单个元素构建层次结构。在我们的示例中,有六个元素{a} {b} {c} {d} {e}和{f}。第一步是确定在集群中合并哪些元素。通常,我们希望根据选定的距离获取两个最接近的元素。
还可以选择在这个阶段构造一个距离矩阵 distance matrix,其中第i行第j列中的数字是 i和j,即为两个元素之间的距离。然后,随着聚类过程的推进,行和列随着聚类的合并和距离的更新而合并。这是实现这类聚类的常用方法,并且具有缓存簇之间的距离的优点。在单连接聚类 single-linkage clustering页面中描述了一个简单的凝聚聚类算法; 它适用于很多连接(见下文)。
假设我们已经合并了两个最接近的元素 b 和c,现在我们有以下簇{a}, {b, c}, {d}, {e} 和{f} ,并希望进一步合并它们。为此,我们需要计算{a} 和 {b c}之间的距离,从而定义两个簇之间的距离。
通常情况下的簇[math]\displaystyle{ \mathcal{A} }[/math]和 簇[math]\displaystyle{ \mathcal{B} }[/math]之间距离如下:
- 每个簇内元素之间的最大距离(又名完全连接聚类 complete-linkage clustering)
- [math]\displaystyle{ \max \{\, d(x,y) : x \in \mathcal{A},\, y \in \mathcal{B}\,\}. }[/math]
- 每个簇内的元素之间的最小距离(也称为单连接聚类 single-linkage clustering):
- [math]\displaystyle{ \min \{\, d(x,y) : x \in \mathcal{A},\, y \in \mathcal{B} \,\}. }[/math]
- 每个簇元素之间的平均距离(也称为平均连接聚类,UPGMA):
- [math]\displaystyle{ {1 \over {|\mathcal{A}|\cdot|\mathcal{B}|}}\sum_{x \in \mathcal{A}}\sum_{ y \in \mathcal{B}} d(x,y). }[/math]
- 所有簇内元素方差之和。
- 候选簇从同一分布函数(V-连接 V-linkage)衍生的概率。
在采用最小距离的情况下,随机选择一对元素,从而能够生成几个结构上不同的树状图。或者,同时连接所有绑定对,生成唯一的树状图。[13]
当簇数足够少时,人们可以停止聚类过程。有些联系也可能保证聚集发生在比先前聚集更大的聚集距离上,直到当聚集距离太远无法合并时可以停止聚集(距离标准)。然而也有例外,如采用质心连接,可能会发生逆转(反转 inversions,偏离超节拍 departures from ultrametricity)[14]。
分裂聚类 Divisive clustering
分裂聚类的基本原理被公布为分裂分析聚类 DIvisive ANAlysis Clustering,(DIANA)算法[15]。最初,所有数据都位于同一个集群中,然后最大的集群被拆分,依此类推,直到每个元素都是独立的。
由于每个聚类存在[math]\displaystyle{ O(2^n) }[/math]种划分方法,所以需要启发式算法。DIANA 选择平均相异度最大的对象,然后将所有对象移动到与新集群更相似的集群中。
软件
开源工具

- ALGLIB在C++ 和 C# 上以 [math]\displaystyle{ \mathcal{O}(2^n) }[/math] 的内存和 [math]\displaystyle{ \mathcal{O}(3^n) }[/math]的运行时间实现了几个层次聚类算法(单连接,完整链接,均值)。
- ELKI包括多种层次聚类算法,各种连接方法,同时包括高效运行,[3] CLINK[4] 安德伯格算法 Anderberg algorithms,从树状图和其他各种聚类分析 cluster analysis算法中进行灵活的聚类提取。
- Octave,与MATLAB类似的GNU在“连接”功能中实现了分层聚类。
- Orange,一个数据挖掘软件套件,包括层次聚类和交互式可视化树形图。
- R 有许多提供分层聚类功能的工具包。
- SciPy在python中实现分层聚类,包括高效的slink算法。
- scikit-learn还实现了Python中的层次聚类。
- Weka 包括层次聚类分析。
收费软件
- MATLAB 包括层次聚类分析。
- SAS PROC CLUSTER中包括层次聚类分析。
- SAS包括在群聚程序中进行层次聚类分析。
- Mathematica 包括层次聚类分析工具包。
- NCSS 包括层次聚类分析。
- SPSS包括层次聚类分析。
- QlucoreOmits 资源管理器包括层次聚类分析。
- Stata 包括层次聚类分析。
- CrimeStat 包括一个能够为地理位置提供图形输出的最近邻层次聚类算法。
参见
- 二进制空间划分 Binary space partitioning
- 层次包围盒 Bounding volume hierarchy
- 布朗群集 Brown clustering
- 遗传分类学 Cladistics
- 聚类分析 Cluster analysis
- 计算系统发生学 Computational phylogenetics
- CURE数据聚类算法 CURE data clustering algorithm
- Dasgupta的目标
- 树状图 Dendrogram
- 确定数据集中的簇数 Determining the number of clusters in a data set
- 网络层次聚类 Hierarchical clustering of networks
- 局部敏感哈希(LSH)方法 Locality-sensitive hashing
- 最近邻搜索 Nearest neighbor search
- 最近邻链算法 Nearest-neighbor chain algorithm
- 数值分类法 Numerical taxonomy
- OPTICS算法 OPTICS algorithm
- 统计距离 Statistical distance
- 持续同调 Persistent homology
参考文献
- ↑ Rokach, Lior, and Oded Maimon. "Clustering methods." Data mining and knowledge discovery handbook. Springer US, 2005. 321-352.
- ↑ Frank Nielsen (2016). "Chapter 8: Hierarchical Clustering". Introduction to HPC with MPI for Data Science. Springer. https://www.researchgate.net/publication/314700681.
- ↑ 3.0 3.1 R. Sibson (1973). "SLINK: an optimally efficient algorithm for the single-link cluster method" (PDF). The Computer Journal. British Computer Society. 16 (1): 30–34. doi:10.1093/comjnl/16.1.30.
- ↑ 4.0 4.1 D. Defays (1977). "An efficient algorithm for a complete-link method". The Computer Journal. British Computer Society. 20 (4): 364–366. doi:10.1093/comjnl/20.4.364.
- ↑ "The DISTANCE Procedure: Proximity Measures". SAS/STAT 9.2 Users Guide. SAS Institute. Retrieved 2009-04-26.
- ↑ "The CLUSTER Procedure: Clustering Methods". SAS/STAT 9.2 Users Guide. SAS Institute. Retrieved 2009-04-26.
- ↑ Székely, G. J.; Rizzo, M. L. (2005). "Hierarchical clustering via Joint Between-Within Distances: Extending Ward's Minimum Variance Method". Journal of Classification. 22 (2): 151–183. doi:10.1007/s00357-005-0012-9.
- ↑ 8.0 8.1 Ward, Joe H. (1963). "Hierarchical Grouping to Optimize an Objective Function". Journal of the American Statistical Association. 58 (301): 236–244. doi:10.2307/2282967.
- ↑ Zhang, Wei; Wang, Xiaogang; Zhao, Deli; Tang, Xiaoou (2012). Fitzgibbon, Andrew; Lazebnik, Svetlana; Perona, Pietro; Sato, Yoichi; Schmid, Cordelia (eds.). "Graph Degree Linkage: Agglomerative Clustering on a Directed Graph". Computer Vision – ECCV 2012. Lecture Notes in Computer Science (in English). Springer Berlin Heidelberg. 7572: 428–441. arXiv:1208.5092. Bibcode:2012arXiv1208.5092Z. doi:10.1007/978-3-642-33718-5_31. ISBN 9783642337185. 见: https://github.com/waynezhanghk/gacluster
- ↑ Zhang, et al. "Agglomerative clustering via maximum incremental path integral." Pattern Recognition (2013).
- ↑ Zhao, and Tang. "Cyclizing clusters via zeta function of a graph."Advances in Neural Information Processing Systems. 2008.
- ↑ Ma, et al. "Segmentation of multivariate mixed data via lossy data coding and compression." IEEE Transactions on Pattern Analysis and Machine Intelligence, 29(9) (2007): 1546-1562.
- ↑ Fernández, Alberto; Gómez, Sergio (2008). "Solving Non-uniqueness in Agglomerative Hierarchical Clustering Using Multidendrograms". Journal of Classification. 25 (1): 43–65. arXiv:cs/0608049. doi:10.1007/s00357-008-9004-x.
- ↑ Legendre, P.; Legendre, L. (2003). Numerical Ecology. Elsevier Science BV.
- ↑ Kaufman, L., & Roussew, P. J. (1990). Finding Groups in Data - An Introduction to Cluster Analysis. A Wiley-Science Publication John Wiley & Sons.
进一步阅读
- Kaufman, L.; Rousseeuw, P.J. (1990). Finding Groups in Data: An Introduction to Cluster Analysis (1 ed.). New York: John Wiley. https://archive.org/details/findinggroupsind00kauf.
- Hastie, Trevor; Tibshirani, Robert; Friedman, Jerome (2009). "14.3.12 Hierarchical clustering". The Elements of Statistical Learning (2nd ed.). New York: Springer. pp. 520–528. Archived from the original on 2009-11-10. http://www-stat.stanford.edu/~tibs/ElemStatLearn/. Retrieved 2009-10-20.
编者推荐
集智文章
棒不打鸳鸯:一种高效的聚类和社团发现算法
根据距离或相似度对数据点聚类,是研究诸多自然和社会问题的有力工具。而在各种聚类算法中,分层聚类具有特别的优势。近日,电子科技大学周涛教授领衔的研究组,在 Information Sciences 杂志发表论文,提出一种新的层次聚类算法。该算法在多领域的数据集中展示出超越同类算法的强大能力,在网络社团检测问题上具有广泛应用前景。
集智课程
聚类与判别
对事物分类是人们认识客观的基本方法,同时群体行为的解释可用分类的方法进行研究。
- 判别分析:在已知分为若干个类的前提下,获得判别模型,并用来判定观察对象的归属。
- 聚类分析:将对象归类的统计学方法。在不知道应分多少类合适的情况下,试图借助数理统计的方法用已收集到的资料找出研究对象的适当归类方法。是发掘海量信息的工具。
本课程中,樊瑛老师对聚类分析与判别分析进行了讲解。
本中文词条作者为Ryan翻译,CecileLi审校,薄荷编辑,欢迎在讨论页面留言。
本词条内容源自wikipedia及公开资料,遵守 CC3.0协议。