蚁群优化算法

此词条暂由Henry翻译。

}}

Ant behavior was the inspiration for the metaheuristic optimization technique

Ant behavior was the inspiration for the metaheuristic optimization technique

蚂蚁行为是元启发式优化技术的灵感来源

When a colony of ants is confronted with the choice of reaching their food via two different routes of which one is much shorter than the other, their choice is entirely random. However, those who use the shorter route reach the food faster and therefore go back and forth more often between the anthill and the food.

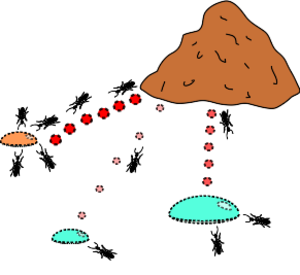
When a colony of ants is confronted with the choice of reaching their food via two different routes of which one is much shorter than the other, their choice is entirely random. However, those who use the shorter route reach the food faster and therefore go back and forth more often between the anthill and the food.

当一群蚂蚁面临选择通过两条不同的路径获取食物时，其中一条路径比另一条路径短得多，它们的选择完全是随机的。然而，那些使用较短的路线到达食物更快，因此往返于蚁丘和食物之间的频率更高。

In computer science and operations research, the ant colony optimization algorithm (ACO) is a probabilistic technique for solving computational problems which can be reduced to finding good paths through graphs. Artificial Ants stand for multi-agent methods inspired by the behavior of real ants.

In computer science and operations research, the ant colony optimization algorithm (ACO) is a probabilistic technique for solving computational problems which can be reduced to finding good paths through graphs. Artificial Ants stand for multi-agent methods inspired by the behavior of real ants.

在计算机科学和运筹学中， 蚁群优化算法ant colony optimization algorithm(ACO)是一种用于解决计算问题的概率技术，它可以简化为通过图表来寻找好的路径。人工蚂蚁是受真蚂蚁行为启发的多智能体方法。

The pheromone-based communication of biological ants is often the predominant paradigm used. Combinations of Artificial Ants and local search algorithms have become a method of choice for numerous optimization tasks involving some sort of graph, e.g., vehicle routing and internet routing. The burgeoning activity in this field has led to conferences dedicated solely to Artificial Ants, and to numerous commercial applications by specialized companies such as AntOptima.

The pheromone-based communication of biological ants is often the predominant paradigm used. Combinations of Artificial Ants and local search algorithms have become a method of choice for numerous optimization tasks involving some sort of graph, e.g., vehicle routing and internet routing. The burgeoning activity in this field has led to conferences dedicated solely to Artificial Ants, and to numerous commercial applications by specialized companies such as AntOptima.

基于信息素的生物蚂蚁通信往往是主要的范例使用。人工蚁群算法和局部搜索算法的结合已经成为许多优化任务的一种选择方法，这些优化任务涉及到一些图形，例如车辆路径和互联网路由。这一领域蓬勃发展的活动导致了专门讨论人工蚂蚁的会议，以及诸如 AntOptima 等专业公司的大量商业应用。

As an example, Ant colony optimization is a class of optimization algorithms modeled on the actions of an ant colony. Artificial 'ants' (e.g. simulation agents) locate optimal solutions by moving through a parameter space representing all possible solutions. Real ants lay down pheromones directing each other to resources while exploring their environment. The simulated 'ants' similarly record their positions and the quality of their solutions, so that in later simulation iterations more ants locate better solutions. One variation on this approach is the bees algorithm, which is more analogous to the foraging patterns of the honey bee, another social insect.

As an example, Ant colony optimization is a class of optimization algorithms modeled on the actions of an ant colony. Artificial 'ants' (e.g. simulation agents) locate optimal solutions by moving through a parameter space representing all possible solutions. Real ants lay down pheromones directing each other to resources while exploring their environment. The simulated 'ants' similarly record their positions and the quality of their solutions, so that in later simulation iterations more ants locate better solutions. One variation on this approach is the bees algorithm, which is more analogous to the foraging patterns of the honey bee, another social insect.

以蚁群算法为例，它是一种提出了一类以蚁群行为为模型的优化算法。人造「蚂蚁」(例如:模拟代理)通过移动的参数空间代表所有可能的解决方案定位最优解。真正的蚂蚁在探索自己的环境时，会产生信息素，互相指引对方寻找资源。模拟的“蚂蚁”类似地记录它们的位置和解决方案的质量，这样在随后的模拟迭代中，更多的蚂蚁找到更好的解决方案。这种方法的一个变种是蜜蜂算法，它更类似于另一种社会昆虫---- 蜜蜂的觅食模式。

This algorithm is a member of the ant colony algorithms family, in swarm intelligence methods, and it constitutes some metaheuristic optimizations. Initially proposed by Marco Dorigo in 1992 in his PhD thesis, the first algorithm was aiming to search for an optimal path in a graph, based on the behavior of ants seeking a path between their colony and a source of food. The original idea has since diversified to solve a wider class of numerical problems, and as a result, several problems have emerged, drawing on various aspects of the behavior of ants. From a broader perspective, ACO performs a model-based search and shares some similarities with estimation of distribution algorithms.

This algorithm is a member of the ant colony algorithms family, in swarm intelligence methods, and it constitutes some metaheuristic optimizations. Initially proposed by Marco Dorigo in 1992 in his PhD thesis, the first algorithm was aiming to search for an optimal path in a graph, based on the behavior of ants seeking a path between their colony and a source of food. The original idea has since diversified to solve a wider class of numerical problems, and as a result, several problems have emerged, drawing on various aspects of the behavior of ants. From a broader perspective, ACO performs a model-based search and shares some similarities with estimation of distribution algorithms.

这个算法是蚁群算法家族的一员，在群体智能方法中，它构成了一些元启发式优化。最初由 Marco Dorigo 在1992年的博士论文中提出，第一个算法的目的是在图中寻找最佳路径，基于蚂蚁的行为寻找一条在它们的群体和食物来源之间的路径。最初的想法已经多样化，以解决更广泛的数值问题，结果，出现了几个问题，借鉴了蚂蚁行为的各个方面。从更广泛的角度来看，蚁群算法实现了基于模型的搜索，并与分布估计算法具有一定的相似性。

Overview

概览

In the natural world, ants of some species (initially) wander randomly, and upon finding food return to their colony while laying down pheromone trails. If other ants find such a path, they are likely not to keep travelling at random, but instead to follow the trail, returning and reinforcing it if they eventually find food (see Ant communication).

In the natural world, ants of some species (initially) wander randomly, and upon finding food return to their colony while laying down pheromone trails. If other ants find such a path, they are likely not to keep travelling at random, but instead to follow the trail, returning and reinforcing it if they eventually find food (see Ant communication).

在自然世界中，一些物种的蚂蚁(最初)随机徘徊，一发现食物便回到它们的群落，同时产生信息素的踪迹。如果其他蚂蚁找到了这样一条路径，它们很可能不会继续随机行走，而是沿着这条路径前进，如果它们最终找到了食物，就会返回并加固这条路径(参见蚂蚁通讯)。

Over time, however, the pheromone trail starts to evaporate, thus reducing its attractive strength. The more time it takes for an ant to travel down the path and back again, the more time the pheromones have to evaporate. A short path, by comparison, gets marched over more frequently, and thus the pheromone density becomes higher on shorter paths than longer ones. Pheromone evaporation also has the advantage of avoiding the convergence to a locally optimal solution. If there were no evaporation at all, the paths chosen by the first ants would tend to be excessively attractive to the following ones. In that case, the exploration of the solution space would be constrained. The influence of pheromone evaporation in real ant systems is unclear, but it is very important in artificial systems.

Over time, however, the pheromone trail starts to evaporate, thus reducing its attractive strength. The more time it takes for an ant to travel down the path and back again, the more time the pheromones have to evaporate. A short path, by comparison, gets marched over more frequently, and thus the pheromone density becomes higher on shorter paths than longer ones. Pheromone evaporation also has the advantage of avoiding the convergence to a locally optimal solution. If there were no evaporation at all, the paths chosen by the first ants would tend to be excessively attractive to the following ones. In that case, the exploration of the solution space would be constrained. The influence of pheromone evaporation in real ant systems is unclear, but it is very important in artificial systems.

然而，随着时间的推移，信息素的踪迹开始蒸发，从而减少了它的吸引力。蚂蚁沿着路径往返需要的时间越长，信息素蒸发的时间就越长。相比之下，短路径更频繁地穿越，因此短路径上的信息素密度比长路径上的高。信息素蒸发还具有避免收敛到局部最优解的优点。如果根本没有蒸发，那么第一批蚂蚁选择的路径对于后面的蚂蚁来说就会非常有吸引力。在这种情况下，对解空间的探索将受到限制。信息素蒸发对实际蚂蚁系统的影响尚不清楚，但在人工系统中具有重要意义。

The overall result is that when one ant finds a good (i.e., short) path from the colony to a food source, other ants are more likely to follow that path, and positive feedback eventually leads to many ants following a single path. The idea of the ant colony algorithm is to mimic this behavior with "simulated ants" walking around the graph representing the problem to solve.

The overall result is that when one ant finds a good (i.e., short) path from the colony to a food source, other ants are more likely to follow that path, and positive feedback eventually leads to many ants following a single path. The idea of the ant colony algorithm is to mimic this behavior with "simulated ants" walking around the graph representing the problem to solve.

总的结果是，当一只蚂蚁找到一条从蚁群到食物来源的好的(即短的)路径时，其他蚂蚁更有可能遵循这条路径，正反馈最终导致许多蚂蚁走同一条路径。蚁群算法的思想是通过“模拟蚂蚁”在代表要解决问题的图上走来模拟这种行为。

Ambient networks of intelligent objects

智能物体的周围网络 New concepts are required since “intelligence” is no longer centralized but can be found throughout all minuscule objects. Anthropocentric concepts have been known to lead to the production of IT systems in which data processing, control units and calculating forces are centralized. These centralized units have continually increased their performance and can be compared to the human brain. The model of the brain has become the ultimate vision of computers. Ambient networks of intelligent objects and, sooner or later, a new generation of information systems which are even more diffused and based on nanotechnology, will profoundly change this concept. Small devices that can be compared to insects do not dispose of a high intelligence on their own. Indeed, their intelligence can be classed as fairly limited. It is, for example, impossible to integrate a high performance calculator with the power to solve any kind of mathematical problem into a biochip that is implanted into the human body or integrated in an intelligent tag which is designed to trace commercial articles. However, once those objects are interconnected they dispose of a form of intelligence that can be compared to a colony of ants or bees. In the case of certain problems, this type of intelligence can be superior to the reasoning of a centralized system similar to the brain.

New concepts are required since “intelligence” is no longer centralized but can be found throughout all minuscule objects. Anthropocentric concepts have been known to lead to the production of IT systems in which data processing, control units and calculating forces are centralized. These centralized units have continually increased their performance and can be compared to the human brain. The model of the brain has become the ultimate vision of computers. Ambient networks of intelligent objects and, sooner or later, a new generation of information systems which are even more diffused and based on nanotechnology, will profoundly change this concept. Small devices that can be compared to insects do not dispose of a high intelligence on their own. Indeed, their intelligence can be classed as fairly limited. It is, for example, impossible to integrate a high performance calculator with the power to solve any kind of mathematical problem into a biochip that is implanted into the human body or integrated in an intelligent tag which is designed to trace commercial articles. However, once those objects are interconnected they dispose of a form of intelligence that can be compared to a colony of ants or bees. In the case of certain problems, this type of intelligence can be superior to the reasoning of a centralized system similar to the brain.

我们需要新的概念，因为“智能”不再是集中的，而是可以在所有微小的物体中找到。以人为中心的概念已经被认为导致了 IT 系统的产生，其中数据处理、控制单元和计算力量是集中的。这些集中的单位不断地提高他们的表现，可以与人类的大脑相比较。大脑模型已经成为计算机的终极愿景。由智能物体构成的环境网络，以及基于纳米技术的新一代信息系统，迟早会深刻地改变这一概念。可以与昆虫相比较的小型设备本身并不具备高智能。事实上，他们的智力可以归类为相当有限。例如，不可能将一个有能力解决任何数学问题的高性能计算器集成到植入人体的生物芯片中，或者集成到一个用于跟踪商业文章的智能标签中。然而，一旦这些物体互相连接起来，它们就拥有了一种可以与一群蚂蚁或蜜蜂相提并论的智慧。在某些问题的情况下，这种类型的智能可能优于类似大脑的集中式系统的推理。

Nature offers several examples of how minuscule organisms, if they all follow the same basic rule, can create a form of collective intelligence on the macroscopic level. Colonies of social insects perfectly illustrate this model which greatly differs from human societies. This model is based on the co-operation of independent units with simple and unpredictable behavior. They move through their surrounding area to carry out certain tasks and only possess a very limited amount of information to do so. A colony of ants, for example, represents numerous qualities that can also be applied to a network of ambient objects. Colonies of ants have a very high capacity to adapt themselves to changes in the environment as well as an enormous strength in dealing with situations where one individual fails to carry out a given task. This kind of flexibility would also be very useful for mobile networks of objects which are perpetually developing. Parcels of information that move from a computer to a digital object behave in the same way as ants would do. They move through the network and pass from one knot to the next with the objective of arriving at their final destination as quickly as possible.

Nature offers several examples of how minuscule organisms, if they all follow the same basic rule, can create a form of collective intelligence on the macroscopic level. Colonies of social insects perfectly illustrate this model which greatly differs from human societies. This model is based on the co-operation of independent units with simple and unpredictable behavior. They move through their surrounding area to carry out certain tasks and only possess a very limited amount of information to do so. A colony of ants, for example, represents numerous qualities that can also be applied to a network of ambient objects. Colonies of ants have a very high capacity to adapt themselves to changes in the environment as well as an enormous strength in dealing with situations where one individual fails to carry out a given task. This kind of flexibility would also be very useful for mobile networks of objects which are perpetually developing. Parcels of information that move from a computer to a digital object behave in the same way as ants would do. They move through the network and pass from one knot to the next with the objective of arriving at their final destination as quickly as possible.

大自然提供了几个例子，说明如果微小的生物体都遵循同样的基本规律，它们是如何在宏观层面上创造出一种集体智慧的。社会性昆虫的群落完美地说明了这个模型，它与人类社会有很大的不同。该模型基于独立单元之间的合作，具有简单和不可预测的行为。他们穿过周围地区执行某些任务，但只掌握非常有限的信息。例如，一群蚂蚁代表了许多特性，这些特性也可以应用到环境对象的网络中。蚂蚁群体具有很高的适应环境变化的能力，并且在处理个体无法完成某项任务的情况时具有巨大的力量。这种灵活性对于不断发展的移动对象网络也是非常有用的。从计算机到数字物体的信息包和蚂蚁的行为一样。它们穿过网络，从一个节点传到下一个节点，目的是尽快到达最终目的地。

Artificial pheromone system

人工信息素系统 Pheromone-based communication is one of the most effective ways of communication which is widely observed in nature. Pheromone is used by social insects such as

Pheromone-based communication is one of the most effective ways of communication which is widely observed in nature. Pheromone is used by social insects such as

基于信息素的通信是自然界中普遍存在的最有效的通信方式之一。信息素用于社会昆虫，如

bees, ants and termites; both for inter-agent and agent-swarm communications. Due to its feasibility, artificial pheromones have been adopted in multi-robot and swarm robotic systems. Pheromone-based communication was implemented by different means such as chemical or physical (RFID tags, light, sound) ways. However, those implementations were not able to replicate all the aspects of pheromones as seen in nature.

bees, ants and termites; both for inter-agent and agent-swarm communications. Due to its feasibility, artificial pheromones have been adopted in multi-robot and swarm robotic systems. Pheromone-based communication was implemented by different means such as chemical or physical (RFID tags, light, sound) ways. However, those implementations were not able to replicate all the aspects of pheromones as seen in nature.

蜜蜂、蚂蚁和白蚁; 都用于内部代理和代理群通信。由于其可行性，人工信息素已被应用于多机器人和群机器人系统中。基于信息素的通信是通过化学或物理(RFID 标签、光、声)方式实现的。然而，这些实现并不能复制信息素的所有方面。

Using projected light was presented in an 2007 IEEE paper by Garnier, Simon, et al. as an experimental setup to study pheromone-based communication with micro autonomous robots. Another study that proposed a novel pheromone communication method, COSΦ, for a swarm robotic system is based on precise and fast visual localization.

Using projected light was presented in an 2007 IEEE paper by Garnier, Simon, et al. as an experimental setup to study pheromone-based communication with micro autonomous robots. Another study that proposed a novel pheromone communication method, COSΦ, for a swarm robotic system is based on precise and fast visual localization.

2007年，由 Garnier，Simon 等人在 IEEE 的一篇论文中提出了使用投射光作为研究信息素与微型自主机器人通信的实验装置。另一项针对群机器人系统的研究提出了一种新颖的信息素通信方法 cosφ，该方法基于精确快速的视觉定位。

The system allows simulation of a virtually unlimited number of different pheromones and provides the result of their interaction as a gray-scale image on a horizontal LCD screen that the robots move on. In order to demonstrate the pheromone communication method, Colias autonomous micro robot was deployed as the swarm robotic platform.

The system allows simulation of a virtually unlimited number of different pheromones and provides the result of their interaction as a gray-scale image on a horizontal LCD screen that the robots move on. In order to demonstrate the pheromone communication method, Colias autonomous micro robot was deployed as the swarm robotic platform.

该系统可以模拟几乎无限数量的不同信息素，并在机器人移动的水平 LCD 屏幕上以灰度图像的形式提供它们相互作用的结果。为了演示信息素通信方法，自主微型机器人Colias调动为群体机器人平台。

Algorithm and formulae

算法和公式 In the ant colony optimization algorithms, an artificial ant is a simple computational agent that searches for good solutions to a given optimization problem. To apply an ant colony algorithm, the optimization problem needs to be converted into the problem of finding the shortest path on a weighted graph. In the first step of each iteration, each ant stochastically constructs a solution, i.e. the order in which the edges in the graph should be followed. In the second step, the paths found by the different ants are compared. The last step consists of updating the pheromone levels on each edge.

In the ant colony optimization algorithms, an artificial ant is a simple computational agent that searches for good solutions to a given optimization problem. To apply an ant colony algorithm, the optimization problem needs to be converted into the problem of finding the shortest path on a weighted graph. In the first step of each iteration, each ant stochastically constructs a solution, i.e. the order in which the edges in the graph should be followed. In the second step, the paths found by the different ants are compared. The last step consists of updating the pheromone levels on each edge.

在蚁群算法中，人工蚂蚁是一种简单的计算代理，可以为给定的最佳化问题寻找好的解决方案。为了应用蚁群算法，需要将最佳化问题问题转化为在加权图上寻找最短路径的问题。在每个迭代的第一步，每个随机构造一个解，即。图中的边应遵循的顺序。在第二步中，比较了不同蚂蚁发现的路径。最后一步是更新每个边上的信息素水平。

procedure ACO_MetaHeuristic is

procedure ACO_MetaHeuristic is

过程 ACO _ 元启发式是

    while not_termination do

    while not_termination do

而不是终止合同

        generateSolutions()

        generateSolutions()

概要解答()

        daemonActions()

        daemonActions()

daemonActions ()

        pheromoneUpdate()

        pheromoneUpdate()

信息素更新()

    repeat

    repeat

重复

end procedure

end procedure

结束过程

Edge selection

Each ant needs to construct a solution to move through the graph. To select the next edge in its tour, an ant will consider the length of each edge available from its current position, as well as the corresponding pheromone level. At each step of the algorithm, each ant moves from a state [math]\displaystyle{ x }[/math] to state [math]\displaystyle{ y }[/math], corresponding to a more complete intermediate solution. Thus, each ant [math]\displaystyle{ k }[/math] computes a set [math]\displaystyle{ A_k(x) }[/math] of feasible expansions to its current state in each iteration, and moves to one of these in probability. For ant [math]\displaystyle{ k }[/math], the probability [math]\displaystyle{ p_{xy}^k }[/math] of moving from state [math]\displaystyle{ x }[/math] to state [math]\displaystyle{ y }[/math] depends on the combination of two values, the attractiveness [math]\displaystyle{ \eta_{xy} }[/math] of the move, as computed by some heuristic indicating the a priori desirability of that move and the trail level [math]\displaystyle{ \tau_{xy} }[/math] of the move, indicating how proficient it has been in the past to make that particular move. The trail level represents a posteriori indication of the desirability of that move.

Each ant needs to construct a solution to move through the graph. To select the next edge in its tour, an ant will consider the length of each edge available from its current position, as well as the corresponding pheromone level. At each step of the algorithm, each ant moves from a state [math]\displaystyle{ x }[/math] to state [math]\displaystyle{ y }[/math], corresponding to a more complete intermediate solution. Thus, each ant [math]\displaystyle{ k }[/math] computes a set [math]\displaystyle{ A_k(x) }[/math] of feasible expansions to its current state in each iteration, and moves to one of these in probability. For ant [math]\displaystyle{ k }[/math], the probability [math]\displaystyle{ p_{xy}^k }[/math] of moving from state [math]\displaystyle{ x }[/math] to state [math]\displaystyle{ y }[/math] depends on the combination of two values, the attractiveness [math]\displaystyle{ \eta_{xy} }[/math] of the move, as computed by some heuristic indicating the a priori desirability of that move and the trail level [math]\displaystyle{ \tau_{xy} }[/math] of the move, indicating how proficient it has been in the past to make that particular move. The trail level represents a posteriori indication of the desirability of that move.

每只蚂蚁都需要构造一个解来移动图形。为了在它的旅行中选择下一条边，蚂蚁会考虑每条边从它当前位置可以获得的长度，以及相应的信息素水平。在算法的每个步骤中，每个蚂蚁从一个状态 < math > x </math > 移动到状态 < math > y </math > ，对应于一个更完整的中间解。因此，每个蚂蚁在每次迭代中计算一组可行展开式到它的当前状态，并移动到其中一个概率上。对于蚂蚁来说，从数学状态到数学状态的概率取决于两个值的组合---- 吸引力，数学状态到数学状态的概率。试验水平代表了一个后验指示的愿望，这一举动。

In general, the [math]\displaystyle{ k }[/math]th ant moves from state [math]\displaystyle{ x }[/math] to state [math]\displaystyle{ y }[/math] with probability

In general, the [math]\displaystyle{ k }[/math]th ant moves from state [math]\displaystyle{ x }[/math] to state [math]\displaystyle{ y }[/math] with probability

一般来说，蚂蚁从状态“数学”移动到状态“数学”移动到状态“数学”移动到状态“数学”

[math]\displaystyle{ \lt math\gt 《数学》 p_{xy}^k = p_{xy}^k = 1 = 0 = 0 = 0 \frac \frac 压裂 { (\tau_{xy}^{\alpha}) (\eta_{xy}^{\beta}) } { (\tau_{xy}^{\alpha}) (\eta_{xy}^{\beta}) } {(tau _ { xy } ^ { alpha })(eta _ { xy } ^ { beta })} { \sum_{z\in \mathrm{allowed}_x} (\tau_{xz}^{\alpha}) (\eta_{xz}^{\beta}) } { \sum_{z\in \mathrm{allowed}_x} (\tau_{xz}^{\alpha}) (\eta_{xz}^{\beta}) } { sum _ { z in mathrm { allowed } _ x }(tau _ { xz } ^ { alpha })(eta _ { xz } ^ { beta })} }[/math]

</math>

数学

where

where

在哪里

[math]\displaystyle{ \tau_{xy} }[/math] is the amount of pheromone deposited for transition from state [math]\displaystyle{ x }[/math] to [math]\displaystyle{ y }[/math], 0 ≤ [math]\displaystyle{ \alpha }[/math] is a parameter to control the influence of [math]\displaystyle{ \tau_{xy} }[/math], [math]\displaystyle{ \eta_{xy} }[/math] is the desirability of state transition [math]\displaystyle{ xy }[/math] (a priori knowledge, typically [math]\displaystyle{ 1/d_{xy} }[/math], where [math]\displaystyle{ d }[/math] is the distance) and [math]\displaystyle{ \beta }[/math] ≥ 1 is a parameter to control the influence of [math]\displaystyle{ \eta_{xy} }[/math]. [math]\displaystyle{ \tau_{xz} }[/math] and [math]\displaystyle{ \eta_{xz} }[/math] represent the trail level and attractiveness for the other possible state transitions.

[math]\displaystyle{ \tau_{xy} }[/math] is the amount of pheromone deposited for transition from state [math]\displaystyle{ x }[/math] to [math]\displaystyle{ y }[/math], 0 ≤ [math]\displaystyle{ \alpha }[/math] is a parameter to control the influence of [math]\displaystyle{ \tau_{xy} }[/math], [math]\displaystyle{ \eta_{xy} }[/math] is the desirability of state transition [math]\displaystyle{ xy }[/math] (a priori knowledge, typically [math]\displaystyle{ 1/d_{xy} }[/math], where [math]\displaystyle{ d }[/math] is the distance) and [math]\displaystyle{ \beta }[/math] ≥ 1 is a parameter to control the influence of [math]\displaystyle{ \eta_{xy} }[/math]. [math]\displaystyle{ \tau_{xz} }[/math] and [math]\displaystyle{ \eta_{xz} }[/math] represent the trail level and attractiveness for the other possible state transitions.

是从状态 < math > x </math > 到 < math > y </math > 的信息素沉积量，0≤ < math > alpha </math > 是一个控制 < math > tau { xy > </math > 影响的参数,状态转换的可取性是指状态转换对数学的可取性(先验知识，通常是数学知识，其中数学知识是距离)和数学知识是控制数学知识影响的参数。< math > tau _ { xz } </math > 和 < math > eta _ { xz } </math > 表示其他可能的状态转换的轨迹级别和吸引力。

Pheromone update

Trails are usually updated when all ants have completed their solution, increasing or decreasing the level of trails corresponding to moves that were part of "good" or "bad" solutions, respectively. An example of a global pheromone updating rule is

Trails are usually updated when all ants have completed their solution, increasing or decreasing the level of trails corresponding to moves that were part of "good" or "bad" solutions, respectively. An example of a global pheromone updating rule is

当所有的蚂蚁都完成了他们的解决方案，路径通常更新，增加或减少路径的水平对应的移动，是“好”或“坏”的解决方案的一部分，分别。全局信息素更新规则的一个例子是

[math]\displaystyle{ \lt math\gt 《数学》 \tau_{xy} \leftarrow \tau_{xy} \leftarrow 左眼 (1-\rho)\tau_{xy} + \sum_{k}\Delta \tau^{k}_{xy} (1-\rho)\tau_{xy} + \sum_{k}\Delta \tau^{k}_{xy} (1-rho) tau _ { xy } + sum _ { k } Delta tau ^ { k } _ { xy } }[/math]

</math>

数学

where [math]\displaystyle{ \tau_{xy} }[/math] is the amount of pheromone deposited for a state transition [math]\displaystyle{ xy }[/math], [math]\displaystyle{ \rho }[/math] is the pheromone evaporation coefficient and [math]\displaystyle{ \Delta \tau^{k}_{xy} }[/math] is the amount of pheromone deposited by [math]\displaystyle{ k }[/math]th ant, typically given for a TSP problem (with moves corresponding to arcs of the graph) by

where [math]\displaystyle{ \tau_{xy} }[/math] is the amount of pheromone deposited for a state transition [math]\displaystyle{ xy }[/math], [math]\displaystyle{ \rho }[/math] is the pheromone evaporation coefficient and [math]\displaystyle{ \Delta \tau^{k}_{xy} }[/math] is the amount of pheromone deposited by [math]\displaystyle{ k }[/math]th ant, typically given for a TSP problem (with moves corresponding to arcs of the graph) by

其中，tau { xy } </math > 是一个状态转换的信息素沉积量 < math > xy </math > ，< math > rho </math > 是信息素蒸发系数，< math > Delta tau ^ { xy } </math > 是数学 < k </math > 蚂蚁沉积的信息素沉积量，通常用于 TSP 问题(与图中弧线相对应的移动)

[math]\displaystyle{ \lt math\gt 《数学》 \Delta \tau^{k}_{xy} = \Delta \tau^{k}_{xy} = 3. d \begin{cases} \begin{cases} 开始{ cases } Q/L_k & \mbox{if ant }k\mbox{ uses curve }xy\mbox{ in its tour} \\ Q/L_k & \mbox{if ant }k\mbox{ uses curve }xy\mbox{ in its tour} \\ Q/L _ k & mbox { if ant } k mbox { use curve } xy mbox { in its tour } 0 & \mbox{otherwise} 0 & \mbox{otherwise} 0 & mbox { otherwise } \end{cases} \end{cases} 结束{ cases } }[/math]

</math>

数学

where [math]\displaystyle{ L_k }[/math] is the cost of the [math]\displaystyle{ k }[/math]th ant's tour (typically length) and [math]\displaystyle{ Q }[/math] is a constant.

where [math]\displaystyle{ L_k }[/math] is the cost of the [math]\displaystyle{ k }[/math]th ant's tour (typically length) and [math]\displaystyle{ Q }[/math] is a constant.

其中 l _ k </math > 是蚂蚁旅行的费用(通常是长度) ，q </math > 是一个常数。

Common extensions

Here are some of the most popular variations of ACO algorithms.

Here are some of the most popular variations of ACO algorithms.

下面是一些最流行的 ACO 算法变体。

Ant System (AS)

The Ant System is the first ACO algorithm. This algorithm corresponds to the one presented above. It was developed by Dorigo.

The Ant System is the first ACO algorithm. This algorithm corresponds to the one presented above. It was developed by Dorigo.

蚁群算法是第一种蚁群算法。此算法与上述算法相对应。它是由 Dorigo 开发的。

Ant Colony System (ACS)

In the Ant Colony System algorithm, the original Ant System was modified in three aspects: (i) the edge selection is biased towards exploitation (i.e. favoring the probability of selecting the shortest edges with a large amount of pheromone); (ii) while building a solution, ants change the pheromone level of the edges they are selecting by applying a local pheromone updating rule; (iii) at the end of each iteration, only the best ant is allowed to update the trails by applying a modified global pheromone updating rule.

In this algorithm, the global best solution deposits pheromone on its trail after every iteration (even if this trail has not been revisited), along with all the other ants.

在这种算法中，全局最优解在每次迭代之后(即使这条路径没有被重新访问)与其他所有蚂蚁一起将信息素存放在它的路径上。

Elitist Ant System

In this algorithm, the global best solution deposits pheromone on its trail after every iteration (even if this trail has not been revisited), along with all the other ants.

This algorithm controls the maximum and minimum pheromone amounts on each trail. Only the global best tour or the iteration best tour are allowed to add pheromone to its trail. To avoid stagnation of the search algorithm, the range of possible pheromone amounts on each trail is limited to an interval [τ_max,τ_min]. All edges are initialized to τ_max to force a higher exploration of solutions. The trails are reinitialized to τ_max when nearing stagnation.

该算法控制每条路线上信息素的最大和最小数量。只有全局最优旅行或迭代最优旅行才允许在其轨迹中添加信息素。为了避免搜索算法的停滞不前，每条路径上可能的信息素数量范围被限制在一个区间[ τ < sub > max ，τ < sub > min ]。所有边都被初始化为 τ < sub > > max ，以迫使更高的解决方案探索。当接近停滞状态时，轨迹重新初始化为 τ < sub > max 。

Max-Min Ant System (MMAS)

This algorithm controls the maximum and minimum pheromone amounts on each trail. Only the global best tour or the iteration best tour are allowed to add pheromone to its trail. To avoid stagnation of the search algorithm, the range of possible pheromone amounts on each trail is limited to an interval [τ_max,τ_min]. All edges are initialized to τ_max to force a higher exploration of solutions. The trails are reinitialized to τ_max when nearing stagnation.

All solutions are ranked according to their length. Only a fixed number of the best ants in this iteration are allowed to update their trials. The amount of pheromone deposited is weighted for each solution, such that solutions with shorter paths deposit more pheromone than the solutions with longer paths.

所有的解决方案都是根据它们的长度来排序的。在这个迭代中，只有一定数量的最优秀的蚂蚁被允许更新它们的试验。信息素沉积量的权重每个解决方案，使解决方案与短路径沉积更多的信息素比较长的路径。

Rank-based Ant System (ASrank)

All solutions are ranked according to their length. Only a fixed number of the best ants in this iteration are allowed to update their trials. The amount of pheromone deposited is weighted for each solution, such that solutions with shorter paths deposit more pheromone than the solutions with longer paths.

The pheromone deposit mechanism of COAC is to enable ants to search for solutions collaboratively and effectively. By using an orthogonal design method, ants in the feasible domain can explore their chosen regions rapidly and efficiently, with enhanced global search capability and accuracy. The orthogonal design method and the adaptive radius adjustment method can also be extended to other optimization algorithms for delivering wider advantages in solving practical problems.

COAC 的信息素存储机制是使蚂蚁能够协同有效地寻找解决方案。利用正交设计方法，可行域中的蚂蚁可以快速有效地搜索所选区域，提高了全局搜索能力和准确性。正交设计法和自适应半径调整法也可以推广到其他优化算法中，在解决实际问题时具有更广泛的优势。

Continuous Orthogonal Ant Colony (COAC)

The pheromone deposit mechanism of COAC is to enable ants to search for solutions collaboratively and effectively. By using an orthogonal design method, ants in the feasible domain can explore their chosen regions rapidly and efficiently, with enhanced global search capability and accuracy. The orthogonal design method and the adaptive radius adjustment method can also be extended to other optimization algorithms for delivering wider advantages in solving practical problems.

It is a recursive form of ant system which divides the whole search domain into several sub-domains and solves the objective on these subdomains. The results from all the subdomains are compared and the best few of them are promoted for the next level. The subdomains corresponding to the selected results are further subdivided and the process is repeated until an output of desired precision is obtained. This method has been tested on ill-posed geophysical inversion problems and works well.

它是蚂蚁系统的一种递归形式，将整个搜索域划分为若干子域，并在这些子域上求解目标。对所有子域的结果进行比较，并将其中最好的几个子域提升到下一个级别。与选定结果相对应的子区域被进一步细分，并重复这个过程，直到获得所需精度的输出。该方法在不适定地球物理反演问题中得到了验证，效果良好。

Recursive Ant Colony Optimization

It is a recursive form of ant system which divides the whole search domain into several sub-domains and solves the objective on these subdomains. The results from all the subdomains are compared and the best few of them are promoted for the next level. The subdomains corresponding to the selected results are further subdivided and the process is repeated until an output of desired precision is obtained. This method has been tested on ill-posed geophysical inversion problems and works well.

For some versions of the algorithm, it is possible to prove that it is convergent (i.e., it is able to find the global optimum in finite time). The first evidence of convergence for an ant colony algorithm was made in 2000, the graph-based ant system algorithm, and later on for the ACS and MMAS algorithms. Like most metaheuristics, it is very difficult to estimate the theoretical speed of convergence. A performance analysis of a continuous ant colony algorithm with respect to its various parameters (edge selection strategy, distance measure metric, and pheromone evaporation rate) showed that its performance and rate of convergence are sensitive to the chosen parameter values, and especially to the value of the pheromone evaporation rate. In 2004, Zlochin and his colleagues showed that COAC-type algorithms could be assimilated methods of stochastic gradient descent, on the cross-entropy and estimation of distribution algorithm. They proposed these metaheuristics as a "research-based model".

对于某些版本的算法，可以证明它是收敛的(也就是说，它能在有限时间内找到全局最优解)。蚁群算法的收敛性在2000年首次得到证实，基于图的蚂蚁系统算法，以及后来的 ACS 和 MMAS 算法。和大多数启发式算法一样，很难估计理论上的收敛速度。通过对连续蚁群算法各参数(边缘选择策略、距离测度和信息素蒸发率)的性能分析，表明蚁群算法的性能和收敛速度对参数的选择，特别是信息素蒸发率的选择非常敏感。在2004年，Zlochin 和他的同事们展示了 coac 类型的算法可以同化随机梯度下降的方法，比如交叉熵和分布估计算法。他们提出这些元启发式作为一个“基于研究的模型”。

Convergence

For some versions of the algorithm, it is possible to prove that it is convergent (i.e., it is able to find the global optimum in finite time). The first evidence of convergence for an ant colony algorithm was made in 2000, the graph-based ant system algorithm, and later on for the ACS and MMAS algorithms. Like most metaheuristics, it is very difficult to estimate the theoretical speed of convergence. A performance analysis of a continuous ant colony algorithm with respect to its various parameters (edge selection strategy, distance measure metric, and pheromone evaporation rate) showed that its performance and rate of convergence are sensitive to the chosen parameter values, and especially to the value of the pheromone evaporation rate. In 2004, Zlochin and his colleagues showed that COAC-type algorithms could be assimilated methods of stochastic gradient descent, on the cross-entropy and estimation of distribution algorithm. They proposed these metaheuristics as a "research-based model".

[背包问题: 相对于数量更多但营养更少的糖，蚂蚁更喜欢小滴的蜂蜜]

Ant colony optimization algorithms have been applied to many combinatorial optimization problems, ranging from quadratic assignment to protein folding or routing vehicles and a lot of derived methods have been adapted to dynamic problems in real variables, stochastic problems, multi-targets and parallel implementations.

从二次赋值到蛋白质折叠或路径选择问题，蚁群算法已经被应用于许多组合优化问题，许多派生方法已经被应用于实变量、随机问题、多目标和并行实现的动态问题。

Applications

It has also been used to produce near-optimal solutions to the travelling salesman problem. They have an advantage over simulated annealing and genetic algorithm approaches of similar problems when the graph may change dynamically; the ant colony algorithm can be run continuously and adapt to changes in real time. This is of interest in network routing and urban transportation systems.

它也被用来产生接近最佳的解决方案的旅行推销员问题。当图形可能发生动态变化时，它们比模拟退火算法和遗传算法具有优势; 蚁群算法可以连续运行并实时适应变化。这是在网络路由和城市交通系统的兴趣。

Knapsack problem: The ants prefer the smaller drop of honey over the more abundant, but less nutritious, sugar

Ant colony optimization algorithms have been applied to many combinatorial optimization problems, ranging from quadratic assignment to protein folding or routing vehicles and a lot of derived methods have been adapted to dynamic problems in real variables, stochastic problems, multi-targets and parallel implementations.

The first ACO algorithm was called the ant system and it was aimed to solve the travelling salesman problem, in which the goal is to find the shortest round-trip to link a series of cities. The general algorithm is relatively simple and based on a set of ants, each making one of the possible round-trips along the cities. At each stage, the ant chooses to move from one city to another according to some rules:

第一个蚁群算法被称为蚂蚁系统，它的目标是解决旅行推销员问题，其中的目标是找到最短的往返连接一系列城市。一般算法相对简单，基于一组蚂蚁，每个蚂蚁沿着城市进行一次可能的往返旅行。在每个阶段，蚂蚁都会根据一些规则从一个城市迁移到另一个城市:

It has also been used to produce near-optimal solutions to the travelling salesman problem. They have an advantage over simulated annealing and genetic algorithm approaches of similar problems when the graph may change dynamically; the ant colony algorithm can be run continuously and adapt to changes in real time. This is of interest in network routing and urban transportation systems.

It must visit each city exactly once;

它必须每个城市只参观一次;

A distant city has less chance of being chosen (the visibility);

一个遥远的城市被选中的机会较少(能见度) ;

The first ACO algorithm was called the ant system and it was aimed to solve the travelling salesman problem, in which the goal is to find the shortest round-trip to link a series of cities. The general algorithm is relatively simple and based on a set of ants, each making one of the possible round-trips along the cities. At each stage, the ant chooses to move from one city to another according to some rules:

The more intense the pheromone trail laid out on an edge between two cities, the greater the probability that that edge will be chosen;

在两个城市之间的边缘上布置的信息素踪迹越强烈，那条边缘被选择的概率就越大;

1. It must visit each city exactly once;

Having completed its journey, the ant deposits more pheromones on all edges it traversed, if the journey is short;

旅程结束后，如果旅程很短，蚂蚁会在所经过的边缘释放更多的信息素;

1. A distant city has less chance of being chosen (the visibility);

After each iteration, trails of pheromones evaporate.

每次迭代后，信息素的踪迹蒸发。

1. The more intense the pheromone trail laid out on an edge between two cities, the greater the probability that that edge will be chosen;

1. Having completed its journey, the ant deposits more pheromones on all edges it traversed, if the journey is short;

center

中心

1. After each iteration, trails of pheromones evaporate.

Scheduling problem

• Sequential Ordering Problem (SOP)

• Job-shop scheduling problem (JSP)

• Open-shop scheduling problem (OSP)

• Permutation flow shop problem (PFSP)

• Single machine total tardiness problem (SMTTP)

• Single machine total weighted tardiness problem (SMTWTP)

• Resource-constrained project scheduling problem (RCPSP)

• Group-shop scheduling problem (GSP)

• Single-machine total tardiness problem with sequence dependent setup times (SMTTPDST)

• Multistage flowshop scheduling problem (MFSP) with sequence dependent setup/changeover times

Vehicle routing problem

• Capacitated vehicle routing problem (CVRP)

• Multi-depot vehicle routing problem (MDVRP)

• Period vehicle routing problem (PVRP)

• Split delivery vehicle routing problem (SDVRP)

• Stochastic vehicle routing problem (SVRP)

• Vehicle routing problem with pick-up and delivery (VRPPD)

• Vehicle routing problem with time windows (VRPTW)

• Time dependent vehicle routing problem with time windows (TDVRPTW)

• Vehicle routing problem with time windows and multiple service workers (VRPTWMS)

Assignment problem

• Quadratic assignment problem (QAP)

• Generalized assignment problem (GAP)

• Frequency assignment problem (FAP)

• Redundancy allocation problem (RAP)

Set problem

• Set cover problem (SCP)

• Partition problem (SPP)

• Weight constrained graph tree partition problem (WCGTPP)

• Arc-weighted l-cardinality tree problem (AWlCTP)

• Multiple knapsack problem (MKP)

• Maximum independent set problem (MIS)

Device sizing problem in nanoelectronics physical design

• Ant colony optimization (ACO) based optimization of 45 nm CMOS-based sense amplifier circuit could converge to optimal solutions in very minimal time.

Loopback vibrators 10×10, synthesized by means of ACO algorithm

采用蚁群算法合成回路振子10 × 10

• Ant colony optimization (ACO) based reversible circuit synthesis could improve efficiency significantly.

[[File:ANT antenna 2.jpg|thumb|Unloopback vibrators 10×10, synthesized by means of ACO algorithm loopback and unloopback vibrators 10×10

[文件: ANT antenna 2. jpg | thumb | Unloopback 振子10 × 10，由 ACO 算法回环和未回环振子10 × 10合成

Antennas optimization and synthesis

The graph here is the 2-D image and the ants traverse from one pixel depositing pheromone. The movement of ants from one pixel to another is directed by the local variation of the image's intensity values. This movement causes the highest density of the pheromone to be deposited at the edges.

这里的图形是二维图像和蚂蚁遍历从一个像素沉积信息素。蚂蚁从一个像素移动到另一个像素是由图像灰度值的局部变化引导的。这一运动导致最高密度的信息素沉积在边缘。

Loopback vibrators 10×10, synthesized by means of ACO algorithm

Unloopback vibrators 10×10, synthesized by means of ACO algorithm

The following are the steps involved in edge detection using ACO:

以下是使用 ACO 进行边缘检测的步骤:

To optimize the form of antennas, ant colony algorithms can be used. As example can be considered antennas RFID-tags based on ant colony algorithms (ACO), loopback and unloopback vibrators 10×10

Step1: Initialization:
Randomly place [math]\displaystyle{ K }[/math] ants on the image [math]\displaystyle{ I_{M_1 M_2} }[/math] where [math]\displaystyle{ K= (M_1*M_2)^\tfrac{1}{2} }[/math] . Pheromone matrix [math]\displaystyle{ \tau_{(i,j)} }[/math] are initialized with a random value. The major challenge in the initialization process is determining the heuristic matrix.

Step1: 初始化: 随机地点 < math > k </math > 图像上的蚂蚁 < math > i _ { m _ 1 m _ 2} </math > where < math > k = (m _ 1 * m _ 2) ^ tfrac {1} </math > 。信息素矩阵 < math > tau _ {(i，j)} </math > 由一个随机值初始化。在初始化过程中的主要挑战是确定启发式矩阵。

Image processing

The ACO algorithm is used in image processing for image edge detection and edge linking.

There are various methods to determine the heuristic matrix. For the below example the heuristic matrix was calculated based on the local statistics:

确定启发式矩阵的方法有多种。对于下面的例子，启发式矩阵是根据当地统计数据计算出来的:

• Edge detection:

the local statistics at the pixel position (i,j).

像素位置(i，j)的局部统计。

The graph here is the 2-D image and the ants traverse from one pixel depositing pheromone. The movement of ants from one pixel to another is directed by the local variation of the image's intensity values. This movement causes the highest density of the pheromone to be deposited at the edges.

[math]\displaystyle{ \eta_{(i,j)}= \tfrac{1}{Z}*Vc*I_{(i,j)} }[/math]

< math > eta _ (i，j)} = tfrac {1}{ z } * Vc _ (i，j)} </math >

The following are the steps involved in edge detection using ACO:

Where [math]\displaystyle{ I }[/math] is the image of size [math]\displaystyle{ M_1*M_2 }[/math]

大小如下的图像在哪里

Step1: Initialization:
Randomly place [math]\displaystyle{ K }[/math] ants on the image [math]\displaystyle{ I_{M_1 M_2} }[/math] where [math]\displaystyle{ K= (M_1*M_2)^\tfrac{1}{2} }[/math] . Pheromone matrix [math]\displaystyle{ \tau_{(i,j)} }[/math] are initialized with a random value. The major challenge in the initialization process is determining the heuristic matrix.

[math]\displaystyle{ Z =\sum_{i=1:M_1} \sum_{j=1:M_2} Vc(I_{i,j}) }[/math], which is a normalization factor

[ math ] z = sum { i = 1: m _ 1} sum { j = 1: m _ 2} Vc (i _ { i，j }) </math > ，这是一个归一化因子

There are various methods to determine the heuristic matrix. For the below example the heuristic matrix was calculated based on the local statistics:

[math]\displaystyle{ \begin{align}Vc(I_{i,j}) = &f \left( \left\vert I_{(i-2,j-1)} - I_{(i+2,j+1)} \right\vert + \left\vert I_{(i-2,j+1)} - I_{(i+2,j-1)} \right\vert \right. \\ \lt math \gt begin { align } Vc (i _ { i，j }) = & f left (left vert i _ {(i-2，j-1)}-i _ {(i + 2，j + 1)}右垂直 + 左垂直 i _ {(i-2，j + 1)}-i _ (i + 2，j-1)}右垂直。\\ the local statistics at the pixel position (i,j). & +\left\vert I_{(i-1,j-2)} - I_{(i+1,j+2)} \right\vert + \left\vert I_{(i-1,j-1)} - I_{(i+1,j+1)} \right\vert\\ & +\left\vert I_{(i-1,j-2)} - I_{(i+1,j+2)} \right\vert + \left\vert I_{(i-1,j-1)} - I_{(i+1,j+1)} \right\vert\\ & +\left\vert I_{(i-1,j)} - I_{(i+1,j)} \right\vert + \left\vert I_{(i-1,j+1)} - I_{(i-1,j-1)} \right\vert\\ & +\left\vert I_{(i-1,j)} - I_{(i+1,j)} \right\vert + \left\vert I_{(i-1,j+1)} - I_{(i-1,j-1)} \right\vert\\ \lt math\gt \eta_{(i,j)}= \tfrac{1}{Z}*Vc*I_{(i,j)} }[/math]

& + \left. \left\vert I_{(i-1,j+2)} - I_{(i-1,j-2)} \right\vert + \left\vert I_{(i,j-1)} - I_{(i,j+1)} \right\vert \right) \end{align}</math>

左边。(i-1，j + 2)}-i _ {(i-1，j-2)}右 vert + 左 vert i _ {(i，j-1)}-i _ {(i，j + 1)}右 vert 右 vert { align } </math >

Where [math]\displaystyle{ I }[/math] is the image of size [math]\displaystyle{ M_1*M_2 }[/math]

[math]\displaystyle{ f(\cdot) }[/math] can be calculated using the following functions:
[math]\displaystyle{ f(x) = \lambda x, \quad \text{for x ≥ 0; (1)} }[/math]
[math]\displaystyle{ f(x) = \lambda x^2, \quad \text{for x ≥ 0; (2)} }[/math]
[math]\displaystyle{ f(x) = \lt math \gt f (cdot) }[/math] 可以用以下函数计算: < br/> < math > f (x) = lambda x，quad text { for x ≥0; (1)} </math > < br/> < math > f (x) = lambda x ^ 2，quad text { for x ≥0; (2)} </math > < br/> < math > f (x) =

[math]\displaystyle{ Z =\sum_{i=1:M_1} \sum_{j=1:M_2} Vc(I_{i,j}) }[/math], which is a normalization factor

\begin{cases}

开始{ cases }

\sin(\frac{\pi x}{2 \lambda}), & \text{for 0 ≤ x ≤} \lambda \text{; (3)} \\

Sin (frac { pi x }{2 lambda }) ，& text { for 0≤ x ≤} lambda text { ; (3)}

[math]\displaystyle{ \begin{align}Vc(I_{i,j}) = &f \left( \left\vert I_{(i-2,j-1)} - I_{(i+2,j+1)} \right\vert + \left\vert I_{(i-2,j+1)} - I_{(i+2,j-1)} \right\vert \right. \\ 0, & \text{else} 0，& text { else } & +\left\vert I_{(i-1,j-2)} - I_{(i+1,j+2)} \right\vert + \left\vert I_{(i-1,j-1)} - I_{(i+1,j+1)} \right\vert\\ \end{cases} }[/math]
[math]\displaystyle{ f(x) = 结束{ cases } }[/math] < br/> < math > f (x) =

& +\left\vert I_{(i-1,j)} - I_{(i+1,j)} \right\vert + \left\vert I_{(i-1,j+1)} - I_{(i-1,j-1)} \right\vert\\

\begin{cases}

开始{ cases }

& + \left. \left\vert I_{(i-1,j+2)} - I_{(i-1,j-2)} \right\vert + \left\vert I_{(i,j-1)} - I_{(i,j+1)} \right\vert \right) \end{align}</math>

\pi x \sin(\frac{\pi x}{2 \lambda}), & \text{for 0 ≤ x ≤} \lambda \text{; (4)} \\

\pi x \sin(\frac{\pi x}{2 \lambda}), & \text{for 0 ≤ x ≤} \lambda \text{; (4)} \\

0, & \text{else}

0，& text { else }

[math]\displaystyle{ f(\cdot) }[/math] can be calculated using the following functions:
[math]\displaystyle{ f(x) = \lambda x, \quad \text{for x ≥ 0; (1)} }[/math]
[math]\displaystyle{ f(x) = \lambda x^2, \quad \text{for x ≥ 0; (2)} }[/math]
[math]\displaystyle{ f(x) = \end{cases} }[/math]
The parameter [math]\displaystyle{ \lambda }[/math] in each of above functions adjusts the functions’ respective shapes.
Step 2 Construction process:
The ant's movement is based on 4-connected pixels or 8-connected pixels. The probability with which the ant moves is given by the probability equation [math]\displaystyle{ P_{x,y} }[/math]
Step 3 and Step 5 Update process:
The pheromone matrix is updated twice. in step 3 the trail of the ant (given by [math]\displaystyle{ \tau_{(x,y)} }[/math] ) is updated where as in step 5 the evaporation rate of the trail is updated which is given by the below equation.
[math]\displaystyle{ 上面每个函数中的参数 \lt math \gt lambda }[/math] 调整函数各自的形状。< br/> 步骤2构建过程: < br/> 蚂蚁的移动是基于4个连接的像素或8个连接的像素。根据概率方程 < math > p _ { x，y } </math > < br/> 步骤3和步骤5更新过程给出蚂蚁移动的概率: < br/> 信息素矩阵更新两次。在步骤3中，蚂蚁的踪迹(由 < math > tau _ {(x，y)} </math > 给出)被更新，在步骤5中，蚂蚁的踪迹蒸发率被更新，这个更新是由下面的方程给出的。[数学]

\begin{cases}

\tau_{new} \leftarrow

左塔罗

\sin(\frac{\pi x}{2 \lambda}), & \text{for 0 ≤ x ≤} \lambda \text{; (3)} \\

(1-\psi)\tau_{old} + \psi \tau_{0}

(1-psi) tau _ { old } + psi tau _ {0}

0, & \text{else}

</math>, where [math]\displaystyle{ \psi }[/math] is the pheromone decay coefficient [math]\displaystyle{ 0\lt \tau \lt 1 }[/math]

这里是信息素衰变系数

\end{cases}</math>
[math]\displaystyle{ f(x) = \begin{cases} Step 7 Decision Process:\lt br /\gt Once the K ants have moved a fixed distance L for N iteration, the decision whether it is an edge or not is based on the threshold T on the pheromone matrixτ. Threshold for the below example is calculated based on Otsu's method. 步骤7决策过程: 一旦 k 蚂蚁在 n 次迭代中移动了一个固定的距离 l，判断它是否是一个边缘是基于信息素矩阵 τ 上的阈值 t。下面例子的阈值是根据 Otsu 的方法计算的。 \pi x \sin(\frac{\pi x}{2 \lambda}), & \text{for 0 ≤ x ≤} \lambda \text{; (4)} \\ 0, & \text{else} Image Edge detected using ACO:\lt br /\gt The images below are generated using different functions given by the equation (1) to (4). 使用 ACO 检测图像边缘: \lt br/\gt 下面的图像是使用方程(1)至(4)给出的不同函数生成的。 \end{cases} }[/math]
The parameter [math]\displaystyle{ \lambda }[/math] in each of above functions adjusts the functions’ respective shapes.
Step 2 Construction process:
The ant's movement is based on 4-connected pixels or 8-connected pixels. The probability with which the ant moves is given by the probability equation [math]\displaystyle{ P_{x,y} }[/math]
Step 3 and Step 5 Update process:
The pheromone matrix is updated twice. in step 3 the trail of the ant (given by [math]\displaystyle{ \tau_{(x,y)} }[/math] ) is updated where as in step 5 the evaporation rate of the trail is updated which is given by the below equation.
[math]\displaystyle{ thumb 拇指 \tau_{new} \leftarrow (1-\psi)\tau_{old} + \psi \tau_{0} }[/math], where [math]\displaystyle{ \psi }[/math] is the pheromone decay coefficient [math]\displaystyle{ 0\lt \tau \lt 1 }[/math]

Step 7 Decision Process:
Once the K ants have moved a fixed distance L for N iteration, the decision whether it is an edge or not is based on the threshold T on the pheromone matrixτ. Threshold for the below example is calculated based on Otsu's method.

Image Edge detected using ACO:
The images below are generated using different functions given by the equation (1) to (4).

• Edge linking: ACO has also been proven effective in edge linking algorithms too.

Other applications

• Bankruptcy prediction

• Classification

• Connection-oriented network routing

• Connectionless network routing

• Data mining

• Discounted cash flows in project scheduling

• Distributed information retrieval

• Energy and electricity network design

• Grid workflow scheduling problem

• Inhibitory peptide design for protein protein interactions

• Intelligent testing system

• Power electronic circuit design

• Protein folding

The inventors are Frans Moyson and Bernard Manderick. Pioneers of the field include Marco Dorigo, Luca Maria Gambardella.

发明者是 Frans Moyson 和 Bernard Manderick。这一领域的先驱包括马可 · 多里戈、卢卡 · 玛利亚 · 甘巴德拉。

• System identification

Colors=

Chronology of ant colony optimization algorithms.

蚁群算法年表。

  id:fond     value:white #rgb(0.95,0.95,0.98)

  id:marque   value:rgb(1,0,0)

  id:marque_fond value:rgb(1,0.9,0.9)

BackgroundColors = canvas:fond

Define $dx = 7 # décalage du texte à droite de la barre

Define $dy = -3 # décalage vertical

Define $dy2 = 6 # décalage vertical pour double texte

PlotData=

 bar:Leaders color:marque_fond width:5 mark:(line,marque) align:left fontsize:S

 from:1989  till:1989 shift:($dx,$dy)    text:studies of collective behavior

 from:1991  till:1992 shift:($dx,$dy)    text:ant system (AS)

 from:1995  till:1995 shift:($dx,$dy)    text:continuous problem (CACO)

 from:1996  till:1996 shift:($dx,$dy)    text:ant colony system (ACS)

 from:1996  till:1996 shift:($dx,$dy2)   text:max-min ant system (MMAS)

 from:2000  till:2000 shift:($dx,$dy)   text:proof to convergence (GBAS)

 from:2001  till:2001 shift:($dx,$dy)   text:multi-objective algorithm

</timeline>|caption=Chronology of COA algorithms

}}

Chronology of ant colony optimization algorithms.

• 1959, Pierre-Paul Grassé invented the theory of stigmergy to explain the behavior of nest building in termites;

• 1983, Deneubourg and his colleagues studied the collective behavior of ants;

• 1988, and Moyson Manderick have an article on self-organization among ants;

• 1989, the work of Goss, Aron, Deneubourg and Pasteels on the collective behavior of Argentine ants, which will give the idea of ant colony optimization algorithms;

• 1989, implementation of a model of behavior for food by Ebling and his colleagues;

• 1991, M. Dorigo proposed the ant system in his doctoral thesis (which was published in 1992). A technical report extracted from the thesis and co-authored by V. Maniezzo and A. Colorni was published five years later;

• 1994, Appleby and Steward of British Telecommunications Plc published the first application to telecommunications networks

• 1995, Gambardella and Dorigo proposed ant-q, the preliminary version of ant colony system as first estension of ant system; .

• 1996, Gambardella and Dorigo proposed ant colony system

• 1996, publication of the article on ant system;

• 1996, Hoos and Stützle invent the max-min ant system;

• 1997, Dorigo and Gambardella proposed ant colony system hybridized with local search;

• 1997, Schoonderwoerd and his colleagues published an improved application to telecommunication networks;

• 1998, Dorigo launches first conference dedicated to the ACO algorithms;

• 1998, Stützle proposes initial parallel implementations;

• 1999, Gambardella, Taillard and Agazzi proposed macs-vrptw, first multi ant colony system applied to vehicle routing problems with time windows,

• 1999, Bonabeau, Dorigo and Theraulaz publish a book dealing mainly with artificial ants

• 2000, special issue of the Future Generation Computer Systems journal on ant algorithms

• 2000, first applications to the scheduling, scheduling sequence and the satisfaction of constraints;

• 2000, Gutjahr provides the first evidence of convergence for an algorithm of ant colonies

• 2001, the first use of COA algorithms by companies (Eurobios and AntOptima);

• 2001, Iredi and his colleagues published the first multi-objective algorithm

• 2002, first applications in the design of schedule, Bayesian networks;

• 2002, Bianchi and her colleagues suggested the first algorithm for stochastic problem;

• 2004, Dorigo and Stützle publish the Ant Colony Optimization book with MIT Press

• 2004, Zlochin and Dorigo show that some algorithms are equivalent to the stochastic gradient descent, the cross-entropy method and algorithms to estimate distribution

• 2005, first applications to protein folding problems.

• 2012, Prabhakar and colleagues publish research relating to the operation of individual ants communicating in tandem without pheromones, mirroring the principles of computer network organization. The communication model has been compared to the Transmission Control Protocol.

• 2016, first application to peptide sequence design.

• 2017, successful integration of the multi-criteria decision-making method PROMETHEE into the ACO algorithm (HUMANT algorithm).

Publications (selected)

Category:Articles which contain graphical timelines

类别: 包含图形时间表的文章

• M. Dorigo, 1992. Optimization, Learning and Natural Algorithms, PhD thesis, Politecnico di Milano, Italy.

Category:Nature-inspired metaheuristics

类别: 自然启发的启发式元推理

• M. Dorigo, V. Maniezzo & A. Colorni, 1996. "Ant System: Optimization by a Colony of Cooperating Agents", IEEE Transactions on Systems, Man, and Cybernetics–Part B, 26 (1): 29–41.

Category:Optimization algorithms and methods

类别: 优化算法和方法

This page was moved from wikipedia:en:Ant colony optimization algorithms. Its edit history can be viewed at 蚁群优化算法/edithistory